BADANIE WYMIENNIKÓW CIEPŁA                                       

 
 
 
 
 
 
 

 

1.  Rodzaje wymienników ciepła 

2.  Zarys teorii przeponowego wymiennika ciepła 

3.  Efektywność wymiennika ciepła 

4.  Cel i zakres badań 

5.  Przygotowanie i wykonanie pomiarów 

6.  Instrukcja wykonania ćwiczenia laboratoryjnego 

LITERATURA 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.  Rodzaje wymienników ciepła.                                                                                   

 

Wymiennik ciepła (przenośnik ciepła) jest to urządzenie, w którym ciepło przekazywane jest 

od jednego płynu o temperaturze wyższej (gorącego) do drugiego płynu (zimnego) o 

temperaturze niższej. Znajduje on zastosowanie w różnego rodzaju technologiach i w 

zależności od przeznaczenia posiada zróżnicowane nazwy np.. podgrzewacz, grzejnik, 

chłodnica, wytwornica pary, przegrzewacz, skraplacz, parownik, regenerator i wiele innych. 

         Ze względu na zasadę działania rozróżnić możemy następujące grupy wymienników 

ciepła: 

a)  Wymienniki przeponowe, gdzie dwa płyny (gorący i zimny) oddzielone są od siebie 

ścianką (przeponą) wykonaną z materiału zapewniającego długotrwałe działanie. 

b)    Wymienniki powierzchniowe (regeneratory), gdzie powierzchnia tych samych 

elementów (ceramicznych lub metalowych) wypełniających wymiennik jest na 

przemian omywana przez płyn gorący ( np. gorące spaliny) i płyn zimny ( np. świeże 

powietrze), które po ogrzaniu wykorzystywane jest do celów technologicznych. 

c)  Wymienniki mieszalnikowe, w których następuje bezpośrednie mieszanie się płynu 

gorącego i zimnego. Wymienniki tego typu stosowane są w przypadkach, gdy oba 

płyny mogą być mieszane np. (woda – woda,  para wodna – powietrze,  powietrze – 

powietrze) lub jeśli za wymiennikiem można łatwo je rozdzielić np. (powietrze – woda) 

W ostatnim przypadku procesowi przekazywania ciepła  towarzyszy zjawisko wymiany 

masy (parowanie wody). 

d)  Wymienniki z wewnętrznymi źródłami ciepła posiadają tylko jeden płyn spełniający 

rolę nośnika ciepła. Płyn ten omywa powierzchnię elementów, elementów których 

wydziela się ciepło( np. elementy paliwowe reaktorów jądrowych, elementy 

nagrzewane energią elektryczną). 

 

2.  Zarys teorii przeponowego wymiennika ciepła. 

 

Obliczenie cieplne wymiennika mogą mieć charakter projektowy lub sprawdzający. 

Nowoczesne metody projektowania kompletnych instalacji technologicznych polegają na 

wyborze najodpowiedniejszego typu konstrukcji wymiennika i złożeniu ich z typowych 

elementów (np. wymiennik płytowy w oparciu o dane katalogowe i obliczenia 

sprawdzające. Celem obliczeń sprawdzających jest wyznaczenie mocy cieplnej 

wymiennika i temperatur końcowych płynu. 

    

 W przypadku budowy pojedynczych wymienników o dużej mocy (np. kocioł    

energetyczny, reaktor  jądrowy) lub masowej produkcji wymienników  małej mocy (np. 

grzejniki centralnego ogrzewania, chłodnice samochodowe) opłacalne staje się 

przeprowadzenie optymalizacji parametrów przepływowych i wymiarów geometrycznych 

konstrukcji opartej na obliczeniach projektowych. Celem obliczeń projektowych jest 

wyznaczenie powierzchni wymiany ciepła.  

 

Równania bilansu cieplnego odniesione do elementarnej powierzchni wymiennika ciepła 

dA (rys 1) są następujące:  

  

                                       dQ = - m

1

 di

1

 = m

2

 di

2

  

                                                  

( 1 )

 

 

lub dla całej powierzchni 

 

Q = m

1

 (i

1

’ – i

1

’’) = m

2

 (i

2

’’ – i

2

’)    [W ]                                               ( 2 ) 

Ponieważ  di = c

p

 dT,  dla c

p

 = const mamy 

 

Q = m

1

 c

p1

 (T

1

’ – T

2

’’) = m

2

 c

p2

 (T

2

’’ –T

2

’)                                                ( 3 ) 

 

Wprowadzając współczynnik C = m c

p

 otrzymujemy: 

 

C

1

/C

2

 = (T

2

’’ – T

2

’)/(T

1

’ – T

1

’’) = T

2

/T

1

 = dT

2

/dT

1

                            ( 4 ) 

 

Równanie przenikania ciepła przez element powierzchni przepony w kształcie ścianki 

płaskiej jest następujące:  

 

dQ = k T dA                                                             ( 5 ) 

 
gdzie:   T = T

2

 – T

1

  [ K ]   =  różnica temperatur   

 
 
                        1 
k =  ----------------------------------------        [ W/m

2

 K]  - współczynnik przenikania         

          1/

1

  +  ∑(/)

i

  +  1/

2  

                                          ciepła 

 
W większości przypadków współczynnik k zmienia się nieznacznie i w obliczeniach 

można przyjmować, jest stały i równy jego uśrednionej wartości. 

 

                            

 

gdzie A

1

 – fragment powierzchni wymiennika, na którym praktycznie współczynnik 

przenikania ciepła k

i

 jest stały. 

Zatem Równanie ( 5 ) przyjmuje postać: 

                                          A 

  Q = k    T dA = k T A   [ W ]                                                      ( 7 ) 

                                         0 
Średnia różnica temperatur zgodnie z równaniem ( 7 ) wynosi: 

                                         A         
                                           T dA 
                                         0 

T = ----------------                                                                      ( 7a ) 

                                               A 
 
Aby obliczyć całkę w powyższym równaniu należy ustalić zależność T od powierzchni A 

Równanie  ( 1 ) dla współprądowego wymiennika ciepła ( rys,  1 ) możemy zapisać 

następująco: 

 
                                       dQ = - C

1

 dT

1

 = C

2

 dT

2 

 

  
a stąd            dT

1

 = -dQ/C

1

                i                     dT

2

 = dQ/C

2

   

 

oraz    d ( T

1

 – T

2

 ) = dT

1

 – dT

2

 = - ( 1/C

1

 + 1/C

2

 ) dQ = - m dQ                             ( 8 )   

 

gdzie:                       m = (1/C

1

 + 1/C

2

)     przeciwprąd   

 
Podstawiając równanie ( 5 ) do ( 8 ) mamy:     
 
                        d ( T

1

 – T

2

 ) = d(T) = - m k T dA  

 
lub                            d(T) / T = - m k dA      
 
przyjmując, że  m i k    są stałe  całkowanie powyższego równania w granicach od A = 0 
do A daje: 
 
                                       ln (T/T’) = - m k A                                                                ( 9 ) 
 

lub                                T = T’ e 

– m k A

                                                                   ( 9a ) 

 

                n 

               ∑   (A

i

 k)

i 

                      n = 1 
         

k = ------------                                                                                   ( 6 )                                                

                 A 

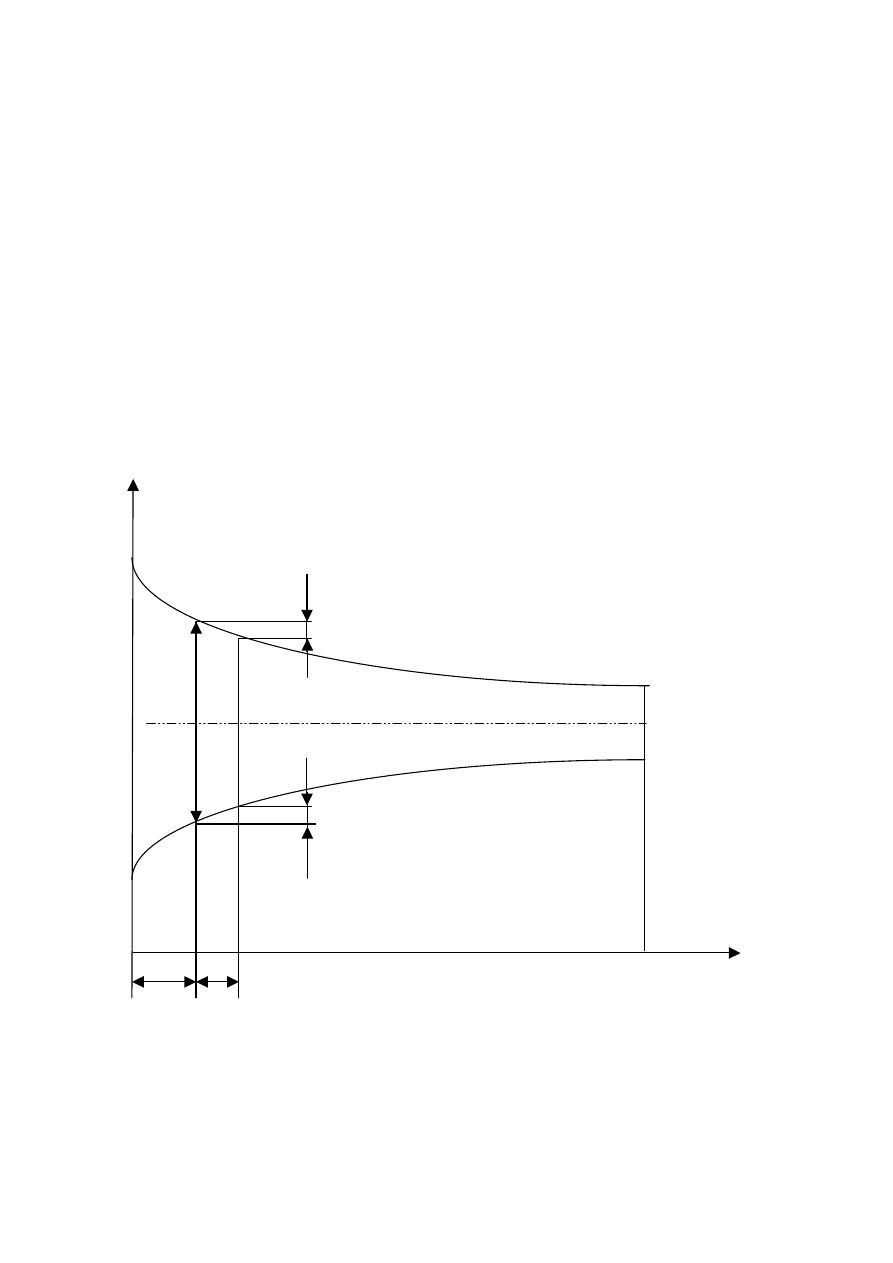
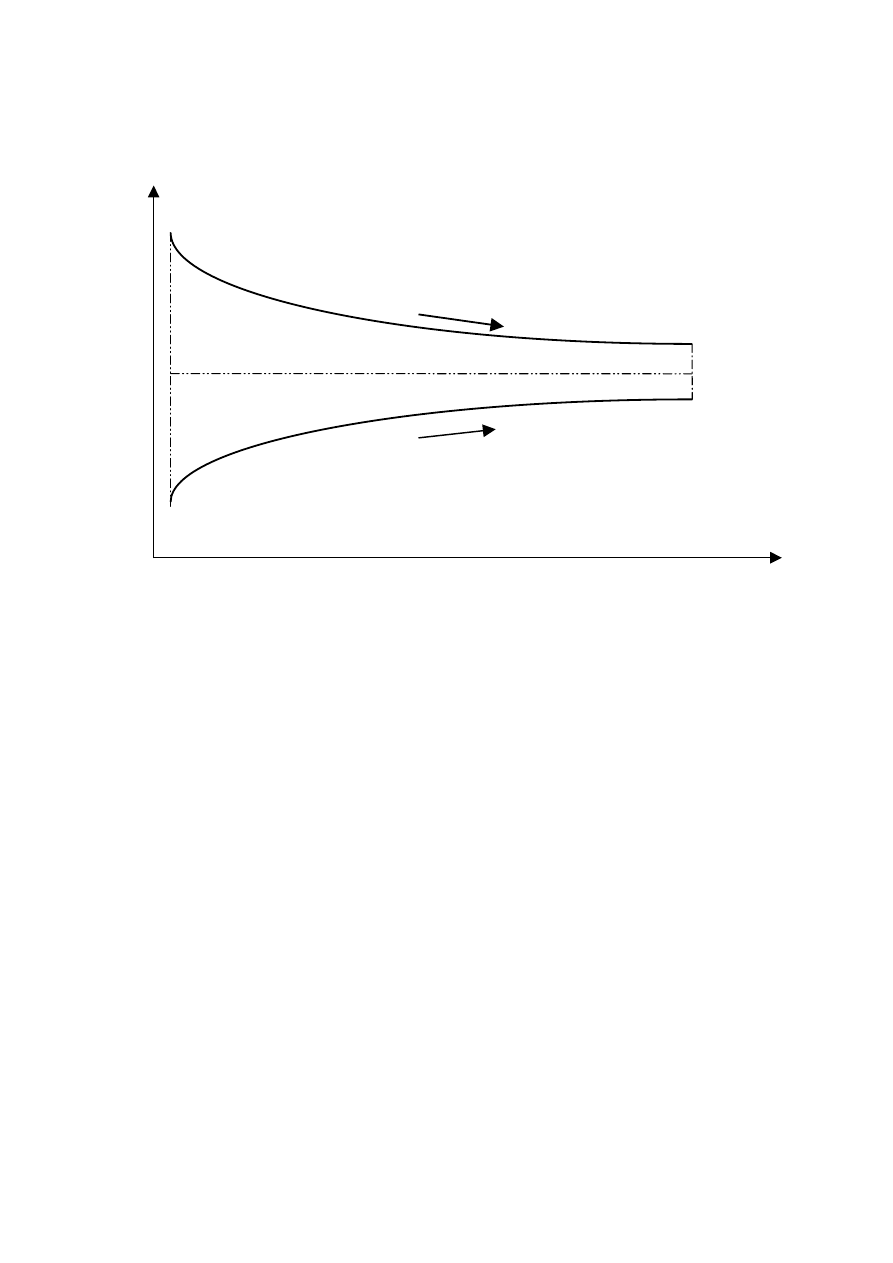
Powyższy rezultat pokazuje, że różnice temperatur T zmienia się wzdłuż powierzchni 

wymiennika wg. funkcji eksponencjalnej. 

 
        Podstawiając zależności ( 9a ) do wzoru ( 7a ) mamy:  
                         A 
  T = T’ / A    e 

– m k A

 dA =  T’/ - m k A ( e 

m k A

 = 1 ) 

                        0 
 
Następnie podstawiając za wielkość m k A  i   e 

– m k A

 zależność ( 9 ) i ( 9a ) powyższy 

wzór przyjmuje formę 

                                             T’’ – T’ 
                                 T = -----------------                                                                    ( 10 ) 
                                            ln (T’’/ T’) 
 
Przyjmując, że T = T’’ dla A = A

k

 mamy: 

 
                                     T’’ – T’ 
                        T = --------------------                                                                        ( 10a ) 
                                  ln ( T’’ / T’ ) 
 
Powyższy wzór jest zapisywany również w formie: 
 
                                        T

max

 – T

min

 

                          T = ----------------------------                                                           ( 10b ) 
                                     ln ( T

max

 / T

min

 ) 

 
która jest ważna dla wymienników współprądowych jak i dla przeciwprądowych.  

Dla innych układów ( np. krzyżowy ) średnią różnicę temperatur obliczamy z wzoru: 

 

                                        T = T

przeciwprąd

, 



T

                                                       ( 10c) 

gdzie: 

             



T

 = f ( P = T

2

 / T

max

  ,      R = T

1

 / T

2

 )  - współczynnik poprawkowy. 

 
Obliczenia temperatur końcowych..  

Bardzo często znane są temperatury początkowe płynów T

1

’ i T

2

’, natężenie przepływów 

m

1

 i m

2

 , powierzchnie wymiany ciepła A oraz współczynnik przenikania ciepła k.  

Aby wyznaczyć moc cieplną wymiennika należy obliczyć temperatury końcowe płynów. 

   Podstawą obliczeń temperatur końcowych dla współprądu może być wzór ( 9a )  

( dla A = A

k

  mamy T = T’’), który przyjmie postać: 

                          T’’ = T’ e

 – m k A

k 

Odejmując od obu stron T’ = T

1

’ – T

2

’ mamy

: 

                                 T

1

’’ – T

2

’’ – T

1

’ + T

2

’ = T’ ( e 

– m k A

k 

 - 1 ) 

Po przekształceniach otrzymujemy: 

 

                                         T

1

 + T

2

 = T ’ ( 1 – e 

– m k A

k 

) 

 

Następnie eliminujemy wielkość T

2

  za pomocą bilansu cieplnego ( 4 ) w postaci  

T

2

 = T

1

 ( C

1

 / C

2

 )  

   otrzymujemy    T

1

 + T

1

 (C

1

 / C

2

 ) = T’ ( 1 – e 

– m k A

k 

) 

lub 

 

                                          1 – e

 –(k A

k

 / 

C1) (1 + C1/C2 )

 

                       T

1

 = T '  -----------------------------------                                              ( 11a ) 

                                                       1 + C

1

 / C

2

      

 
 
w rezultacie temperatura końcowa płynu „gorącego“ jest równa   
 
                                             T

1

’’ = T

1

’ – T



 
Z równania ( 4 ) obliczamy temperaturę końcową płynu „zimnego”: 
 
                      T

2

 = T

1

 (C

1

 / C

2

 )      oraz     T

2

’’ = T

2

’ + T

2

                                    ( 11b ) 

 
Podobne obliczenia dla przeciwprądowego wymiennika prowadzą do wzorów: 
 
                                             1 – e

 –(k A

k

 / 

C1) (1 - C1/C2 )

 

              T

1

 = ( T

1

’ – T

2

’ )  -----------------------------------                                          ( 12a ) 

                                              (1 - C

1

 / C

2

 ) e

 –(k A

k

 / 

C1) (1 - C1/C2 )

    

 
                                                 T

2

 = T

1

 ( C

1

 / C

2

 )                                                    ( 12b ) 

 
3 Efektywność wymiennika ciepła. 
 
    Oceniając efektywność rzeczywistego wymiennika ciepła jako punkt odniesienia 

przyjmijmy idealny przeciwprądowy wymiennik ciepła o powierzchni A, w którym opory 

cieplne są równe zero. Lokalna różnica temperatur pomiędzy płynem gorącym i zimnym 

T  jest tu równa zero i z termodynamicznego punktu widzenia realizowany jest proces 

odwracalny. Początkowo „zimny” płyn „2” opuszcza wymiennik o temperaturze rownej 

temperaturze początkowej płynu „gorącego”. W rzeczywistym wymienniku ciepła jest to 

oczywiście niemożliwe i stopień jego doskonałości czyli jego efektywność definiowana 

jest jako stosunek mocy cieplnej wymiennika rzeczywistego do mocy cieplnej wymiennika 

idealnego. 

                                                    Q

rzeczywistego 

 

                                              



 = ---------------                                                               ( 13 ) 

                                                    Q

idealnego

  

   
Dla wymiennika przeciwprądowego mamy: 
 
                                            Q

rz

.            T

1

’ – T

1

’’ 

                                     E = -------    =    -------------                                                      ( 14 ) 
                                             Qi

d

.            T

1

’ – T

2

’    

 
Ponieważ dla  k =    z wzoru ( 12b ) wynika, że T

1

 = T

1

’’ – T

1

’ = T

1

’ – T

2

’  

Dla wymiennika współprądowego otrzymujemy natomiast:  

 

                                  Q

rz

.          C

1

 + C

2

         T

1

’’ – T

1

’   

                          



 =  -----    =   -----------  =  -----------------------                                  ( 15 ) 

                                  Q

id

                 C

2

           ( T

1

’ – T

2

’)/T

1

’ 

                

ponieważ dla  k =    z wzoru ( 11a ) wynika, że 

T

1

 = T

1

’’ – T

1

’ = C

2

 ( C

1

 + C

2

) (T

1

’ – T

2

’). 

Należy zauważyć, że do tych wyników dochodzimy przyjmując, że idealny wymiennik 

posiada nieskończenie dużą powierzchnię A. 

 

Moc mechaniczna zużyta na przetłaczanie nośników ciepła. 

W przeponowym wymienniku ciepła nośnikami ciepła są płyny, których przepływ przez 

kanały wymiennika odbywa się ze stratami ciśnienia (na pokonanie tzw. oporów 

przepływu). Przepływ nawet przez najprostsze wymienniki ciepła jest  bardzo złożony i 

obliczenia teoretyczne dają wyniki jedynie przybliżone. Toteż pewne informacje o 

oporach przepływu dają jedynie bezpośrednie pomiary. 

    Energia mechaniczna przeznaczona na pokonanie oporów przepływu „wytraca się” 

(dysypuje) wskutek wpływu lepkości płynu na ciepło tarcia. Zwykle można przyjmować, 

że występujące w wymiennikach zmiany ciśnienia oraz temperatur płynów nie powodują 

istotnych zmian gęstości tych płynów. Wtedy moc przeznaczoną na przetłaczanie jednego 

z płynów przez wymiennik obliczamy z wzoru. 

 

                                                  V P        m P 

                                         M =  -------  =  -------- 
              

 

 
gdzie:     V [m

3

 / s ]  – strumień objętości płynu 

               m [kg / s]   – strumień masy płynu 

             P [N / m3] – całkowite straty ciśnienia 

                 [kg / m3] – średnia gęstość płynu    

 - współczynnik sprawności pompy lub wentylatora 

   Wymiennik ciepła o określonej geometrii i danej powierzchni oraz temperaturach posiada 

optymalne warunki pracy, przy których zużycie mocy mechanicznej ( na pokonanie oporów 

przepływu) na jednostkę przekazywanego ciepła jest najmniejsze. Jakkolwiek należy pamiętać, 

że ostateczne optymalne wymiary geometryczne i parametry pracy wymiennika ciepła są 

określone przez minimum sumy kosztów budowy i eksploatacji urządzenia. 

 

Cel i zakres badań. 

     W przypadku badań o charakterze podstawowym mającym na celu sprawdzenie 

istniejących teorii i ustalenie ilościowych związków opisujących procesy cieplno – 

przepływowe opory cieplne i hydrauliczne) pomiary przeprowadza się zwykle w warunkach 

laboratoryjnych, gdzie modeluje się poszczególne elementarne procesy cieplne i przepływowe. 

    W oparciu o podstawowe i uogólnione dane doświadczalne i teoretyczne powstają metody i 

procedury obliczeń konkretnych konstrukcji wymienników ciepła. Ostateczne sprawdzenie 

tych metod obliczeniowych odbywa się najczęściej na rzeczywistych konstrukcjach w 

warunkach eksploatacyjnych. 

    Jak z powyższego wynika możemy rozróżnić dwa rodzaje badań wymienników ciepła. 

Pierwszy bardziej szczegółowy i wymagający pomiaru rozkładu temperatury, lokalnych 

gęstości strumienia ciepła, naprężeń stycznych na powierzchni ścianki (przepony) oraz 

pomiaru pól temperatur i prędkości płynu w kanałach wymiennika ciepła. Umożliwia to 

wyznaczenie współczynnika przenikania ciepła  k,  współczynnika poprawkowego 



T

 oraz 

strat ciśnienia w funkcji masowych natężeń przepływu płynu „gorącego” m

1

 lub „zimnego” 

m

2

. Ze względu na konieczność wbudowania w powierzchnię ścianki wymiennika czujników 

takie badania mają charakter modelowy i przeprowadzone są w warunkach laboratoryjnych. 

    Drugi rodzaj badań przeprowadzane są w warunkach eksploatacyjnych i wymaga jedynie 

pomiaru strumienia masy płynu ‘gorącego” m

1

  i  :”zimnego”  m

2

 oraz temperatur płynów na 

wlocie i wylocie wymiennika ciepła.  

    Umożliwia to jedynie wyznaczenie mocy cieplnej wymiennika Q funkcji masowych natężeń 

przepływu, oraz średniej wartości współczynnika przenikania ciepła. Wyniki badań mogą być 

przedstawione w postaci wykresów. 

                                              Q = f ( m

1

,  m

2

 – parametr ) 

oraz dla wymienników w układzie współprądowym i przeciwprądowym w postaci np. 

                                               k = Q / A T  = ( m

1

, m

2

 – parametr ) 

a dla wymienników w układach złożonych w postaci np. 

                           ( 



T

 k ) =  Q / A T

przeciwprąd

   =   f (m

1

,  m

2

  - parametr ) 

    Badania eksperymentalne wymienników ciepła dostarcza zarówno wielu informacji 

podstawowych jak również ma ogromne znaczenie praktyczne. Ponieważ teoretyczne 

obliczenia mocy cieplnej lub powierzchni wymiennika nie są najczęściej dostatecznie 

dokładne. Bardzo często niedokładność obliczeń sięga  ±  25 %. Wymienić można następujące 

przyczyny niedokładności obliczeń: 

1)  niedokładność wzorów na współczynniki przejmowania ciepła ( rzędu ± 3 – 15 %) 

2)  rozbieżność pomiędzy sytuacją, przy której ustalono wzory na współczynniki 

przejmowania ciepła i rzeczywistym zjawiskiem zachodzącym w wymienniku 

ciepła ( od kilku do kilkudziesięciu procent ). 

3)   niedokładność danych fizycznych płynów ( rzędu 0.5 – 5 % ) 

4)  niedokładność wykonania wymiennika ciepła 

5)  wpływ zanieczyszczeń powierzchni wymiany ciepła 

6)  zmienność współczynnika przenikania ciepła wzdłuż powierzchni wymiennika, 

która w teorii wymiennika ciepła jest pomijana 

7)  niedokładność wyznaczania współczynnika poprawkowego 



T

.  

 

            Przygotowanie i wykonanie pomiarów 

    Po ustaleniu zakresu badań, określa się mierzone wielkości i wymaganą dokładność 

pomiarów. Następnie po określeniu technik pomiarowych ustala się punkty zabudowy 

czujników i dobiera mierniki. Wykonuje się również schemat badanego układu i ustala dane 

techniczne i wymiary wymiennika ciepła. 

   

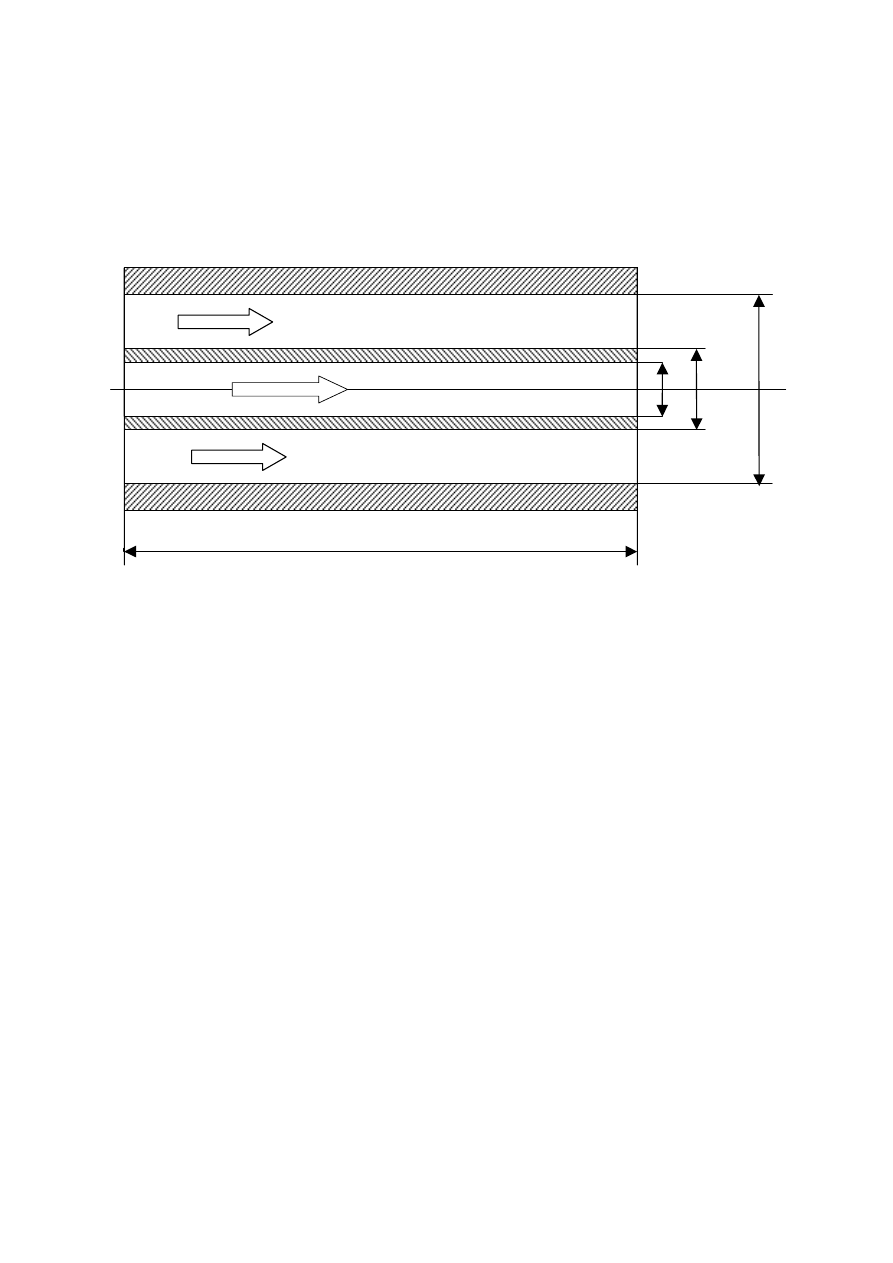
               I   Wymiennik ciepła  „rura w rurze”  (rys. 2) 

   Urządzenie wykonano specjalnie do celów dydaktycznych. zespół umożliwia zrealizowanie 

przepływu współprądowego lub przeciwprądowego uzyskując w rezultacie takie przebiegi 

temperatur jakie pokazano przykładowo na rys. 4. 

Powierzchnia wymiany ciepła – rura miedziana niklowana o wymiarach: 

- średnica  d

zewn

. = 16.0 mm,   średnica  d

wewn

. = 14 mm 

- długość  L = 1230 mm 

Płaszcz zewnętrzny stanowi rura wykonana ze szkła organicznego o wymiarach: 

średnica:    d

zewn

. = 40.0 mm,    d

wewn

. = 31.6 mm 

 

            II  Chłodnica oleju (rys. 3) 

    Urządzenie jest typową chłodnicą oleju pracującą np. w obiegu olejowym turbiny parowej. 

Do celów dydaktycznych bieg olejowy zastąpiono wodą. 

Dane techniczne 

- powierzchnia wymiany ciepła   ( rurek )                             A = 1.615 m

2

  

- średnica rurek                                                                 d

z

/d

w

 =  14 / 12 mm 

- długość rurek                                                                        L =  507 mm 

- ilość rurek                                                                              n =  78 szt. 

- materiał rurek                                                                           mosiądz M85 

    Strumienie masy ( masowe natężenie przepływu ) przepływających płynów są mierzone 

rotametrami. Temperatury są mierzone termoparami  Cu – Konst. i rejestrowane w funkcji 

czasu. Umożliwia to dokładne ustalenie czy wymiennik po uruchomieniu lub zmianie 

parametrów pracy osiągnął stan równowagi cieplnej. 

    Bezpośrednim celem ćwiczenia jest wyznaczenie mocy cieplnej wymiennika w kilku 

punktach pracy czyli fragmentu jego charakterystyki. Porównując otrzymane rezultaty z 

wynikami obliczeń sprawdzających opartych o dane literaturowe dokonujemy analizy metody 

obliczeniowej z pomiarami. 

 

Instrukcja wykonania ćwiczenia laboratoryjnego. 

1)  Zapoznanie się z literaturą i katalogami dotyczącymi wymienników ciepła. 

2)  Zapoznanie się z budową i działaniem stanowisk badawczych. 

3)  Uruchomienie stanowiska 

a)  wymiennik ciepła „rura w rurze”  ( rys. 2 ) za pomocą zaworów zrealizować 

układ współprądowy i przeciwprądowy. 

b)  Chłodnica oleju ( rys. 3 ) sprawdzić podłączenie zasilania wodą :gorącą” i 

„zimną”. 

c)  Uruchomić przepływ płynów, odpowietrzyć układ, uruchomić rejestracje 

pomiaru. 

4)  Po osiągnięciu równowagi cieplnej dokonać odczytu wskazań. 

5)  W oparciu o dane techniczne i odczyty wykonać obliczenia wyników pomiaru ( Tablica 

poz. 9 – 35 )  

6)  W oparciu o zmierzone temperatury początkowe płynów ( T

1

’, T

2

’ ) i strumienie masy 

(m

1

, m

2

) oraz dane literaturowe wykonać obliczenia „teoretyczne” mocy wymiennika 

ciepła a wyniki obliczeń porównać z wynikami pomiarów ( Tablica   poz. 36 – 39). 

7)  W miarę możliwości wykonać wykresy: Q = f ( m

1

, m

2

 ) oraz P = f (m ) i  

 Q / N = f (m

1

, m

2

 ). 

       8)  W oparciu o uzyskane wyniki opracować wnioski dotyczące dokładności pomiarów i                          

 teoretycznej metody obliczeniowej oraz prawidłowości działania urządzenia i    

 położenia punktów pracy wymiennika. 

8)  Sporządzić sprawozdanie, które powinno zawierać: 

a)  cel badania 

b)  schemat pomiarowy i dane techniczne badanego urządzenia 

c)  wykaz i dane techniczne użytej aparatury 

d)  wypełnioną tabele pomiarowo – obliczeniową 

e)  obliczenia teoretyczne mocy cieplnej wymiennika 

f)  ocenę dokładności i wnioski wypływające z wyników badań 

g)  wykaz literatury ( w tym „źródeł” własności fizycznych) 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                   LITERATURA 

1)  F. J. BALEY,  J, M. OWEN,  A. B. TURNER:  Heat Transfer. Thomas Nelson and 

Sons  LTD  1972. 

2)  N. AFGAN,  E.U. SCHLUNDER  Editors:  Heat Exchangers: Design and Theo 

Sourcebook.  McGraw – Hill Book Company 1974. 

3)  K. BRODOWICZ: Wymienniki ciepła i masy. Wydawnictwo Politechniki 

Warszawskiej, Warszawa  1977. 

4)  W. P. ISACZENKO,  W. A. OSIPOWA,  A. S. SUKOMIEŁ:  Tiepłopieredacza, 

Energia – Moskwa  1969. 

5)  J. MADEJSKI: Teoria wymiany ciepła.  PWN  1963. 

6)  Katalogi: Typowe wymienniki ciepła płaszczowo – rurowe i „rura w rurze”. Zakłady 

Urządzeń Chemicznych i Aparatury Przemysłowej  CHEMAR,  Kielce  1973. 

7)  Katalog Maszyn i Urządzeń Przemysłu Spożywczego,  SPOMASZ,  1974. 

 

   

 

 

 

 

  

  

 

          

 

 
     

 

 

 
 
 
 
 

 
 

OBLICZENIA MOCY CIEPLNEJ WYMIENNIKA 

typu  „rura w rurze”. 

1. Geometria wymiennika 

 

 
2 Równanie opisujące przejmowanie ciepła po stronie wewnętrznej i zewnętrznej przepony 

 

W zakresie  R

f

 < 2000  

 
                      Nu

f

 = 0.15 Re

f

0.33

 Pr

f

0.43

 Gr

f

0.1

  (Pr

f

 /Pr

w

 )

0.25

 

 
W zakresie 10

4

 <Re

f

 < 5 10

3 

 

                                  

Nu

f

 = 0.021 Re

f

0.8 

Pr

f

0.43

  ( Pr

f

 / Pr

w

 )

0.25

  

 
Gdzie:   Re

f

 = v d

h

 /         .  

 
              Nu

f 

=  d

h

 /       

 
                         G d

3

  

               Gr  =  ----------   ( T

w

 – T

f

 ) 

                               

2




       T

w

 = (T

w1

 + T

w2

 ) /2    -  T

w1

, T

w2

 – temp. wody ciepłej na wlocie i wylocie 

 
                 T

f

 = ( T

f1

 + T

f2

 ) / 2     -  T

f1

,  T

f2

 – temp. wody zimnej na wlocie i wylocie 

      
                         4 A      4 przekroje przepływu 
                d

h

 =  ----- = -----------------------------   

                           O         obwód zwilżany 

      

        – lepkość kinematyczna 

L  

        – przewodność cieplna  

        – współczynnik rozszerzalności termicznej 

A  Metoda dokładna 

3a  Współczynnik przenikania ciepła przez przegrodę cylindryczną odniesionej do       

       jednostkowej długości. 

 
                                                      2   

                      k = ----------------------------------------------------       [ W / m

2

 K ]    

                                1              1              d

z

               1 

                             ------   +     -----    ln ------   +    ------ 
                             r

w

                             d

w

            r

z

 

z

   

 

4a Logarytmiczna różnica temperatur 

 
                                            t

max

 - t

min 

                                  t = ------------------                                            [ K ] 
                                                   t

max

 

                                             Ln --------- 
                                                    t

min 

 

5a  Moc cieplna przekazywana przez przeponę wymiennika. 

 

                                         Q = L 

q

L

 = L k

l

 t

m

                                     [ W ] 

 

B  Metoda przybliżona 

 

      W przypadku spełnienia warunku d

z

 / d

w

 < 2 przegrodę cylindryczną można obliczyć  

przy wykorzystaniu zależności dla przegrody płaskiej przyjmując obliczeniową powierzchnię 

przepływu ciepła. 

                                             A

o

 =  d

o

 L    gdzie: 

                           d

o

 = d

w

     jeśli     

z

  >> 

w

 

                           d

o

 = d

z

      jeśli     

w

 >> 

z

 

                           d

o

 = ( d

w

 + d

z

 ) /2     jeśli     

w

    

z

  

 

                             Współczynnik przenikania ciepła 

                                                1 
                            k = ---------------------------------                               [ W / m

2

 K ] 

                                      1                1 
                                   ----  +  ---  +  ---- 
                                     

w

              

z 

 

 

                                
                          Logarytmiczna różnica temperatur 
                                           
                                                

tmax

 – 

tmin

 

                                      t

ln

 =  --------------------- 

                                                         t

max

 

                                                     ln ---------- 
                                                         t

min

 

Moc cieplna przekazywana przez przeponę wymiennika 
 
                                             Q = k A

o

 t

ln

    

 
 
 
 
 
 
 
 
T

1

’ 

 
                 
               .                                dT

1

  

                                                      
 
                                                                                                                           T

1

’’ 

              T 
 
 
                                                                                                                            T

2

’’ 

 
 
                                                  dT

2

 

                               

T

2

’ 

 

 

          A         dA                                                                                            A 
 
 
 
 
 
 
 
 
 

 
 
 

 
 
 
 

T

1

’ 

T

2

’ 

        T

 1

’’ 

 T

2

’’ 

T

min

 

 

T

max

 

 

A 

T 

Przepływ współprądowy 
 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

T

max

 

T

min

 

T

1

’ 

T

2

’ 

T

1

’’ 

T

2

’

’ 

A 

Przepływ przeciwprądowy 

T 

 

 

POMIAR MOCY CIEPLNEJ PŁASZCZOWO – RUROWEGO WYMIENNIKA CIEPŁA 

 

1.  Zapoznać się z układem pomiarowym. 

2.  Zidetyfikować wymiennik i określić jego wymary. 

3.  Określić sposób podłączenia wymiennika 

4.  Wykonać pomiary temperatur na wlotach i wylotach oraz strumienie masy czynnika 

grzejnego i podgrzewanego. 

5.  Wykonać obliczenia mocy cieplnej badanego wymiennika i porównać z 

bezpośrednimi pomiarami. 

6.  Określić charakterystykę wymiennika dla wybranych parametrów 

m

grzewczego

  T

A

,  T

B

 

 

 

                     

                                 Q 

 

 

 

 

 

 

 

                                                                                                                                                                                             

                                                                                          m

p