Dynamika punktu

materialnego

Za pomocą równań kinematycznych potrafimy
opisać ruch, ale nie potrafimy odpowiedzieć na
pytanie, dlaczego jedne ciała poruszają się
ruchem jednostajnym, a inne zmiennym, jedne
prostoliniowym inne krzywoliniowym itd. Dział
fizyki stawiający sobie takie pytania i próbujący
na nie odpowiadać nazywamy

dynamiką

.

Masa i siła

Z doświadczenia wiemy, że jedne ciała łatwiej
wprawić w ruch, zatrzymać lub ogólnie zmienić ich
prędkość (szybkość, kierunek ruchu lub jedno i
drugie), a inne trudniej. Tę cechę ciał nazywamy

bezwładnością

. Miarą bezwładności ciał w ruchu

postępowym jest wielkość fizyczna nazywana

masą

.

Doświadczenie uczy nas również, że za ruch ciał
odpowiedzialne są wzajemne oddziaływania między
nimi. Miarą tych oddziaływań jest wielkość fizyczna
nazywana

siłą

. Doświadczalnie można łatwo pokazać,

że jest to wielkość wektorowa.

Oddziaływania podstawowe (fundamentalne)

Można podawać wiele przykładów sił, z jakimi
spotykamy się w życiu codziennym. Okazuje się
jednak, że wszystkie one sprowadzają się do kilku
tzw.

oddziaływań podstawowych

.

Obecnie znamy cztery oddziaływania
fundamentalne:

•

oddziaływanie grawitacyjne

•

oddziaływanie elektromagnetyczne

•

oddziaływanie słabe

•

oddziaływanie silne

Oddziaływanie grawitacyjne

Pierwszym odkrytym oddziaływaniem było

oddziaływanie grawitacyjne

. Prawo opisujące ten typ

oddziaływanie zostało odkryte i opublikowane w
1687 roku w pracy Phylosophiae naturalis principa
mathematica przez Izaaka Newtona i nosi nazwę
prawa powszechnego ciążenia. Siła grawitacyjna
pochodzi od mas i działa między wszystkimi ciałami.
Ma ona charakter oddziaływania długozasięgowego
(obserwacje każą nam wierzyć, że ten typ sił działa
nawet w odległościach o skali kosmicznej). Ze
wszystkich znanych sił fundamentalnych siła
grawitacyjna jest najsłabsza.

Oddziaływanie elektromagnetyczne

Drugim typem oddziaływań są

oddziaływania

elektromagnetyczne

. Kiedyś traktowane było ono

jak dwa niezależne oddziaływania: elektryczne i
magnetyczne. Dopiero Teoria Maxwella z drugiej
połowy XIX wieku połączyła oba typy oddziaływań
w jedno oddziaływanie elektromagnetyczne, w
którym siły elektryczne i magnetyczne są jedynie
różnymi przejawami jednego typu pola sił.
Źródłem sił elektromagnetycznych są ładunki
elektryczne i działają na ładunki. Siły elektro-
magnetyczne, podobnie jak grawitacyjne są
dalekozasięgowe.

Oddziaływanie słabe

Trzecim znanym dziś typem oddziaływań jest tzw.

oddziaływanie słabe

. Jest to oddziaływanie o

najkrótszym zasięgu, który jest rzędu 10

m.

Ten typ oddziaływania ma miejsce między
cząstkami elementarnymi i jest odpowiedzialny
m.in. za rozpady promieniotwórcze jąder
atomowych (np. rozpad typu ), a także rozpady
niektórych cząstek elementarnych np. mionów.

Oddziaływanie silne

Kolejnym typem oddziaływań podstawowych jest

oddziaływanie silne

zwane też jądrowym.

Oddziaływanie silne jest odpowiedzialne m.in. za
trwałość jąder atomowych pomimo występowania w
nich ogromnego odpychania kulombowskiego
między protonami. Występuje ono pomiędzy
cząstkami elementarnymi nazywanymi kwarkami,
antykwarkami i gluonami. Jest to najsilniejsze ze
znanych oddziaływań. Jego cechą charakterystyczna
jest to, że siła rośnie ze wzrostem odległości
pomiędzy cząstkami, ale zakres tego oddziaływania
jest bardzo krótki rzędu 10

m.

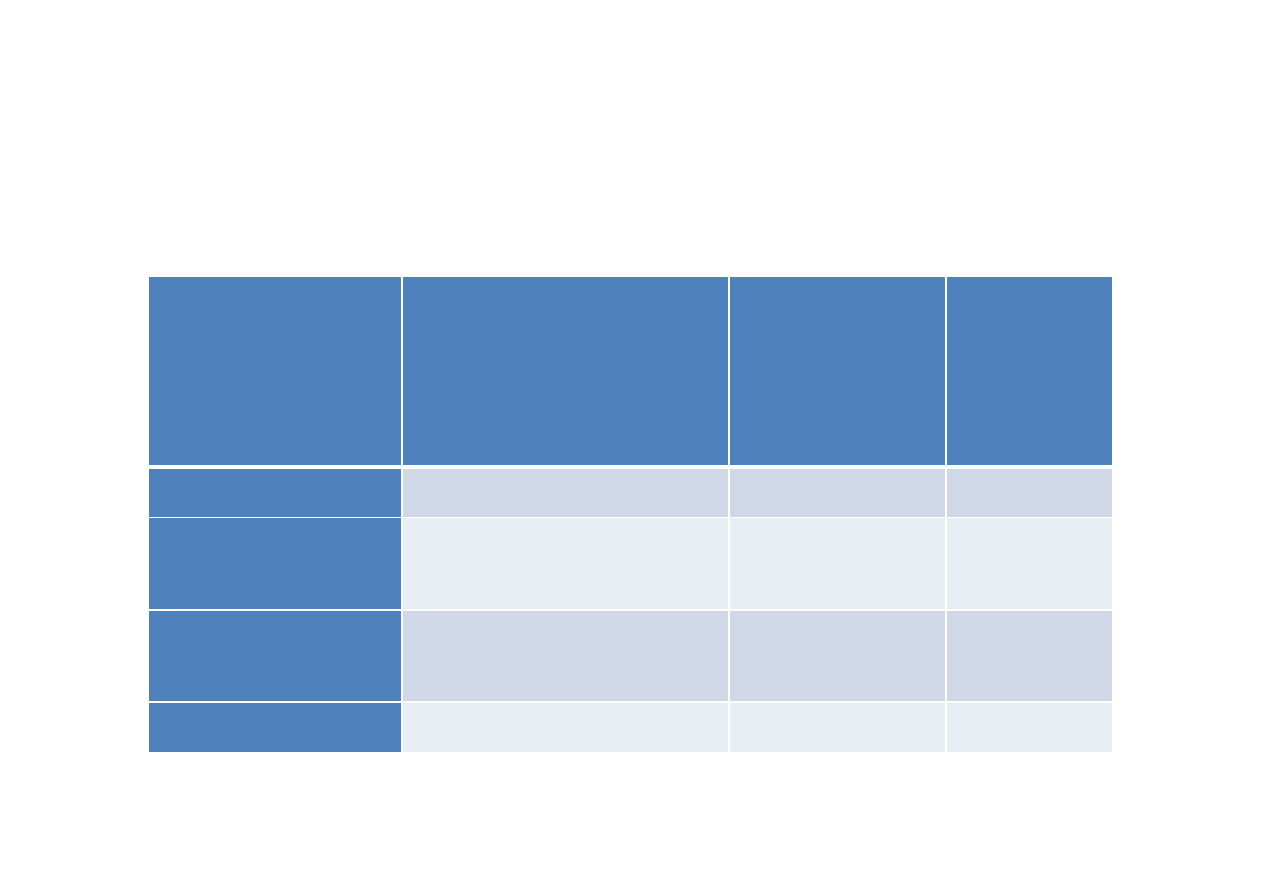
Każdemu typowi oddziaływania możemy przypisać
tzw. stałą sprzężenia, która charakteryzuje nam
wielkość siły.

Oddziaływanie

Źródło

oddziaływania

Względna

stała

sprzężenia

Zasięg

Grawitacyjne

Masa

10

∞

Elektromagnety

czne

Ładunki elektryczne

10

∞

Silne (jądrowe)

Kwarki, antykwarki,

gluony

1

10

m

Słabe

Cząstki elementarne

10

10

m

W wieku XIX Maxwell stworzył teorię, która
połączyła dwie formy oddziaływań: oddziaływanie
elektryczne i magnetyczne uznawane wcześniej za
dwie odrębne i nie związane ze sobą formy
oddziaływań. Fizycy sądzą, że wszystkie
oddziaływania fundamentalne da się opisać jedną
spójną teorią, tzw.

Teorią Wielkiej Unifikacji

. Nad

taką teorią pracował Albert Einstein, ale niestety
nie udało mu się stworzyć takiej teorii.

W 1979 roku nagrodę Nobla w dziedzinie fizyki
otrzymali fizycy Sheldon Glashow, Abdus Salam i
Steven Weinberg za stworzenie tzw. Teorii Małej
Unifikacji, która połączyła w jedną teorię
oddziaływania słabe i elektromagnetyczne.
Istnieje kilka teorii łączących odziaływania
elektrosłabe z oddziaływaniami silnymi, ale żadna
jak dotąd nie znalazła potwierdzenia
doświadczalnego.
Do teorii unifikacyjnych najtrudniej dodać
oddziaływanie grawitacyjne.

Czy istnieją inne formy odziaływań?
Być może tak. Pojawiły się fakty doświadczalne,
których na razie nie potrafimy wytłumaczyć.

Ciemna materia

– hipotetyczna materia, która nie

emituje ani nie odbija fal elektromagnetycznych.
Jej obecnością tłumaczymy szybszy ruch materii w
galaktykach niż wynikałoby to z oddziaływań
grawitacyjnych.

Ciemna energia

– hipotetyczna forma energii

wypełniającej wszechświat i powodującej, że
wszechświat rozszerza się coraz szybciej.

Siły kontaktowe

W życiu codziennym mamy do czynienia z siłami
wymagającymi kontaktu między ciałami. Jeśli
ciała są do siebie dociskane np. w wyniku
działania siły ciężkości lub przez nas, gdy np.
popychamy jakieś ciało, to pojawiają się siły
nazywane

siłami kontaktowymi

. Ich źródłem jest

oddziaływanie elektromagnetyczne, czyli jedno z
oddziaływań podstawowych. Gdy atomy dwóch
ciał zbliżają się do siebie odpowiednio blisko,
chmury elektronowe atomów zbliżanych ciał
zaczynają się przekrywać i odpychają się tym
silniej im bliżej zbliżymy do siebie ciała

Źródłem sił kontaktowych pojawiających się
podczas rozciągania np. sznurka są również siły
elektromagnetyczne. Atomy lub cząsteczki
tworzące rozciągany materiał tworzą stabilną
strukturę dzięki oddziaływaniu
elektromagnetycznemu, które przeciwdziała
siłom próbującym oddalić od siebie te atomy.
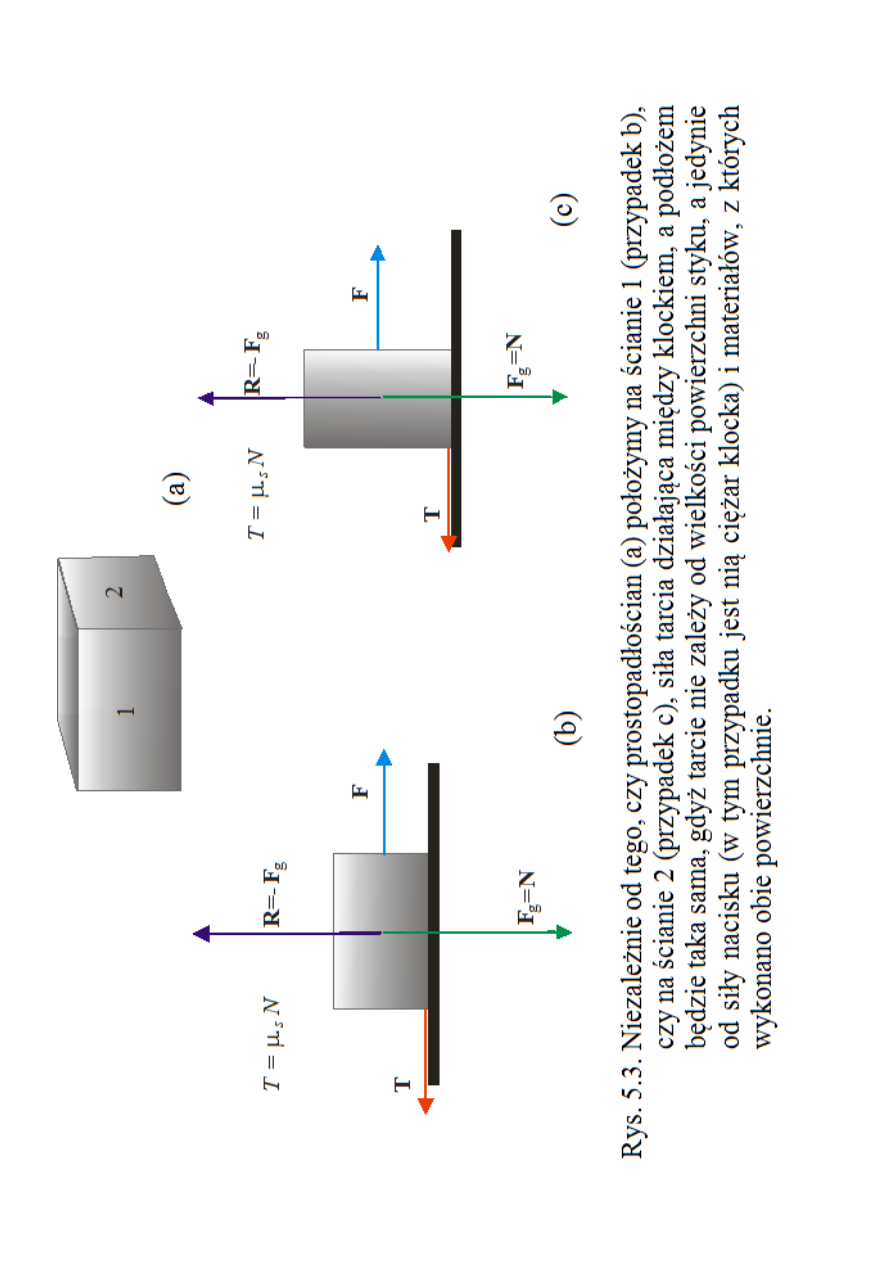
Cechą charakterystyczną siły kontaktowych jest
to, że są one zawsze prostopadłe do powierzchni
ciał, pomiędzy którymi działają.

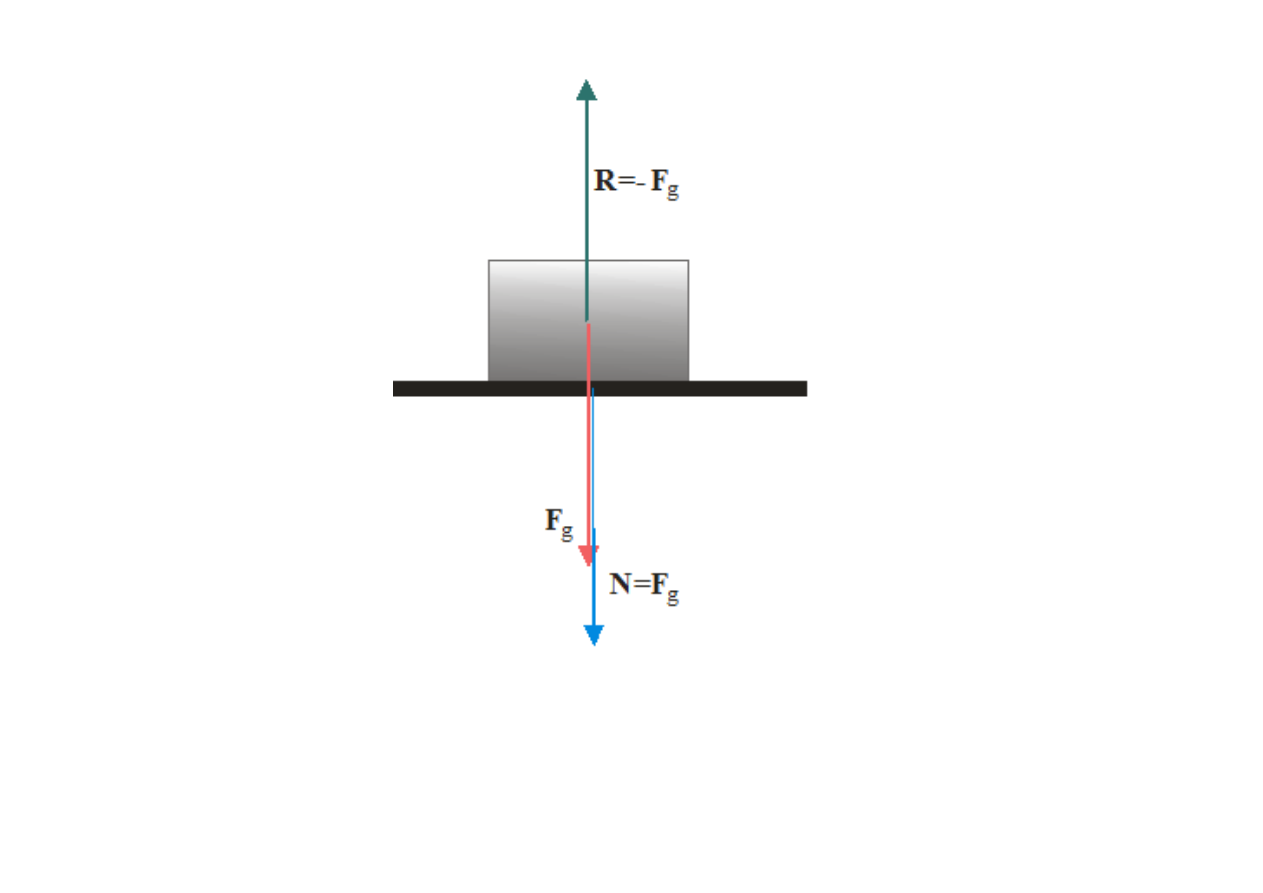
Siły działające na klocek leżący na poziomym blacie stołu
oraz siła, z jaką klocek naciska na blat

Tarcie

Oprócz sił opisanych powyżej istnieje inna ważna siła
kontaktowa, która jest styczna do powierzchni ciał
działających na siebie. Wyobraźmy sobie, że klocek
leżący na stole próbowalibyśmy poruszyć
przykładając do niego siłę równoległą do podłoża.
Jeśli siła ta byłaby dostatecznie mała, zauważyli-
byśmy, że klocek się nie porusza. Wynika z tego, że
naszej sile przeciwdziała inna siła równoważąca
naszą. Siłę tą nazywamy

tarciem

. Klocek zacznie się

poruszać dopiero wówczas, gdy nasza siła przekroczy
pewną graniczną wartość, charaktery-styczną dla
tego klocka oraz podłoża, na którym on leży.

Opisaną tu siłę tarcia działającą między nierucho-
mymi powierzchniami nazywamy

tarciem statycznym

.

Maksymalna wartość tarcia statycznego , jest równa
krytycznej wartości siły, którą musimy przyłożyć do
ciała, aby je poruszyć.

Tarcie statyczne ma dwie ciekawe cechy, które znamy
z doświadczeń:

•

Wartość siły

jest proporcjonalna do siły, z jakimi

powierzchnie naciskają na siebie

•

Wartość siły

z dobrym przybliżeniem nie zależy

od powierzchni styku obu ciał.

Z pierwszej z tych cech wynika, że stosunek
maksymalnej wartości siły tarcia statycznego

do siły

nacisku

między ciałami jest wielkością stałą (dla

danego typu obu powierzchni). Wielkość tę nazywamy
współczynnikiem tarcia statycznego

=

.

Po wprawieniu ciała w ruch na ciało nadal będzie
działać siła tarcia. Na ogół będzie ona nieco mniejsza od
siły tarcia statycznego. Tarcie występujące podczas
ruchu ślizgających się po sobie ciał nazywamy

tarciem

kinetycznym

. Tarcie kinetyczne

ma takie same cechy

jak tarcie statyczne, tzn. nie zależy od powierzchni styku
oraz jest proporcjonalne do siły, z jaką ciała naciskają na
siebie. Współczynnik tarcia kinetycznego

definiujemy

jako stosunek tarcia kinetycznego do siły nacisku między
ciałami

=

.

Współczynnik tarcia kinetycznego

jest na ogół nieco

mniejszy od współczynnika tarcia statycznego .

Opisane tarcie kinetyczne dotyczy ruchu postępowego
(ślizgania się ciała). Z nieco innym rodzajem tarcia
mamy do czynienia w przypadku toczenia się ciał (opis
tzw. tarcia tocznego pominiemy). Współczynniki tarcia
statycznego i kinetycznego są bezwymiarowe,
natomiast wymiarem współczynnika tarcia tocznego
w układzie SI jest metr.

Współczynniki tarcia zależą od rodzaju materiałów
obu trących powierzchni oraz struktury tych
powierzchni. Czym gładsze, czyli lepiej wypolerowane
będą powierzchnie, tym mniejszy będzie współczynnik
tarcia (dotyczy to zarówno tarcia statycznego jak i
kinetycznego). Istnieje jednak granica dokładności
polerowania powierzchni. Po przekroczeniu tej granicy
tarcie zamiast spadać zaczyna bardzo szybko rosnąć, a
przyłożone do siebie idealnie wypolerowane ciała
przylegają do siebie tak mocno, że trudno je rozdzielić.

Tarcie występujące pomiędzy naciskającymi na
siebie ciałami nazywamy

tarciem suchym

albo

kulombowskim

. Zjawisko to jest bardzo

skomplikowane i jak dotąd nie istnieje żadna
ścisła teoria opisująca je. Źródłem tarcia są trudne
do opisania oddziaływania pomiędzy atomami
tworzącymi powierzchnie ciał wcale nie takie
równe i gładkie jak mogłoby się wydawać.

Oprócz tarcia suchego spotykamy również tzw.

tarcie

wiskotyczne

. Jest to tarcie, jakie występuje w cieczach

lub gazach i jest związane ze zjawiskiem nazywanym

lepkością

. W przeciwieństwie do tarcia suchego, tarcie

wiskotyczne zależy od prędkości oraz rozmiarów ciała
poruszającego się w cieczy lub gazie. W pewnych
warunkach tarcie wiskotycznego jest proporcjonalne do
prędkości ciała. Zjawisko to opisał w 1851 roku irlandzki
matematyk i fizyk George Stokes. Prawo nazywane
dzisiaj prawem Stokesa opisuje siłę oporu, jakiego
doznaje kulka o promieniu poruszająca się z
szybkością w cieczy lub gazie o współczynniku lepkości

. W odpowiednich warunkach siła ta jest równa

= −6

.

Zasada Bezwładności (I zasada dynamiki)

Zasadą bezwładności

nazywamy zasadę sformułowaną

przez Newtona i nazywane też pierwszą zasadą dynamiki.
W myśl te zasady ciało, nie podlegające żadnym
oddziaływaniom porusza się ruchem jednostajnym
prostoliniowym lub pozostaje w spoczynku. Nie istnieje
żaden dowód, że ta zasada jest słuszna. We współczesnej
fizyce przyjmujemy ją jako postulat istnienia układu
odniesienia, w którym ta zasada jest spełniona. O jego
słuszności przekonuje nas zgodność z doświadczeniem
wszystkich przewidywań opartych na tym postulacie.
Układ odniesienia, w którym dowolny punkt materialny
nie oddziałujący z innymi ciałami poruszałby się ruchem
jednostajnym prostoliniowym lub spoczywał nazywamy

układem inercjalnym

.

Tabela 1.2. Szacunkowe wartości przyspieszeń związanych z
ruchami Ziemi i Słońca.

Przyspieszenie dośrodkowe związane z
ruchem obrotowym Ziemi

≈ 3,4 ∙ 10

m/s

Przyspieszenie dośrodkowe związane z
ruchem Ziemi wokół Słońca

≈ 6 ∙ 10

m/s

Przyspieszenie dośrodkowe związane z
ruchem Słońca wokół centrum Galaktyki

≈ 3 ∙ 10

&

m/s

Najlepszym przybliżeniem układu inercjalnego jest
układ związany z tzw. gwiazdami stałymi. Pojęcie gwiazd
stałych jest już dzisiaj pojęciem historycznym używano
go w odniesieniu do gwiazd, które w przeciwieństwie do
planet wydawały się nie zmieniać swego położenia
względem siebie. Newton był pierwszy, który związał z
gwiazdami układ inercjalny.

Myśl zawarta w pierwszym prawie Newtona została
wcześniej wypowiedziana przez Galileusza (Galileusz
żył latach 1564 – 1642, Newton urodził się rok po
śmierci Galileusza i zmarł w 1727). Przed Galileuszem
ludzie sądzili, że ciało, na które nie działają siły musi
być w spoczynku. Uważano, że każdy ruch, w tym
także ruch jednostajny potrzebuje jakiejś przyczyny.

II zasada dynamiki

Druga zasada dynamiki, nazywana też drugim
prawem Newtona określa w sposób ilościowy związek
pomiędzy siłą działająca na punkt materialny, a
przyśpieszeniem, jakie uzyska ten punkt. Przykładając
tę samą siłę do różnych ciał zauważamy, że
przyśpieszenia tych ciał będą różne. Jak mówiliśmy
wcześniej miarą bezwładności ciała w ruchu
postępowym jest masa ciała. Doświadczenie pokazuje,
że przyśpieszenia ciał uzyskiwane pod wpływem sił są
proporcjonalne do tych sił, a odwrotnie
proporcjonalne do ich mas.

Treść drugiej zasady dynamiki:
punkt materialny, na który działa niezrównoważona
siła F uzyskuje w inercjalnym układzie odniesienia
przyśpieszenie a o kierunku i zwrocie zgodnym z
kierunkiem i zwrotem tej siły i wprost proporcjonalne
do jej wartości oraz odwrotnie proporcjonalne do
masy m tego punktu.

Drugą zasadę dynamiki często zapisujemy w postaci
równania = '(. Zauważmy, że w przypadku
zerowej siły z równania opisującego drugą zasadę
dynamiki dostajemy, że również przyspieszenie ciała
jest zerowe. Można zatem powiedzieć, że pierwsza
zasada dynamiki jest przypadkiem szczególnym
drugiej zasady. Mimo to traktujemy pierwszą zasadę
jako odrębną zasadę i przypisujemy jej duże
znaczenie, gdyż, jak wcześniej mówiliśmy, pierwsza
zasada dynamiki postuluje istnienie układów
inercjalnych.

Pęd ciała

Bardzo ważną wielkością fizyczną jest pęd ciała.
Pęd ciała jest wielkością wektorową definiowaną
jako iloczyn masy ciała i jego prędkości

) = ' .

Ogólniejsze sformułowanie II zasady dynamiki

Bardziej ogólne od podanego wyżej sformułowania
drugiej zasady dynamiki jest sformułowanie
następujące: szybkość zmiany pędu ciała (pochodna
pędu względem czasu) jest równa sile działającej na
ciało

*)

*+

= .

Równanie to pozwala opisywać ruch ciał w przypadku
zmiennej masy. Dla układów, których masa się nie
zmienia, czyli ' = ,-./+ równanie powyższe
przechodzi w prostszą postać, podaną poprzednio

= '(.

Korzystając z definicji przyśpieszenia możemy (dla
układów o stałej masie) napisać

'( = '

*

*+

= '

* 0

*+

= .

Powyższe równanie stanowi tzw.

dynamiczne

równanie ruchu

. W kartezjańskim układzie

współrzędnych dostajemy z niego trzy skalarne
równania

'

*

1

*+

=

1

,

'

*

2

*+

=

2

,

'

*

3

*+

=

3

,

lub

'

* 4

*+

=

1

,

'

* 5

*+

=

2

,

'

* 6

*+

=

3

.

Znając siłę działającą na ciało i korzystając z równań
ruchu możemy opisać ruch ciała. Mówimy wówczas o
rozwiązywaniu równań ruchu. W przypadku zerowej
siły dostajemy równania identyczne do tych, jakie
rozwiązywaliśmy omawiając ruch jednostajny
prostoliniowy, natomiast w przypadku stałej siły
dostajemy równania, jakie rozwiązywaliśmy w
przypadku ruchu jednostajnie zmiennego. Nie zawsze
jednak mamy do czynienia z tak prostymi sytuacjami.
W wielu przypadkach rozwiązywanie równań ruchu
może być skomplikowane, gdyż siła w ogólności może
zależeć od położenia, prędkości ciała i czasu

= (0, , +).

III zasada dynamiki

Z trzeciej zasady dynamiki Newtona wynika, że w
przyrodzie nie mogą występować pojedyncze siły.
Siły występują zawsze parami. Jeżeli jedno ciało
działa na drugie jakąś siłą, to to drugie działa na to
pierwsze siłą taką samą co do kierunku i wartości
lecz o przeciwnym zwrocie. Jeżeli jedną z sił
wzajemnego oddziaływania między ciałami
nazwiemy akcją, a drugą reakcją, to możemy
powiedzieć, że każdej akcji towarzyszy reakcja. się.

Rozważmy klocek leżący na poziomym blacie stołu. Na
klocek działa siła ciężkości

9

, gdyby była to jedyna

siła działająca na klocek, to zgodnie z drugim prawem
Newtona powinien on poruszać się ruchem
jednostajnie przyśpieszonym prostoliniowym w dół.
Wiemy jednak, że leży on na stole nieruchomo.
Dlaczego tak jest? Klocek naciska na blat stołu siłą
równą swojemu ciężarowi, a ten odpowiada reakcją
przyłożoną do klocka o tej samej wartości i kierunku,
lecz skierowaną przeciwnie : = −

9

. Siła ciężkości i

siła reakcji blatu stołu działające na klocek równoważą
się, dzięki czemu klocek może spoczywać nieruchomo
na stole.

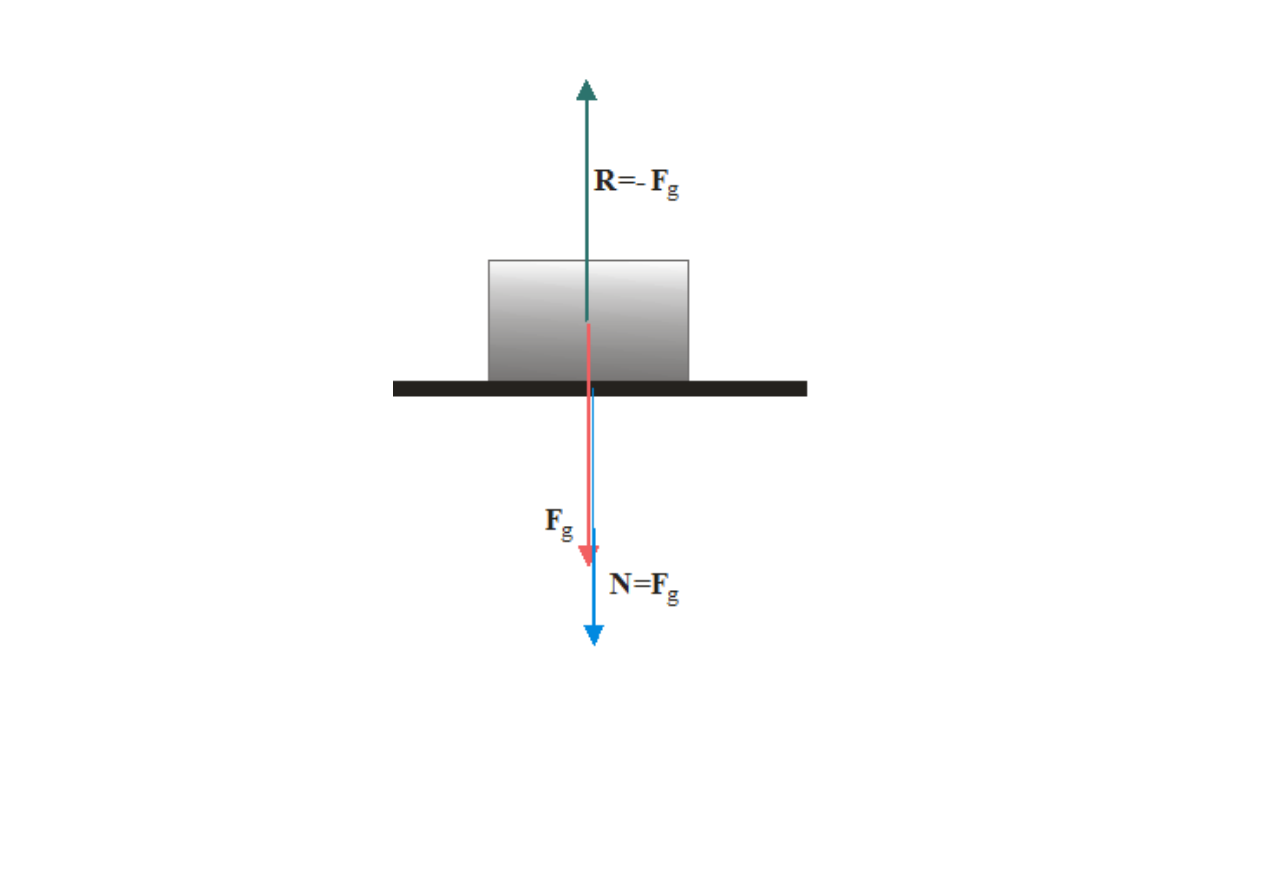
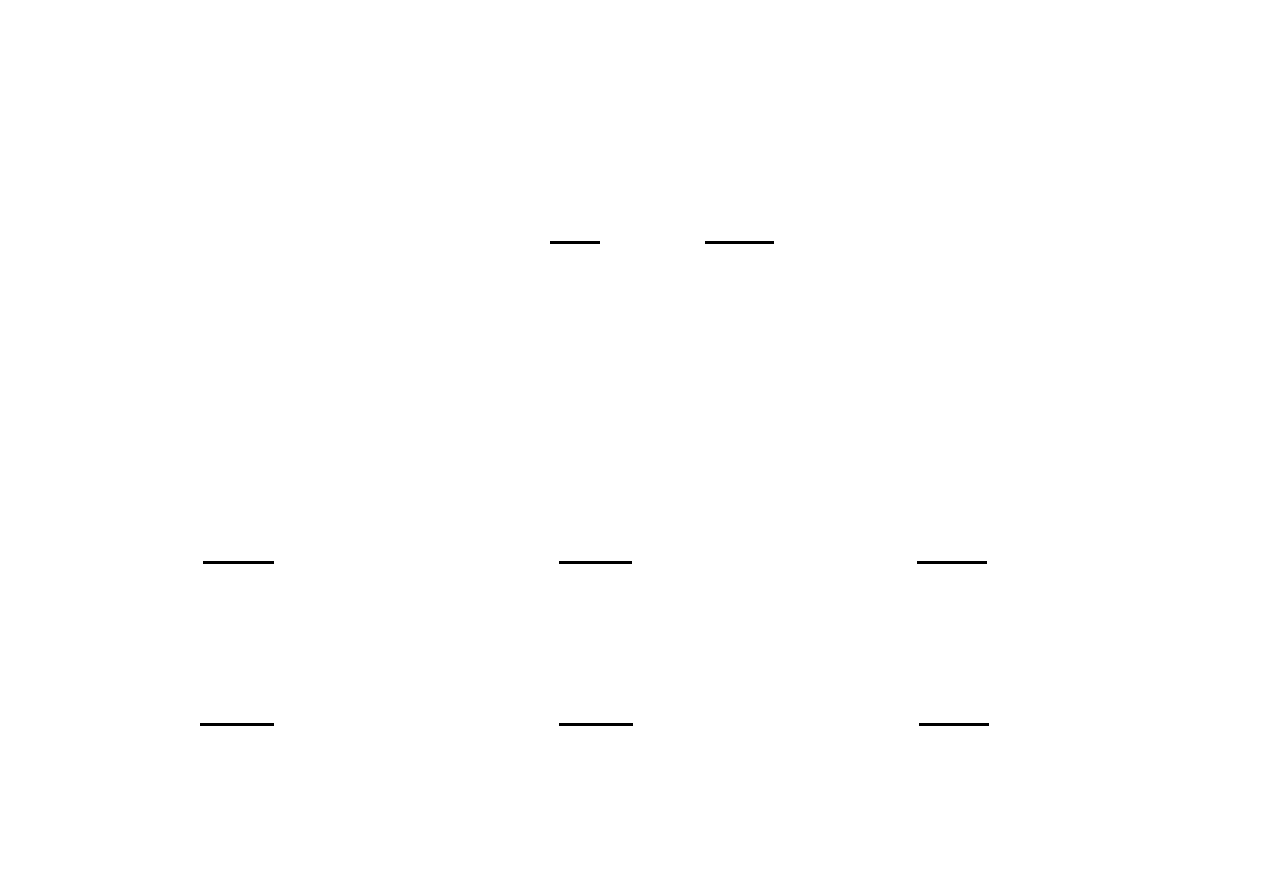
Siły działające na klocek leżący na poziomym blacie stołu
oraz siła, z jaką klocek naciska na blat

Zauważmy, że przedstawione na rysunku siły
przyłożone do klocka, nie są siłami akcji i reakcji, o
którym jest mowa w trzecim prawie Newtona.
Pierwsza z nich to siła ciężkości

9

, czyli siła, z jaką

Ziemia przyciąga klocek, a reakcją towarzysząca tej
sile jest siła, z jaką klocek przyciąga Ziemię (nie ma
jej na rysunku). Drugą jest siła reakcji stołu : na
nacisk ; =

9

, jaki klocek na niego wywiera.

Zwróćmy uwagę na to, że siła ; nacisku klocka na
blat jest przyłożona do blatu, a siła : reakcji blatu
jest przyłożona do klocka.

Ograniczenia III zasady dynamiki
Trzecia zasada dynamiki Newtona ma swoje
ograniczenia. Zasada ta milcząco zakłada, że
oddziaływania przenoszą się nieskończenie szybko.
Fizykom w czasach Newtona, a nawet później
wydawało się to oczywiste. Dziś wiemy, że
oddziaływania rozchodzą się z ogromną, lecz
skończoną prędkością równą prędkości światła.
Dlatego też w przypadku bardzo szybkich
procesów np. zderzeń bardzo szybko
poruszających się cząstek elementarnych, trzecia
zasada dynamiki nie zawsze jest prawdziwa.

Układy nieinercjalne

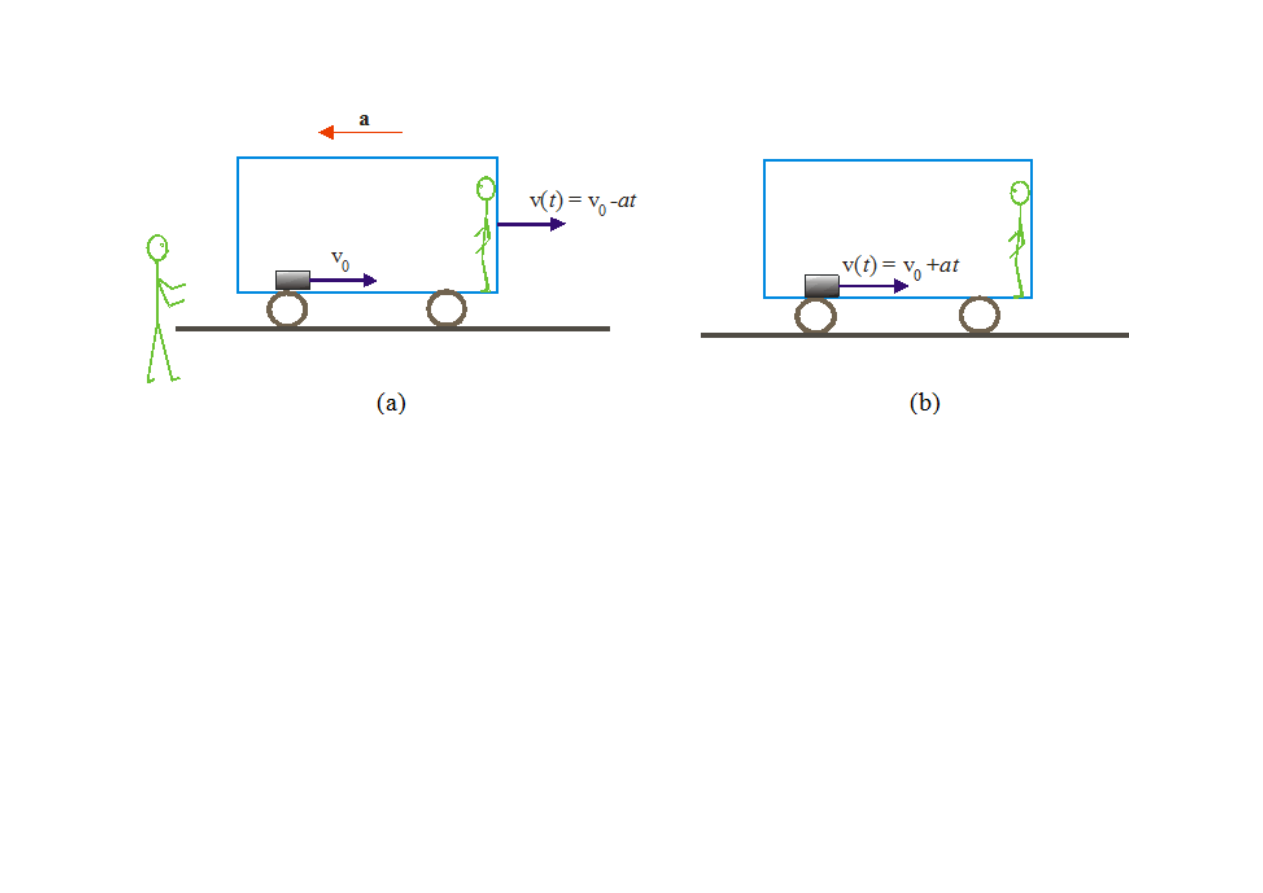
Obserwacja zachowania się ciała wewnątrz hamu-
jącego pojazdu z punktu widzenia obserwatora
zewnętrznego (z układu inercjalnego) (a) oraz z
punktu widzenia pasażera tego pojazdu (b).

Obserwator z układu inercjalnego nie ma żadnego
problemu z opisaniem zachowania ciała. Wszystko jest
zgodne z zasadami dynamiki Newtona. Inaczej wygląda to
z punktu widzenia pasażera pojazdu poruszającego się ze
zmieniająca się prędkością, czyli obserwatora w

układzie

nieinercjalnym

. Aby móc nadal stosować prawa Newtona,

musi on założyć, że w jego układzie oprócz sił, których
źródłem są oddziaływania pojawia się jeszcze siła równa
iloczynowi masy danego ciała i przyspieszenia – (

&

, gdzie

(

&

jest przyspieszeniem jego układu względem

dowolnego układu inercjalnego

=

= −'(

&

.

Te dodatkowe siły, jakie musimy wprowadzić do opisu
zjawisk w układzie nieinercjalnym nazywamy

siłami

bezwładności

. Siły bezwładności nie są zwykłymi

siłami, takimi, o których mówiliśmy do tej pory, nie są
one wynikiem oddziaływań między ciałami, nie mają
one również swojego odpowiednika wynikającego z III
zasady dynamiki Newtona, gdyż zasada akcji i reakcji
dotyczy jedynie oddziaływań między ciałami. Sił
bezwładności nie ma, gdy opisujemy jakieś zjawisko z
punktu widzenia układu inercjalnego. Potrzebne nam
są tylko wówczas, gdy chcemy dokonać opisu zjawiska
w układzie nieiner-cjalnym, czyli poruszającym się
ruchem przyśpieszonym względem dowolnego układu
inercjalnego.

Z wymienionych wyżej powodów siły bezwładności często
nazywane są również

siłami pozornymi

. W odróżnieniu od

sił pozornych siły rzeczywiste występują zarówno w
układach inercjalnych, jak i w nieinercjalnych i w obu są
takie same.

Układ odniesienia obracający

się ruchem jednostajnym

względem stałej osi

Bardzo ważnym układem nieinercjalnym jest układ
obracający się ruchem jednostajnym względem stałej osi.
Takim układem jest np. Ziemia. Przy opisie ruchu
obrotowego wygodniej jest używać pojęcia prędkości
kątowej zamiast dotychczas używanego przez nas pojęcia
prędkości, nazywanej dla odróżnienia prędkością liniową.

Prędkość kątową

definiujemy jako wektor

(dokładniej

pseudowektor)

, którego kierunek pokrywa się z kierunkiem

osi obrotu ciała (układu), zwrot określony jest regułą
prawej dłoni, a długość określa szybkość zmiany kąta w
czasie.

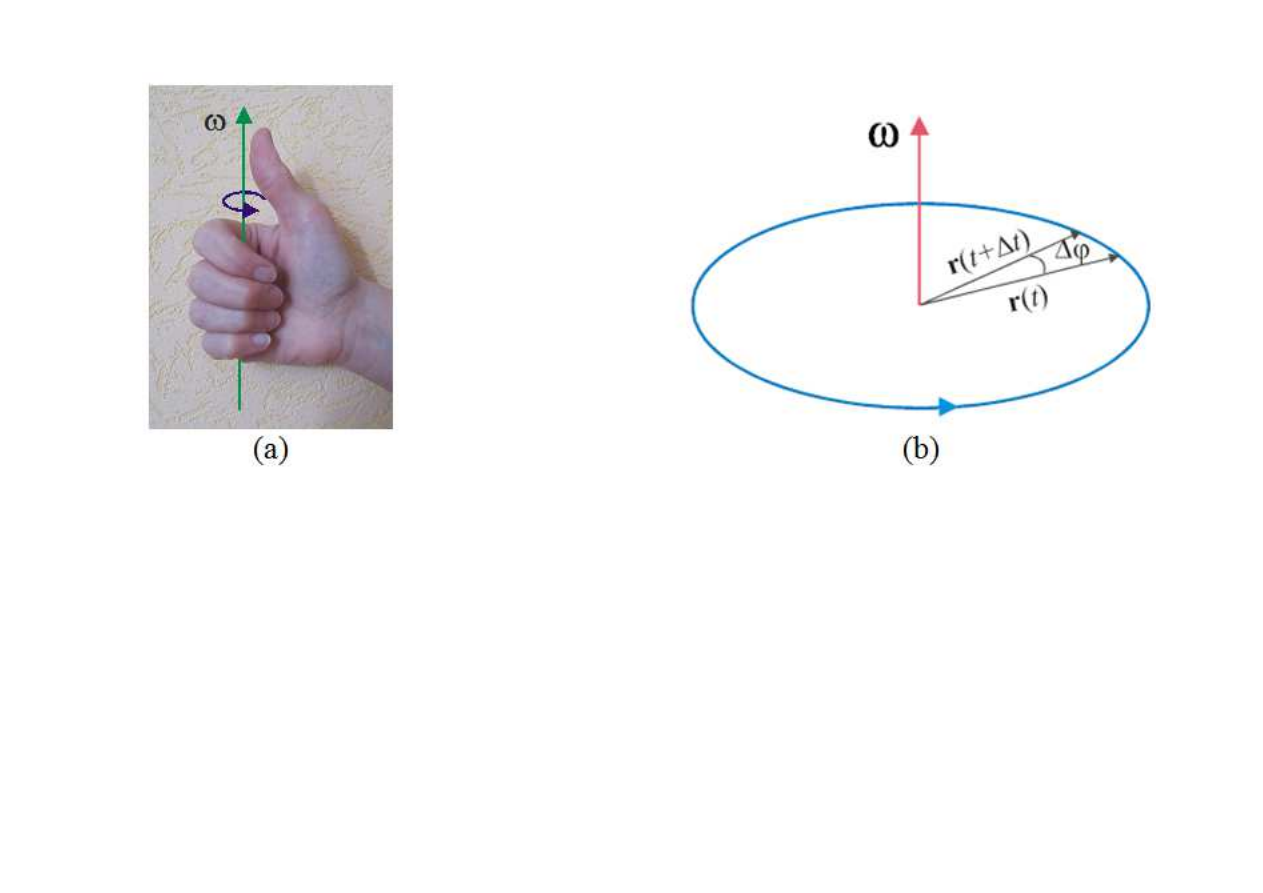
Definicja prędkości kątowej: kierunek i zwrot prędkości
kątowej pokazuje rysunek (a), zmianę kąta ∆? w czasie
∆+ pokazuje rysunek (b).

Podobnie jak w przypadku prędkości liniowej możemy
wprowadzić najpierw pojęcie średniej prędkości kątowej
o długości definiowanej jako stosunek zmiany kąta ∆? do
czasu ∆+, w którym ta zmiana nastąpiła

@

śB.

=

∆?

∆+

,

a następnie chwilową prędkość kątową o długości

@ = lim

∆E→G

∆?

∆+

,

czyli

@ =

*? +

*+

.

W układzie SI jednostką prędkości kątowej jest rad/s.

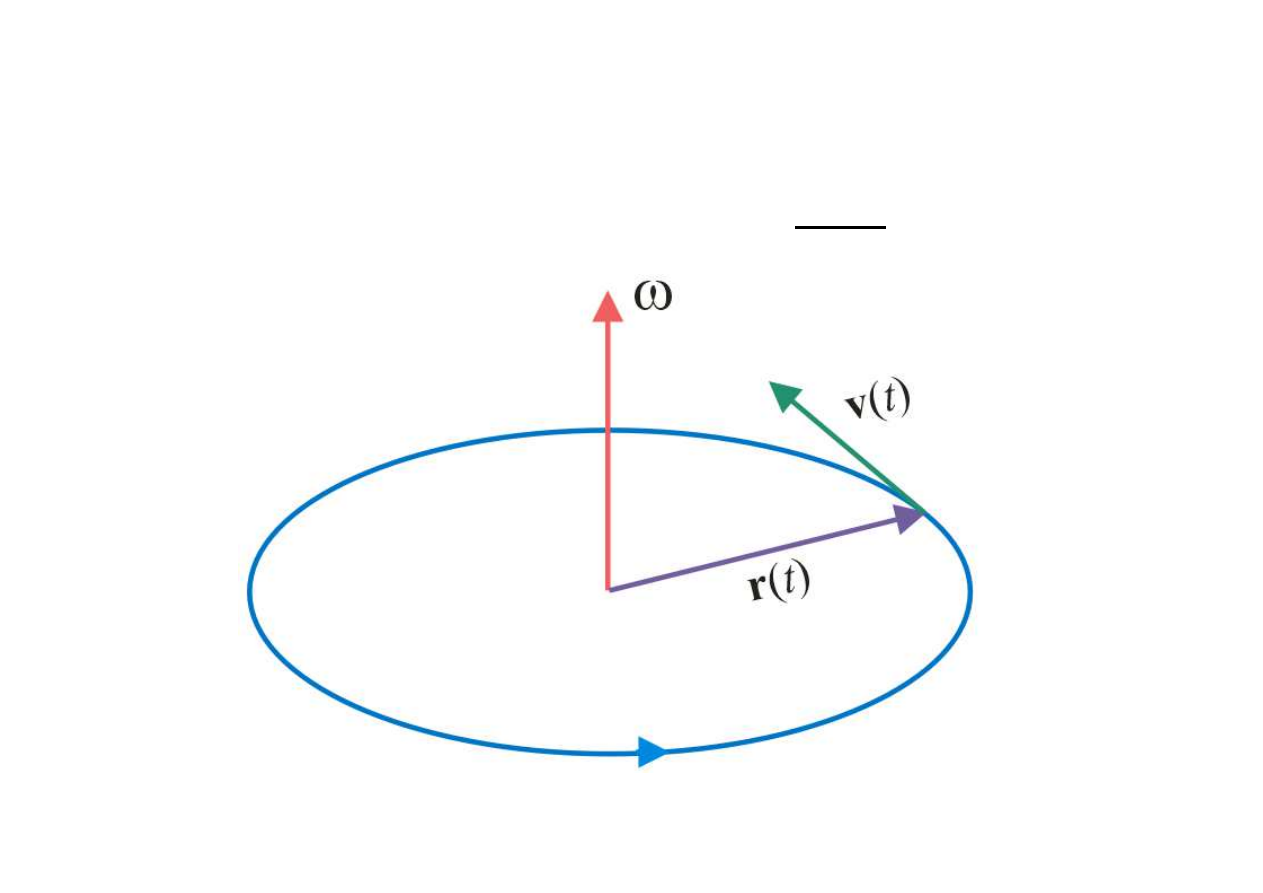
Wektory 0, , H są wzajemnie do siebie prostopadłe i
można pokazać, że

= H × 0lubH =

0 ×

r

.

Siła odśrodkowa

Wyobraźmy sobie ciało nieruchome względem obraca-
jącego się ze stałą prędkością kątową H = ,-./+ układu
odniesienia, np. dziecko na karuzeli, planetę krążącą
wokół Słońca itp. Niech ciało to znajduje się w odległości

> 0 od osi obrotu układu. Względem układu inercjal-

nego, względem którego oś obrotu naszego układu
obracającego się jest nieruchoma, ciało to porusza się
ruchem jednostajnym po okręgu o promieniu . Za ruch
ten odpowiedzialna jest siła nazywana

siłą dośrodkową,

gdyż cały czas jest skierowana do środka okręgu, po
którym krąży ciało.

W przypadku ruchu jednostajnego po okręgu, siła
dośrodkowa jest stała co do wartości. Możemy zapisać w
różnych postaciach:

N śO.

= −'

0P = −'@

0P = 'H ×

= 'H × (H × 0).

W wymienionych powyżej przykładach siłą tą jest siła
naprężająca łańcuch utrzymujący krzesełko na
obracającej się karuzeli i siła grawitacyjna, z jaką Słońce
przyciąga planetę.

Spójrzmy teraz na nasze ciało z układu obracającego się,
czyli tego układu, w którym ciało jest nieruchome. Tak jak
w przypadku poprzednio rozważanego układu nieiner-
cjalnego (poruszającego się ruchem prostoliniowym
zmiennym), pojawia się znowu niezgodność z zasadami
dynamiki. Widzimy, że ciało pozostaje w spoczynku
(względem naszego obracającego się układu), chociaż na
ciało działa siła (dośrodkowa). A zatem tak jak poprze-
dnio, aby móc nadal stosować zasady dynamiki Newtona
musimy założyć, że w obracającym się układzie odnie-
sienia działają siły bezwładności (siły pozorne, gdyż
niewynikające z oddziaływań).

W omawianym przypadku szukana siła bezwładności musi
mieć cały czas ten sam kierunek i wartość, co siła
dośrodkowa, lecz przeciwny do siły dośrodkowej zwrot i
dlatego siłę tę nazywamy siłą odśrodkową

NśO.

= −

N śO.

.

Siła odśrodkowa, tak jak w poprzednim przykładzie siła

Q

= −'(

&

towarzyszy wszystkim ciałom w obracającym

się układzie odniesienia.

Stan nieważkości

w układzie nieinercjalnym

W układzie nieinercjalnym, w którym siła bezwładności
równoważy siłę ciążenia będzie panował stan nazywany

stanem nieważkości

. Krótkotrwale możemy wywołać taki

stan w układzie poruszającym się ruchem prostoliniowym
z przyśpieszeniem równym przyśpieszeniu ziemskiemu R.
W układzie takim na każde ciało oprócz siły ciężkości

9

= 'R działa siła bezwładności

=

= −'(, a ponieważ

przyspieszenie układu wynosi ( = R, to

=

= −'R. Jak

widzimy obie siły równoważą się w związku z czym nie
będziemy odczuwać ciężaru, będziemy w stanie
nieważkości

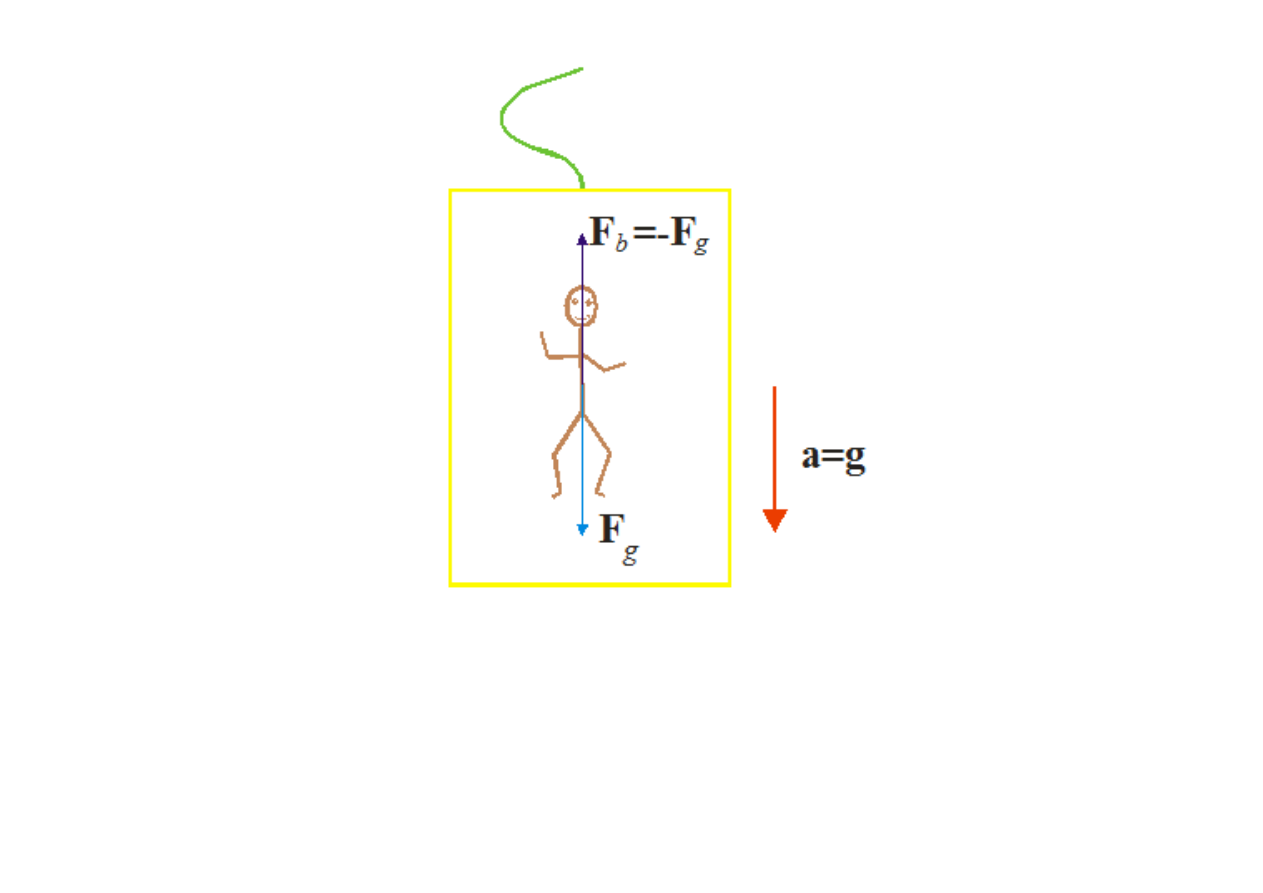
Stan nieważkości w kabinie spadającej swobodnie na linie
bungee.

Podobny stan możemy osiągnąć w układzie
obracającym się, jeśli ruch zrealizujemy w taki
sposób, żeby siła odśrodkowa (siła bezwładności
w układzie obracającym się) zrównoważyła siłę
grawitacji. Krótkotrwale (i tylko w przybliżeniu)
możemy to zrealizować w samolocie
poruszającym się po odpowiednim torze
zakrzywionym. Natomiast w sposób trwały
osiągamy stan nieważkości w stacji kosmicznej
poruszającej się na orbicie wokółziemskiej.

Załóżmy dla uproszczenia, że stacja orbitalna porusza się
na orbicie kołowej. Ruch jednostajny po okręgu wymaga,
jak pamiętamy, siły dośrodkowej o stałej wartości. W
przypadku ruchu na orbicie wokółziemskiej źródłem tej
siły jest grawitacja. Na stację i wszystkie znajdujące się w
niej ciała działa siła ciężkości (przyciągania ziemskiego),
która sprawia, że ciała te poruszają się ruchem
jednostajnym po okręgu. Układ związany ze stacją jest
układem nieinercjalnym obracającym się ruchem
jednostajnym, a zatem na każde ciało w tym układzie
działa również siła odśrodkowa równa dokładnie co do
wartości sile dośrodkowej, a że siłą dośrodkową jest tu
siła ciężkości, to siła odśrodkowa (bezwładności)
równoważy siłę ciężkości, co prowadzi do stanu
nieważkości.

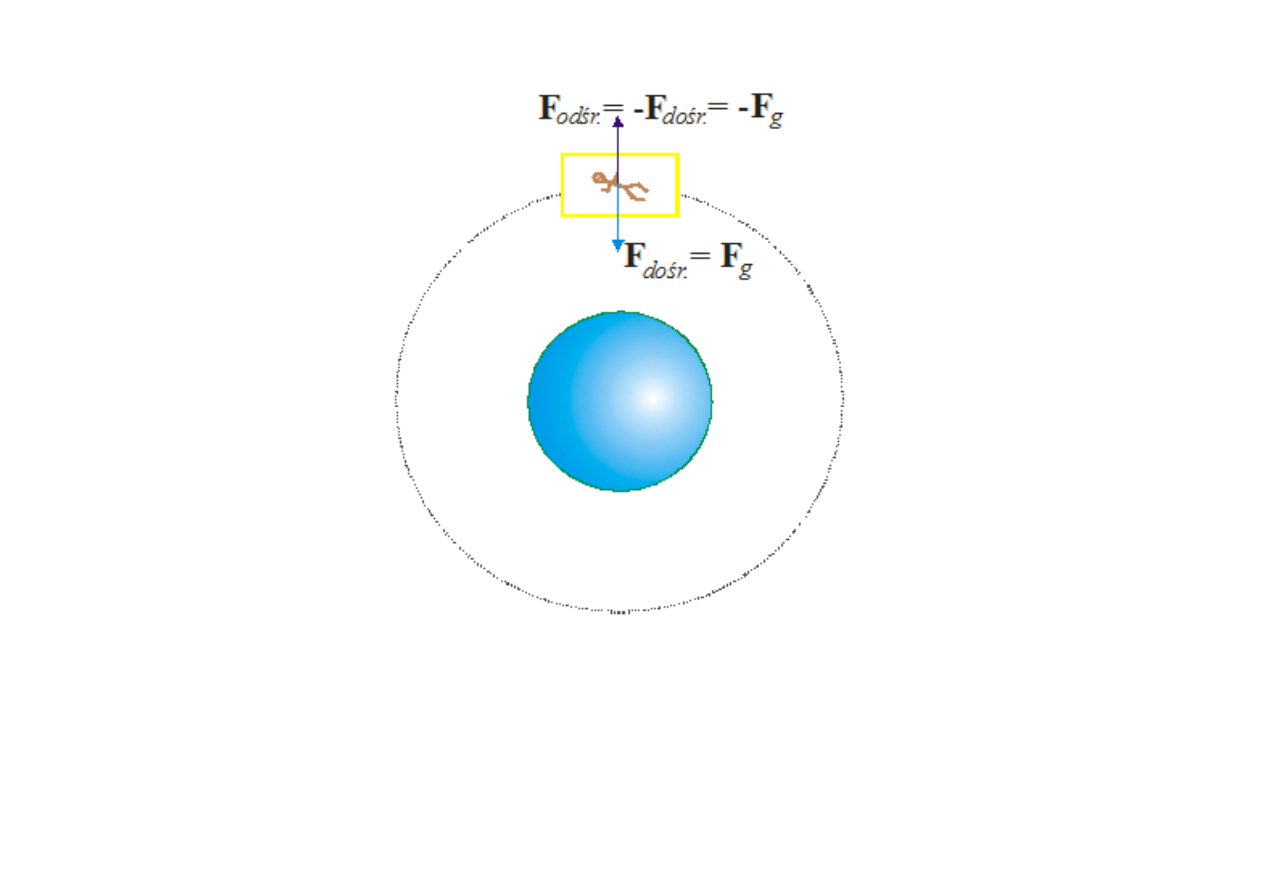
Stan nieważkości w stacji orbitalnej.

Siła Coriolisa

W przypadku ciał nieruchomych względem obracającego
się układu siła odśrodkowa jest jedyną siłą bezwładności.
Jednak okazuje się, że na ciała będące w ruchu względem
układu obracającego się ruchem jednostajnym oprócz siły
odśrodkowej działa jeszcze inna siła bezwładności. Aby
się o tym przekonać wyobraźmy sobie, że będąc w środku
wirującej ruchem jednostajnym tarczy strzelamy w
kierunku obiektu umieszczonego na krawędzi tarczy
naprzeciwko nas. Spróbujmy opisać ten eksperyment z
punktu widzenia obserwatora obracającego się wraz z
tarczą oraz obserwatora zewnętrznego (nieruchomego).

Obserwator zewnętrzny stwierdzi, że pocisk po
wystrzeleniu porusza się ruchem jednostajnym
prostoliniowym z prędkością, jaką osiągnął po
wystrzeleniu. Jest tak, ponieważ po opuszczeniu lufy nie
działają na niego żadne siły (dla uproszczenia rozważań
pomińmy siłę grawitacji). Tymczasem wirująca tarcza cały
czas obraca się, więc zanim pocisk pokona dystans równy
promieniowi tarczy, jaki dzielił go od obiektu, do którego
strzelaliśmy, tarcza obróci się wraz z obiektem o pewien
kąt i pocisk nie trafi w wycelowany obiekt.

Jak ten eksperyment opisze obserwator na wirującej
tarczy? Otóż ze zdziwieniem zauważy, że pocisk nie
porusza się po linii prostej, lecz po torze zakrzywionym
spychany z toru prostoliniowego jakąś tajemniczą siłą.
Obserwator nie jest w stanie wskazać źródła tej siły, więc
musi to być siła bezwładności. Nie jest nią poznana
wcześniej siła odśrodkowa, gdyż tamta działa wzdłuż
promienia, czyli właśnie w takim kierunku, w jakim pocisk
został wystrzelony. Siłą bezwładności, którą w ten sposób
odkryliśmy jest siła nazywana, od nazwiska odkrywcy
efektu jej działania na Ziemi,

siłą Coriolisa

.

W przypadku układów obracających się ruchem
niejednostajnym oprócz siły odśrodkowej i siły Coriolisa
pojawi się jeszcze inna siła bezwładności.

Siła Coriolisa jest siłą bezwładności, jaka działa w
obracających się układach odniesienia na ciała
poruszające się względem tego układu. Wyraża się ona
wzorem

S

= −2'H ×

B

,

gdzie

B

oznacza prędkość względem układu obracające-

go się.

Pamiętając o własnościach iloczynu wektorowego
możemy wymienić następujące cechy siły Coriolisa:

•

Siła Coriolisa jest prostopadła do osi obrotu oraz
prędkości, jaką ma ciało względem układu
obracającego się

•

Siła Coriolisa jest zerowa wtedy, gdy

•

układ nie obraca się H = 0,

•

ciało spoczywa względem układu obracającego się

B

= 0,

•

ciało porusza się w kierunku równoległym do osi
obrotu.

Wypadkową siłą bezwładności w układzie obracającym
się ruchem jednostajnym jest suma siły Coriolisa i siły
odśrodkowej

=

=

S

+

VWś.

= −2'H ×

B

− 'H × H × 0 .

W powyższym wyrażeniu 0 jest wektorem wodzącym
wychodzącym z początku układu obracającego się.

Siła Coriolisa na Ziemi

W normalnych warunkach, z jakimi mamy do czynienia
przy powierzchni Ziemi siła ta jest bardzo mała i dlatego w
życiu codziennym jej nie dostrzegamy. Na przykład nie
widzimy, że ciało, które upuścimy nie spada na Ziemię po
linii prostej, lecz po torze zakrzywionym. Analizując
kierunek i zwrot działania siły Coriolisa na ciała spadające
swobodnie na powierzchnię Ziemi, widzimy, że ciała będą
odchylane na wschód. Gdyby nie uwzględniać oporów
powietrza, wiatru itd., to ciało zrzucone z wieży Eiffla
spadłoby w punkcie odchylonym od pionu zaledwie o ok.
6,5 cm na wschód.

Jak można wytłumaczyć zbaczanie w kierunku wschodu
ciała spadających na Ziemię, z punktu widzenia układu
inercjalnego? Jak już podkreślaliśmy w układzie
inercjalnym nie ma sił bezwładności, a więc również nie
ma siły Coriolisa odpowiedzialnej za zakrzywianie toru.
Pozornie wydawać by się mogło, ze ciało spadające na
Ziemię powinno spaść w punkcie przesuniętym na
Zachód. Przecież zanim ciało upadnie Ziemia nieco obróci
się, a obraca się w kierunku z zachodu na wschód.

Zauważmy jednak, że ciało puszczone swobodnie, bez
prędkości początkowej względem Ziemi z wysokości X nad
powierzchnią Ziemi, ma względem układu inercjalnego
niezerową prędkość wynikającą z ruchu obrotowego Ziemi,
więc nie porusza się po prostej, lecz po (w przybliżeniu)
paraboli, wzdłuż ramienia paraboli skierowanego na
wschód.

Prędkość ta wynosi (na równiku) @

W

(Y

Z

+ X),

gdzie @

W

jest prędkością kątową Ziemi w jej ruchu

obrotowym wokół osi, a Y

Z

jest promieniem Ziemi i jest

większa od prędkości liniowej punktów na powierzchni
Ziemi, która na równiku wynosi @

W

Y

Z

i dlatego w efekcie

uzyskujemy przesunięcie na wschód, a nie na zachód.

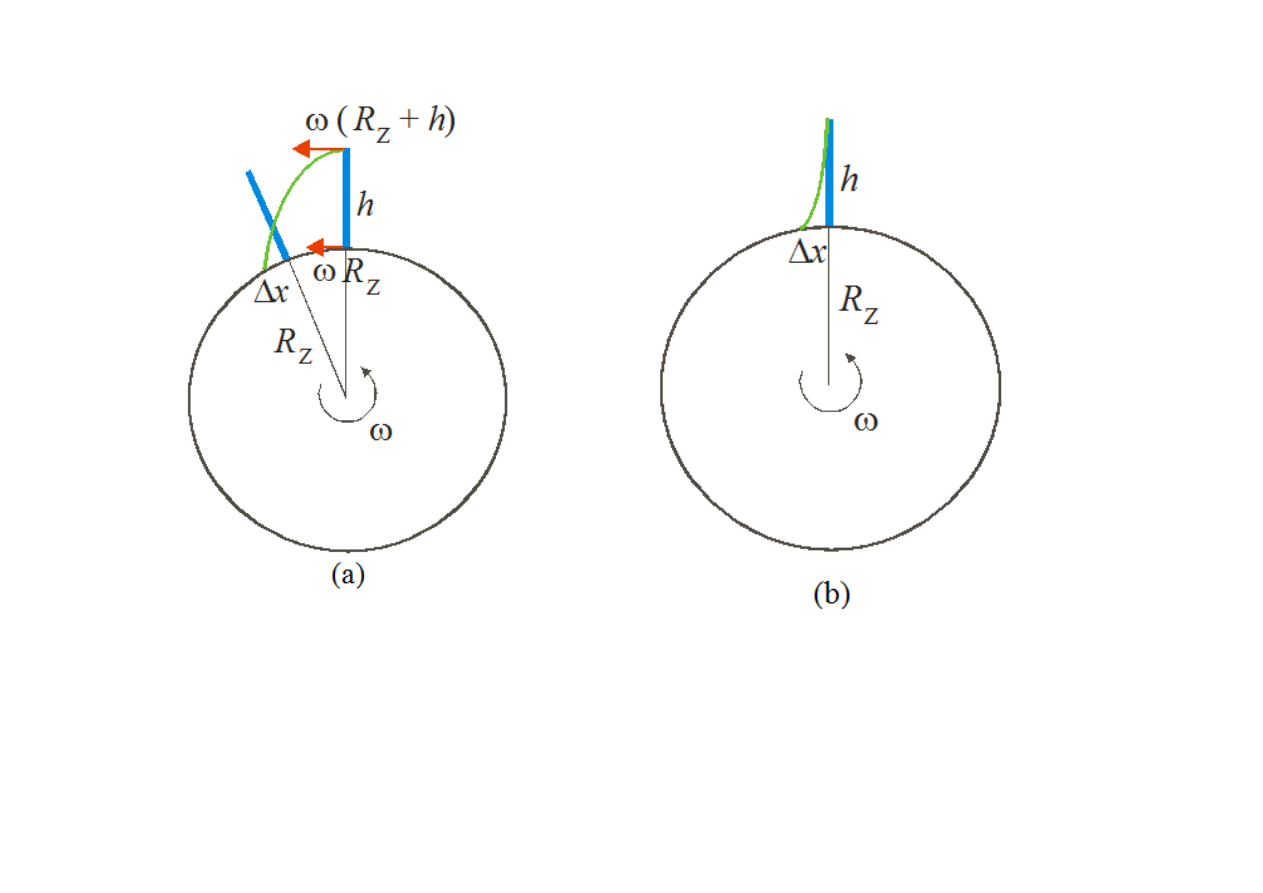
Kształty torów spadające swobodnie ciała na równiku
widziane z układu inercjalnego (a) oraz nieinercjalnego
związanego z obracającą się Ziemią (b).

Jak widzieliśmy na przykładzie spadku z wieży Eiffla
odchylenie jest niewielkie, ale już w przypadku pocisków
balistycznych, których prędkości są rzędu kilku kilometrów
na sekundę, a czas lotu rzędu kilkudziesięciu sekund
zboczenie od toru, po jakim poruszałby się pocisk, gdyby
siły Coriolisa nie było (Ziemia nie obracałaby się wokół
swojej osi) jest rzędu 100 m i należy taką poprawkę
uwzględnić.

Pomimo małej wartości siły Coriolisa ma ona kolosalny
wpływ na wiele zjawisk zachodzących na Ziemi. To siła
Coriolisa odpowiedzialna jest m.in. za kierunki wiatrów
(przeważają wiatry w kierunku wschód-zachód), kierunki
prądów morskich, czy cyrkulacje powietrza w obszarach
wyższego ciśnienia, czyli wyżach (cyklony) lub niższego
ciśnienia, czyli niżach (antycyklony), które są różne na obu
półkulach – północnej i południowej. Na półkuli północnej
masy powietrza wokół wyżów obracają się w kierunku
zgodnym z ruchem wskazówek zegara, a wokół niżów w
kierunku przeciwnym, zaś na półkuli południowej jest
odwrotnie.

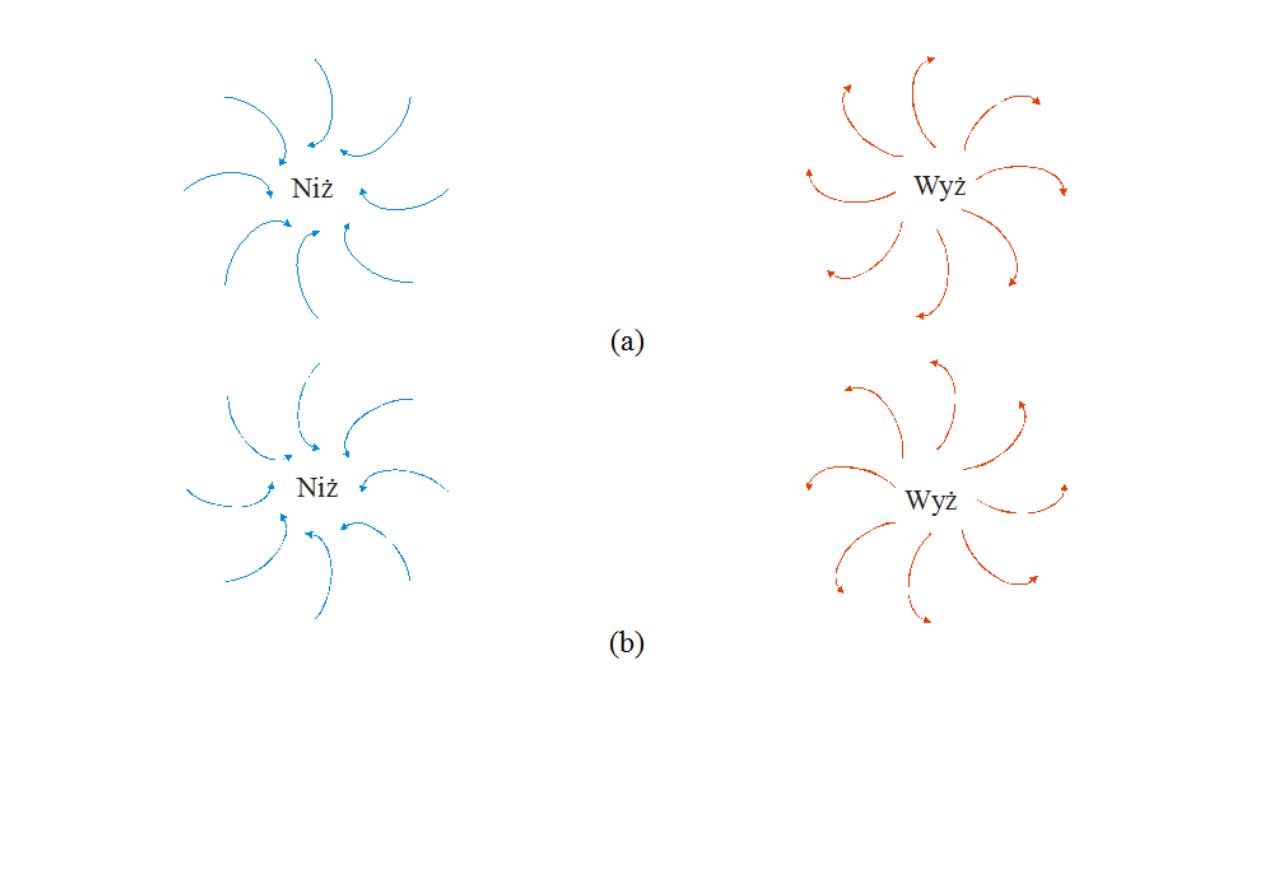
Cyrkulacja powietrza wokół ośrodków niżowych i
wyżowych na półkuli północnej (a) i południowej (b).

Niektóre efekty działania siły Coriolisa na Ziemi

•

na półkuli północnej wiatr ma tendencję do skręcania
w prawo, a na południowej – w lewo;

•

na półkuli północnej mocniej podmywane są prawe
brzegi rzek, na południowej – lewe;

•

na półkuli północnej cyklony poruszają się odwrotnie
do ruchu wskazówek zegara, a na południowej zgodnie
z nim;

•

płaszczyzna, w której porusza się wahadło, ulega
skręceniu na półkuli północnej w prawo, a na
południowej – w lewo.

Wahadło Foucaulta

Bardzo ciekawym przykładem doświadczenia obrazującego
działanie siły Coriolisa, czy mówiąc inaczej dowodem na
ruch obrotowy Ziemi jest tzw. wahadło Foucaulta.
Pod pojęciem wahadła Foucaulta rozumiemy bardzo
długie (co najmniej kilkunastometrowe) i ciężkie (aby
zminimalizować wpływ tłumienia) wahadło mające
możliwość wykonywania wahań w dowolnej płaszczyźnie
pionowej. Na skutek ruchu obrotowego Ziemi płaszczyzna
drgań tego wahadła obraca się stopniowo. Najłatwiej
można wytłumaczyć ten efekt dla wahadła umieszczonego
na biegunie. Ponieważ wahadło zachowuje płaszczyznę
drgań w układzie inercjalnym np. względem gwiazd, a
Ziemia pod nim się obraca, więc w ciągu doby płaszczyzna
drgań wahadła obróci się względem Ziemi o 360°.

W układzie związanym z Ziemią obrót płaszczyzny wahań
wahadła tłumaczymy obecnością siły Coriolisa. Na innych
szerokościach geograficznych okres obrotu płaszczyzny
wahadła będzie większy niż na biegunie rośnie on
odwrotnie proporcjonalnie do sinusa kąta szerokości
geograficznej, czyli na równiku staje się nieskończony. W
związku z tym na równiku nie obserwujemy efektu obrotu
płaszczyzny drgań wahadła. Tor, jaki zakreśla wahadło jest
krzywą nazywaną rozetą. Możliwe są dwa kształty rozety
zależne od sposobu wprawienia w ruch wahadła.

Jeśli wahadło wprawimy w ruch wypychając je z położenia
równowagi, to otrzymamy rozetę o zaokrąglonych
końcach, przechodzącą zawsze przez punkt równowagi, z
którego ruch się rozpoczął. Jeśli natomiast wychylimy je z
położenia równowagi i puścimy swobodnie, bez
nadawania prędkości początkowej, to rozeta będzie miała
ostre końce i nie będzie przechodzić przez punkt
równowagi. W pierwszym przypadku ruch wahadła
względem gwiazd stałych będzie się odbywał w
płaszczyźnie, a w drugim przypadku wahadło względem
gwiazd będzie poruszać się po elipsie.

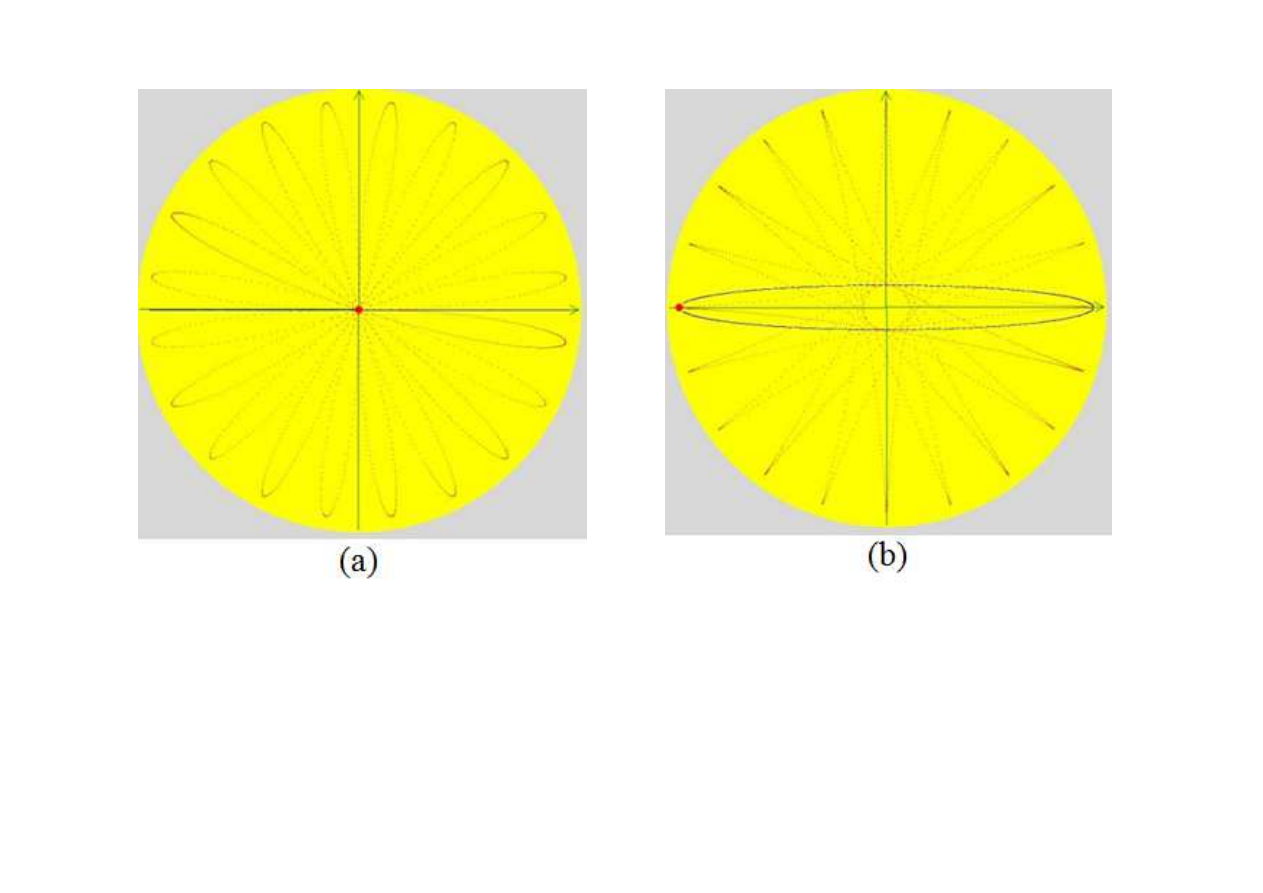
Kształty torów wahadła Foucaulta w zależności od warunków
początkowych.