INSTYTUT METROLOGII I INŻYNIERII BIOMEDYCZNEJ
Politechniki Warszawskiej
Laboratorium Podstaw Metrologii
Semestr I
Ćwiczenie nr 4
Wyznaczanie niepewności pomiarów pośrednich na przykładzie
przepływomierza zwężkowego
Warszawa
Wyznaczanie niepewności pomiarów pośrednich na przykładzie przepływomierza
zwężkowego
Opracował: prof. nzw. dr hab. inż. Mateusz Turkowski
1. Cel ćwiczenia
Celem ćwiczenia jest zapoznanie się z praktycznym wyznaczaniem niepewności pomiarów
bezpośrednich i pośrednich oraz zmniejszeniem wpływu błędów systematycznych na wynik
pomiaru poprzez wprowadzenie poprawek. Dodatkowy cel to zapoznanie się zasadą
zwężkowego pomiaru strumienia płynu.
2. Wprowadzenie teoretyczne
2.1. Wyprowadzenie wzoru umożliwiającego obliczenie strumienia objętości płynu przy
pomiarze zwężkowym
Strumień objętości qv jest to objętość płynu przepływającego przez poprzeczny przekrój
rurociągu w jednostce czasu.
Najczęściej stosowaną zwężką pomiarową, umożliwiającą pomiar strumienia płynu, jest
kryza – płaska tarcza z okrągłym otworem o średnicy d, współosiowa z rurociągiem o
średnicy wewnętrznej D.
Przepływomierze zwężkowe oparte o kryzę są szeroko stosowane zarówno do pomiarów
technologicznych we wszystkich praktycznie gałęziach przemysłu a także do pomiarów
rozliczeniowych takich strategicznych surowców jak gaz ziemny i ropa naftowa.
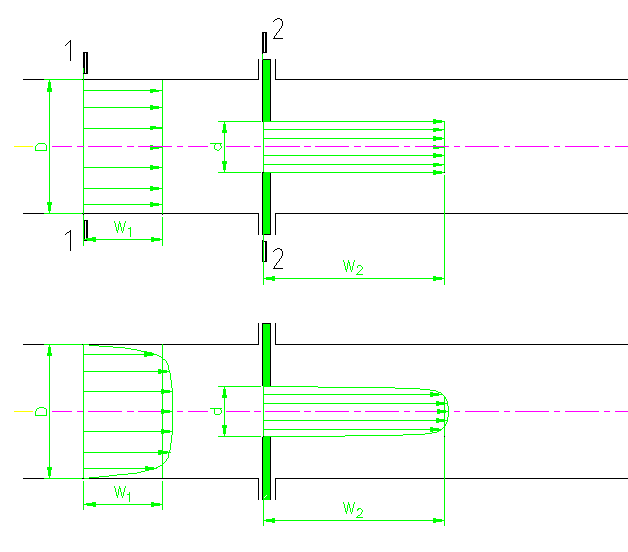
Załóżmy na razie, dla uproszczenia, że rozkład prędkości jest równomierny, czyli
prędkość w każdym przekroju jest stała, równa prędkości średniej w (patrz rys. 1a).
Zgodnie z zasadą ciągłości przepływu (będącą jedną z form powszechnie
obowiązującego w przyrodzie prawa zachowania masy) do każdego przekroju dopływa i
odpływa w jednostce czasu taka sama masa płynu. Obowiązuje więc, dla przekroju rurociągu
A 1 = π D 2 /4 i dla przekroju otworu kryzy A 2 = π d 2 /4 równanie ciągłości: q
ρ
ρ
m = A 1 1 w 1 = A 2 2 w 2
(1)
gdzie ρ 1, w1 – prędkość średnia i gęstość płynu w rurociągu przed kryzą, ρ 2, w2 – prędkość średnia i gęstość płynu w otworze kryzy. Dla płynów nieściśliwych ρ = const, wówczas
qv = A 1 w 1 = A 2 w 2
(2)
Drugie równanie wyprowadza się z zasady zachowania energii. Zgodnie z tą zasadą
wzrost energii kinetycznej (związanej z prędkością) może nastąpić tylko kosztem spadku
energii potencjalnej (ciśnienia). Zwiększeniu prędkości w okolicach kryzy towarzyszy więc
spadek ciśnienia w tej strefie, co wyraża równanie Bernoulliego:
ρ w 2
ρ w 2
1 + p =
2
(3)
1
+ p 2 = const
2
2
Rozwiązując układ równań (2) i (3) otrzymujemy
2
p
2
( 1 − 2)
w
(4)
2 =
2
ρ
A
1−
1
A 2
Zdefiniujmy jeszcze tzw. przewężenie zwężki β = d/D. Wówczas
2
A
d
2
2
=
= β
(5)
2
A
D
1
Uwzględniając jeszcze związki qv = A 2 w 2 oraz A2 = π d 2 /4 i oznaczając różnicę ciśnień p1 – p2 = ∆ p otrzymujemy uproszczony związek między strumieniem objętości a spadkiem ciśnienia na zwężce
1
π d 2 2 p
∆
q =
⋅
(6)
v
− β 4
4
1
ρ
Przy wyprowadzaniu powyższego wzoru przyjęto jednak szereg założeń upraszczających.
M.in. rozkład prędkości w otworze zwężki i rurociągu nie jest równomierny (płaski), a
wyostrzony (rys. 1b). Dla nierównomiernego rozkładu prędkości energia strumienia jest
większa niż dla płaskiego, tak więc równanie Bernoulliego nie opisuje zupełnie ściśle stanu
faktycznego.
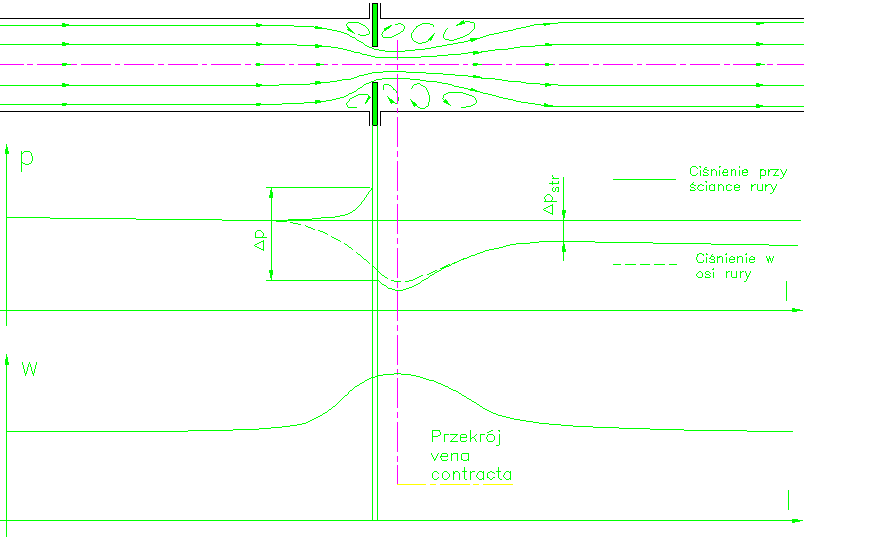
Ponadto najsilniejsze przewężenie strumienia nie występuje w samym otworze kryzy a
poza nią, ponadto przekrój strumienia w miejscu najsilniejszego przewężenia jest mniejszy
niż w otworze kryzy. Dzieje się tak dlatego, że elementy płynu, dopływając do kryzy, mają
pewną doosiową składową prędkości, która nie może zaniknąć od razu (patrz obraz linii prądu
na rys. 1 c). Przekrój o najsilniejszym przewężeniu nazywamy „vena contracta”.
Ani stopnia kontrakcji ani rzeczywistych profili prędkości nie da się jednak wyznaczyć z
taką dokładnością, aby na drodze teoretycznej skorygować wyprowadzony powyżej,
uproszczony wzór. Dlatego wpływ wymienionych czynników (oraz szeregu innych) ujmuje
się za pomocą jednego, sumarycznego, tzw. współczynnika przepływu C. Wzór (6) przybierze
wówczas postać
C
π d 2 2 p
∆
q =
⋅
(7)
v
− β 4
4
1
ρ
Współczynnik przepływu można wyznaczyć poprzez wzorcowanie szeregu podobnych
geometrycznie zwężek o różnych przewężeniach β. Wyznaczone wartości zależą jednak od
szeregu innych czynników, jak średnica rurociągu, prędkość przepływu czy lepkość płynu.
Dla wykorzystania w przyszłości tych wyników wzorcowań posługujemy się więc teorią
podobieństwa przepływów.
Wprowadźmy tzw. liczbę Reynoldsa, jedną z bezwymiarowych liczb podobieństwa
stosowanych w technice. Jest to stosunek występujących w przepływie sił bezwładności do sił
lepkości. Dla rurociągu o przekroju kołowym można ją obliczyć z wzoru:
w D
Re
1
= ν
(8)
3
gdzie ν - kinematyczny współczynnik lepkości płynu.
Zgodnie z teorią podobieństwa przepływów dla różnych rozpatrywanych przepływów,
przy podobnych geometrycznie powierzchniach opływanych, (czyli dla zwężek o takich
samych przewężeniach β) i dla takich samych wartości liczby Reynoldsa zachodzi
podobieństwo pól ciśnień i pól prędkości.
Podobieństwo pól prędkości zapewnia podobieństwo rozkładów prędkości i
podobieństwo linii prądu, co z kolei zapewnia taki sam stopień kontrakcji. Dzięki temu, przy
takich samych liczbach Reynoldsa taka sama będzie wartość współczynnika przepływu,
uwzględniającego wpływ tych zjawisk. Wystarczy więc wyznaczyć poprzez wzorcowanie
szeregu zwężek o różnych wartościach przewężenia β wartości współczynnika przepływu dla
różnych przewężeń w funkcji liczby Reynoldsa, aby móc później, wykorzystując wyniki tych
wzorcowań, obliczać zwężki dla innych średnic rurociągów czy innych płynów, niż
stosowane podczas tych badań.
Kolejne uproszczenie jakie wprowadzono powyżej, to założenie nieściśliwości płynu
(ρ = const). Dla gazów uproszczenie to może być źródłem znacznych błędów pomiaru.
Wskutek spadku ciśnienia w strefie zwężki wystąpi tu rozprężanie – zmniejszenie gęstości i
dodatkowe zwiększenie prędkości. Dla uwzględnienia tych zjawisk stosowany jest mnożnik
poprawkowy ∈, zwany liczbą ekspansji. Wyznacza się go eksperymentalnie poprzez
porównanie charakterystyk zwężki dla nieściśliwych cieczy z charakterystykami dla gazów.
Liczba ekspansji jest funkcją przewężenia β, wykładnika izentropy κ, oraz stosunku ∆ p/p:
∈ = f(β, κ, ∆ p/p)
(9)
Dla cieczy, które są praktycznie nieściśliwe, przyjmuje się ∈ = 1.
Po tym uściśleniu ostateczny wzór na strumień objętości ma postać
C ∈
π d 2 2 p
∆
q =
⋅
(10)
v
− β 4
4
1
ρ
2.2. Normalizacja zwężek
Uzyskanie wystarczająco obszernych wyników badań zależności C = f( Re, β) i ∈ = f(β, κ, ∆ p/p) umożliwia normalizację zwężek. Warunkiem jest jednak uzyskanie zgodności
wyników badań uzyskanych w różnych laboratoriach. W wyniku opracowania statystycznego
wyników tych badań zostaje sformułowana ostateczna postać zależności C = f( Re, β) i ∈ =
f(β, κ, ∆ p/p) a z analizy statystycznej tych wyników – niepewności wyznaczenia C i ∈.
Normalizacja zwężek umożliwia projektowanie przepływomierzy zwężkowych i
wyznaczanie ich charakterystyki obliczeniowo, tylko na podstawie znajomości parametrów
płynu i pomiarów geometrycznych zwężki. Eliminuje się więc konieczność indywidualnego
wzorcowania, często w ogóle niemożliwego, a zawsze kosztownego i pracochłonnego.
Polska Norma PN-EN ISO 5167:2005 dotycząca zwężkowych pomiarów parametrów
przepływu jest odpowiednikiem normy międzynarodowej, przyjętej powszechnie w Europie i
większości krajów świata.
Poza kryzami znormalizowane są dysze o płynnie ukształtowanym wlocie (rys. 2 a).
Należy je stosować tam, gdzie korozyjne lub korozyjne oddziaływanie płynu powodowałoby
szybkie stępienie krawędzi kryzy.
W przypadkach gdy niedopuszczalne są duże straty ciśnienia należy stosować oraz
zwężki o małych stratach ciśnienia – dysze Venturiego (rys. 2 b) i klasyczne zwężki
Venturiego (rys. 2 c). Dzięki łagodnemu rozszerzeniu strumienia przez stożkową część
4
rozbieżną mniejsze są szkodliwe straty energii potencjalnej (ciśnienia), przez co niezbędna
jest większa moc pomp/sprężarek.
Wartości C i ∈ wyznacza się z podanych w normie równań empirycznych. Np. dla
znormalizowanej kryzy współczynnik przepływu obliczamy z równania Reader-Harrisa
6
0,7
10 β
6
0,3
10
C = 0,5961+0,0261β2 - 0,216β8 + 0,000521
+ (0,0188+0,0063 A) β3,5
(11)
Re
Re
Liczbę ekspansji dla znormalizowanych kryz oblicza się z wzoru empirycznego
∆ p
∈ = 1 - (0,41+0,35 β4)
(12)
p
κ
1
2.3. Wyznaczenie parametrów płynu
Dla obliczenia strumienia płynu niezbędna jest znajomość gęstości i lepkości. Dla cieczy
korzystamy z danych tablicowych. W przypadku cieczy można pominąć wpływ ciśnienia na
te parametry, a jedynie uwzględnić wpływ temperatury. Dla gazów gęstość wyznaczamy z
wzoru
pT n
ρ = ρ n
(13 )
p TK
n
gdzie ρ n – gęstość gazu w warunkach normalnych, tj. Tn = 273.15 K, pn = 101.325 kPa (dla
powietrza ρ n = 1.2928 kg/m3); p i T – ciśnienie i temperatura absolutna przed zwężką, K –
względny współczynnik ściśliwości przy ciśnieniu p i temperaturze T (współczynnik
ściśliwości uwzględnia odchylenia właściwości gazu rzeczywistego od właściwości gazu
doskonałego).
Jeżeli gaz jest wilgotny to wzór (16) trzeba zmodyfikować do postaci
( p −ϕ p T
p ) n
ρ = ρ
+ ϕρ
n
p , s
(15 )
p TK
n
gdzie ϕ - wilgotność względna, pp – ciśnienie pary wodnej w temperaturze T, ρ p,s – gęstość
pary wodnej nasyconej w temperaturze T.
Niezbędną do obliczenia liczby Reynoldsa wartość lepkości oblicza się dla gazów z wzoru
C
1+ 27 .315
T
η =η0
C
273 1
. 5
(16 )
1+ T
gdzie C – stała Sutherlanda (dla powietrza C = 112 K), η 0 – lepkość gazu w warunkach
normalnych (dla powietrza η 0 = 17.1·10-6 kg/m·s).
5
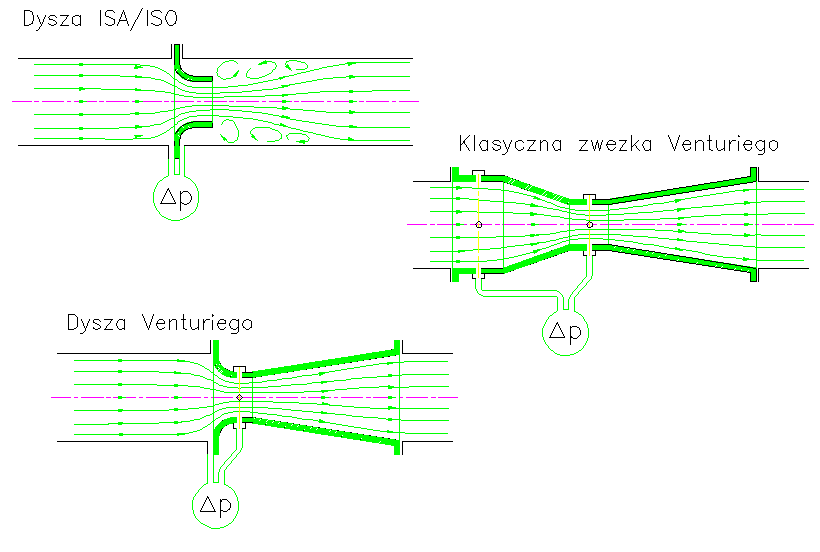
Rys. 2. Inne zwężki znormalizowane i linie prądu przy przepływie
przez te zwężki.
Rys. 1. Przepływ płynu przez kryzę: a) model uproszczony do wypro-
wadzenia wzoru, rzeczywiste profile prędkości i obraz linii prądu przy
przepływie przez kryzę.
2.4. Analiza niepewności zwężkowego pomiaru strumienia płynu
Pomiar strumienia płynu za pomocą zwężki jest pomiarem pośrednim, tj. wartość
strumienia płynu uzyskiwana jest drogą pośrednią, poprzez wstawienie do wzoru (11)
wartości innych wielkości, mierzonych bądź bezpośrednio (np. ∆ p), bądź także pośrednio; np.
gęstość ρ obliczana jest pośrednio, z zależności (14) lub (15).
Z wykładów Podstaw Metrologii wiadomo, że niepewność pomiaru można obliczyć jako
pierwiastek z sumy kwadratów niepewności cząstkowych, będących iloczynami niepewności
danej wielkości przez tzw. współczynnik wrażliwości. Dla pomiaru zwężkowego wzór na
niepewność pomiaru strumienia płynu ma postać
2
2
U ( q =
+
∈ +
+
+
∆ +
(17)
v )
2
2
1
1
2
u ( C) u ( )
β 4
2
2
u D
u d
u
p
u
4
( )
2
4
( )
2 ( )
2 (ρ)
1− β
1− β
4
4
Najczęściej przyjmuje się podawanie wyniku pomiaru przy poziomie ufności 0.95, tak
więc wszystkie niepewności występujące w powyższym wzorze to niepewności tzw.
„dwusigmowe”, czyli ze współczynnikiem rozszerzenia równym k = 2.
Założono też, że wszystkie błędy systematyczne pomiarów zostały wyeliminowane.
2.5. Najistotniejsze niepewności pomiaru zwężkowego
Jak wiadomo z wykładu Podstawy Metrologii niepewności najogólniej można podzielić na
dwie grupy: niepewności typu A – obliczane metodami statystycznymi i niepewności typu B
– wyznaczane innymi metodami. W trakcie ćwiczenia będą stosowane obie metody.
2.5.1. Niepewność wyznaczenia współczynnika przepływu u( C)
Niepewność u( C) wynosi dla kryzy
0.6% dla β < 0.6 lub β (%) dla 0.6 < β < 0.75.
Informacje o tej niepewności są zaczerpnięte z normy [1], i pomimo, że przez autorów
normy były wyznaczone metodami statystycznymi, to z punktu widzenia użytkownika normy
są to niepewności typu B.
2.5.2. Niepewność wyznaczenia liczby ekspansji
Dla kryzy niepewność ta, wg normy [1] wynosi
p
∆
u( )
∈ = 4
(%)
p
Podobnie jak dla niepewności współczynnika przepływu jest to niepewność typu B.
2.5.3. Niepewność pomiaru parametrów geometrycznych zwężki i rurociągu
Metody pomiaru parametrów geometrycznych takich jak np. średnica otworu zostały
zmierzone w laboratorium pomiarów wielkości geometrycznych Instytutu. Niepewności u( D)
i u( d) obliczone w trakcie tych pomiarów poda prowadzący ćwiczenie, w zależności od tego,
jaki rurociąg i kryza będą wykorzystane w trakcie ćwiczenia. Należy je traktować jako
niepewności typu B, chociaż wykonujący pomiary prawdopodobnie stosował metody
statystyczne do oszacowania tych niepewności.
2.5.4. Niepewność pomiaru ciśnienia różnicowego
7
Niepewność pomiaru ciśnienia różnicowego u(∆ p) na zwężce wyznaczyć można poprzez
wykonanie serii pomiarów (co najmniej 10) tej wielkości. Będzie to więc niepewność typu
A, czyli wyznaczana metodami statystycznymi.
2.5.5. Niepewność pomiaru ciśnienia w rurociągu
Także ta niepewność u( p) będzie wyznaczona poprzez wykonanie serii pomiarów (co
najmniej 10). Będzie to więc także niepewność typu A.
2.5.6. Niepewność pomiaru temperatury
Temperatura będzie mierzona za pomocą czujnika Pt 100 (platynowy rezystor o rezystancji
100 Ω w temperaturze 0 °C). Współpracuje on z przetwornikiem przekształcający zmiany
rezystancji na sygnał cyfrowy temperatury. W świadectwie wzorcowania podano jego
niepewność ze współczynnikiem rozszerzenia k = 2. Jest to także niepewność typu B.
2.5.7. Niepewność wyznaczenia gęstości
Gęstość gazu suchego obliczamy z wzoru (14). Jest to wiec też pomiar pośredni,
niepewność obliczenia gęstości można wyznaczyć z wzoru
u(ρ )
2
= u (ρ +
+
+
n )
2
u ( p)
2
u ( T )
2
u ( K )
Niepewność gęstości w warunkach normalnych z danych tablicowych (a więc typu B)
u(ρ n) = 0.002 kg/m3.
Niepewność względna współczynnika ściśliwości (typu B, wyznaczanego w trakcie
obliczeń z wzoru Redlicha – Kwonga) wynosi u( K) = 20(1 – K) %.
Należy pamiętać, że p - ciśnienie absolutne w rurociągu - wyznacza się czasem (o ile nie
ma do dyspozycji przetwornika ciśnienia absolutnego) pośrednio, jako sumę ciśnienia
atmosferycznego pb i zmierzonego nadciśnienia w rurociągu.
Uwzględniając dodatkowe czynniki występujące we wzorze (15), tj. ϕ, pp i ρ p,s , można też
uwzględnić niepewność obliczenia gęstości gazu wilgotnego.
3. Opis stanowiska
W ćwiczeniu wykorzystuje się niskociśnieniowe stanowisko powietrzne. Składa się ono z
wentylatora wymuszającego przepływ, zaworu do regulacji przepływu, zestawu gazomierzy
kontrolnych (w ćwiczeniu nie będą one wykorzystywane), komory filtrów chroniących
gazomierze kontrolne oraz z ciągu przepływomierza sprawdzanego, w którym będzie
zamontowany rurociąg z kryzą, stosowaną do pomiaru w niniejszym ćwiczeniu.
Do pomiaru ciśnienia absolutnego i ciśnienia różnicowego zastosowane zostaną
inteligentne przetworniki firmy Rosemount. Do pomiaru temperatury zastosowano platynowy
czujnik rezystancyjny Pt100 z przetwornikiem Rosemount.
4. Wykonanie ćwiczenia
Wstępne dane o instalacji i badanym płynie będą podane na ćwiczeniach przez
prowadzącego zajęcia. Dane te należy zamieścić w otrzymanym protokole.
Następnie należy wykonać pomiary parametrów otoczenia, tj. ciśnienia atmosferycznego,
temperatury i wilgotności, określając przy tym niepewności pomiarów tych wielkości na
podstawie oznaczeń na podzielni lub świadectw przyrządów.
Kolejna czynność to sprawdzenie długości prostych odcinków pomiarowych przed i za
zwężką i porównanie ich z wymaganiami normy [1].
8
Następnie, po uruchomieniu wentylatora wymuszającego przepływ w rurociągu należy
dokonać serii pomiarów nadciśnienia (lub ciśnienia absolutnego) w rurociągu, ciśnienia
różnicowego i temperatury. Wyniki zapisać w otrzymanym formularzu protokołu.
5. Opracowanie wyników pomiarów
Po wykonaniu części pomiarowej należy wykonać obliczenia za pomocą odpowiedniego
komputerowego arkusza kalkulacyjnego. Program umożliwia śledzenie toku obliczeń i
wyników posrednich, oblicza też, poza strumieniem płynu, niepewności pomiaru
spowodowane rożnymi czynnikami i niepewność złożoną.
Jeżeli jest możliwość porównania wyniku pomiaru za pomocą zwężki z wynikiem pomiaru
wykonanym innym przepływomierzem (zainstalowanym szeregowo) to należy sprawdzić czy
wyniki te są zgodne (w granicach niepewności obu przepływomierzy)
6. Treść sprawozdania
W sprawozdaniu należy zamieścić:
1. Schemat instalacji pomiarowej
2. Protokół pomiarów
3. Wyniki obliczeń
4. Analizę niepewności wykonana na podstawie wyliczonych wartości niepewności poszcze-
gólnych parametrów i niepewności złożonej. Analiza powinna obejmować ocenę, które ze
źródeł błędów są najistotniejsze, a wiec jakie czynności należy podjąć aby efektywnie
podwyższyć dokładność pomiaru. Ponadto należy dokonać oceny, które niepewności (lub
ich grupa) są pomijalnie małe.
6. Jeżeli jest możliwość porównania wyniku pomiaru za pomocą zwężki z wynikiem pomiaru
wykonanym innym przepływomierzem (zainstalowanym szeregowo) to należy sprawdzić
czy wyniki te są zgodne (w granicach niepewności obu przepływomierzy)
7. Zasady opracowywania oraz kryteria oceny sprawozdań z ćwiczeń laboratoryjnych
wykonywanych w Laboratorium Przepływów IMiSP
Zasady ogólne
Należy przestrzegać zapisów instrukcji do ćwiczeń. W każdej instrukcji (zwykle w
końcowej części) podano, co ma zawierać sprawozdanie. Poniżej podano bliższą interpretację
poszczególnych pozycji sprawozdania. Interpretacja ta jest podstawą do oceny sprawozdania.
Opis przeprowadzonych badań (przebieg ćwiczenia) oraz schemat stanowiska
Te dwa punkty sprawozdania łącznie powinny być opracowane tak, aby na ich podstawie
eksperyment będący przedmiotem ćwiczenia można było odtworzyć w dowolnym innym
laboratorium na świecie.
Zdarzały się przypadki, że odkrycia warte nagrody Nobla (np. wykrycie antygrawitacji)
wskutek złego udokumentowania nie mogły być zweryfikowane w innych laboratoriach, a w
takich przypadkach wyniki badań uznaje się za niewiarygodne. Podczas pracy w laboratorium
należy więc opanować zasady właściwego opracowywania wyników badań. Jest to istotny
element oceny sprawozdania.
Szczególnie starannie należy wykonać schemat stanowiska. Czy schemat ten będzie w
formie bardziej realistycznej czy bardziej umownej, symbolicznej, nie ma to większego
znaczenia. Ważne, żeby były na nim wszystkie istotne z punktu widzenia określonego
badania urządzenia, aparatura pomiarowa i pomocnicza, połączone logicznie w całość.
Wszystkie elementy schematu należy opisać w legendzie podając conajmniej typ
urządzenia, producenta, zakres pomiarowy i niepewności wskazań. Jeśli jest dostępne
9
świadectwo legalizacji, wzorcowania lub uwierzytelnienia – podać jego numer i kto je
sporządził.
Jeżeli istotne dla badanych zjawisk są wymiary geometryczne należy je też podać (np.
średnica i długość rurociągu, w którym zainstalowany jest badany przepływomierz).
Fotografia stanowiska lub/i jego fragmentów może być pożytecznym elementem
uzupełniającym, nie może jednak zastąpić schematu.
Opracowanie wyników badań
Należy załączyć wyniki pomiarów wykonywanych bezpośrednio, wyniki obliczeń
pośrednich i wyniki końcowe. Bardzo ważna jest analiza niepewności lub analiza błędów.
Jeśli tylko jest to możliwe, wyniki końcowe należy przedstawiać w postaci graficznej (np.
charakterystyka badanego przyrządu, krzywa błędów). Przy opracowywaniu wykresów
należy dobrze dopracować opis osi – standardowe wykresy generowane np. przez MSExcel
zwykle nie są zadowalające.
Wnioski
Czasem instrukcja zawiera wskazówki jakie najważniejsze elementy należy przeanalizować i
ująć we wnioskach. Jeśli nie, to należy posłużyć się własną dociekliwością i zmysłem
krytycznym. Wnioski są zwykle dobrym materiałem dla sprawdzenia i oceny, czy ćwiczenie
było wykonywane świadomie i ze zrozumieniem badanych zjawisk, czy mechanicznie, bez
zaangażowania potencjału intelektualnego.
Bibliografia:
[1] PN-ISO 5167:2005. Pomiar strumienia płynu za pomocą zwężek
[2] Turkowski M. Przemysłowe sensory i przetworniki pomiarowe, OWPW, Warszawa, 2002
10
Wyszukiwarka
Podobne podstrony:
PEM 1 cwiczenie 5 protokół
PEM-1 cwiczenie 5 protokół
PEM 1 cwiczenie 3 id 354576 Nieznany
PEM 1 cwiczenie 6 id 354582 Nieznany
PEM 1 cwiczenie 6 protok%c3%b3%c5%82
PEM-1 cwiczenie 3 protokół
PEM-1 cwiczenie 4 protokół
PEM 1 cwiczenie 5 id 354580 Nieznany
PEM 1 cwiczenie 4 protokół
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
PEM 1
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
więcej podobnych podstron