WM

Z5/14. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 14

1

Z5/14. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH –

ZADANIE 14

Z5/14.1. Zadanie 14

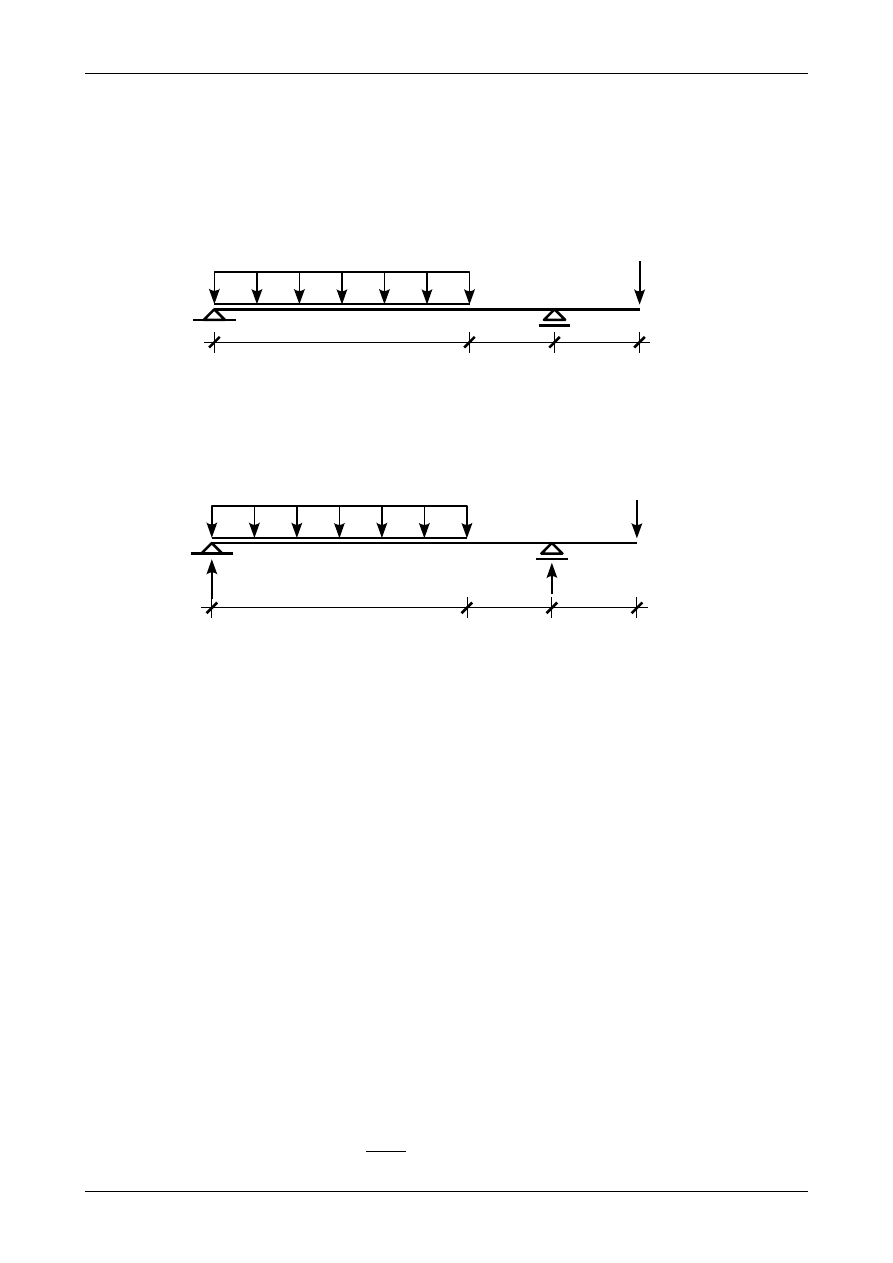
Narysować metodą punktów szczególnych wykresy sił przekrojowych dla belki przedstawionej na

rysunku Z5/14.1. Wymiary belki podane są w metrach.

A

B

C

D

18,0 kN

27,0 kN/m

6,0

2,0

2,0

[m]

Rys. Z5/14.1. Belka prosta

Analiza kinematyczna belki przedstawionej na rysunku Z5/14.1 znajduje się w zadaniu 13. Zgodnie

z tamtym zadaniem rysunek Z5/14.2 przedstawia wartości i zwroty reakcji podporowych.

A

B

C

D

18,0 kN

27,0 kN/m

6,0

2,0

2,0

[m]

96,75 kN

83,25 kN

Rys. Z5/14.2. Prawidłowe wartości i zwroty reakcji w belce prostej

Z5/14.2. Wykres siły poprzecznej

Zgodnie z rozdziałem 5 w przedziale AB siła poprzeczna będzie funkcją liniową natomiast w pozos-

tałych przedziałach będzie miała wartość stałą. Pionowe reakcje na podporach A i C będą powodowały skok
siły poprzecznej o wartości bezwzględnej równej danej reakcji.

Rysowanie wykresu siły poprzecznej zaczniemy od punktu A. W punkcie tym działa reakcja o war-

tości 96,75 kN do góry. Siła poprzeczna w tym punkcie wynosi więc

T

A

=

96,75 kN

.

(Z5/14.1)

W przedziale AB działa obciążenie ciągłe równomiernie rozłożone o wartości 27,0 kN/m w dół więc

siła poprzeczna w tym przedziale będzie liniowo opadać a w punkcie B tego przedziału wynosi

T

B



L



=

96,75−27,0⋅6,0=−65,25 kN

.

(Z5/14.2)

Jak widać siła poprzeczna na obu końcach przedziału AB ma wartości przeciwnych znaków. W przedziale
tym będzie ona miała więc miejsce zerowe. Zgodnie ze wzorem (5.127) jego odległość od punktu A wynosi

x

L

=

96,75

27,0

=

3,583 m

(Z5/14.3)

Dr inż. Janusz Dębiński

WM

Z5/14. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 14

2

natomiast od punktu B, zgodnie ze wzorem (5.128) miejsce zerowe znajduje się w odległości

x

P

=

65,25

27,0

=

2,417 m

.

(Z5/14.4)

W punkcie B nie działa żadna siła skupiona więc wartość siły poprzecznej z prawej strony punktu

B wynosi

T

B



P



=−

65,25 kN

.

(Z5/14.5)

W przedziale BC nie działa żadne obciążenie ciągłe więc siła poprzeczna ma w całym przedziale oraz

z lewej strony punktu C wartość stałą równą

T

BC

=

T

C



L



=−

65,25 kN

.

(Z5/14.6)

W punkcie C działa reakcja o wartości 83,25 kN w górę. Wartość siły poprzecznej z prawej strony

punktu C wynosi więc

T

C



P



=−

65,2583,25=18,0 kN

.

(Z5/14.7)

W przedziale CD nie działa żadne obciążenie ciągłe więc siła poprzeczna ma w całym przedziale oraz

w punkcie D wartość stałą równą

T

CD

=

T

D

=

18,0 kN

.

(Z5/14.8)

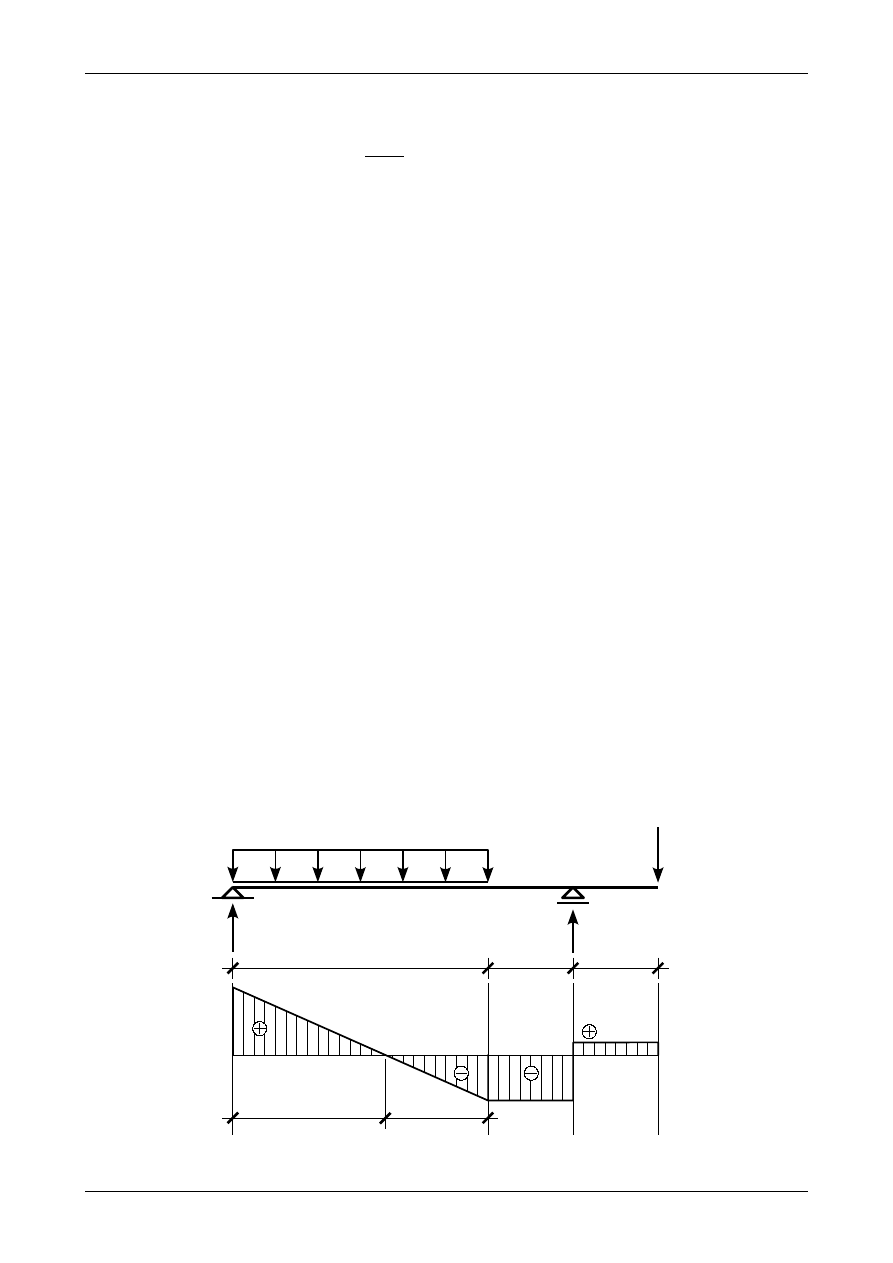
Rysunek Z5/14.3 przedstawia ostateczną postać wykresu siły poprzecznej w całej belce prostej

wyznaczonego metodą punktów charakterystycznych.

A

B

C

D

18,0 kN

27,0 kN/m

2,0

2,0

[m]

96,75 kN

83,25 kN

T(x) [kN]

6,0

96

,75

65,25

18,0

3,583

2,417

Rys. Z5/14.3. Wykres siły poprzecznej w belce prostej

Dr inż. Janusz Dębiński

WM

Z5/14. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 14

3

Z5/14.3. Wykres momentu zginającego

Zgodnie z rozdziałem 5 w przedziale AB moment zginający będzie funkcją kwadratową natomiast

w pozostałych przedziałach będzie funkcją liniową. Wykres momentu będzie w całej belce ciągły. W dalszej
części, przy obliczaniu wartości momentu zginającego w punktach charakterystycznych, siły, które kręcą
zgodnie z założonym momentem zginającym będziemy zapisywać z minusem, siły które kręcą przeciwnie
z plusem.

A

27,0 kN/m

6,0

96,75 kN

[m]

M

B

(L)

A

96,75 kN

M

A

a)

b)

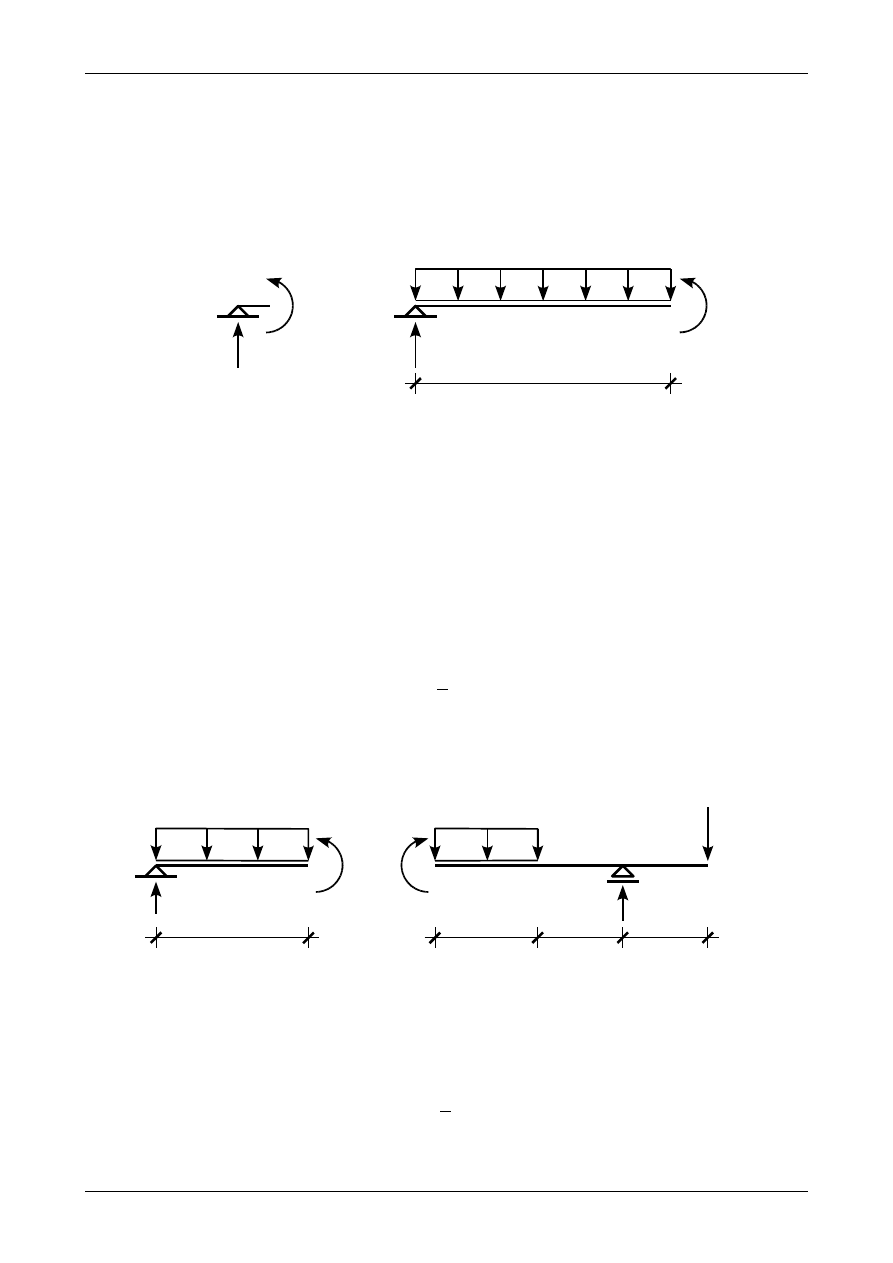
Rys. Z5/14.4. Momenty zginające na obu końcach przedziału AB

Rysunek Z5/14.4 a) przedstawia moment zginający w punkcie A. Zgodnie z tym rysunkiem moment

ten ma wartość

M

A

=

0,0kNm

.

(Z5/14.9)

Rysunek Z5/14.4 b) przedstawia moment zginający w punkcie B z lewej strony. Zgodnie z tym

rysunkiem moment ten ma wartość

M

B



L



=

96,75⋅6,0−27,0⋅6,0⋅

1
2

⋅

6,0=94,5 kNm

.

(Z5/14.10)

Znak plus oznacza, że rozciąga on dolną część belki.

B

C

D

18,0 kN

2,0

2,0

[m]

83,25 kN

2,417

27,0 kN/m

A

27,0 kN/m

3,583

96,75 kN

M

1

M

1

a)

b)

Rys. Z5/14.5. Ekstremalny moment zginający w przedziale AB

Rysunek Z5/14.5 przedstawia ekstremalny moment zginający w przedziale AB. Zgodnie z rysunkiem

Z5/14.5 a) wynosi on

M

1

=

96,75⋅3,583−27,0⋅3,583⋅

1
2

⋅

3,583=173,3 kNm

(Z5/14.11)

Zgodnie z rysunkiem Z5/14.5 b) wynosi on

Dr inż. Janusz Dębiński

WM

Z5/14. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 14

4

M

1

=

83,25⋅



2,02,417



−

18,0⋅



4,02,417



−

27,0⋅2,417⋅

1
2

⋅

2,417=173,3 kNm

.

(Z5/14.12)

Jak widać ekstremalne momenty zginające w przedziale AB obliczone dla lewej i prawej części belki są
takie same. Znak plus oznacza, że rozciąga on dolną część belki.

C

D

18,0 kN

2,0

[m]

83,25 kN

2,0

M

B

(P)

C

D

18,0 kN

2,0

[m]

83,25 kN

M

C

(L)

a)

b)

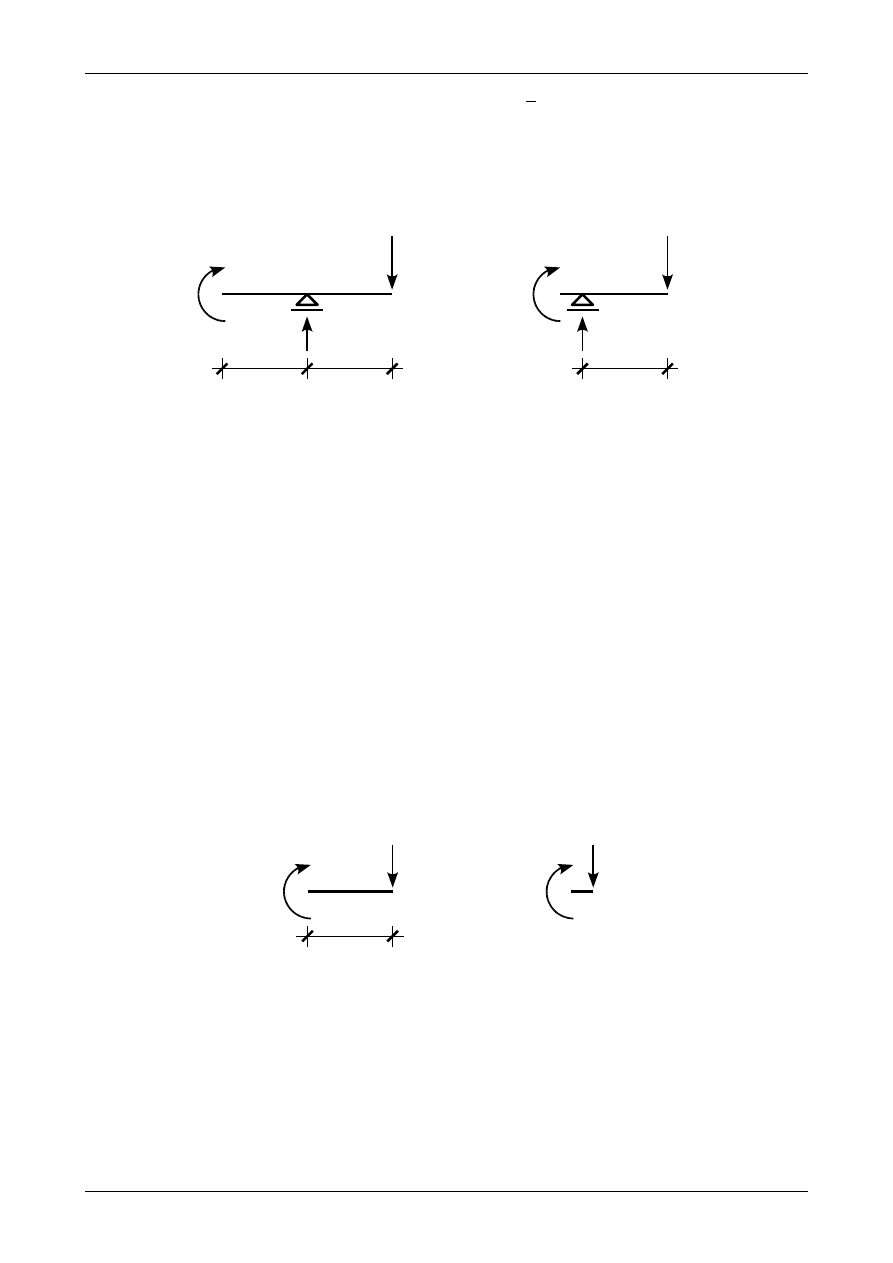
Rys. Z5/14.6. Momenty zginające na na obu końcach przedziału BC

Rysunek Z5/14.6 a) przedstawia moment zginający w punkcie B z prawej strony tego punktu. Zgodnie

z tym rysunkiem moment ten ma wartość

M

B



P



=

83,25⋅2,0−18,0⋅4,0=94,5 kNm

.

(Z5/14.13)

Moment ten jest równy momentowi wyznaczonemu ze wzoru (Z5/14.10). Znak plus oznacza, że rozciąga on
dolną część belki.

Rysunek Z5/14.6 b) przedstawia moment zginający w punkcie C z lewej strony tego punktu. Zgodnie

z tym rysunkiem moment ten ma wartość

M

C



L



=−

18,0⋅2,0=−36,0 kNm

.

(Z5/14.14)

Znak minus oznacza, że rozciąga on górną część belki.

D

2,0

18,0 kN

[m]

M

C

(P)

D

18,0 kN

M

D

a)

b)

Rys. Z5/14.7. Momenty zginające na na obu końcach przedziału CD

Rysunek Z5/14.7 a) przedstawia moment zginający w punkcie C z prawej strony tego punktu. Zgodnie

z tym rysunkiem moment ten ma wartość

M

C



P



=−

18,0⋅2,0=−36,0 kNm

.

(Z5/14.15)

Moment ten jest równy momentowi wyznaczonemu ze wzoru (Z5/14.14). Znak minus oznacza, że rozciąga
on górną część belki.

Dr inż. Janusz Dębiński

WM

Z5/14. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 14

5

Rysunek Z5/14.7 b) przedstawia moment zginający w punkcie D. Zgodnie z tym rysunkiem moment

ten ma wartość

M

D

=

0,0 kNm

.

(Z5/14.16)

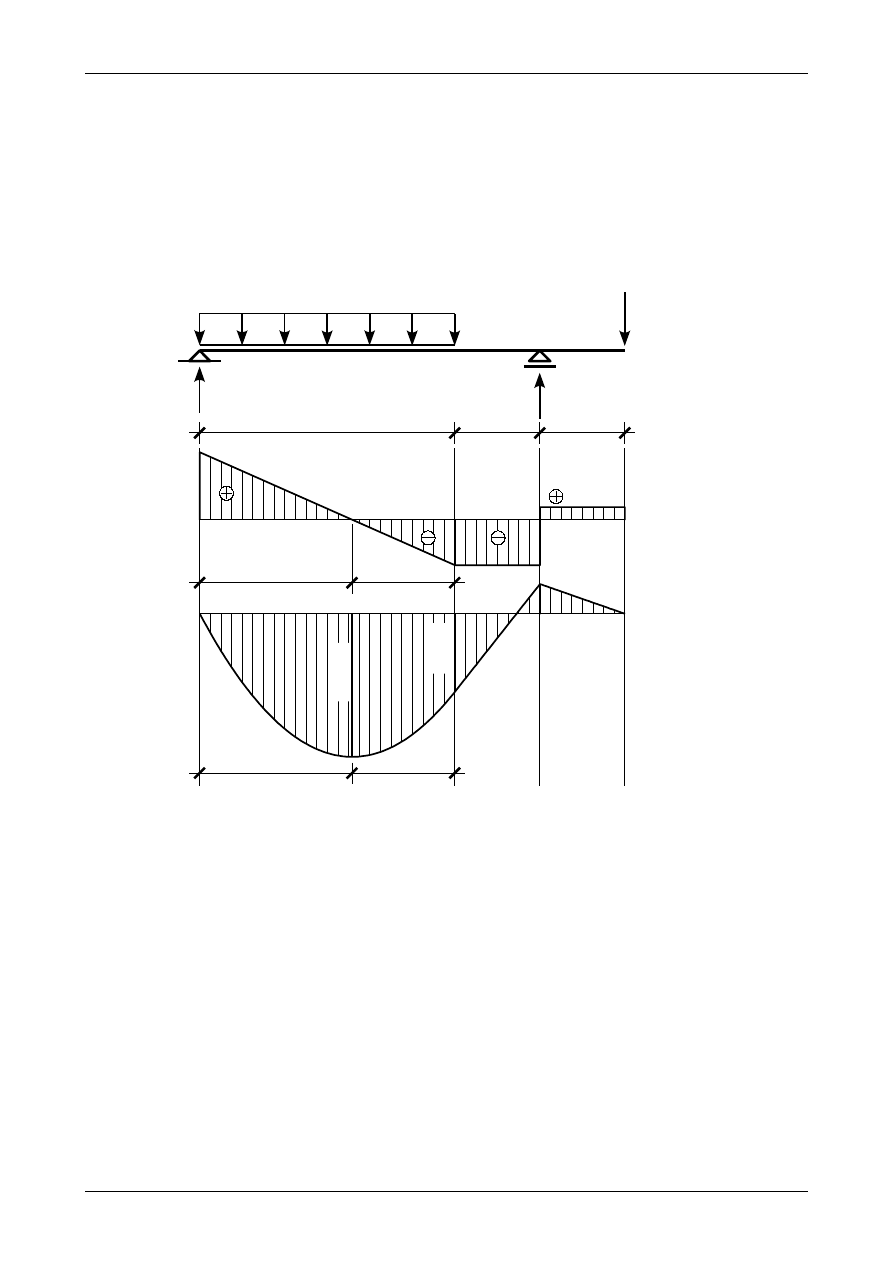
Rysunek Z5/14.8 przedstawia ostateczne wykresy siły poprzecznej i momentu zginającego w belce

prostej wyznaczone metodą punktów charakterystycznych.

A

B

C

D

18,0 kN

27,0 kN/m

2,0

2,0

[m]

96,75 kN

83,25 kN

T(x) [kN]

M(x) [kNm]

6,0

96

,75

65,25

18,0

0,

0

94

,5

36

,0

0,

0

3,583

2,417

3,583

2,417

17

3,3

Rys. Z5/14.8. Ostateczne wykresy siły poprzecznej i momentu zginającego wyznaczone metodą punktów

charakterystycznych

Dr inż. Janusz Dębiński