Matematyka Dyskretna

Andrzej Szepietowski

25 czerwca 2002 roku

Rozdział 1

Teoria liczb

1.1

Dzielenie całkowitoliczbowe

Zacznijmy od przypomnienia szkolnego algorytmu dzielenia liczb naturalnych. Podziel-
my 1743 przez 12.

1

4

5

1

7

4

3

:

1

2

1

2
5

4

4

8
6

3

6

0
3

W wyniku dzielenia otrzymali´smy iloraz 145 i reszt˛e 3. Liczby te spełniaj ˛

a równanie

i reszta jest mniejsza od dzielnika. Podobnie mo˙zemy post ˛

api ´c dla dowolnych liczb natu-

ralnych

i

pod warunkiem, ˙ze

.

Twierdzenie 1.1 Dla dowolnych liczb naturalnych

oraz

istnieje dokładnie jedna

para liczb naturalnych

i

spełniaj ˛

acych warunki:

!

#"$

nazywa si˛e ilorazem całkowitoliczbowym

przez

, a

nazywa si˛e reszt¸a z dzielenia

Zauwa˙zmy, ˙ze iloraz

jest zaokr¸agleniem w dół normalnego ilorazu

&%

(')+*

. Iloraz

całkowitoliczbowy liczb

i

b¸edziemy oznacza´c przez

-,.

/10(2

43651789

3

4

Rozdział 1. Teoria liczb

a reszt˛e przez

63

9

Przykład 1.2

)

,

!

oraz

)

63

!

, poniewa˙z

-.

oraz

$

"

.

W przypadku, gdy

i

s ˛

a liczbami całkowitymi iloraz i ró˙znice mo˙zna róznie definiowa ´c.

Na przykład w j¸ezyku Pascal iloraz dwóch liczb typu całkowitego oznacza si¸e przez

a div b

i jest to

%

6')+*

— zaokr¸aglenie ilorazu

6')

w dół, gdy

6')

jest dodatnie i

(')

, —

zaokr¸aglenie ilorazu

('

w gór¸e, gdy

(')

jest ujemne. Reszta, któr¸a oznacza si¸e przez

a mod b,

jest okre´slona wzorem:

a mod b = a-(a div b)*b.

Mamy wi¸ec, na przykład:

22 div 4 = 5; (-22)div 4 = -5; 22 div(-4)= -5; (-22)div(-4)= 5;

22 mod 4 = 2; (-22)mod 4 = -2; 22 mod(-4)= 2; (-22)mod(-4)= -2.

1.2

Podzielno´s´c liczb

Mówimy, ˙ze liczba całkowita

dzieli liczb¸e całkowit¸a

, je˙zeli istnieje liczba całko-

wita

, taka ˙ze:

9

B¸edziemy to oznacza´c przez

. Zauwa˙zmy, ˙ze zachodzi wtedy:

63

9

Liczb¸e

nazywamy dzielnikiem liczby

.

Przykład 1.3

,

oraz

.

Lemat 1.4 Je˙zeli

oraz

, to

oraz

Dowód. Je˙zeli

i

, to istniej¸a dwie liczby całkowite

i

, takie ˙ze:

oraz

9

Mamy wi¸ec:

oraz

czyli

dzieli

oraz

.

1.3. Relacja kongruencji

5

1.3

Relacja kongruencji

Niech

b¸edzie dowoln¸a liczb¸a naturaln¸a

. Powiemy, ˙ze dwie liczby całkowite

i

s¸a równowa˙zne (lub przystaj¸a) modulo

, je˙zeli

9

B¸edziemy wtedy pisa´c:

63

9

Przykład 1.5

63

,

63

,

63

,

63

.

Je˙zeli

i

s ˛

a dodatnie, to

63

wtedy i tylko wtedy, gdy

i

maj ˛

a takie

same reszty z dzielenia przez

.

Lemat 1.6 Relacja przystawania modulo jest relacj¸a równowa˙zno´sci, czyli spełnia nast¸epuj¸ace
trzy warunki:

zwrotno´

s´

c, dla ka˙zdego

zachodzi

63

,

symetri¸e, dla ka˙zdego

i

, je˙zeli

63

to

63

,

przechodnio´

s´

c, dla ka˙zdego

,

i

,

je˙zeli

63

i

63

to

63

.

Dowód. Udowodnimy tylko przechodnio´s´c relacji. Je˙zeli

oraz

to

czyli

.

Ponadto relacja modulo jest zgodna z dodawaniem, odejmowaniem i mno˙zeniem.

Twierdzenie 1.7 Je˙zeli

3

oraz

3

to:

63

3

63

9

Dowód. Z zało˙zenia mamy:

z tego za´s łatwo wynika, ˙ze

dzieli:

oraz

!

czyli zachodzi teza twierdzenia.

Przykład 1.8 Twierdzenie 1.7 mo˙ze by´c u˙zyte do obliczania reszty z dzielenia Je˙zeli chce-
my policzy´c na przykład

63

6

Rozdział 1. Teoria liczb

to pytamy, która z trzech liczb

przystaje do 1999 modulo 3. Zróbmy najpierw

kilka prostych obserwacji. Po pierwsze:

63

bo

. Z twierdzenia 1.7 wynika, ˙ze ka˙zda pot¸ega liczby dziesi¸e´c przystaje do 1

modulo 3, czyli:

3

dla ka˙zdego

. Mamy teraz:

)8

)84

63

9

Podobnie, dla dowolnej liczby

, je˙zeli zapiszemy

w postaci dziesi¸etnej:

to

63

czyli

ma takie same reszty modulo 3 co suma cyfr w zapisie dziesi¸etnym.

Przykład 1.9 Aby przekona´c si˛e, ˙ze

)8

(

wystarczy zauwa˙zy´c, ˙ze liczba

jest parzysta, wi˛ec tak˙ze wynik mno˙zenia powinien

by˙z parzysty. Mówi ˛

ac inaczej

)

63

oraz

63

, wi˛ec na

podstawie twierdzenia 1.7 mamy

63

, a liczba

(

przystaje

do jedynki modulo 2. Podobnie mo˙zemy si˛e przekona´c, ˙ze

)8

(

wystarczy zauwa˙zy´c, ˙ze w iloczynie

)#

ostatni ˛

a cyfr ˛

a powinno by´c 8 a nie 6.

Inaczej

63

oraz

3

, wi˛ec na podstawie twierdze-

nia 1.7 mamy

.

63

, a liczba

)

przystaje do 6 modulo

10.

1.4

Klasy abstrakcji

Dla relacji przystawania modulo

definiujemy klasy abstrakcji. Dla dowolnej liczby

całkowitej

, klas¸e abstrakcji elementu

definiujemy w nast¸epuj¸acy sposób:

3

9

Innymi słowy, klasa abstrakcji liczby

to zbiór wszystkich liczb z ni¸a równowa˙znych.

Przykład 1.10 Dla

mamy trzy klasy abstrakcji

1.5. Pier´scie´n

7

9

99

9

99

99

9

9

99

99

9

)

9

99

Zauwa˙zmy, ˙ze klasy abstrakcji elementów równowa˙znych pokrywaj¸a si¸e.

Lemat 1.11 Je˙zeli

63

to

.

Dowód. Je˙zeli

to

63

i z przechodnio´sci relacji

63

, czyli:

a wi¸ec pokazali´smy, ˙ze:

9

Identycznie pokazujemy zawieranie odwrotne

.

Nast¸epna wa˙zna własno´s´c klas abstrakcji to ich rozł¸aczno´s´c.

Lemat 1.12 Je˙zeli

to

,

inaczej, dwie klasy abstrakcji

i

albo s¸a identyczne, albo s¸a rozł¸aczne.

Dowód. Przypu´s´cmy, ˙ze klasy

i

maj¸a wspólny element

. Wtedy:

63

63

9

Z przechodnio´sci mamy wtedy

63

, a z lematu 1.11

.

1.5

Pier´scie ´n

Klasy abstrakcji relacji modulo

wygl¸adaj¸a nast¸epuj¸aco:

99

9

9

Dla dowolnego

z przedziału

#

, klasa

jest postaci:

(

oznacza zbiór liczb całkowitych). Zbiór klas abstrakcji modulo

oznacza si¸e przez

.

Poniewa˙z relacja modulo jest zgodna z działaniami dodawania i mno˙zenia, mo˙zemy

zdefiniowa´c dodawanie i mno˙zenie na klasach abstrakcji. Mówi¸ac w skrócie, aby wyko-
na´c działanie na dwóch klasach abstrakcji, wybieramy dowolnych przedstawicieli tych

8

Rozdział 1. Teoria liczb

klas i wykonujemy działania na tych przedstawicielach. Dokładniej, dodawanie klas abs-
trakcji definiujemy nast¸epuj¸aco:

9

Podobnie definiujemy odejmowanie i mno˙zenie:

9

Poni˙zszy lemat pokazuje, ˙ze działania te s¸a dobrze zdefiniowane; ˙ze wynik działania na
dwóch klasach nie zale˙zy od wyboru reprezentantów.

Lemat 1.13 Je˙zeli

oraz

to:

9

Dowód. Z zało˙zenia mamy:

63

63

9

a z twierdzenia 1.7:

oraz

9

Przykład 1.14 Niech

. Dla dowolnych dwóch liczb

i

ich suma

nale˙zy do

a iloczyn do

)

.

Lemat 1.15 Działania na klasach abstrakcji

9

99

spełniaj¸a nast¸epuj¸ace warunki:

dodawanie oraz mno˙zenie s¸a przemienne i ł¸aczne,

klasa

jest elementem neutralnym dodawania, to znaczy dla ka˙zdego

mamy

,

dla ka˙zdej klasy

istnieje klasa do niej przeciwna

8

, taka ˙ze

8

,

klasa

jest elementem neutralnym mno˙zenia, to znaczy dla dowolnego

mamy

,

mno˙zenie jest rozdzielne wzgl¸edem dodawania, czyli dla ka˙zdych trzech klas

,

,

mamy

.

Zbiór z dwoma działaniami spełniaj¸acymi powy˙zsze warunki nazywa si¸e pier´scieniem
przemiennym z jedynk¸a.

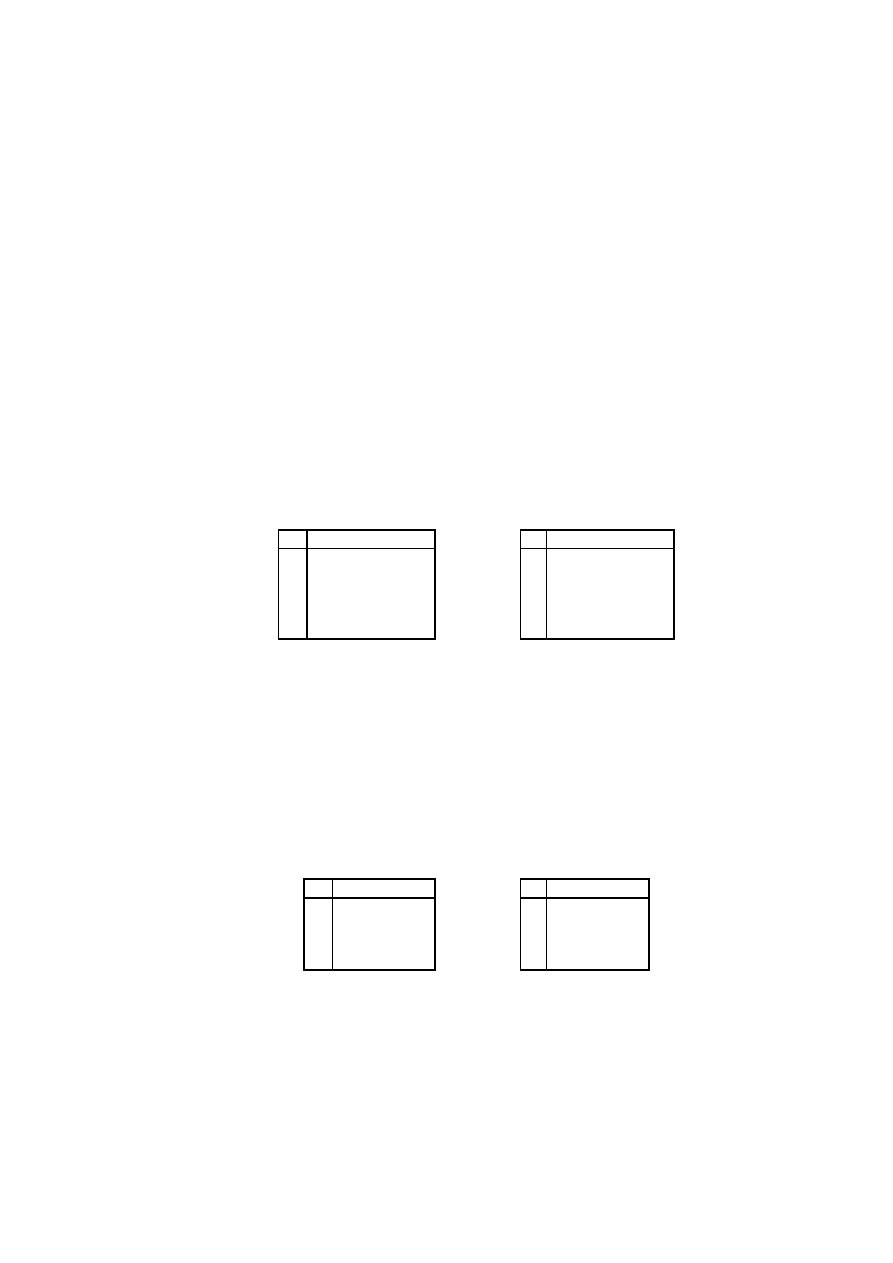
1.5. Pier´scie´n

9

Dowód: Udowodnimy tylko rozdzielno´s´c:

9

Skorzystali´smy w tym dowodzie z rozdzielno´sci mno˙zenia wzgl¸edem dodawania dla liczb
całkowitych.

Przykład 1.16 Rozwa˙zmy zbiór reszt modulo 5. Składa si¸e on z pi¸eciu klas:

dla prostoty b¸edziemy dalej opuszcza´c nawiasy. Mamy wi¸ec zbiór:

z dodawaniem i mno˙zeniem okre´slonym nast¸epuj¸acymi tabelami:

+

0

1

2

3

4

0

0

1

2

3

4

1

1

2

3

4

0

2

2

3

4

0

1

3

3

4

0

1

2

4

4

0

1

2

3

0

1

2

3

4

0

0

0

0

0

0

1

0

1

2

3

4

2

0

2

4

1

3

3

0

3

1

4

2

4

0

4

3

2

1

Zauwa˙zmy, ˙ze ka˙zdy element oprócz zera ma w

element odwrotny wzgl¸edem mno˙zenia,

czyli dla ka˙zdego

istnieje

taki ˙ze

:

9

Dlatego

jest ciałem, czyli pier´scieniem przemiennym z jedynk¸a i z odwrotno´sci¸a wzgl¸edem

mno˙zenia.

Przykład 1.17 Rozwa˙zmy teraz pier´scie´n reszt modulo 4:

gdzie dodawanie i mno˙zenie jest okre´slone nast¸epuj¸acymi tabelami:

+

0

1

2

3

0

0

1

2

3

1

1

2

3

0

2

2

3

0

1

3

3

0

1

2

0

1

2

3

0

0

0

0

0

1

0

1

2

3

2

0

2

0

2

3

0

3

2

1

nie jest ciałem, poniewa˙z nie ma w nim elementu odwrotnego do 2. Ponadto w

mamy:

-

czyli zero mo˙zna przedstawi´c jako iloczyn dwóch liczb ró˙znych od zera.

10

Rozdział 1. Teoria liczb

Łatwo zauwa˙zy´c, ˙ze je˙zeli liczba

jest zło˙zona,

dla

"

"

, to w

pier´scieniu

mamy

i ani , ani

nie maj¸a elementów odwrotnych. Przypu´s´cmy

bowiem, ˙ze istnieje

. Mamy wtedy:

czyli

, sprzeczno´s´c. Tak wi¸ec

nie jest ciałem, je˙zeli

jest liczb¸a zło˙zon¸a.

W dalszej cz¸e´sci tego rozdziału zobaczymy, ˙ze je˙zeli

jest liczb¸a pierwsz¸a, to

jest

ciałem.

1.6

Najwi¸ekszy wspólny dzielnik

Dla dwóch liczb całkowitych

i

, ich najwi¸ekszy wspólny dzielnik to po prostu najwi¸eksza

liczba całkowita

, która dzieli

i

. Najwi¸ekszy wspólny dzielnik liczb

i

b¸edziemy

oznacza´c przez

. Na przykład:

,

.

1.7

Algorytm Euklidesa

Najwi¸ekszy wspólny dzielnik dwóch liczb dodatnich mo˙zna obliczy ´c za pomoc¸a algoryt-
mu Euklidesa.

Algorytm Euklidesa. Aby obliczy´c najwi¸ekszy wspólny dzielnik dwóch dodatnich liczb
naturalnych

,

, powtarzamy a˙z do skutku:

je˙zeli

, to koniec,

,

je˙zeli

, to

,

je˙zeli

"

, to

.

Powy˙zszy algorytm odejmuje od wi¸ekszej liczby mniejsz¸a tak długo, a˙z liczby b¸ed¸a rów-
ne. Wtedy wynikiem działania algorytmu jest wspólna warto´s´c tych liczb. W uproszczo-
nej wersji j¸ezyka Pascal algorytm Euklidesa mo˙zna zapisa´c w nast¸epuj¸acy sposób:

p:=a;q:=b;

while p<>q do

if p>q then p:=p-q

else q:=q-p;

NWD(a,b):=p

W poni˙zszej tabeli pokazano kolejne kroki działania algorytmu Euklidesa na parze

liczb 36 i 15:

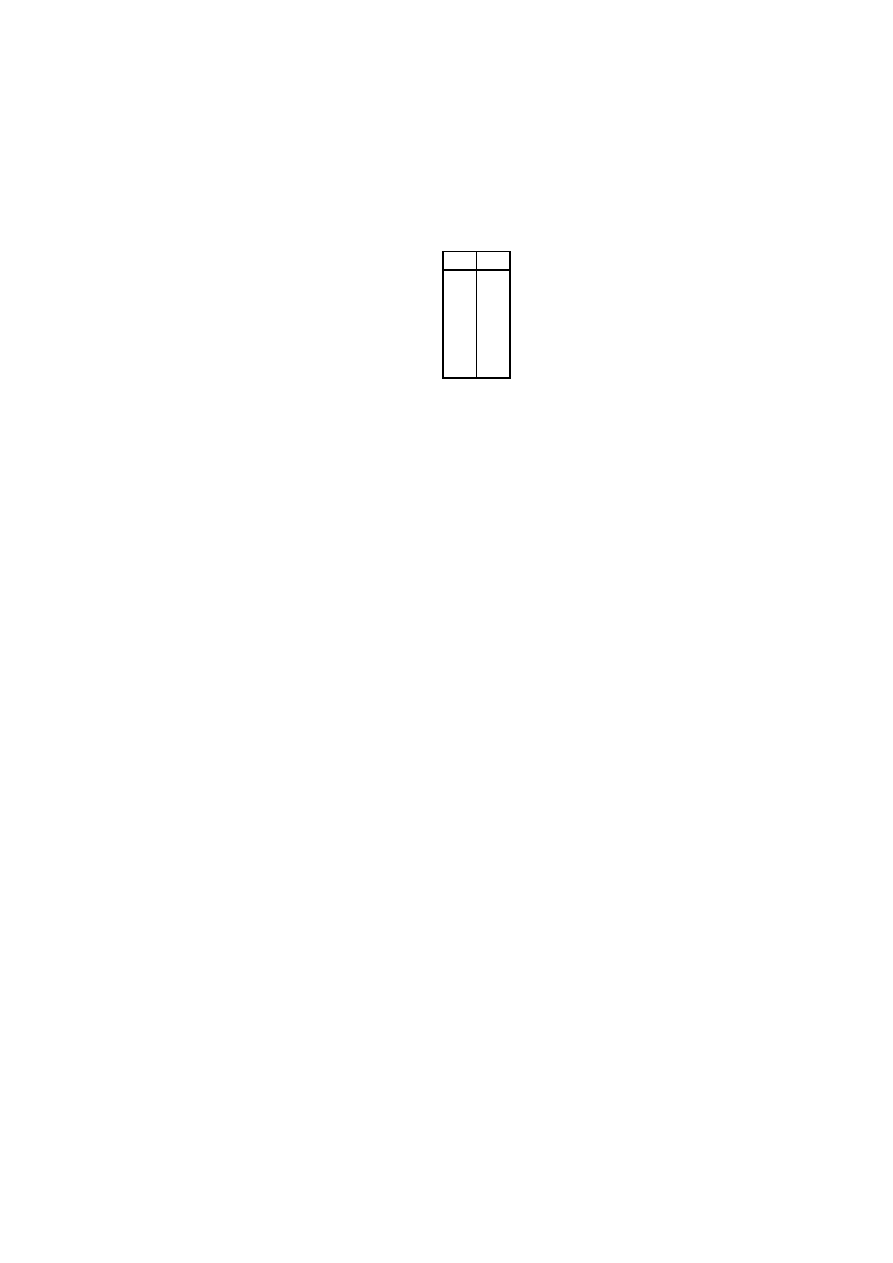
1.7. Algorytm Euklidesa

11

36

15

21

15

6

15

6

9

6

3

3

3

Tak wi¸ec 3 jest najwi¸ekszym wspólnym dzielnikiem liczb 15 i 36.

Poprawno´s´c algorytmu Euklidesa wynika z poni˙zszego lematu.

Lemat 1.18 Niech

i

b¸ed¸a dwoma liczbami naturalnymi i niech

"

"

. Wtedy

para

ma taki sam zbiór wspólnych dzielników jak para

,

.

Dowód. Je˙zeli liczba

jest wspólnym dzielnikiem pary

, to

dzieli tak˙ze

, czyli

jest wspólnym dzielnikiem pary

,

.

Na odwrót, je˙zeli liczba

jest wspólnym dzielnikiem pary

,

, to

dzieli tak˙ze

, czyli

jest wspólnym dzielnikiem pary

.

Tak wi¸ec po ka˙zdej iteracji p¸etli

while

para

ma taki sam zbiór wspólnych dziel-

ników, a wi¸ec tak˙ze taki sam najwi¸ekszy wspólny dzielnik. Na ko ´ncu, gdy

, wów-

czas oczywi´scie

.

Nale˙zy jeszcze pokaza´c, ˙ze dla ka˙zdej pary dodatnich liczb naturalnych

i

algorytm

zatrzyma si¸e. Ale to wynika z faktu, ˙ze po ka˙zdej iteracji p¸etli

while

liczba

jest coraz mniejsza, a poniewa˙z jest to zawsze liczba naturalna dodatnia, wi¸ec nie mo˙ze
zmniejsza´c si¸e w niesko ´nczono´s´c. Zauwa˙zmy przy okazji, ˙ze je˙zeli jedna z dwóch liczb,

lub

, jest zerem, to algorytm nie zatrzyma si¸e.

Twierdzenie 1.19 Niech

i

b¸ed¸a dwoma dodatnimi liczbami naturalnymi i niech

. Wtedy istniej¸a liczby całkowite

i

, takie ˙ze:

(

lub mówi¸ac inaczej,

jest kombinacj¸a całkowitoliczbow¸a liczb

i

.

Dowód. Poka˙zmy, ˙ze wszystkie warto´sci, jakie przyjmuj¸a zmienne

i

w trakcie wy-

konywania algorytmu Euklidesa, s¸a całkowitoliczbowymi kombinacjami liczb

i

. Na

pocz¸atku, gdy

i

, mamy:

9

Załó˙zmy teraz, ˙ze po

-tej iteracji p¸etli

$

oraz ˙ze zachodzi:

)

9

Wtedy w

iteracji

b¸edzie pomniejszone o

i b¸edziemy mieli:

9

Z tego wynika, ˙ze tak˙ze ostateczna warto´s´c zmiennej (która jest równa

) jest całkowitoliczbow¸a

kombinacj¸a liczb

i

.

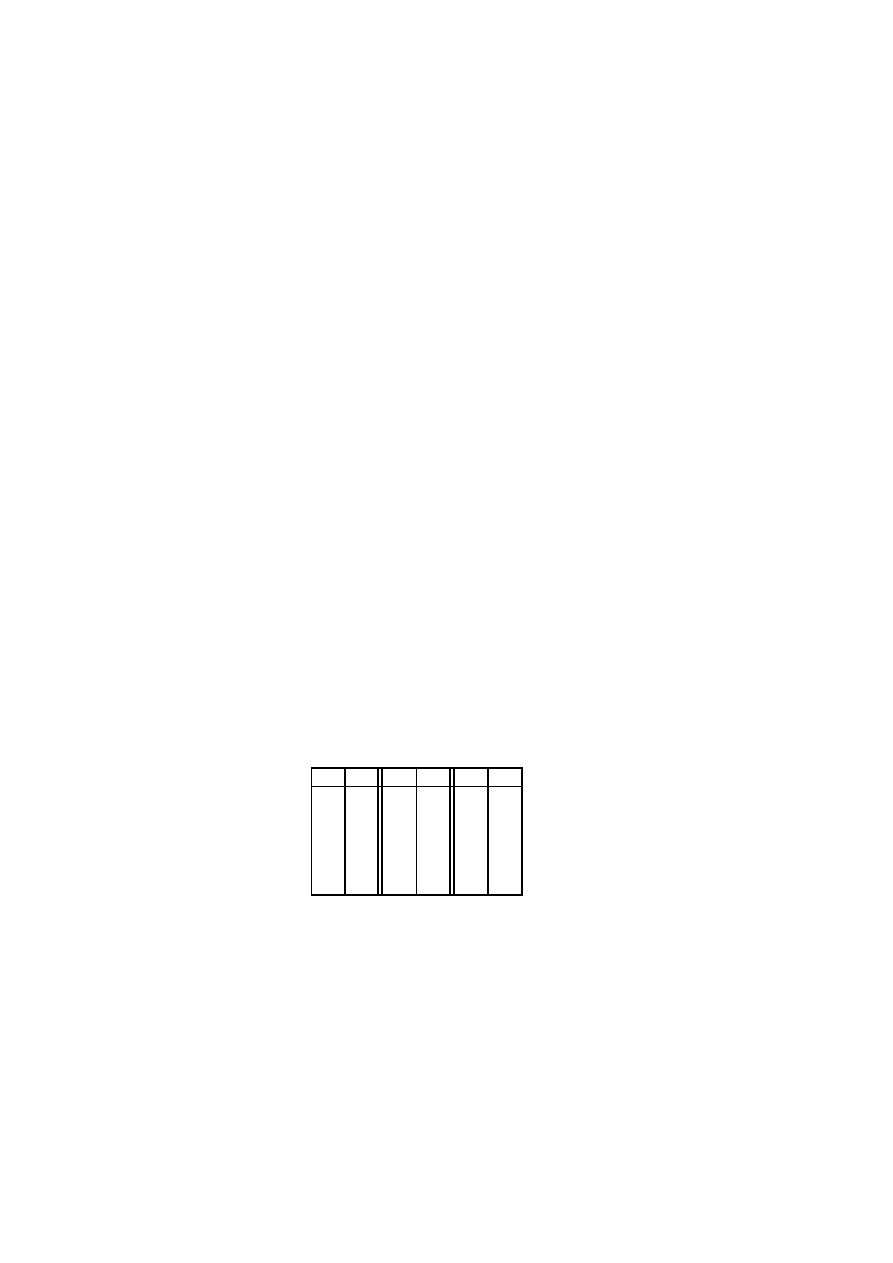
12

Rozdział 1. Teoria liczb

Algorytm Euklidesa mo˙zna tak zmodyfikowa´c, aby oprócz najwi¸ekszego wspólnego

dzielnika

, wyliczał tak˙ze liczby

i

, takie ˙ze:

(

9

Oto ten algorytm w j¸ezyku Pascal:

p:=a;q:=b;

xp:=1;yp:=0;

xq:=0;yq:=1;

while p<>q do

if p>q then

begin

p:=p-q;

xp:=xp-xq;

yp:=yp-yq

end

else

begin

q:=q-p;

xq:=xq-xp;

yq:=yq-yp

end;

NWD(a,b):=p;

x:=xp,y:=yp

W poni˙zszej tabeli pokazano kolejne kroki działania rozszerzonego algorytmu Eukli-

desa na parze liczb 36 i 15:

6

36

15

1

0

0

1

21

15

1

-1

0

1

6

15

1

-2

0

1

6

9

1

-2

-1

3

6

3

1

-2

-2

5

3

3

3

-7

-2

5

Tak wi¸ec liczb¸e 3 mo˙zna przedstawi´c jako kombinacj¸e liczb 15 i 36 w nast¸epuj¸acy sposób:

)

9

Zauwa˙zmy, ˙ze je˙zeli jaka´s liczba

dzieli liczby

i

, to dzieli tak˙ze ka˙zd¸a ich kombinacj¸e

całkowit¸a

(

a wi¸ec dzieli tak˙ze najwi¸ekszy wspólny dzielnik

. Udowodnili´smy poni˙zszy

lemat.

1.8. Liczby pierwsze i wzgl¸ednie pierwsze

13

Lemat 1.20

jest podzielny przez ka˙zdy wspólny dzielnik liczb

i

.

Z lematu 1.20 wynika, ˙ze najwi¸ekszy wspólny dzielnik

mo˙ze by ´c rów-

nowa˙znie zdefiniowany jako taki wspólny dzielnik liczb

i

, który jest podzielny przez

ka˙zdy wspólny dzielnik

i

.

Lemat 1.21 Liczba

jest najwi¸ekszym wspólnym dzielnikiem liczb

i

wtedy i tylko

wtedy gdy

b¸edzie wspólnym dzielnikiem

i

oraz istniej¸a liczby całkowite

i

, takie

˙ze

!

(

.

Dowód Je˙zeli

to

,

oraz (z twierdzenia 1.19) istniej¸a liczby całko-

wite

i

, takie ˙ze:

!

(

.

Na odwrót, je˙zeli

dzieli

i

oraz

(

, to ka˙zdy wspólny dzielnik

i

dzieli

, a wi¸ec

jest najwi¸ekszym wspólnym dzielnikiem

i

.

Wniosek 1.22 Je˙zeli istniej¸a liczby całkowite

i

, takie, ˙ze

(

, to

.

Przykład 1.23 Zastanówmy si¸e, ile wynosi

)

. Poniewa˙z:

)

oraz 2 jest wspólnym dzielnikiem 1998 i 2000, wi¸ec

)

.

Zastanówmy si¸e teraz, ile wynosi

))(

. Poniewa˙z:

))

wi¸ec

))

dzieli 2, a poniewa˙z 2 nie dzieli ani 1999, ani 2001, wi¸ec

(

.

1.8

Liczby pierwsze i wzgl¸ednie pierwsze

Dwie liczby naturalne

i

s ˛

a wzgl¸ednie pierwsze, je˙zeli

, a liczba

naturalna

jest pierwsza, je˙zeli

i jedynymi dzielnikami naturalnymi

s¸a jedynka i

samo .

Oto wszystkie liczby pierwsze mniejsze od 50:

)

)

(

)

9

Liczba

, która nie jest pierwsza jest zło˙zona. Istniej ˛

a wtedy dwie liczby

,

"

,

takie, ˙ze

.

1.9

Rozkład liczb na czynniki pierwsze

W tym rozdziale zobaczymy, ˙ze ka˙zd¸a liczb¸e naturaln¸a

mo˙zna rozło˙zy ´c na czynniki

pierwsze i ˙ze taki rozkład jest jednoznaczny z dokładno´sci¸a do kolejno´sci czynników. Na
przykład:

i

)

9

14

Rozdział 1. Teoria liczb

Twierdzenie 1.24 Ka˙zd¸a liczb¸e naturaln¸a

mo˙zna przedstawi´c jako iloczyn liczb

pierwszych (niekoniecznie ró˙znych):

9

Dowód nie wprost. Przypu´s´cmy, ˙ze istnieje liczba naturalna

, której nie mo˙zna przed-

stawi´c jako iloczynu liczb pierwszych i ˙ze

jest najmniejsz¸a tak¸a liczb¸a.

nie mo˙ze by ´c

liczb¸a pierwsz¸a (bo wtedy

), wi¸ec

jest liczb¸a zło˙zon¸a, czyli jest postaci:

dla

"

. Ale poniewa˙z

i

s¸a mniejsze od

, wi¸ec mo˙zna je rozło˙zy ´c na czynniki

pierwsze

ale wtedy, wbrew zało˙zeniu, mamy rozkład liczby

na czynniki pierwsze:

9

Aby pokaza´c, ˙ze rozkład jest jednoznaczny (z dokładno´sci¸a do kolejno´sci czynników),

musimy najpierw udowodni´c dwa lematy.

Lemat 1.25 Niech

i

b¸ed¸a dodatnimi wzgl¸ednie pierwszymi liczbami naturalnymi.

Wtedy dla dowolnej liczby

, je˙zeli

, to

.

Dowód. Z twierdzenia 1.19, istniej¸a dwie liczby całkowite

i

, takie ˙ze:

6

9

Pomnó˙zmy teraz obie strony tego równania przez

:

(

i zauwa˙zmy, ˙ze

dzieli oba składniki po lewej stronie równania, a wi¸ec dzieli praw¸a

stron¸e, czyli

.

Lemat 1.26 Je˙zeli liczba pierwsza

dzieli iloczyn liczb pierwszych

(niekoniecznie ró˙znych), to wtedy

jest równe jednej z liczb

.

Dowód przez indukcj¸e ze wzgl¸edu na

. Dla

mamy

, a poniewa˙z

jest

pierwsza i

, wi¸ec

.

Załó˙zmy teraz, ˙ze teza zachodzi dla

i przypu´s´cmy, ˙ze

dzieli

9

Mamy dwa przypadki: albo

dzieli

, albo nie. W pierwszym przypadku

.

W drugim przypadku mamy

, bo 1 i

to jedyne dzielniki liczby

. Z lematu 1.25 wynika teraz, ˙ze

dzieli

a z zało˙zenia indukcyjnego, ˙ze

dla jakiego´s

4

.

.

1.10. Elementy odwracalne

15

Udowodnimy teraz, ˙ze rozkład liczby na czynniki pierwsze jest jednoznaczny, z dokładno´sci¸a
do kolejno´sci czynników.

Twierdzenie 1.27 Ka˙zd¸a liczb¸e naturaln¸a

mo˙zna w dokładnie jeden sposób przed-

stawi´c w postaci iloczynu:

9

99

gdzie

s¸a dodatnimi liczbami naturalnymi,

s¸a liczbami pierwszymi oraz zachodzi

"

"

99

9("

.

Dowód. Twierdzenie 1.24 orzeka, ˙ze liczba ma rozkład na czynniki pierwsze. Trzeba
pokaza´c, ˙ze jest to rozkład jednoznaczny.

jako liczba pierwsza ma jednoznaczny

rozkład. Przypu´s´cmy, ˙ze

jest najmniejsz¸a liczb¸a z dwoma ró˙znymi rozkładami:

999

99

9

9

(1.1)

Wtedy z jednej strony

nie mo˙ze wyst¸epowa´c po prawej stronie równania (1.1), bo

'

byłoby mniejsz¸a liczb¸a z niejednoznacznym rozkładem. Z drugiej strony

dzieli praw¸a

stron¸e, a wi¸ec, z lematu 1.26 wyst¸epuje po prawej stronie. Mamy wi¸ec sprzeczno´s´c.

Lemat 1.28 Je˙zeli

i

s¸a wzgl¸ednie pierwsze, to ich rozkłady s¸a rozł¸aczne, to znaczy

maj¸a rozł¸aczny zbiór liczb pierwszych wyst¸epuj¸acych w ich rozkładach.

1.10

Elementy odwracalne

Definicja 1.29 Element

jest odwracalny, je˙zeli istnieje

, takie, ˙ze

63

9

nazywamy elementem odwrotnym do

i oznaczamy przez

.

Przykład 1.30

jest odwracalna w

bo

3

. Oprócz 3 w

odwra-

calne s ˛

a tak˙ze ,

i

.

Lemat 1.31 Liczba

jest odwracalna wtedy i tylko wtedy, gdy

.

Dowód. Je˙zeli

, to istniej¸a liczby całkowite

i

, takie ˙ze:

a wi¸ec

dzieli

, czyli:

63

9

Teraz wystarczy przyj¸a´c za

tak¸a liczb¸e z przedziału od 1 do

, która przystaje

do

modulo

.

Z drugiej strony je˙zeli istnieje element

odwrotny do

to

63

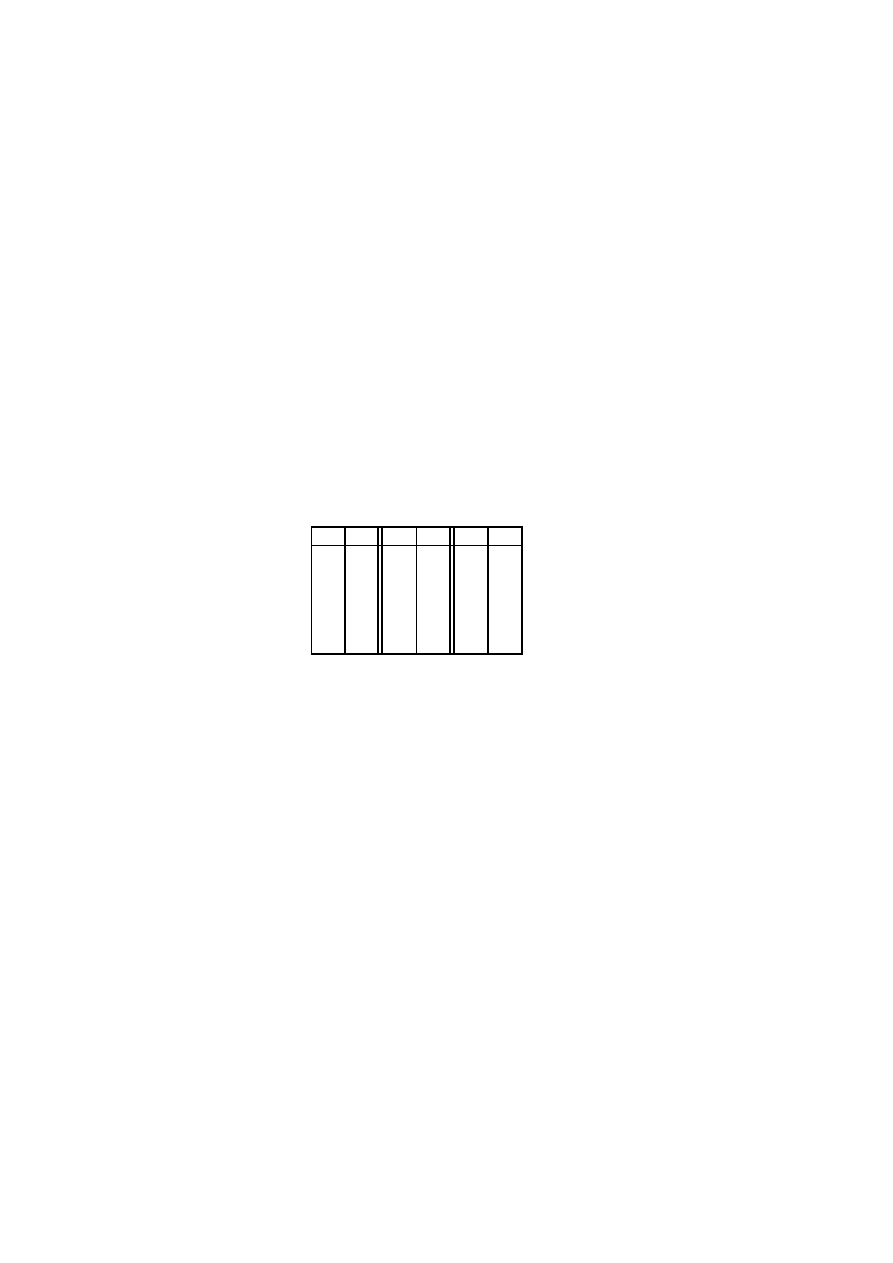
16

Rozdział 1. Teoria liczb

czyli

dla jakiego´s

. Mamy wi¸ec

czyli

(wniosek 1.22).

Z powy˙zszego dowodu wynika, ˙ze element odwrotny do

mo˙zna wyliczy ´c stosuj¸ac

algorytm Euklidesa. Na przykład policzmy element odwrotny do 12 w pier´scieniu

.

Najpierw zastosujemy algorytm Euklidesa, aby obliczy´c

i

, takie ˙ze:

9

Kolejne kroki algorytmu przedstawiono w tabeli:

6

17

12

1

0

0

1

5

12

1

-1

0

1

5

7

1

-1

-1

2

5

2

1

-1

-2

3

3

2

3

-4

-2

3

1

2

5

-7

-2

3

Mamy wi¸ec:

-)

czyli:

63

ale:

3

czyli 10 jest elementem odwrotnym do 12 w pier´scieniu

.

Definicja 1.32 Zbiór elementów odwracalnych w

oznaczamy przez

.

Przykład 1.33

.

Lemat 1.34 Je˙zeli liczba

jest pierwsza, to ka˙zdy element

,

, jest odwra-

calny, czyli pier´scie´n

jest ciałem.

Lemat 1.35 Je˙zeli

to

oraz

.

To oznacza, ˙ze

z mno˙zeniem jest grup¸a.

Dowód: Elementem odwrotnym do iloczynu

6

jest

, a elementem odrotnym do

jest

.

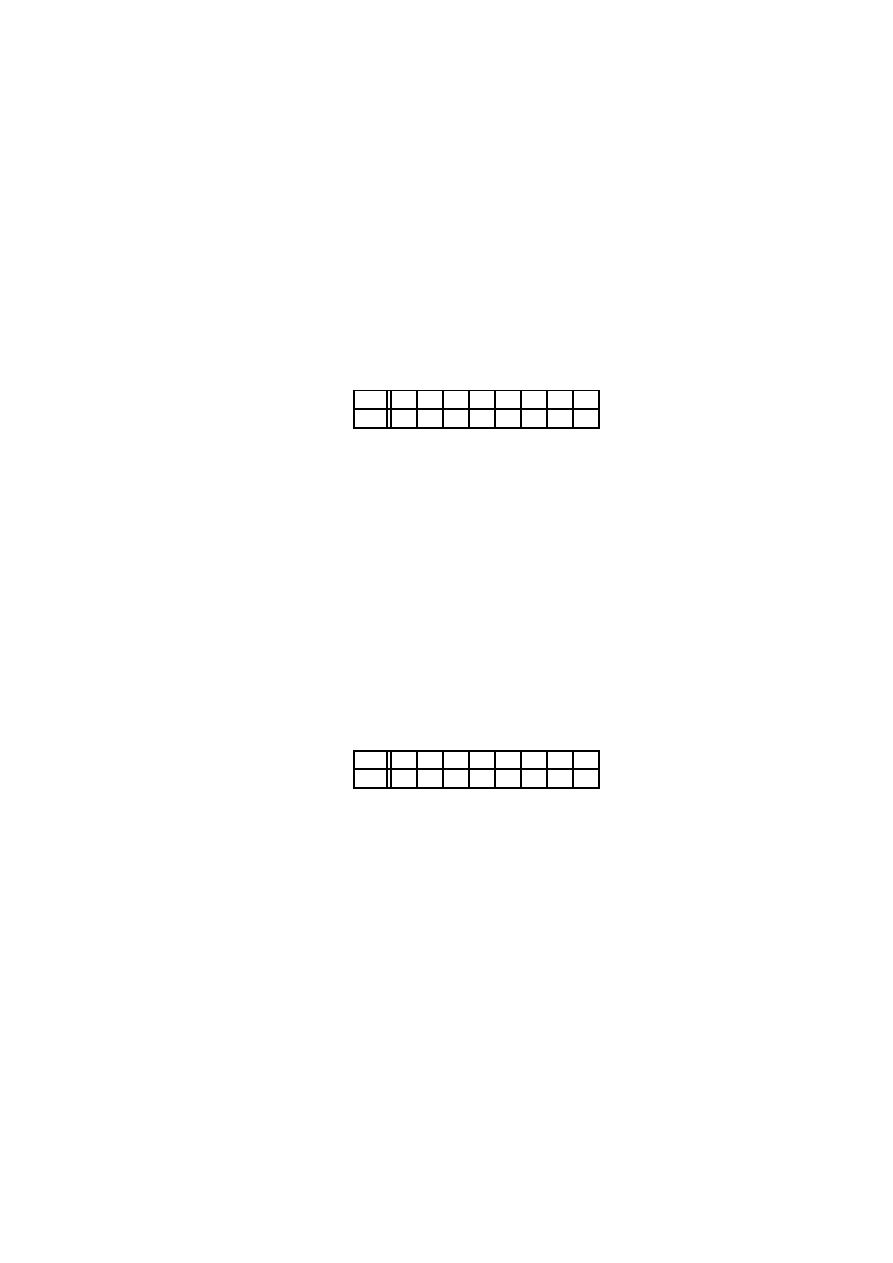
1.11. Funkcja liniowa

17

1.11

Funkcja liniowa

Zastanówmy si¸e jak w pier´scieniu

działa funkcja liniowa

63

9

Rozpatrzmy najpierw przypadek, gdy

i

s¸a wzgl¸ednie pierwsze, czyli gdy

. Dla

i

warto´sci funkcji przedstawia tabela

x

0

1

2

3

4

5

6

7

3x

0

3

6

1

4

7

2

5

W takim przypadku istnieje

element odwrotny do

i funkcja

, która

jest odwrotna do . Rzeczywi´scie

9

Z tego wynika, ˙ze

jest wzajemnie jednoznaczna i "na" oraz, ˙ze dla ka˙zdego

równanie

ma dokładnie jedno rozwi¸azanie w pier´scieniu

, jest ono równe

.

Funkcja

jest permutacj¸a w

i wykorzystuje si¸e j¸a, gdy trzeba wymiesza´c (prze-

permutowa´c) elementy

. Zauwa˙zmy, ˙ze

jest tak˙ze permutacj ˛

a w

. Rzeczywi´scie,

je˙zeli

, to na podstawie lematu 1.35

. Mamy wi¸ec

Lemat 1.36 Je˙zeli

, to funkcja

jest funkcj¸a wzajemnie

jednoznaczn¸a w

i w

.

Rozpatrzmy teraz przypadek, gdy

i

nie s¸a wzgl¸ednie pierwsze, czyli gdy

. Dla

i

warto´sci funkcji przedstawia tabela

x

0

1

2

3

4

5

6

7

6x

0

6

4

2

0

6

4

2

Zauwa˙zmy, ˙ze je˙zeli

jest warto´sci¸a funkcji , czyli gdy

63

to istnieje takie

, ˙ze

a poniewa˙z

dzieli

i

, to

dzieli

, a wi¸ec warto´sciami funkcji

mog¸a by´c tylko

liczby podzielne przez

.

Lemat 1.37 Je˙zeli

oraz

, to równania

63

oraz

('

'

63

'

s¸a równowa˙zne, czyli maj¸a ten sam zbiór rozwi¸aza´n w zbiorze liczb całkowitych.

18

Rozdział 1. Teoria liczb

Dowód

3

wtedy i tylko wtedy, gdy istnieje

takie ˙ze

a to zachodzi wtedy i tylko wtedy, gdy istnieje

takie, ˙ze

('

'

'

czyli wtedy i tylko wtedy, gdy

('

'

63

'

9

Przypu´s´cmy teraz, ˙ze

dzieli

i rozwi¸a˙zmy równanie

(1.2)

w pier´scieniu

, czyli szukamy takich

99

9

, ˙ze

3

(1.3)

Z lematu 1.37, to równanie jest równowa˙zne równaniu

('

'

63

'

(1.4)

Ale teraz

('

'

i równanie (1.4) ma dokładnie jedno rozwi¸azanie

99

9

'

takie ˙ze

('

'

3

'

9

Ale równania (1.4) i (1.3) s¸a spełnione tak˙ze przez liczby

'

.

'

99

9

'

9

S¸a to wszystkie liczby ze zbioru

9

99

spełniaj¸ace równania (1.4) i (1.3), czyli

wszystkie rozwi¸azania równania (1.2) w pier´scieniu

.

Przykład 1.38 Rozwi¸a˙zmy równanie

63

9

(1.5)

Poniewa˙z

, wi¸ec najpierw rozwi¸azujemy równanie

63

W

mamy

wi¸ec rozwi¸azaniem jest

. Tak wi¸ec rozwi¸azaniami

równaia (1.5) w

s¸a liczby

9

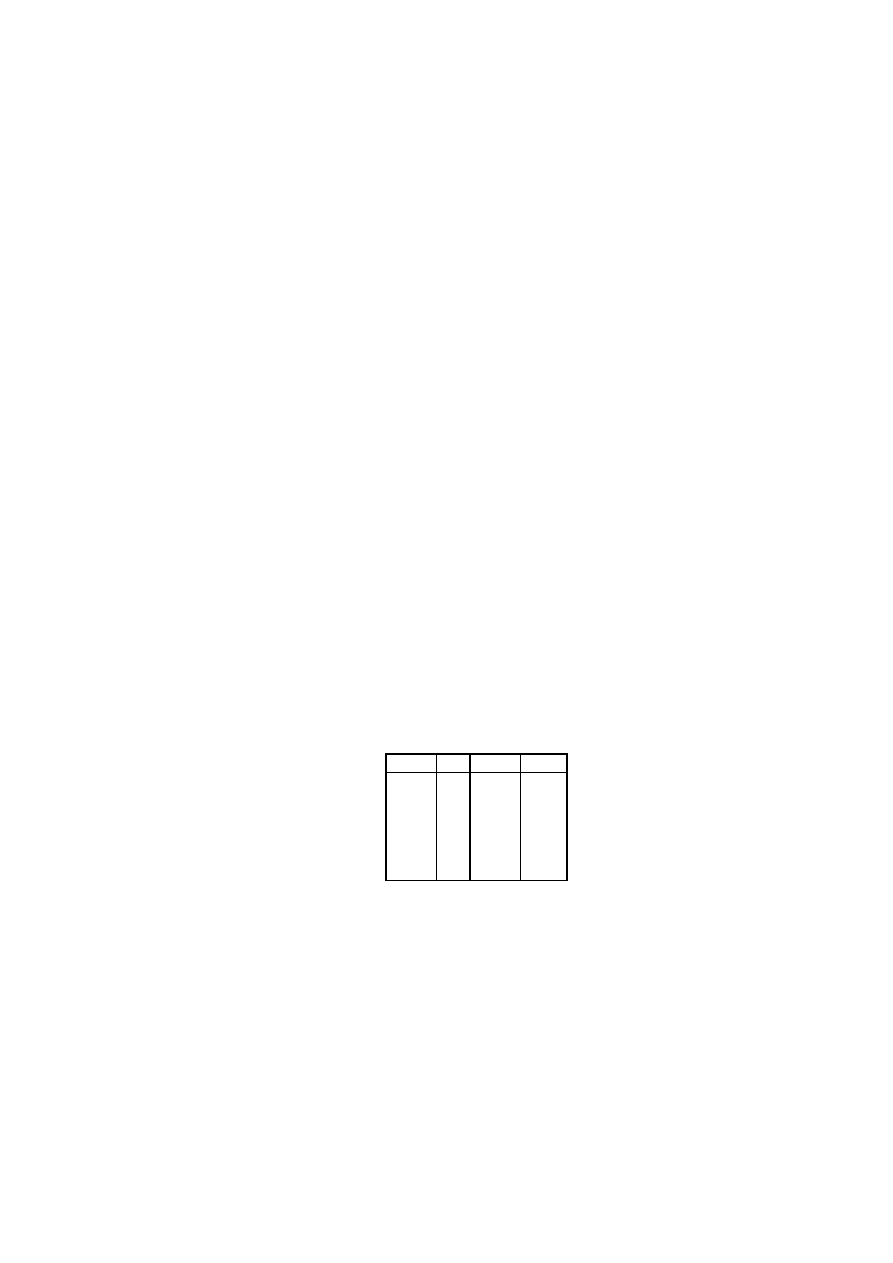
1.12. Szyfry liniowe

19

1.12

Szyfry liniowe

Przypu´s´cmy, ˙ze mamy tekst zapisany za pomoc¸a 26 liter alfabetu łaci ´nskiego:

i chcemy ten tekst zaszyfrowa´c. W tym celu uto˙zsamiamy zbiór liter z elementami pier-
´scienia

:

9

99

wybieramy dwie liczby

, takie ˙ze

, i szyfrujemy litera po

literze według wzoru:

3

9

Funkcja deszyfruj¸aca jest okre´slona wzorem:

63

9

Rzeczywi´scie:

9

Z tego wynika, ˙ze funkcja szyfruj¸aca

jest wzajemnie jednoznaczna.

Przykład 1.39 Wybierzmy

i

)

i zaszyfrujmy słowo

6

9

W tym celu musimy zaszyfrowa´c 6 liter:

,

,

, ,

oraz

. Obliczenia przedstawiono w

tabeli:

litera

szyfr

m

12

10

k

a

0

20

u

t

19

15

p

e

4

8

i

y

24

0

a

k

10

16

q

Słowo

6

po zaszyfrowaniu wygl¸ada tak:

9

Je˙zeli za´s zastosujemy ten sam szyfr do pocz¸atkowego zdania z wiersza Lokomotywa Ju-
liana Tuwima:

stoi na stacji lokomotywa,

to otrzymamy:

spewhuspuotwneqekepagu.

20

Rozdział 1. Teoria liczb

A oto program w j¸ezyku Pascal, który szyfruje teksty zapisane za pomoc¸a 26 liter alfabetu
łaci´nskiego:

var

t:string;

a,b,i,m:integer;

begin

writeln(’podaj klucz’);

write(’a=’);

readln(a);

write(’b=’);

readln(b);

writeln(’podaj tekst do zaszyfrowania’);

readln(t);

for i:=1 to length(t) do

begin

m:=((ord(t[i])-97)*a+b)mod(26)+97;

write(chr(m))

end

end.

Komentarz. Zmienna

t

jest typu

string

, czyli ła ´ncuch. Tak¸a zmienn¸a mo˙zna traktowa´c

jak tablic¸e z indeksami od 1 do

length(t)

i z warto´sciami typu

char

(znak). Zmienne

typu

char

s¸a przechowywane w jednym bajcie i mog¸a zawiera ´c jeden znak. List¸e znaków

wraz z odpowiadaj¸acymi im numerami (od 0 do 255) zawiera tak zwany kod ASCII. Małe
litery alfabetu łaci ´nskiego maj¸a tam numery od 97 —

a

, do 122 —

z

.

Instrukcja

readln(t)

czyta z klawiatury tekst do zaszyfrowania i zapisuje go do zmiennej

t

. Elementy tablicy

t[i]

, dla

i

od 1 do

length(t)

, zawieraj¸a poszczególne znaki naszego tekstu.

Funkcja

ord

przypisuje znakom ich numery w kodzie ASCII, a funkcja

chr

działa

na odwrót, przypisuje znak numerowi. P¸etla

for

, dla ka˙zdego znaku tekstu

t

po kolei,

wylicza numer tego znaku po zakodowaniu:

m:=((ord(t[i])-97)*a+b)mod(26)+97,

a nast¸epnie drukuje zakodowany znak na ekranie:

write(chr(m)).

Klucz do kodowania przechowywany jest w postaci dwóch liczb,

a

i

b,

typu integer.

Szyfry liniowe s¸a bardzo starym wynalazkiem. W prostszej wersji z

sto-

sował je ju˙z Juliusz Cezar. Ich wad¸a jest to, ˙ze bardzo łatwo daj¸a si¸e łama ´c. Czasami
wystarcza odgadn¸a´c, jak zaszyfrowano dwie litery. Mo˙zna to zrobi´c analizuj¸ac cz¸esto´sci
wyst¸epowania liter w zaszyfrowanym tek´scie.

Przykład 1.40 (kontynuacja przykładu 1.39) W naszym drugim zaszyfrowanym tek´scie
litera wyst¸epuje cztery razy, a litery i

po trzy razy. Mo˙ze to nam pomóc w odgadni¸eciu,

1.13. Chi ´nskie twierdzenie o resztach

21

˙ze litera

koduje liter¸e

, a litera

koduje liter¸e

. Mamy wi¸ec dwa równania:

63

63

9

Po odj¸eciu tych równa´n stronami mamy:

63

9

Korzystaj¸ac z algorytmu Euklidesa, mo˙zemy teraz wyliczy´c element odwrotny do 5 w pier-
´scieniu

. Jest to 21, poniewa˙z:

.

oraz

(

63

tak wi¸ec:

(

)

(8

63

9

Teraz z drugiego równania mo˙zemy wyliczy´c

:

-

63

9

1.13

Chi ´nskie twierdzenie o resztach

W staro˙zytnych Chinach generałowie u˙zywali pewnego ciekawego sposobu liczenia swo-
ich ˙zołnierzy. Dla kilku niewielkich liczb parami wzgl¸ednie pierwszych, na przykład dla:

obliczano i zapami¸etywano reszty z dzielenia liczby ˙zołnierzy przez te liczby. W celu
obliczenia reszt kazano ˙zołnierzom ustawi´c si¸e trójkami, pi¸atkami i siódemkami. Je˙zeli
przy nast¸epnym apelu wszystkie trzy reszty były takie same, to znaczyło, ˙ze nie brakuje

˙zadnego ˙zołnierza.

Zobaczmy, jak ten sposób działa. We´zmy najpierw dwie liczby:

9

W poni˙zszej tabeli mamy zestawione reszty modulo 2 i 3 liczb od 0 do 5:

a

63

3

0

0

0

1

1

1

2

0

2

3

1

0

4

0

1

5

1

2

22

Rozdział 1. Teoria liczb

Ka˙zda z liczb od 0 do

.

ma inny zestaw reszt oraz dla ka˙zdej pary reszt

, spełniaj¸acych warunek

"

,

"

, istnieje liczba

, taka ˙ze:

63

63

9

Oczywi´scie 6 ma takie same reszty jak 0:

63

63

i ogólnie, je˙zeli dwie liczby

i

ró˙zni¸a si¸e o wielokrotno´s´c liczby

-

, czyli:

dla jakiego´s całkowitego

, to

63

63

63

63

9

Z tego wida´c, ˙ze sposób chi ´nskich generałów, z liczbami 2 i 3, liczy ˙zołnierzy z dokładno´sci¸a
do pi¸eciu.

Sytuacja jest inna, je˙zeli

i

nie s¸a wzgl¸ednie pierwsze. Je˙zeli, na przykład,

i

, to w´sród liczb od 0 do

)

istniej¸a takie, które maj¸a takie

same reszty, na przykład 1 i 13:

63

3

63

3

9

Ponadto nie istnieje taka liczba

, dla której:

63

63

9

Rzeczywi´scie, z pierwszej równo´sci wynika, ˙ze

powinno by´c nieparzyste, a z drugiej,

˙ze parzyste.

Je˙zeli jednak

i

s¸a wzgl¸ednie pierwsze, to ka˙zda z liczb od 0 do

ma

inny zestaw reszt oraz dla ka˙zdej pary reszt

, spełniaj¸acych warunek

"

,

#

"

, istnieje liczba

, taka ˙ze:

63

63

zachodzi bowiem poni˙zsze twierdzenie.

Twierdzenie 1.41 (chi ´

nskie twierdzenie o resztach) Niech

999

b¸ed¸a dodatnimi liczbami wzgl¸ednie pierwszymi, to znaczy dla ka˙zdej pary

"

mamy

, oraz niech

999

1.13. Chi ´nskie twierdzenie o resztach

23

b¸ed¸a dowolnymi resztami. Wtedy istnieje liczba całkowita

, taka ˙ze:

63

63

(1.6)

9

99

3

9

Ponadto je˙zeli liczby

i

s¸a rozwi¸azaniami układu kongruencji (1.6), to ich ró˙znica

dzieli si¸e przez iloczyn wszystkich liczb

, czyli przez:

9

Dowód. Najpierw udowodnimy drug¸a cz¸e´s´c twierdzenia. Dla ka˙zdego

mamy:

63

3

9

Po odj¸eciu stronami tych dwóch równa ´n mamy:

3

czyli

wi¸ec ka˙zda spo´sród liczb

dzieli

!

, a skoro liczby

99

9

s¸a wzgl¸ednie pierwsze,

wi¸ec tak˙ze ich iloczyn

dzieli

. Rzeczywi´scie, przypu´s´cmy bowiem, ˙ze

ma

rozkład

9

We´zmy teraz dowolne

. Poniewa˙z rozkłady liczb

99

9

s¸a rozł¸aczne, wi¸ec

wyst˛epuje w rozkładzie jakiego´s

, czyli dzieli

oraz

, a wi¸ec w rozkładzie

liczby

, liczba

wyst¸epuje z wykładnikiem

. Dlatego

dzieli

.

Zobaczymy teraz, ˙ze układ (1.6) ma rozwi¸azanie. Niech

'

, czyli:

999

9

Poniewa˙z

i

maj¸a rozł¸aczne rozkłady, wi¸ec

oraz istnieje

,

takie ˙ze:

63

9

We´zmy teraz:

9

Zauwa˙zmy, ˙ze je˙zeli

, to

, oraz:

63

co daje:

3

dla ka˙zdego

, a wi¸ec

jest rozwi¸azaniem układu równa ´n (1.6).

24

Rozdział 1. Teoria liczb

Przykład 1.42 Ka˙zda z liczb od 0 do

!

ma inny zestaw reszt wzgl¸edem

liczb 3, 5 i 7. Tak wi¸ec stosuj¸ac sposób chi´nskich generałów z liczbami 3, 5, 7 mo˙zemy
liczy´c ˙zołnierzy z dokładno´sci¸a do 104.

Ale sposób chi´nskich generałów pozwala tak˙ze stwierdzi´c, o ile zmieniła si¸e liczba

˙zołnierzy. Przypu´s´cmy bowiem, ˙ze na porannym apelu było

˙zołnierzy i uzyskano reszty:

63

63

63

a na apelu wieczornym było

˙zołnierzy i otrzymano reszty:

63

63

63

wtedy ró˙znica

spełnia nast¸epuj¸acy układ kongruencji:

63

63

63

9

Jak wida´c, chi´nskie twierdzenie o resztach pozwala wnioskowa´c o du˙zych liczbach za

pomoc¸a operacji na małych liczbach. Zobaczmy teraz inne zastosowanie tego twierdzenia.

Przykład 1.43 Zastanówmy si¸e, ile wynosi reszta z dzielenia liczby

przez 15. Łatwo mo˙zna policzy´c, ˙ze:

63

oraz

63

, a wi¸ec:

63

poniewa˙z 4 jest jedyn¸a liczb¸a z przedziału

9

99

, która posiada reszty

63

oraz

63

.

1.14

Pierwiastki kwadratowe

Definicja 1.44 Liczb¸e

nazywamy pierwiastkiem kwadratowym liczby

w pier´scieniu

, je˙zeli

3

9

Przykład 1.45 W

pierwiastkami 4 s¸a 2 i 3, a liczba 2 nie posiada pierwiastka.

Zauwa˙zmy, ˙ze je˙zeli

63

to

63

czyli

63

, te˙z jest pierwiastkiem

.

Lemat 1.46 Je˙zeli

jest liczb¸a pierwsz¸a i

, to

i

s¸a jedynymi pierwiastkami

z

.

1.15. Funkcja Eulera

25

Dowód Je˙zeli

3

, to

dzieli

, a poniewa˙z

jest pierwsze to

dzieli

lub

. W pierwszym przypadku

63

, w

drugim

63

.

Przykład 1.47 Tak nie musi by´c, je˙zeli

nie jest liczb¸a pierwsz¸a. Na przykład w

mamy cztery pierwiastki z , s¸a to ,

,

i

.

Ogólnie rozwa˙zmy liczb¸e

która jest iloczynem dwóch ró˙znych liczb pierwszych

.#

. We´zmy teraz dowoln¸a liczb¸e

, dla której

63

lub

63

oraz

3

lub

63

Wtedy

63

oraz

63

czyli z chi´nskiego twierdzenia o resztach wynika, ˙ze

63

9

Poniewa˙z

, to

3

oraz

63

i mamy wtedy

cztery ró˙zne pierwiastki z 1,

. S¸a to liczby dla których

63

63

63

63

63

63

63

63#

9

Zauwa˙zmy, ˙ze

3

oraz

63

.

1.15

Funkcja Eulera

Definicja 1.48 Funkcja Eulera, jest to funkcja, która liczbie

przypisuje

liczb¸e

elementów odwracalnych w

. Z definicji przyjmujemy

.

Przykład 1.49

, bo w

odwracalne s ˛

a

.

Podobnie

,

,

,

,

.

Lemat 1.50

a) Je˙zeli

jest liczb¸a pierwsz¸a, to dla dowolnego

,

. W szczególno´sci

.

b) Je˙zeli

i

s¸a wzgl¸ednie pierwsze, to

26

Rozdział 1. Teoria liczb

Dowód:

a)

Zauwa˙zmy ˙ze, w´sród liczb

99

9

wzgl¸ednie pierwsze z

nie s¸a te, które s¸a po-

dzielne przez , jest ich

'

, czyli

9

b)

Najpierw zauwa˙zmy, ze dla dowolnej liczby

,

#

"

wtedy i tylko wtedy gdy

oraz

a to zachodzi wtedy i tylko wtedy gdy reszty

3

oraz

3

spełniaj¸a warunki

oraz

(1.7)

Par reszt

spełniaj¸acych warunek (1.7) jest

, a z chi ´nskiego twierdzenia

o resztach ka˙zdej liczbie

,

"

odpowiada dokładnie jedna para reszt, i na

odwrót ka˙zdej parze reszt odpowiada jedna liczba. Tak wi¸ec liczb wzgl¸ednie pierwszych
z

jest

9

1.16

Szybkie pot¸egowanie

Teraz zastanowimy si¸e jak mo˙zna pot¸egowa´c, czyli jak obliczy´c

63

dla

oraz

. Pierwszy nasuwaj¸acy si¸e algorytm pot¸egowania polega na

krotnym mno-

˙zeniu przez

:

y:=1;

for i:=0 to k do y:=y*a mod n

W kryptografii oblicza si¸e pot¸egi z wykładnikami posiadaj¸acymi po kilkaset bitów. Do
takich zastosowa ´n powy˙zszy algorytm jest nieprzydatny (wymaga on

mno˙ze ´n).

Poka˙zemy teraz jak mo˙zna pot¸egowa´c du˙zo szybciej. Zauwa˙zmy, ˙ze

i ogólnie

9

Dlatego, aby obliczy´c pot¸eg¸e o wykładniku, który jest pot¸eg¸a dwójki

nale˙zy

wykona´c

y:=a;

for i:=1 to j do y:=y*y mod n

1.16. Szybkie pot¸egowanie

27

Przykład 1.51 Aby obliczy´c

w

obliczmy

-

3

,

!

3

,

3

,

63

.

Je˙zeli wykładnik jest sum¸a pot¸eg dwójki

, to

9

Przykład 1.52 Aby obliczy´c

63

trzeba wymno˙zy´c

)

63

.

Zauwa˙zmy, ˙ze ka˙zda liczba naturalna

jest sum¸a pot¸eg dwójki

gdzie

to cyfry rozwini¸ecia dwójkowego

.

Powy˙zsze uwagi sugeruj¸a nast¸epuj¸acy algorytm obliczania pot¸egi

.

Algorytm szybkiego pot˛egowania

Dane wej´sciowe: podstawa

a

oraz wykładnik

k=(dj,...,d0)

w postaci binarnej.

x:=a; y:=1

if d0=1 then y:=y*a mod n

for i:=1 to j do

x:=x*x mod n;

if di=1 then y:=y*x mod n

Zmienna

x

zawiera kolejne pot¸egi

o wykładnikach b¸ed¸acych pot¸egami 2. Na pocz¸atku

. Po

tej iteracji p¸etli for

. Je˙zeli

to mno˙zymy

przez

.

Na ko´ncu

8

9

Przykład 1.53 Prze´sled´zmy działanie algorytmu podczas obliczania

63

.

w zapisie dwójkowym ma posta´c

)

)

. Poni˙zsza tabela zawiera warto´sci zmiennej

x

i

y

przed wej´sciem do p˛etli

for i=0

) oraz po ka˙zdej iteracji.

i

x

y

0

2

2

1

4

8

2

3

8

3

9

8

4

3

11

Zauwa˙zmy, ˙ze wyniki po´srednie, i ostateczny, nale˙z ˛

a do

i algorytm nie potrzebuje

zbyt du˙zej pami¸eci. Algorytmu tego nie mo˙zna stosowa´c do obliczania

w liczbach

całkowitych, je˙zeli

jest du˙ze, to wynik ostateczny oraz po´srednie b¸ed ˛

a zbyt du˙ze, ˙zeby

mógł si¸e zmie´sci´c w pami¸eci komputera.

28

Rozdział 1. Teoria liczb

1.17

Małe twierdzenie Fermata

Twierdzenie 1.54 (Fermata) Niech

, wtedy

63

9

Dowód Niech

99

9

to b¸ed¸a wszystkie elementy

. Je˙zeli pomno˙zymy je przez

9

99

to zgodnie z lematem 1.36 otrzymamy te same elementy tylko w innej kolejno´sci.

Wymnó˙zmy teraz elemnty obu ci¸agów

63

9

Po pomno˙zeniu przez odwrotno´s´c

otrzymamy tez¸e twierdzenia.

Wniosek 1.55 Je˙zeli

jest liczb¸a pierwsz¸a, to dla ka˙zdego

wzgl¸ednie pierwszego z

mamy

3

9

1.18

Szyfry RSA

W szyfrach one-pad opisanych w rozdziale o funkcjach boolowskich klucz do szyfrowa-
nia jest ten sam co klucz do deszfrowania. W szyfrach liniowych wprawdzie klucze do
szyfrowania i deszyfrowania s¸a ró˙zne, ale jaden łatwo mo˙zna wyliczy ´c z drugiego. Takie
szyfry nazywamy symetrycznymi.

Teraz zapoznamy si¸e ze sposobem szyfrowania, w których klucz do szyfrowania mo˙ze

by´c jawny, nawet ogłaszany publicznie, a klucz do deszyfrowania jest tajny i jest praktycz-
nie niemo˙zliwe wyliczenie klucza tajnego z klucza jawnego. Sposób ten zaproponowali
Rivest, Shamir i Adleman. Przypu´s´cmy, ˙ze Alicja chce utworzy´c swój klucz. Bierze w
tym celu dwie du˙ze liczby pierwsze

i

, ka˙zda mo˙ze zawiera´c po kilkaset bitów. Tworzy

ich iloczyn

. Funkcja Eulera

. Nast¸epnie Alicja losuje liczb¸e

, która jest wzgl¸ednie pierwsza z

. Skoro

to istnieje liczba

, taka, ˙ze

3

. Teraz para

jest jawnym kluczem Alicji i mo˙ze

by´c publicznie ogłoszona. Para

jest kluczem prywatnym Alicji, nie powinna go ona

nikomu zdradza´c. Alicja nie powinna te˙z zdradza´c rozkładu liczby

na czynniki. Je˙zeli

kto´s zna

i

, to mo˙ze wyliczy´c

oraz

.

Przypu´s´cmy, ˙ze Bob chce przesła´c Alicji jak¸a´s zaszyfrowan¸a wiadomo´s´c

. Traktuje-

my t¸e wiadomo´s´c jako liczb¸e

"

. (Je˙zeli wiadomo´s´c jest ci¸agiem znaków, to kodujemy

1.19. Testy pierwszo´sci

29

ka˙zdy znak jako 8 bitów i cały ci¸ag mo˙ze by´c traktowany jako liczba w postaci dwójko-
wej.) Bob szyfruje wiadomo´s´c przy pomocy funkcji szyfruj¸acej

63

i przesyła j¸a Alicji. Alicja odszyfrowuje za pomoc¸a funkcji deszyfruj¸acej

63

9

Poka˙zemy teraz, ˙ze je˙zeli

, to

9

Mamy

63

9

Poniewa˙z

!

63

, wi¸ec istnieje

takie, ˙ze

4

, czyli

63

ale je˙zeli

, to

63

. Tak wi¸ec

. Do powy˙zszego potrzebne było zało˙zenie, ˙ze

. Ale gdy kto´s trafi na

wiadomo´s´c

, która nie jest wzgl¸ednie pierwsza z

, to Alicja ma pecha, poniewa˙z wtedy

mo˙zna dokona´c rozkładu liczby

i złama´c jej szyfr.

Łatwo te˙z mo˙zna pokaza´c, ˙ze

.

Niesymetryczne szyfry daj¸a nowe mo˙zliwo´sci. Mo˙zna ich na przykład u˙zywa´c do

podpisu. Aby podpisa´c jak¸a´s wiadomo´s´c

, Alicja szyfruje j¸a swoim szyfrem prywat-

nym

i jest to podpis wiadomo´sci

. Alicja wysyła Bobowi par¸e

.

˙

Zeby sprawdzi´c, ˙ze wszystko si¸e zgadza Bob szyfruje podpis publicznym kluczem Alicji
i sprawdza czy

9

1.19

Testy pierwszo´sci

W tym rozdziale zajmiemy si¸e zagadnieniem jak sprawdzi´c, czy liczba

jest pierwsza.

Mo˙zemy sobie wyobrazi´c, ˙ze

ma kilkaset bitów. Jak wida´c z poprzedniego rozdziału

du˙ze liczby pierwsze mog¸a by´c przydatne.

1.19.1

Test naiwny

Najprostszy sposób to, dzieli´c

przez kolejne liczby (pierwsze) a˙z do

. Jednak ten

test jest zupełnie niepraktyczny, je˙zeli

ma kilkaset bitów.

30

Rozdział 1. Teoria liczb

1.19.2

Test Fermata

Drugi test jest algorytmem probabilistycznym i opiera si¸e na twierdzeniu Fermata 1.54.

Losujemy liczb¸e

"

i najpierw sprawdzamy, czy

. Je˙zeli

i

nie s¸a wzgl¸ednie pierwsze, i

, to

jest dzielnikiem

i

nie jest

pierwsza.

Je˙zeli

, to obliczamy

63

. Je˙zeli

63

, to

mamy pewno´s´c, ˙ze

nie jest liczb¸a pierwsz¸a.

Definicja 1.56 Tak¸a liczb¸e

, dla której

oraz

63

b¸edziemy nazywa´c ´swiadkiem Fermata dla

, poniewa˙z za´swiadcza ona, ˙ze

jest zło˙zona.

Je˙zeli

63

, to orzekamy, ˙ze liczba

jest pierwsza. W tym przypadku

mo˙zemy si¸e pomyli´c. Liczba

mo˙ze by´c zło˙zona a mimo to wylosowali´smy pechowo i

3

. Ale zachodzi nast¸epuj¸acy lemat.

Lemat 1.57 Je˙zeli istnieje takie

, ˙ze

63

, to przynajmniej poło-

wa elementów

jest ´swiadkiem Fermata dla

.

Dowód. Przypu´s´cmy, ˙ze

9

99

s ˛

a to wszystkie elementy

, dla których

3

. Wtedy po pomno˙zeniu

przez

otrzymamy

elementów

6

9

99

6

ró˙znych mi¸edzy sob¸a (lemat 1.36), z których ka˙zdy jest ´swiadkiem Fermata. Rzeczywi-
´scie

63

9

A wi¸ec ´swiadków zło˙zono´sci jest co najmniej połowa.

Je˙zeli

jest pierwsze, to z Twierdzenia Fermata, algorytm zawsze orzeknie dobrze.

Z lematu 1.57 wynika, ˙ze je˙zeli

jest zło˙zona i istnieje ´swiadek Fermata dla

, to takich

´swiadków jest co najmniej połowa, i nasz algorytm pomyli si¸e z prawdopodobie ´nstwem

"

'

. Prawdopodobie ´nsto, to mo˙zna zmniejszy´c poprzez powtórzenie algorytmu

razy,

z ró˙znymi wylosowanymi

.

Istniej¸a jednak liczby zło˙zone

, które nie maj¸a ´swiadków zło˙zono´sci. Na przykład

. Kłopot bierze si¸e st¸ad, ˙ze

!

)

, a

dzieli si¸e przez

,

oraz przez

. Dlatego dla dowolnego

, je˙zeli

, to

jest wzgl¸ednie pierwsze z

,

i

oraz mamy

63

63

63

i z chi´nskiego twierdzenia o resztach wynika, ˙ze

63

Takie liczby nazywaj¸a sie liczbami Carmichaela. Pierwsze trzy z nich to 561, 1105 i 1729.
Wyst¸epuj¸a one bardzo rzadko, jest ich tylko 255 w´sród liczb mniejszych od 100 000 000.

1.19. Testy pierwszo´sci

31

1.19.3

Test Millera-Rabina

Zakładamy, ˙ze

jest nieparzyste (2 jest jedyn¸a parzyst¸a liczb¸a pierwsz¸a). Najpierw spraw-

dzamy, czy

jest pot¸eg¸a jakiej´s liczby naturalnej. Dla

od 2 do

/

sprawdzamy czy

, dla jakiego´s

. W rozdziale o arytmetyce opisano jak za pomoc¸a binary search

stwierdzi´c, czy liczba jest pot¸eg¸a innej liczby. Je˙zeli

jest pot¸eg¸a, to jest zło˙zona.

Poniewa˙z

jest nieparzyste, to

mo˙zemy przedstawi´c w postaci

9

dla jakiego´s

nieparzystego.

Losujemy

"

. Sprawdzamy, czy

(je˙zeli

8

, to

jest zło˙zona).

Nast¸epnie obliczamy

63

. Je˙zeli

63

, to koniec, stwierdzamy, ˙ze

jest pierwsza. Je˙zeli

63

, to obliczamy po kolei

3

63

99

9

63

9

Zauwa˙zmy, ˙ze w tym ci¸agu ka˙zda liczba jest kwadratem poprzedniej. Je˙zeli w´sród tych
liczb nie ma jedynki, to z twierdzenia Fermata wynika, ˙ze

jest zło˙zona, bo wtedy

3

9

Je˙zeli w tym ci¸agu jest jedynka, na przykład

3

to patrzymy na poprzedni element

. Je˙zeli

, to znale˙zli´smy nietrywial-

ny pierwiastek z 1. Z twierdzenia 1.46 wynika, ˙ze jest to mo˙zliwe tylko wtedy gdy

nie

jest pierwsze. Je˙zeli

, to orzekamy, ˙ze

jest pierwsze.

Łatwo wi¸ec wida´c, ˙ze je˙zeli

jest pierwsze, to test zawsze odpowie prawidłowo,

niezale˙znie od losowania. Wiadomo te˙z, ˙ze je˙zeli

jest zło˙zona i nie jest pot¸eg¸a licz-

by pierwszej, to z prawdopodobie ´nstwem wi¸ekszym ni˙z

'

wykryjemy to (dowód tego

faktu wybiega poza zakres tej ksi¸a˙zki i pomijamy go).

W praktyce stosujemy wszystkie trzy testy na raz. Maj¸ac nieparzyst¸a liczb¸e

, naj-

pierw sprawdzamy, czy dzieli si¸e ona przez kilka kolejnych liczb pierwszych

9

99

9

Dobór

zale˙zy od tego jak du˙ze liczby sprawdzamy. W ten sposób eliminujemy du˙z¸a

cz¸e´s´c liczb. Zauwa˙zmy, ˙ze obliczaj¸ac iloczyn tych liczb

i sprawdzaj¸ac, czy

&

mo˙zemy za jednym razem sprawdzi´c, czy

dzieli

si¸e przez któr¸a´s z tych liczb.

32

Rozdział 1. Teoria liczb

Po przej´sciu pierwszego testu stosujemy test drugi, a gdy liczba

go przejdzie stosu-

jemy test trzeci.

Poniewa˙z liczby Carmichaela s¸a do´s´c rzadkie, wi¸ec drugi test wyeliminuje wi¸ekszo´s´c

liczb zło˙zonych.

Je˙zeli chcemy wyklosowa´c liczb¸e pierwsz¸a to losujemy nieparzyst¸a liczb¸e, a mast¸epnie

sprawdzamy, czy jest ona pierwsza. Je˙zeli nie, to sprawdzamy nast¸epne liczby

91919

.

1.20

Zadania

1. Dla ka˙zdej z liczb:

,

,

oraz

)

znajd´z liczb˛e

tak ˛

a,

˙ze

63

.

2. W pier´scieniu

wykonaj działania

oraz

.

3. W pier´scieniu

rozwi ˛

a˙z równania: a)

, b)

, c)

8

, d)

8

.

4. W pier´scieniu

rozwi ˛

a˙z równania: a)

, b)

.

5. W pier´scieniu

rozwi ˛

a˙z równania: a)

-

, b)

.

6. Dla liczb

i

)

oblicz

oraz liczby całkowite

i

spełniaj¸ace równanie

6

.

7. Oblicz

(

.

8. W pier´scieniu

rozwi ˛

a˙z równania: a)

3

.

9. W pier´scieniu

rozwi ˛

a˙z równania: a)

, b)

.

10. Znajd´z całkowite rozwi¸azanie

spełniaj¸ace równanie:

.

11. Podaj rozkład na czynniki pierwsze liczb

oraz

)

.

12. Ile dzielników ma liczba

?

13. Podaj tabliczk¸e dodawania i mno˙zenia w ciele

. Podaj elementy odwrotne do 5 i

6 w

.

14. Znajd´z elementy odwrotne do wszystkich elementów dwracalnych w

.

15. Dla jakich par reszt

istniej¸a liczby

spełniaj¸ace układ kongruencji:

63

63

9

16. Niech

i

b¸ed¸a dowolnymi dodatnimi liczbami całkowitymi. Dla jakich par

reszt

istniej¸a liczby

spełniaj¸ace układ kongruencji:

63

63

9

1.21. Problemy

33

1.21

Problemy

1.21.1

Najwi˛ekszy wspólny dzielnik

Udowodnij, ˙ze

jest najmniejsz¸a dodatni¸a liczb¸a

, dla której istnieje

i

całkowite, takie ˙ze

(

.

Udowodnij, ˙ze ka˙zda liczba postaci

(

, dla

i

całkowitych, jest wielokrotno´sci¸a

, i na odwrót, ka˙zda wielokrotno´s´c

jest postaci

(

, dla jaki´s

i

całkowitych.

Udowodnij, ˙ze poni˙zszy algorytm poprawnie oblicza najwi¸ekszy wspólny dzielnik

, je˙zeli

$

:

var a,b,p,q,r,:integer;

begin

readln(a,b);

p:=a;q:=b;

while q >0 do

begin

r:=p mod q;

p:=q; q:=r

end;

writeln(’NWD(’,a,’,’,b,’)=’,p)

end.

Zmodyfikuj powy˙zszy program, tak aby oprócz

, obliczał tak˙ze współ-

czynniki

i

, takie ˙ze

6

.

1.21.2

Najmniejsza wspólna wielokrotno´

s´

c

Niech

oznacza najmniejsz¸a wspóln¸a wielokrotno´s´c liczb

i

.

Udowodnij, ˙ze

dzieli ka˙zd¸a inn¸a wspóln¸a wielokrotno´s´c liczb

i

.

Poka˙z, ˙ze

1.21.3

Liczby wzgl˛ednie pierwsze

Udowodnij, ˙ze je˙zeli

jest wzgl¸ednie pierwsze z

i

, to

jest wzgl¸ednie pierwsze z

iloczynem tych liczb

6

.

Jako wniosek udowodnij, ˙ze je˙zeli

jest wzgl¸ednie pierwsze z ka˙zd¸a z liczb

919

9

,

to

jest wzgl¸ednie pierwsze z iloczynem tych liczb

9

34

Rozdział 1. Teoria liczb

1.21.4

Układ kongruencji

Istnieje inny sposób rozwi¸azywania układu kongruencji. Poka˙zemy go na przykładzie
układu

63

(1.8)

63

Najpierw szukamy dwóch liczb

i

spełniaj¸acych warunki

63

63

63

63

Udowodnij, ˙ze rozwi¸azaniem układu (1.8) jest

63

9

Jak policzy´c

oraz

? Poniewa˙z 3 i 5 s¸a wzgl¸ednie pierwsze, wi¸ec istniej¸a

i

takie,

˙ze

Poka˙z, ˙ze je˙zeli podstawimy

63

oraz

63

, to b¸edzie

dobrze.

1.21.5

Chi ´

nskie twierdzenie o resztach

Z chi´nskiego twierdzenia o resztach wynika, ˙ze je˙zeli

, to funkcja

63

63

stanowi wzajemnie jednoznaczne odwzorowanie pomi¸edzy

a iloczynem kartezja ´n-

skim

.

Na iloczynie kartezja ´nskim

mo˙zemy okre´sli´c działania dodawania i mno˙ze-

nia w nast¸epuj¸acy sposób:

9

Łatwo mo˙zna sprawdzi´c, ˙ze zbiór

z tak okre´slonymi działaniami, jest pier´scie-

niem. Ponadto funkcja

spełnia warunki

oraz

.