Badanie zależności pomiędzy dwiema cechami 

 

SKALA INTERWAŁOWA 

 
współczynnik korelacji liniowej r Pearsona 
 

 

 
  -1 <=r<= 1 
r – współczynnik korelacji liniowej w próbie 
n – liczebność próby 

i

x

- 

poszczególne wartości cechy x 

i

y

 - 

poszczególne wartości cechy y 

 

Po wyznaczeniu współczynnika korelacji liniowej w próbie należy sprawdzić 

jego istotność.  

 

Test  t  Studenta  dla  sprawdzania  istotności  współczynnika  korelacji   r 
Pearsona  
 
Test  służy  do  weryfikacji  hipotezy  o  braku  zależności  pomiędzy  dwiema  cechami 
pochodzącymi z dwóch populacji. 
 
W ar u nk i   st o so wan i a t e st u:    

 

Pomiar obydwu cech na skali interwałowej 

  

Badane  zmienne  w  obydwu  populacjach  mają  rozkład  zgodny  z rozkładem 
normalnym ( sprawdzić korzystając z testu normalności) 

 
H

0

: R

 =

 0                                   R- współczynnik korelacji liniowej w populacji 

H

1

:

 

R

 ≠

  0 

 

t=

2

1

2

n

r

r

 

 

Jeżeli p<=0,05 to H

0

 odrzucamy,  przyjmując H

1

 

Jeżeli p>0,05 to nie ma podstaw do odrzucenia H

0

 

 

Jeżeli,  za pomocą testu t Studenta dla sprawdzania istotności współczynnika 

korelacji stwierdzimy, że istnieje zależność liniowa pomiędzy badanymi cechami, to 
możemy  wtedy  wyznaczyć  jeszcze  równanie  tej  zależności,  zwane  równaniem 
regresji liniowej. 

n

i

n

i

i

i

n

i

n

i

i

i

n

i

n

i

n

i

i

i

i

i

y

n

y

x

n

x

y

x

n

y

x

r

1

2

1

2

1

2

1

2

1

1

1

1

1

1

 
y=a+bx,   gdzie b – współczynnik regresji           a - odległość linii regresji od osi X 
 
Interpretacja współczynnika korelacji Pearsona, gdy jest on istotny. 
Jeżeli  współczynnik  korelacji  liniowej  r>0  oraz  istnieje  zależność  pomiędzy 
badanymi cechami, to wraz ze wzrostem cechy x, rosną wartości cechy y. Natomiast, 
jeżeli współczynnik korelacji liniowej r<0 oraz istnieje zależność pomiędzy badanymi 
cechami, to wzrost cechy x, powoduje spadek wartości cechy y. 
 
Oprócz współczynnika korelacji r wyznacza sie także współczynnik determinacji r

2

. 

Współczynnik ten określa, jaką część ogólnej zmienności zmiennej zależnej y, można 
przypisać zależności od zmiennej x.      
 
 

SKALA PORZĄDKOWA 

 
współczynnik korelacji rangowej r

s

 Spearmana 

 

r

s

=

n

n

d

n

i

i

3

1

2

6

1

                        -1<=r

s

<=1 

 
 r

s

 – współczynnik korelacji rangowej w próbie,  n – liczebność próby 

d

i

 – różnica pomiędzy rangami odpowiadających sobie wartości cechy x oraz cechy y 

 

Po wyznaczeniu współczynnika korelacji rangowej w próbie należy sprawdzić 

jego istotność.  

 

Test  t  Studenta  dla  sprawdzania  istotności  współczynnika  korelacji   r

s

 

Spearmana  
 
Test  służy  do  weryfikacji  hipotezy  o  braku  zależności  pomiędzy  dwiema  cechami 
pochodzącymi z dwóch populacji. 
 
W ar u nk i   st o so wan i a t e st u:    

 

Pomiar  co  najmniej  jednej  z  cech,  na  skali  porządkowej  lub  na  skali 
interwałowej z brakiem normalności rozkładu 

H

0

: R

s =

 0                                   R

s

- współczynnik korelacji rangowej w populacji 

H

1

:

 

R

s ≠

  0 

 

t=

2

1

2

n

r

r

s

s

 

 

Jeżeli p<=0,05 to H

0

 odrzucamy,  przyjmując H

1

 

Jeżeli p>0,05 to nie ma podstaw do odrzucenia H

0

 

 

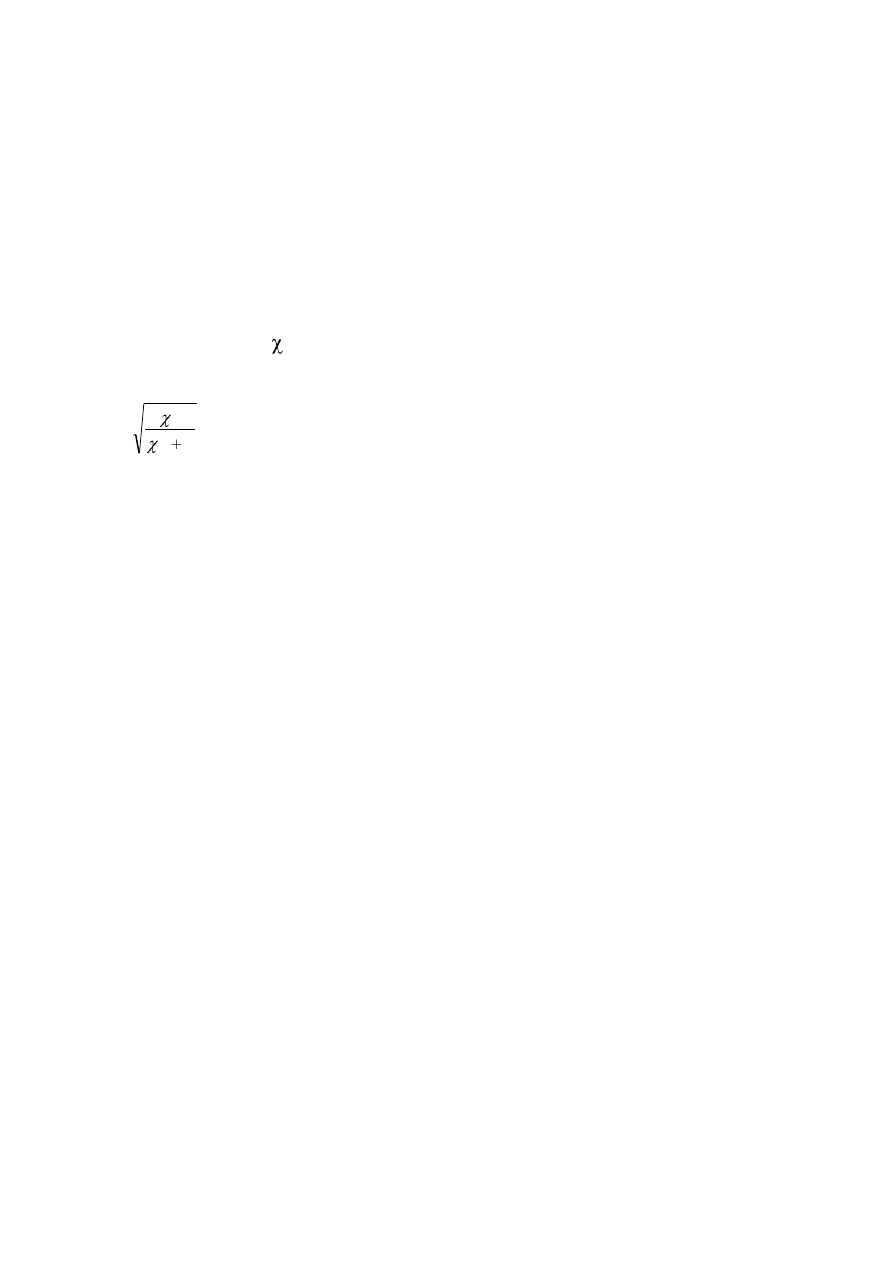
Interpretacja współczynnika korelacji Spearmana, gdy jest on istotny. 
Jeżeli  współczynnik  korelacji  rangowej  r

s

>0  oraz  istnieje  zależność  pomiędzy 

badanymi cechami, to wraz ze wzrostem cechy x, rosną wartości cechy y. Natomiast, 
jeżeli  współczynnik  korelacji  rangowej  r

s

<0  oraz  istnieje  zależność  pomiędzy 

badanymi cechami, to wzrost cechy x, powoduje spadek wartości cechy y. 

 

SKALA NOMINALNA 

 
współczynnik C Pearsona 

Współczynnik  ten  wyznaczamy  tylko  wtedy,  jeżeli  uprzednio  przy  użyciu 

testu  niezależności 

2

,  

stwierdzimy,  że  istnieje  zależność  pomiędzy  badanymi 

cechami. Wówczas współczynnik C oznacza siłę tej zależności. 

 

C=

n

2

2

              0 < C<1 

 

Interpretacja współczynnika C Pearsona 

 

Jeżeli C<0.3 , to zależność jest słaba, 

 

jeżeli 0.3 <=C<0.6 , to zależność jest średnia, 

 

jeżeli C>=0.6 , to zależność jest silna.