Projekt "Modernizacja oferty kształcenia zawodowego w powiązaniu z potrzebami lokalnego/
regionalnego rynku pracy" współfinansowany ze środków Unii Europejskiej w ramach Europejskiego
Funduszu Społecznego.
1 z 5
Instrukcja do ćwiczenia 10
Dział – Pomiary wielkości elektrycznych.
Temat: Minimalizacja funkcji – tablicami
Karnaugh
.
Cel ćwiczenia: poznanie sposobu minimalizacji funkcji logicznych.
I.
Wprowadzenie
W informatyce często staje się przed problemem minimalizacji funkcji logicznych.
Zanim jednak przejdziemy do omówienia tego zagadnienia, musimy przejść przez wszystkie
definicje, które powiedzą nam, czym tak naprawdę jest funkcja logiczna. Zagadnienie
związane z minimalizacją funkcji logicznych można sformułować na wiele sposobów. Przede
wszystkim jest to problem, jak uprościć funkcję logiczną tak, by jej zapis był jak najbardziej
zwięzły. Innymi słowy, problem sprowadza się także do znalezienia funkcji minimalnej, która
pod względem logicznym będzie równoważna naszej wyjściowej funkcji.
Jednak, jakie są kryteria, które mówią, jak bardzo funkcja jest skomplikowana? Całe
szczęście jest to określone. Mianowicie, wprowadzone zostało pojęcie, które mówi
o współczynniku skomplikowania funkcji. Najczęściej definiuje się go jako ilość spójników
logicznych w zapisie funkcji, oczywiście w zależności od ilości zmiennych funkcja będzie
mniej lub bardziej skomplikowana. Jednak zawsze daną funkcję da się zapisać jako funkcję
o dużo większym skomplikowaniu, używając do tego tak zwanych iloczynów pełnych.
Metoda tablic Karnaugh
Najpopularniejszą algorytmiczną metodą upraszczania funkcji logicznych jest metoda tablic
Karnaugh, zwana także metodą Veitcha. Stosuje się tutaj diagramy, przypominające
kwadratowe lub prostokątne tablice. W zależności od ilości zmiennych, od których jest
uzależniona funkcja, tablica ta jest większa. Konkretnie dla n zmiennych mamy 2
n
pól
w tablicy, dlatego dla wielu zmiennych ta metoda jest dość żmudna i raczej niemożliwa do
przeprowadzenia. Jednak w ręcznym minimalizowaniu funkcji do czterech-pięciu zmiennych
jest chyba najwygodniejszą.
Tablica Karnaugh wygląda w sposób następujący. Przede wszystkim, każde z pól
posiada swój określony numer, który odpowiada numerowi iloczynu pełnego. Często pomija
się ten numer, ponieważ używa się łatwych do zapamiętania tablic, jednak warto zawsze
w rogu komórki pisać, jaki numer odpowiada danemu polu, zwłaszcza na początku. Oprócz
numeru komórki w danym polu wprowadza się jeden z trzech symboli. Pierwszy z nich to
symbol 1, kiedy w zapisie funkcji znajduje się iloczyn pełny oznaczony numerem komórki, 0,
kiedy danego iloczynu pełnego nie ma w zapisie funkcji. Możliwe jest także, że niektóre
iloczyny pełne są tak zwanymi iloczynami nieistotnymi, gdzie nie jest ważne, jaka wartość
funkcji jest dla niektórych wartości argumentów. Wówczas w kratce tablicy Karnaugh stawia
się trzeci symbol - może to być na przykład znak X.
Najczęściej używa się następujących uporządkowań dla tablic Karnaugh (kolejność
zmiennych od a):
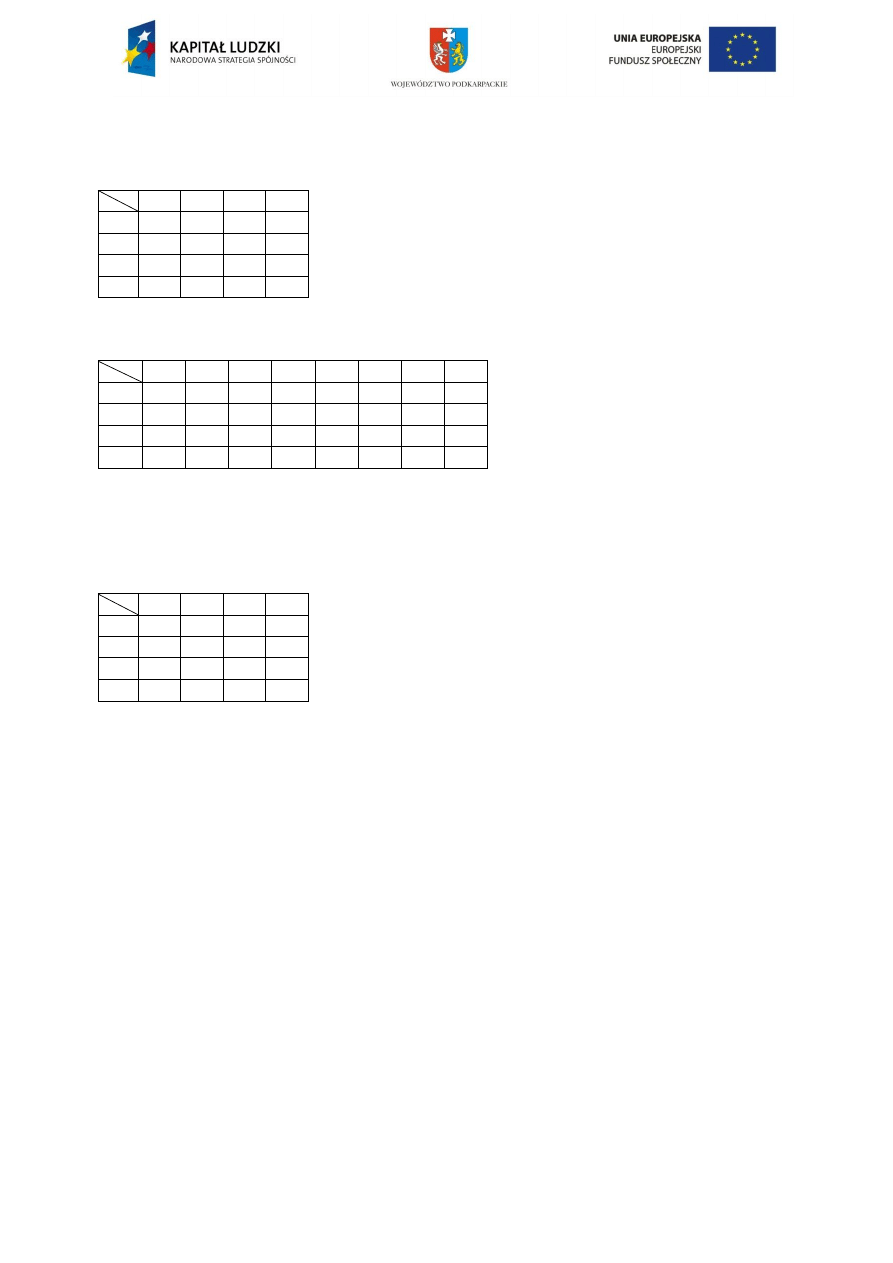
Projekt "Modernizacja oferty kształcenia zawodowego w powiązaniu z potrzebami lokalnego/
regionalnego rynku pracy" współfinansowany ze środków Unii Europejskiej w ramach Europejskiego
Funduszu Społecznego.
2 z 5
Tablica dla czterech zmiennych:
ab
cd
00
01
11
10
00
0
1
3
2
01
4
5
7
6
11
12
13
15
14
10
8
9
11
10
Tablica dla pięciu zmiennych:
ab
cde
000 001 011 010 110 111 101 100
00
0
1
3
2
6
7
5
4
01
8
9
11
10
14
15
13
12
11
24
25
27
26
30
31
29
28
10
16
17
19
18
22
23
21
20
Mając daną funkcję f(a,b,c,d) = Σ(1,2,3,6)+ Σn(5,9,12,13)należy przepisać ją do tablicy
Karnaugh dla czterech zmiennych. Tam, gdzie mamy iloczyny pod znakiem "sumy"
wpisujemy jedynkę, tam gdzie mamy iloczyny pod znakiem "sumy nieistotnej" wstawiamy
gwiazdkę, w reszcie pól wstawiamy zera.
ab
cd
00
01
11
10
00
0
1
1
1
01
x
0
0
1
11
x
x
0
0
10
0
x
0
0
Minimalizacja polega na tym, by zawsze szukać w diagramie par, dwójek, czwórek
lub innych potęg dwójki pól, które znajdują się obok siebie, przy czym należy przyjąć, że
tablica Karnaugh jest "zawijalna", to znaczy skrajne pola są sąsiadujące. Przy poszukiwaniu
takich grup pól bierzemy pod uwagę tylko te pola, w których widnieją jedynki lub X, które
można potraktować jako jedynki lub zera, ponieważ nie jest istotne, jaką wartość przyjmuje
funkcja dla tego iloczyny pełnego.
Następnym krokiem jest określenie, jaki adres ma całość grupy wybranej i sklejonej.
Jeśli na przykład w diagramie czterech zmiennych wybierzemy grupę ośmiu elementów, to
może ona mieć adres ZM lub
, gdzie ZM jest nazwą pewnej zmiennej.
Istnieje szereg zasad, według których należy wybierać elementy grup. Przede wszystkim
należy pamiętać o tym, by każda jedynka była reprezentowana w jakiejś grupie. Jeżeli nie da
się dołożyć jedynki do żadnej grupy, wówczas należy w rozwiązaniu podać także jej pełny
adres, czyli iloczyn pełny, który jest przez nią reprezentowany. Oczywiście należy pamiętać,
by nie szastać ilością grup - musi ich być jak najmniej by otrzymać funkcję o jak
najmniejszym współczynniku skomplikowania. Jeśli oda nam się wybrać taki minimalny
zbiór "pokrycia" diagramu, możemy uważać powstałą formułę za minimalną.
Projekt "Modernizacja oferty kształcenia zawodowego w powiązaniu z potrzebami lokalnego/
regionalnego rynku pracy" współfinansowany ze środków Unii Europejskiej w ramach Europejskiego
Funduszu Społecznego.
3 z 5
Wszystko to brzmi na pewno bardzo niejasno, dlatego najlepszym rozwiązaniem będzie
obejrzenie przykładu.
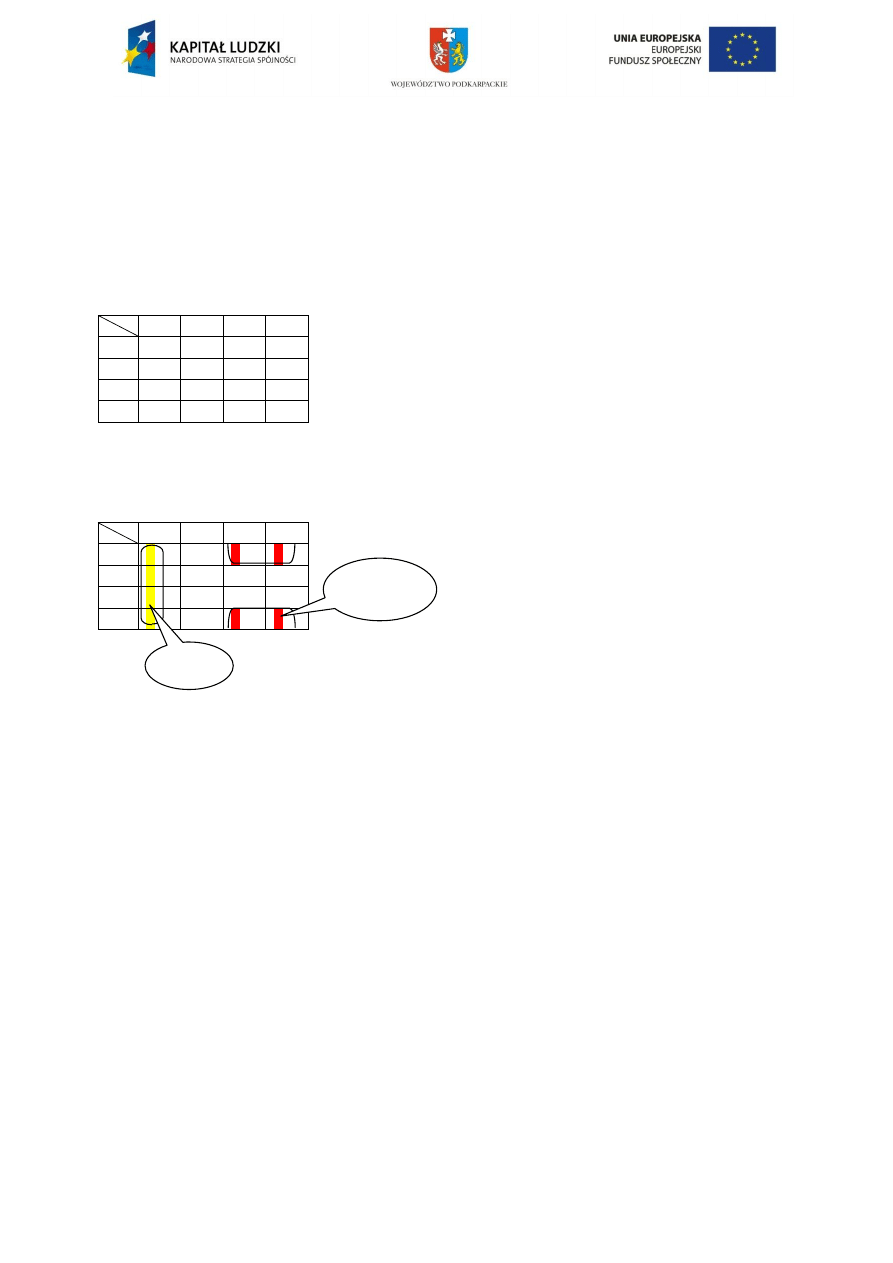
Mamy funkcję logiczną
f(a,b,c,d) = Σ(0,2,3,4,8,10,11,12).
Na razie bez iloczynów nieistotnych. Odpowiadający jej diagram będzie wyglądał
następująco:
ab
cd
00
01
11
10
00
1
0
1
1
01
1
0
0
0
11
1
0
0
0
10
1
0
1
1
Teraz naszym zadaniem jest odnalezienie elementów sąsiadujących ze sobą w grupach po
dwa, cztery lub osiem. Ósemek nie mamy, mamy za to dwie czwórki:
ab
cd
00
01
11
10
00
1
0
1
1
01
1
0
0
0
11
1
0
0
0
10
1
0
1
1
Pamiętajmy, że skrajne elementy też są sąsiadujące, dlatego grupę numer dwa można było
stworzyć właśnie w taki sposób. Teraz należy określić adresy zaznaczonych grup.
Grupa pierwsza znajduje się zarówno w pasie zmiennej
̅ oraz w pasie zmiennej ̅. Dlatego
adres tej grupy będzie
̅ ̅.
Grupa druga leży na przecięciu pasów oraz c, dlatego jej adresem będzie c.
W ten sposób otrzymaliśmy formułę funkcji:
f(a,b,c,d) = c +
̅ ̅
II. Treść zadania.
Przy użyciu tablic
Karnaugh zminimalizuj funkcje i zaprojektuj układ logiczny na bramkach 2
wejściowych. Wykonaj układy logiczny i sprawdź jego działanie, wyniki umieść w tabeli prawdy.
Funkcje:
a)
( , , , ) = ∑(0,2,5,8,10) + ∑ (13)
b)
( , , , ) = ∑(1,3,7,9,11) + ∑ (6)
c)
( , , , ) = ∑(4,5,6,12,13) + ∑ (14)
Grupa1
Grupa 2
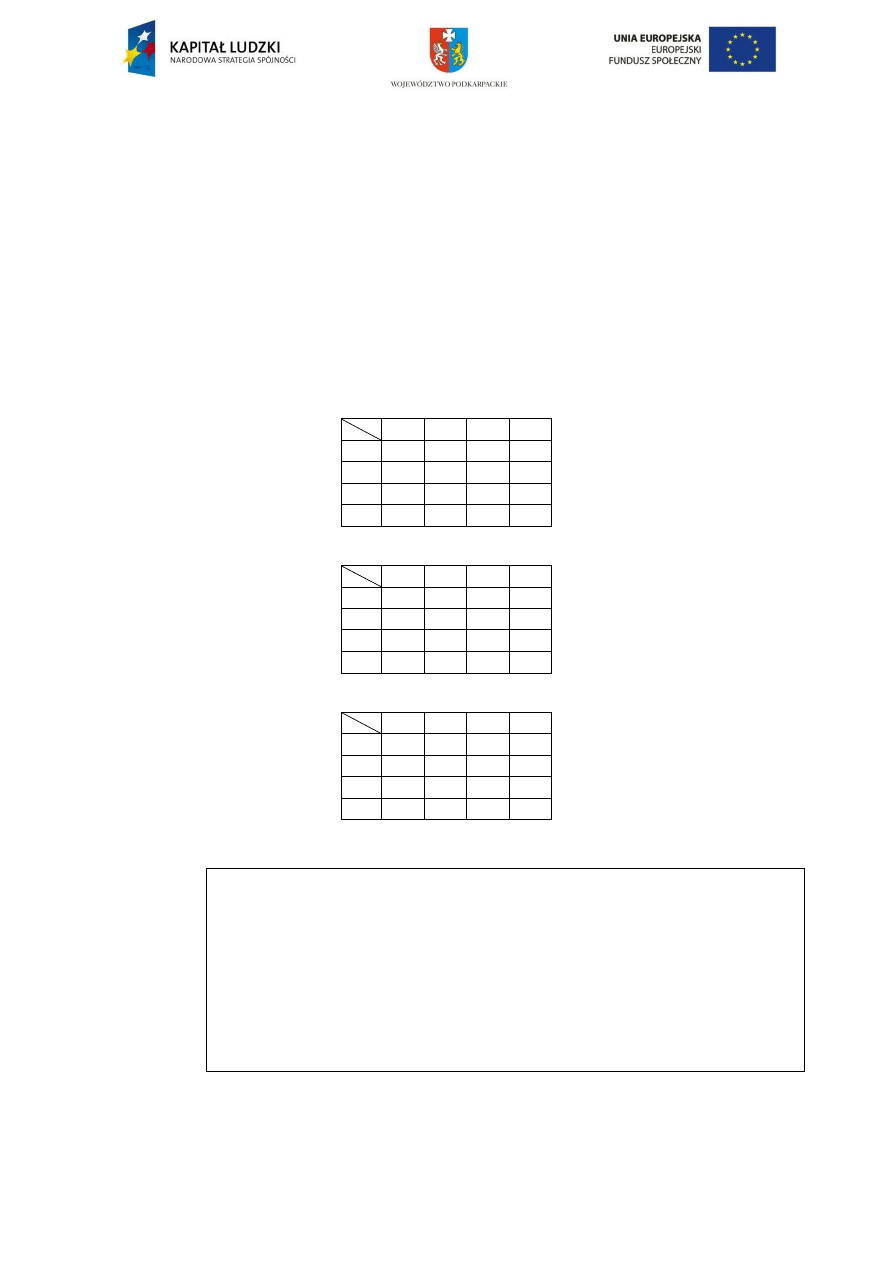
Projekt "Modernizacja oferty kształcenia zawodowego w powiązaniu z potrzebami lokalnego/
regionalnego rynku pracy" współfinansowany ze środków Unii Europejskiej w ramach Europejskiego
Funduszu Społecznego.
4 z 5
Sposób postępowania:
1.
Zapoznać się z treścią zadania.
2.
Dokonać minimalizacji funkcji.
3.
Na podstawie otrzymanej funkcji, narysuj schemat składający się z bramek 2
wejściowych.
4.
Połącz układ i sprawdź jego działanie.
5.
Wyniki wpisz do tabeli prawdy.
6.
Zapisz wnioski i spostrzeżenia
III. Sprawozdanie z przeprowadzonego ćwiczenia.
1.
Tablice
Karnaugh funkcji
a)
f(a,b,c,d)=
ab
cd
00
01
11
10
00
0
1
3
2
01
4
5
7
6
11
12
13
15
14
10
8
9
11
10
b)
f(a,b,c,d)=
ab
cd
00
01 11
10
00
0
1
3
2
01
4
5
7
6
11
12
13
15
14
10
8
9
11
10
c)
f(a,b,c,d)=
ab
cd
00
01 11
10
00
0
1
3
2
01
4
5
7
6
11
12
13
15
14
10
8
9
11
10
2.
Schemat układu pomiarowego.
Projekt "Modernizacja oferty kształcenia zawodowego w powiązaniu z potrzebami lokalnego/
regionalnego rynku pracy" współfinansowany ze środków Unii Europejskiej w ramach Europejskiego
Funduszu Społecznego.
5 z 5
3.
Tablica prawdy.
Wejścia
Wyjścia funkcji
a
b
c
d
Y
A
Y
B
Y
C
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
4.
Uwagi i wnioski.