INFORMATYKA I ROK STUDIA INŻYNIERSKIE NIESTACJONARNE SAN

SEMESTR LETNI 2016 ĆWICZENIA Z FIZYKI

ZADANIA KONTROLNE

Dział I: Podstawy mechaniki.

Zadania.

Dla wszystkich zadań należy przyjąć wartość przyspieszenia ziemskiego g=10m/s2.

1. Motocyklista przebył 1/3 drogi z prędkością 60km/h, a pozostałą część drogi z prędkością

30km/h. Jaka była średnia prędkość motocyklisty na całej drodze ?

2. Jaki kąt powinna tworzyć oś symetrii kajaka płynącego względem wody z prędkością

v=3m/s z linią brzegu rzeki płynącej z prędkością u=1,5m/s, aby kajak płynął prostopadle do

brzegu rzeki ? Z jaką prędkością płynie kajak względem brzegu ?

3. W czwartej sekundzie ruchu jednostajnie zmiennego bez prędkości początkowej ciało

przebyło drogę s=2m. Jaką prędkość osiągnie to ciało pod koniec siódmej sekundy ruchu?

4. Znajdź szybkość kuli, jeżeli po wystrzale z pistoletu w kierunku poziomym kula przebiła

dwie pionowe kartki papieru ustawione w odległości l=20m od siebie, przy czym okazało się,

że otwór w drugiej kartce znajduje się o h=5cm niżej niż otwór w pierwszej kartce.

5. Pod jakim kątem do poziomu wyrzucono ciało, jeżeli wiadomo, że maksymalna wysokość

na jaką wzniosło się ciało, jest cztery razy mniejsza od zasięgu rzutu ?

6. Z wieży o wysokości 20m wyrzucono w kierunku poziomym ciało z szybkością 10m/s.

Napisz równanie toru tego ciała. Jaka jest szybkość ciała w chwili upadku ? Jaki kąt tworzy

wtedy wektor prędkości z płaszczyzną poziomą ?

7. O ile trzeba zmniejszyć szybkość jednej z gąsienic ciągnika, poruszającego się z szybkością

v=24km/h, aby jego środek ciężkości mógł poruszać się po okręgu o promieniu R=9m, jeżeli

odległość między gąsienicami wynosi d=1,5m ?

8. Z jakim przyspieszeniem zsuwa się ciało z równi pochyłej o kącie nachylenia α=30

o

, jeżeli

współczynnik tarcia ciała o równię ma wartość f=0,2 ?

9. Na jaką wysokość wsunie się ciało na równię pochyłą o kącie nachylenia, α=30

o

, jeżeli u

podstawy równi nadano mu prędkość v

0

=10m/s, a wartość współczynnika tarcia ciała o

równię ma wartość f=0,1 ?

10. Przez nieważki bloczek zamocowany na szczycie równi pochyłej o kącie nachylenia

α=30

o

przerzucono nieważką, nierozciągliwą nić na końcach której zamocowano dwa ciała o

takich samych masach m

1

=m

2

=2kg. Oblicz przyspieszenie ciał oraz naciąg nici, jeżeli

współczynnik tarcia ciała o równię ma wartość f=0,1.

11. Z jaką siłą naciska ciało o masie m=4kg na podłogę windy:

a/ ruszającej do góry z przyspieszenie; 2m/s

2

b/ hamującej w ruchu do góry z opóźnieniem 2m/s

2

?

12. Z jaką siłą naciska motocyklista o masie 60kg na siodełko motocykla, przejeżdżając

najwyższy punkt mostu o promieniu krzywizny R=40m z prędkością v=36km/h ? Z jaką

prędkością musiałby jechać motocyklista, aby w najwyższym punkcie mostu nie naciskać na

siodełko (być w chwilowym stanie nieważkości) ?

13. Pod jakim kątem do poziomu musi nachylić się rowerzysta wjeżdżający w zakręt o

promieniu r=50m z prędkością v=10m/s ?

14. O jaki kąt odchyli się od pionu linka o długości l=2m, jeżeli okres obiegu kulki na niej

zawieszonej w płaszczyźnie poziomej wynosi T=2s ?

15. Z jaką maksymalną prędkością może wjechać samochód w zakręt o promieniu r=20m,

jeżeli współczynnik tarcia pomiędzy kołami a nawierzchnią ma wartość f=0,6 ?

16. Na poziomej płaszczyźnie spoczywa drewniana kula o masie m1=1kg. Pocisk pistoletowy

o masie m2=5g przebija kulę wzdłuż poziomej średnicy. Prędkość pocisku przed zderzeniem

z kulą wynosiła v1=500m/s, a po przebiciu kuli ma wartość v2=150m/s. Z jaką prędkością

porusza się kula po przejściu przez nią pocisku ?

17. Po poziomym torze powietrznym (bez tarcia) porusza się z prędkością v

0

=2m/s układ

dwóch ciał o masach: m

1

=1kg oraz m

2

=0,5kg, pomiędzy które wciśnięto sprężynę. W pewnej

chwili sprężynę zwalniamy. Jaką jest prędkość ciała o masie m

2

względem ciała o masie m

1

,

jeżeli po zwolnieniu sprężyny ciało o masie m

1

zatrzymało się ?

18. Wyznacz odległość, na jaką przesunie się łódź stojąca nieruchomo na wodzie, jeżeli

człowiek o masie m

1

=70kg przejdzie z dziobu na rufę, jeżeli długość łodzi wynosi l=2,5m, a

jej masa m

2

=140kg.

19. Samochód jedzie z prędkością v=54km/h. Współczynnik tarcia statycznego kół o podłoże

ma wartość f=0,6. Oblicz najkrótszą drogę na jakiej samochód może wyhamować do

zatrzymania.

20. Oblicz siłę ciągu silnika samochodowego o mocy P=150kW, jeżeli samochód porusza się

ruchem jednostajnym z prędkością v=15m/s.

21. Piłkę rzucono pionowo do góry z prędkością początkową v

0

=8m/s. Jaką prędkość będzie

miała piłka na wysokości równej połowie maksymalnego wzniesienia ?

22. W pudełko z piaskiem o masie m

1

=4kg, swobodnie zawieszone na nici, uderza pocisk o

masie m

2

=10g i grzęźnie w nim. Odległość od punktu zaczepienia nici do środka masy

pudełka wynosi l=1m. Oblicz prędkość pocisku, jeżeli na skutek uderzenia pudełko odchyliło

się od położenia równowagi tak, że nitka tworzyła z pionem kąt α=60

o

.

23. Ciało zsuwa się z równi pochyłej bez oporów ruchu i wpada do pierścienia ustawionego w

płaszczyźnie pionowej o promieniu R=80cm. Z jakiej najmniejszej wysokości powinno

zsuwać się ciało, aby mogło zatoczyć pełny okrąg bez oderwania się w najwyższym punkcie ?

24. Z wiatrówki strzelono do drewnianego klocka leżącego w odległości l=50cm od końca

stołu. Śrut o masie m=1g lecący poziomo z prędkością v=150m/s przebija klocek i leci dalej z

prędkością v

1

=75m/s. Masa klocka wynosi M=50g. Przy jakiej wartości współczynnika tarcia

klocka o stół nie spadnie on ze stołu ?

25. Przez bloczek zamocowany na szczycie równi pochyłej o kącie nachylenia α=30

o

przerzucono nieważką, nierozciągliwą nić, na końcach której zamocowano dwa ciała o takich

samych masach m

1

=m

2

=2kg. Oblicz przyspieszenie ciał oraz naciąg nici, jeżeli współczynnik

tarcia ciała o równię ma wartość f=0,1, a masa bloczka ma wartość M=0,1kg.

26. Jednorodna deska oparta jest o ścianę i podłogę. Przyjmując, że tarcie występuje tylko

między deską i podłogą, wyznacz najmniejszy kąt α, jaki deska pozostająca w równowadze

może tworzyć z poziomem, jeżeli współczynnik tarcia deski o podłogę ma wartość f=0,1.

Dział II: Drgania mechaniczne.

Zadania.

Dla wszystkich zadań należy przyjąć wartość przyspieszenia ziemskiego g=10m/s2.

1. Po jakim czasie od chwili początkowej punkt materialny wykonujący drgania harmoniczne

przesunie się na odległość równą połowie amplitudy, jeżeli faza początkowa jest równa zeru,

a okres T=6s ?

2. Oblicz okres drgań punktu materialnego, jeżeli po czasie t=1s jego wychylenie z położenia

równowagi wynosi x(t

1s)

A 2 / 2

=

=

, gdzie A jest amplitudą. Przyjmij, że faza początkowa

ruchu ma wartość zero.

3. Oblicz średnią prędkość w ruchu harmonicznym, dla którego amplituda ma wartość

A=10cm, a okres wynosi T=0,4s.

4. Oblicz fazę początkową w ruchu harmonicznym, jeżeli wychylenie w tym ruchu dla t=0

jest równe 0.25 wartości A amplitudy.

5. Wyprowadź wzór pozwalający obliczyć okres wahadła sprężynowego składającego się z

ciężarka o masie m i sprężyny o współczynniku sprężystości k.

6. Wyprowadź wzór pozwalający obliczyć okres wahadła matematycznego, które jest

utworzone z masy punktowej m zawieszonej na nieważkiej nici o długości l.

7. Wyprowadź wzór pozwalający obliczyć okres drgań wahadła fizycznego utworzonego z

bryły o masie m zawieszonej w odległości d od środka masy, jeżeli moment bezwładności tej

bryły względem osi obrotu wahadła ma wartość I.

8. Oblicz częstotliwość drgań cieczy o gęstości i masie m umieszczonej w rurce wygiętej w

kształcie litery U o polu przekroju o wartości S, gdy ciecz wyprowadzimy z położenia

równowagi (np. dmuchając w jedno z ramion).

9. Na sprężynie wisi pewien ciężarek i drga ruchem harmonicznym z okresem T=0,5s. Po

doczepieniu dodatkowego obciążenia okres drgań zwiększył się do T’=0,6s. O ile wydłużyła

się sprężyna wskutek tego dodatkowego obciążenia ?

10. Narysuj wykres zależności energii potencjalnej od wychylenia E

p

(x) dla ruchu

harmonicznego z fazą początkową wynoszącą zero.

11. Narysuj wykres zależności energii kinetycznej od wychylenia E

k

(x) dla ruchu

harmonicznego z fazą początkową wynoszącą zero.

12. Narysuj wykres zależności energii całkowitej od wychylenia E

c

(x) dla ruchu

harmonicznego.

13. Znajdź okres drgań układu sprężyn połączonych równolegle oraz szeregowo, jeżeli

współczynniki sprężystości sprężyn wynoszą k

1

i k

2

, zaś masa ciężarka jest równa m.

14. Z wysokości H na wagę sprężynową skacze człowiek o masie M. Zakładając, że drgania

nie są tłumione i współczynnik sprężystości sprężyny wagi wynosi k, oblicz amplitudę drgań

wagi.

15. Wyznacz amplitudę drgań harmonicznych punktu materialnego, jeżeli jego całkowita

energia drgań jest równa 0.004J, a działająca nań siła przy wychyleniu do połowy amplitudy

ma wartość 2N.

16. Wyznacz okres drgań wahadła matematycznego o długości L i masie m umieszczonego:

a/ w windzie ruszającej do góry z przyspieszeniem a;

b/ w windzie ruszającej w dół z przyspieszeniem a;

c/ w ruszającym z przyspieszeniem a autobusie.

17. Wyznacz częstotliwość drgań ciężarka o masie m=0,2kg zawieszonego na sprężynie o

współczynniku sprężystości k=50N/m i zanurzonego w oleju o współczynniku oporu

b=0,5kg/s.

18. Oblicz okres drgań tarczy (traktowanej jako wahadło fizyczne), którą oś obrotu przebija w

połowie promienia R.

Dział III: Elektrostatyka. Obwody prądu

stałego.

1. Dwa ładunki tego samego znaku i o tej samej wartości wynoszącej 4 µC umieszczono w

odległości 1 m od siebie. Wyznacz natężenie pola elektrostatycznego w punkcie leżącym w

odległości 2 m od odcinka łączącego oba ładunki i należącym do symetralnej tego odcinka.

2. Wyznacz natężenie pola elektrostatycznego pochodzącego od naładowanego ładunkiem Q

pierścienia o promieniu r w punkcie należącym do prostej przechodzącej przez środek

pierścienia i prostopadłej do płaszczyzny wyznaczonej przez pierścień, odległym o d od jego

środka.

3. Dwa ładunki o wartościach 9µC i 4µC znajdują się w odległości 5 cm od siebie. Wyznacz

odległość od większego ładunku punktu, w którym natężenie pola elektrostatycznego

przyjmuje wartość zero.

4. W jednorodne pole elektrostatyczne wytworzone między dwoma równoległymi płytami,

naładowanymi ładunkami przeciwnego znaku, odległymi od siebie o d wpada, prostopadle do

linii sił pola, z prędkością v

0

, ładunek o wartości q i masie m. Wyznacz kąt jaki będzie

tworzyć kierunek prędkości ładunku po przejściu całej przestrzeni między płytami z

kierunkiem v

0

, jeżeli napięcie między płytami ma wartość U, a ich długość w kierunku ruchu

początkowego ładunku wynosi L.

5. Jaką wartość ma natężenie pola elektrostatycznego w odległości r od nieskończonego,

naładowanego pręta, jeżeli gęstość liniowa ładunku na pręcie wynosi λ ?

6. Jakie pole elektrostatyczne jest w pobliżu płaskiej naładowanej z gęstością powierzchniową

σ

płaszczyzny ? Określ kierunek i wartość tego natężenia.

7. Wyznacz natężenie pola elektrostatycznego między dwoma równoległymi płaszczyznami

naładowanymi ładunkami o przeciwnych znakach i takich samych gęstościach

powierzchniowych

σ

.

8. Wyznacz natężenie pola elektrostatycznego między dwoma równoległymi płaszczyznami

naładowanymi ładunkami o takich samych znakach i takich samych gęstościach

powierzchniowych

σ

.

9. Długi przewodzący walec o promieniu r, na którym umieszczono ładunek +q, otoczony jest

przez przewodzącą, cylindryczną powłokę o promieniu R i ładunku –2q. Wyznacz wartość

natężenia pola elektrostatycznego w obszarze między powłoką i walcem.

10. Dwa ładunki tego samego znaku i o tej samej wartości wynoszącej 4µC umieszczono w

odległości 1 m od siebie. Wyznacz potencjał pola elektrostatycznego w punkcie leżącym w

odległości 2 m od odcinka łączącego oba ładunki i należącym do symetralnej tego odcinka.

11. Trzy ładunki o wartościach +q, -4q i +2q umieszczono w wierzchołkach trójkąta

równobocznego o boku a. Oblicz pracę potrzebną do takiego ustawienia ładunków.

12. Udowodnij, że powierzchnia przewodnika jest powierzchnią ekwipotencjalną.

13. Jaki jest potencjał pola elektrostatycznego pola centralnego w odległości 20cm od źródła,

jeżeli natężenie pola w tym punkcie wynosi E=0,1N/C ?

14. Dwie kule o promieniach r

1

=10cm i r

2

=40cm oraz potencjałach V

1

=4000V i V

2

=1000V

połączono przewodnikiem o znikomej pojemności. Jaka jest wartość potencjału na pierwszej

kuli po połączeniu?

15. Kondensator cylindryczny składa się z dwóch współosiowych cylindrów o promieniach r i

R oraz długości l. Wyprowadź wzór na pojemność takiego kondensatora.

16. Wyprowadź wzór na pojemność kondensatora płaskiego, którego okładki oddalone są o d,

a ich powierzchnia wynosi S.

17. Dwa kondensatory o pojemnościach C

1

i C

2

połączono szeregowo. Oblicz pojemność

zastępczą takiego układu.

18. Dwa kondensatory o pojemnościach C

1

i C

2

połączono równolegle. Oblicz pojemność zastępczą

takiego układu.

19. Jak zmieni się pojemność i natężenie pola elektrostatycznego wewnątrz kondensatora

płaskiego, jeżeli jego okładki rozsuniemy na dwukrotnie większą odległość i będzie on po

naładowaniu odłączony od źródła napięcia ?

20. Jak zmieni się pojemność i natężenie pola elektrostatycznego wewnątrz kondensatora

płaskiego, jeżeli jego okładki rozsuniemy na dwukrotnie większą odległość i będzie on po

naładowaniu podłączony do źródła napięcia przez cały czas?

21. Jak zmieni się energia zgromadzona w naładowanym kondensatorze płaskim

podłączonym do źródła napięcia, jeżeli zmniejszymy dwukrotnie odległość między jego

okładkami?

22. Jak zmieni się energia zgromadzona w naładowanym kondensatorze płaskim odłączonym

od źródła napięcia, jeżeli zmniejszymy dwukrotnie odległość między jego okładkami?

23. Przewód aluminiowy o średnicy 2,54 mm jest połączony z przewodem miedzianym o

średnicy 1,65 mm . Przez tak połączone przewody przepływa prąd o natężeniu 10A. Jaka jest

gęstość prądu i spadek napięcia w każdym z przewodów ?

24. Jaka jest prędkość unoszenia elektronów w przewodniku miedzianym o średnicy 1,63mm,

jeżeli gęstość miedzi wynosi 9 g/cm3, masa molowa ma wartość 64 g/mol, a przez

przewodnik przepływa prąd o natężeniu 10 A. Obliczenia przeprowadź, zakładając, że 1 atom

miedzi uwalnia 1 elektron.

25. Ile metrów przewodnika z chromonikieliny o oporze właściwym ρ = 9,8•10

-7

Ω

m i

średnicy 2r = 0,5 mm musimy użyć do wykonania grzałki o mocy P = 250 W, pracującej pod

napięciem U = 220 V ?

26. Jaki prąd przepływa przez przewodnik o długości

∆

x i polu przekroju poprzecznego A,

jeżeli do jego końców przyłożona jest różnica potencjału

∆

V, przewodnictwo właściwe

materiału, z którego wykonano przewodnik wynosi

σ

?

27. Jak zmieni się opór kawałka drutu, jeżeli przy zachowanej masie jego średnicę

zmniejszymy dwa razy ?

28. W obwodzie składającym się z ogniwa o SEM E = 4 V i oporze wewnętrznym r = 1

Ω

zmieniono opór zewnętrzny z R

1

= 2

Ω

na R

2

= 10

Ω

. Oblicz różnicę pomiędzy wskazaniami

woltomierza mierzącego napięcie na oporze zewnętrznym.

29. Jeżeli elektrody ogniwa połączymy oporem R

1

= 5

Ω

to woltomierz dołączony do ogniwa

wskazuje napięcie U

1

= 10 V. Przy oporze R

2

= 2

Ω

napięcie to jest równe U

2

= 8 V. Oblicz

SEM ogniwa oraz jego opór wewnętrzny.

30. Mamy do dyspozycji dwie identyczne grzałki. Za pomocą jednej grzałki doprowadzamy

do wrzenia pewną ilość wody w czasie t = 2 minuty. Ile czasu potrzeba, aby (zaniedbując

straty) doprowadzić do wrzenia tę samą ilość wody za pomocą dwu grzałek połączonych:

a/ szeregowo;

b/ równolegle ?

31. Przewodnik o oporze 5

Ω

połączono z baterią o SEM wynoszącą 2 V i oporze

wewnętrznym 1

Ω

. Ile energii chemicznej przekształci się w energię elektryczną ? Ile energii

pojawi się w oporniku jako ciepło Joule’a ? Oblicz wydajność obwodu.

32. Ogniwo o sile elektromotorycznej E i oporze wewnętrznym r połączono ze zmiennym

oporem R. Narysuj wykres zależności mocy wydzielanej na oporze R w zależności od

natężenia prądu P(I) w obwodzie. Oblicz maksymalną moc P wydzielaną na oporze

zewnętrznym.

33. Bieguny ogniwa spinano dwoma różnymi oporami R

1

i R

2

, przy czym w obu przypadkach

wydzielone ilości ciepła w tych oporach były takie same. Oblicz opór wewnętrzny ogniwa r.

34. Za pomocą amperomierza o oporze wewnętrznym r = 2

Ω

przystosowanego do pomiaru

natężenia prądu w zakresie 0 – 0,1 A, należy dokonać pomiaru natężenia prądu w zakresie 0 –

0,5 A. Jaki opornik i jak należy dołączyć do amperomierza, aby przeprowadzenie pomiaru

było możliwe ?

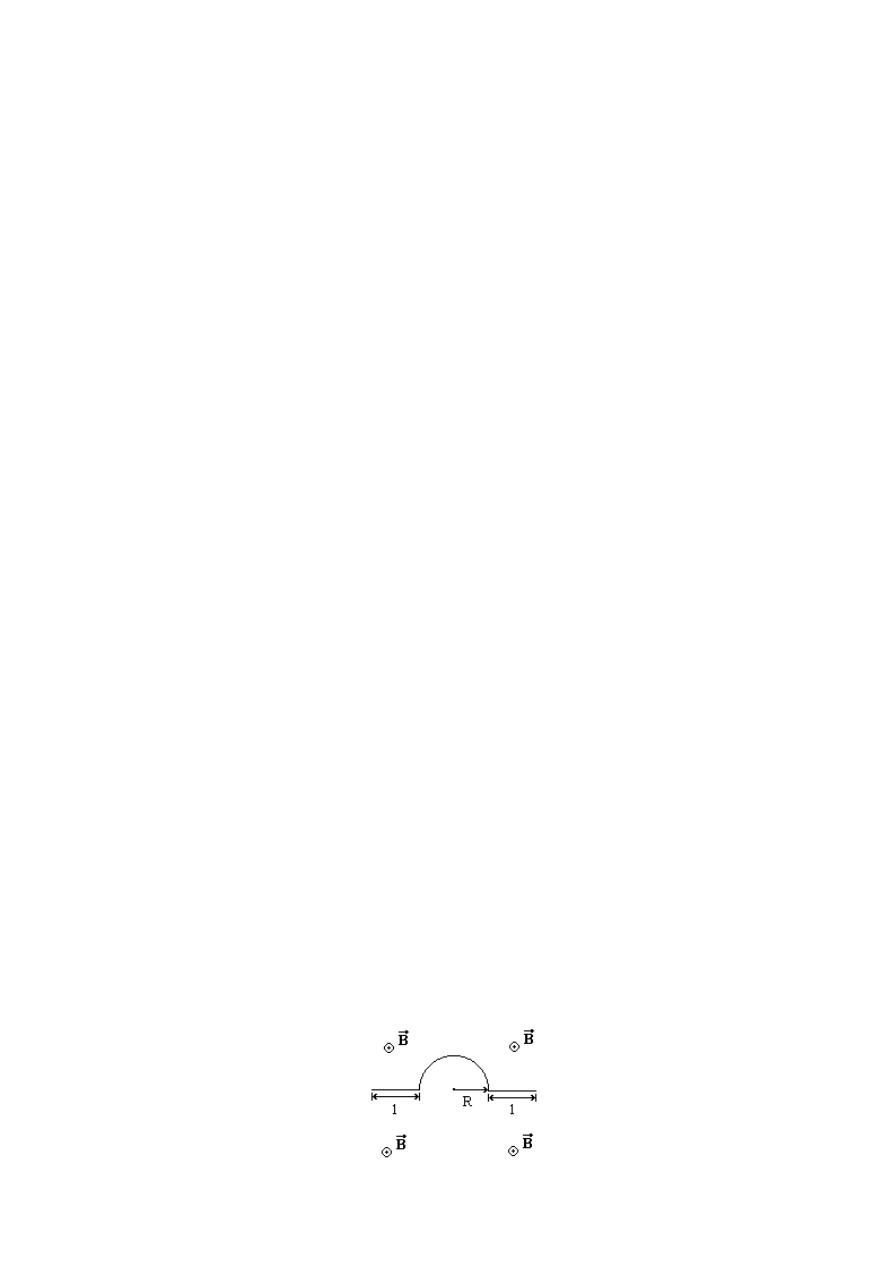
35. Za pomocą woltomierza o oporze wewnętrznym r = 2

Ω

przystosowanego do pomiaru

napięcia w zakresie 0 – 1 V, należy dokonać pomiaru napięcia w zakresie 0 – 5 V. Jaki

opornik i jak należy dołączyć do woltomierza, aby przeprowadzenie pomiaru było możliwe ?

36. Prądnica o oporze wewnętrznym r1=0,5

Ω

ładuje akumulator o oporze wewnętrznym

r

2

=0,3

Ω

prądem o natężeniu I=10A i napięciu U=15V. Oblicz siłę elektromotoryczną

prądnicy E

1

oraz siłę elektromotoryczną akumulatora E

2

.

Dział IV: Magnetyzm. Indukcja

elektromagnetyczna i prądy zmienne.

Zadania

1. Po szynach tworzących równię pochyłą o kącie nachylenia

α

może zsuwać się bez tarcia

pręt o masie m, przez który przepuszczono prąd o natężeniu I. Linie sił pola magnetycznego

są prostopadłe do podstawy równi (nie do torów). Wyznacz minimalną wartość indukcji pola

magnetycznego, w którym należy umieścić układ, aby pręt pozostawał w spoczynku, jeżeli

odległość między szynami wynosi L. W którą stronę musi płynąć prąd w pręcie, jeżeli

założymy, że pole magnetyczne jest skierowane „do góry”?

2. Przewodnik prostoliniowy AB o długości l = 50cm i o ciężarze P = 0,1N zawieszono

poziomo na dwóch niciach AD i BC. Przewodnik ten, przez który płynie prąd o natężeniu I =

2A, umieszczono w jednorodnym polu magnetycznym, którego linie mają kierunek poziomy i

są prostopadłe do przewodnika. Oblicz naciąg nici, jeżeli indukcja pola magnetycznego ma

wartość B = 0.005T. Zbadać dwa możliwe przypadki. Jaka musiałaby być wartość indukcji

pola magnetycznego i w którą stronę musiałby płynąć prąd przez przewodnik, aby naciąg nici

miał wartość zero ?

3. Przewód wygięty tak na rysunku, przewodzący prąd I jest umieszczony w jednorodnym

polu magnetycznym o indukcji magnetycznej B, skierowanej przed płaszczyznę rysunku.

Oblicz wartość siły działającej na cały przewodnik.

4. Wyznacz wartość momentu pary sił działających na ramkę prostokątną o długości boków

a=10cm i b=20cm, jeżeli płynie przez nią prąd o natężeniu I=5A i jeśli znajduje się ona w

jednorodnym polu magnetycznym o indukcji B=0,01T . Linie sił pola magnetycznego są:

a/ prostopadłe do powierzchni ramki;

b/ równoległe do powierzchni ramki;

c/ tworzą z powierzchnią ramki kąt 45

o

.

5. Jednorodne pole magnetyczne o indukcji B = 1,5T skierowane jest poziomo z południa na

północ. Jaka siła będzie działała na proton o energii 5MeV poruszający się pionowo w dół w

tym polu ? Na odpowiednim rysunku narysuj kierunek i zwrot tej siły. Przyjmij ładunek

protonu e = 1,6

*

10

-19

C i jego masę mp = 1,672

*

10

-27

kg.

6. Oblicz stosunek promieni okręgów, jakie zatoczą cząstka

α

i proton, jeżeli ich energie są

równe, a cząstki wpadają w to samo pole magnetyczne prostopadle do linii sił pola. (Przyjmij:

m

α

=4m

p

, q

α

=2qp).

7. Proton poruszający się z prędkością v = 10

5

m/s wpada w jednorodne pole magnetyczne o

indukcji B = 0,4T pod kątem

α

= 45

o

do kierunku wektora indukcji pola magnetycznego.

Wyznacz promień i skok linii śrubowej, po której będzie poruszał się proton. Przyjmij

ładunek protonu q=1,6*10

-19

C i jego masę mp = 1,672*10

-27

kg.

8. Jaką prędkość ma proton (e = 1,6

*

10

-19

C, m

p

= 1,672

*

10

-27

kg), jeżeli bez odchylenia od

swojego pierwotnego kierunku przechodzi przez układ wzajemnie prostopadłych pól:

magnetycznego o indukcji B = 2T i elektrycznego o natężeniu E = 1000V/m. Proton porusza

się w kierunku prostopadłym zarówno do wektora E jak i B.

9. Oblicz przy pomocy prawa Ampere’a wartość natężenia pola magnetycznego w odległości

r od prostoliniowego, nieskończenie długiego przewodnika, przez który przepływa prąd o

natężeniu I.

10. Wyznacz przy pomocy prawa Biota – Savarta natężenie pola magnetycznego w środku

pętli z przewodnika o promieniu r, jeżeli wartość natężenia płynącego w pętli prądu wynosi I.

11. Wyznacz przy pomocy prawa Ampere’a wartość natężenia pola magnetycznego wewnątrz

cewki o długości l, składającej się z N zwojów, przez które przepływa prąd o natężeniu I.

12. Na prostym, nieskończenie długim przewodniku utworzono pętle o promieniu r=8cm.

Jakie jest natężenie prądu w przewodniku, jeżeli natężenie pola w środku pętli (w punkcie O

na rysunku) wynosi 100 A/m ?

13. W dwóch równoległych, nieskończenie długich przewodnikach odległych od siebie o 2m,

płyną prądy o wartościach odpowiednio równych I

1

= 1A i I

2

= 4A. W jakiej odległości od

przewodnika z mniejszym prądem znajduje się punkt, w którym natężenie pola

magnetycznego ma wartość zero, jeżeli prądy w przewodnikach płyną:

a/ w tych samych kierunkach,

b/ w przeciwnych kierunkach?

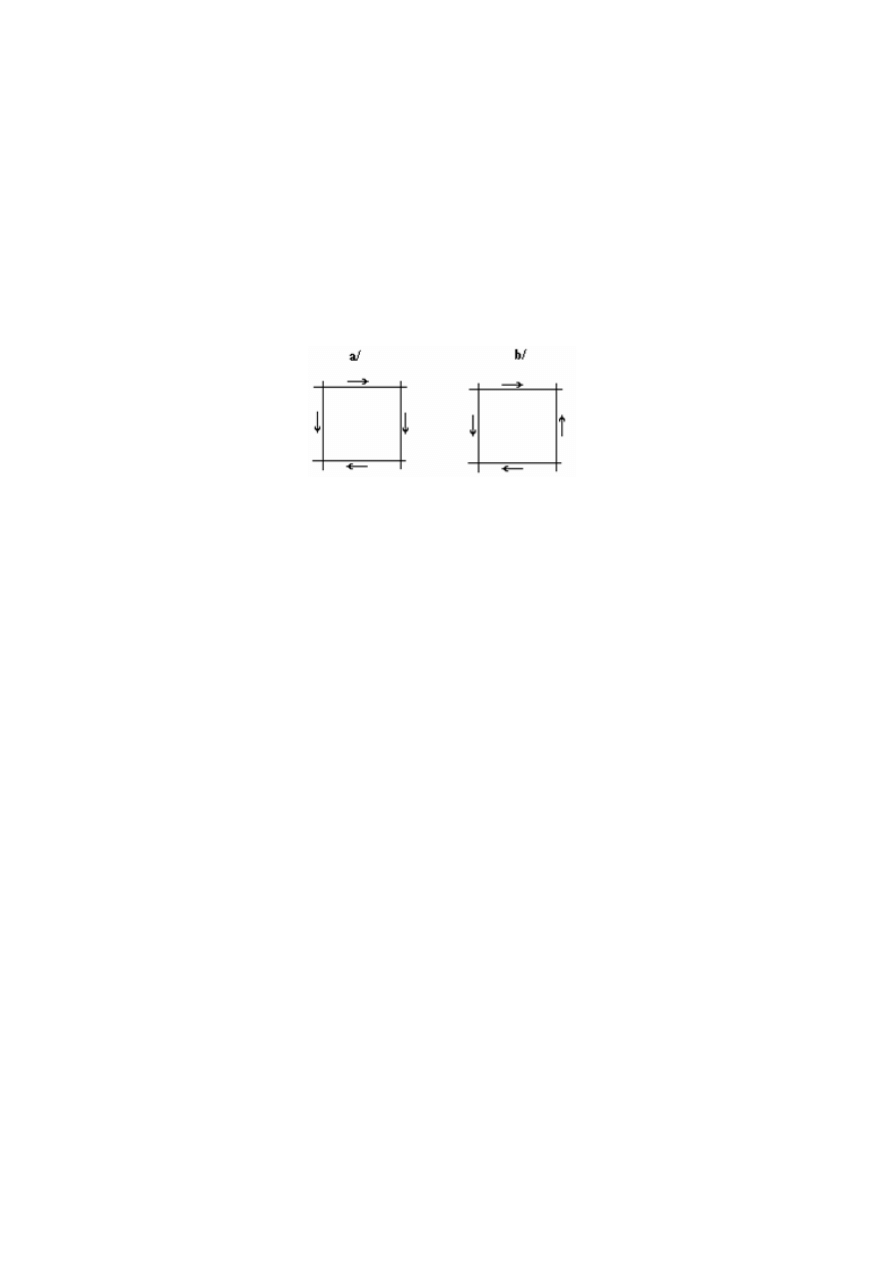
14. Oblicz natężenie pola magnetycznego w środku kwadratu, w podanych na rysunkach

przypadkach, jeżeli natężenie prądu płynącego w każdym z przewodników ma wartość I=1 A,

a bok kwadratu ma długość a = 10cm.

15. W jednorodnym polu magnetycznym obraca się ze stałą prędkością kątową

ω

=20rad/s

pręt o długości l=1m. Oś obrotu jest równoległa do linii pola, przechodzi przez koniec pręta i

jest do niego prostopadła. Wyznacz napięcie U między końcami pręta, jeżeli indukcja pola

magnetycznego ma wartość B=0,05T.

16. W jednorodnym polu magnetycznym o indukcji B=2T porusza się po równoległych

szynach odległych od siebie o d=50cm przewodnik. Linie sił pola magnetycznego są

prostopadłe do płaszczyzny wyznaczonej przez szyny i przewodnik, a wektor prędkości

przewodnika leży w tej płaszczyźnie i jest prostopadły do wektora indukcji pola

magnetycznego i przewodnika. Szyny, na jednym z końców są spięte opornikiem o oporze

R=4

Ω

. Jaki prąd przepływa przez opornik, jeżeli wartość jego prędkości wynosi v=50m/s i

porusza się on:

a/ w kierunku opornika;

b/ oddalając się od opornika.

17. Przez wnętrze cewki ustawionej pionowo przelatuje magnes. Narysuj wykres zależności

od czasu indukowanego w cewce natężenia prądu.

18. Wyznacz pracę wykonaną przy przesuwaniu przewodnika o długości d=20cm w

prostopadłym polu magnetycznym o indukcji B=2T. Natężenie prądu w przewodniku wynosi

I=5A. Przewodnik przesunięto na odległość l=1m ruchem jednostajnym.

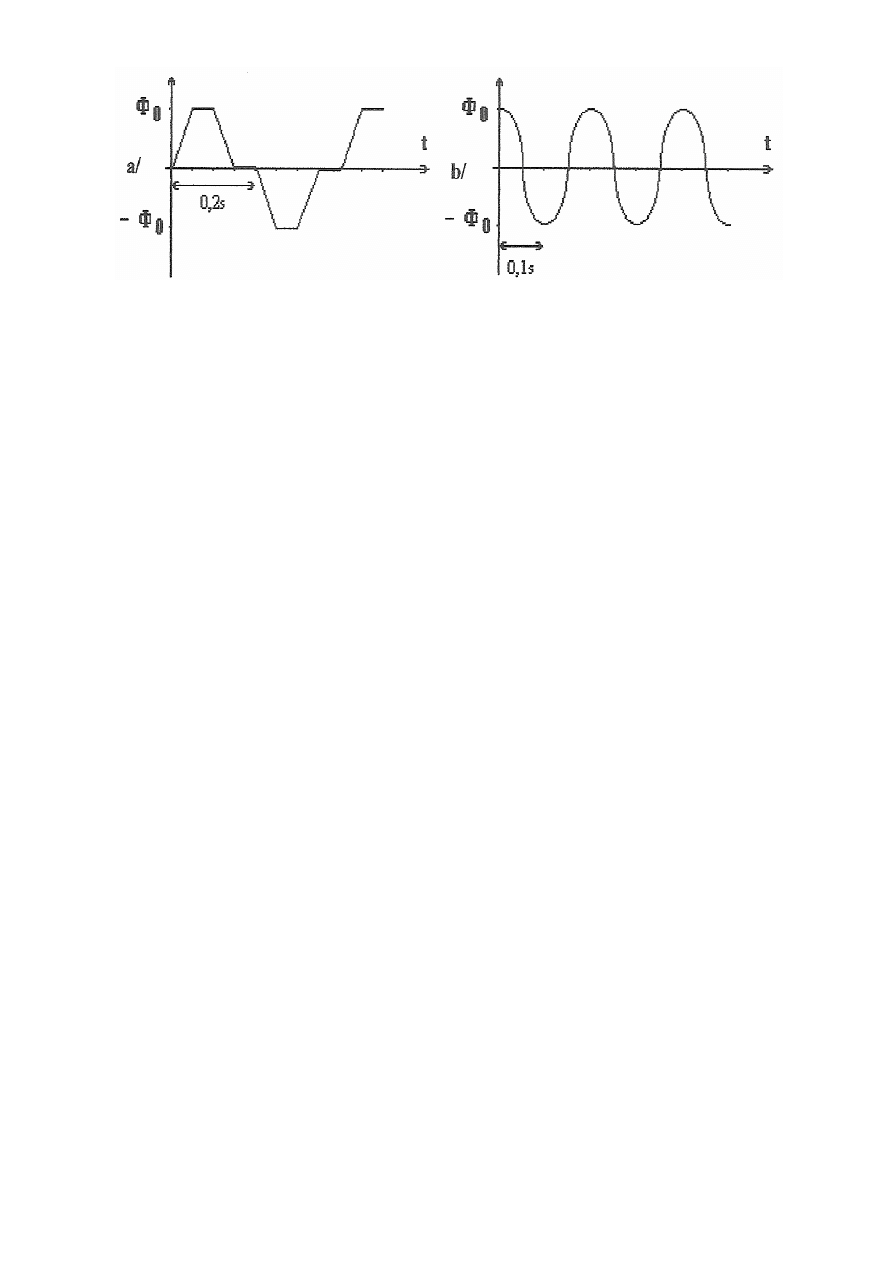
19. Dysponując wykresem przedstawiającym zależność strumienia indukcji pola

magnetycznego od czasu (rysunek), naszkicować zależność SEM indukcji powstałej w

pojedynczym zwoju, jeżeli

Φ

0

=0,1Wb.

20. Cewka o promieniu r=10cm ma N=500 zwojów. Cewka znajduje się w jednorodnym polu

magnetycznym prostopadłym do jej przekroju poprzecznego. W ciągu czasu

∆

t=0,3s indukcja

pola wzrosła od B

1

=1T do B

2

=1,6T. Obliczyć wzbudzoną w tej cewce średnią siłę

elektromotoryczną indukcji.

Dział V: Obwody drgające. Prawa Maxwella.

Optyka.

1. Wyprowadź wzór pozwalający obliczyć gęstość energii pola elektrostatycznego(oblicz

energię kondensatora jako funkcję natężenia pola elektrycznego).

2. Wyprowadź wzór pozwalający obliczyć gęstość energii pola magnetycznego(j.w. dla cewki

i pola magnetycznego).

3. Wewnątrz nieskończonego cylindra o promieniu R wytworzono jednorodne pole

magnetyczne, którego wektor indukcji B jest równoległy do ścian cylindra. Wartość indukcji

pola magnetycznego wzrasta jednostajnie w funkcji czasu z szybkością dB/dt. Wykreśl

wykres zależności natężenia pola elektrycznego od odległości od wzdłużnej osi cylindra.

4. Narysuj wykres zależności wartości natężenia prądu przepływającego przez opornik o

oporze R od czasu, jeżeli jest on szeregowo podłączony z idealną cewką o indukcyjności L i

cały układ jest podłączony do źródła o sile elektromotoryczne E i znikomym oporze

wewnętrznym. Za początek osi czasu przyjmij chwilę podłączenia układu do źródła.

5. Okładki kondensatora o pojemności C=2µF, na którym był zgromadzony pewien ładunek

elektryczny, zwarto zwojnicą o indukcyjności L=0,01H i znikomym oporze omowym. Po

jakim czasie od momentu połączenia okładek kondensatora energia pola w kondensatorze

będzie równa energii pola magnetycznego w zwojnicy ?

6. Obwód drgający składa się z kondensatora o pojemności C=0,1µF oraz cewki o pewnej

indukcyjności i bardzo małym oporze omowym R. Po naładowaniu kondensatora ładunkiem

Q=10

-4

C i zamknięciu obwodu powstały w nim gasnące drgania elektryczne. Oblicz

maksymalną ilość ciepła, która mogłaby wydzielić się w obwodzie do momentu całkowitego

wygaśnięcia drgań. Dlaczego w rzeczywistości ilość wydzielanego ciepła jest mniejsza od

obliczonej ?

7. Na jaką długość fali nastawiony jest radioodbiornik, jeżeli obwód antenowy zawiera cewkę

o samoindukcji 1,5mH i kondensator o pojemności 450pF ?

8. W jakiej odległości od punktowego źródła monochromatycznej fali świetlnej o długości λ

=600nm w chwili t= T/2 wektor świetlny ma długość równą połowie długości maksymalnej ?

Prędkość światła w próżni ma wartość c=3*10

8

m/s.

9. Nad środkiem okrągłego pokoju o promieniu r=2m umieszczono żarówkę, której wysokość

nad podłogą można zmieniać. Na jakiej wysokości winna być zawieszona żarówka, aby

natężenie oświetlenia brzegów podłogi było najsilniejsze ?

10. Korzystając z zasady Huygensa udowodnij prawo odbicia światła.

11. Korzystając z zasady Huygensa udowodnij prawo załamania światła.

12. Na dnie naczynia napełnionego wodą do wysokości h=20cm umieszczono punktowe

źródło światła. Po powierzchni wody pływa okrągła nieprzezroczysta płyta, której środek

znajduje się dokładnie nad źródłem światła. Wyznacz minimalny promień pływającej płyty,

przy którym ani jeden promień światła emitowanego przez źródło nie przejdzie przez

powierzchnię wody, jeżeli współczynnik załamania dla wody wynosi n=4/3.

13. Cienka płytka szklana została oświetlona światłem białym padającym na nią pod bardzo

małym kątem. Obserwator patrzący na płytkę stwierdza, że odbite od niej światło ma

zabarwienie żółte (λ=530nm). Oblicz grubość tej płytki, jeżeli wiadomo, że jest ona mniejsza

od dmax=0,2µm, a wartość współczynnika załamania szkła, z którego zrobiona jest płytka

wynosi n=1,5.

14. Na siatkę dyfrakcyjną o stałej a=2,5*10

-6

m pada prostopadle wiązka fal

monochromatycznych o długości λ =560nm. Jaki jest maksymalny rząd widma, który można

jeszcze zaobserwować ?

Dla wszystkich kolejnych zadań przyjęto następujące wartości stałych:

Stała Plancka h=6,6310

-34

Js

stała Wiena b=2,9*10

-3

mK

stała Stefana – Boltzmanna =5,67*10

-8

W/(m

2

K

4

)

prędkość światła c=3*10

8

m/s

masa elektronu me=9,1*10

-31

kg

stała Rydberga R=1,1*10

7

1/m

15. Oblicz, przy jakiej temperaturze maksimum krzywej w rozkładzie widma energii ciała

doskonale czarnego wystąpi dla fali o długości λ =556nm, na którą jest najbardziej czułe oko

ludzkie.

16. Na powierzchnię S=5cm

2

pada wiązka fotonów o natężeniu m=10

18

fotonów na sekundę.

Jakie ciśnienie wywiera wiązka na powierzchnię, jeżeli długość fali padającego światła

wynosi λ =500nm i powierzchnia pochłania światło w 50% ?

17. Płaski pyłek o masie m=10

-10

kg i polu powierzchni S=10

-11

m

2

jest utrzymywany przez

padające nań od dołu światło monochromatyczne nad powierzchnią Ziemi. Jakie musi być

natężenie tego światła, jeżeli założymy, że światło całkowicie się od niego odbija.

18. Temperatura ciała doskonale czarnego wynosi T

0

=1000K. Oblicz, ile razy wzrośnie

całkowita energia emitowana przez to ciało oraz o ile zmieni się długość fali, na którą

przypada maksimum natężenia, jeżeli temperatura wzrośnie o

∆

T=100K.

19. Ile razy zwiększy się moc promieniowania ciała doskonale czarnego, jeżeli maksimum

energii w widmie przesunęło się z λ

1

=700nm do λ

2

=400nm?

20. Narysuj wykres przedstawiający zależność energii kwantu od:

a/ częstotliwości,

b/ długości fali.

21. Znając długofalową granicę zjawiska fotoelektrycznego dla rubidu wynoszącą λ

1

=540nm,

oblicz pracę wyjścia i maksymalną energię elektronów wybijanych z tego materiału przez

światło o długości fali λ

2

=400nm.

22. Izolowana elektrycznie płytka cezowa jest oświetlona światłem monochromatycznym o

długości fali λ=450nm. Do jakiego potencjału naładuje się ta płytka pod wpływem stałego

działania tego promieniowania, jeżeli praca wyjścia dla cezu wynosi W=1,9eV ?

23. Jaka długość fali de Broglie’a odpowiada elektronom przyspieszanym napięciem

U=105V?

24. Oblicz stosunek energii potencjalnej do energii kinetycznej elektronu krążącego po

dowolnej orbicie kołowej w atomie.

25. Jaki jest stosunek prędkości elektronu krążącego w atomie wodoru po czwartej orbicie do

jego prędkości, jeśli krąży on po drugiej orbicie?

26. Oblicz prędkość liniową i kątową elektronu na pierwszej orbicie bohrowskiej w atomie

wodoru. Jak zmieni się ta prędkość, gdy elektron przejdzie z pierwszej orbity na drugą?

27. Oblicz energię oraz potencjał jonizacji atomu wodoru.

28. Jaka musi być długość fali padającego promieniowania elektromagnetycznego, aby mogło

ono wybić elektron krążący po trzeciej orbicie w atomie wodoru, tak aby opuścił on atom z

prędkością v=2,2*10

6

m/s.

29. Atom wodoru, znajdujący się w stanie podstawowym, został przeprowadzony w stan

wzbudzony, charakteryzujący się główną liczbą kwantową n=3. Oblicz energię wzbudzenia

dla tego stany oraz długości fal dla linii, które mogą powstać w widmie podczas przejścia ze

stanu wzbudzonego do stanu podstawowego.

30. Jaką wartość ma stosunek promienia trzeciej orbity elektronu w atomie wodoru wyliczony

z teorii Bohra do promienia pierwszej orbity?

31. Oblicz długość fali odpowiadającej granicom serii:

a/ Lymanna (przejścia z wyższych powłok na powłokę pierwszą),

b/ Balmera (przejścia z wyższych powłok na powłokę drugą),

c/ Bracketta (przejścia z wyższych powłok na powłokę czwartą).

32. Znajdujący się w pierwszym stanie zbudzonym (E

2

=-3,4eV) atom wodoru przechodzi do

stanu podstawowego (E

1

=-13,6eV) emitując kwant promieniowania nadfioletowego o energii

E

f

. Wykaż, że prawo zachowania pędu wymaga, aby wartość E

f

była nieco mniejsza od

wartości E

2

-E

1

(ze względu na zjawisko odrzutu).

Dział VI: Budowa ciał stałych. Elektryczne i

magnetyczne właściwości materii.

1. Jaka jest wartość modułu Younga stali, jeżeli wykonany z niej pręt o polu przekroju 1mm2,

pod wpływem działania siły 100N doznaje wydłużenia względnego o wartości 0,001?

2. Wyznacz natężenie pola elektrostatycznego dipola w punkcie należącym do osi

poprzecznej tego dipola, leżącym w odległości r od jego środka, jeżeli elektryczny moment

dipolowy ma wartość p, a odległość r jest dużo większa od długości dipola.

3. Jaki moment sił działa na dipol o elektrycznym momencie dipolowym p, umieszczony w

jednorodnym polu elektrostatycznym o natężeniu E, tak, że oś dipola tworzy z liniami sił pola

kąt

α

?

4. Wyznacz potencjał pola elektrostatycznego dipola w punkcie należącym do osi poprzeczne

tego dipola, leżącym w odległości r od jego środka, jeżeli elektryczny moment dipolowy ma

wartość p.

5. Jak zmieni się pojemność i natężenie pola elektrostatycznego wewnątrz kondensatora

płaskiego, jeżeli między jego okładki wsuniemy dielektryk o stałej dielektrycznej er i będzie

on po naładowaniu odłączony od źródła napięcia ?

6. Jak zmieni się pojemność i natężenie pola elektrostatycznego wewnątrz kondensatora

płaskiego, jeżeli między jego okładki wsuniemy dielektryk o stałej dielektrycznej er i będzie

on po naładowaniu podłączony do źródła napięcia przez cały czas ?

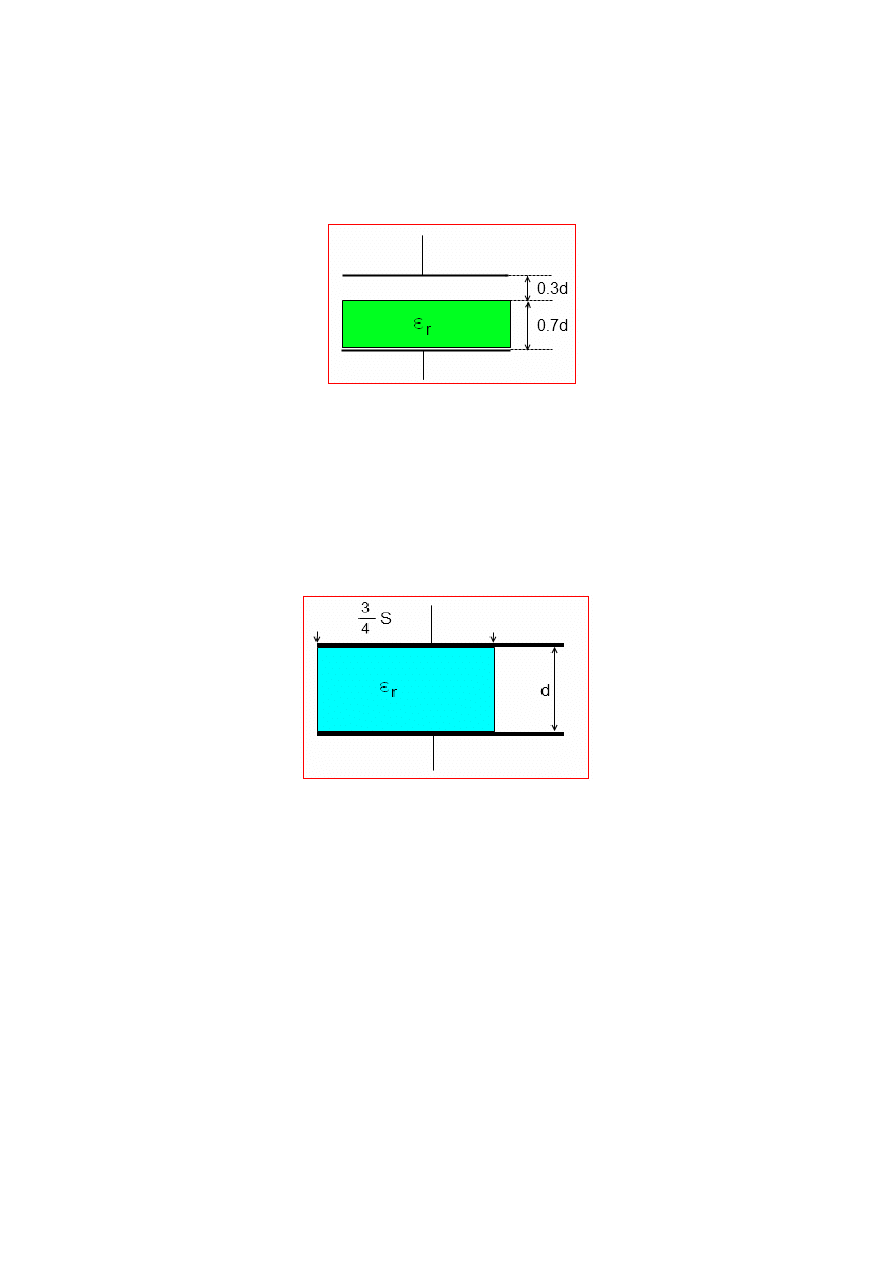
7. Oblicz pojemność następującego kondensatora wiedząc, że pojemność tego kondensatora

bez dielektryka wynosi C.

8. Jaką pracę należy wykonać, aby do kondensatora o pojemności C wsunąć dielektryk o

stałej dielektrycznej

ε

r

wypełniając dokładnie przestrzeń między okładkami, jeżeli

kondensator jest cały czas podłączony do źródła napięcia U ?

9. Oblicz pojemność następującego kondensatora, wiedząc, że pojemność tego kondensatora

bez dielektryka wynosi C.

10. Jaką pracę należy wykonać, aby do kondensatora o pojemności C wsunąć dielektryk o

stałej dielektrycznej

ε

r

wypełniając dokładnie przestrzeń między okładkami, jeżeli

kondensator jest naładowany ze źródła napięcia U, a następnie, w czasie wsuwania

dielektryka, od źródła odłączony ?

11. Wykreśl zależność wartości natężenia pola elektrostatycznego dla naładowanej ładunkiem

Q kuli od odległości od środka tej kuli, dla kul wykonanych z:

a/ przewodnika;

b/ dielektryka.

12. Oblicz i wykreśl zależność wartości potencjału pola elektrostatycznego dla naładowanej

ładunkiem Q kuli od odległości od środka tej kuli, dla kul wykonanych z:

a/ przewodnika;

b/ dielektryka.

13. Przyjmując, że orbita elektronu (e = 1,6•10

-19

C , m

e

= 9,1•10

-31

kg ) w nie wzbudzonym

atomie wodoru jest okręgiem o promieniu r=5,3•10

-11

m, znajdź natężenie pola

magnetycznego wytwarzanego przez elektron w środku jego orbity, jeżeli jego prędkość na tej

orbicie wynosi w=2,2•10

6

m/s.

14. Wyprowadź związek między orbitalnym dipolowym momentem magnetycznym elektronu

na dowolnej orbicie w atomie wodoru

µ

m

, a jego orbitalnym momentem pędu L

m

, przyjmując

za dane e – ładunek elektronu i m – masę elektronu.

15. Jaką pracę należy wykonać, aby z cewki o N = 500 zwojach i długości l = 20cm, przez

którą przepływa prąd o natężeniu I = 2A, wyciągnąć rdzeń, którego względna przenikalność

magnetyczna wynosi µ=20?

16. Obliczyć koercję magnetyczną cienkiego pręta żelaznego o długości l = 20cm, jeżeli po

włączeniu prądu okazało się, że pole magnetyczne w pobliżu końców pręta jest równe zeru.

Prąd o natężeniu I = 2A płynie przez N = 500 zwojów cienkiego izolowanego przewodu

nawiniętego na ten pręt.