
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
MINISTERSTWO EDUKACJI
NARODOWEJ
Henryka Lisowska
Stosowanie podstawowych pojęć z zakresu mechaniki
technicznej 322[13].Z2.01
Poradnik dla ucznia
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
1
Recenzenci:
lek med. Mariusz Długosz
dr n. med. Piotr Majcher
Opracowanie redakcyjne:
mgr Henryka Lisowska
Konsultacja:
mgr Ewa Łoś
Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 322[13].Z2.01
„Stosowanie podstawowych pojęć z zakresu mechaniki technicznej”, zawartego
w modułowym programie nauczania dla zawodu technik ortopeda.
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
2
SPIS TREŚCI
1.
Wprowadzenie
4
2.
Wymagania wstępne
6
3.
Cele kształcenia
7
4.
Materiał nauczania
8
4.1. Siła. Rachunek wektorowy sił. Płaski układ sił. Przestrzenny układ sił.
Moment siły
8
4.1.1. Materiał nauczania
8
4.1.2. Pytania sprawdzające
10
4.1.3. Ćwiczenia
10
4.1.4. Sprawdzian postępów
13
4.2. Tarcie
14
4.2.1. Materiał nauczania
14
4.2.2. Pytania sprawdzające
15
4.2.3. Ćwiczenia
16
4.2.4. Sprawdzian postępów
17
4.3. Masa i ciężar ciała
18
4.3.1. Materiał nauczania
18
4.3.2. Pytania sprawdzające
21
4.3.3. Ćwiczenia
21
4.3.4. Sprawdzian postępów
24
4.4. Ruch. Rodzaje ruchu. Ruch punktu materialnego
25
4.4.1. Materiał nauczania
25
4.4.2. Pytania sprawdzające
31
4.4.3. Ćwiczenia
32
4.4.4. Sprawdzian postępów
35
4.5. Ruch bryły. Składanie ruchu
36
4.5.1. Materiał nauczania
36
4.5.2. Pytania sprawdzające
37
4.5.3. Ćwiczenia
37
4.5.4. Sprawdzian postępów
39
4.6. Zasady dynamiki Newtona. Dynamika punktu i bryły sztywnej.
Ruch środka masy. Dynamika ruchu obrotowego ciała sztywnego
40
4.6.1. Materiał nauczania
40
4.6.2. Pytania sprawdzające
41
4.6.3. Ćwiczenia
41
4.6.4. Sprawdzian postępów
44
4.7. Energia i praca mechaniczna
45
4.7.1. Materiał nauczania
45
4.7.2. Pytania sprawdzające
46
4.7.3. Ćwiczenia
46
4.7.4. Sprawdzian postępów
48

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
3
4.8. Podstawy wytrzymałości materiałów
49
4.8.1. Materiał nauczania
49
4.8.2. Pytania sprawdzające
53
4.8.3. Ćwiczenia
54
4.8.4. Sprawdzian postępów
56
5.
Sprawdzian osiągnięć
57
6.
Literatura
65

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
4
1. WPROWADZENIE
Poradnik będzie Ci pomocny w przyswajaniu wiedzy z zakresu mechaniki technicznej.
W poradniku zamieszczono:
−
wymagania wstępne- umiejętności potrzebne do realizacji programu nauczania,
−
cele kształcenia- umiejętności, jakie opanujesz podczas pracy z poradnikiem,
−
materiał nauczania- wiadomości teoretyczne niezbędne do opanowania treści jednostki
modułowej,
−
zestaw pytań sprawdzających, czy już opanowałeś określone treści,
−
ć
wiczenia, pomogą ci zweryfikować wiadomości teoretyczne oraz ukształtować
umiejętności praktyczne,
−
sprawdzian postępów,
−
sprawdzian osiągnięć, przykładowy zestaw zadań. Zaliczenie testu potwierdzi
opanowanie wiadomości i umiejętności określonych w programie jednostki modułowej,
−
literaturę uzupełniającą.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
5
Schemat układu jednostek modułowych
322[13].Z2
Podstawy biomechaniki ortopedycznej
322[13].Z2.01
Stosowanie podstawowych pojęć
z zakresu mechaniki technicznej
322[13].Z2.02
Stosowanie układów biomechanicznych
w protetyce ortopedycznej

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
6
2.
WYMAGANIA WSTĘPNE
Przystępując do realizacji programu jednostki modułowej powinieneś umieć:
−
stosować jednostki układu SI,
−
przeliczać jednostki,
−
posługiwać się podstawowymi pojęciami z zakresu statyki, dynamiki i kinematyki,
budowy materii,
−
rozróżniać wielkości skalarne i wektorowe,
−
posługiwać się płaskim i przestrzennym układem współrzędnych,
−
rozwiązywać równania matematyczne,
−
przekształcać wzory,
−
korzystać z różnych źródeł informacji,
−
współpracować w grupie,
−
posługiwanie się podstawowymi pojęciami z zakresu mechaniki.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
7
3. CELE KSZTAŁCENIA
W wyniku realizacji programu jednostki modułowej powinieneś umieć:
−
wyjaśnić pojęcia: siła, układ sił, moment siły,
−
wykonać rachunek wektorowy sił,
−
wyznaczyć graficznie siłę wypadkową i wypadkowy moment siły,
−
zastosować pojęcia: masa i ciężar ciała, środek masy,
−
rozróżnić rodzaje równowagi,
−
obliczyć siłę tarcia,
−
wyjaśnić pojęcie ruchu,
−
rozróżnić rodzaje ruchu,
−
wyjaśnić różnice w ruchu punktu i bryły sztywnej,
−
zapisać zasady dynamiki punktu materialnego i bryły sztywnej za pomocą wzorów,
−
zastosować zasady dynamiki punktu materialnego i bryły sztywnej,
−
wyjaśnić pojęcie energia, praca mechaniczna,
−
obliczyć siłę sprężystości i zastosować prawo Hooke’a,
−
wyjaśnić zjawisko odkształcenia ciał pod wpływem działających sił,
−
wyjaśnić zjawisko naprężeń,
−
wyjaśnić proces odkształcania materiałów spowodowany rozciąganiem, ściskaniem,
zginaniem, skręcaniem,
−
scharakteryzować wytrzymałość złożoną i wytrzymałość zmęczeniową materiałów,
−
wykonać obliczenia wytrzymałościowe.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
8
4. MATERIAŁ NAUCZANIA
4.1.
Siła. Rachunek wektorowy sił. Płaski układ sił. Przestrzenny
układ sił. Moment siły
4.1.1. Materiał nauczania
Siła
Siła jest miarą oddziaływania ciał.
Skutki oddziaływania ciał:
–
statyczne - polegające na zmianie kształtu ciała,
–
dynamiczne - polegające na zmianie ruchu (wprowadzenie w ruch, zatrzymanie go,
zmianie kierunku ruchu).
Siła (F), jest to wielkość fizyczna, wektorowa.
Aby określić siłę należy podać jej wartość liczbową, jednostkę miary, kierunek, zwrot i punkt
przyłożenia.
Jednostką siły w układzie SI jest niuton (N):
1N= 1
2
*
s
m
kg
Oznaczenia wektorów siły:
–
w druku grube litery F
–
lub strzałka nad literą F
.
Wartość liczbowa wektora:
–
litera F pisana kursywą,
–
lub |F|.
Krótki przegląd sił
–
Siła ciężkości.
Na wszystkie ciała na Ziemi i w jej pobliżu działa siła przyciągania, której źródłem jest
Ziemia. Jest ona skierowana pionowo w dół.
Wyrażona jest wzorem
P= m * g
gdzie: g – przyspieszenie ziemskie; średnia wartość 9,81 N/kg
m – masa ciała
–
Siła sprężystości.
Siła sprężystości występuje przy wszelkich odkształceniach ciał stałych, np. przy rozciąganiu
sprężyny. Jej wartość obliczyć można ze wzoru:
F
s
= k*
∆
l
gdzie:
∆
l – przyrost długości ( l-lo)
k – współczynnik sprężystości, jednostka [N/m].
Wzór ten jest słuszny tylko w pewnym zakresie sił. Dla zbyt dużych sił nie jest słuszny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
9
–
Siła reakcji więzów.
Przyczyny powodujące ograniczenia ruchu ciała (lub ciał) nazwami więzami.
Rachunek wektorowy sił.
–
Dodawanie wektorów sił.
Stosuje się – regułę równoległoboku lub trójkąta.
–
Mnożenie wektora przez liczbę (skalar).
Powoduje zwiększenie długości wektora tyle razy, ile wynosi moduł liczby, przez którą
mnożymy. Kierunek wektora pozostaje bez zmiany, zwrot nie zmienia się, jeśli liczba jest
dodatnia, natomiast zmienia się na przeciwny jeżeli liczba jest ujemna.
–
Odejmowanie wektorów sił.
F
1
– F
2
= F
1
+ (- F
2
)
–
Iloczyn skalarny.
F
1 *
F
2
= |F
1
| * |F
2
| * cos
α
gdzie:
α
– kąt między wektorami sił
|F
1
| i |F
2
| – długość wektorów (wartości liczbowe sił)
–
Iloczyn wektorowy.
W wyniku wektorowego mnożenia dwóch wektorów otrzymujemy wektor:
F
= F
1 x
F
2
o następujących właściwościach:
–
wartość; |F|= |F1| |F2| *sin
α
–
kierunek: F
⊥
F
1 F
⊥
F
2
–
zwrot: określony jest regułą prawej dłoni.
Składanie sił.
Siła wypadkowa jest to siła, która może zastąpić działanie dwóch lub więcej
sił składowych. Wyznaczanie wielkości i kierunku wypadkowej nosi nazwę składania sił lub
sumowania geometrycznego.
Rozkładanie sił.
Rozkładanie sił jest czynnością odwrotną do składania sił.
Składanie i rozkładanie sił ułatwia korzystanie z układu współrzędnych.
Płaski układ sił.
Wektory sił leżą w jednej płaszczyźnie. Korzystamy z układu współrzędnych (x,y) płaskiego.
|F|=
2
2
y
x
F
F
+
|F| - wartość siły
F
x
- składowa siły (x)
F
y
- składowa siły (y)
Przestrzenny układ sił.
Wektory sił leżą w przestrzeni.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
10
Korzystamy z przestrzennego układu sił (x,y,z)
|F|=
2
2
2
z
y
x
F
F
F
+
+
|F|- wartość siły
F
x
- składowa siły (x)
F
y
- składowa siły (y)
F
z
- składowa siły (z)
Moment siły.
Momentem siły nazywamy iloczyn wektorowy siły i jej ramienia.
r
F
M
×
=
r
-
ramię siły (odległość punktu przyłożenia siły od wybranego punktu 0)
F
- działająca siła
M
- moment siły
Jednostka [ M]= 1N * m
4.1.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jak należy określić siłę?
2.
Co jest jednostką siły w układzie SI?
3.
Co to jest siła ciężkości?
4.
Gdzie występują siły sprężystości?
5.
Jakie działania można wykonać na wektorach sił?
6.
Na czym polega składanie sił?
7.
Na czym polega rozkładanie sił?
8.
Co to jest siła wypadkowa?
9.
Jaki układ sił nazywamy płaskim?
10.
Jaki układ sił nazywamy przestrzennym?
11.
Co to jest moment siły?
4.1.3. Ćwiczenia
Ćwiczenie 1
Na ciało działa płaski układ sił zbieżnych F
1 ,
F
2,
F
3
o składowych:
F
1
=
=
=
2
4
1
1
y
x
F
F
=
=
=
3
0
2
2
2
y
x
F
F
F
−
=
=
=
3
2
3
3
3
y
x
F
F
F
Znajdź wektor siły F
(wypadkowy) będący sumą wektorów F
1 ,
F
2,
F
3
. Oblicz jego
wartość.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
11
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
narysować układ współrzędnych x,y,
2)
narysować wektory sił F
1 ,
F
2,
F
3
w układzie współrzędnych x,y w odpowiedniej skali,
3)
wyznaczyć współrzędne wektora wypadkowego F
,
4)
narysować wektor siły wypadkowej F
,
5)
obliczyć wartość bezwzględną wektora wypadkowego F
|F|.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
papier milimetrowy,
–
pisaki, długopisy,
–
linijka,
–
poradnik ucznia,
–
tabela funkcji trygonometrycznych,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Na ciało działa siła F
1
= 4 N w kierunku wschodnim oraz sił F
2
= 3 N w kierunku
północno-wschodnim.
Znajdź wartość i kierunek siły wypadkowej F.
Sposób wykonania ćwiczenia.
Aby wykonać ćwiczenie, powinieneś:
1)
narysować układ współrzędnych x,y,
2)
narysować wektory sił F
1 ,
F
2,
F
3
w układzie współrzędnych x,y w odpowiedniej skali,
3)
wyznaczyć współrzędne wektora wypadkowego F
,
4)
narysować wektor siły wypadkowej F
,
5)
obliczyć wartość bezwzględną wektora wypadkowego F
|F|.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
papier milimetrowy,
–
pisaki, długopisy,
–
linijka,
–
poradnik ucznia,
–
tabela funkcji trygonometrycznych,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Kulkę o ciężarze P = 30N, zawieszono na nitce i wychylono z położenia równowagi o kąt
α
a)
30°
b)
50°
c)
90°

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
12
Wyznacz składowe:
P
1
- powodujące ruch oraz P
2
- napinające nitkę
1)
wykonać rysunek przedstawiający sytuację przedstawioną w zadaniu,
2)
narysować układ współrzędnych (x,y),
3)
narysować składową P
1
,
4)
narysować składową P
2
,
5)
obliczyć wartości składowych P
1
i P
2
.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
papier milimetrowy,
–
pisaki, długopisy,
–
linijka,
–
poradnik ucznia,
–
tabela funkcji trygonometrycznych,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 4
Na punkt materialny leżący w środku układu współrzędnych (x,y) działają dwie siły F
1 ,
F
2,
o składowych:
(
)
(
)
4
,
1
5
,
7
2
2
1
1
=
−
=
=
=
y
x
y
x
F
F
F
F
F
F
1)
wyznacz siłę wypadkową F w sposób graficzny,
2)
wyznacz siłę wypadkową F w sposób analityczny tzn. oblicz jej wartość liczbową,
3)
określ jej kierunek.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenia powinieneś:
1)
narysować układ współrzędnych (x,y),
2)
narysować wektory sił F
1 ,
F
2
w odpowiedniej skali,
3)
narysować siłę wypadkową F
,
4)
wyznaczyć składowe siły wypadkowej F
,
5)
obliczyć wartość siły F
,
6)
wyznaczyć jej kierunek.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
papier milimetrowy,
–
długopis, ołówek,
–
linijka,
–
poradnik ucznia,
–
tabela funkcji trygonometrycznych,
–
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
13
4.1.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
określić siłę i jej jednostkę?
2)
określić siłę ciężkości i sprężystości?
3)
posłużyć się rachunkiem wektorowym sił?
4)
wyznaczyć składowe siły?
5)
wyznaczyć siłę wypadkową kilku sił?
6)
wyznaczyć wartość siły wypadkowej?
7)
określić moment siły?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
14
4.2.
Tarcie
4.2.1. Materiał nauczania
Tarcie statyczne.
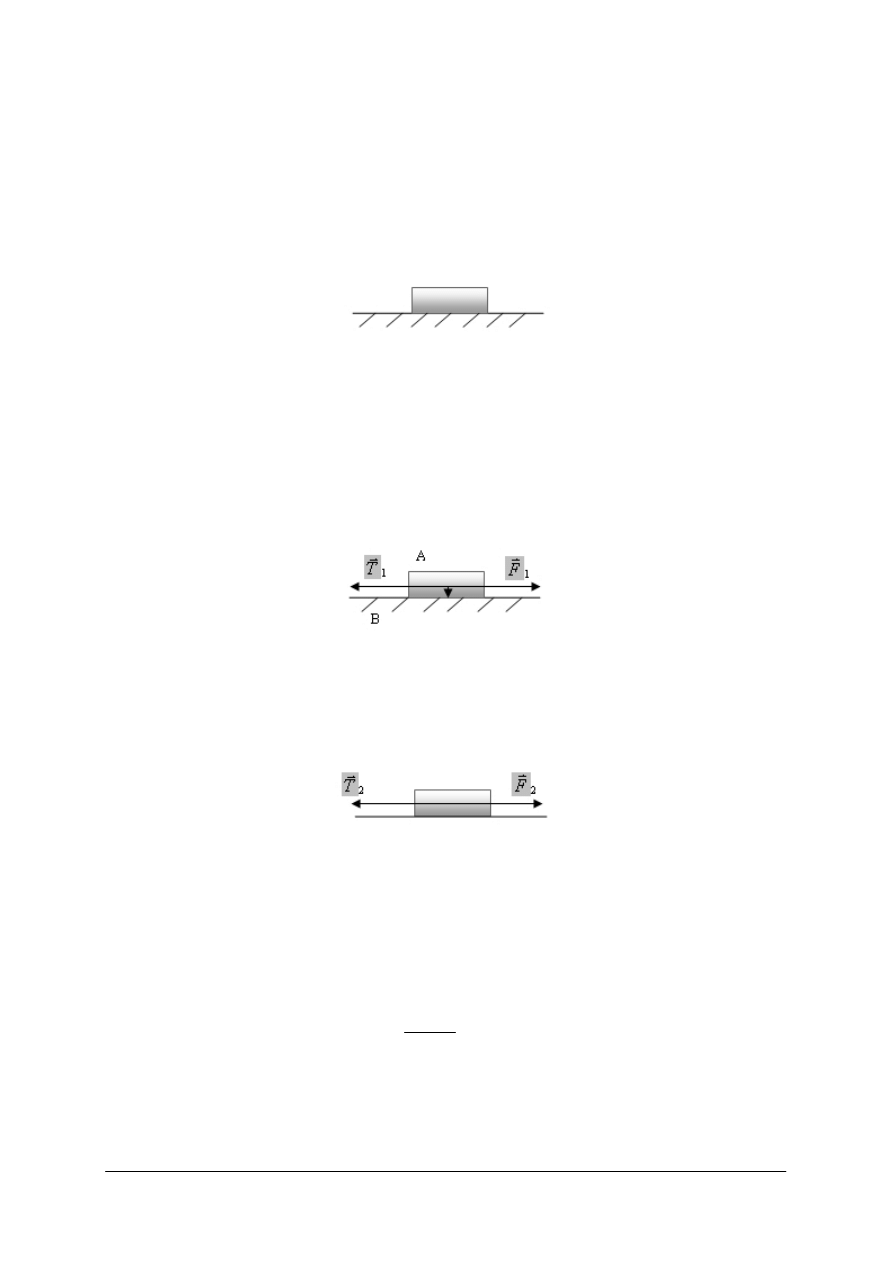
Na poziomej powierzchni leży klocek (rys. 1)
Rys. 1
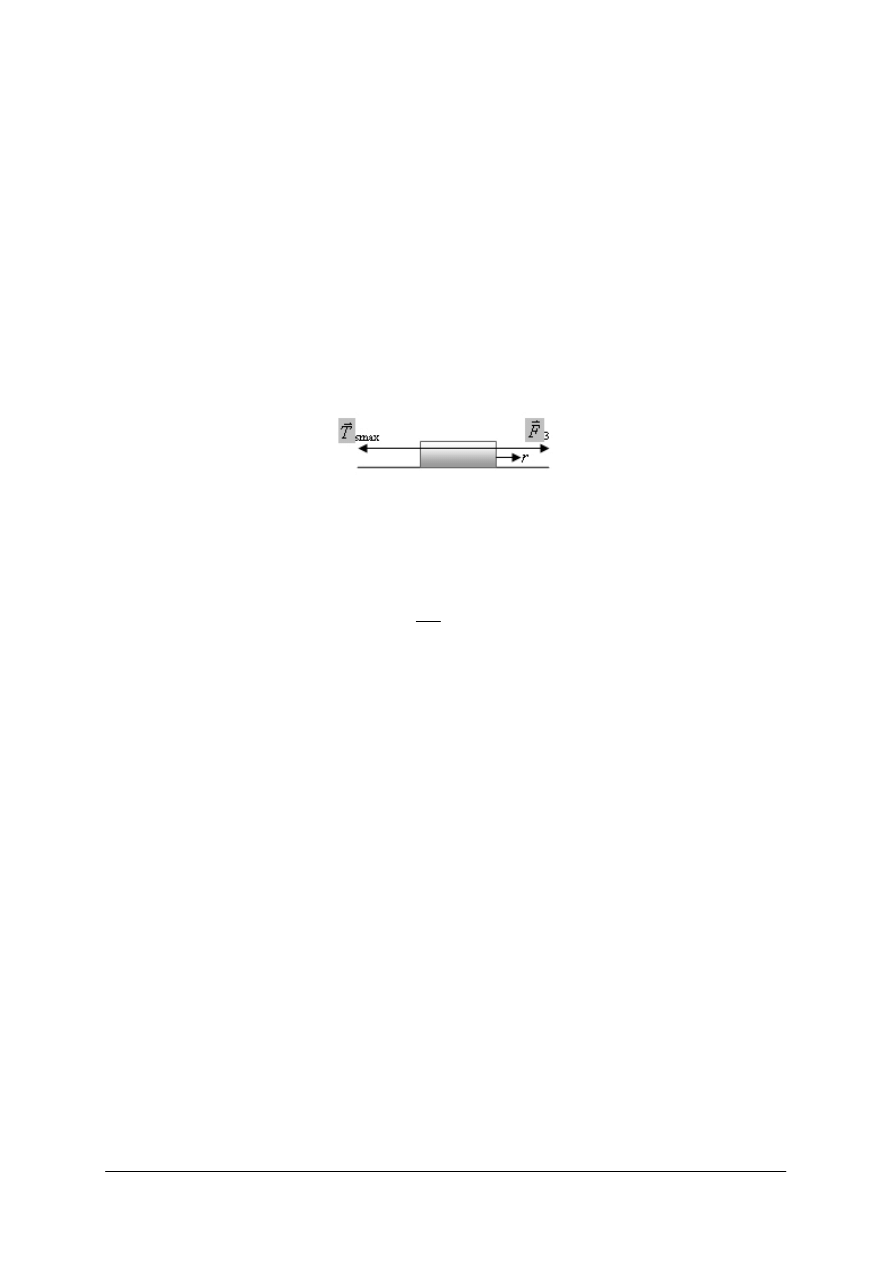
Jeżeli na klocek zadziałamy małą siłą F
1
równolegle do powierzchni zetknięcia
z podłożem (rys. 2), to nadal pozostanie w spoczynku. Na klocek działają siły, które się
równoważą.
Klocek działa na podłoże siłą F
AB
, a podłoże na klocek siłą F
BA
(zgodnie z trzecią zasadą
dynamiki), natomiast siła F
1
, jest zrównoważona siłą zwaną siłą tarcia T
1
.
Rys. 2
Jeżeli zwiększymy siłę działającą na klocek do F
2
(rys. 3) a klocek nadal nie ruszy z miejsca,
znaczy to, że wzrośnie także siła tarcia do T
2
i równoważy siłę F
2 .
Rys. 3
Siłę tarcia działającą na ciało spoczywające nazywa się siłą tarcia spoczynkowego lub
statycznego. Wartość siły tarcia statycznego może wzrosnąć tylko do pewnej wartości
maksymalnej T
s max
.
Maksymalna wartość siły tarcia statycznego T
smax
jest wprost proporcjonalna do wartości siły
nacisku F
N
ciała na podłoże.
s
f
=
N
max
s
F
T
Iloraz tych sił zależy tylko od rodzaju stykających się ciał (powierzchni).
Nazywa się go współczynnikiem tarcia statycznego f
s
.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
15
Siła tarcia statycznego T
s
:
−
występuje między stykającymi się powierzchniami ciał stałych,
−
jest styczna do powierzchni przylegania,
−
jest przeciwna do kierunku ruchu,
−
jest wprost proporcjonalna do siły nacisku normalnego,
−
zależy od rodzaju i gładkości stykających się powierzchni (fs),
−
nie zależy od wielkości stykających się powierzchni.
Tarcie kinetyczne.
Jeżeli na klocek zadziałamy odpowiednio dużą siłą
3
F
(rys. 4), siła tarcia
s
T
max nie jest
w stanie jej równoważyć i klocek rusza. Gdy ciało zaczyna się poruszać, siła tarcia maleje
i przyjmuje stałą wartość. Nazywa się ją siłą tarcia kinetycznego T
k
.
Rys. 4
Stosunek wartości siły tarcia kinetycznego T
k
do wartości siły nacisku F
N
nazywamy
współczynnikiem tarcia kinetycznego f
k.
k
N
k
f
F
T
=
Współczynnik tarcia kinetycznego jest mniejszy od współczynnika tarcia statycznego i zależy
od szybkości ruchu.
f
k <
f
s
W technice wprowadza się wielkość zwaną współczynnikiem przyczepności, który zależy od
kształtu stykających się powierzchni, szybkości ruchu, temperatury, ciśnienia i przylegania
(adhezja).
4.2.2. Pytania
sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jak określisz siłę tarcia?
2.
Jak określa się siłę tarcia statycznego?
3.
Co to jest współczynnik tarcia statycznego?
4.
Jak określa się tarcie kinetyczne?
5.
Co to jest współczynnik tarcia kinetycznego?
6.
Od czego zależy wielkość współczynnika tarcia statycznego?
7.
Od czego zależy wielkość współczynnika tarcia kinetycznego?
8.
Jaka jest zależność między f
s.
i f
k.
?
9.
Od czego zależy wielkość współczynnika przyczepności?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
16
4.2.3. Ćwiczenia
Ćwiczenie 1
Samochód porusza się po poziomym odcinku szosy z prędkością 80 km/h. Oblicz
najmniejszą drogę hamonowania, po przebyciu której samochód zatrzyma się.Współczynnik
tarcia kinetycznego opony gumowej po asfalcie wynosi 0,60.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
odszukać w materiale nauczania potrzebne wzory i zależności,
3)
zapisać je,
4)
dokonać przekształceń i podstawień,
5)
wyznaczyć drogę hamowania.
Wyposażenia stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis,
–
poradnik dla ucznia,
–
kalkulator,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Wyznaczanie siły tarcia za pomocą równi.
Na równi pochyłej tworzącej z poziomem kąt 30°
.Leży blok stalowy o ciężarze 1500 N.
Wyznacz siłę F
, która działając w kierunku równi utrzyma ciężar w równowadze.
Współczynnik tarcia statycznego dla stali wynosi 0,15.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać wielkości dane,
3)
zapisać wielkości szukane,
4)
naszkicować rysunek obrazujący przedstawioną sytuację,
5)
zaznaczyć występujące siły,
6)
zapisać potrzebne wzory, zależności,
7)
zaznaczyć siłę F
, obliczyć jej wartość.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis, ołówek, linijka, kątomierz,
–
poradnik ucznia,
–
tabela funkcji trygonometrycznych,
–
kalkulator,
–
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
17
4.2.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
Określić silę tarcia kinetycznego?
2)
Określić siłę tarcia statycznego?
3)
Określić współczynnik tarcia statycznego i kinetycznego?
4)
Określić zależność między f
s.
i f
k.
?
5)
Wyznaczyć siłę tarcia?
6)
Określić współczynnik przyczepności?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
18
4.3.
Masa i ciężar ciała
4.3.1. Materiał nauczania
Masa - podstawowa cecha ciała fizycznych, charakteryzuje bezwładność ciał. Jednostką masy
(m) jest kilogram (kg).
Ś
rodek - masy- punkt geometryczny, reprezentujący pewne średnie położenie układu punktów
materialnych. Wektor położenia środka masy:
i
i
r
m
M
R
∑
=
1
gdzie: M = masa całego układu,
Σ
m
i
- masa i-tego punktu materialnego
r
i
- wektor położenia i-tej masy.
Współrzędne wektora R
:
R
x
=
i
x
i
r
m
M
∑
1
,
R
y =
i
y
i
r
m
M
∑
1
,
R
z
=
i
z
i
r
m
M
∑
1
,
Gdzie: R
= [
R
x,
R
y,
R
z
]
r
- [r
xi
, r
yi
, r
zi
]
Moment bezwładności (I)
I= m
1 *
2
1
r + m
2
*
2
2
r
+………m
n
*
2
n
r
=
2
1
i
h
i
i
r
m
∑
=
r - odległość punktów układu od pewnej osi.
Jednostką momentu bezwładności jest [kg*m
2
].
Moment bezwładności dotyczy ruchu obrotowego ciała sztywnego, określa rozkład masy ciała
względem punktu lub osi obrotu ciała. Jest miarą bezwładności ciała sztywnego w ruchu
obrotowym. Można z dużym uproszczeniem powiedzieć, że zastępuje masę w ruchu
obrotowym, tzn. tam gdzie w ruchu postępowym występuje masa, to w ruchu obrotowym
występuje moment bezwładności.
Moment bezwładności zależy od:
–
wyboru osi obrotu,
–
kształtu ciała,
–
sposobu rozmieszczenia masy ciała.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
19
Przykład
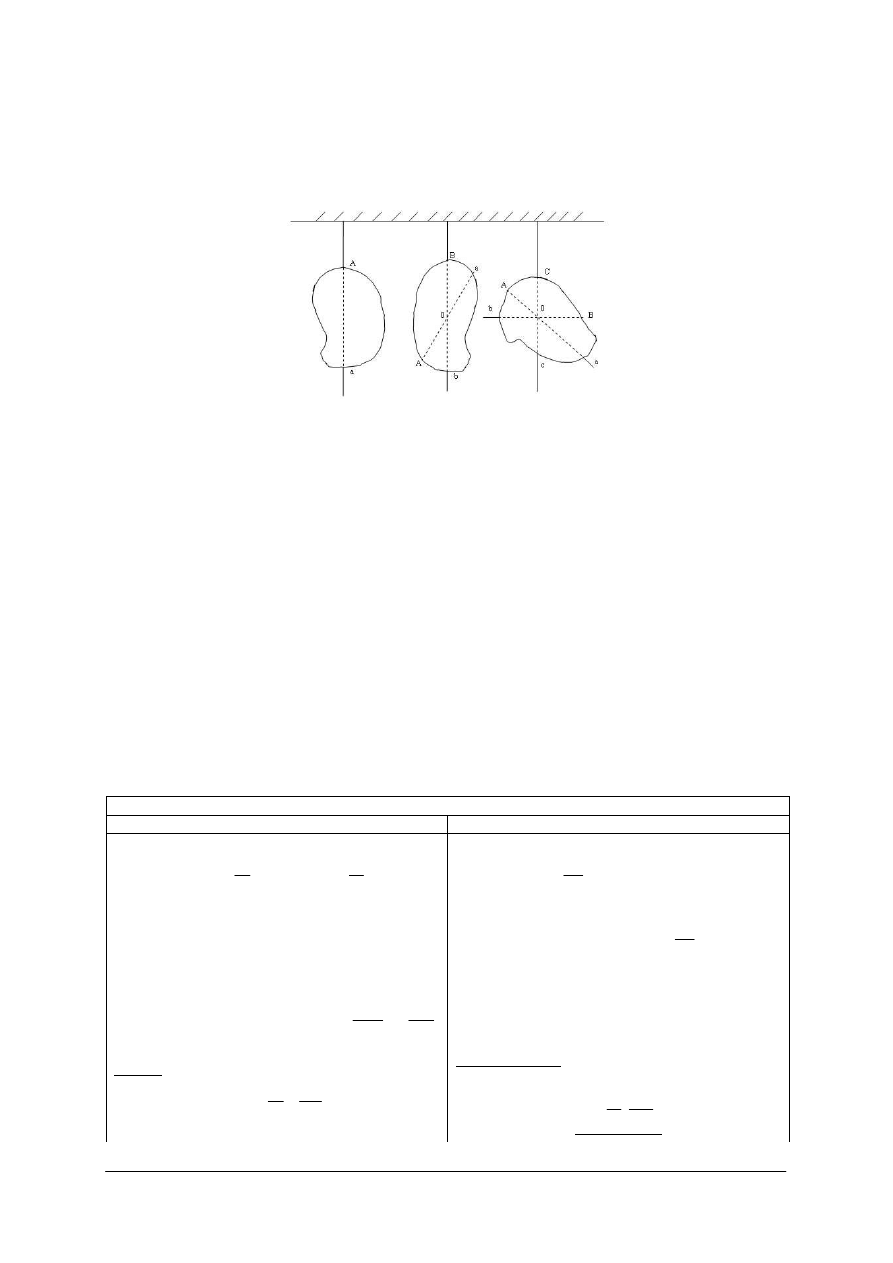
Doświadczalne wyznaczanie środka masy (środka ciężkości) przedmiotów jednorodnych
o nieregularnych kształtach. (rys. 5)
Rys. 5
Ś
rodek masy (środek ciężkości) znajduje się zawsze pod punktem zawieszenia.
Punkt 0 – środek masy,
– środek ciężkości.
Sposób postępowania:
–
ciało zawieszamy na sznurku w pewnym punkcie A znajdującym się na krawędzi tego
ciała.
Po ustaleniu się równowagi, przeprowadzamy linię pionową A na której musi znajdować się
ś
rodek masy,
–
następnie zawieszamy ciało w punkcie B i przeprowadzamy linię Bb, na której znajduje
się środek masy. Jedynym punktem wspólnym jest punkt 0 – to właśnie środek masy
(ciężkości),
–
można jeszcze to samo zrobić zawieszając w punkcie C- linia Cc. Również przetnie się
w punkcie 0.
Tabela. 1
MASA I CIĘśAR CIAŁA
MASA [m]
CIĘśAR CIAŁA [p]
Określa
ciężkość
ciała
wynikającą
z
jego
bezwładności
a
F
m
=
i ciążenia
g
P
m
=
- wielkość skalarna
- jednostka: 1kg
-masa ciała jest jednakowa w każdym miejscu
Stosunek mas dwóch ciał
Gęstość- to stosunek masy ciała do jego objętości
ϱ
=
v
m
[
3
m
kg
]
-zależy od temperatury
Siła grawitacyjna, z jaką Ziemia przyciąga ciała
P= m *g = 9,807
2
s
m
- wielkość wektorowa (do środka Ziemi)
- jednostka: 1N , 1kG= 1kg * 9,807
2
s
m
- ciężar ciała jest różny w różnych miejscach na Ziemi
(różne g)
- stosunkowi ich ciężarów (WAśENIE)
Ciężar właściwy- stosunek ciężaru ciała do jego
objętości.
]
[
3
m
N
v
P
=
γ
2
1
2
1
P
P
m
m
=

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
20
Ś
rodek masy- punkt geometryczny reprezentujący
pewne
ś
rednie
położenie
układu
punktów
materialnych.
Wektor położenia środka masy:
i
i
r
m
M
R
*
1
∑
=
=
=
v
g
m *
γ
ϱ*g -(iloczyn gęstości i
przyspieszenia ziemskiego)
Ś
rodek ciężkości- punkt przyłożenia wypadkowej siły
ciężkości.
Dla ciał znajdujących się w jednorodnym polu sił ciężkości (na wszystkie punkty ciała
działa jednakowe g):
Ś
RODEK MASY POKRYWA SIĘ ZE ŚRODKIEM CIĘśKOŚCI
Każde ciało to układ punktów materialnych. Na każdy taki punkt działa siła ciężkości. Czyli
na całe ciało działa wypadkowa siła ciężkości.
−
Ciężar ciała- to wypadkowa siła ciężkości (wszystkich sił działających na poszczególne
punkty materialne).
P=m * g
gdzie: P- ciężar ciała
m- masa ciała
g- przyspieszenie ziemskie
Jednostką ciężaru jest niuton [N].
−
Ciężar właściwy- ciężar substancji zawartej w jednostce objętości, wyraża się przez
stosunek ciężaru ciała (P) do jego objętości (V).
V
P
=
γ
Jednostka [
3
m
N
]
−
Ś
rodek ciężkości- to punkt przyłożenia wypadkowej siły ciężkości (P). Dla brył
jednorodnych środek ciężkości pokrywa się ze środkiem masy. Dla brył regularnych
ś
rodek masy (środek ciężkości) pokrywa się ze środkiem geometrycznym.
Ś
rodek ciężkości brył nieregularnych można wyznaczyć doświadczalnie.
Rodzaje równowagi.
−
Równowaga trwała- jeżeli po wytrąceniu ciała ze stanu równowagi pojawiają się siły
przywracające ten stan.
Ś
rodek ciężkości ciała zajmuje najniższe z możliwych położenie (rys. 6a).
−
Równowaga chwiejna- małe zaburzenie niszczy stan równowagi (rys. 6c) Środek
ciężkości zajmuje najwyższe położenie.
−
Równowaga obojętna- małe wychylenie nie powoduje pojawiania się ani sił
przyciągania ani odpychania (rys. 6b). Środek ciężkości jest na tym samym poziomie.
Rys. 6 Rodzaje równowagi.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
21
Warunki równowagi.
1.
Suma geometryczna wszystkich zewnętrznych sił działających na ciało w stanie
równowagi musi równać się zero.
0
...
2
1
=
+
+
+
=
n
F
F
F
F
,
2.
Dla wagi lub dźwigni (maszyna prosta)- suma geometryczna zewnętrznych momentów sił
równa się 0.
0
2
1
=
+
M
M
,
lub
2
2
1
1
*
*
r
F
r
F
=
gdzie:
M - moment siły
r
F
M
*
=
F
- siła
r
1
i r
2
-ramię siły.
4.3.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jak określisz masę ciała?
2.
Co to jest środek masy?
3.
Co to jest moment bezwładności?
4.
Jak określisz ciężar ciała?
5.
Jak określisz środek ciężkości?
6.
Jak wyznacza się środek masy?
7.
Jak wyznacza się środek ciężkości?
8.
Jakie są rodzaje równowagi?
9.
Jakie są warunki równowagi?
4.3.3. Ćwiczenia
Ćwiczenie 1
Wyznacz środek masy następujących ciał:
a)
kuli,
b)
sześcianu,
c)
równoległoboku,
d)
pręta,
e)
trójkątnej płyty.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
określić rodzaj ciał ze względu na kształt,
2)
określić położenie środka masy ciał o kształcie regularnym,
3)
narysować te ciała,
4)
wyznaczyć środki mas.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
22
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis, ołówek,
–
linijka, cyrkiel,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Wyznacz środek masy.
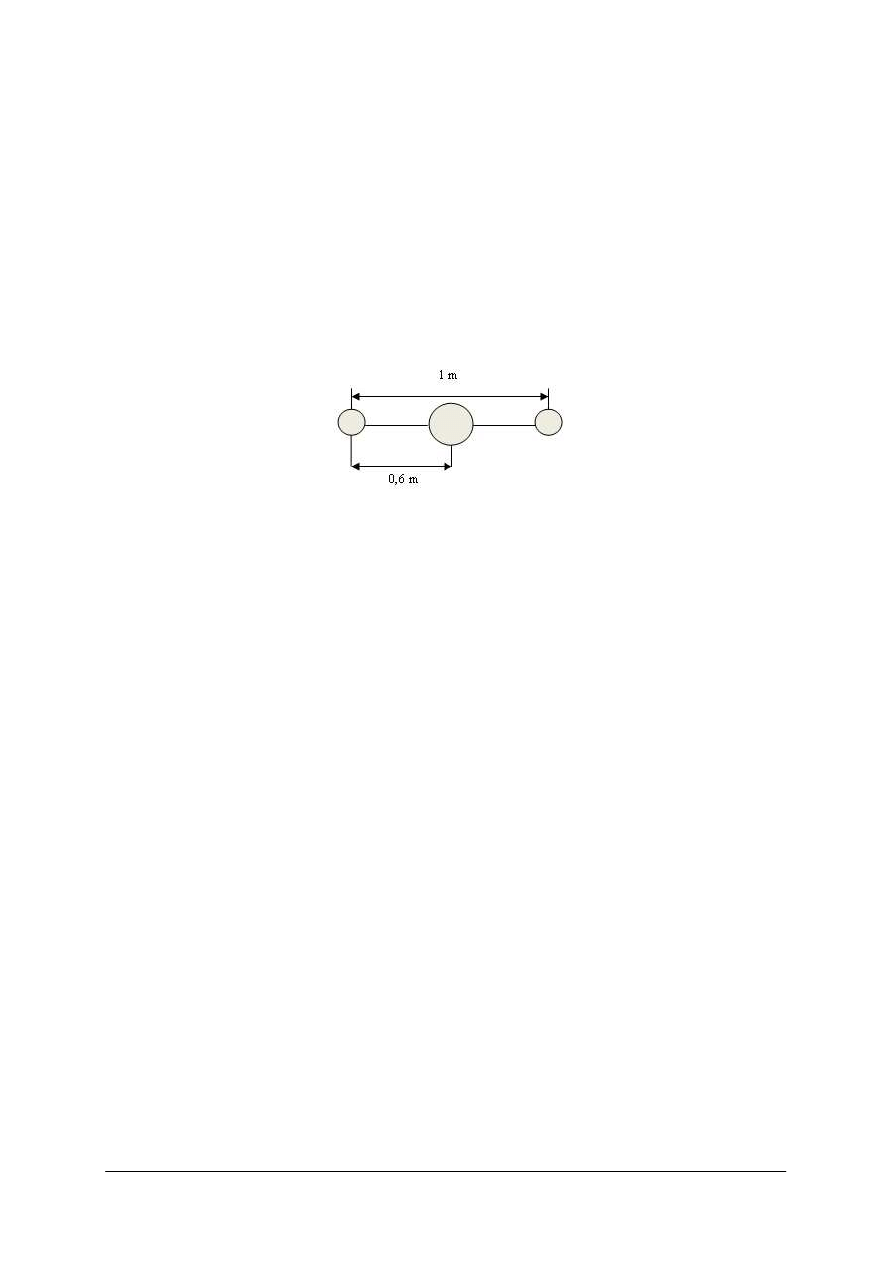
Trzy kule o różnych masach m
A
,m
B
,m
C
połączono prętami (rys. 7).
Rys. 7
Masy kul są odpowiednio równe: 1 kg, 2 kg, 0,5 kg. Układ ten może obracać się względem
osi przechodzącej przez jego środek masy. Masy prętów pomijamy.
1.
Wyznacz środek masy tego układu.
2.
Oblicz moment bezwładności tego układu względem osi obrotu.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
dokonać analizy rysunku,
3)
zapisać wyrażenie na środek masy,
4)
wyznaczyć środek masy,
5)
zapisać wzór na moment bezwładności,
6)
wyznaczyć moment bezwładności,
7)
określić jednostki.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis, ołówek,
–
tabela podstawowych stałych fizycznych,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Oblicz ciężar (w niutonach N) człowieka ważącego 70 kg.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
23
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
odszukać w materiale nauczania i zapisać wyrażenie na ciężar,
2)
zapisać wielkości dane,
3)
zapisać wielkości szukane,
4)
odszukać i zapisać w tabeli wartość potrzebnej wielkości,
5)
podstawić dane,
6)
obliczyć.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis, ołówek,
–
tabela podstawowych stałych fizycznych,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 4
Jednorodna belka stalowa o długości 1 m opiera się swymi końcami o dwie wagi
sprężynowe. Ciężar belki wynosi 4 N.
1.
Określ wskazania wag.
2.
Na belce zawieszono ciało o ciężarze 6 N w odległości 25 cm od jej końca. Określ jakie
teraz będą wskazania wag.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
naszkicować rysunek obrazujący przedstawioną sytuację, dokonać analizy,
2)
określić i narysować działające siły,
3)
odszukać i zapisać potrzebne zależności, warunki,
4)
zapisać wielkości dane,
5)
zapisać wielkości szukane,
6)
podstawić dane liczbowe,
7)
dokonać obliczeń.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń, papier milimetrowy,
–
długopis, ołówek,
–
linijka,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
24
4.3.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
określić masę ciała?
2)
określić środek masy (środek ciężkości)?
3)
wyznaczyć środek masy ciał o kształtach regularnych?
4)
wyznaczyć środek masy ciał o kształtach nieregularnych?
5)
określić ciężar ciała?
6)
obliczyć ciężar ciała?
7)
zastosować odpowiednie jednostki masy i ciężaru ciała?
8)
określić rodzaje równowagi?
9)
określić warunki równowagi ciał?
10)
zastosować warunki równowagi ciał?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
25
4.4.
Ruch. Rodzaje ruchu. Ruch punktu materialnego
4.4.1. Materiał nauczania
Spoczynek i ruch. Względność ruchu. Przemieszczenie.
Położenie ciała określa się zawsze w stosunku do innego ciała lub zespołu innych ciał
zwanych układem odniesienia.
Ruchem nazywamy zachodzącą w czasie zmianę położenia ciała względem wybranego
układu odniesienia.
Jeżeli położenie ciała względem przyjętego układu odniesienia nie zmienia się, to ciało
znajduje się w stanie spoczynku, jeżeli zaś ulega zmianie, to znajduje się ono w stanie ruchu
względem tego układu.
W tej samej chwili ciało może być w spoczynku względem jednego układu odniesienia
a względem drugiego- w ruchu. Tę właściwość ruchu nazywamy względnością.
Np. pasażer w autobusie jest w spoczynku względem autobusu, ale w ruchu względem
drogi, domów przy drodze.
Do opisu zmiany położenia ciała służy wielkość wektorowa zwana przemieszczeniem.
Przemieszczenie to wektor o początku w początkowym położeniu ciała i końcu w jego
położeniu końcowym.
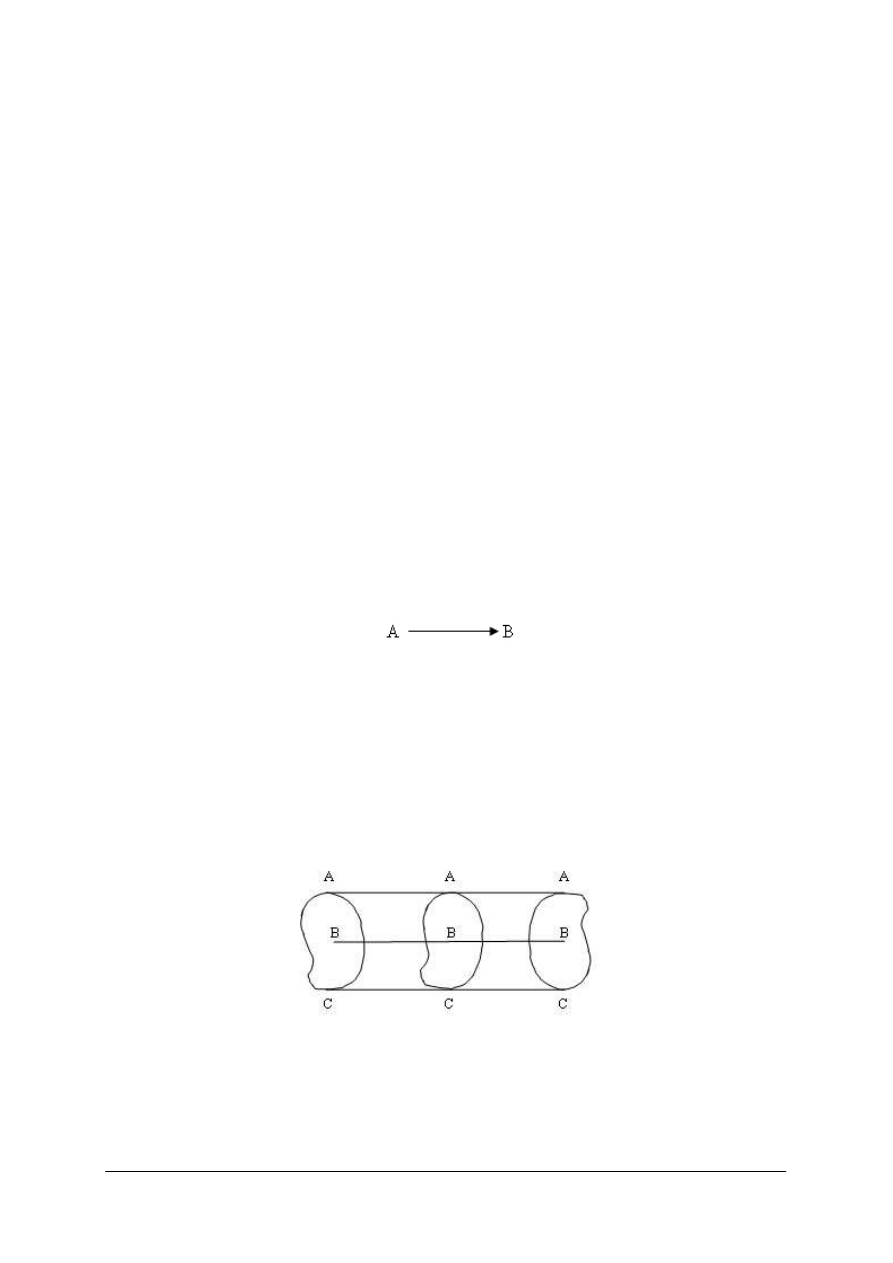
Np. z Warszawy wystartował samolot i przebył po linii prostej na wschód 500 km. Jeżeli
przyjmiemy, że odległości 250 km odpowiada odcinek długości 1cm, to przemieszczenie
samolotu opisuje wektor o długości 2 cm (rys. 8)
Rys. 8
Punkt A to początek wektora, B jego koniec. Prosta, na której leży wektor to kierunek
wektora, a grot strzałki określa jego zwrot.
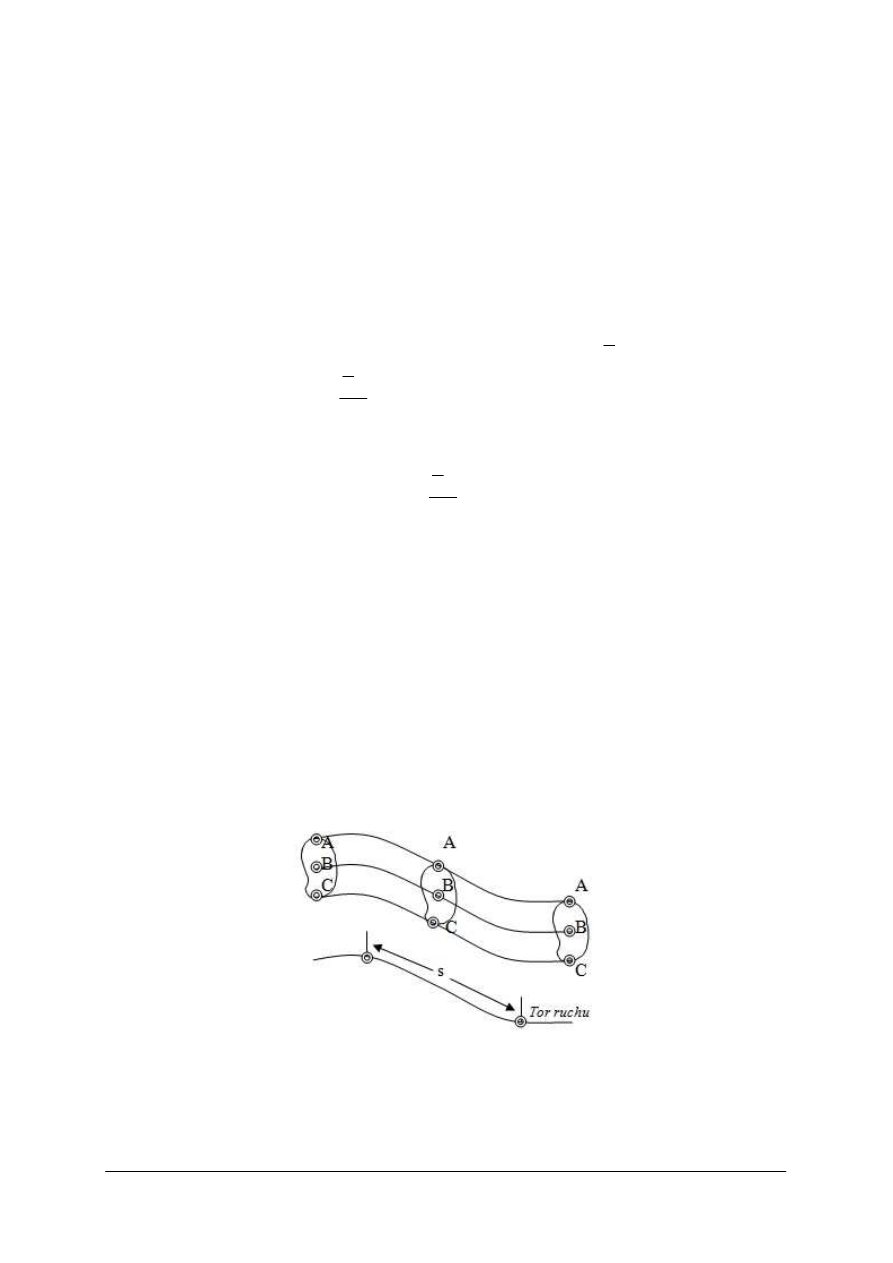
Tor ruchu.
Linia ciągła, którą tworzą kolejne położenia rozpatrywanego punktu poruszającego się ciała
(np. położenie A,B,C na rys. 9) nazywa się torem ruchu.
Rys. 9
Tor ruchu może być linią prostą lub krzywą.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
26
Droga. Prędkość ruchu.
Odcinek toru przebyty przez punkt poruszającego się ciała w pewnym odstępie czasu to
droga. Poszczególne odcinki toru, czyli drogi mogą być przebywane w jednakowych
odstępach czasu- ciało porusza się ze stałą prędkością lub w różnych odstępach czasu- ciało
porusza się z prędkością zmienną.
Prędkość v
jest wielkością wektorową.
Aby ją określić należy podać:
–
kierunek- jest zgodny z kierunkiem przemieszczenia,
–
zwrot- jest zgodny ze zwrotem przemieszczenia,
–
wartość.
Wartość wektora prędkości nazywamy szybkością ciała.
Prędkością średnią v
ś
r
nazywamy iloraz wektora przemieszczenia
B
A
i czasu, w którym to
przemieszczenie nastąpiło v
ś
r
=
t
B
A
.
Prędkością chwilową v
chwil
,nazywamy iloraz wektora przemieszczenia ciała w bardzo
krótkim czasie i czasu t, w którym to przemieszczenie nastąpiło
v
chwil
=
t
B
A
∆
*
∆
t
→
0
Droga a przemieszczenie (przesunięcie):
–
przemieszczenie jest wielkością wektorową,
–
jeżeli położenie ciała przed i po przemieszczeniu jest takie samo, to całkowite
przemieszczenie jest równe zeru,
–
droga nie jest wielkością wektorową, jest wielkością skalarną,
–
jeżeli położenie ciała przed i po przemieszczeniu jest takie samo, to całkowita droga jest
różna od zera.
Rodzaje ruchów.
Ze względu na tor ruchu:
Ruch postępowy- gdy tory po których poruszają się poszczególne jego punkty, są równe
i równoległe. (rys. 10)
Rys. 10
Ruch obrotowy- gdy poszczególne punkty ciała zakreślają okręgi współśrodkowe a ich środki
leżą w linii prostej nie biorącej udziału w ruchu i zwanej osią obrotu. (rys. 11)

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
27
Rys. 11
Ruch złożony- z obydwu ruchów.
Np. ruch koła jadącego samochodu jest złożony z ruchu obrotowego koła dookoła osi i ruchu
postępowego osi koła względem drogi.
Ruch prostoliniowy - tory ruchu to linie proste.
Ruch krzywoliniowy- tory ruchu to linie krzywe.
Ze względu na prędkość ruchu:
Ruch jednostajny - w równych, dowolnie małych odstępach czasu ciało przebywa jednakowe
drogi, czyli droga jest wprost proporcjonalna do czasu ruchu.
Ruch niejednostajny, zmienny- proporcjonalność ta nie jest zachowana.
Często zdarza się, że rozpatrywany jest ruch ciała o wymiarach znikomo małych
w porównaniu z odległościami innych ciał, przyjętych za układ odniesienia. Pojęcie ciała
można w takich przypadkach zastąpić punktem, w którym ześrodkowana jest jego masa,
nazywamy punktem materialnym.
W kolejnym punkcie omawiać będziemy ruch punktu materialnego- zagadnienia kinematyki
punktu materialnego.
Ruch jednostajny.
Ruch jednostajny prostoliniowy.
Punkt materialny porusza się ruchem jednostajnym prostoliniowym, jeżeli torem tego
ruchu jest linia prosta, a droga s przebyta w dowolnym czasie t , liczonym od chwili
rozpoczęcia obserwacji (t
0
=0), jest wprost proporcjonalna do czasu ruchu.
Stosunek drogi s - do odpowiadającego jej czasu t ma wartość stałą i jest miarą prędkości v
tego ruchu (ściślej miarą wartości liczbowej prędkości v).
v =
t
s
,
Jednostką prędkości (w układzie SI) jest m/s i jednostki pochodne, np. km/h.
Wartość przebytej drogi s wyraża równanie
s = v * t
zwane równaniem ruchu jednostajnego.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
28
Jeżeli obserwacje ruchu ciała rozpoczęto w chwili t
0
w której znajdowało się ono w odległości
s od przyjętego punktu odniesienia, to wartość prędkości v tego ruchu wyrazi się wzorem:
v=
t
s
∆
∆
;
gdzie:
0
s
s
s
−
=
∆
to przyrost drogi
0
t
t
t
−
=
∆
to przyrost czasu
to
0
0
t
t
s
s
v
−
−
=
i
)
(
0
o
t
t
v
s
s
−
+
=
Jest to ogólna postać równania ruchu jednostajnie prostoliniowego.
Wykres równania drogi i prędkości w ruchu jednostajnym prostoliniowym.
Ruchy ciał mogą być ilustrowane graficznie za pomocą wykresów w układzie
współrzędnych.
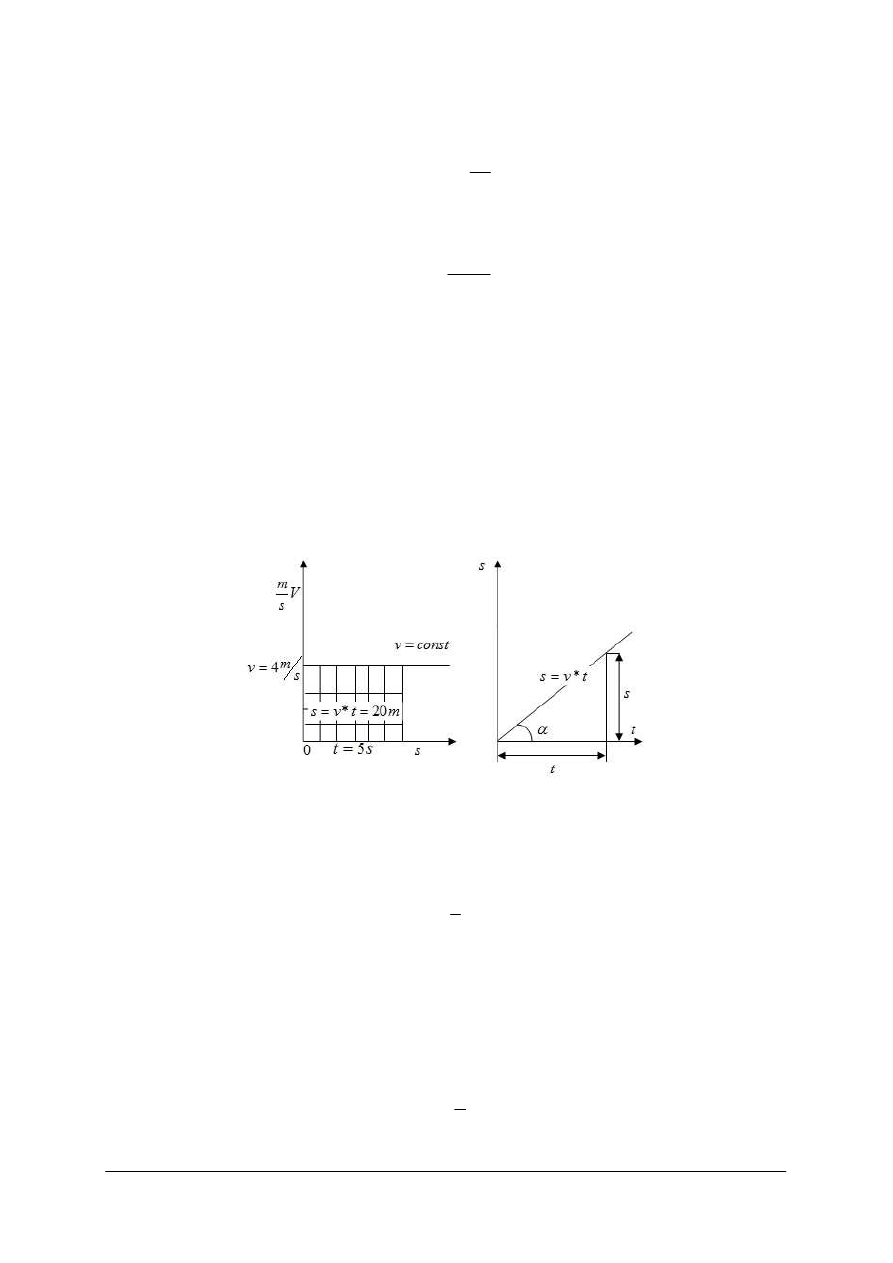
Wykres prędkości w układzie współrzędnych v,t (rys. 12) oraz drogi w układzie
współrzędnych s,t (rys. 13)
Rys. 12 Rys. 13
Wykresem równania drogi ruchu jednostajnego jest linia prosta (rys. 13) nachylona do osi
czasu po kątem
α
, którego tangens jest równy prędkości v.
v
t
s
tg
=
=
α
Wykresem równania prędkości ruchu jednostajnego jest linia prosta równoległa do osi czasu
(rys. 12). Droga (s) przebyta w czasie (t), równa iloczynowi v*t jest na wykresie polem
prostokąta.
Dla pełnego określenia ruchu potrzebna jest znajomość wartości prędkości, ale również jej
kierunku, w którym zachodzi ruch.
Prędkość jest wektorem.
t
s
v
=
Podlega wice prawu dodawania wektorów.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
29
Często spotykane są takie ruchy, w których bierze udział nie tylko rozpatrywane ciało, ale również
układ odniesienia. Ciało wykonuje wówczas równocześnie dwa ruchy: ruch względem
poruszającego się układu z prędkością względną v
w
. oraz – łącznie z układem odniesienia- ruch
względem innego nieruchomego układu, przyjętego za układ odniesienia, z prędkością unoszenia
v
u
. Ruch ciała odbywa się wówczas z prędkością v
,będącą sumą geometryczną prędkości
w
v
i
u
v
.
Ruch prostoliniowy zmienny.
Ruch, w którym droga przebywana przez punkt materialny nie jest wprost proporcjonalna
do czasu, nazywa się ruchem zmiennym.
Ruch prostoliniowym jednostajnie zmienny.
Prędkość zmienia się
0
v
v
v
−
=
∆
gdzie: v
∆
- przyrost prędkości,
v
0
- prędkość początkowa,
v
- prędkość po upływie czasu t.
Stosunek przyrostu prędkości
v
∆
do przyrostu czasu
t
∆
, w którym zachodzi nazywa się
przyspieszeniem a.
t
v
v
t
v
a
∆
−
=
∆
∆
=
0
,
Jednostką przyspieszenia w układzie SI jest m/s
2
.
Przyspieszenie podobnie jak prędkość jest wielkością wektorową.
t
v
a
∆
∆
=
Jeżeli przyspieszenie jest dodatnie, czyli skierowane tak samo jak prędkość, to taki ruch jest
ruchem prostoliniowym jednostajnie przyspieszonym, jeżeli przyspieszenie skierowane
przeciwnie niż prędkość, jest to ruch prostoliniowy jednostajnie opóźniony.
Równanie prędkości w ruchu jednostajnie zmiennym prostoliniowym jest następujące.
t
a
v
v
*
0
+
=
Obraz graficzny tego równania przedstawia rys. 15.
a)
dla ruchu jednostajnie przyspieszonego
b)
dla ruchu jednostajnie opóźnionego
a
t
v
v
tg
=
−
=
0
α
Rys. 15
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
30
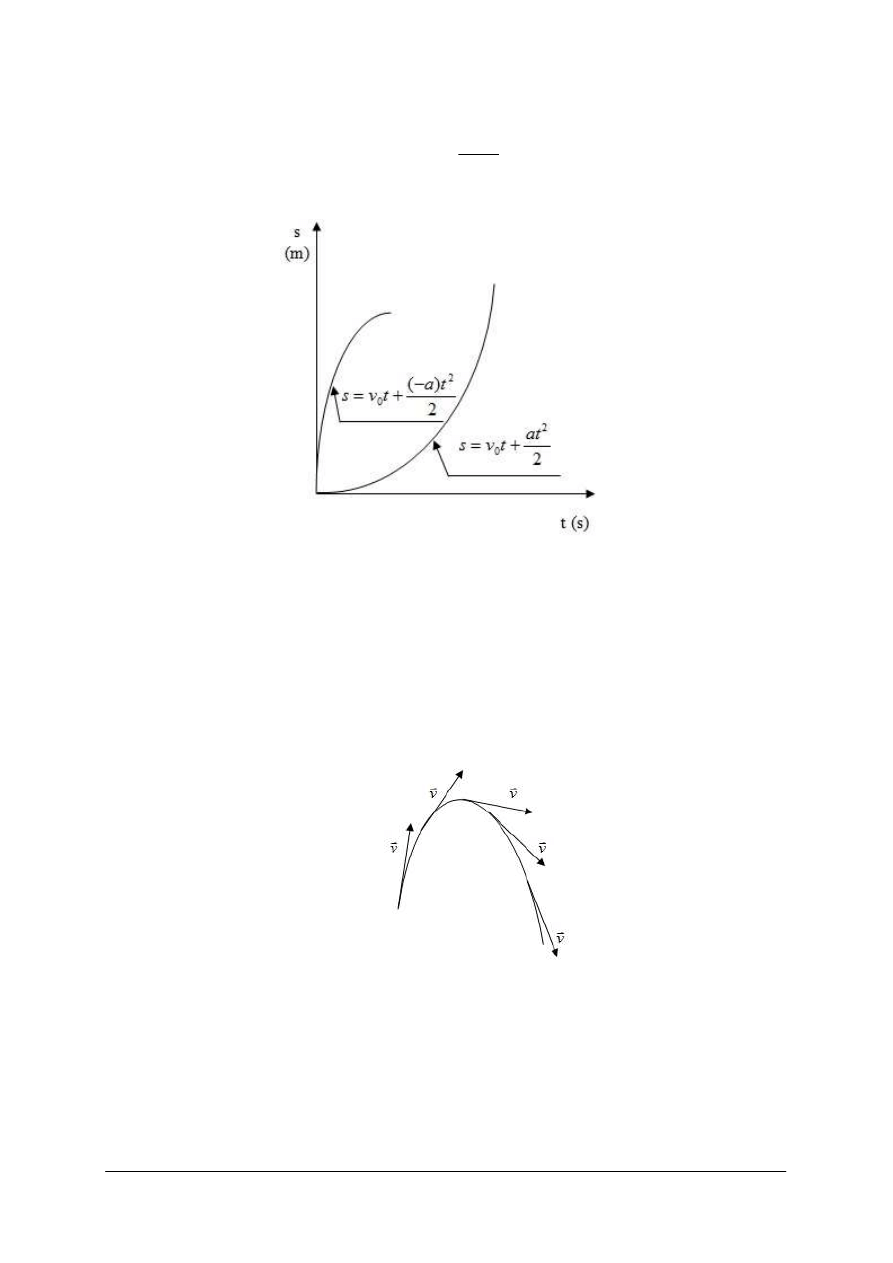
Równanie drogi w ruchu jednostajnie zmiennym prostoliniowym jest następujące:
2
*
2
0
t
a
t
v
s
+
=
Wykres tego równania przedstawia rys. 16.
Rys. 16
Jeżeli wartość podczas ruchu zmienia się i jest funkcją czasu , to taki ruch nazywamy ruchem
niejednostajnie zmiennym.
Jeżeli wartość prędkości wzrasta – to ruch nazywa się przyspieszonym, jeżeli maleje-
opóźnionym.
Ruch krzywoliniowy.
W ruchu krzywoliniowym torem ruchu punktu materialnego jest linia krzywa.
Kierunek prędkości poruszającego się punktu materialnego jest styczny do krzywej w jej
poszczególnych punktach (rys. 17)
Rys. 17
Kierunek prędkości w ruchu krzywoliniowym ulega więc ciągłym zmianom.
Jeżeli wartość prędkości się nie zmienia- jest to ruch krzywoliniowy jednostajny.
Jeżeli zmienia się również wartość prędkości, jest to ruch krzywoliniowy zmienny.
Fakt, że kierunek prędkości w ruchu krzywoliniowym jest w każdym punkcie styczna do toru,
potwierdzają liczne doświadczenia, np. iskry przy szlifowaniu poruszają się w kierunku
stycznym do tarczy; kamień uwiązany na sznurku i obracany dookoła ręki po zerwaniu się
sznurka biegnie po stycznej do okręgu, po którym się poruszał.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
31
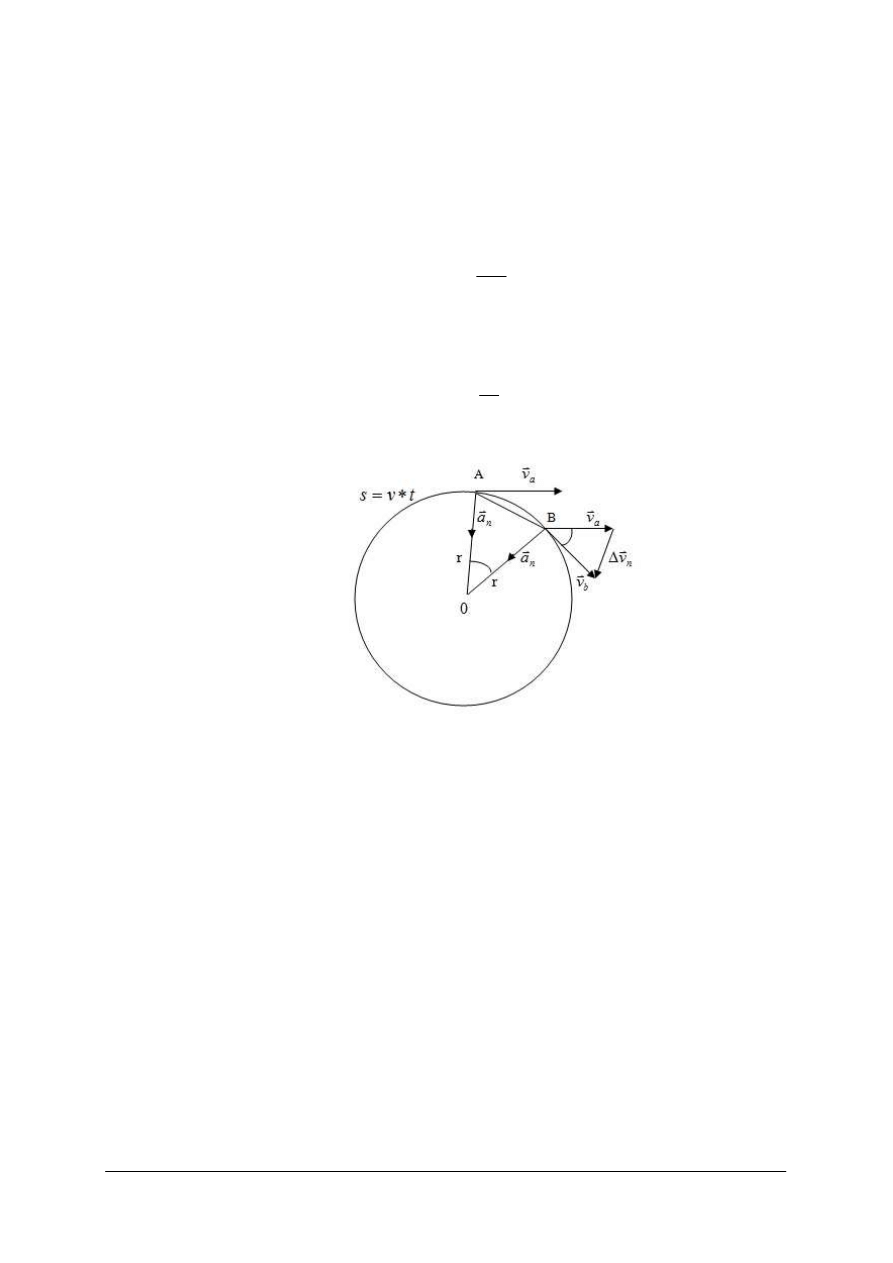
Ruch jednostajny po okręgu.
Jest to ruch, w którym punkt materialny zakreśla w równych odstępach czasu jednakowe
odcinki łuku.
W związku ze zmianą kierunku prędkości występuje więc geometryczny przyrost prędkości
n
v
∆
.
Stosunek przyrostu geometrycznego
n
v
∆
do czasu t , w którym ten przyrost zachodzi jest
miarą przyspieszenia
n
a
, zwanego przyspieszeniem dośrodkowym lub normalnym.
t
v
a
n
n
∆
=
Przyspieszenie dośrodkowe
n
a
w ruchu jednostajnym po okręgu powoduje zmianę kierunku
prędkości, jest w każdym punkcie toru skierowane wzdłuż promienia r do środka okręgu (rys. 18)
Wartość przyspieszenia dośrodkowego określa wyrażenie.
r
v
a
n
2
=
,
gdzie: v- wartość prędkości,
r
- promień okręgu.
Rys. 18
4.4.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jak określa się położenie ciała?
2.
Co to jest ruch?
3.
Jak wyjaśnisz pojęcie względność ruchu?
4.
Jak można określić pojęcie tor ruchu?
5.
Jakie są rodzaje toru ruchu?
6.
Jakie są kryteria podziału ruchów?
7.
Jakie są rodzaje ruchów?
8.
Jaki ruch nazywa się ruchem jednostajnym prostoliniowym?
9.
Jak wyraża się równanie ruchu jednostajnie prostoliniowego?
10.
Jak przedstawia się wykres równania drogi i prędkości w ruchu jednostajnie
prostoliniowym?
11.
Jaki ruch nazywa się ruchem jednostajnie zmiennym prostoliniowym?
12.
Jaki ruch jest ruchem prostoliniowym jednostajnie przyspieszonym, a jaki jednostajnie
opóźnionym?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
32
13.
Jak wyraża się równanie drogi i prędkości w ruchu jednostajnie zmiennym
prostoliniowym?
14.
Jak przedstawia się wykres równania drogi i prędkości w ruchu jednostajnie zmiennym
prostoliniowym?
15.
Jaki ruch nazywa się ruchem krzywoliniowym?
16.
Jakie znasz ruchy krzywoliniowe?
17.
Jak należy wyjaśnić termin geometryczny przyrost prędkości?
18.
Co to jest przyspieszenie dośrodkowe?
4.4.3. Ćwiczenia
Ćwiczenie 1
Sklasyfikuj poznane rodzaje ruchów. Podaj przykłady.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
odszukać w materiałach dydaktycznych kryteria klasyfikacji ruchów,
2)
zapisać kryteria,
3)
zapisać obok kryteriów odpowiednie rodzaje ruchów,
4)
zapisać przy rodzaju ruchu jego charakterystykę,
5)
przy nazwie rodzaju ruchu podać jego przykład.
Wyposażenie stanowiska pracy:
–
papier formatu A4,
–
flamastry, długopis, linijka,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Samochód jedzie z szybkością 90km/h. Sprinter biegnie z szybkością 10 m/s. Wyraź
szybkość:
a)
samochodu w m/s,
b)
sprintera w km/h.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
Zapisać, że 1 km = …….. m,
2)
Zapisać, że 1 h = …….. s,
3)
Dokonać wyliczenia szybkości samochodu w m/s wstawiając w miejsce km metry
a w miejsce godziny sekundy,
4)
Obliczyć szybkość sprintera w km/h wstawiając w miejscu metrów km, a w miejsce
sekund godziny.
Wyposażenie stanowiska pracy:
–
papier, zeszyt,
–
długopis,
–
tabela jednostek miar, tabela przeliczeń,
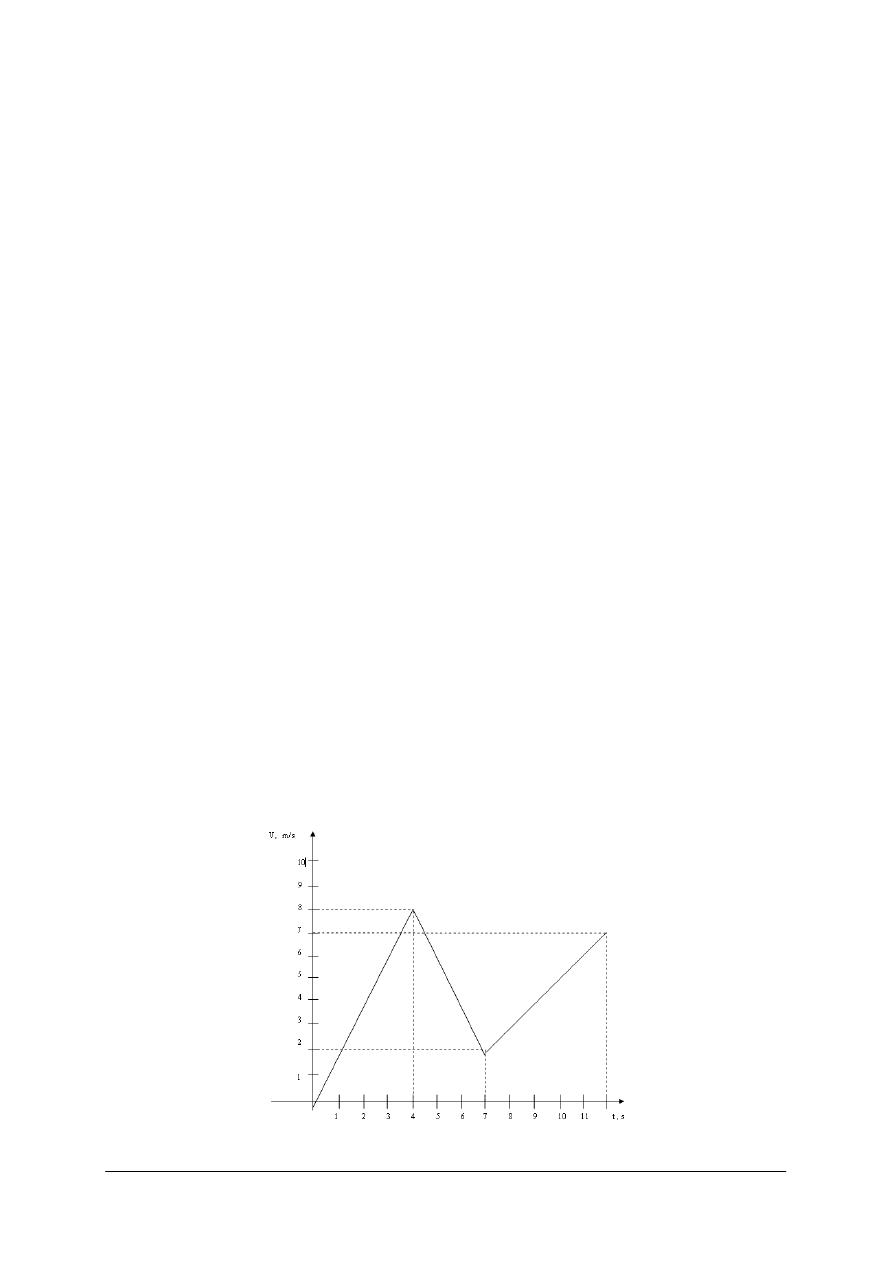
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
33
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
W odległości 1200 m od stacji pociąg zaczął się poruszać ruchem jednostajnym
z szybkością 72 km/h. W jakim czasie przebędzie on drogę 2,4 km? W jakiej odległości
od stacji znajdzie się po upływie 4 min? Oblicz.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy treści fizycznej zadania,
2)
wyszukać i zapisać wielkości dane,
3)
dokonać przeliczenia jednostek aby je ujednolicić,
4)
zapisać wielkości szukane,
5)
zapisać wzory z jakich należy skorzystać aby obliczyć czas,
6)
podstawić dane i obliczyć czas,
7)
zapisać wzór z jakiego należy skorzystać aby obliczyć drogę,
8)
podstawić dane i obliczyć drogę,
9)
zapisać wyniki.
Wyposażenie stanowiska pracy:
–
zeszyt,
–
długopis,
–
tabela przeliczeń jednostek miar,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 4
Na rys. 19 pokazano zależność prędkości ciała od czasu ruchu. Oblicz:
1.
Przyspieszenie ciała dla: t
1
= 1 s, t
2
= 5 s, t3 = 10 s.
2.
Drogę pokonaną przez ciało podczas całego ruchu,
3.
Prędkość średnią w poszczególnych etapach ruchu i w całym ruchu.
Rys.19

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
34
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
rozróżnić etapy ruchu,
2)
rozróżnić rodzaje ruchów w poszczególnych etapach,
3)
zapisać wzór na przyspieszenie,
4)
odczytać z wykresu wartości prędkości i czasu potrzebne do wyliczenia a
1
, a
2
, a
3
,
5)
zapisać wzory na drogę w tym ruchu, wybrać wygodniejszy,
6)
odczytać z wykresu potrzebne dane,
7)
wyliczyć drogę s,
8)
zapisać wzór na prędkość średnią,
9)
podstawić dane i wyliczyć v
ś
r1
, v
ś
r2
, v
ś
r3
,
10)
obliczyć prędkość średnią w całym ruchu,
11)
zapisać wyniki.
Wyposażenie stanowiska pracy:
–
zeszyt,
–
długopis,
–
poradnik ucznia,
–
wykres ruchu,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 5
W naszym otoczeniu zachodzą np. następujące ruchy:
1.
ruch cząsteczek w gazie między zderzeniami,
2.
ruch Ziemi wokół Słońca,
3.
ruch krzesełka kolejki liniowej ze stałą prędkością,
4.
ruch autobusu dojeżdżającego do przystanku,
5.
ruch krzesełka karuzeli,
6.
ruch wahadła w zegarze,
7.
ruch spadającej piłki- przy pominięciu oporu powietrza,
8.
ruch piłki rzuconej pionowo w górę,
9.
ruch sanek z oblodzonej górki.
Dokonaj klasyfikacji wymienionych ruchów wpisując je do tabelki.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zapisać rodzaje ruchów,
2)
rozpoznać rodzaje ruchów podanych przez nauczyciela,
3)
narysować tabelę z liczbą rubryk odpowiadającą liczbie rozpoznanych rodzajów ruchów,
4)
wpisać nazwy ruchów do tabeli,
5)
wpisać rozpoznane rodzaje ruchu w odpowiedniej rubryce,
6)
sprawdzić prawidłowość zapisu.
Wyposażenie stanowiska pracy:
–
papier formatu A4,
–
flamastry, długopis,
–
linijka,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
35
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
4.4.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
określić położenie ciała?
2)
wyjaśnić pojęcie względność ruchu?
3)
określić ruch postępowy?
4)
określić ruch obrotowy?
5)
określić ruch złożony?
6)
podać przykłady ruch postępowego, obrotowego i złożonego?
7)
określić ruch prostoliniowy?
8)
określić ruch krzywoliniowy?
9)
określić ruch jednostajny?
10)
określić ruch zmienny?
11)
rozróżnić rodzaje ruchów?
12)
podać i zastosować równania prędkości i drogi w poszczególnych
rodzajach ruchu?
13)
przeliczyć wartości podane w jednych jednostkach na inne?
14)
scharakteryzować (określić) przyspieszenie dośrodkowe?
15)
podać związki między drogą, prędkością, czasem i wartością
przyspieszenia w ruchach: jednostajnym i jednostajnie przyspieszonym?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
36
4.5.
Ruch bryły. Składanie ruchów
4.5.1. Materiał nauczania
Bryła to zbiór wielu punktów.
Bryła sztywna to takie ciało, w którym siły zewnętrzne nie zmieniają odległości między
dowolnymi jego punktami. W rzeczywistości nie ma takich ciał- jest to przybliżenie, ale
często wystarczające.
Ruch bryły sztywnej możemy podzielić na dwie kategorie:
1.
Ruch postępowy- wszystkie punkty bryły poruszają się tak samo, po torach równoległych
do siebie.
2.
Ruch obrotowy- punkty bryły poruszają się po współśrodkowych okręgach.
Ś
rodki tych okręgów leżą na jednej prostej, nie biorą udziału w ruchu. Prosta ta nazywa
się osią obrotu.
Drogi s poszczególnych punktów są różne –w zależności od położenia punktu w stosunku do
osi obrotu (s-droga liniowa).
Kąt obrotu ciała
α
jest jednakowy dla wszystkich punktów biorących udział w ruchu, nosi
nazwę drogi kątowej
α
.
Droga liniowa s dowolnego punktu obracającego się ciała jest równa iloczynowi drogi
kątowej (
α
) i jego promienia wodzącego (r).
s=
α
*r
Stosunek przyrostu drogi kątowej
α
∆
do przyrostu czasu
t
∆
, w którym została ona
zakreślona nosi nazwę prędkości kątowej (
ω
)
t
∆
∆
=
α
ω
Jednostki: [
s
s
rad 1
,
]
Częstotliwość obrotów: f
=
r
v
π
π
ω
2
2
=
[obroty/min, obroty/s].
Rodzaje ruchu obrotowego:
–
ruch obrotowy jednostajny- ruch, w którym zakreślona droga kątowa jest wprost
proporcjonalna do czasu, czyli prędkość kątowa ma stałą wartość.
–
ruch obrotowy zmienny- proporcjonalność ta nie jest zachowana, prędkość kątowa się
zmienia.
Tabela 2 zawiera wielkości i wzory występujące w ruchu obrotowym i porównuje je z ruchem
postępowym punktu materialnego.
Tabela. 2
Porównanie wielkości i wzorów ruchu postępowego i obrotowego
Wielkość
Ruch postępowy
Ruch obrotowy
Zależność
Ruch jednostajny
Droga
Prędkość
t
v
s
*
=
t
*
ω
α
=
r
s
*
α
=
t
s
v
=
t
α
ω
=
r
v
*
ω
=

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
37
Ruch jednostajnie zmienny
Droga
2
2
0
at
t
v
s
±
=
2
2
0
t
t
ε
ω
α
+
=
)
2
(
2
t
ε
−
r
s
*
α
=
Prędkość
at
v
v
+
=
0
)
( at
−
t
ε
ω
ω
+
=
0
)
(
t
ε
−
r
v
*
ω
=
Przyspieszenie
t
v
v
a
0
−
=
t
0
ω
ω
ε
−
−
r
a
*
ε
=
gdzie:
s – droga liniowa,
v – prędkość liniowa,
t – czas ruchu,
a – przyspieszenie,
v
0
– prędkość początkowa,
α
– droga kątowa,
ω
– prędkość kątowa (omega),
ε
– przyspieszenie kątowe (epsilon)
0
ω
– prędkość początkowa,
r – promień wodzący.
4.5.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz czy jesteś przygotowany do wykonania ćwiczeń.
1.
Co to jest bryła sztywna?
2.
Jakie ruchy może wykonywać bryła sztywna?
3.
Jak określisz ruch postępowy bryły?
4.
Jak określisz ruch obrotowy bryły?
5.
Jakie znasz rodzaje ruchu obrotowego?
6.
Jak określisz drogę kątową?
7.
Jak określisz prędkość kątową?
8.
Co to jest przyspieszenie kątowe?
9.
Jaka jest zależność pomiędzy drogą liniową a kątową?
10.
Jaka jest zależność pomiędzy prędkością liniową a kątową?
11.
Jaka jest zależność pomiędzy przyspieszeniem kątowym i liniowym?
4.5.3. Ćwiczenia
Ćwiczenie 1
Prędkość kątowa kół samochodu w ciągu 12 s wzrosła z 1200 obrotów/min do 3000
obrotów/min.
Oblicz:
a)
Przyspieszenie kątowe kół przyjmując, że jest ono stałe,
b)
Ile obrotów wykonały koła w ciągu tego czasu.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
38
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać wielkości dane,
3)
zapisać wielkości szukane,
4)
odszukać i zapisać potrzebne zależności,
5)
podstawić dane liczbowe,
6)
dokonać obliczeń.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2.
Samochód jedzie z prędkością v = 60 km/h. Zewnętrzna średnica opon r = 60 cm.
Oblicz:
a)
ile obrotów na sekundę robią koła samochodu, jeżeli toczą się po szosie bez poślizgu,
b)
wielkość przyspieszenia dośrodkowego zewnętrznej warstwy gumowej na oponach jego kół.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać wielkości dane,
3)
dokonać ujednolicenia jednostek,
4)
zapisać wielkości szukane,
5)
określić zależność prędkości liniowej punktów zewnętrznych opony i prędkości
postępowej ruchu samochodu,
6)
zapisać potrzebne wzory, zależności,
7)
postawić wartości dane,
8)
dokonać obliczenia.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis,
–
poradnik ucznia,
–
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
39
4.5.4. Sprawdzian osiągnięć
Czy potrafisz:
Tak
Nie
1)
określić bryłę sztywną?
2)
określić ruch postępowy bryły?
3)
określić ruch obrotowy bryły?
4)
określić drogę kątową?
5)
określić prędkość kątową?
6)
określić przyspieszenie kątowe?
7)
wyznaczyć drogę, prędkość, przyspieszenie kątowe?
8)
określić zależność pomiędzy drogą liniową a drogą kątową?
9)
określić zależność pomiędzy prędkością liniową a prędkością
kątową?
10)
określić
zależność
pomiędzy
przyspieszeniem
liniowym
a przyspieszeniem kątowym?
11)
wyznaczyć częstotliwość obrotów?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
40
4.6.
Zasady dynamiki Newtona. Dynamika punktu i bryły. Ruch
środka masy. Dynamika ruchu obrotowego bryły sztywnej
4.6.1. Materiał nauczania
Pierwsza zasada dynamiki.
Istnieje taki układ odniesienia, w którym jeżeli na ciało nie działają żadne siły lub działające
siły się równoważą, to ciało to jest w spoczynku lub porusza się ruchem jednostajnym po linii
prostej.
Taki układ nazywamy układem inercjalnym.
Druga zasada dynamiki.
Jeżeli na ciało o masie m działa wypadkowa siła ( F
), to ciało porusza się z przyspieszeniem
)
(a
proporcjonalnym do działającej siły i odwrotnie proporcjonalnym do masy ciała (
m).
Co możemy zapisać:
m
F
a
=
lub
a
m
F
*
=
gdzie:
F
- siła wypadkowa, czyli wektorowa suma wszystkich sił działających na ciało.
m- masa [kg]
a – przyspieszenie [m/s
2
]
Siła wypadkowa i przyspieszenie ciała mają zgodne zwroty.
Jeżeli na ciało działa stała siła wypadkowa, to jego ruch jest jednostajnie przyspieszony lub
opóźniony po linii prostej.
Trzecia zasada dynamiki.
Jeżeli ciało A działa na ciało B siłą
AB
F
, to ciało B działa na ciało A siłą
BA
F
o takiej samej
wartości i kierunku, lecz przeciwnym zwrocie.
AB
F
= -
BA
F
Jest to zasada „akcji i reakcji”, czyli siły zawsze występują parami.
Trzecia zasada dynamiki jest bardzo ważna. Jest pomocna, gdy określamy jakie siły działają
na ciało w danych warunkach.
Dynamika w ruchu po okręgu.
W ruchu po okręgu, przyspieszenie jest różne od zera, jest to przyspieszenie dośrodkowe.
r
v
a
d
2
=
gdzie:
a
d
– przyspieszenie dośrodkowe,
v – prędkość,
r – promień okręgu.
Z drugiej zasady dynamiki wynika, że
r
v
m
a
m
F
d
d
2
*
*
=
=
Siłę
F
d
nazywamy siłą dośrodkową.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
41
Pęd (p) - to iloczyn masy ciała i jego prędkości,
p= m*v Jednostka [kg*m/s].
Dynamika bryły sztywnej.
Druga zasada dynamiki dla bryły sztywnej przybiera postać.
I
M
I
M
*
lub
ε
ε
=
=
gdzie:
ε
– przyspieszenie kątowe,
M – moment siły lub moment obrotowy,
I – moment bezwładności.
Kręt (L)- to iloczyn momentu bezwładności (I) i prędkości kątowej (
ω
)
L= I *
ω
L- kręt lub moment pędu.
4.6.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jak określa się pierwszą zasadę dynamiki?
2.
Jak określa się drugą zasadę dynamiki dla ruchu postępowego?
3.
Jak określa się drugą zasadę dynamiki dla ruchu po okręgu?
4.
Jak określa się drugą zasadę dynamiki dla ruchu obrotowego?
5.
Co to jest pęd i kręt?
6.
Co to jest moment obrotowy?
4.6.3. Ćwiczenia
Ćwiczenie 1
Z równi pochyłej o kącie nachylenia
α
do poziomu zsuwa się ciało o masie
m. Zadanie
do wykonania:
1.
Wyznacz siłę tarcia T, jeśli współczynnik tarcia wynosi
f.
2.
Wyznacz przyspieszenie ciała.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
zastosować zasady dynamiki, funkcje trygonometryczne,
2)
znaleźć wszystkie siły działające na ciało,
3)
zaznaczyć te siły na rysunku,
4)
wybrać układ współrzędnych,
5)
rozłożyć na składowe te siły, które tego wymagają,
6)
zsumować składowe sił wzdłuż wszystkich osi układu współrzędnych,
7)
zapisać równanie wynikające z zasady dynamiki,
8)
wyznaczyć siłę tarcia,
9)
wyznaczyć przyspieszenie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
42
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
papier milimetrowy,
–
pisaki, długopis,
–
tabela wartości funkcji trygonometrycznych,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenia 2
Do koła o promieniu r = 0,5 m i momencie bezwładności I = 20 kg * m
2
, przyłożono stały
moment siły M = 50 N*m.
Wyznacz:
1.
Przyspieszenie kątowe
ε
,
2.
Prędkość liniową punktów na obwodzie koła w końcu dziesiątej sekundy (10 s), prędkość
początkową v
0
= 0.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać wielkości dane,
3)
zapisać wielkości szukane,
4)
odszukać i zapisać potrzebne wzory i zależności,
5)
dokonać odpowiednich przekształceń wzorów,
6)
podstawić wartości liczbowe,
7)
dokonać obliczeń,
8)
zapisać jednostki.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Wyznacz przyspieszenie.
Za pomocą toru powietrznego sprawdzono zależność przyspieszenia wózka od działającej
siły. Wyniki pomiaru zapisano w tabeli.
F[ ]
5
10
15
20
25
30
a[ ]
4,9
9,8
15,2
20,1
25
29,9
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
wstawić jednostki siły (F) i przyspieszenia (a),
2)
narysować wykres zależności przyspieszenia wózka od działającej siły,
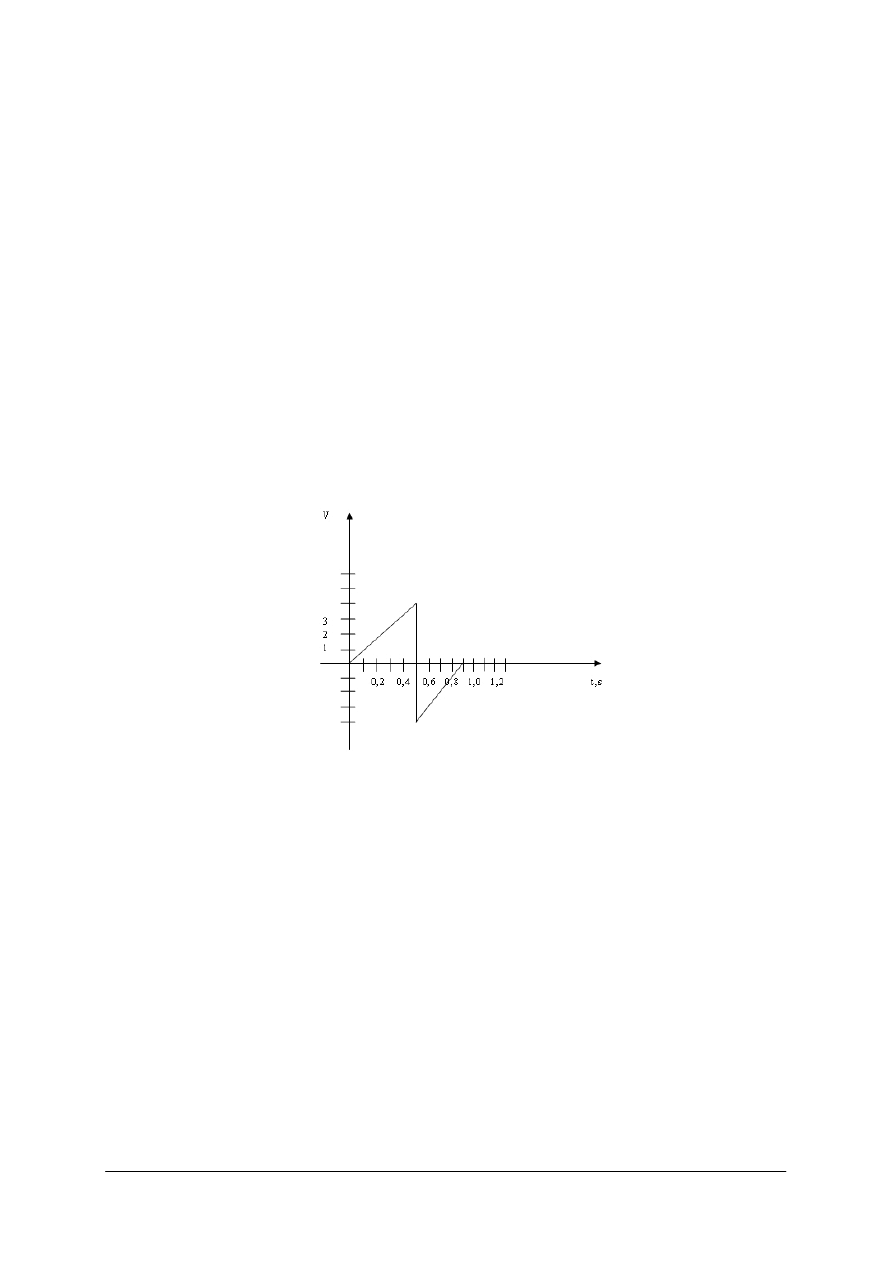
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
43
3)
zapisać wniosek wynikający z tego doświadczenia,
4)
na wykonanym wykresie, narysować przebieg zmian przyspieszenia od działającej siły dla
wózka o dwukrotnie większej masie.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
papier milimetrowy,
–
długopis, ołówek,
–
poradnik ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 4
Zbadaj ruch bryły sztywnej. Wyznacz przyspieszenie.
Za pomocą detektora prędkości sprzężonego z komputerem badano prędkość swobodnie
spadającej w powietrzu piłki o masie m = 0,2 kg. Na ekranie monitora pojawił się wykres
zależności prędkości piłki od czasu ruchu.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
określić, jakimi ruchami poruszała się piłka,
2)
obliczyć wysokość, z której spadła piłka,
3)
narysować wykres zależności przyspieszenia piłki od czasu jej ruchu,
4)
zderzenie piłki z podłożem trwało 60 ms. obliczyć siłę działającą na piłkę podczas
odbicia.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
papier milimetrowy,
–
długopis, ołówek,
–
poradnik ucznia,
–
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
44
4.6.4.
Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
określić pierwszą zasadę dynamiki?
2)
określić drugą zasadę dynamiki w ruchu postępowym?
3)
określić drugą zasadę dynamiki w ruchu obrotowym?
4)
określić pęd i kręt?
5)
wyznaczyć przyspieszenie liniowe?
6)
wyznaczyć przyspieszenie kątowe?
7)
wyznaczyć reakcję dynamiczną?
8)
dokonać analizy i porównania ruchu punktu materialnego i bryły
sztywnej?
9)
dokonać analizy i porównania ruchu postępowego i obrotowego?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
45
4.7.
Energia i praca mechaniczna
4.7.4.
Materiał nauczania
Praca
Praca jest iloczynem skalarnym wektora siły (F) i wektora przesunięcia (s).
α
cos
*
*
*
s
F
W
s
F
W
=
=
Kąt
α
jest kątem między wektorem siły działającej na ciało i wektora przesunięcia.
Praca (fizyczna) może być ujemna lub zerowa.
Jednostką pracy jest dżul:
J
m
N
W
=
=
*
]
[
Moc.
Moc (P) jest ilorazem wykonanej pracy (W) i czasu (t) jej wykonania.
t
W
P
=
Jednostką mocy jest wat. [P] = 1J/s= 1W
Energia kinetyczna.
Energia kinetyczna związana jest z ruchem ciała. Wyraża się następująco:
2
*
2
v
m
E
k
=
gdzie: m – masa ciała
v – prędkość
E
k
– energia kinetyczna
Jednostką energii kinetycznej jest dżul (I)
Energia potencjalna ciężkości.
Energię tą posiada ciało podniesione w polu siły ciężkości na pewną wysokość. Wyraża się
wzorem:
h
g
m
E
p
*
*
=
gdzie: m- masa ciała
g- przyspieszenie ziemski
h- wysokość, na jakiej ciało się znajduje
–
Energia potencjalna sprężystości.
Energia sprężystości sprężyny zależy od jej współczynnika sprężystości (k) i zmiany długości
sprężyny (x)
2
*
2
x
k
E
p
=
Jednostką energii potencjalnej jest dżul [J].
Zasada zachowania energii.
W izolowanym układzie ciał, w którym działają siły zachowawcze, energia mechaniczna
(tj. suma energii kinetycznych i potencjalnych) jest stała.
.
const
E
E
p
k
=
+
∑
∑

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
46
Tabela.3 Porównuje dynamikę, pracę , energię i moc w ruchu postępowym i obrotowym.
Tabela 3.
Wielkość
Ruch postępowy
Ruch obrotowy
Zależności
PRACA
s
F
W
*
=
α
*
M
W
=
r
F
M
*
=
MOC
v
F
P
*
=
ω
*
M
P
=
ENERGIA
KINETYCZNA
2
*
2
v
m
E
k
=
2
*
2
ω
J
E
k
=
2
*
n
n
r
m
J
∑
=
II ZASADA
NEWTONA
a
m
F
*
=
ε
*
J
M
=
PED, KRĘT
v
m
p
*
=
ω
*
J
L
=
gdzie:
W – praca,
F – siła,
s – droga liniowa,
P – moc,
E
k
– energia kinetyczna,
m – masa,
v – prędkość liniowa,
a – przyspieszenie liniowe,
p – pęd,
M – moment siły, moment obrotowy,
α
– droga kątowa,
I – moment bezwładności,
ε
– przyspieszenie kątowe,
L – kręt, moment pędu,
r – ramię siły.
4.7.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz czy jesteś przygotowany do wykonania ćwiczeń.
1.
Jak określa się pracę mechaniczną?
2.
Co jest jednostką pracy mechanicznej?
3.
Jak określa się moc?
4.
W jakich jednostkach jest wyrażana moc?
5.
Jak określa się energię kinetyczną?
6.
Jak określa się energię potencjalną?
7.
W jakich jednostkach wyraża się energię mechaniczną?
8.
Jak wyjaśnisz zasadę zachowania energii mechanicznej?
4.7.3. Ćwiczenia
Ćwiczenie 1
Samochód mający energię kinetyczną 400kJ zmniejsza swoją prędkość dwukrotnie.
Oblicz zmianę jego energii kinetycznej.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
47
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać potrzebne zależności,
3)
zapisać wielkości dane,
4)
zapisać wielkości szukane,
5)
podstawić wartości liczbowe do wzoru,
6)
dokonać obliczenia.
Wyposażenie stanowiska pracy:
–
poradnik dla ucznia,
–
zeszyt do ćwiczeń,
–
długopis,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Wisząca nad podłogą na wysokości 3 m lampa ma energię potencjalną 60 J. Oblicz masę
lampy.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać potrzebne zależności,
3)
zapisać wielkości dane,
4)
zapisać wielkości szukane,
5)
podstawić wartości liczbowe do wzoru,
6)
dokonać obliczenia.
Wyposażenie stanowiska pracy:
–
poradnik ucznia,
–
zeszyt do ćwiczeń,
–
długopis,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Na ciało o masie 8 kg działa siła nadająca mu przyspieszenia 4 m/s
2
. Oblicz jaką pracę
wykona to ciało na drodze 100 m.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać potrzebne zależności,
3)
zapisać wielkości dane,
4)
zapisać wielkości szukane,
5)
podstawić wartości liczbowe do wzoru,
6)
dokonać obliczenia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
48
Wyposażenie stanowiska pracy:
–
poradnik dla ucznia,
–
zeszyt do ćwiczeń,
–
długopis,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 4
Zbadaj ruch. Zbdaj zasady zachowania energii. Zbadaj reakcję dynamiczną.
Oblicz energię potencjalną, kinetyczną oraz całkowitą ciała o masie 300 g wzniesionego
na wysokość 10 m i puszczonego swobodnie. Obliczenie przeprowadź dla wysokości 10 m,
8 m, 5 m, 4 m i 0 m.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania, ruchu ciała,
2)
zapisać wielkości dane,
3)
zapisać wielkości szukane,
4)
odszukać w materiale nauczania potrzebne wzory i zależności,
5)
podstawić dane liczbowe,
6)
obliczyć energię kinetyczną, potencjalną i całkowitą na poszczególnych wysokościach.
7)
wyjaśnić zasadę zachowania energii, na podstawie dokonanych obliczeń.
Wyposażenie stanowiska pracy;
–
zeszyt do ćwiczeń,
–
długopis,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
4.7.4.
Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
określić pracę mechaniczną w ruchu postępowym i obrotowym?
2)
określić moc w ruchu postępowym i obrotowym?
3)
określić energię kinetyczną w ruchu postępowym i w ruchu
obrotowym?
4)
określić energię potencjalną?
5)
wyznaczyć: pracę mechaniczną?
6)
wyznaczyć moc
7)
wyznaczyć energię kinetyczną
8)
wyznaczyć energię potencjalną?
9)
wyjaśnić zasadę zachowania energii?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
49
4.8.
Podstawy wytrzymałości materiałów
4.8.1. Materiał nauczania
Strukturalne właściwości materii.
Elementy strukturalne materii to: atomy, jony, cząsteczki, które w odpowiednich
warunkach wiążą się w większe zespoły.
W zależności od tych warunków oraz od właściwości samych elementów, tworzą się struktury
nadające danej substancji określone właściwości fizyczne takie jak: elektryczne, magnetyczne,
cieplne, optyczne oraz mechaniczno- sprężyste.
Struktury te są zależne od stanu w jakim występuje dana substancja- stały, ciekły, gazowy.
W dalszym ciągu zajmiemy się ciałami stałymi i ich właściwościami mechaniczno-
sprężystymi.
Właściwości mechaniczno- sprężyste substancji opisane są za pomocą pewnych
współczynników wyrażających odporność lub podatność danej substancji na działanie sił
zewnętrznych wywołujących odkształcenie.
Odkształcenie.
Odkształcenie, to zmiana wymiarów i kształtu ciał stałych, zachodząca pod wpływem
działania sił zewnętrznych.
Ze względu na trwałość odkształceń wyróżniamy:
–
ciała sprężyste- po ustaniu działania sił zewnętrznych, powracają do stanu pierwotnego.
Tę własność ciał nazywa się sprężystością postaci:
–
ciała plastyczne- po ustaniu działania sił nie powracają do pierwotnej postaci.
–
ciała kruche- ulegają mechanicznemu uszkodzeniu.
Rodzaje odkształceń:
1.
Wydłużenie - pod wpływem rozciągania
2.
Skrócenie - pod wpływem ściskania.
3.
Wygięcie - pod wpływem zginania.
4.
Skręcenie
5.
Ś
cinanie.
6.
Proste odkształcenie postaci.
7.
Proste odkształcenie objętości.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
50
Tabela 4
Rodzaj odkształcenia
(działania)
Skutek
Wielkości,
Współczynniki,
zależności
Określenia,
jednostki
s
l
F
k
l
0
*
*
=
∆
PRAWO HOOKE’A
k
E
1
=
Moduł
YOUNGA
[N/m
2
]
(moduł
sprężystości
podłużnej)
s
F
=
σ
NAPRĘśENIE [N/m
2
]
E
l
l
0
*
σ
=
∆
PRAWO HOOKE’A
Po wprowadzeniu E
i
σ
0
l
l
∆
Wydłużenie względne
R
r
Wytrzymałość na
rozciąganie
Przyrost długości
0
l
l
l
l
−
=
∆
∆
n
R
r
k
=
σ
Naprężenie
dopuszczalne
n-wsp. bezpieczeństwa
0
_
d
d
∆
Przewężenie względne
1.
Rozciąganie
Przewężenie
-
0
d
d
d
−
=
∆
d-średnica
0
0
_
l
l
d
d
∆
=
∆
µ
Wzór Poissona
µ
-wsp. POISSONA
s
l
F
k
l
0
*
*
=
∆
−
PRAWO HOOKE’A
0
l
l
∆
−
Skrócenie względne
Skrócenie
0
l
l
l
−
=
∆
−
E
l
l
σ
=
∆
−
0
PRAWO HOOKE’A
k
E
s
F
1
;
=
=
σ
Rozszerzenie
0
d
d
∆
Rozszerzenie
względne
2.
Ś
ciskanie
0
0
l
l
d
d
∆
=
∆
µ
=
Wzór Poissona
3.
Zginanie
Odkształcenie (belki, pręta, płyty), podczas którego przekroje poprzeczne ulegają
sztywnemu przesunięciu względem siebie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
51
Skutkiem zginania jest wygięcie (y).
I
E
M
y
*
=
gdzie:
y – wygięcie (wychylenie od położenia pierwotnego prostopadłe do osi belki),
M – moment siły zginającej (M=F*r),
E – moduł Younga,
I – moment bezwładności przekroju poprzecznego względem osi belki.
Rodzaje zginania.
–
Zginanie czyste- gdy do końców belki przyłożone są dwa momenty sił skręcających,
działających w przeciwne strony.
–
Zginanie poprzeczne- powstaje podczas obciążenia belki podpartej na jednym lub dwu
końcach, siłą prostopadłą do osi belki w jej środku masy (ciężkości).
–
Zginanie skośne- siły zginające leżą w płaszczyźnie przechodzącej przez oś belki ale nie
będącej jej płaszczyzną symetrii.
–
Wyboczenie- występuje gdy działające siły są skierowane wzdłuż osi belki (ściskanie).
Pojawiają się skokowo po przekroczeniu pewnej granicznej wartości naprężeń.
4.
Skręcanie
Odkształcenie ciała stałego pod wpływem pary sił działających w płaszczyźnie
prostopadłej do osi pręta. Każdy przekrój poprzeczny pręta ulega obróceniu o pewien kąt
ϕ
.
Wielkość skręcenia zależy od momentu sił działających. Jeśli siły nie są zbyt duże, to obie
wielkości są do siebie proporcjonalne.
ϕ
*
D
M
=
;
D
M
=
ϕ
M – moment sił skręcających
D – współczynnik proporcjonalności- zwany momentem kierującym- zależy od własności
materiału
l
r
G
D
2
*
*
4
π
=
r – promień przekroju pręta
l – długość pręta
G – współczynnik stały dla danego materiału zwany:
- modułem sztywności na skręcanie lub – modułem torsyjnym.
Jednostka modułu [N/m
2
]
G
1
- nosi nazwę liczby poślizgowej materiału.
5.
Ś
cinanie.
Odkształcenie wywołane naprężeniami (siłami) stycznymi do powierzchni ciała.
Ciało można podzielić na małe równoległościany. Odkształcenie polega na zmianie
kątów w tych równoległościanach. Jest to odkształcenie postaci:
G
s
σ
ϕ
=
gdzie:
σ
-kąt skręcenia (efektem ścinania jest skręcenie proste),
G -współczynnik sprężystości postaci lub moduł sztywności,
s
σ
-naprężenie styczne.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
52
s
F
s
=
σ
; F- siła, s-pole powierzchni
6.
Proste odkształcenie postaci.
Odkształcenie postaci bez zmiany objętości. Powstaje podczas skręcania i ścinania.
Jego miarą jest kąt skręcania prostego.
G
σ
ϕ
=
gdzie:
σ
- naprężenie styczne,
G- moduł sztywności.
7.
Proste odkształcenie objętości.
Wywołane jest ciśnieniem działającym równomiernie na ciało ze wszystkich stron. Miarą
odkształcenia objętościowego jest względna zmiana objętości.
k
v
v
σ
=
∆
0
;
gdzie: v
∆
- zmiana objętości ( v
∆
=v-v
0
),
V
0
- objętość początkowa,
σ
- naprężenie normalne,
k- moduł sprężystości objętościowej
Zdolność ciała do zmiany objętości pod wpływem zmian ciśnienia zewnętrznego nazywamy
ś
ciśliwością.
Współczynnik ściśliwości
χ
.
p
V
V
∆
∆
−
=
*
1
χ
k
1
=
χ
gdzie: V
∆
- zmiana objętości,
p
∆
- zmiana ciśnienia.
Podsumowanie
Każde odkształcenie jest proporcjonalne do naprężenia i do odpowiedniego współczynnika.
Można więc zapisać ogólny wzór.
O=
σ
* W
gdzie:
O- odkształcenie,
σ
- naprężenie,
W – współczynnik.
Do zmiany długości i objętości ciała dochodzi również pod wpływem zmiany temperatury:
ogrzewania lub oziębiania.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
53
Przy ogrzewaniu dochodzi do:
1.
rozszerzalności liniowej.
2.
rozszerzalności objętościowej.
Przy oziębianiu dochodzi do:
1.
kurczliwości liniowej.
2.
kurczliwości objętościowej.
Tabela 5
OGRZEWANIE
OZIĘBIANIE
1.
Rozszerzalność liniowa-
przyrost długości
0
0
0
0
)
1
(
*
0
l
l
t
l
l
t
l
l
l
l
l
l
t
t
t
>
∆
+
=
∆
=
∆
>
∆
−
=
∆
α
α
α
-współczynnik rozszerzalności
liniowej [
]
1
lub
1
0
C
K
2.
Kurczliwość liniowa- przyrost
(zmiana) długości
0
0
0
0
0
)
(
)
1
(
0
0
l
l
t
t
t
l
l
t
l
l
l
l
l
l
t
t
t
<
<
∆
∆
−
∆
+
=
∆
=
∆
<
∆
<
−
=
∆
α
α
α
3.
Rozszerzalność objętościowa-
przyrost objętości
0
0
0
0
0
)
1
(
*
0
V
V
t
t
V
V
t
V
V
V
V
V
V
t
t
t
>
>
∆
∆
+
=
∆
=
∆
>
∆
−
=
∆
β
β
β
-współczynnik rozszerzalności
objętościowej
α
β
3
=
3.
Kurczliwość objętościowa
0
0
0
0
0
)
(
)
1
(
0
V
V
t
V
t
t
V
V
t
V
V
V
t
t
<
<
∆
<
∆
∆
−
∆
+
=
∆
=
∆
<
∆
β
β
β
gdzie:
l
o
- długość początkowa,
l
t
- długość w temperaturze T (końcowej),
t- temperatura końcowa,
t
o
- temperatura początkowa,
t
∆
-zmiana temp,
V
o
- objętość początkowa,
V
t
- objętość końcowa (w temp. T końcowej).
4.8.2. Pytania sprawdzające
Odpowiadając na pytania sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1.
Co to jest odkształcenie?
2.
Jakie znasz rodzaje odkształceń?
3.
Co jest miarą poszczególnych odkształceń?
4.
Od czego zależy zmiana długości przy rozciąganiu?
5.
Jak objaśnisz prawo Hooke’a?
6.
Co to jest naprężenie?
7.
Co to jest wydłużenie względne?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
54
8.
O czym informuje wzór Poissona?
9.
Co to jest naprężenie dopuszczalne?
10.
Jakie prawa stosuje się do ściskania?
11.
Co jest skutkiem zginania?
12.
Jakie znasz rodzaje zgnania?
13.
Na czym polega skręcanie?
14.
Co to jest ścinanie?
15.
Na czym polega proste odkształcenie postaci?
16.
Na czym polega proste odkształcenie objętości?
17.
Do czego dochodzi podczas ogrzewania ciał?
18.
Do czego dochodzi podczas oziębiania ciał?
4.8.3. Ćwiczenia
Ćwiczenie 1
ś
elazny pręt o długości l = 1,5 m przy obciążeniu P = 5000 N nie powinien wydłużyć się
więcej niż o 0,3 mm. Oblicz jaki ma być przekrój pręta.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
odszukać w materiale nauczania informacji dotyczących rozciągania,
2)
oszukać i zapisać zależności, wzory,
3)
zapisać wielkości dane,
4)
zapisać wielkości szukane,
5)
przeliczyć jednostki,
6)
odszukać w tabeli moduł Younga dla żelaza,
7)
przekształcić odpowiednie zależności,
8)
podstawić znane wartości,
9)
obliczyć i sprawdzić wynik.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń, kartka papieru,
–
długopis,
–
tabela modułów Younga,
–
kalkulator,
–
poradnik dla ucznia,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Oblicz minimalną długość l. przy której zostanie rozerwany pod wpływem własnego
ciężaru zawieszony pręt metalowy:
a)
ze stali,
b)
z ołowiu.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
55
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać wzory i zależności związane z tematem zadania,
3)
zapisać wielkości dane,
4)
odszukać w odpowiednich tabelach potrzebne wartości,
5)
zapisać wielkości szukane,
6)
podstawić wartości liczbowe,
7)
dokonać obliczenia, sprawdzić.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis,
–
tabela ciężarów właściwych ciał,
–
kalkulator,
–
poradnik dla ucznia,
–
tabele: własności ciał sprężystych, właściwości sprężyste i wytrzymałościowe ciał
stałych,
–
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Oblicz rozszerzalność i kurczliwość objętościową pod wpływem zmian temperatury.
Oblicz wytrzymałość materiałową.
Lina stalowa o przekroju 3 cm² jest zamocowana w swym górnym końcu i zwisa pionowo
w dół. Oblicz ciężar, który należy zawiesić na dalszym końcu liny, aby nie dopuścić do
zmniejszenia jej długości mimo, że temperatura otoczenia spadła o 20°C.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1)
dokonać analizy zadania,
2)
zapisać wzory i zależności związane z tematem zadania,
3)
zapisać wielkości dane,
4)
odszukać w odpowiednich tabelach potrzebne wartości,
5)
zapisać wielkości szukane,
6)
podstawić wartości liczbowe,
7)
dokonać obliczenia, sprawdzić.
Wyposażenie stanowiska pracy:
–
zeszyt do ćwiczeń,
–
długopis,
–
kalkulator,
–
tabele: własności ciał sprężystych, właściwości sprężyste i wytrzymałościowe ciał
stałych,
–
poradnik dla ucznia
–
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
56
4.8.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1)
zdefinjować odkształcenie?
2)
określić rodzaje odkształceń?
3)
określić od czego i jak zależy zmiana długości przy rozciąganiu
i ściskaniu?
4)
wyjaśnić prawo Hooke’a?
5)
wyjaśnić prawo Poissona?
6)
wyznaczyć wydłużenie przy rozciąganiu?
7)
wyznaczyć przewężenie przy rozciąganiu?
8)
wyznaczyć zmianę długości i średnicy pręta przy ściskaniu?
9)
określić naprężenie dopuszczalne?
10)
określić skutki zginania?
11)
kreślić skutki skręcania?
12)
określić skutki ścinania?
13)
określić od czego i jak zależą skutki zginania, skręcania i ścinania?
14)
bliczyć wytrzymałość materiałów na ściskanie, rozciąganie, zginanie,
skręcanie i ścinanie?
15)
określić wpływ zmiany temperatury na wymiary ciała?
16)
obliczyć zmianę długości i objętości pod wpływem zmiany
temperatury?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
57
5. SPRAWDZIAN OSIĄGNIĘĆ
INSTRUKCJA DLA UCZNIA
1.
Przeczytaj uważnie instrukcję.
2.
Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3.
Zapoznaj się z zestawem zadań testowych.
4.
Test zawiera 30 zadań.
5.
Do każdego zadania dołączone są 4 możliwości odpowiedzi. Tylko jedna jest prawidłowa.
6.
Udzielaj odpowiedzi na załączonej karcie odpowiedzi, stawiając w odpowiedniej rubryce
znak X.
7.
W przypadku pomyłki należy błędną odpowiedź zaznaczyć kółkiem, a następnie
ponownie zakreślić odpowiedź prawidłową.
8.
Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.
9.
Jeśli udzielenie odpowiedzi na któreś zadanie będzie Ci sprawiało trudność, wtedy odłóż
jego rozwiązanie na później i wróć do niego, gdy zostanie Ci wolny czas.
10.
Obliczeń dokonaj na osobnym arkuszu papieru.
Powodzenia!
ZESTAW ZADAŃ TESTOWYCH
1.
Która z podanych jednostek nie jest jednostką podstawową układu SI?
a)
Amper.
b)
Niuton.
c)
Kelwin.
d)
Kandela.
2.
Po dwóch równoległych torach kolejowych jadą w przeciwne strony dwa pociągi: jeden
z prędkością 60 km/h, a drugi z prędkością 40 km/h. Prędkość pociągów względem siebie
ma wartość
a)
100 km/h przy zbliżaniu się, a 20 km/h przy oddalaniu.
b)
20 km/h przy zbliżaniu się, a 100 km/h przy oddalaniu.
c)
50 km/h zarówno przy zbliżaniu się, jak i przy oddalaniu.
d)
100 km/h zarówno przy zbliżaniu się, jak i przy oddalaniu.
3.
Na samochód poruszający się poziomo ruchem przyspieszonym działają cztery siły: siła
ciężaru
G
, siła sprężystości podłoża
R
, siła napędu
P
, siła oporów
T
. Przyspieszenie,
z którym porusza się samochód nadaje
a)
Siła
P
.
b)
Wypadkowa wszystkich sił.
c)
Siła
P
-
T
.
d)
Siła
G
-
R
+
P
-
T
.
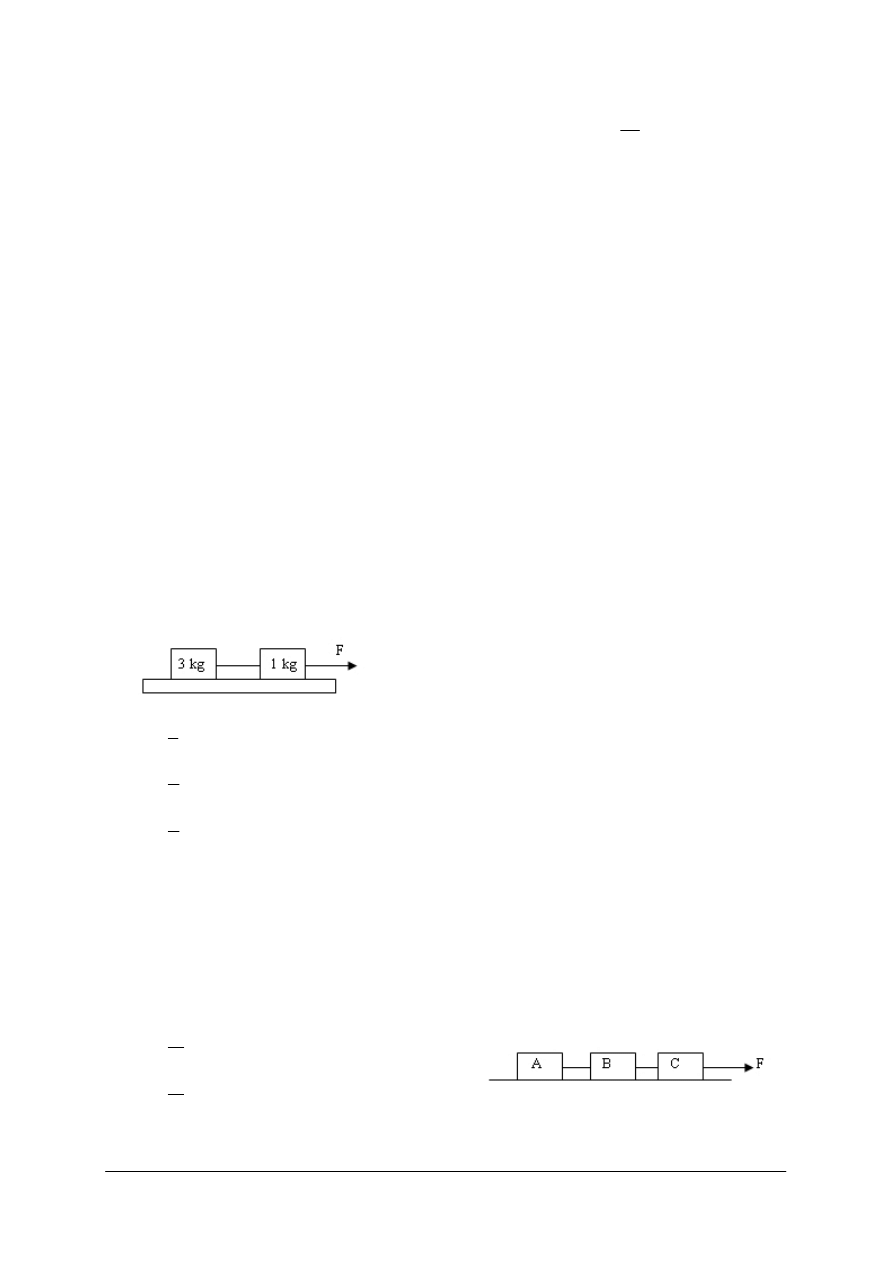
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
58
4.
Na ciało o masie 8 kg działa siła nadająca mu przyspieszenie 4
2
s
m
. Na drodze 100 m
wykona ono pracę
a)
200 J.
b)
400 J.
c)
800 J.
d)
3200 J.
5.
Silnik samochodu poruszający się ze stałą prędkością 72 km/h wytwarza siłę napędową
o wartości 1000N. Silnik ten ma moc
a)
2 kW.
b)
20 kW.
c)
50 kW.
d)
72 kW.
6.
Na ciało poruszające się po okręgu o promieniu 1 m działa siła dośrodkowa o wartości
10 N. Energia kinetyczna tego ciała ma wartość
a)
5 J.
b)
10 J.
c)
20 J.
d)
100 J.
7.
W sytuacji przedstawionej na rysunku (tarcie zaniedbujemy) siła napinająca nitkę
ma wartość
a)
F
3
1
.
b)
F
2
1
.
c)
F
4
3
.
d)
F
1 .
8.
Trzy klocki o jednakowych masach
m są połączone nieważkimi nitkami. Klocek C jest
ciągnięty w prawo siłą
F nadającą całemu układowi przyspieszenie. Jeżeli założymy,
ż
e nie ma tarcia między klockami i podłożem, to wypadkowa siła działająca na klocek
B wynosi
a)
zero.
b)
.
3
F
c)
.
2
F
d)
F.
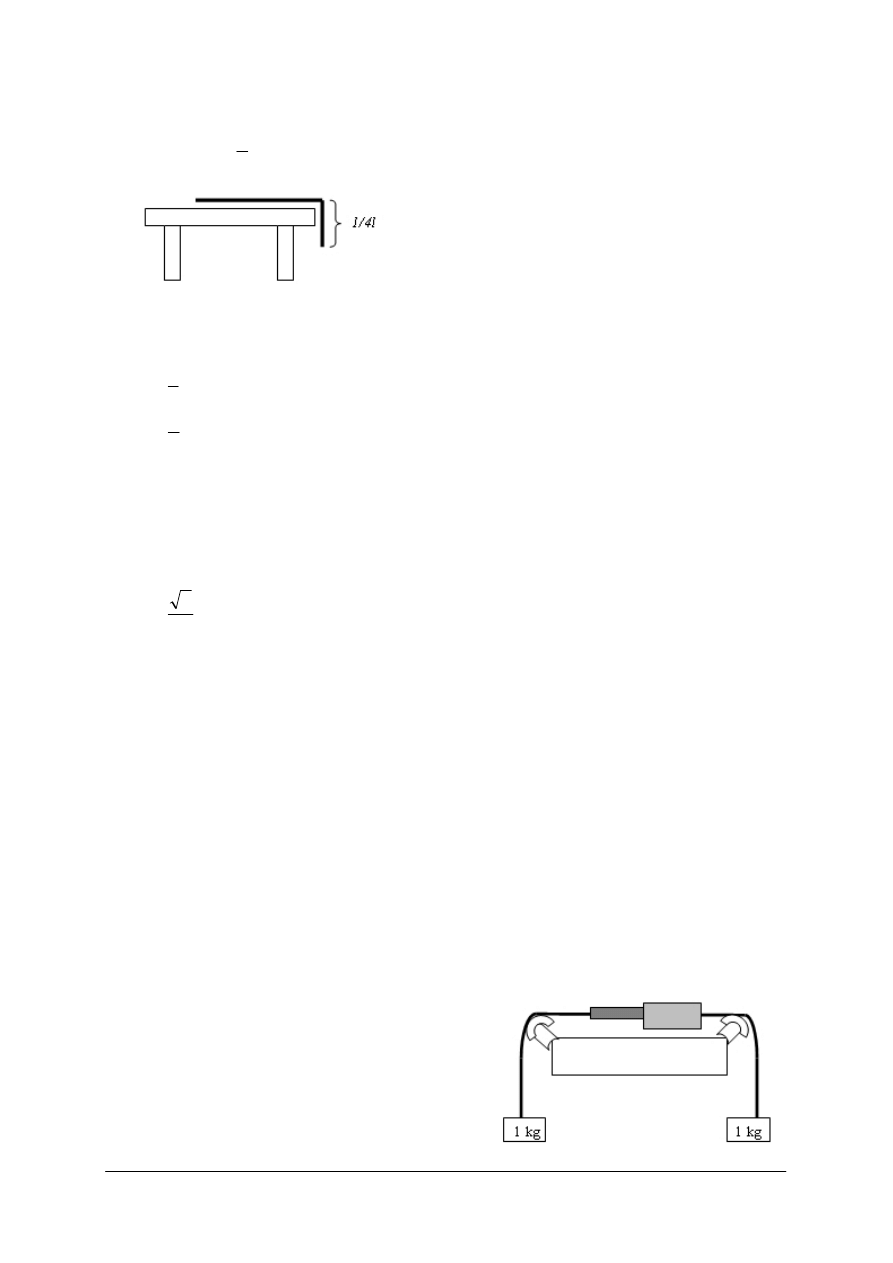
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
59
9.
Jednorodna linka o długości l w sytuacji przedstawionej na rysunku zaczyna się zsuwać
ze stołu, gdy
4
1
jej długości zwisa.
Możemy wywnioskować , że współczynnik tarcia statycznego linki o stół wynosi
a)
4.
b)
3.
c)
3
1
.
d)
4
1
.
10.
Na równi pochyłej leży klocek. Klocek zaczyna się zsuwać z równi przy kącie nachylenia
równym 45
º
. Współczynnik tarcia statycznego w tym przypadku wynosi
a)
zero.
b)
0,5.
c)
1.
d)
2
2
.
11.
Na równi znajduje się ciało o masie
m pozostające w spoczynku. Jeżeli zwiększymy
nachylenie równi w zakresie od zera do kąta, przy którym ciało zaczyna się zsuwać,
to siła tarcia ma wartość: (
α
-kąt nachylenia równi,
f- współczynnik tarcia statycznego)
1.
fmgcos
α
.
2.
mgcos
α
.
3.
fmgsin
α
.
4.
mgsin
α
Poprawne są:
a)
tylko 1.
b)
tylko 1 i 4.
c)
tylko 2 i 3.
d)
tylko 4.
12.
Na obu końcach wagi sprężynowej, pokazanej na rysunku zawieszono dwa ciężarki
o masie 1 kg. Na podziałce wagi odczytamy
a)
około 0 N.
b)
około 9,8 N.
c)
około 19,6 N.
d)
około 4,9 N.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
60
13.
Masa ciała o ciężarze 19,6 N wynosi
a)
około 19,6 kg.
b)
około 19,6 kg.
c)
około 2 kg.
d)
około 2 kg.
14.
Z wysokości 5 m swobodnie spada piłka kauczukowa. Podczas ruchu piłki pomijamy siły
oporu powietrza. Wybierz z poniżej zamieszczonych stwierdzeń zdanie nieprawdziwe.
a)
Podczas spadania piłki nie jest wykonywana praca.
b)
Prędkość piłki wzrasta bo maleje energia potencjalna piłki.
c)
Energia mechaniczna spadającej piłki ma stałą wartość.
d)
Prędkość spadającej piłki nie zależy od jej masy.
15.
Na poruszające się po linii prostej ciało o masie m działa siła F, której zależność od czasu
przedstawiono na rysunku. Możemy wnioskować, że w przedstawionej sytuacji ciało
będzie się poruszało
a)
ruchem jednostajnie przyspieszonym.
b)
ruchem niejednostajnie przyspieszonym.
c)
ruchem jednostajnie opóźnionym.
d)
ruchem jednostajnym.
16.
Jeżeli na ciało działa kilka sił w tym tylko jedna z nich np.
F
1
ma zwrot zgodny
ze zwrotem przyspieszenia tego ciała, to siłą nadającą temu ciału przyspieszenie jest
a)
właśnie siła
F
1
b)
różnica
F
1
-
F
2,
gdzie
F
2
jest wypadkową wszystkich sił zwróconych przeciwnie
do przyspieszenia.
c)
wypadkowa, będąca sumą geometryczną wszystkich działających na to ciało sił.
d)
wypadkowa wszystkich sił o kierunkach zgodnych z kierunkiem przyspieszenia tego
ciała.
17.
Jeżeli na poruszające się ciało działa siła wypadkowa o kierunku równoległym do jego
prędkości o wartości stałej w czasie ruchu, to ciało będzie się poruszało ruchem
a)
jednostajnym prostoliniowym.
b)
jednostajnie przyspieszonym.
c)
jednostajnie opóźnionym.
d)
jednostajnie zmiennym (opóźnionym lub przyspieszonym).
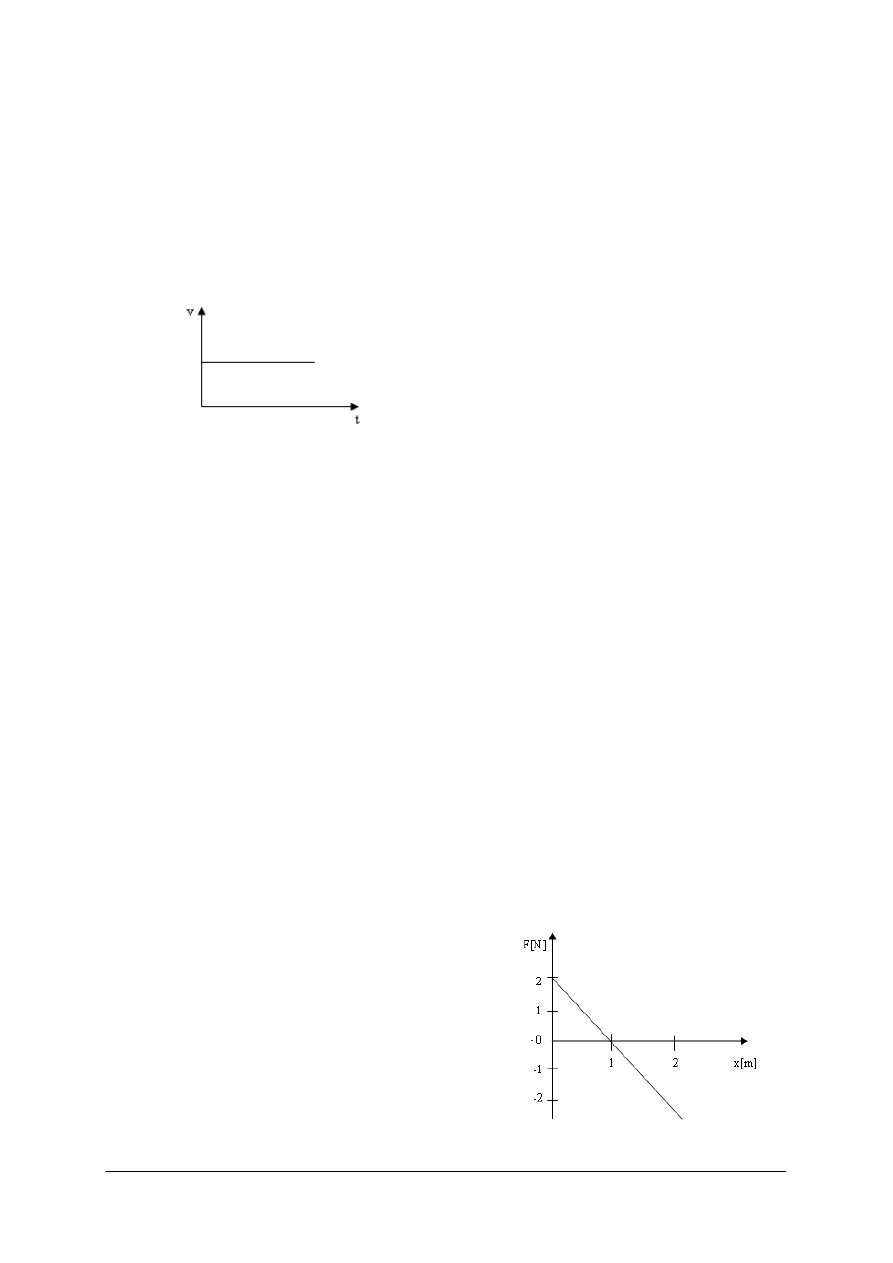
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
61
18.
Na nici w polu sił ciężkości waha się kulka. W chwili przechodzenia przez położenie
równowagi o siłach działających na kulkę powiedzieć można, że
a)
wypadkowa siła jest styczna do toru i nadaje ruch kulce.
b)
siła ciężkości jest zrównoważona przez siłę dośrodkową.
c)
na kulkę działa niezrównoważona siła dośrodkowa.
d)
siła ciężkości jest zrównoważona przez siłę reakcji nitki.
19.
Na wykresie przedstawiono zależność prędkości od czasu w pewnym ruchu
prostoliniowym. Wypadkowa siła działająca na ciało w tym przypadku
a)
jest stała i zwrócona w kierunku ruchu.
b)
jest stała i zwrócona przeciwnie do kierunku ruchu.
c)
jest równa zeru.
d)
jednostajnie maleje z czasem.
20.
Na ciało o masie 1 kg pozostające w chwili początkowej w spoczynku na poziomej
płaszczyźnie działa równolegle do płaszczyzny siła 2 N. Współczynnik tarcia wynosi 0,1.
Praca wykonana przez siłę wypadkową na drodze 1 m wynosi
a)
0,2 J.
b)
2 J.
c)
1,02 J.
d)
2,98 J.
21.
Siła wypadkowa działająca na punkt materialny poruszający się ruchem jednostajnym po
okręgu jest
a)
różna od zera i styczna do okręgu.
b)
różna od zera i skierowana do środka okręgu na zewnątrz.
c)
różna od zera i skierowana do środka okręgu.
d)
równa zeru.
22.
Pod działaniem siły F ciało porusza się po osi x. Na rysunku przedstawiono wykres
zależności wartości siły F od położenia ciała. Nap odstawie wykresu możemy
wnioskować, że praca wykonana przez tą siłę o drodze 2 m wynosi
a)
0 J.
b)
2 J.
c)
4 J.
d)
-2 J.
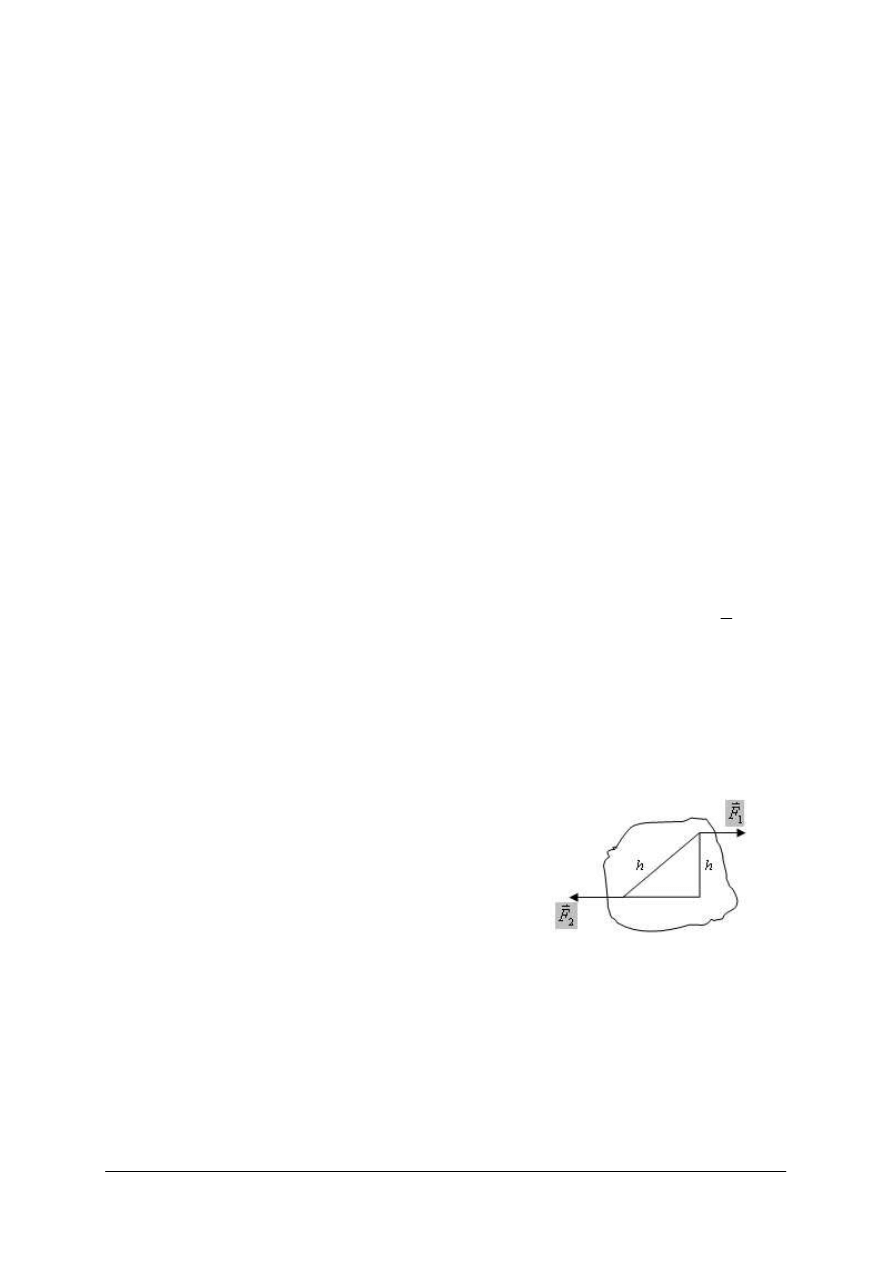
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
62
23.
W pierwszej sekundzie ruchu ciało przebyło drogę 1 m. W drugiej sekundzie 2 m,
a w trzeciej 3m. Jakim ruchem poruszało się ciało w czasie tych trzech sekund?
a)
jednostajnym.
b)
jednostajnym zmiennym.
c)
jednostajnym przyspieszonym.
d)
zmiennym.
24.
Ciało poruszające się po linii prostej ruchem jednostajnie przyspieszonym (v
0
= 0)
przebywa w pierwszej sekundzie ruchu drogę 1 m. Droga przebyta w drugiej sekundzie
ruchu wynosi
a)
1 m.
b)
2 m.
c)
3 m.
d)
4 m.
25.
Z zasady zachowania energii mechanicznej wynika, że
a)
w układzie zamkniętym energia kinetyczna jest równa energii potencjalnej.
b)
suma energii kinetycznej i potencjalnej układu jest stała, gdy w układzie działają
tylko siły zachowawcze i siły zewnętrzne nie wykonują pracy nad układem.
c)
suma energii kinetycznej i potencjalnej jest równa zeru.
d)
energia mechaniczna jest równa sumie energii kinetycznej i potencjalnej.
26.
Co można powiedzieć o energiach kinetycznych ruchu postępowego E
kp
i obrotowego E
ko
pełnego walca toczącego się po poziomej równi (moment bezwładności walca wynosi
2
1
mr
2
).
a)
E
kp
=
E
ko
.
b)
E
kp
>
E
ko.
c)
E
kp
<
E
ko.
d)
E
kp
>
E
ko
, lub
E
kp
<
E
ko
, w zależności od masy walca.
27.
Na ciało działa para sił (
F
1
=
F
2
=
F). Moment obrotowy tej pary sił ma wartość
(
l
1
– odległość pomiędzy liniami sił), (
l
2
– odległość między punktami przyłożenia sił)
a)
F*l
1
.
b)
2F*l
1
.
c)
F*l
2
.
d)
2F*l
2.
28.
Rozciągnięcie nieodkształconej początkowo sprężyny o pewną długość wymaga
wykonania określonej pracy. Dodatkowe wydłużenie tej sprężyny (przy założeniu idealnej
sprężystości) o tę samą długość wymaga wykonania:
a)
takiej samej pracy.
b)
dwa razy większej pracy.
c)
trzy razy większej pracy.
d)
dwa razy mniejszej pracy.
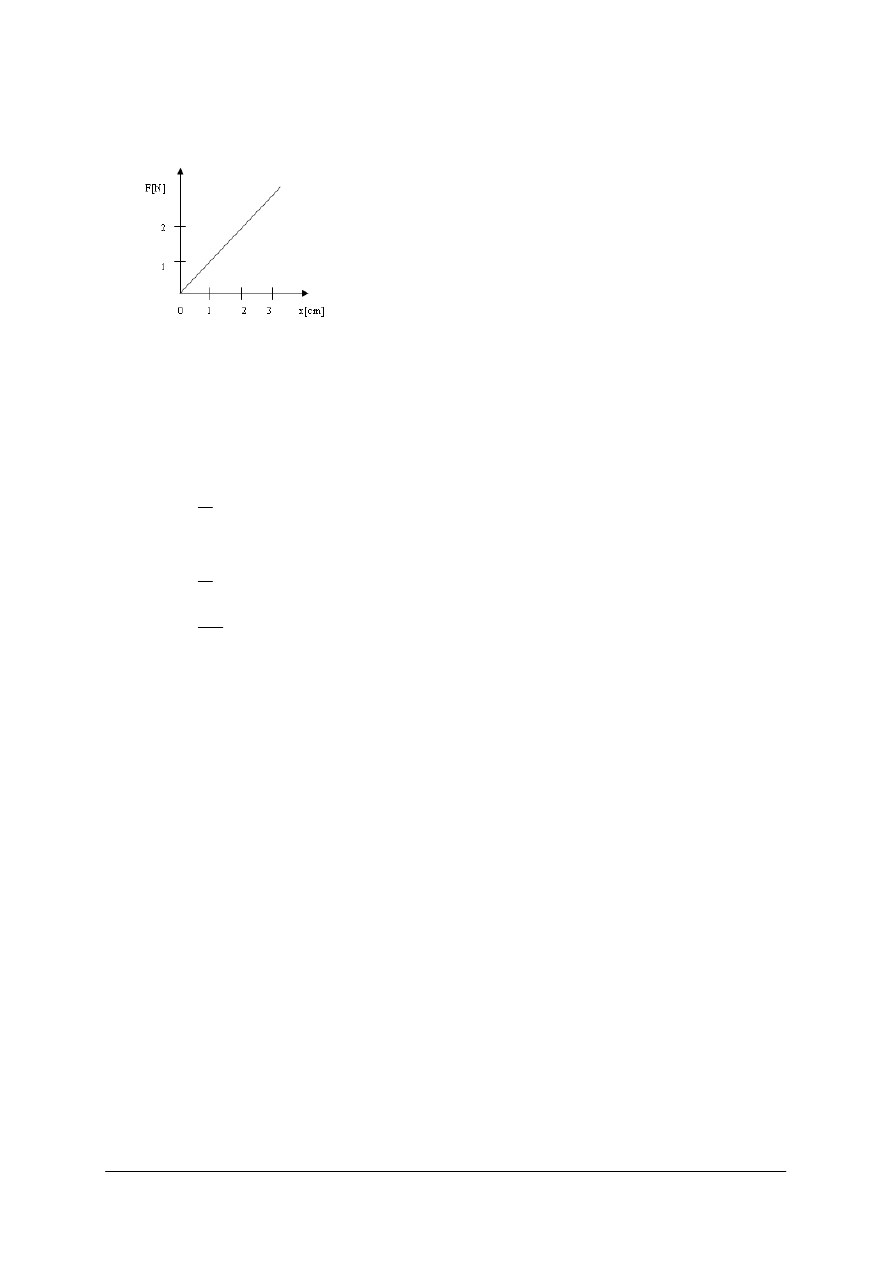
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
63
29.
Na rysunku przedstawiono zależność siły F potrzebnej do ściśnięcia sprężyny,
od odkształcenia sprężyny x. Praca wykonana przy ściśnięciu sprężyny o 3 cm wynosi
a)
0,09 J.
b)
0,045 J.
c)
4,5 J.
d)
0,9 J.
30.
Jaką siłą F należy rozciągać drut o przekroju S, aby jego długość nie uległa zmianie przy
oziębieniu go o
∆
T (
η
- moduł Younga,
α
- liniowy współczynnik rozszerzalności)?
a)
F =
T
S
∆
η
α
.
b)
F =
α η
T
S
∆
.
c)
F
=
T
S
∆
α
η
.
d)
F
=
T
S
∆
αη
.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
64
KARTA ODPOWIEDZI
Imię i nazwisko..........................................................................................
Stosowanie podstawowych pojęć z zakresu mechaniki technicznej
Zakreśl poprawną odpowiedź
.
Nr
zadania
Odpowiedź
Punkty
1
a
b
c
d
2
a
b
c
d
3
a
b
c
d
4
a
b
c
d
5
a
b
c
d
6
a
b
c
d
7
a
b
c
d
8
a
b
c
d
9
a
b
c
d
10
a
b
c
d
11
a
b
c
d
12
a
b
c
d
13
a
b
c
d
14
a
b
c
d
15
a
b
c
d
16
a
b
c
d
17
a
b
c
d
18
a
b
c
d
19
a
b
c
d
20
a
b
c
d
21
a
b
c
d
22
a
b
c
d
23
a
b
c
d
24
a
b
c
d
25
a
b
c
d
26
a
b
c
d
27
a
b
c
d
28
a
b
c
d
29
a
b
c
d
30
a
b
c
d
Razem:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
65
6. LITERATURA
1.
Błaszczyk J.W.: Biomechanika kliniczna, PWZL, Warszawa 2004
2.
Bober T., Zawadzki J.: Biomechanika układu ruchu człowieka. Wydawnictwo BK,
Wrocław 2001.
3.
Cach R., Ciszewska A., Kołaczkiewicz J., Styrkowiec R.: Słownik fizyczny.
Wydawnictwo Europa. Wrocław 2003.
4.
Dega W., Senger A.: Ortopedia i rehabilitacja, PWZL, Warszawa 1996.
5.
Gaździk T.: Ortopedia i traumatologia. PWZL, Warszawa 2005.
6.
Górecki A.: Technologia ogólna. WSiP. Warszawa 2004.
7.
Holiday D, Resnick R, Walker I.: Podstawy fizyki. PWN Warszawa 2003.
8.
Jemielity S.: Fizyka. Vademecum maturzysty. Wydawnictwo Oświata, Warszawa 2004.
9.
Kamiński Z.: Fizyka dla kandydatów na wyższe uczelnie techniczne. WNT. Warszawa.
10.
Kiwerski J.: Rehabilitacja medyczna. PWZL, Warszawa 2003.
11.
Marciniak W., Szulc A. (red): Wiktora Degi,: Ortopedia i rehabilitacja. PWZL, Warszawa
2005.
12.
Myśliborski T.: Zaopatrzenie ortopedyczne. PWZL, Warszawa 1985.
13.
Potyński A.: Podstawy technologii i konstrukcji mechanicznych. WSiP, Warszawa 2004
14.
Prosnak M, Łuczak E.: Podstawy biomechaniki ortopedycznej. Materiały pomocnicze.
CMDNŚSM, Warszawa 1988.
15.
Prosnak M.: Podstawy protetyki ortopedycznej. Materiały pomocnicze. CMDNŚSM,
Warszawa 1988.
16.
Prosnak M.: Podstawy technologii ortopedycznej. Materiały pomocnicze. CMDNŚSM,
Warszawa 1987.
17.
Przeździak B.: Zaopatrzenie rehabilitacyjne. Via Media, Gdańsk 2003.
18.
Rutkowski A.: Części maszyn. WSiP, Warszawa 2004
19.
Sagnowska B. red.: Fizyka i astronomia dla każdego. Zam Kor, Kraków 2007.
20.
Siuta W.: Mechanika techniczna. WSiP, Warszawa 1995.
Wyszukiwarka
Podobne podstrony:
15 Stosowanie podstawowych pojęć z zakresu mechaniki
Stosowanie praw i pojęć z zakresu mechaniki,mechatroniki oraz technologii dróg i mostów
słownik podstawowych pojęć z zakresu ochrony osób i mienia
Definicje podstawowych pojęć stosowanych w?daniach statystycznych wypadków przy pracy
15 Stosowanie typowych powiązań podstawowych
Wykład II Analiza podstawowych pojęć eksploatacyjnych i użytkowanie obiektów ED
Zmiany w podstawie programowej w zakresie edukcji matematycznej, Wczesna edukacja, Materiały do prac
Podstawowe wielkosci elektromagnetyczne i mechaniczne
Podstawowe pojęcia w zakresie motywacji i motywowania
dydaktyka zarys podstawowych pojec modele ogniwa i metody ksztalcenia, Pedagogika op-wych, Dydaktyka
Podstawowe pojęcia z zakresu położnictwa, Zdrowie, medycyna itp, Położnictwo, Różne
podstawowe wiadomosci z zakresu profilaktyki przeciwpo¬arowej
ĆWICZENIA Z PODSTAWOWYCH POJĘĆ ZWIĄZANYCH Z KULTURĄ JĘZYKA
socjologia kilka podstawowych pojęć
slowniczek podstawowych pojęć (5 str), S?OWNICZEK PODSTAWOWYCH POJ??
więcej podobnych podstron