1

Dynamika punktu materialnego w mechanice klasycznej

##########################################################################################
Autor : R. Waligóra ; data powstania dokumentu : 2008-11-05 ; ostatnie poprawki z dnia: 2008-11-05
##########################################################################################

1. Siła (oddziaływanie)

Podstawowym pojęciem dynamiki jest pojęcie „siły”. Mówimy : na ciało materialne (punkt materialny, układ
punktów materialnych) działa siła F ; ciało A działa na ciało B siłą F i podobnie. Jak widać siłę wiążemy z
działaniem - oddziaływaniem (lub możliwością działania -oddziaływania) jednego ciała materialnego na drugie
ciało materialne. Pod pojęciem oddziaływania rozumiemy wzajemny wpływ ciał materialnych (lub układów ciał)
na inne ciało materialne (lub układ ciał ) polegający na zmianie własności mechanicznych (deformacja
plastyczna w przypadku bryły materialnej) lub kinetycznych (zmiana kształtu toru, prędkości , przyspieszenia
itp. ). Wpływ jednego ciała na drugie dokonuje się za pośrednictwem pewnego pola fizycznego. Oczywiście
rozpatrując jedynie zjawiska mechaniczne trudno dociekać konkretnej natury takich pól , może to być bowiem
pole elektromagnetyczne, grawitacyjne lub inne. Zazwyczaj ograniczamy się do stwierdzenia, że ciało
posiadające pewną własność (mechaniczną ) zmienia inną własność (mechaniczną) ciała na które oddziałuje.
Mówimy wówczas, że ciało A działa na ciało B z pewną siłą , zazwyczaj też przyjmujemy że ciała działają na
siebie przez bezpośredni kontakt. Naturalnie, należy sobie zdawać sprawę z ograniczoności zakresu stosowania
takiego wyobrażenia i skromnych możliwości wyjaśnień uzyskiwanych w takim prostym – mechanicznym
modelu dotyczących „natury” oddziaływania. Wiadomo bowiem, że większość oddziaływań związanych jest z
siłami natury elektromagnetycznej, pozostającymi wobec poza zakresem możliwości eksplanacji dynamiki
klasycznej. Wiadomo również, że każdemu oddziaływaniu towarzyszy pewne pole fizyczne, jest więc oczywiste,
ż

e wyjaśnień natury takiego pola będziemy poszukiwali badając konkretną teorię polowa. Model oddziaływania

w mechanice klasycznej ma podobny zakres stosowania jak omówiony wcześniej schemat pojęciowy kinematyki
klasycznej.
Generalnie powiemy , że na ciało A działa siła (nie wnikając na razie w jej źródło) jeżeli zmienia się w czasie
wektor prędkości ciała A. Zmiana ta może mieć charakter chwilowy lub ciągły , odpowiednio siła może działać
w pewnym odcinku czasu lub stale.
Jak pokazuje doświadczenie siła ma charakter wektorowy – może być przedstawiana jako wektor zaczepiony
(jej punktem zaczepienia jest punkt w którym przyłożono siłę - polem sił zajmiemy się później). Stwierdzenie to
jest z matematycznego punktu widzenia „silnym” stwierdzeniem, wiąże się ono bowiem z zastosowaniem całego
matematycznego aparatu rachunku wektorowego.
Czasami przyjmuje się jako IV prawo dynamiki twierdzenie :
Siła jest wektorem.
Co jest aksjomatycznym sformułowaniem powyższego stwierdzenia.
Siły działające na punkt materialny (układ punktów materialnych (spełniają zasadę superpozycji)
(do tego zagadnienia powrócę przy omawianiu zasad dynamiki Newtona)
W zależności od sytuacji fizycznej (rodzaju siły ) siła może mieć być funkcją postaci :
F = F ( a, v, r, t ) tj. może zależeć od przyspieszenia, prędkości, wektora wodzącego , czasu.
Zazwyczaj jednak przyjmujemy :
F = F (v, r, t )
lub nawet :
F = F ( r, t ) tj. siła zależy jedynie od położenia punktu materialnego i czasu.
Przykładami fizycznymi sił mogą być siły :
a) sprężystości
F = k r ; k – pewna stała zwana współczynnikiem sprężystości.
b) siła grawitacyjna.

F = (

γ

/ r2 ) ř ; ř - wersor

c) siła oporu ośrodka - siła tarcia
F =

µ

F

µ

.

d) siła elektromagnetyczna działająca na cząstkę o ładunku e.
F = F (v, r, t ) = e E + k [ v, B]
gdzie : E – to wektor natężenia pola elektrycznego, B – to wektor natężenia pola magnetycznego.

Jednostka siły jest Newton [ N].
Mówimy , że na ciało o masie 1 [kg] działa siła równa 1[ N] , jeżeli ciało to porusza się z przyspieszeniem

1 [ m/s2 ] pod działaniem tej i tylko tej siły. Mamy zatem : [ N = kg m /s2 ]

2

2. Cząstka swobodna – prawo bezwładności.

Dynamika przejmuje od kinematyki pojęcia czasu i przestrzeni bez ich modyfikacji (zobacz tekst dotyczący
kinematyki ). Cząstki materialne umieszczone są (poruszają się ) w trójwymiarowej (absolutnej ) przestrzeni
Euklidesa a ich stan określony być może jako funkcja absolutnego czasu.
Mamy zatem arenę zdarzeń oraz „aktorów” na tej arenie tj. punkty (układy punktów, bryły) materialne.
Dynamika wprowadza na tą arenę pojęcie siły tj. miary działania cząstek między sobą. Konsekwencją
oddziaływania cząstek (lub ogólnie – działania na nie siły ) jest zmiana parametrów ruchu – toru , prędkości
przyspieszenia.
Załóżmy na początku, że na tej arenie istnieje tylko jedna cząstka , oczywiste jest , że jej parametry ruchu będą
niezmienne w czasie, jednak jak wiemy takie pojęcie kinetyczne jak np. prędkość nie maj sensu dla jednej
jedynej cząstki , celowe zatem jest wprowadzenie drugiej cząstki. Jednak w takiej sytuacji moglibyśmy
przypuszczać , że między tymi cząstkami działa pewna siła. Oczywiście tak być nie musi i jest to uwarunkowane
rodzajem cząstek i rodzajem działających między nimi sił. Nadto wiadomo również, że dla większości
działających sił – siła zmniejsza się wraz z odległością (tak jest np. dla najuniwersalniejszej z sił – siły
grawitacji). Mamy więc dwie (nie oddziałujące lub o zaniedbywalnej sile oddziaływania ) cząstki, możemy
zatem określić sensownie pewne wielkości kinetyczne. Pytanie jest następujące : jak będą się poruszały takie
cząstki ? ( zgodnie z zasadą względności, z każdą z nich możemy związać równoprawny układ odniesienia )
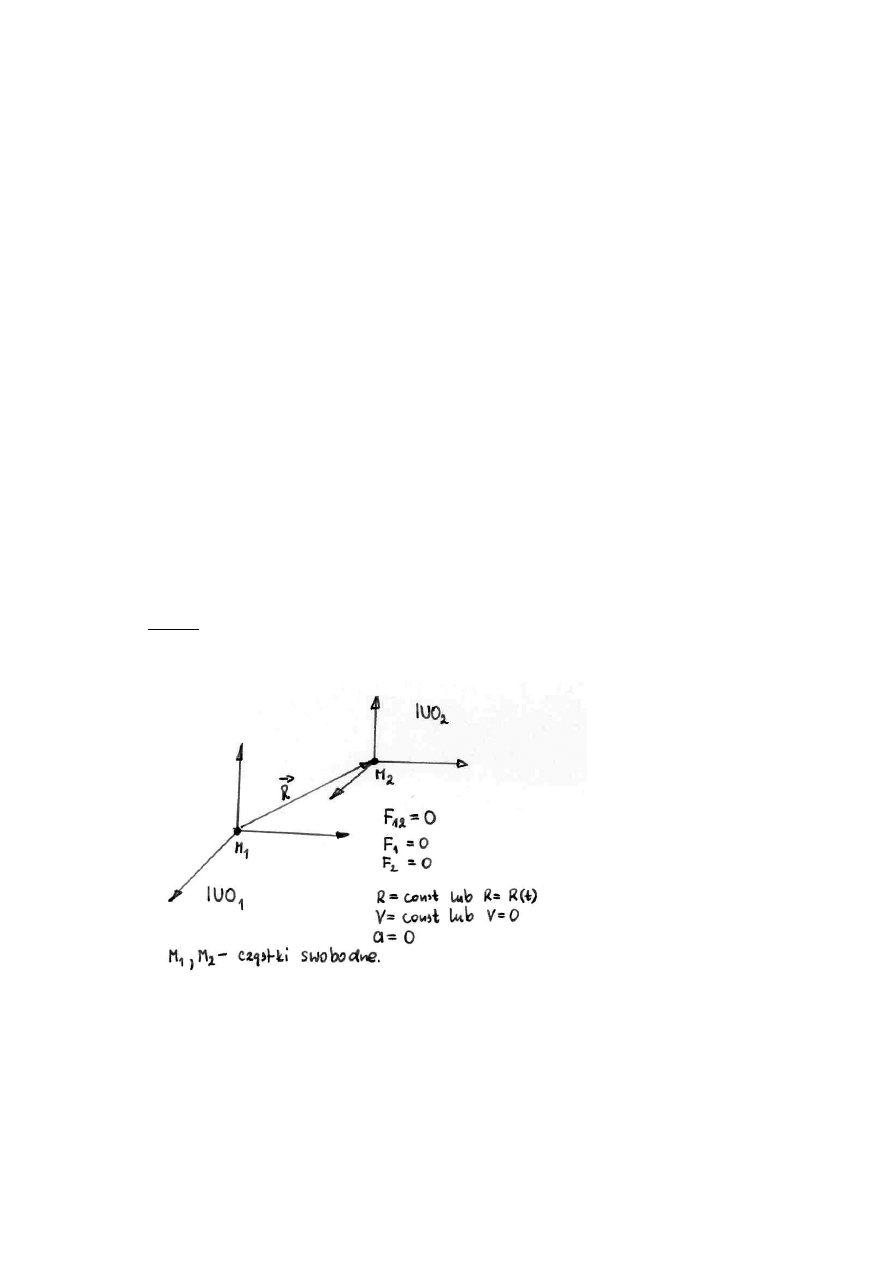
Przyjmijmy następująca definicję: cząstki lub cząstkę na którą nie działają żadne siły zewnętrzne (lub działające
siły równoważą się ) nazywamy „cząstką swobodną”. Pojęcie to, oczywiście pewną abstrakcją fizyczną w
rzeczywistości nie ma cząstek swobodnych , warunki swobody tj. nie działania żadnych sił ,mogą być spełnione
jedynie w przybliżeniu.
Postulujemy , że cząstka swobodna porusza się ruchem jednostajnym , prostoliniowym ( ruchem swobodnym)
lub spoczywa. Układ odniesienia dla którego spełnione są powyższe warunki nazywamy „układem inercjalnym”
Postulat ten nazywamy „prawem bezwładności” (Galileusza ).
Wypowiedzmy go jasno :
Istnieje taki układ odniesienia – zwany : inercjalnym układem odniesienia ( w skrócie IUO ) w którym cząstka
(cząstki) swobodne poruszają się ruchem swobodnym.
Jest to postulat (zgodny z eksperymentem w granicach przyjętych przez model ) – cząstka swobodna mogła by
poruszać się np. ruchem jednostajnie przyspieszonym lub mogła by tylko spoczywać (tak przyjmował np.
Arystoteles w swojej dynamice )

Rys. 1 Inercjalne układy odniesienia to układy w których cząstki swobodne poruszają się ruchem swobodnym.

3

3. Prawa dynamiki Newtonowskiej.

Zajmiemy się teraz podstawowymi prawami dynamiki sformułowanymi przez Newtona.
I prawo dynamiki Newtona ( zwane prawem bezwładności) głosi :
Ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym , jeżeli działające na niego
siły są równe zeru.
Jak widać jest to zasada bezwładności Galileusza.
Prawo to możemy sformułować następująco :
Istnieje IUO.
I jak już powiedziałem jest to postulat. W kinematyce wszystkie układy odniesienia były równouprawnione
dynamika uprzywilejowaną rolę przypisuje pewnej wyróżnionej klasie układów odniesienia , są to IUO.
W praktyce jako IUO możemy przyjąć układ odniesienia w którym ruch swobodny jest swobodnym w pewnych
granicach. Jak łatwo zauważyć (wynika to ze szczególnego przekształcenia Galileusza ) jeżeli istnieje jeden IUO
to istnieje nieskończenie wiele IUO. W praktyce takim IUO może być , jak wiadomo, nawet układ który tak
naprawdę układem inercjalnym nie jest. Przykładowo obliczając ruch pocisku wystrzelonego z niedużą
prędkością , w pobliżu powierzchni Ziemi i o niedużym zasięgu , możemy jako IUO przyjąć np. układ związany
ze środkiem Ziemi.

II prawo dynamiki Newtona ( zwane prawem ruchu) głosi :
Przyspieszenie cząstki jest proporcjonalne do działającej na nią siły.
k a = F ; k – stała proporcjonalności (3.1)
Siła F może być wypadkową kilku (ogólnie wielu ) sił działających na dana cząstkę. Ze wzoru (3.1) wynika , że
wektor przyspieszenia ma kierunek działającej siły.
I teraz najważniejsza uwaga – II prawo dynamiki jest spełnione ( w powyższej formie) tylko w IUO. To znaczy ,
ż

e przyspieszenie określone jest względem IUO związanego z daną cząstką. Można więc powiedzieć, że IUO to

układ w którym spełnione jest II prawo Newtona. Jak zobaczymy dalej NIUO (nie inercjalny układ odniesienia )
możemy sprowadzić do IUO wprowadzając pewną modyfikację II prawa dynamiki.
Jeżeli obserwator O związany z IUO stwierdzi, że cząstka porusza się ruchem przyspieszonym (ogólnie nie
jednostajnym lub krzywoliniowym ) może powiedzieć , że na cząstkę ta działa pewna siła F. ( jest jeszcze jedna
możliwość obserwatorowi O może się wydawać , że znajduje się w IUO i do tej kwestii powrócę później )
Obecnie omówię bardzo ważną kwestię , mianowicie - czym jest (co to jest ) stała proporcjonalności k.
Po pierwsze jak widać jest to skalar. Skalar ten nazywamy „masą bezwładną”. Masa bezwładna charakteryzuje
konkretną cząstkę (jest własnością konkretnej cząstki). W dynamice klasycznej przyjmujemy, że masa
bezwładna może być funkcją jedynie czasu (chociaż zazwyczaj przyjmujemy ją jako stałą ). Wymiarem tej stałej
jest kilogram [kg] – właściwiej było ,opuszczając przedrostek „kilo”, powiedzieć : gram [g] . Jak dotąd wzorzec
kilograma nie doczekał się definicji „uniwersalnej” i należy odwoływać się do pewnego etalonu.
Przyjmijmy zatem zgodnie z tradycją : k = m. Masa jest wielkością addytywną tj. możemy sumować
poszczególne masy cząstek otrzymując masę wypadkową. Newton definiuje masę ( na samym początku
Principiów ) jako „ilość materii” proporcjonalną do objętości i gęstości. Jest to oczywiście znany wzór na masę
m =

ρ

V ;

ρ

- gęstość substancji, V – objętość zajmowana przez tą substancje.

Ogólnie - pojęcie masy we współczesnej fizyce jest interesującym zagadnieniem. Zainteresowanego czytelnika
odsyłam do książek :
Max Jammer - „Concepts of mass in classical and modern physics” – jest przekład rosyjski
Progres Moskwa 1967
Fridrich S. Zawielski - „ Masa w fizycznym obrazie świata” WP 1979
lub przeglądowego artykułu Michała Hellera w książce pt. „Filozofować w kontekście nauki” PTT Kraków 1987

II prawo dynamiki ma oczywiście oparcie (mocne) w doświadczeniu. Stała siła działająca na ciała o różnej masie
bezwładnej wywołuje oczywiście różne przyspieszenia, tym sposobem możemy wyznaczać doświadczalnie
wielkości m lub F. Możemy powiedzieć, że masa bezwładna jest miarą oporu (bezwładności) z jakim ciało
przeciwstawia się próbie zmiany ruchu czyli działającej na nie sile F.

III prawo dynamiki Newtona ( zwane prawem akcji i reakcji ) głosi :
Jeżeli ciało A działa na ciało B siłą F , to ciało B działa na ciało A siłą – F.
Prawo to ma również oparcie eksperymentalne. Wiadomo bowiem z doświadczenia , że jeśli jedno ciało działa
pewną siłą na drugie ciało – to drugie ciało działa również pewną siłą na ciało pierwsze. Stwierdzono , że siły te
są równe co do wartości bezwzględnej , działają na tej samej prostej (łączącej oba ciała) i maja przeciwne
zwroty. Pojedyncze siły nie mogą więc występować w przyrodzie. Jeżeli jedną z takich sił nazwiemy „siłą akcji”

4

to drugą nazwiemy „siłą reakcji”. Nie jest istotne którą z tych dwóch sił ( jest to para sił ) jak nazwiemy, ważne
jest to że mamy do czynienia z działaniem równoczesnym. O tej własności sił po raz pierwszy mówił Newton w
swojej II zasadzie dynamiki. Oczywiście z relatywistycznego punktu widzenia to równoczesne działanie jest
działaniem natychmiastowym i powinno być zastąpione działaniem w sensie relatywistycznym.
Siły akcji i reakcji są siłami działającymi na różne ciała – gdyby działały na jedno i to samo ciało ich
wypadkowa była by równa zeru i II zasada dynamiki nie miała by szans funkcjonować.
Jeżeli mamy pewien układ ciał (punktów ) materialnych i m-ty punkt działa na n-ty punkt siłą Fmn to n-ty punkt
działa na m-ty punkt siłą Fnm = - Fmn .
Z powyższej równości wynika w szczególności dla m = n znikanie sił samoodziaływania tj. :
Fnn = Fmm = 0

W literaturze spotkać możemy różne postaci sformułowań praw dynamiki Newtona. Możemy prawa te podać,
przykładowo w formie :
I Prawo. Ciało pozostaje w spoczynku lub ruchu jednostajnym po linii prostej , jeśli działające na niego siły nie
zmuszą go do zmiany tego stanu.
II Prawo. Zmiana pędu w czasie jest proporcjonalna do siły powodującej ruch i zachodzi w kierunku linii prostej
,którą wyznacza kierunek działania siły.
III Prawo. Działaniu towarzyszy zawsze przeciwdziałanie, równe co do wielkości , lecz przeciwnie skierowane.

Jako IV prawo dynamiki przyjmuje się zasadę superpozycji sił ( lub wektorowego liniowego charakteru siły)
Jeżeli na punkt materialny działają niezależnie siły F1 , F2 ... Fn . To możemy zsumować wektorowo te siły i
przyjąć , że działa jedna siła wypadkowa :
n
F =

ΣΣΣΣ

Fi .

i =1
I odpowiednio z II prawem :
a = a1+ a2 + .. .+ an = (1/m)(F1 + F2 + ... + Fn )
Możemy również przyjąć , że każda siła działająca na dany punkt materialny może być przedstawiona jako
pewna suma niezależnie działających sił składowych. Zasada ta ma oczywiście oparcie w doświadczeniu.
Uwaga !. Zasada superpozycji sił nie jest spełniona dla sił które są zależne od drugiej i wyższych pochodnych
wektora wodzącego punktu materialnego na które działa ta siła. To oznacza , że rozważane w mechanice siły
mogą być funkcjami czasu, położenia i prędkości ale nie przyspieszeń tj.
F = F ( r , v , t )
Uogólniając pojęcie siły możemy wprowadzić tzw. „pole siły” (pole siłowe). Mówimy , że w pewnym obszarze
przestrzennym zostało zdefiniowane pole siłowe jeżeli każdemu punktowi należącemu do tego obszaru został
przyporządkowany wektor reprezentujący siłę jaka działała by na ciało materialne jeżeli znalazłoby się w tym
punkcie. Z punktu widzenia matematyki zadanie pola siły jest równoważne zadaniu pewnego pola wektorowego.

4. Równanie ruchu punktu (układu punktów) materialnego.

Zajmiemy się teraz dokładniej II prawem dynamiki. Na początek wprowadźmy pojęcie pędu.
Pędem nazywamy iloczyn masy i prędkości punktu materialnego lub układu punktów materialnych.
p = mv (4.1)
Pęd jest wielkością wektorową ( Newton nazywa go „ilością ruchu” ). W dalszej części przyjmuje , że masa jest
wielkością stałą w czasie tj. m = const. Oczywiście można rozpatrywać układy mechaniczne o masie zmiennej w
czasie.
Jeżeli układ materialny składa się z n punktów o masach odpowiednio : m1, ... ,mn poruszających się
odpowiednio z prędkościami : v1, .. , vn to pęd tego układu jest dany :
n n
p =

ΣΣΣΣ

pi =

ΣΣΣΣ

mi vi (4.2)

i=1 i=1
II zasada dynamiki (dla punktu materialnego) w sformułowaniu pierwotnym ma postać :
dp /dt = F (2.3)

lub , równoważnie : d/dt ( mv ) = F ; ma = F ; md2r/dt2 = F ;
Dla układu punktów materialnych mamy :
n n

ΣΣΣΣ

dpi /dt =

ΣΣΣΣ

Fi (4.3a)

i=1 i=1

5

Równanie (4.3) jest to równanie wektorowe - w przestrzeni Euklidesa równoważne jest ono trzem równaniom
skalarnym :

md2x/dt2 = Fx
md2y/dt2 = Fy
md2z/dt2 = Fz
Z matematycznego punktu widzenia jest to układ równań różniczkowych zwyczajnych drugiego rzędu.
Rozwiązaniem tego równania ( jest to tzw. rozwiązanie podstawowego zagadnienia dynamiki tj. mamy podaną
siłę a wyznaczamy wektor wodzący ) jest pewna funkcja wektorowa :
r = x(t) i + y(t) j + z(t) k (4.4)
Jeżeli funkcja ta spełnia odpowiednie warunki ( jest regularna ) to równania ruchu maja dokładnie jedno
rozwiązanie. Rozwiązanie to zawiera w ogólności sześć stałych całkowania , mianowicie :
- trzy składowe wektora położenia początkowego ( tj. wektora wodzącego w chwili t0 ) :
r0 = (x0 , y0 , z0 )
- trzy składowe wektora prędkości początkowej :
v0 = (vx0 , vy0 , vz0 )
Rozwiązanie znajdujemy poprzez dwukrotne całkowanie postaci :
t1

τ

1

r(t) = (1/m)

∫ ∫

F dt d

τ

+ v0 t + r0 (4.5)

t0

τ

0

W ogólnym przypadku rozwiązanie analityczne takiego równania jest niemożliwe , stosujemy wtedy metody
numeryczne.
Znajomość postaci funkcji siły F = F( r, t) – działającej na cząstkę materialną o stałej masie m jak również
znajomość wartości wektorów r0 , v0 dla (dowolnej ) chwili początkowej t0 pozawala jednoznacznie określić
(obliczyć ) wartość funkcji r = r ( t ) dla dowolnej chwili czasu t , tym samym pozwala nam określić

jednoznacznie tor ruchu tej cząstki. Stwierdzenie to stanowi podstawę dla sformułowania klasycznej zasady
przyczynowości ( zasady determinizmu), w myśl której znajomość praw ruchu i wartości wielkości ruchu w
jednej dowolnie ustalonej chwili pozwala na ustalenie parametrów ruchu w dowolnej chwili w przyszłości jak i
przeszłości.
Można pokazać (prostymi rachunkami ), że równanie (4.3) nie zależy od wyboru IOU. Zatem siła jest
niezmiennicza wobec przekształcenia Galileusza. tj.
F’ = F dla IUO U i U’

Jeżeli działająca siła jest równa zeru to :
dp /dt = 0 => p = const => v = const
lub :
dp /dt = 0 => ma = 0 => a = 0 => v = const
Czyli jeżeli na punkt materialny nie działa żadna siła ( lub wypadkowa działających sił jest równa zeru )
to punkt ten porusza się ze stałą prędkością tj. ruchem jednostajnym prostoliniowym czyli swobodnym.
Jest to tzw. zasada zachowania pędu punktu materialnego.
Rozważmy równanie :
t1

p(t1) – p(t0 ) =

∫

F dt (4.6)

t0
Równanie to otrzymujemy przez scałkowanie równania (4.3). Wielkość :
t1

∫

F dt = I

t0
nazywamy „popędem siły“. Możemy zatem sformułować następujące prawo :
„Przyrost w czasie pędu jest równy popędowi siły“.

5. Rozwiązania równania dynamiki dla różnych postaci siły.

Przykład 1. Rozważmy jednowymiarowy ruch punktu materialnego, na który działa stała w czasie siła F.
Ponieważ ruch zachodzi na jednej prostej , przyjmijmy że jest to prosta wyznaczona przez oś Ox.
równanie wektorowe : ma = F , możemy zapisać w postaci skalarnej :

6

md2x/dt2 = Fx
Fx = F = const. => a = F/m = const

v (t) = (1/m)

∫

F dt = at + v0

r (t) =

∫

v (t) dt = ½ at2 + v0 t + r0

Co jest oczywiście znanym wzorem dla ruchu jednostajnie przyspieszonego ( na prostej )

Przykład 2. Napisać równanie ruchu punktu materialnego w polu grawitacyjnym ziemi (pominąć opory
powietrza)

Siła działająca równa jest ciężarowi ciała (mamy zatem siłę o postaci F = F(r ) – jest to przykład siły centralnej )
, zatem :

md2r/dt2 = -mg k
Czyli :

md2x/dt2 = 0

md2y/dt2 = 0

md2z/dt2 = -mg

(przyjmujemy, że oś z (o wersorze k ) skierowana jest przeciwnie do działania siły ciężkości )
Po scałkowaniu :

r (t) = - ½ g t2 k + v0 t + r0

Przykład 3. Rozważyć ogólną postać rozwiązań równań dynamiki dla siły zależnej tylko od czasu tj. F = F(t).
Ogólna postać rozwiązań jest następująca :

v (t) = (1/m)

∫

F(t) dt + v0

r (t) = (1/m)

∫∫

F(t) dt + v0 t + r0

Przykład 4. Punkt materialny A został wyrzucony z powierzchni Ziemi pionowo w górę z prędkością
początkową v0. Pomijając opór powietrza znaleźć prędkość tego punktu jako funkcję odległości od środka
Ziemi.

Punkt materialny jest przyciągany zgodnie z prawem ciążenia siłą F = k mM / r2. ( m- masa punktu , M –masa
Ziemi , r- odległość od środka Ziemi do punktu A, k – stała grawitacyjna )
Wybierzmy początek układu odniesienia ( współrzędnych ) tak aby jego środek pokrywał się ze środkiem Ziemi,
a oś Ox miała kierunek ruchu punktu A. Wtedy warunki początkowe będą następujące : przy t = 0 r0 = R
dx/dt = v0. Wyrażenie na siłę przyciągania przyjmuje postać : F = k mM / x

2. Równanie ruchu zgodnie z II

prawem Newtona ma postać :

md2x/dt2 = - F = - k mM / x2.
Na powierzchni Ziemi : F = mg dlatego przy x = R mamy : F = mg = kmM/R2 => kM = gR2 i równanie
różniczkowe przyjmie postać :

md2x/dt2 = dv/dt = - g R2 / x2.

W równaniu tym mamy trzy zmienne : x, v ,t a my potrzebujemy znaleźć zależność między dwoma ( x i v ),
dlatego wykluczymy zmienną t i przejdziemy do zmiennych v i t następująco :
dv/dt = (dv/dx ) (dx/dt ) = v (dv/dx). Otrzymamy zatem równanie o zmiennych rozdzielonych :

v (dv/dx) = - g R2 / x2 lub v dv = - g R ( dx / x2 )
Mamy następujące równanie :
v x v x

∫

v dv = -

∫

( gR / x2 ) dx => ½ v2 | = gR / x |

v0 R v0 R
lub : ½ ( v2 – v20 ) = ( gR

2 / x ) – gR

skąd :

v =

±

sqrt [ v20 + 2 gR ( R – x ) / x ]

W chwili osiągnięcia przez punkt A wysokości maksymalnej H = xmax , jej prędkość staje się zerowa , zatem :

7

0 = sqrt [ v20 + 2 gR ( R – x ) / x ] => H = 2gR

2 / ( 2gR - v2

0 )

Z tego wyrażenia wynika , że jeśli v20 < 2gR to punkt osiągnie wysokość maksymalną H a następnie zacznie
opadać na Ziemie. Przy : v20

≥

2gR punkt będzie cały czas oddalał się od Ziemi. Przyjmując R = 6400 [ km]

g = 0,0098 [ km/s2 ] znajdujemy , że punkt będzie oddalał się cały czas od Ziemi przy prędkości :
v0 = 11,2 [ km/s ] – jest to tzw. druga prędkość kosmiczna.
( pierwszą prędkością kosmiczną nazywamy prędkość przy której ciało rzucone stycznie do Ziemi nie upada na
nią tj. stanie się jej sztucznym satelitą ( oczywiście pomijając opór powietrza przy jej powierzchni) . Jak
wiadomo pierwsza prędkość kosmiczna jest równa w przybliżeniu 7,9 [ km/s ] )

6. Ruch w nieinercjalnych układach odniesienia

Jak już powiedziano układem inercjalnym nazywamy układ odniesienia w którym słuszne jest II prawo
dynamiki. Jeżeli wyznaczymy ( dokonując odpowiednich pomiarów ) , że pewien układ odniesienia jest układem
inercjalnym to tak naprawdę wyznaczymy cała klasę IUO – do tej klasy należą wszystkie układy odniesienia
poruszające ruchem jednostajnym prostoliniowym względem pierwotnie wyznaczonego IUO. Analizując
przykłady transformacji układów odniesienia ( patrz tekst pt. „Kinematyka punktu materialnego w mechanice
klasycznej” ) widać wyraźnie dlaczego tak jest – w IUO nie pojawiają się żadne siły pozorne. Jeżeli punkt
porusza się bez przyspieszenia w jednym z wybranych IUO to będzie poruszał się bez przyspieszenia w każdym
innym IUO. Z odmienną sytuacją mamy do czynienia w układach które poruszają się względem siebie z
niezerowym przyspieszeniem względnym. Rozważmy klasyczny przykład : mamy dwóch obserwatorów jeden
znajduje się w IUO a drugi w układzie wirującym ze stałą prędkością kątową ω względem pierwszego
obserwatora. Rozważmy teraz punkt materialny , w najprostszej sytuacji – spoczywający względem pierwszego
obserwatora. Obserwator związany z IUO stwierdzi słuszność II prawa dynamiki, obserwator drugi stwierdzi , że
II prawo dynamik nie jest słuszne – na punkt materialny ( według niego – przyjmujemy , że nie wie on o tym ,że
jego układ odniesienia jest układem wirującym ) działa pewna siła. Rozważmy ogólny wzór transformacyjny
poruszających się ruchem dowolnym, układów odniesienia :

a’ = a + A + acor + adośr. +

α

αα

α

×

r

acor = 2 ω

×

r - przyspieszenie Coriolisa.

adośr. = ω

×

( ω

×

r ) – przyspieszenie dośrodkowe.

Mnożąc go przez masę punktu materialnego m otrzymujemy :
ma’ = ma + mA + macor + madośr. + m(

α

αα

α

×

r)

Jak widać równanie to jest równaniem określającym pewne siły ( iloczyny przyspieszeń i masy ).
Dla IUO mamy : ma’ = 0. Dla naszego przypadku : ma’ = madośr. tj. drugi z obserwatorów stwierdzi, że punkt
materialny posiada niezerowe przyspieszenie dośrodkowe – działa na niego więc pewna niezerowa siła.
Jeżeli teraz na punkt materialny w IUO działa siła F , to w układzie wirującym działa siła F + Fdośr.
W ogólności dla NIUO ( nie inercjalnego układu odniesienia ) mamy :
F’ = F + FA + Fcor + Fdośr. + F

α

Jest to ogólny wzór transformacyjny siły.

Siłę F – nazywamy siłą rzeczywistą , siły : FA , Fcor , Fdośr. , F

α

- są to siły pozorne (siły bezwładności ).

Siły pozorne nie są związane z oddziaływaniami – są wynikiem stosowania NIUO. W NIUO aby II prawo
dynamiki było spełnione należy je zmodyfikować – do siły rzeczywistej należy dodać ( wektorowo) siły
bezwładności Fb :
ma = F + Fb .
Rozwiązanie prostego zagadnienia dynamiki wiąże się teraz z koniecznością znajomości nie tylko postaci siły
rzeczywistej ale i postaci ( sumy ) sił bezwładności. Dynamika punktu materialnego rozpatrywana w IUO, jak
widać ma dużo prostszą postać niż dynamika rozpatrywana w NIUO.
Ogólnie możemy stwierdzić, że siły pozorne możemy wyeliminować poprzez odpowiedni wybór układu
odniesienia. Jeżeli działające siły nie mają charakteru pozornego tj. wiążą się z konkretnym oddziaływaniem to
nie można ( w ogólności ) wskazać takiego układu odniesienia ( inercjalnego lub nieinercjalnego ) w którym
były by one równe zeru. Jak również widać siły pozorne mogą być siłami zależnymi od czasu , wektora
wodzącego i prędkości tj. Fb = Fb ( r, v, t ).

8

7. Ruch punktu materialnego o zmiennej masie.

Rozważmy ruch punktu materialnego którego masa jest ( w ogólnym przypadku ) funkcja czasu i prędkości tj.
m = m(t, v). Bilans pędu (zgodny z zasadą zachowania ) będzie miał postać :
dp = F dt + dm ( v + a )
Zatem :
dp /dt = F + (dm/dt) ( v + a )
Jeżeli w szczególności masa dm spoczywa w układzie inercjalnym to :
dp /dt = F => d (mv) = F => (dm/dt )v + m(dv/dt) = F
m(dv/dt) = F + (dm/dt )v
Składowa : (dm/dt )v – jest to siła powstała wskutek zmiany masy cząstki ( siła ciągu ).

8. Absolutność IUO ?

W kinematyce rozpatrywaliśmy m.in. następującą sytuacje : Jeżeli układ U poruszał się ruchem jednostajnym
prostoliniowym z prędkością v, względem innego układu U’ – to żadne doświadczenie fizyczne ( mechaniczne)
nie było w stanie rozsądzić czy to U porusza się względem U’ z prędkością v czy też U’ porusza się względem U
z prędkością – v. Oczywiście chodzi tu o klasycznie rozumiana względność spoczynku i ruchu Galileusza ,
mająca potwierdzenie w odpowiednich wzorach transformacyjnych. Zatem pytanie o to który z układów
„rzeczywiście” się porusza nie ma sensu. Obecnie możemy postawić to samo pytanie dla układów
poruszających się ruchem przyspieszonym. Niech układ U porusza się ( w szczególności ) ruchem jednostajnie
przyspieszonym – z przyspieszeniem a ,względem układu U’. Czy zasadne było by równouprawnienie układów
U i U’ ? tj. stwierdzenie , że to U’ porusza się ruchem jednostajnie przyspieszonym względem U.
Jak wiadomo z II prawa dynamiki ruch przyspieszenie jest wynikiem działania siły ( rzeczywistej ) – siła jest
związana z oddziaływaniem, można zatem , w pierwszej kolejności wykazać , że ten z układów na którego
działa siła, porusza się z przyspieszeniem. Problem jednak nie jest tak trywialny, ponieważ samo stwierdzenie ,
ż

e któryś z układów porusza się z przyspieszeniem wymaga ustalenia względem jakiego IUO mierzymy to

przyspieszenie. Podstawą zatem jest ustalenie, który z tych układów jest inercjalny. Może to wykazać jedynie
doświadczenie. Z teorii wiemy jedynie , że IUO istnieje. Wiemy również , jak sprawdzić czy dany układ jest
inercjalny – wystarczy wziąć cząstkę swobodną i sprawdzić jej ruch, lub poddać cząstkę swobodną działaniu
znanej siły i sprawdzić jej ruch. ( osobiście jestem, zatem zdania, że dynamika Newtonowska powinna być
uzupełniona jeszcze jednym postulatem – „istnieje cząstka swobodna” tj. cząstka na którą nie działają żadne siły
Istnienie cząstki swobodnej nie wynika jak mi się wydaje, z żadnego prawa fizycznego – jest raczej odwrotnie
np. siły grawitacyjne są siłami o zasięgu nieskończonym i tylko dzięki ich własności malenia wraz z odległością,
można w dostatecznie odległym punkcie przyjąć ich zerowy wpływ na ruch cząstek materialnych. Należało by
również mieć na uwadze, że z przyjętego schematu rozumowania : IUO + cząstka swobodna => ruch swobodny
cząstki swobodnej – zapostulowano tylko pierwszy składnik. Należy również wspomnieć, że właśnie z takiej a
nie innej postaci II zasady dynamiki wynika taka a nie inna definicja IUO. TO druga pochodna wektora
wodzącego jest proporcjonalna do działającej siły , gdyby proporcjonalna była np. trzecia pochodna należało by
inaczej zdefiniować IUO. Wtedy to względny byłby nie tylko spoczynek i ruch jednostajny ale również
przyspieszenie jednostajne )
Układ będzie inercjalnym jeśli spełniona jest w nim II zasada dynamiki.
IUO jest jak widać pewnym układem (absolutnym – po jego ustaleniu ) bazowym.
Przyspieszenie jest zatem zjawiskiem absolutnym. Po wyznaczeniu względem jakiego IUO układ przyspiesza
ustalamy klasę układów przyspieszonych.
W kontekście tego co powiedziałem należy mieć na uwadze problem absolutności (istnienia absolutnego układu
odniesienia ) przyspieszenia rozpatrywany już przez Newtona.
(zobacz m.in. „Wstęp do fizyki współczesnej” – J. Kociński. PWN 1977 str. 56 )

Bibliografia

Literatura podstawowa
Przedstawiony artykuł został napisany z wykorzystaniem następujących książek :
(podano w kolejności wzrastania stopnia trudności wyłożonego materiału)

1). “Wstęp do fizyki – tom 1 „ – A. K. Wróblewski, J. A. Zakrzewski, PWN 1989
2). „Mechanika klasyczna – tom I, II” – John R. Taylor , WN-PWN 2006
3). „Mechanika teoretyczna” – Piotr Wilde, Mieczysław Wizmur ,PWN 1984
4). „Mechanika Teoretyczna” – W. Rubinowicz, W. Królikowski , WN-PWN 1998
5) „Wstęp do mechaniki klasycznej” – Krzysztof Stefański, WN-PWN 1999

9

6) „Mechanika ogólna” – Zbigniew Osiński , WN-PWN 2000
7) „Mechanika” – Bogdan Skalmierski , WN-PWN 1998
8) „Mechanika klasyczna” – G. Białkowski , PWN 1975
9) „Mechanika teoretyczna” – J. J. Olchowski, PWN 1978
10) „Mechanika” – S. Banach , PWN 1956
11) „Mechanika klasyczna” – R. S. Ingarden, A. Jamiołkowski, PWN 1980
12) „Metody matematyczne mechaniki klasycznej” – W. J. Arnold, PWN 1981

Literatura uzupełniająca
13) „Feynmana wykłady z fizyki” tom 1 cz. 1, WN PWN 2001
14) „Mechanika” – C. Kittel, W.D. Knight, M.A. Ruderman, PWN 1973
15) „Fizyka ruchu i czasoprzestrzeni” – M. Heller, WN-PWN 1993
16) „Mechanika teoretyczna” – G. K .Susłow, PWN 1960
17) „Fizyka matematyczna tom 1 – klasyczne układy dynamiczne” – W. Thirring, PWN 1985

Literatura w języku rosyjskim
18) „Mechanika klasyczna” – G. Goldstein
19) „Podstawy mechaniki teoretycznej” – W. F. Żurawliew, Moskwa Fizmatlit 2001
20) „Wykłady z mechaniki teoretycznej” – Ju. G. Pawlenko, Moskwa Fizmatlit 2002
21) „Mechanika teoretyczna” – A. P. Markjew, Moskwa, 1999

##########################################################################################