XXII SYMPOSIUM – VIBRATIONS IN PHISICAL SYSTEMS – Poznań-Będlewo 2006
WDOWICKI Jacek, FILIPOWICZ Antoni, WDOWICKA Elżbieta
Poznan University of Technology,
ul. Piotrowo 5, 60-965 Poznań, Poland
tel.: +48 61 665 24 62, e-mail:
jacek.wdowicki@put.poznan.pl
ASSESSMENT OF EMPIRICAL EQUATIONS FOR PREDICTING
FUNDAMENTAL PERIODS OF TUNNEL FORM BUILDINGS
1. INTRODUCTION
The paper is concerned with the prediction of fundamental periods of multistorey
shear wall buildings subjected to seismic and paraseismic actions. The determination of
natural frequencies is the key issue in designing of tall buildings. The calculation of
natural frequencies and mode shapes is the first step in evaluation of the dynamic
response of the structure by the modal superposition technique. The values of natural
frequencies are also required in the determination of equivalent static loadings due to
wind actions. In designing it is important to estimate as precisely as possible dynamic
properties of a structure in its preliminary stages. Before all the dimensions of structure
elements are specified the essential decisions are already taken which, in the end,
determine technical and economic properties of the structure. So, in the early stages of
designing it is vital that quite accurate estimation of natural frequencies is at one’s
disposal.
The selection of the best possible estimation of natural frequencies from the proposed
in the literature formulae has been the main aim of the present paper. For the analyses 16
shear wall dominant buildings constructed by using tunnel form techniques [1,
2] have
been applied. The empirical equations presented in the papers [1,
3,
6,
7]
have been
estimated.
Computations have been carried out by using the following specialised computer
programs for shear wall structures: BW for Windows [8, 9] and ETABS [5].
2. ANALYSED BUILDINGS
The buildings which had been investigated during elaboration of the empirical
equations for the fundamental period conducted by the authors [1] were analysed in the
paper. They are shear wall dominant multistorey reinforced concrete structures,
constructed by using a special tunnel form technique, composed of vertical and
horizontal panels set at right angles and supported by struts and props.
There are no beams or columns and these structures generally use all wall elements
as primary load carrying members. In this construction technique, the use of precast load
carrying members is avoided. The walls and slabs, having almost the same thickness are
cast in their place in a single operation. This reduces not only the number of joints, but
also the assembly time. Consequently, the casting of walls and slabs can be completed in
1 day for each floor. The simultaneous casting of walls, slabs and cross-walls results in
368
monolithic structures, which provides high seismic performance and, therefore, they
meet seismic code requirements of many countries located in regions having high
earthquake risk. In addition to their considerable resistance, the speed and ease of
building make them preferable as the multi-unit construction of public and residential
buildings.
The complete database concerning analysed building was categorized into two sub-
data sets according to the plan dimension ratios. If the ratio of the long-side to short-side
dimension is less than 1.5, these plans are accepted as square and those plans having the
same ratio greater or equal to 1.5 are accepted as rectangular.
In the all analysed buildings thickness of both walls and floor slabs equals to 0.12 m.
3. EXAMPLE BUILDING FOR RECTANGULAR CASE
The plan of the selected example building (Plan No.1) has the following dimensions:
long-side 29.70 m, short-side 15.70 m. The height of lintel beams equals to 0.46 m
(in this 0.34 m under the floor slab and 0.12 m of slab). For computations made by using
ETABS program the height of the first storey 2.92 m and the height of next storeys
2.80 m have been assumed. The same storey heights as in ETABS program have been
assumed for calculations in which the program BW for Windows has been applied.
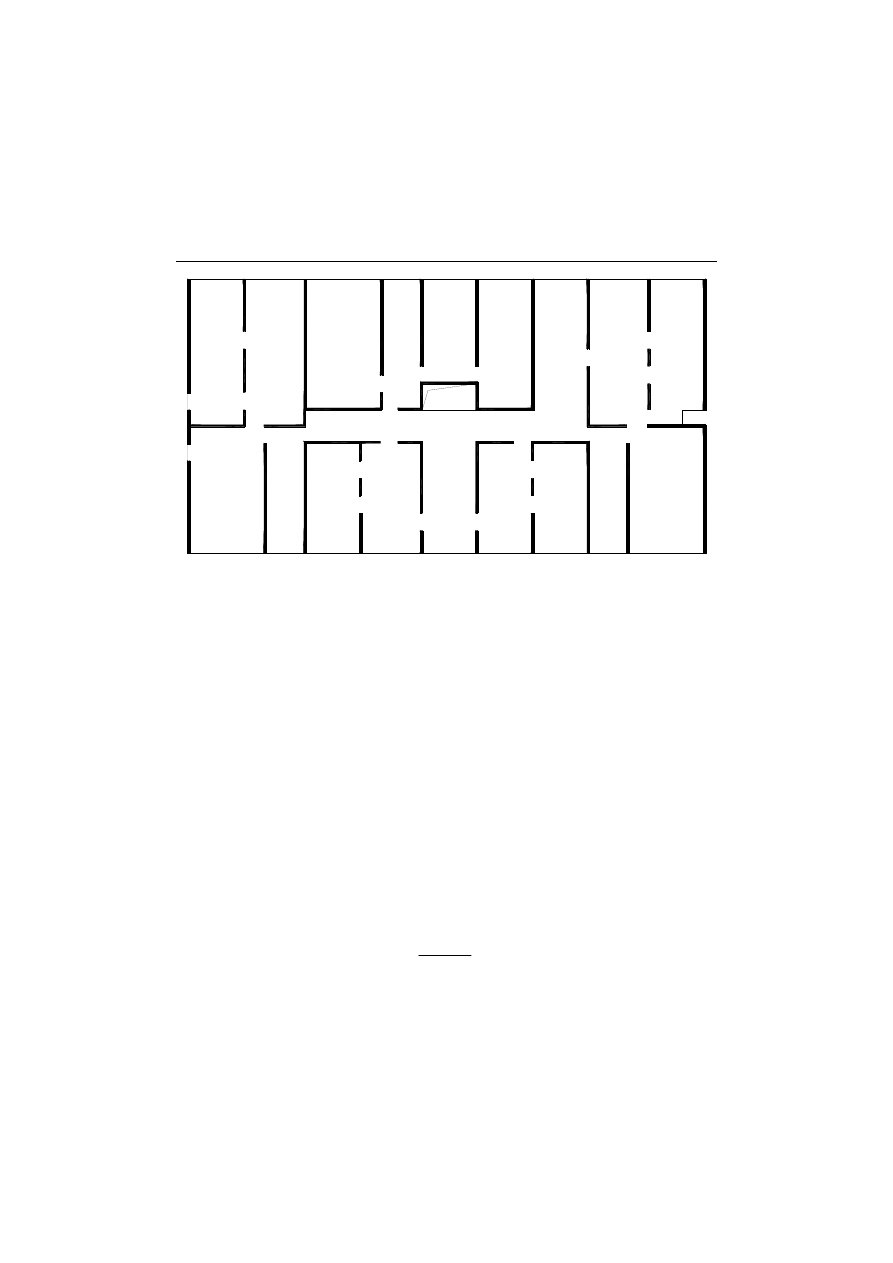
The three-dimensional view for a single storey (Fig.1) and in addition, a building
plan No.1 (Fig.2) has been presented. In Fig. 2 solid lines demonstrate the shear walls in
the plan.
Figure 1. Three-dimensional view for single storey of tunnel form building structure
(Plan No.1).
369
Figure 2. Typical plan view for a rectangular case (Plan No.1).
4. EMPIRICAL EQUATIONS
Below, the compared empirical equations for predicting fundamental periods will be
discussed.
4.1 The formula elaborated by A. Kowalska in the paper [7].
In this paper, based on the analysis of the results of measurements made on 47
buildings which differed in height and structure (a part of them was a masonry
construction, another part constituted precast panel buildings and some others were
framed reinforced buildings), there were determined relations between basic dynamic
characteristics and the building height as well as the material and type of construction
applied.
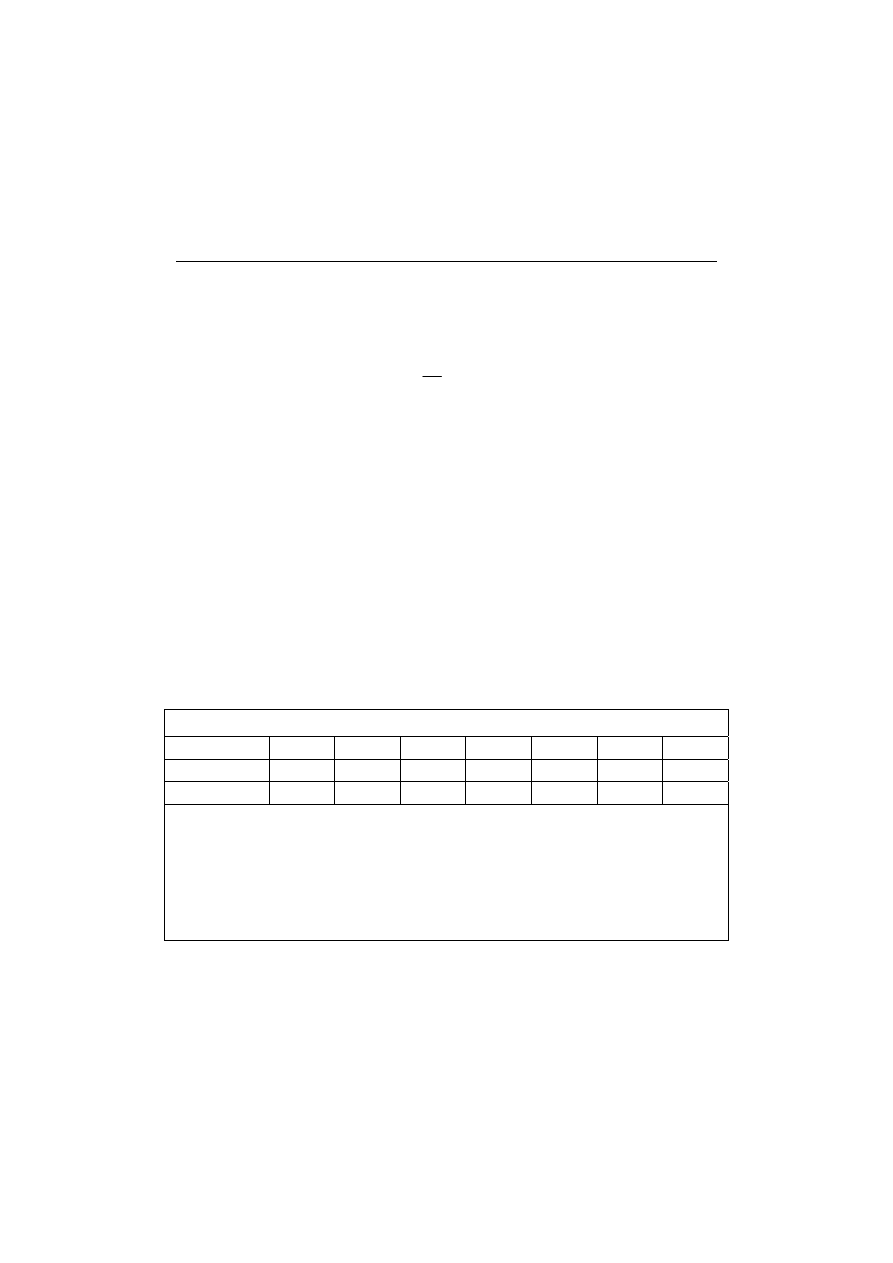
For precast panel buildings it has been given as follows
629
,
55
9174
,
0
H
T
=
(4.1)
where T is the period in s; H is the building height in metres.
370
4.2. The formula proposed by A.P. Jeary in the paper [6].
The author, following [4] recommends the formula for the fundamental period of
multistorey buildings (including shear wall buildings)
H
H
T
⋅
=
=
02174
,
0
46
(4.2)
where T is the period in s; H is the building height in metres.
4.3. The equations which have been developed by C. Balkaya and E. Kalkan in the
paper [1].
In this study the equations from such codes as Uniform Building Code (1997) and
Turkish Seismic Code (1998) have been estimated. It has been observed that the given
empirical equations for prediction of fundamental periods of this specific type of
structures yield inaccurate results.
For that reason, a total of 80 different building configurations were analysed by using
three-dimensional finite element modelling and a set of new empirical equations,
obtained by applying non-linear regression analysis, was proposed. These equations are
different from each other depending on a plan of a building shape. They have been
shown with the accompanying coefficients in Table 1.
Table 1. Empirical equations for predicting fundamental periods
of tunnel form buildings [1].
6
5
min
4
3
2
1
b
b
b
al
b
as
b
b
J
Ch
T
ρ
ρ
ρ
β
=
Plan type
C
1
b
2
b
3
b
4
b
5
b
6
b
Square 0.158 1.400 0.972 0.812 1.165 -0.719 0.130
Rectangular 0.001 1.455 0.170 -0.485 -0.195 0.170 -0.094
T: Period [s]
h: Total building height [m]
β: Ratio of long-side to short-side dimension
ρ
as
: Ratio of short-side shear wall area to total floor area
ρ
al
: Ratio of long-side shear wall area to total floor area
ρ
min
: Ratio of minimum shear wall area to total floor area
J : Plan polar moment of inertia
4.4. The equation presented by C. Balkaya and E. Kalkan in the paper [3].
In this paper the authors continued the research on estimation of the fundamental
period of shear wall buildings using an extended building inventory. A simpler formula
371
that can be applicable for both mid-rise (storey level ≤ 15) and high-rise (storey level
> 15) tunnel form buildings is developed based on the finite element analyses of 20
different buildings (most have as-built plans and were already constructed).
The equation developed to predict the fundamental period of the tunnel form
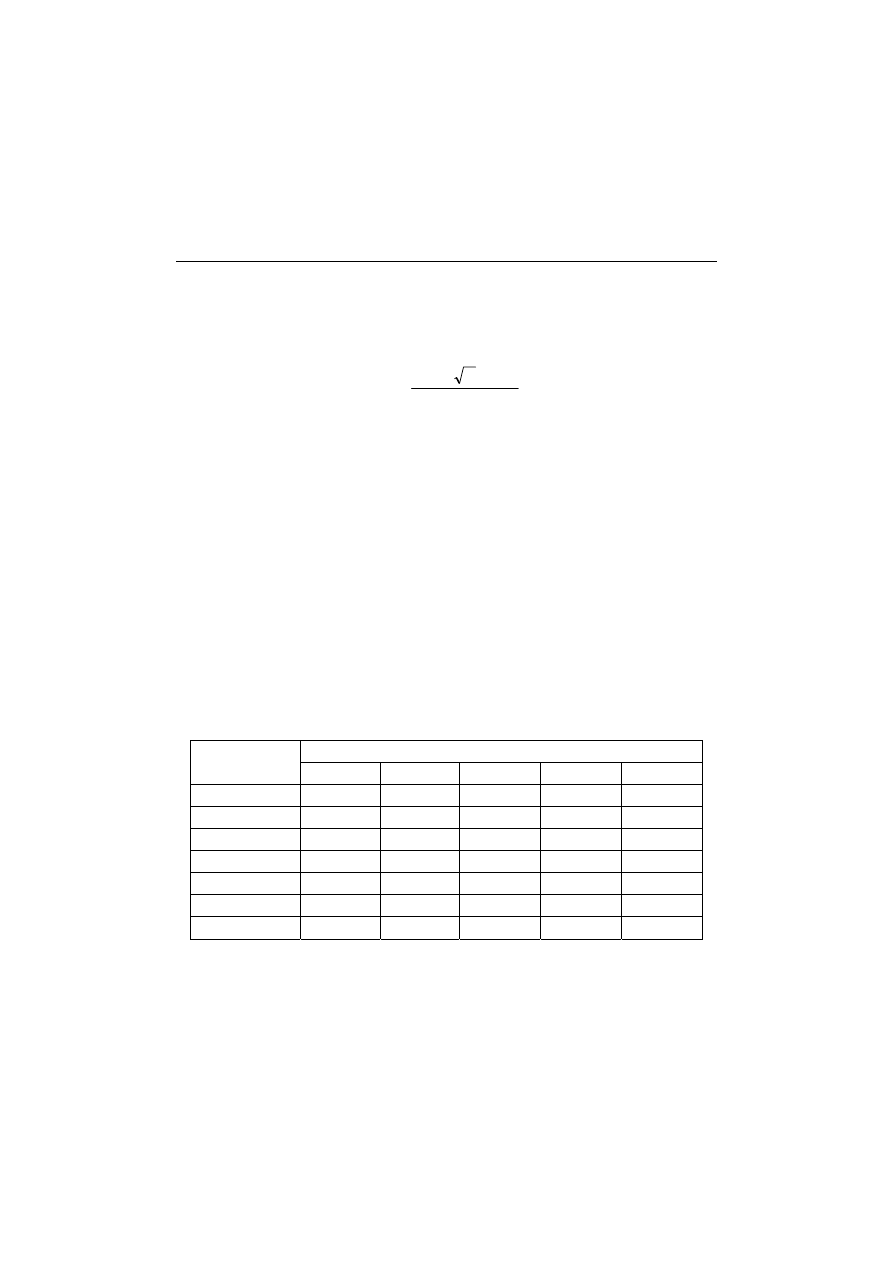
buildings has the following form
(
)
a
width
a
lenght
R
R
R
h
C
T
+
⋅
⋅
=
(4.3)
where
T is the period in s; h is the total height of building in m; R is the ratio of long-
side dimension to short-side dimension of the building;
R
length
is the ratio of shear wall
area oriented along the length to a typical storey area; and
R
width
is the ratio of shear wall
area oriented along the width to typical storey area. In this equation,
C and a are the
estimator parameters obtained from regression analysis, and are equal to 0.138 and -0.4,
respectively.
5. RESULTS OF ANALYSIS
The results for an example building No.1 described in paragraph 3 will be discussed
below. In Table 2 there have been listed values of the fundamental period for five
different building heights (storey levels: 2, 5, 10, 12, 15). The first four rows contain the
values calculated on the basis of the empirical equations discussed in the previous
paragraph. In the next two rows there have been given the values obtained from ETABS
program used by A. Filipowicz and obtained in the study [1]. In the last row the results
obtained from computations using BW program, developed on the basis of the
continuous connections method has been included.
Table 2. Values of fundamental period of building No.1
Fundamental period [s]
Source
2-storey 5-storey 10-storey 12-storey 15-storey
Kow03
-
- 0.387 0.458 0.561
Jea86 0.124 0.308 0.617 0.741 0.925
Bal03 0.030 0.114 0.313 0.408 0.565
Bal04 0.103 0.255 0.511 0.613 0.766
ETABS-Fil 0.048 0.134 0.312 0.393 0.523
ETABS-Bal 0.048 0.129 0.293 0.368 0.489
BW
0.022 0.094 0.263 0.344 0.479
The recommended in paper [1] empirical equations, (see Table 1) are considered to
be appropriate for the estimation of the period of tunnel form building structures for 2–
372
15-storey levels. The results of the proposed equations agree well with finite element
analysis results.
6. CONCLUSIONS
The paper has provided the comparison of fundamental periods of shear wall
buildings, the models of which were discussed in the paper [1]. For more than 10-storey
high buildings the results of computations using the continuous model of shear wall
structure agree well with finite element analysis results. When applying empirical
equations a good agreement is obtained for calculating the fundamental period from the
equation presented in the paper [1]. For buildings more than 15-storey high it should be
replaced by a new formula proposed in the paper [3].
REFERENCES
1. Balkaya C., Kalkan E.:
Estimation of fundamental periods of shear-wall
dominant building structures, Earthquake Engineering & Structural Dynamics,
32, 7, (2003) 985-998.
2. Balkaya C., Kalkan E.:
Nonlinear seismic response evaluation of tunnel form
building structures, Computers and Structures, 81, 3, (2003) 153-165.
3. Balkaya C., Kalkan E.:
Seismic vulnerability, behavior and design of tunnel
form building structures, Engineering Structures, 26, 14 (2004) 2081-2099.
4. Ellis B.R.:
An assessment of the accuracy of predicting the fundamental natural
frequencies of buildings and the implications concerning the dynamic analysis
of structures, Proc. Instn Civ. Engrs, Part 2, 69, Sept. (1980) 763-776.
5. Habibullah
A.:
ETABS, A User's Manual, Computers and Structures, Inc.,
Berkeley, California, USA, 1992.
6. Jeary
A.P.:
Damping in tall buildings - a mechanism and a predictor,
Earthquake Engineering & Structural Dynamics, 14 (1986), 733-750.
7. Kowalska A.:
Prognozowanie podstawowej częstotliwości drgań własnych
i współczynnika tłumienia budynków, Inż. i Bud., 6 (2003) 331-334.
8. Wdowicki J., Wdowicka E.:
Integrated system for analysis of three-dimensio-
nal shear wall structures, Comp. Meth. in Civil Eng., 1, 3-4 (1991) 53-60.
9. Wdowicka E.M., Wdowicki J.A., Błaszczyński T.Z.:
Seismic analysis of the
"South Gate" tall building according to Eurocode 8, The Structural Design of
Tall and Special Buildings, 14, 1 (2005) 59-67.