W Y K Ł A D 4

ZJAWISKA REZONANSOWE W OBWODACH ELEKTRYCZNYCH

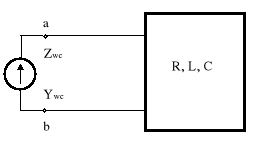
Pulsacje obwodu, dla których część urojona admitancji wejściowej Im{Y_we} lub część urojona impedancji wejściowej Im{Z_we} jest równa zeru, nazywamy pulsacjami drgań nietłumionych (swobodnych) układu R, L, C.

Rys.11.1. Obwód R, L, C

Im {Z_we} = 0, lub Im {Y_we} = 0.

Zjawisko występujące w obwodzie R, L, C, gdy pulsacja zasilania jest równa pulsacji drgań nietłumionych (swobodnych) określonych przez warunki (11.1) i (11.2), nosi nazwę rezonansu, a pulsacja ω pulsacji rezonansowej. Mówimy wówczas o tzw. rezonansie fazowym. Oprócz rezonansu fazowego istnieje również rezonans amplitudowy jako:

• stan ekstremum prądu przy wymuszeniu napięciowym, gdzie częstotliwość rezonansu amplitudowego wyznacza się z warunku
  ,

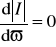
• stan ekstremum napięcia przy wymuszeniu prądowym, gdzie częstotliwość rezonansu amplitudowego wyznacza się z warunku
  

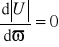
11.1. Obwód szeregowy R, L, C (rezonans napięć)

e (t) = | E_m | sinωt = 
 | E | sinωt.

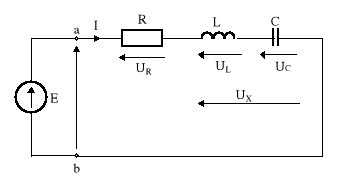
Rys.11.2. Szeregowy obwód R, L, C

, (11.3)

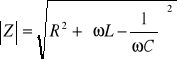
, (11.3a)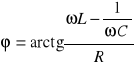

. (11.3b)

(11.4)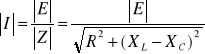
. (11.5)

U_R = RI,     U_L = jX_LI,     U_C = -jX_CI. (11.6)
Zgodnie z definicją rezonans napięć wystąpi dla pulsacji ω, dla której

Im{Z_we} = 0,     czyli     
 = 0    lub    X_L = X_C,  (11.7)
co oznacz równość reaktancji indukcyjnej i reaktancji pojemnościowej.

Warunek ten może być zrealizowany na dwa sposoby:

• dla ω = const. poprzez odpowiedni dobór indukcyjności L w stosunku do pojemności C , tzn.

(11.8) lub odwrotnie, tzn.
(11.9)

• dla ω = variab. oraz L = const. i C = const. poprzez odpowiedni dobór pulsacji ω ( częstotliwości f ) , co wyjaśnia rys.11.3 przedstawiając zależność składników impedancji od pulsacji ω .

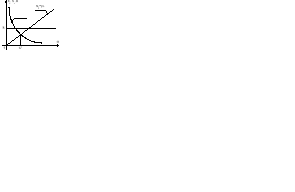
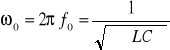
, (11.10)

gdzie: f₀ - częstotliwość rezonansowa równa częstotliwości zasilania, wyrażona w Hz.

Rys.11.3. Charakterystyki częstotliwościowe składników

impedancji obwodu szeregowego R, L, C

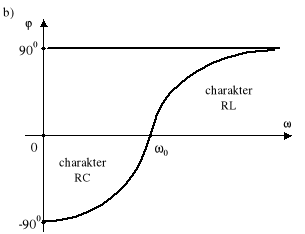
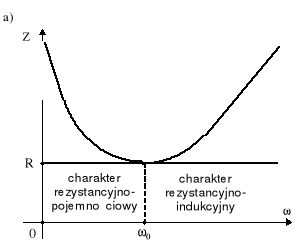
Rys.11.4. Charakterystyki częstotliwościowe obwodu szeregowego R, L, C: a) modułu impedancji; b) argumentu impedancji

I₀ =
,      | I₀ |= | I_max | , (11.11)

(11.12)

U_R0 = R I₀ = E , U_L0 = jX_L0 I₀ = -U_C0 , U_C0 = -jX_C0 I₀ = -U_L0 , U_X0 = U_L0 + U_C0 = 0 .

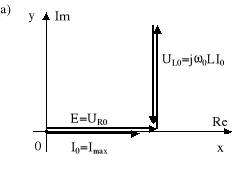
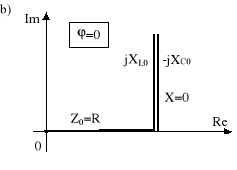
Rys.11.5. Rezonans szeregowy R, L, C ; a) wykres wektorowy prądu i napięć, b) wykres impedancji

11.2. Obwód równoległy R, L, C (rezonans prądów)

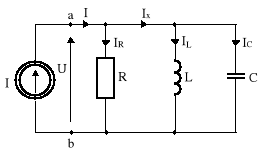
i(t) = | I_m | sinωt,

Rys.11.10. Obwód równoległy R, L, C

,
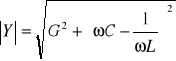
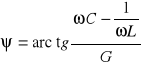
. (11.50b)

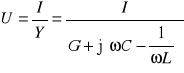
. (11.51)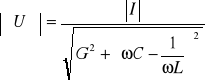
. (11.51a)

(11.52)

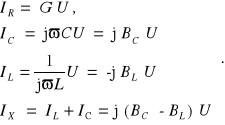
(11.52a)

Gdy Im{Y_we} = 0, to

 = 0. (11.53)    tzn. B_L = B_C , (11.53a)

• dla ω = const. poprzez odpowiedni dobór indukcyjności L w stosunku do pojemności C otrzymując warunek (11.8) lub warunek (11.9)

• dla ω = variab. oraz L = const. i C = const. poprzez odpowiedni dobór pulsacji ω ( częstotliwości f )

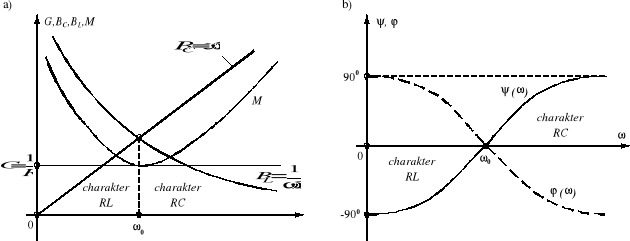
Rys.11.11. Układ równoległy R, L, C a) charakterystyki częstotliwościowe składników admitancji obwodu równoległego R, L, C, b) argument admitancji

|Y| = G.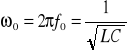
. (11.54)

U₀ = U_max = R I , (11.55)
, (11.56)


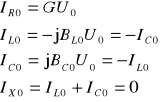
. (11.56a)

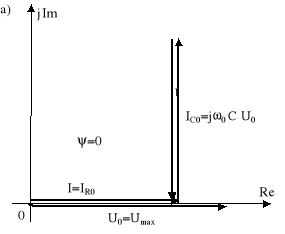
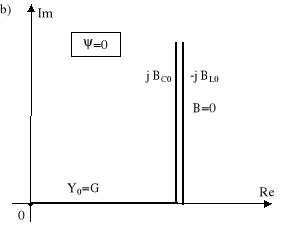
Rys.11.12. Rezonans równoległy R, L, C; a) wykres wektorowy napięcia i prądów b) wykres admitancji

MOCE DLA PRZEBIEGÓW SINUSOIDALNYCH

10.1. Moce dla przebiegów sinusoidalnych i ich zachowawczość

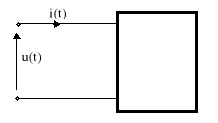
u(t) = 
 |U| sin(ωt + α), (10.1)

i(t) = 
 |I| sin(ωt +β), (10.2)

Rys.10.1. Dwójnik liniowy

• moc chwilową p(t) = u(t) i(t) = |U | |I | cosϕ - |U | |I | cos(2ωt + 2α - ϕ), (10.3)
  

• moc czynną P =
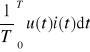
  = |U| |I| cosϕ, (10.4)
  

gdzie: ϕ = α − β ,

• moc bierną Q = |U| |I| sinϕ, (10.5)
  

• moc pozorną |S| = |U| |I| =
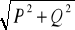
  , (10.6)
  

moc symboliczną S = P + jQ = U I^* (10.7)

gdzie: I^* - wartość skuteczna zespolona sprzężona prądu.

współczynnik mocy źródła
≤ 1 (10.8)

10.2. Znaczenie techniczne współczynnika mocy i jego poprawa

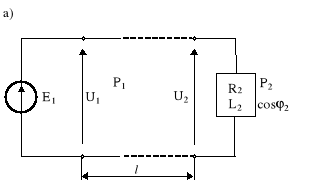
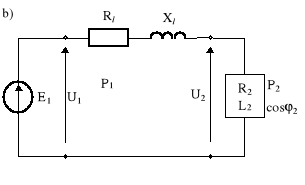
Rys.10.3. Układ: a) źródło - linia transmisyjna - odbiornik; b) schemat zastępczy

R_l = 2R_p = 2
, (10.20) L_l = 
, (10.21)
gdzie: ρ - rezystywność materiału (przewodów), s - przekrój przewodu, l - długość linii,

d - odstęp między przewodami, r- promień przekroju przewodu.

P₂ = |U₂| |I| cosϕ₂, (10.22) a stąd
. (10.23)
Straty mocy czynnej ΔP_l = R_l | I |² =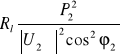
. (10.24)

Straty mocy biernej wzdłuż linii ΔQ_l = X_l | I |² = X_l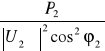
. (10.25)

P₁ = P₂ + ΔP_l = P₂ +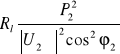 
, (10.26)
Q₁ = Q₂+ΔQ_l = Q₂+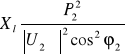 
, (10.27)
|S₁| = |E₁| | I | =
. (10.28)

Nadrzędnym celem kompensacji mocy biernej jest zmniejszenie wartości skutecznej prądu źródła, którego wzrost ponad wartość potrzebną dla zapewnienia mocy czynnej odbiornika P₂ spowodowany jest właśnie przepływem mocy biernej.

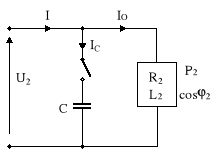
Rys.10.5. Układ: źródło-odbiornik-kompensator

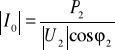
. (10.36)

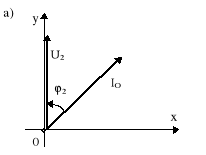
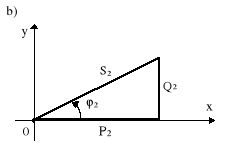
Rys.10.6. Podstawowe wielkości dla układu z rys.10.5: a) wykres wektorowy przy odłączonym kompensatorze; b) trójkąt mocy

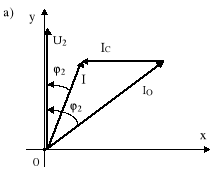
I = I₀ + I_C = I₀ + j ωC U₂ . (10.37)

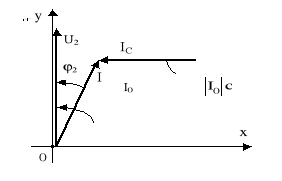
Rys.10.7. Wykres wektorowy dla układu z rys.10.5 przy włączonym kompensatorze (kondensatorze)

Moc czynna odbiornika po włączeniu kondensatora się nie zmieni, gdyż

|I₀| cosϕ₂ = |I| cosϕ₂′, (10.38) P₂ = |U₂| |I_O| cosϕ₂ = |U₂| |I| cosϕ₂ . (10.39)

Zagadnienie poprawy współczynnika mocy możemy rozważać w dwojaki sposób:

1. Dobrać tak pojemność C, aby kąt ϕ₂′= 0, tzn. aby prąd źródła I był w fazie z napięciem U₂ i wówczas mówimy o kompensacji całkowitej (rys.10.8). Dla tak postawionego zagadnienia, po kompensacji zachodzi |S₂′| = P₂ ( rys.10.8b). Z rys.10.8b wynika, że

Q₂ = Q_C = P₂ tgϕ₂ = ωC₀ |U₂|², (10.40)

a stąd

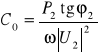
. (10.40a)

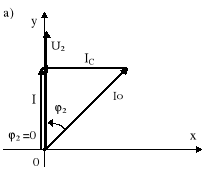
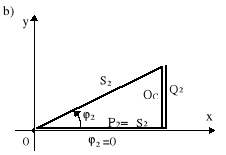
Rys.10.8. Całkowita kompensacja mocy biernej: a) wykres wektorowy; b) trójkąt mocy

2. Dobrać tak pojemność C, aby otrzymać żądany współczynnik mocy cosϕ₂′ > cosϕ₂ (ϕ₂′ < ϕ₂), mówimy wówczas o częściowej kompensacji. Ten rodzaj kompensacji jest praktycznie stosowany, gdyż przy zbliżaniu się pojemności C do pojemności C₀ określonej wzorem (10.40a) wpływ jej na wartość prądu I jest coraz mniejszy i kompensacja całkowita może okazać się nieopłacalna z punktu widzenia ekonomicznego.

Przed doborem kondensatora o pojemności C, tak aby otrzymać żądany współczynnik mocy cosϕ₂ rozważmy wpływ pojemności na zmniejszanie się wartości skutecznej prądu źródła. Wartość skuteczna prądu źródła |I| zmienia się od wartości |I₀| do wartości

| I | = |I₀ + I_C| =
, (10.41)
gdzie:

|I_C| = ωC |U₂| (10.41a)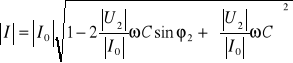
. (10.42)

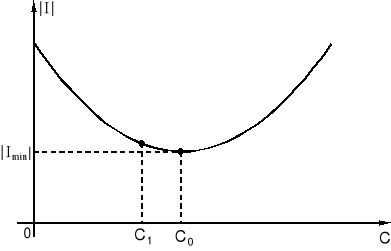
Rys.10.9. Zależność prądu źródła od pojemności kompensującej

Z rys.10.9 wynika, że w otoczeniu pojemności C₀ następuje niewielka zmiana wartości prądu | I |, dlatego też proponuje się niepełną kompensację. Dla tego rodzaju kompensacji wykres wektorowy prądów oraz trójkąt mocy przedstawiono na rys.10.10.

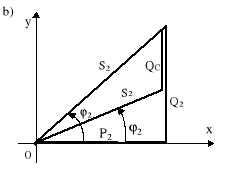
Rys.10.10. Częściowa kompensacja mocy biernej: a) wykres wektorowy; b) trójkąty mocy przed i po kompensacji

Q₂ - Q_C = Q = P₂ tgϕ₂′, (10.43) Q₂ = P₂ tgϕ₂, Q_C = ωC |U₂|²,

stąd szukana pojemność kompensująca wyraża się wzorem

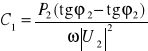
. (10.44)

1

7

---