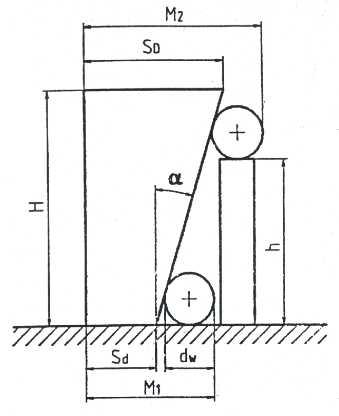
Schemat pomiaru klina długiego o małym pochyleniu za pomocą wałeczków i płytek wzorcowych.

Metoda bezpośrednia - pomiar przy pomocy kątomierza.

Niepewność pomiaru
kąta oblicza się według wzoru:

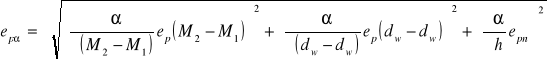
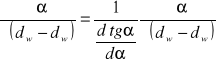
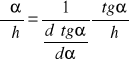
Do wykonania obliczeń można wyliczone pochodne wyrazić jako funkcje mierzonego kąta i długości płytki h.

Schemat pomiaru klina za pomocą wałeczków o różnych średnicach - dużej i małej.

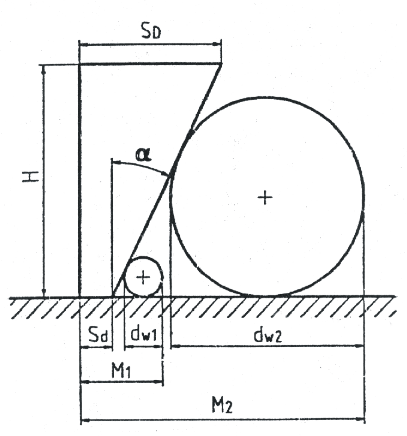
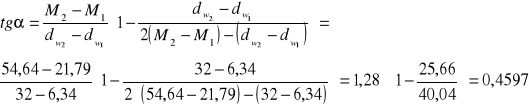
Niepewność pomiarowa kąta

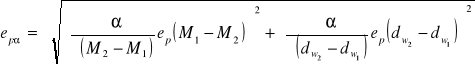
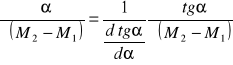
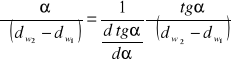
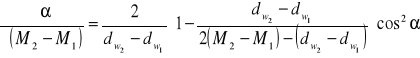
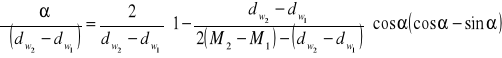
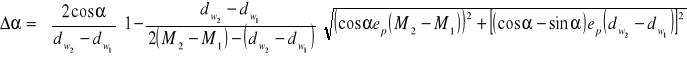
Porównanie wyników pomiarów wykonanych trzema metodami:

Pomiar

Pomiar

Pomiar

Z porównania wyników zauważamy, że metoda I (pomiar bezpośredni kątomierzem) oraz metoda III (pomiar za pomocą wałeczków o różnych średnicach - dużej i małej) są metodami o zbliżonej dokładności. Dają one bowiem dokładność
. Natomiast metoda II (pomiar za pomocą wałeczków i płytek wzorcowych) jest mniej dokładna. Jej dokładność wynosi
. Jest to spowodowane małą statecznością konstrukcji elementów dodatkowych (płytek pomiarowych i wałeczka) użytych do pomiaru wartości
.

Pomiar graniastosłupa kątomierzem optycznym

Szkic podstawy mierzonego graniastosłupa

Suma kątów daje

Zgodnie z teorią graniastosłup ten powinien mieć sumę kątów równą
. Wynika to z podziału podstawy tego graniastosłupa (pięciokąt) na dwie figury: trójkąt (suma kątów wewnętrznych równa
) i czworokąt (suma kątów wewnętrznych równa
).

Zatem błąd pomiarowy wynosi
.

Dzieląc obliczone
na 5 kątów, które mamy w graniastosłupie, otrzymujemy błąd pomiarowy wynoszący
na każdy z kątów.

Uwzględniając dokładność użytego kątomierza, wynoszącą
, otrzymujemy następujące kąty:

4