Wykład 8

Decyzje podmiotów gospodarczych w warunkach niepewności

1. Sytuacja decyzyjna

Załóżmy, że decydent wybiera się na spacer. Wychodząc z domu może podjąć jedną z dwóch decyzji: zabrać ze sobą parasol lub pozostawić parasol w domu. Oznaczmy jego decyzje odpowiednio przez
i
. Załóżmy dalej, że spacerując decydent może natrafić na dobrą pogodę lub na deszcz. O pogodzie decyduje ,,natura”. Oznaczmy stany pogody odpowiednio przez
i
. Jeśli decydent podejmie decyzję
i zrealizuje się stan pogody
(
), decydent poniesie konsekwencje swojego działania w postaci
. Sytuację decyzyjną przedstawiono w poniższej tablicy.

		Stan natury
Decyzja

Niech
(
) będzie funkcją prawdopodobieństwa odzwierciedlającą przekonanie decydenta odnośnie do szansy realizacji stanu natury
(
,
), a
- funkcją odzwierciedlającą zadowolenie decydenta z konsekwencji
(
). Która decyzja jest najlepsza?

2. Funkcja użyteczności oraz reguła oczekiwanej użyteczności

Zauważmy, że użyteczność jest związana bezpośrednio z konsekwencjami
oraz pośrednio - z decyzjami
. Wybór decyzji
-tej oznacza wybór
-tego wiersza tablicy decyzyjnej. Z uwagi na to, że decydent wycenia szansę realizacji stanu
na
, każdy z wierszy tablicy decyzyjnej może być traktowany jako rozkład prawdopodobieństwa decyzji
-tej. W związku z tym rozwiązanie sytuacji decyzyjnej może być analizowane na gruncie wyboru między rozkładami prawdopodobieństwa decyzji. Jak porównywać między sobą rozkłady prawdopodobieństwa?

Oznaczmy przez
decyzję, której niepewne rezultaty
mogą być - według decydenta - uzyskane z prawdopodobieństwami równymi odpowiednio
. Zapiszmy ją jako

.

Funkcją, która ,,wiąże” funkcję odzwierciedlającą zadowolenie decydenta z konsekwencji
,
, z szeregowaniem decyzji
jest ,,reguła oczekiwanej użyteczności” Johna von Neumanna i Oskara Morgrnsterna

.

Użyteczność decyzji
jest wartością oczekiwaną ,,użyteczności elementarnych”, tj. użyteczności jej możliwych konsekwencji
. Zauważmy, że powyższe oznacza, iż
ma taką samą postać dla każdego
.

W celu przybliżenia reguły oczekiwanej użyteczności załóżmy, że decydent może angażować się w niepewne przedsięwzięcie, w wyniku którego uzyska dochód w wysokości
złotych z prawdopodobieństwem
lub dochód w wysokości 0 złotych z prawdopodobieństwem
. Załóżmy także, że przedkłada on większy dochód nad mniejszy. Dajmy mu teraz wybór pomiędzy pewnym dochodem w wysokości
oraz udziałem w tym przedsięwzięciu. Jak zachowa się decydent?

Jeśli
będzie bliskie jedności, decydent zapewne wybierze udział w niepewnym przedsięwzięciu; przy
bliskim zeru - wybierze pewny dochód
. Można zatem przypuszczać, że istnieje takie
(
), przy którym alternatywy staną się jednakowo dobre, czyli

.

Postępując w powyższy sposób dla różnych wielkości dochodu pewnego skonstruujemy całą
. Problem wyboru decydenta zilustrowano na poniższym rysunku.

Rys. 1

Punkt
jest taki, że
.

Uwagi do sposobu konstrukcji
:

• konsekwencje
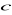
  są liczbami rzeczywistymi reprezentującymi wielkości danego dobra, np. dochodu;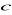
  może być wektorem reprezentującym koszyk dóbr

• postacie funkcji
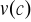
  są takie same dla każdego stanu natury

• sposób konstrukcji
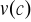
  przesądza, że ma ona charakter kardynalny, natomiast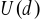
  jest miarą porządkową

Lemat dot. przedsięwzięć złożonych (axiom of complex gambles);

Niech
,
i
będą konsekwencjami decyzji decydenta. Wówczas:

• 
  

• 
  .

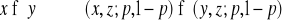
Lemat wyklucza sytuację, w której atrakcyjność
w stosunku do atrakcyjności
zmienia się na skutek pojawienia się
. Bezpośrednim jego rezultatem jest to, że jeśli dwie konsekwencje
i
, takie, że
, są elementami przedsięwzięć złożonych , możemy je sobą wzajemnie zastępować.

Przykład 1:

Załóżmy, że decydent maksymalizuje funkcję użyteczności w postaci
, gdzie (
) opisuje sytuację decyzyjną w dwóch stanach natury. Czy jest on decydentem maksymalizującym wartość oczekiwaną użyteczności w rozumieniu von Neumanna-Morgensterna?

Rozwiązanie.

Tak, z uwagi na to, że
. Stąd
jest funkcją odzwierciedlającą jego zadowolenie z konsekwencji
.

3. Niechęć do ryzyka

Załóżmy, że decydent angażuje się w niepewne przedsięwzięcie, które doprowadza go do ruiny (
) z prawdopodobieństwem
lub bogactwa (
) z prawdopodobieństwem
. Niech funkcją odzwierciedlającą obie konsekwencje jest
, gdzie
- majątek decydenta, taką że decydent przedkłada większy majątek nad mniejszy (
) oraz kolejne równe przyrosty majątku sprawiają mu coraz mniejszą satysfakcję (
). Sytuację taką przedstawiono na rys. 2.

Z rysunku tego wynika, że
jest maksymalną częścią pewnego bogactwa, którą decydent skłonny jest poświęcić po to, żeby uniknąć ryzyka, tzn. z prawdopodobieństwem równym jedności osiągać satysfakcję równą wartości oczekiwanej satysfakcji z sytuacji niepewności. Wielkość tą nazywa się premią za podjęcie ryzyka.

Rys. 2

Warto zauważyć, że możemy wyróżnić 3 rodzaje decydentów:

• 
  

• 
  

• 
  .

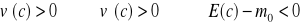
Pierwszy, niechętny ryzyku (risk averse), jest gotowy zapłacić za jego uniknięcie, stąd w jego przypadku premia za podjęcie ryzyka jest dodatnia. Drugi decydent jest neutralny wobec ryzyka (risk neutral). W jego przypadku premia za podjęcie ryzyka jest zerowa. Z kolei trzeci decydent lubi ryzyko (risk lover) i jest gotowy zapłacić za wzięcie udziału w ryzykownym przedsięwzięciu. W jego przypadku premia za podjęcie ryzyka jest ujemna.

Przykład 2:

Która z poniższych funkcji odzwierciedlających konsekwencje:

,
,
,
,

jest właściwa dla decydenta lubiącego ryzyko, neutralnego wobec ryzyka oraz niechętnego ryzyku?

4. Optimum ryzyka dla indywidualnego decydenta

Niech teraz
i
reprezentują konsekwencje podjęcia decyzji przez niechętnego ryzyku decydenta w dwóch, wzajemnie wykluczających się stanach natury, których prawdopodobieństwo wystąpienia jest równe odpowiednio
i
(
). Mogą nimi być np. wielkości konsumpcji pewnego dobra. Funkcją użyteczności decydenta jest więc

,

gdzie
i
. Niech jego ograniczenie budżetowe jest takie, że

,

gdzie
i
są zasobami konsumowanego dobra w każdym ze stanów natury, a
i
- odpowiednio cenami jednostkowymi. Załóż, że decydent podejmuje decyzje wynikające z zasady maksymalizacji oczekiwanej użyteczności konsumpcji i wyznacz optymalne jej wielkości w każdym ze stanów.

Funkcją Lagrange'a dla tego problemu jest

,

Rozwiązaniem powyższego problemu jest taka trójka (
), dla której spełniony jest układ warunków:

,

,

.

Z układu tego wynika, że decydent wybierze taki układ konsumpcji (
), dla którego

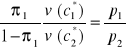
oraz

.

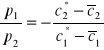
Powyższy wynik jest treścią fundamentalnego twierdzenia o ponoszeniu ryzyka. Głosi ono, że decydent wybierze taki poziom konsumpcji pewnego dobra w dwóch wzajemnie wykluczających się stanach natury (
), dla których iloraz krańcowych użyteczności konsumpcji w tych stanach, zważony prawdopodobieństwami ich realizacji, będzie równy ilorazowi cen rozważanego dobra w tych stanach (
). Twierdzenie zilustrowano na rys. 3

Rys. 3

Paweł Miłobędzki: Wykłady z ekonomii matematycznej

6

Paweł Miłobędzki: Wykłady z ekonomii matematycznej

---