STATYSTYCZNE 

STEROWANIE

 PROCESEM 

PRODUKCYJNYM

On już wie jak to działa 



Statystyczne Sterowanie 

Procesem Produkcyjnym

= 

Statystyczna Kontrola Procesu

 

=

S

tatistical

 P

rocess

 C

ontrol

 

SPC

PO CO STATYSTYKA W 

PRODUKCJI?

Działalność przedsiębiorstwa (DP) można zapisać 
wzorem:

   DP = PROCES 1 + PROCES 2 + ... + 
PROCES n

DP jest więc 

zbiorem różnych procesów. 

Jedne z nich są ważne (proces projektowania 
wyrobu, produkcja), inne mało istotne (np. wywóz 
śmieci z terenu zakładu).

PO CO STATYSTYKA W 

PRODUKCJI?

Cel przedsiębiorstwa

: sukces poprzez 

doskonalenie jakości i obniżanie kosztów

Jak osiągnąć ten cel?:

  Poprzez panowanie nad 

procesami – realizowanie ich w sposób jak 
najbardziej dla siebie korzystny

Jak panować nad procesami?:

 

SPC

IDEA SPC

Każdy proces produkcyjny ma w swojej 
naturze zmienność. Ta zmienność wynika z 
wielu czynników na które często mamy 
ograniczony wpływ. 

SPC pozwala na:

1.monitorowanie czy proces jest statystycznie 

sterowalny (przewidywalny w swoim 
zachowaniu)  

2. odróżnienie zaburzeń jakie się w nim 

pojawiają (przyczyn specjalnych) od 
naturalnej zmienności procesu (przyczyn 
normalnych)

 

NAJCZĘŚCIEJ STOSOWANE 

TECHNIKI SPC

 Histogram
 Karty kontrolne
 Wskaźniki zdolności procesu
 Wskaźniki zdolności maszyn

HISTORIA SPC

Podstawy SPC

 (karty kontrolne) zostały 

opracowane przez Waltera A. Shewharta w 
latach 

20tych XX wieku

. 

SPC było stosowane w 

USA 

podczas 

II wojny 

światowej

 do poprawy procesów 

produkcyjnych (dla wojska). Po wojnie 
przemysł amerykański nie musiał się 
przejmować jakością produkowanych 
wyrobów, gdyż zniszczona działaniami 
wojennymi Europa kupowała wszystko co było 
w USA produkowane. To spowodowało 
znaczący spadek zainteresowania technikami 
statystycznymi na wiele lat. 

HISTORIA SPC

SPC zostało 

"ponownie odkryte"

 w 

USA

 

końcem XX wieku

 i w ostatnich latach jest 

popularyzowane jako jedno z narzędzi Six 
Sigma. Jednocześnie rozwój oprogramowania 
do analizy statystycznej, arkuszy 
kalkulacyjnych i systemów zbierania danych 
znacznie ułatwia stosowanie SPC 

PODSTAWY

 DANE I ICH PREZENTACJA
 ROZKŁADY ZMIENNYCH

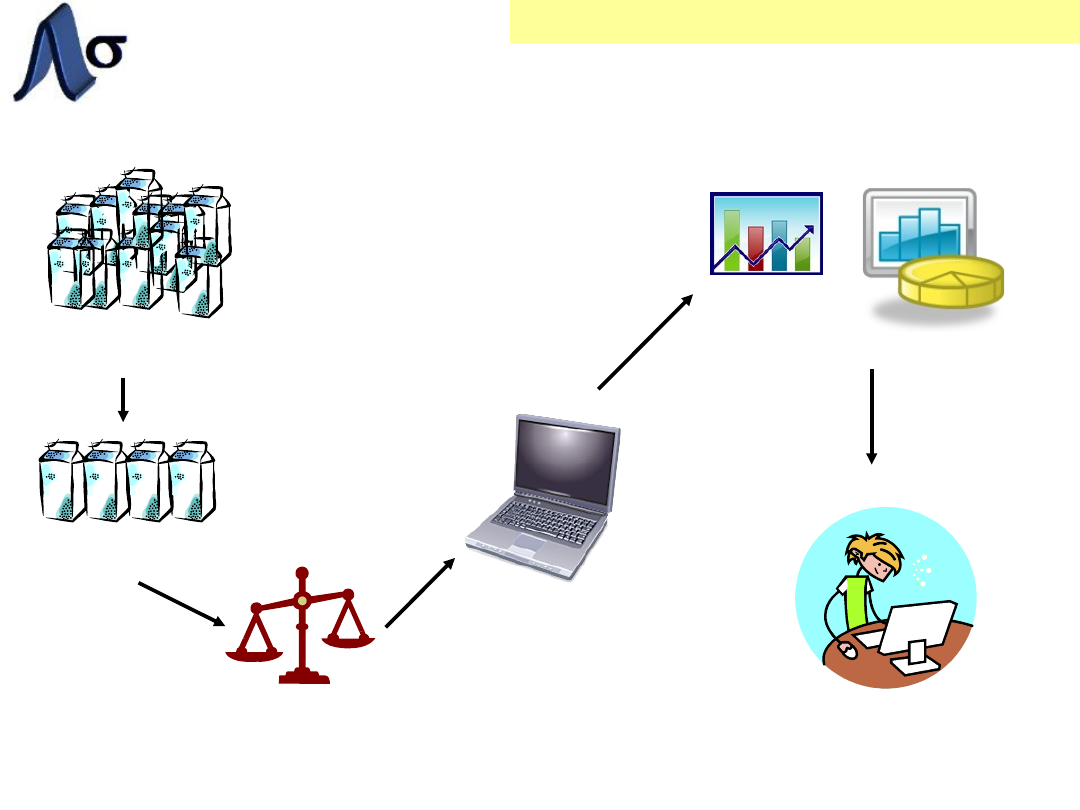
ETAPY ANALIZY 

STATYSTYCZNEJ

PODSTAWY – DANE I ICH PREZENTACJA

POPULACJA

PRÓBKA

POMIARY

OBLICZENIA

WYNIKI

ANALIZA

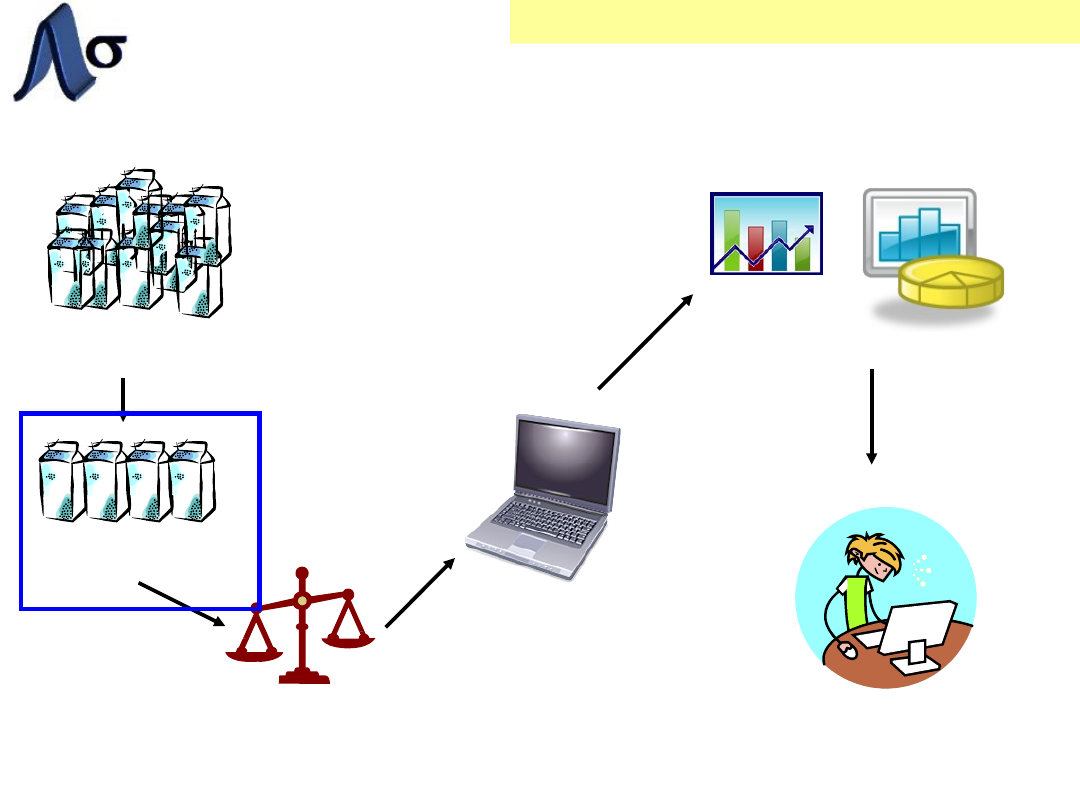
ETAPY ANALIZY 

STATYSTYCZNEJ

PODSTAWY – DANE I ICH PREZENTACJA

POPULACJA

PRÓBKA

POMIARY

OBLICZENIA

WYNIKI

ANALIZA

PRÓBKA

PODSTAWY – DANE I ICH PREZENTACJA

WYBÓR PRÓBKI

:

Próbka wybrana do badania musi być 
odpowiednia
Wybór próbki jest kluczowy etapem z punktu 
widzenia wiarygodności końcowych wyników

CECHY DOBRZE DOBRANEJ PRÓBKI

:

losowa
reprezentatywna

LOSOWOŚĆ PRÓBKI

PODSTAWY – DANE I ICH PREZENTACJA

Próbka losowa: 

pobrana całkowicie 

przypadkowo z pewnej większej liczby 
wyrobów (populacji)

Procedury pomagające zapewnić losowość 
próbki

:

 wykorzystanie tablicy liczb losowych
 losowanie „na ślepo”
 pobieranie systematyczne
 pobieranie wielostopniowe
 pobieranie warstwowe

LOSOWOŚĆ PRÓBKI

PODSTAWY – DANE I ICH PREZENTACJA

Procedury pomagające zapewnić losowość 
próbki:
 

wykorzystanie tablicy liczb losowych

Tablica liczb losowych to zestaw liczb 
wygenerowanych całkowicie losowo i którymi 
posłużyć się można przy wybieraniu 
elementów do badania. 

Podstawowy warunek: ponumerowanie 
wszystkich kontrolowanych jednostek 
produktu.

LOSOWOŚĆ PRÓBKI

PODSTAWY – DANE I ICH PREZENTACJA

Procedury pomagające zapewnić losowość 
próbki:
 

losowanie „na ślepo”

Polega na – z założenia przypadkowym – 
pobieraniu wyrobów do próbki przez 
kontrolera.

Podstawowe warunki: wszystkie elementy z 
badanej partii wyrobów muszą być w takim 
samym stopniu dostępne dla kontrolera; musi 
on pobierać wyroby z różnych miejsc itd.

LOSOWOŚĆ PRÓBKI

PODSTAWY – DANE I ICH PREZENTACJA

Procedury pomagające zapewnić losowość 
próbki:

pobieranie systematyczne

Stosuje się, gdy wyroby są dostarczane w 
sposób ciągły. 

Do kontroli pobiera się wyroby wyprodukowane 
w określonych odstępach czasu lub co 
określoną liczbę wyprodukowanych jednostek.

LOSOWOŚĆ PRÓBKI

PODSTAWY – DANE I ICH PREZENTACJA

Procedury pomagające zapewnić losowość 
próbki:
 

pobieranie wielostopniowe

 pobieranie warstwowe

Stosowane w przypadku dostarczania wyrobów 
do kontroli w postaci partii (również tych 
złożonych z podpartii)

LOSOWOŚĆ PRÓBKI

PODSTAWY – DANE I ICH PREZENTACJA

Szczegółowe zasady losowego pobierania 
przedmiotów do próbek opisane są w 
normie:

PN 83/N-03010 Statystyczna kontrola 
jakości. Losowy wybór jednostek 
produktu do próbki.

REPREZENTATYWNOŚĆ 

PRÓBKI

PODSTAWY – DANE I ICH PREZENTACJA

Próbka reprezentatywna: 

w dobry sposób 

odzwierciedla populację, z której została 
pobrana

Dla zapewnienia reprezentatywności konieczna 
jest odpowiednia liczebność próbki. Im większa 
próbka, tym bardziej wiarygodne wyniki.

Uwaga!

 Liczności nie można zwiększać w 

nieskończoność (koszty kontroli). Należy 
szukać optimum pomiędzy kosztami a 
wiarygodnością wyników.

RODZAJE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Dana:

 każda informacja opisująca proces, 

wyrób, usługę, maszynę itd. 

Typy danych:

 dane kategorialne (uzyskiwane przy ocenie 
metodą alternatywną)
 dane liczbowe (pochodzące z pomiarów)

RODZAJE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Typy danych: 

dane kategorialne

 

Uzyskuje się je w przypadkach:
 dzielenia (klasyfikowania) przedmiotów na 
kategorie
 zliczania liczby przedmiotów w danych 
kategoriach
 zliczania proporcji przedmiotów
 zliczania liczby braków lub niezgodności

RODZAJE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Typy danych: 

dane kategorialne

 

Są one często wykorzystywane w praktyce, bo 
do ich zebrania zazwyczaj nie potrzeba 
skomplikowanych i dokładnych urządzeń 
pomiarowych.

Przykład: zliczanie liczny rys na lakierze 
samochodu; liczba żarówek z danej partii która 
nie świeci

RODZAJE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Typy danych: 

dane kategorialne

 

Zwykle wyroby dzieli się na 2 kategorie: dobre 
i złe.

Można je jednak dzielić na więcej kategorii, 
które odzwierciedlać będą jakość.

Przykład: klasy I, II, III, IV. Klasa I- najwyższej 
jakości, klasa IV- najgorszej.

RODZAJE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Typy danych: 

dane kategorialne

 

Zalety:
 prostota prowadzonej kontroli
 czytelność otrzymanych wyników

Wady:
 nieprecyzyjność

RODZAJE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Typy danych: 

dane liczbowe

 

Uzyskuje się je w przypadkach:
 pomiarów cechy produktu, usługi, procesu
 przeliczania numerycznych wartości z dwóch 
lub więcej pomiarów liczbowych

Wymóg: korzystanie z urządzeń pomiarowych

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Najprostszy sposób: spisywanie w rzędzie np.:

5,6,9,11,6,7,7,6,5,9,7,8,7,6,7,8,4,8,7,8,10,10,9,
7,8,...

Ten zapis jest nieczytelny i mało użyteczny

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Użyteczne metody prezentacji 
danych:
 tabela częstości wystąpień 
(liczności)
 histogram
 wykres punktowy

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Tabela częstości wystąpień

Wartość danej

Wystąpienie 

danej

Liczba wystąpień

3

0

4

2

5

3

6

5

7

1

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Tabela częstości wystąpień

Z tabeli takiej można łatwo odczytać:
 ile pomiarów o danej wartości 
zarejestrowano
 która wartość powtarzała się najczęściej
 w jakim zakresie pojawiają się dane 
(minimum i maksimum)

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Histogram

Jest pewnym rozwinięciem tabeli liczności.
Szczególnie przydatny do prezentowania 
dużej ilości danych liczbowych i 
kategorialnych.

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Histogram

31,820 33,100 33,780 34,650 34,870 35,530 36,750
32,010 33,120 33,790 34,690 34,880 35,620 36,680
32,010 33,260 33,790 34,690 34,900 35,780 36,780
32,050 33,260 33,790 34,720 34,920 35,790 36,850
32,230 33,280 33,820 34,720 34,960 35,860 38,520
32,600 33,300 33,820 34,810 35,090 36,120
32,950 33,360 33,860 34,810 35,120 36,250
33,030 33,540 33,950 34,810 35,160 36,560
33,050 33,560 34,210 34,860 35,280 36,560
33,060 33,750 34,220 34,870 35,290 36,590

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Histogram

Procedura rysowania histogramu:

1.Posortowanie danych w porządku od 

najmniejszej do największej

2. Wyznaczenie wartości najmniejszej i 

największej: 

x

min

, x

max

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Histogram

Procedura rysowania histogramu:

3. Obliczenie szerokości zakresu, w jakim 

pojawiają się dane (rozstępu):                 

R=x

max

-x

min

4. Wyznaczenie liczby przedziałów:               

 

ilość przedziałów= pierwiastek(ilość 

pomiarów)

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Histogram

Procedura rysowania histogramu:

5. Ustalenie szerokości przedziałów:               

  

szerokość przedziału=rozstęp/l-ba 

przedziałów

Otrzymaną wartość zaokrąglamy w taki 

sposób, aby narysowany histogram był jak 
najbardziej czytelny

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Histogram

Procedura rysowania histogramu:

6. Rozpisanie przedziałów i obliczenie, ile w 

każdym z nich znajduje się wyników:

Przedział wartości

Ilość wyników w 

przedziale

(31,32]

1

(32,33]

6

(33,34]

21

(34,35]

17

(35,36]

10

(36,37]

9

(37,38]

0

(38,39]

1

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

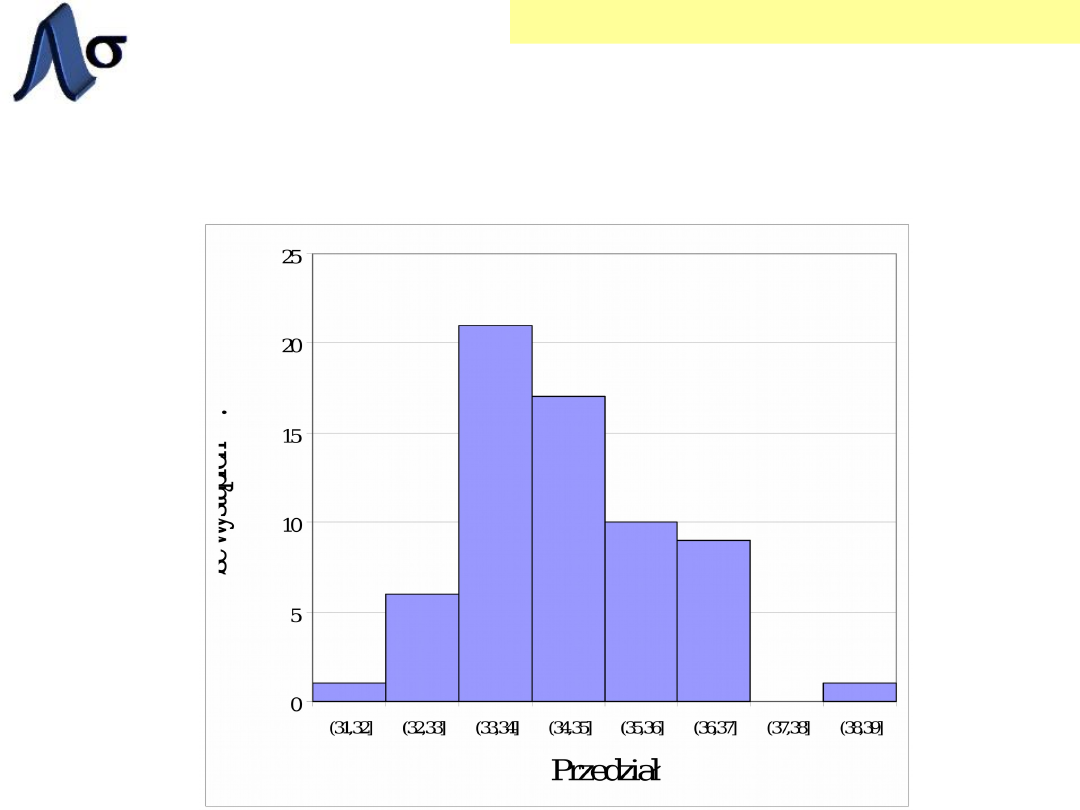
Histogram

Procedura rysowania histogramu:

6. Narysowanie wykresu: 

w zależności od 

liczby wyników w poszczególnych 
przedziałach, rysuje się odpowiednią 
wysokość słupka

.

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Histogram

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Wykres punktowy

Tabela Dane z pomiarów uziarnienia 
mielonego materiału.

Pomiary 

w 

próbce

Obroty młyna [obr/min]

1415

1430

1445

1460

1480

1

32,76

33,37

36,54

36,20

36,74

2

32,72

33,11

35,11

36,58

36,40

3

32,70

33,15

36,02

35,24

36,43

4

32,69

33,25

35,59

36,14

36,72

5

32,67

33,20

36,03

35,52

36,55

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

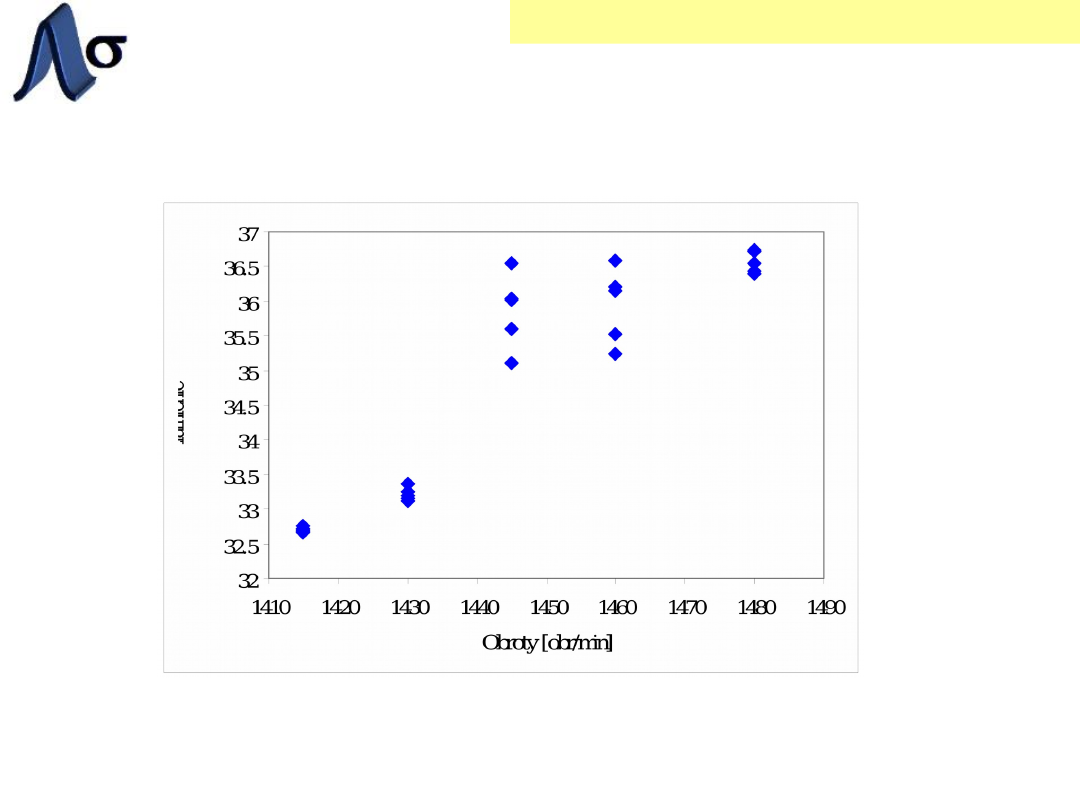
Wykres punktowy

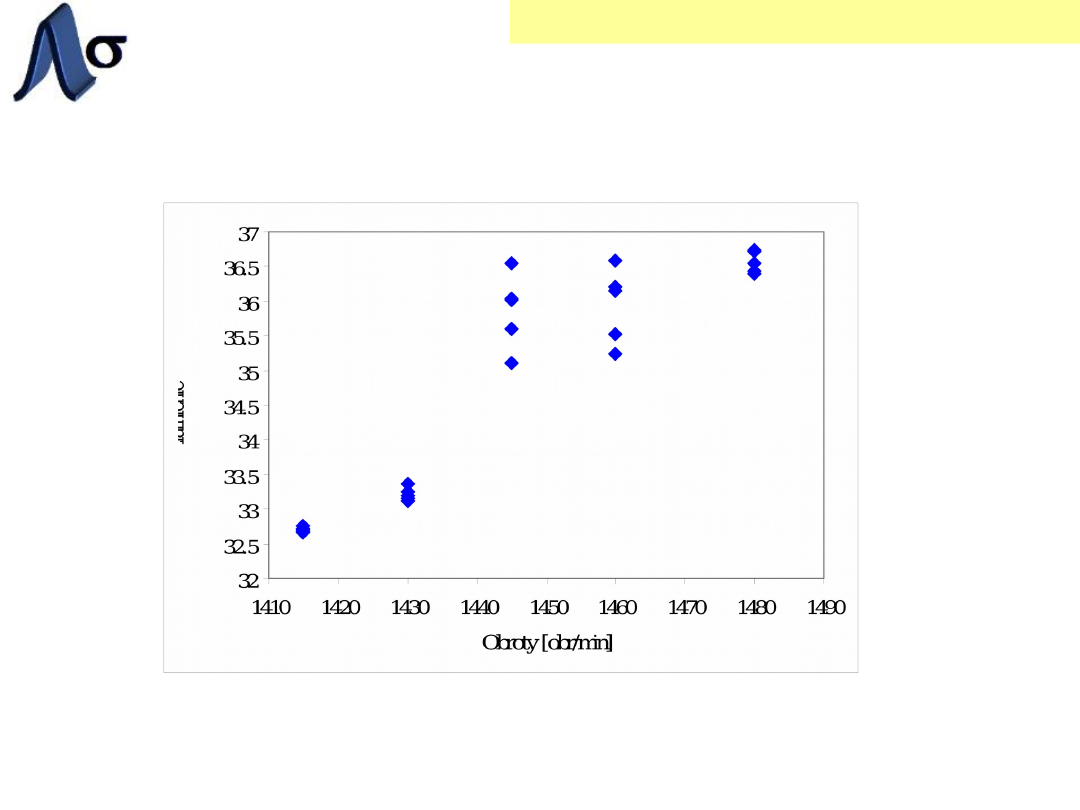
Rys. Wykres punktowy zależności pomiędzy 

uziarnieniem a obrotami młyna.

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

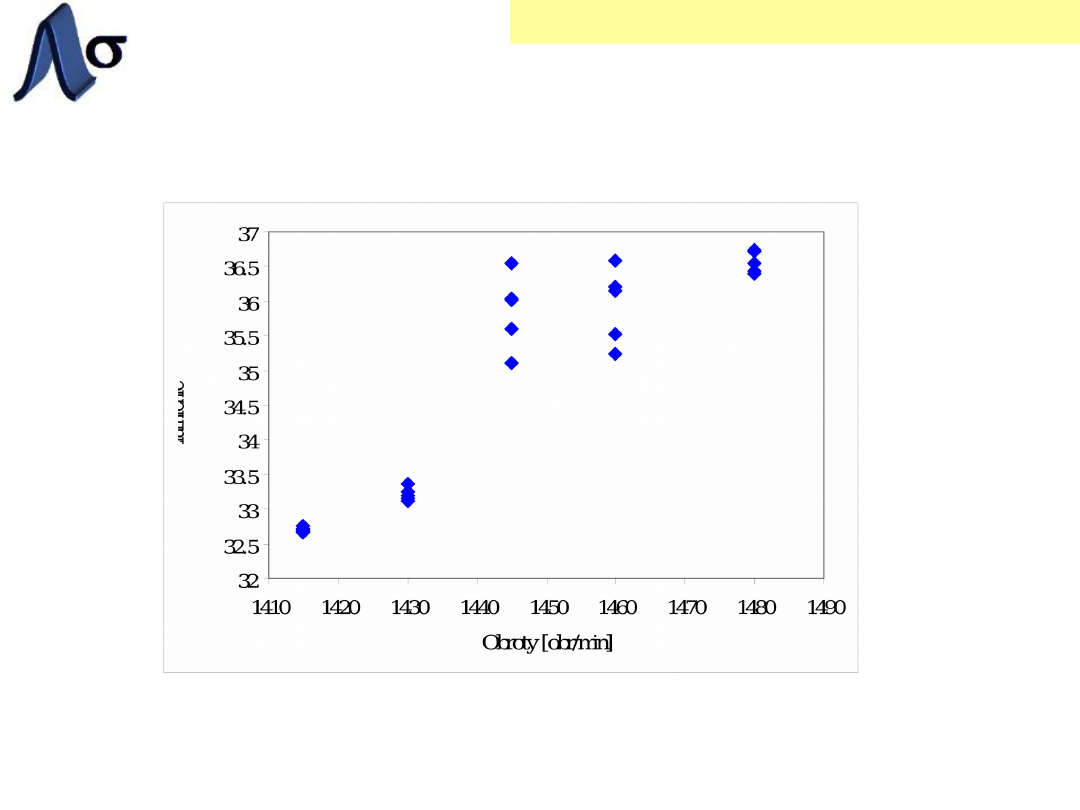
Wykres punktowy

 im większe obroty tym drobniej zmielony 
materiał

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

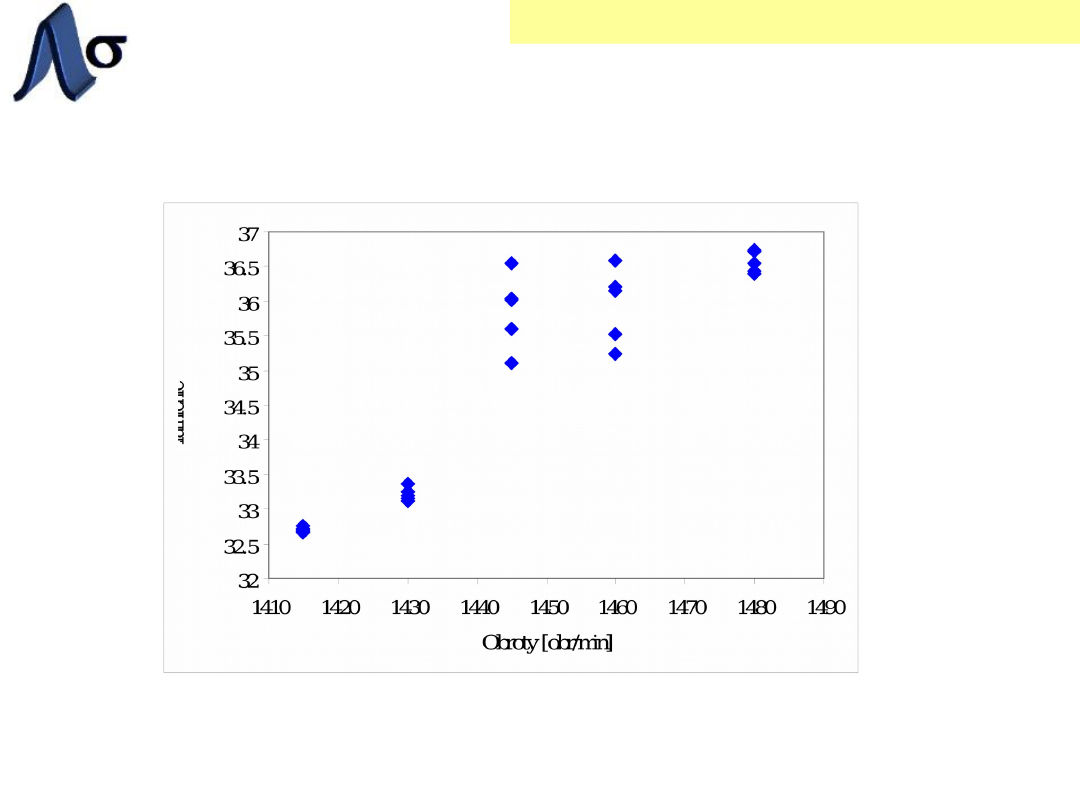
Wykres punktowy

 przy obrotach 1445 i 1460 próbki 
charakteryzują się dużą zmiennością 
(rozrzutem)

PREZENTOWANIE DANYCH

PODSTAWY – DANE I ICH PREZENTACJA

Wykres punktowy

 próbka jest najbardziej jednorodna przy 
obrotach 1415

ROZKŁADY ZMIENNYCH

PODSTAWY – ROZKŁADY ZMIENNYCH

Dane zbierane podczas pomiarów zawsze 
układają się w pewien określony sposób.  To w 
jaki, zależy przede wszystkim od zjawiska, 
które jest obserwowane i od tego jak 
zachowuje się proces, jakimi cechami się on 
charakteryzuje.

Sposób, w jaki układają się dane- 

rozkład 

zmiennej losowej.

Statystycy wyróżniają wiele takich rozkładów 
ale z punktu widzenia SPC ważne jest tylko 
kilka z nich.

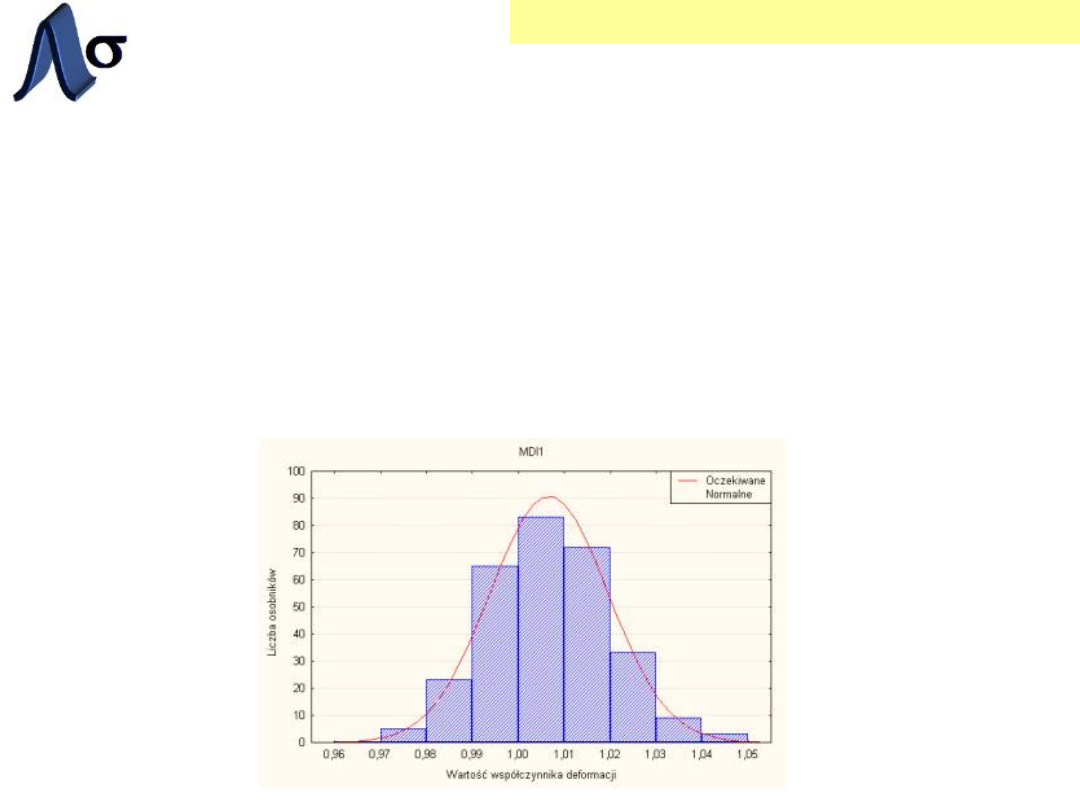
ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

 Najczęściej spotykany w praktyce SPC
 Jest 

symetryczny względem wartości 

średniej

 Jest 

jednomodalny

 (ma jedną określoną 

wartość występującą najczęściej)

ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

Funkcja gęstości prawdopodobieństwa

 

(funkcja opisująca prawdopodobieństwo 
przyjęcia przez zmienną X wybranych 
wartości):

dla -∞ < x< 

∞

2

2

2

)

(

2

1

)

(







m

x

e

x

f







Dystrybuanta:













x

m

x

dx

e

x

F

2

2

2

)

(

2

1

)

(







m- wartość 
oczekiwana (średnia 
arytmetyczna)

σ- odchylenie 
standardowe

ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

m- wartość oczekiwana

 -> opisuje miejsce, w 

jakim znajduje się rozkład zmiennej na 
przyjętej skali 

(miara położenia)

σ- odchylenie standardowe

 ->opisuje rozrzut 

rozkładu 

(miara zmienności)

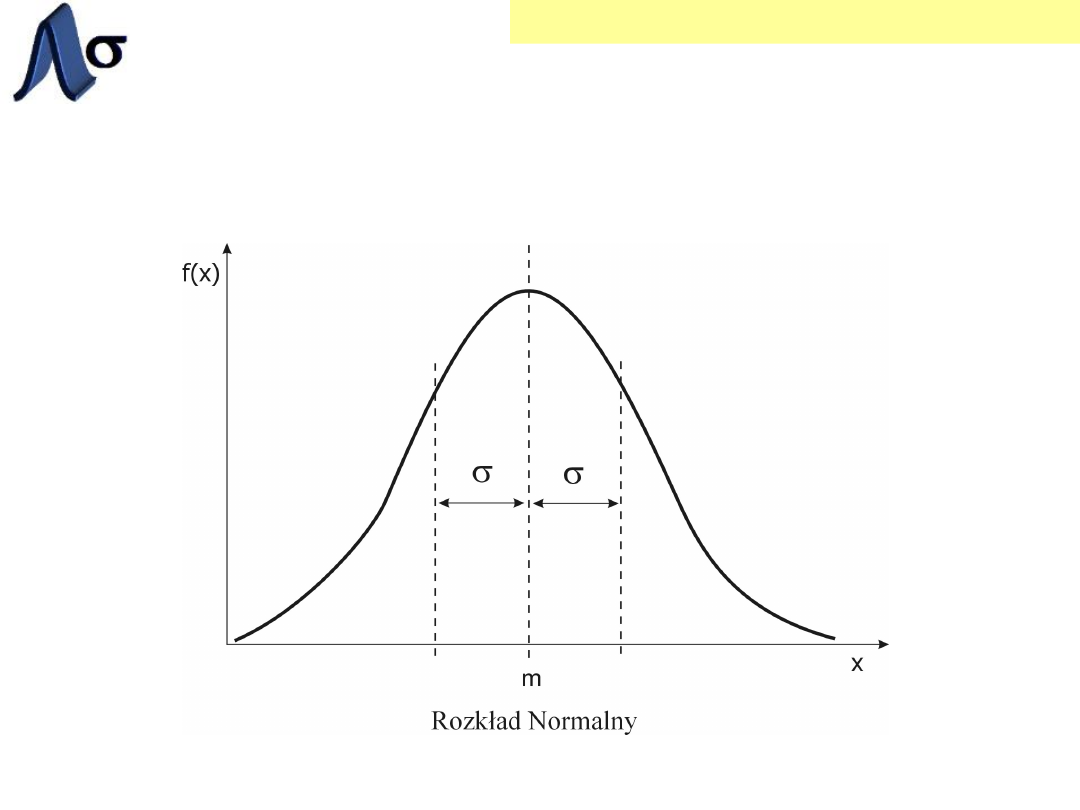
ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

Miary położenia:

 średnia arytmetyczna
 rzadko wykorzystywane: średnia 
geometryczna, średnia harmoniczna, średnia 
ważona
 mediana: wartość środkowa w ciągu danych
 moda (dominanta): wartość występująca 
najczęściej w zbiorze danych















n

i

i

n

śr

x

n

n

x

x

x

x

1

2

1

1

...

ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

Miary zmienności 

(pokazują rozproszenie 

wyników)
 wariancja
 odchylenie standardowe 

UWAGA! Powyższe wzory obowiązują, pod 
warunkiem, że mamy możliwość zbadania 
całej populacji, co jest PRAWIE NIGDY 
SPEŁNIONE









n

i

śr

i

x

x

n

1

2

2

)

(

1



2







ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

Miary zmienności 

(pokazują rozproszenie 

wyników)

Ponieważ opisujemy rozkład opierając się 
jedynie na pewnej próbce wyników, pobranej z 
populacji, stosuje się estymator:











n

i

śr

i

x

x

n

s

1

2

)

(

1

1

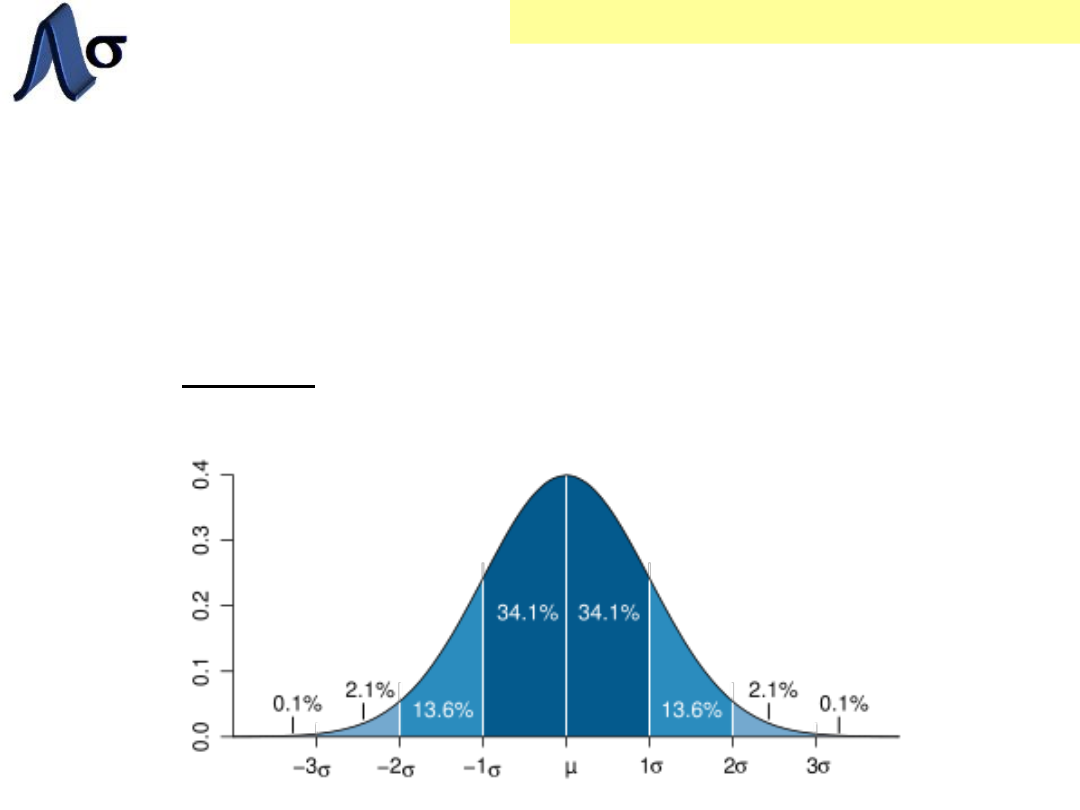
ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

Zasada 3σ

Ponad 68% wszystkich wyników zawiera się w 
przedziale x

śr

 +/- σ

Ponad 99,7% wszystkich wyników mieści się w 
przedziale 

x

śr

 +/- 3σ 

(ten przedział jest 

stosowany SPC)

ROZKŁAD NORMALNY

PODSTAWY – ROZKŁADY ZMIENNYCH

Badanie normalności rozkładu

Ponieważ wiele metod stosowanych w SPC 
opiera się na założeniu, ze zebrane dane mają 
rozkład normalny, należy zawsze sprawdzać, 
czy to założenie jest spełnione.

Testy statystyczne:
 test chi-kwadrat
 test Kołmogorowa-Smirnowa