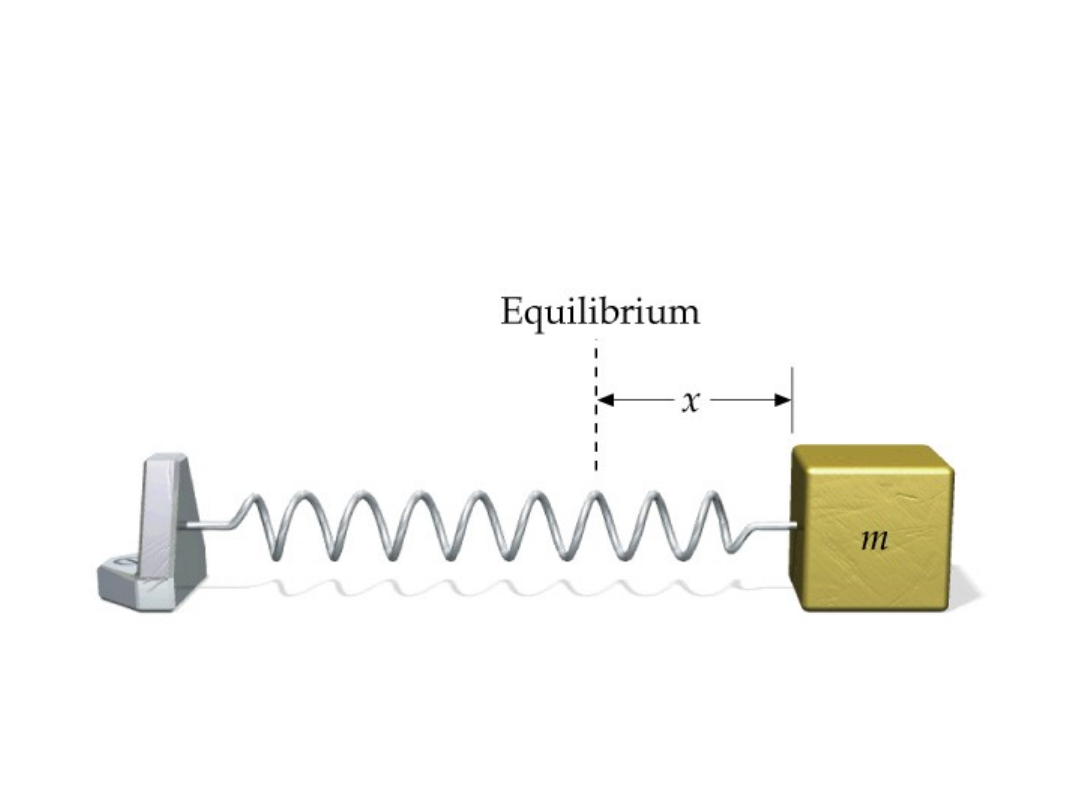
RUCH HARMONICZNY

x

k

F

x







s

d

F

W

y

z

z













Podstawą jest zawsze opis działających sił

Ruch harmoniczny

)

(

)

(

t

x

k

t

F







)

sin(

)

(









t

A

t

x

2

m

k



2



pulsacja (kołowa
częstość drgań
własnych)

Równanie ruchu

)

(t

x

x

dt

t

dx

t

v







)

(

)

(

x

dt

t

x

d

dt

t

dv

t

a









2

2

)

(

)

(

)

(

położeni
e
prędkość

przyspiesze
nie

W kinematyce punktu materialnego
mamy:

3

Mając położenie ciężarka w każdej chwili czasu x(t) możemy podać
prędkość i przyspieszenie
w każdej chwili czasu

Poniżej znajdziecie podsumowanie podstawowych równań i parametrów dla
oscylatora harmonicznego

Równanie ruchu

m

)

(t

F

masa

siła

W dynamice punktu materialnego:





i

i

F

x

m



Czyli równanie ruchu (II zasada dynamiki Newtona) będzie miało
postać:

przyspieszenie

2

2

)

(

dt

t

x

d

suma wszystkich sił
działających na
ciało

4

Ruch harmoniczny

Równanie ruchu harmonicznego – rozwiązanie:

x

k

x

m







0





x

m

k

x



2





m

k

y

podstawiam

0

2





x

x





)

sin(

)

(









t

A

t

x

amplituda

drgań

maksymalne

wychylenie

początkow
a faza
drgań

częstość (pulsacja)

drgań własnych

faza drgań

5

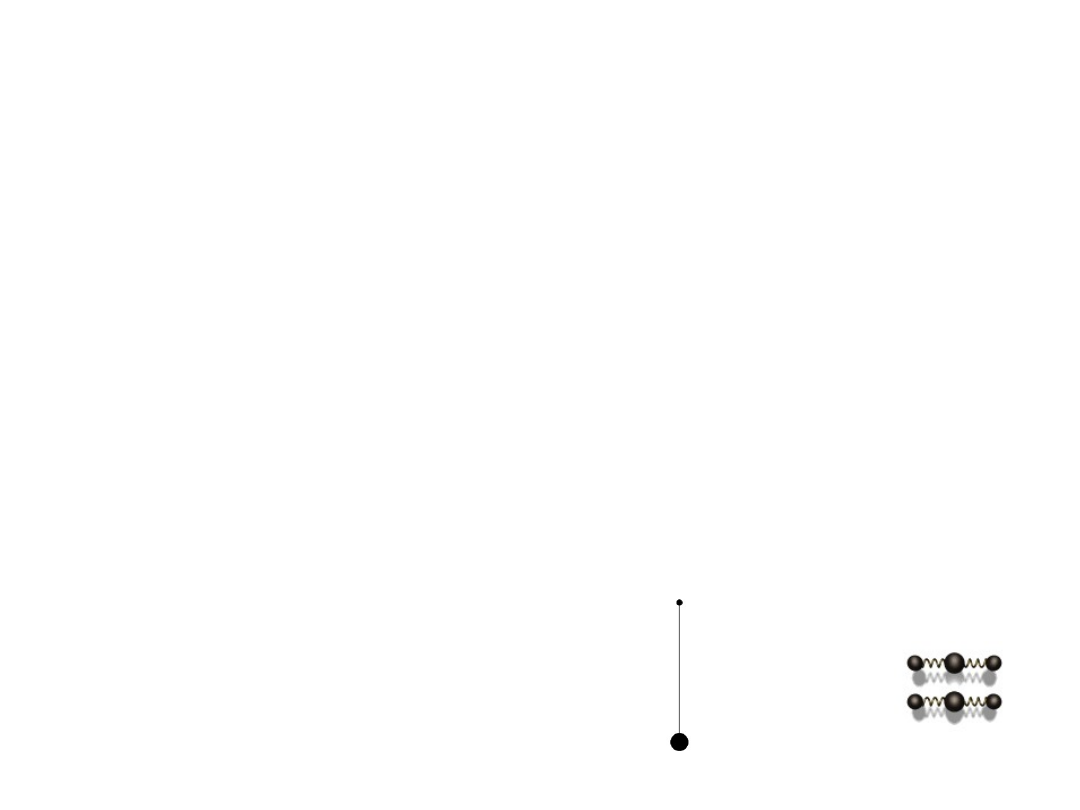
Ruch harmoniczny

Przykłady ruchu harmonicznego:
• ciało na sprężynie (niewielkie

wychylenia)

• wahadło matematyczne (niewielkie

wychylenia)

• wahadło fizyczne (niewielkie wychylenia)
• obciążona próbówka pływająca w wodzie
• ciecz w U-rurce

6

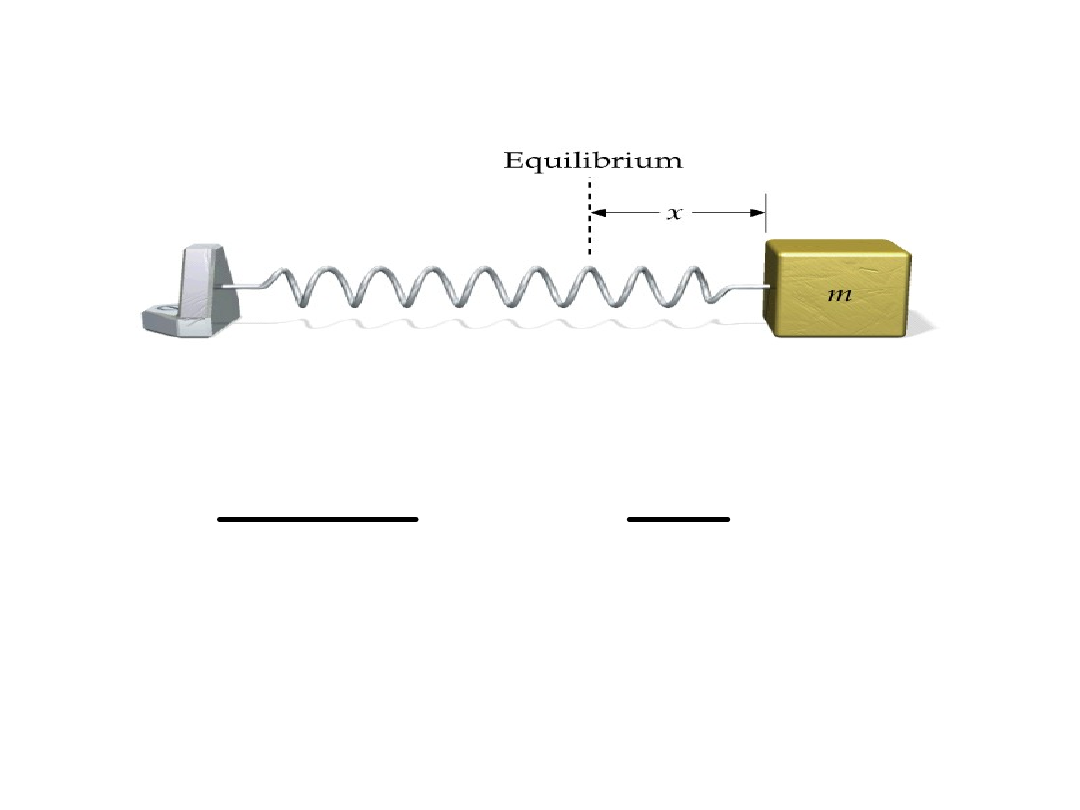
Równanie siły

x

k

dt

x

d

m

x

m

k

a

x

k

a

m

x

x

























2

2

x

k

F

x







powtórzmy jeszcze tok rozumowania w przypadku ciężarka na sprężynie

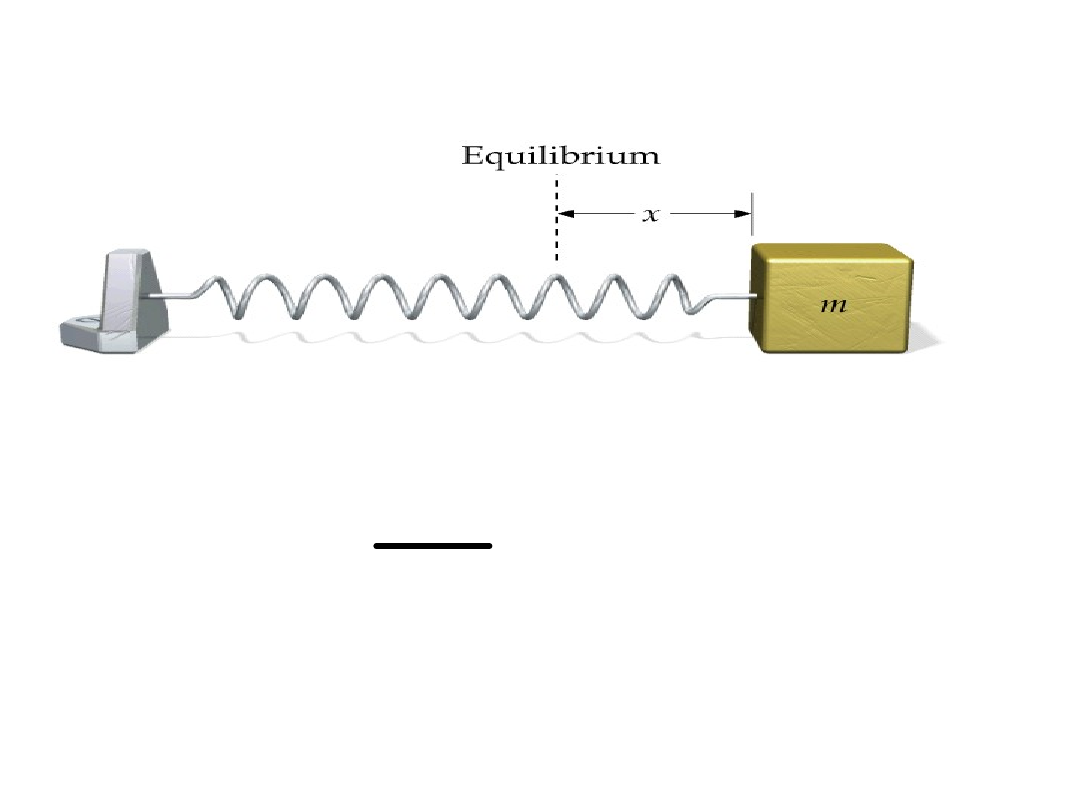
Jest to r.r. drugiego

rzędu

x

m

k

dt

x

d







2

2

Rozwiazaniem r.r. jest funkcja x(t)

x

m

k

x 





Inny zapis tego równania

Rozwiazaniem r.r. jest

funkcja x(t)













t

A

x

cos

























2

sin

cos











t

t

Funkcje sinus i cosinus stosujemy często zamiennie

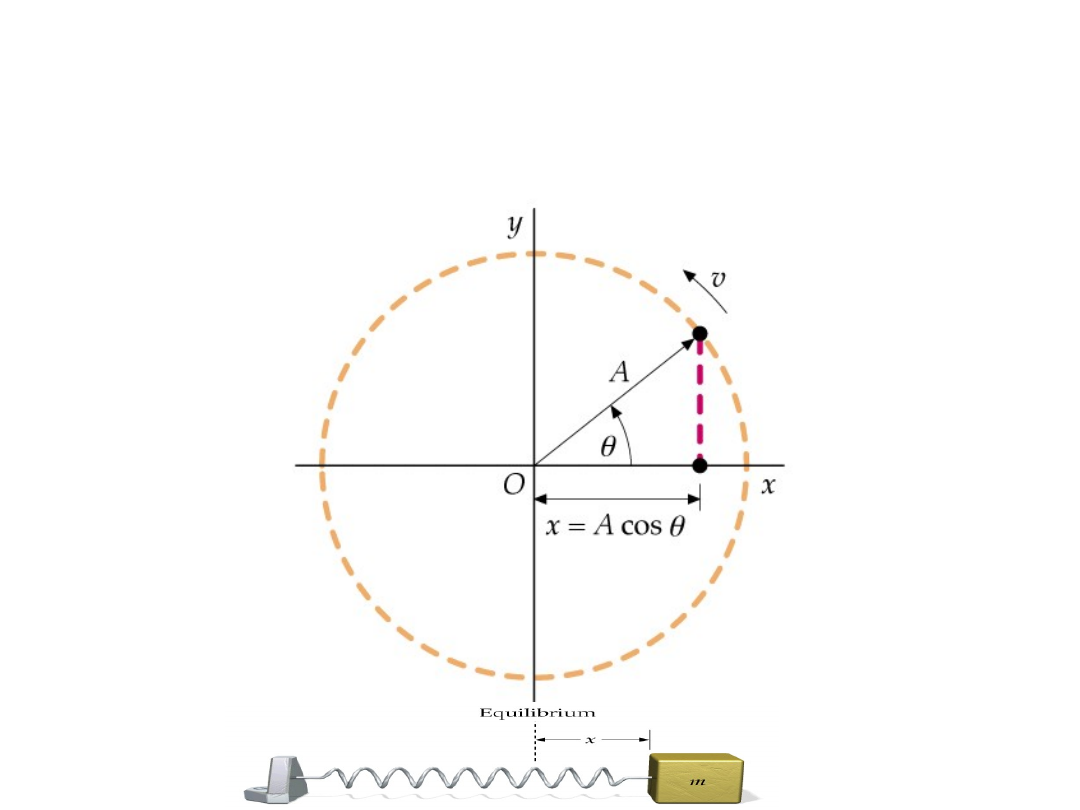
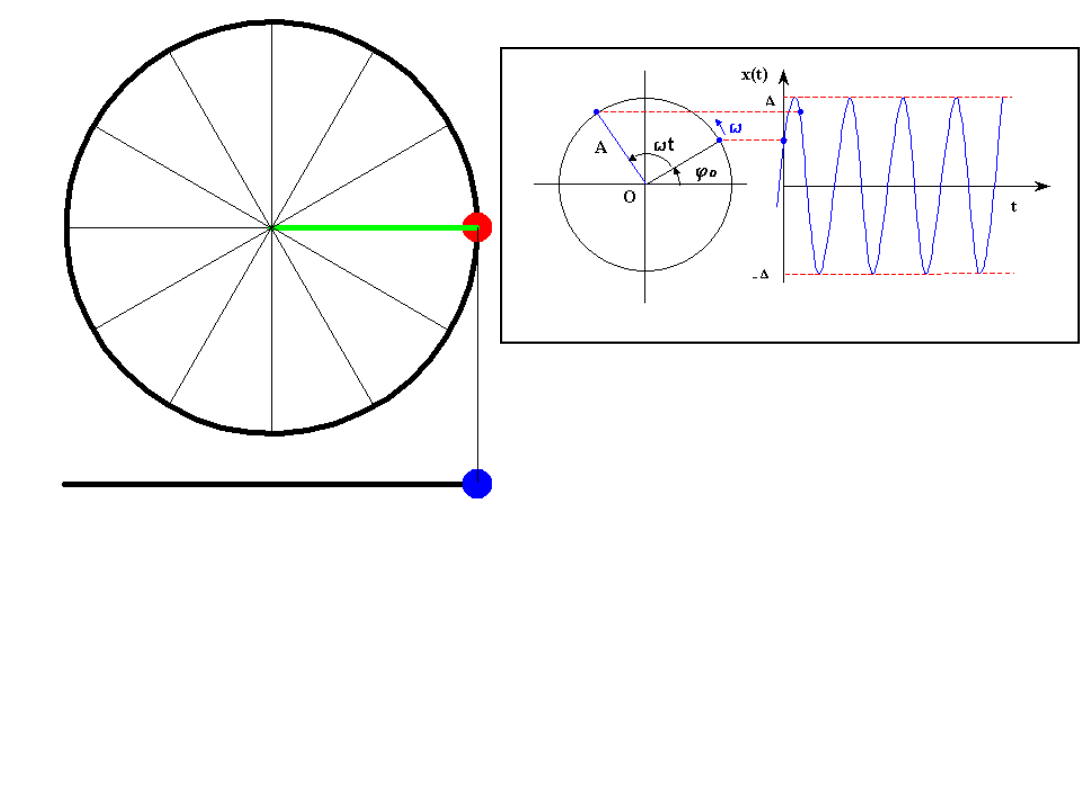
Oscylacje możemy opisać

jako rzuty

w ruchu jednostajnym po

okręgu

 = t + 

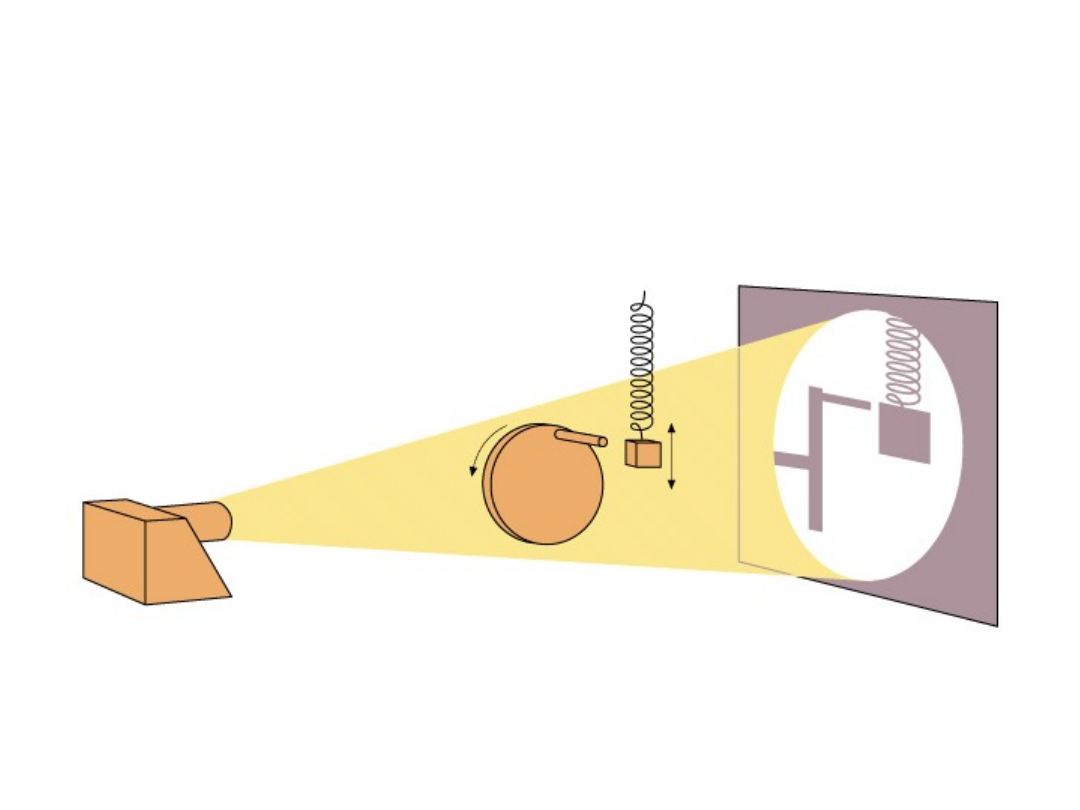
Typowa prezentacja pokazuje

zsynchronizowany ruch ciężarka na sprężynce

oraz rzut punktu poruszającego się ruchem

jednostajnym po okręgu

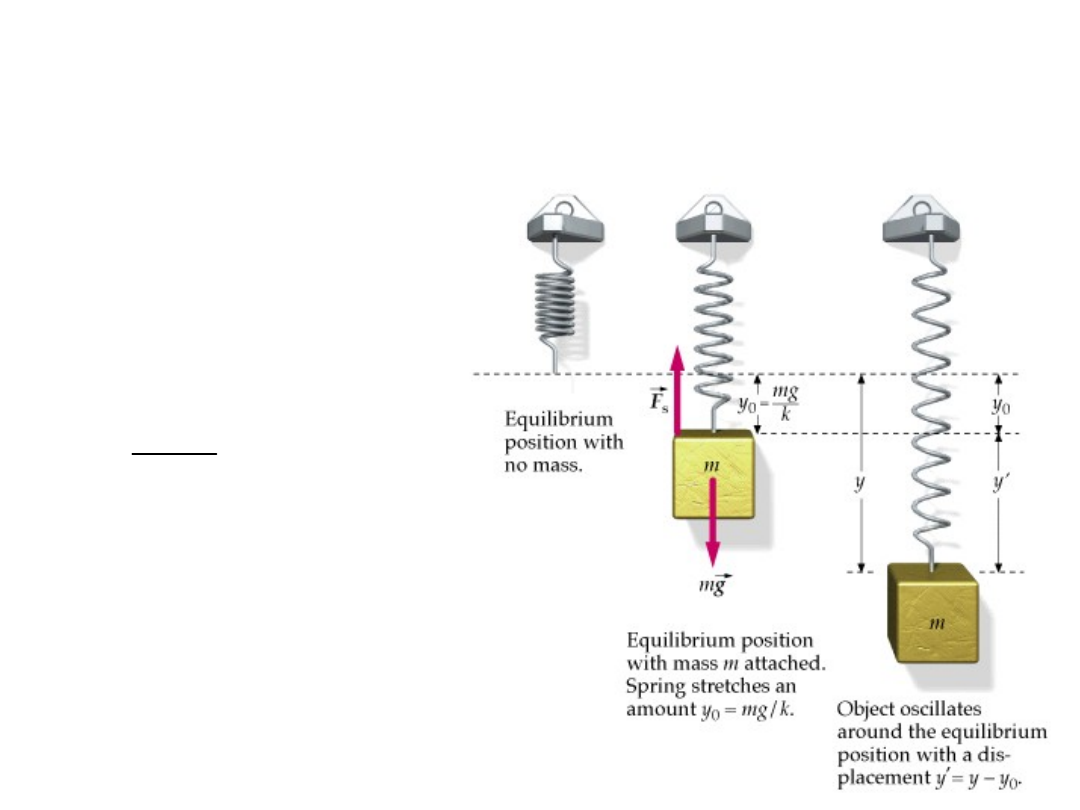
Zadania praktyczne opisują ruch ciężarka
zawieszonego na sprężynce. Wtedy moment
zawieszenia pozwala na wyznaczenie
współczynnika sprężystości k = mg/y

o

ky

dt

y

d

m





2

2

Nowe położenie
równowagi
możemy ustalić po
wychyleniu
się sprężyny o y

o

Wtedy otrzymamy
równanie

Którego rozwiazaniem jest

Funkcja y(t) = y

o

cos ωt

Ale to tylko formalne sztuczki : )

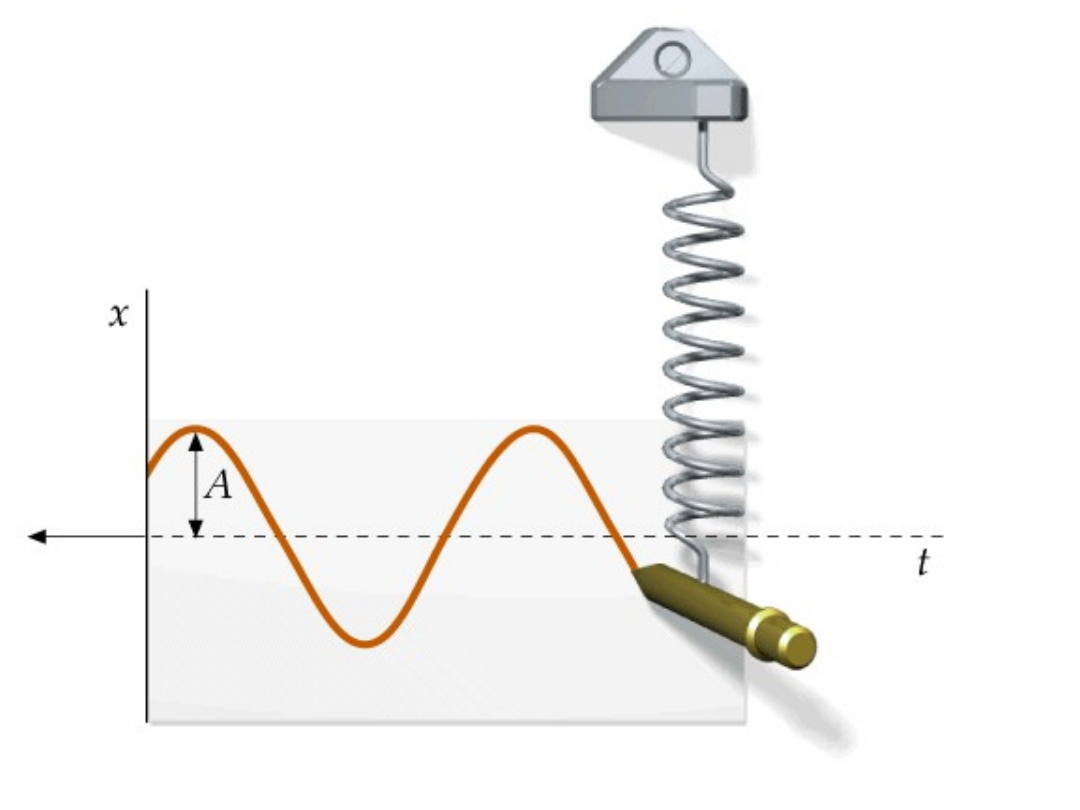
Ruch drgający możemy opisać
W funkcji czasu

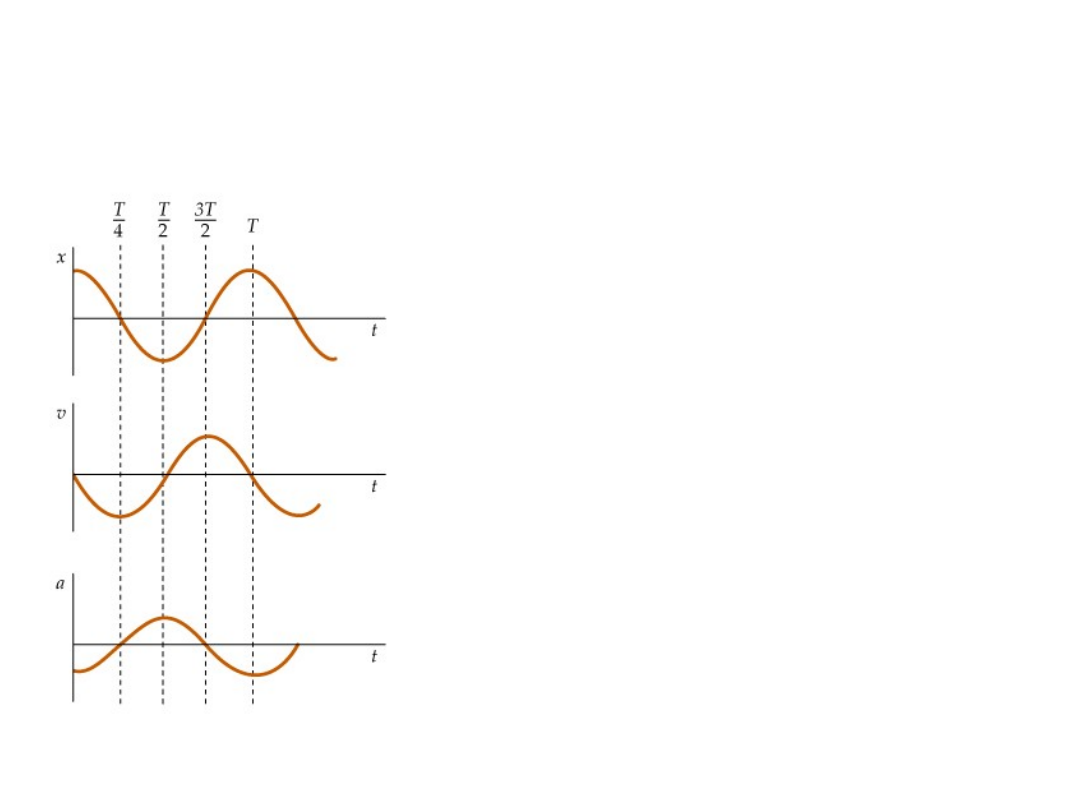
Mając rozwiązanie r.r. możemy wyznaczyć
położenie, prędkość i przyspieszenie w
dowolnej chwili czasu

x(t) = Acos(ωt +
0)

v(t) = dx/dt = -
Aωsin(ωt)

a(t) = dv/dt = - Aωωcos(ωt)

t

A

a

x





cos

2





To już wiemy ale popatrzcie jakie jest przesunięcie fazowe
połozenia, prędkości i przyspieszenia na wykresach

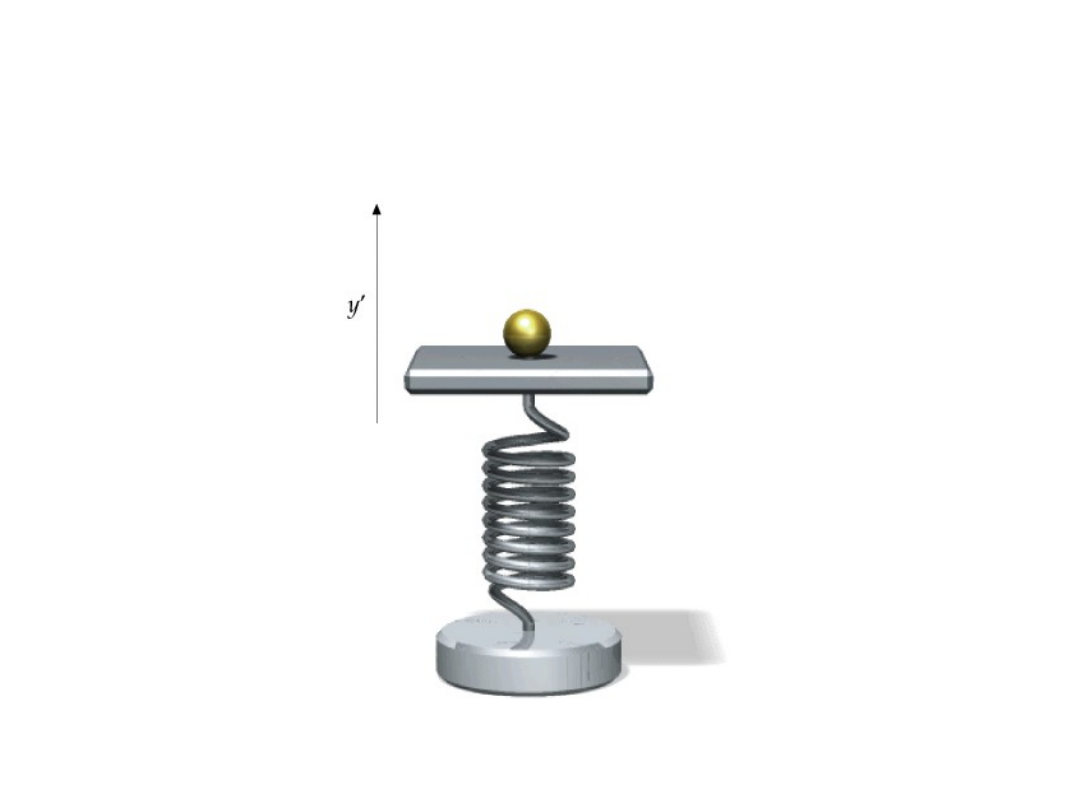
Zadanie dla orłów 

Kulka „spadnie”
(„oderwie się od podłoża”) gdy
przyspieszenie oscylatora
zredukuje przyspieszeni g

Ruch harmoniczny

Energia w ruchu harmonicznym:

2

v

2

m

E

k



Energia
kinetycz
na

Energia
potencja
lna

Energia
całkowit
a

2

2

x

k

E

p



2

2

1

kA

E

E

E

p

k

C







17

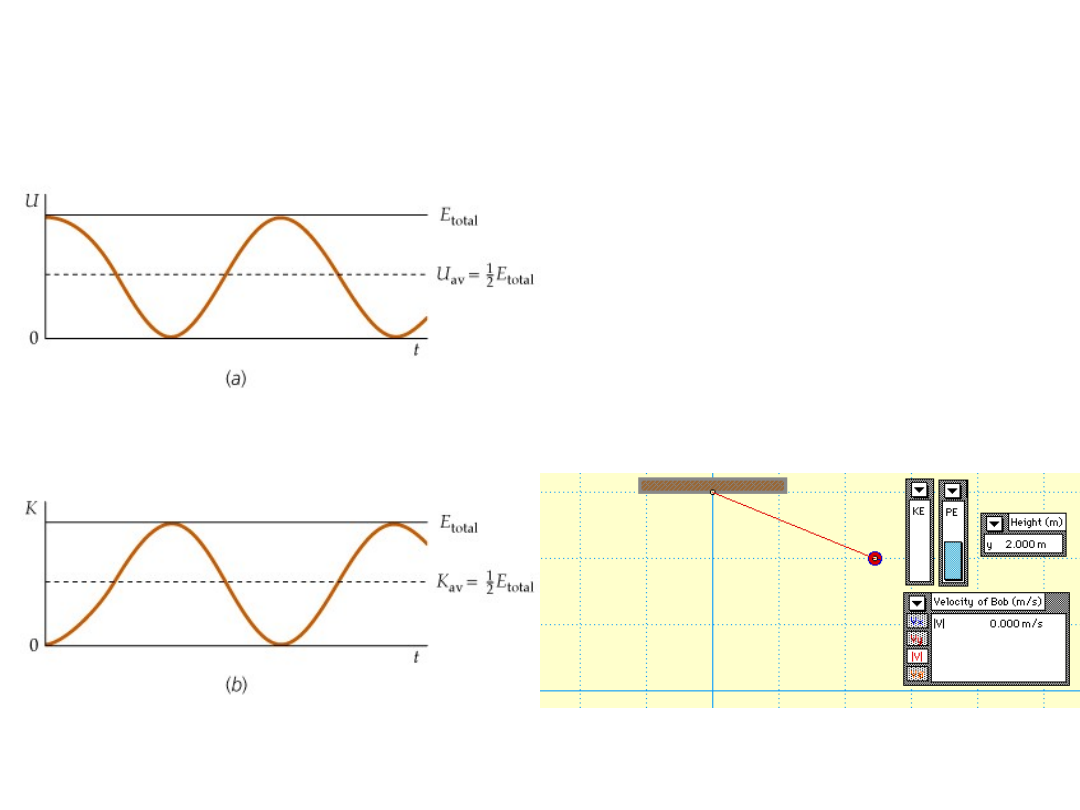
Zmiany energii w czasie

ale suma jest zawsze stała

(oczywiście o ile nie ma strat)



























t

A

m

E

t

kA

E

k

p

2

2

2

2

1

2

2

2

1

sin

cos

1/2

sin

2

ωt

1/2

cos

2

ωt

Poniżej mamy przebieg zmian energii kinetycznej i potencjalnej
w zależności od czasu. Można wykazać albo tylko zauważyć że

zmiany energii są dwa razy częstsze niż zmiany wychylenia

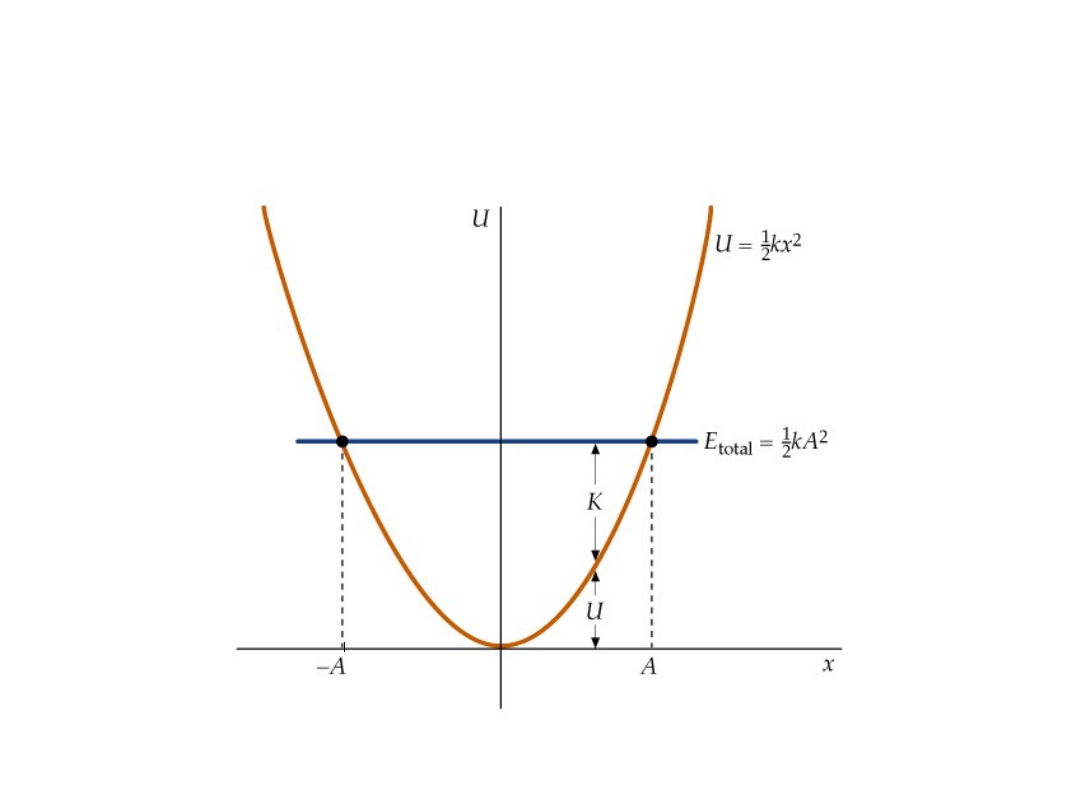
Wykres energii

potencjalnej

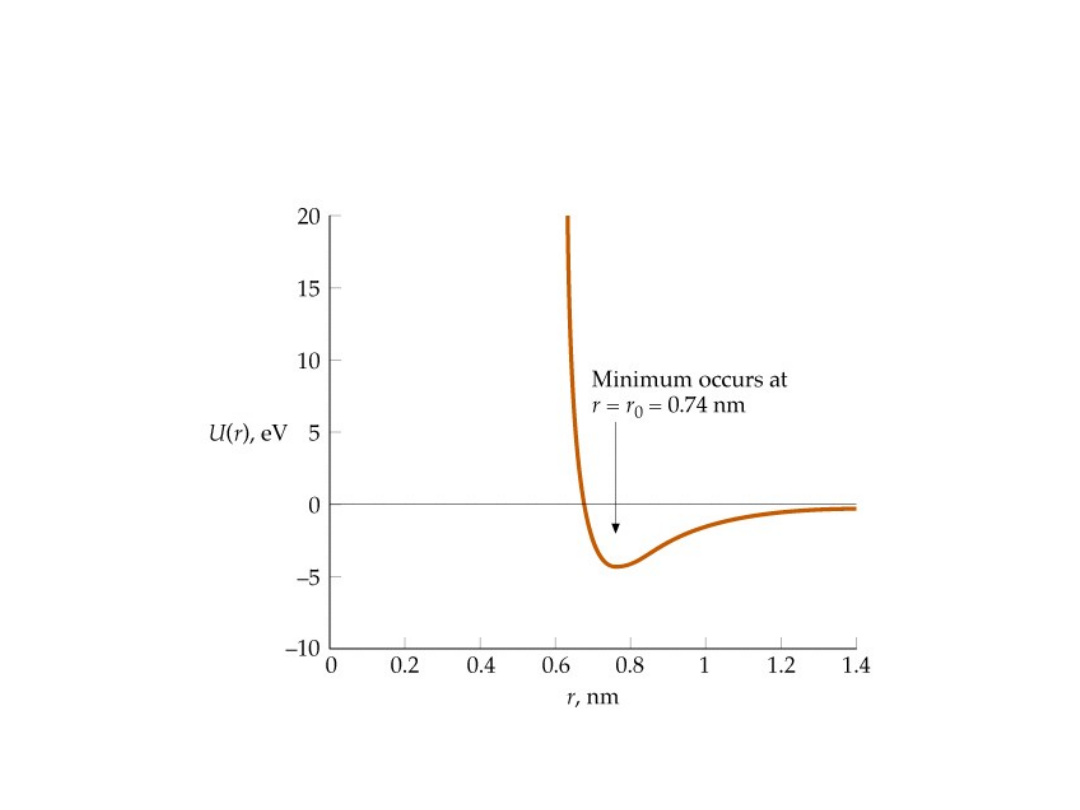
Drobina wodoru

Minimalną wartość energii potencjalnej U = - 4,48 eV ma cząsteczka,
gdy atomy znajdują się we wzajemnej odległości

nm

r

r

74

,

0

0





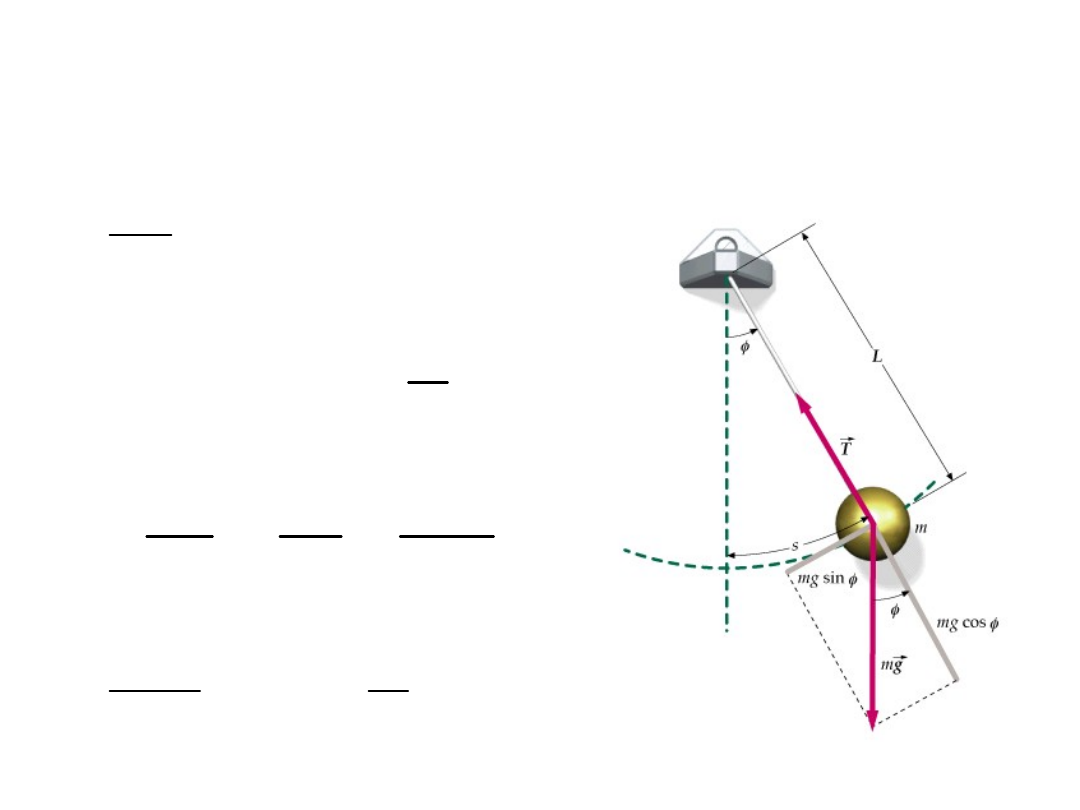
Przyleciał do Was

„niebieski ptak młodości i

kombinuje”

L

S

mg

dt

dS

m

dt

S

d

dt

d

dt

dS

L

S

mg

mg

mg

dt

d

m























2

2

2

2

v

,

,

,

v

sin

v





Kto pamięta wzór na okres drgań ?

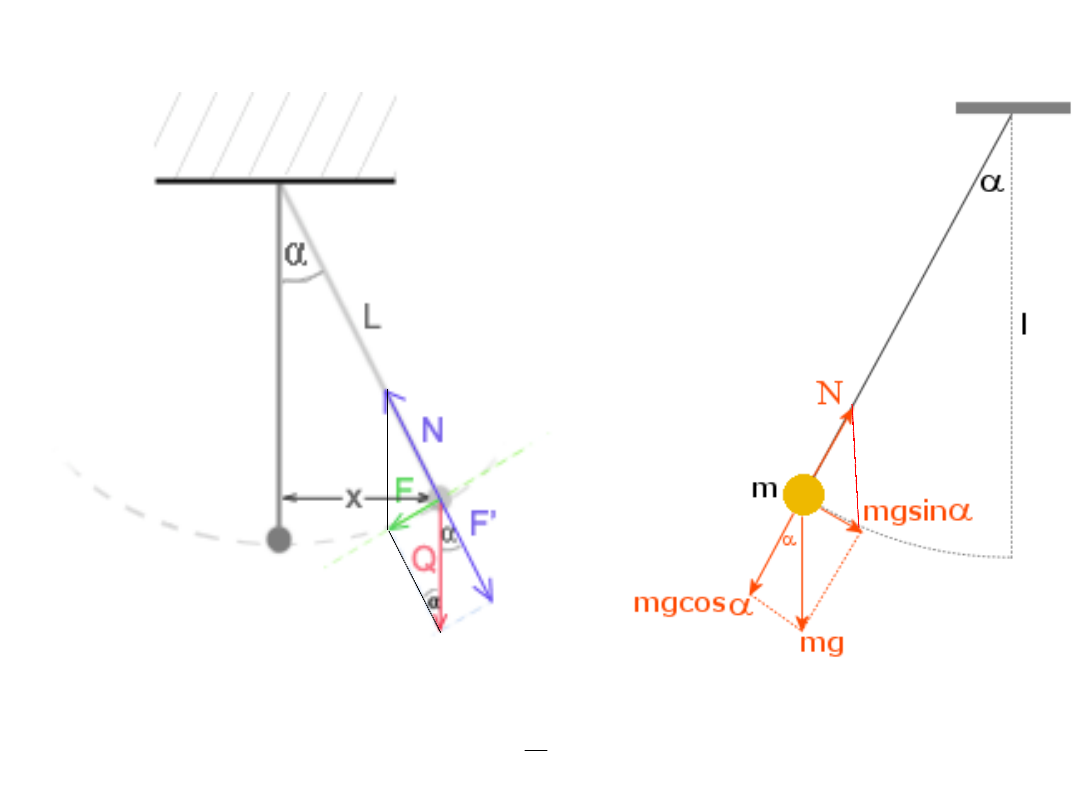
WAHADŁO MATEMATYCZNE

WAHADŁO MATEMATYCZNE

Tu miarą wychylenia jest kąt a przy jednoczesnym założeniu że jest to kąt

Tu miarą wychylenia jest kąt a przy jednoczesnym założeniu że jest to kąt

mały czyli słuszne jest przybliżenie:

mały czyli słuszne jest przybliżenie:

]

rad

[

sin

L

x









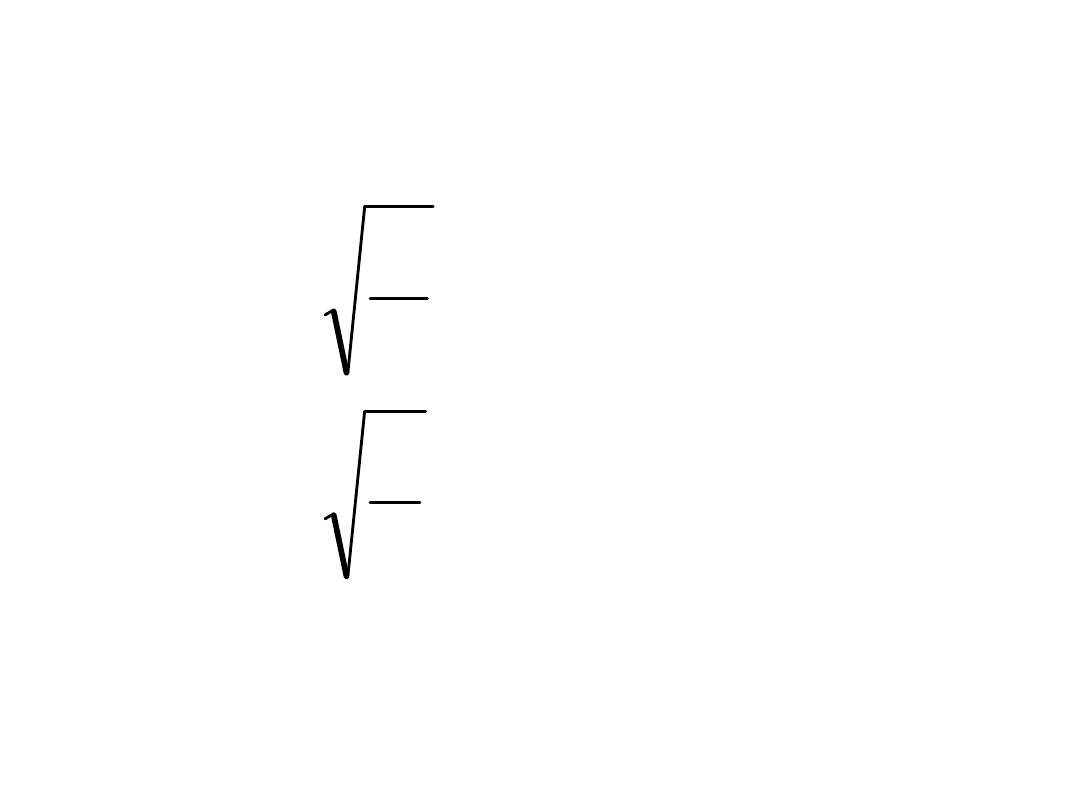
Porównanie wzorów na
pulsację dla ciężarka na
sprężynie i dla wahadła

L

g

m

k









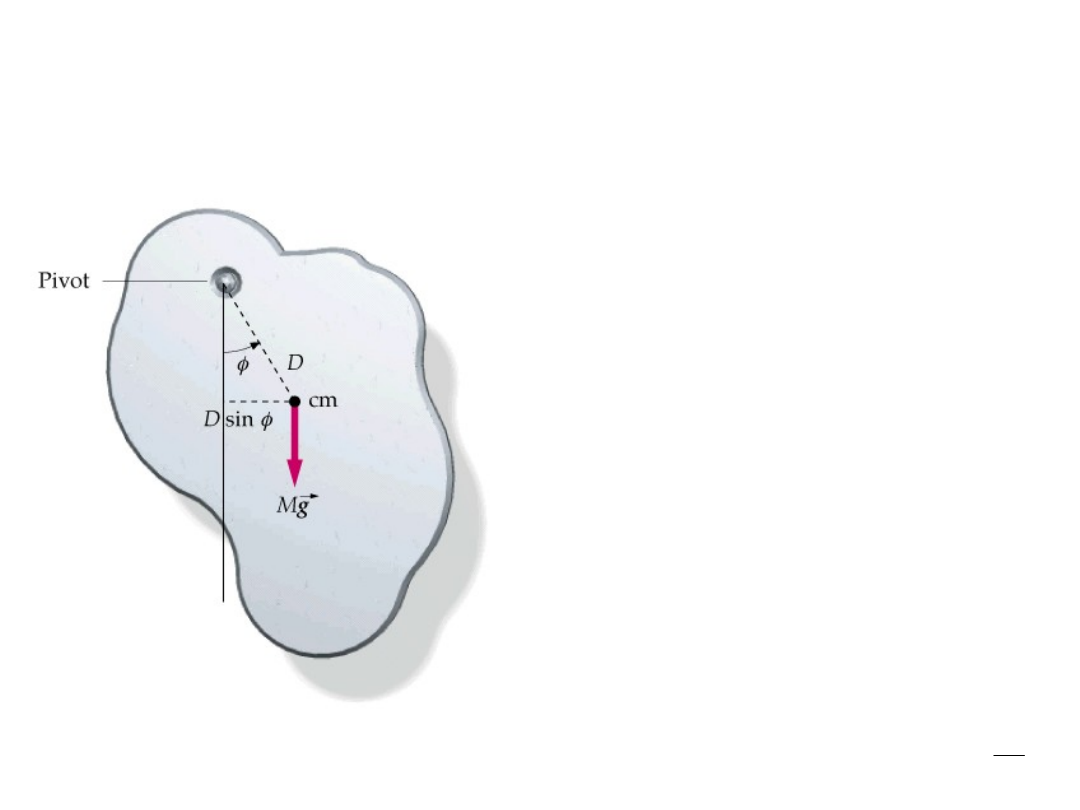
Wahadło fizyczne to też

oscylator

Okazja do wdrożenia nowej procedury myślenia (? ! ?)

Będzie to bryła sztywna
Zawieszona powyżej środka masy

Najlepiej będzie analizować zmiany
kąta wychylenia φ pod wpływem zmie-
niającego się momentu siły M

Procedura jest prosta: trzeba opisać moment siły i moment bezwładności i skorzystać z
drugiego prawa dynamiki bryły sztywnej oraz pamietać, że przyspieszenie katowe to

2

2

dt

d



Moment siły

M

= -





sin

2

2

mgd

dt

d

I







sin

mgd

a równanie różniczkowe przyjmie postać

I

mgd

T

I

mgd

dt

d

























2

2

2

2

2

2

sin













Równanie możemy zapisać w postaci identycznej jak równanie oscylatora harmonicznego

Czy wszyscy pamiętacie dlaczego ?

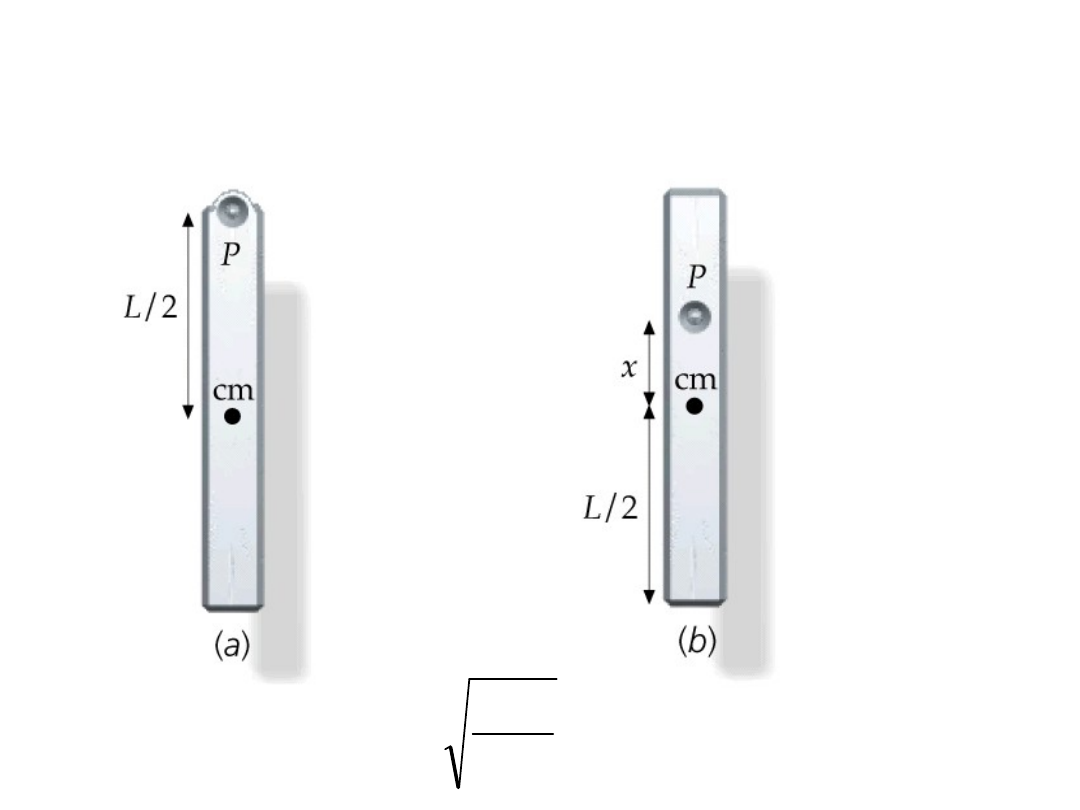
Zadanie: oblicz okres drgań
linijki

zawieszonej jak na rysunku

mgd

I

T



2



d =

d =

W pierwszym przybliżeniu można powiedzieć,
że ruchy następujących ciał są również
ruchami harmonicznymi.

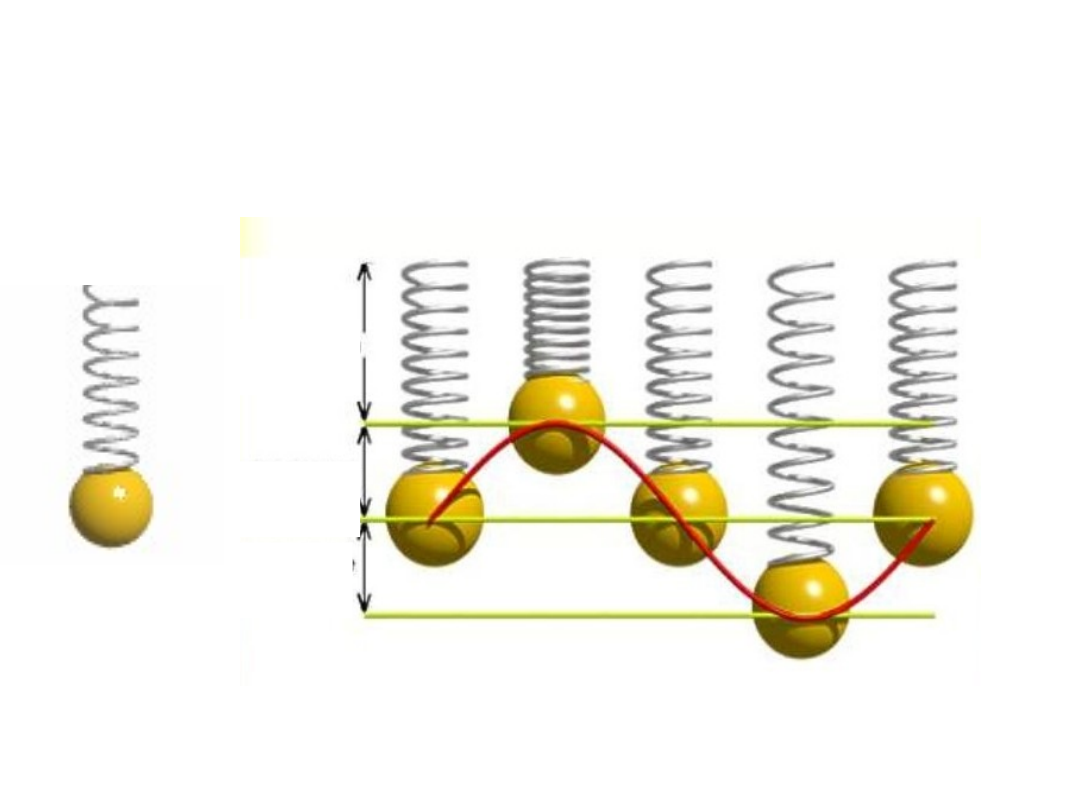
Amplit
uda

Amplit
uda

Minim
um

Zmiany położenia ciężarka na sprężynie

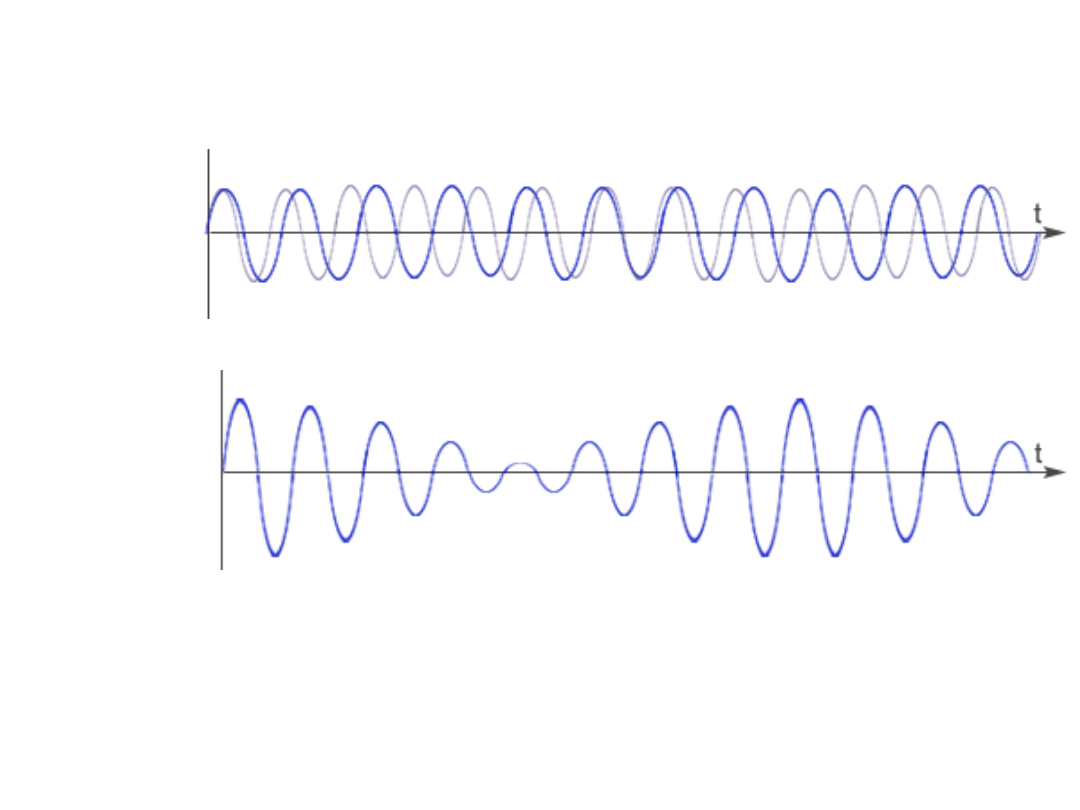
Dudnienia drgań harmonicznych

Dudnienia drgań harmonicznych

W przypadku dwóch drgań harmonicznych o częstościach

W przypadku dwóch drgań harmonicznych o częstościach

ω

ω

1

1

, ω

, ω

2

2

i

i

jednakowej amplitudzie

jednakowej amplitudzie

przebieg drgań można opisać funkcjami:

przebieg drgań można opisać funkcjami:

 

 

                    

                    

 

 

                    

                    

Przebieg powstały w wyniku dodania tych drgań:

Przebieg powstały w wyniku dodania tych drgań:

 

 

                

                

Z sumowania funkcji trygonometrycznych wynika:

Z sumowania funkcji trygonometrycznych wynika:

)

t

sin(

A

)

t

(

x

)

t

sin(

A

)

t

(

x

2

2

1

1









)

t

(

x

)

t

(

x

)

t

(

X

2

1





Lub oznaczając: możemy zapisać wypadkowe drganie:

Lub oznaczając: możemy zapisać wypadkowe drganie:

2

2

2

1

sred

2

1

ul

mod





















)

t

sin(

)

t

cos(

A

2

)

t

(

X

sred

ul

mod













:

 

                                                                                    





















































2

t

)

(

sin

2

t

)

(

cos

A

2

)]

t

sin(

)

t

[sin(

A

2

)

t

(

X

2

1

2

1

2

1

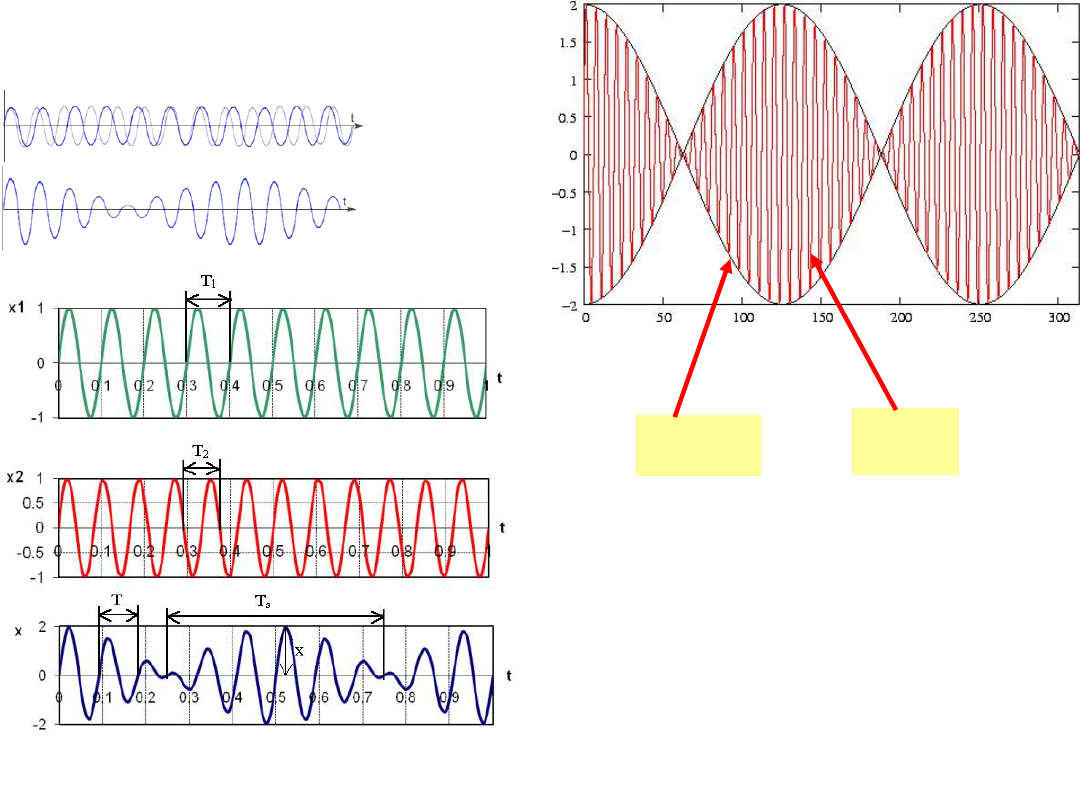
Graficzna ilustracja

Graficzna ilustracja

dudnienia

dudnienia

.

.

sred



ul

mod



Dwa dźwięki o zbliżonych częstościach
Ucho odbiera jako dudnienie - zmianę
głośności o częstości

½

(ω

1

– ω

2

)

dudnienia fal

OSCYLACJE W DWÓCH WYMIARACH - Krzywe Lissajous

OSCYLACJE W DWÓCH WYMIARACH - Krzywe Lissajous

Możliwe jest rozważanie oscylacji w dwóch wymiarach (na płaszczyźnie X,Y).
Będą to jakby dwa oscylatory – jeden X(t) drgający na osi X , drugi zaś Y(t)
drgający na osi Y prostopadłej do X.

)

t

sin(

B

)

t

(

y

)

t

sin(

A

)

t

(

x

y

x













Kształt krzywych na płaszczyźnie (x,y) jest szczególnie uzależniony od ilorazu

Kształt krzywych na płaszczyźnie (x,y) jest szczególnie uzależniony od ilorazu







x

x





y

y









Dla współczynnika

Dla współczynnika





1, krzywa jest elipsą, w specjalnych

1, krzywa jest elipsą, w specjalnych



przypadkach gdy A = B oraz

przypadkach gdy A = B oraz





= 0 lub

= 0 lub





=

=





/2 jest to okrąg.

/2 jest to okrąg.



Inne wartości współczynnika

Inne wartości współczynnika





dają bardziej złożone krzywe, które są zamknięte

dają bardziej złożone krzywe, które są zamknięte



tylko gdy

tylko gdy





jest liczbą wymierną.

jest liczbą wymierną.

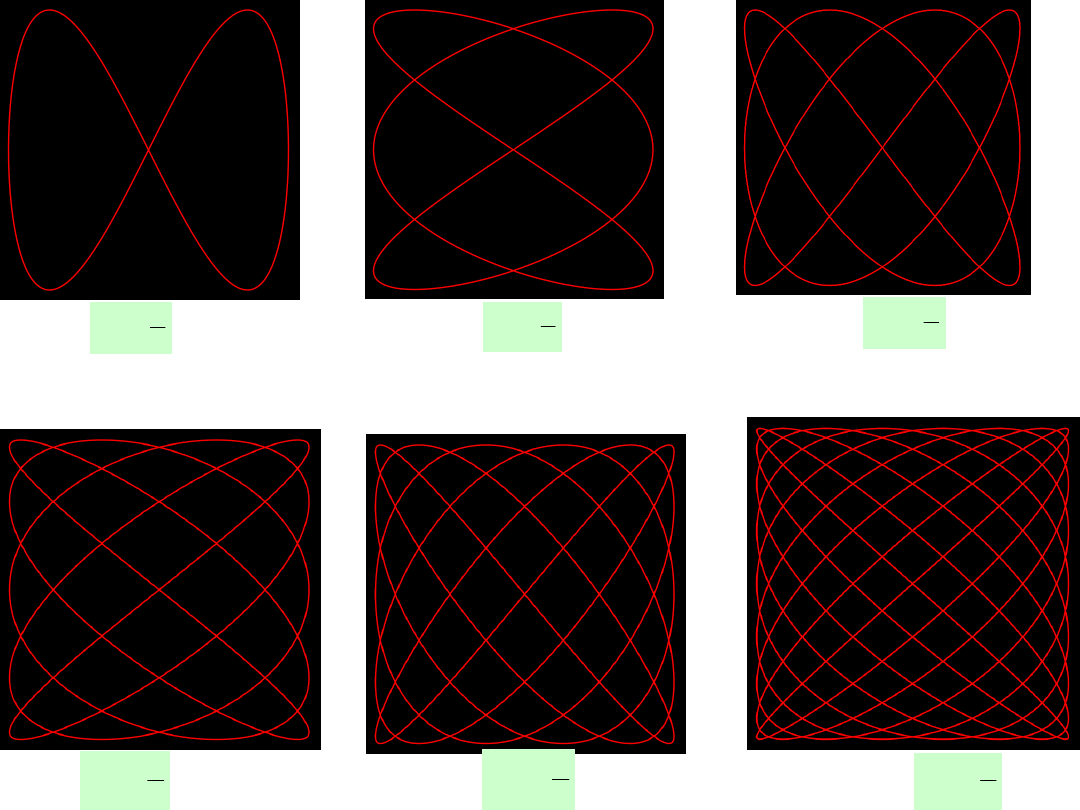
Przykładowe rysunki krzywych Lissajous dla różnych wartości ilorazu

Przykładowe rysunki krzywych Lissajous dla różnych wartości ilorazu









oraz dla różnicy faz

oraz dla różnicy faz





=

=





/2

/2

przedstawia następny slajd.

przedstawia następny slajd.

2

1





2

3





4

3





4

5





6

5





8

9





KRZYWE LISSAJOUS

KRZYWE LISSAJOUS

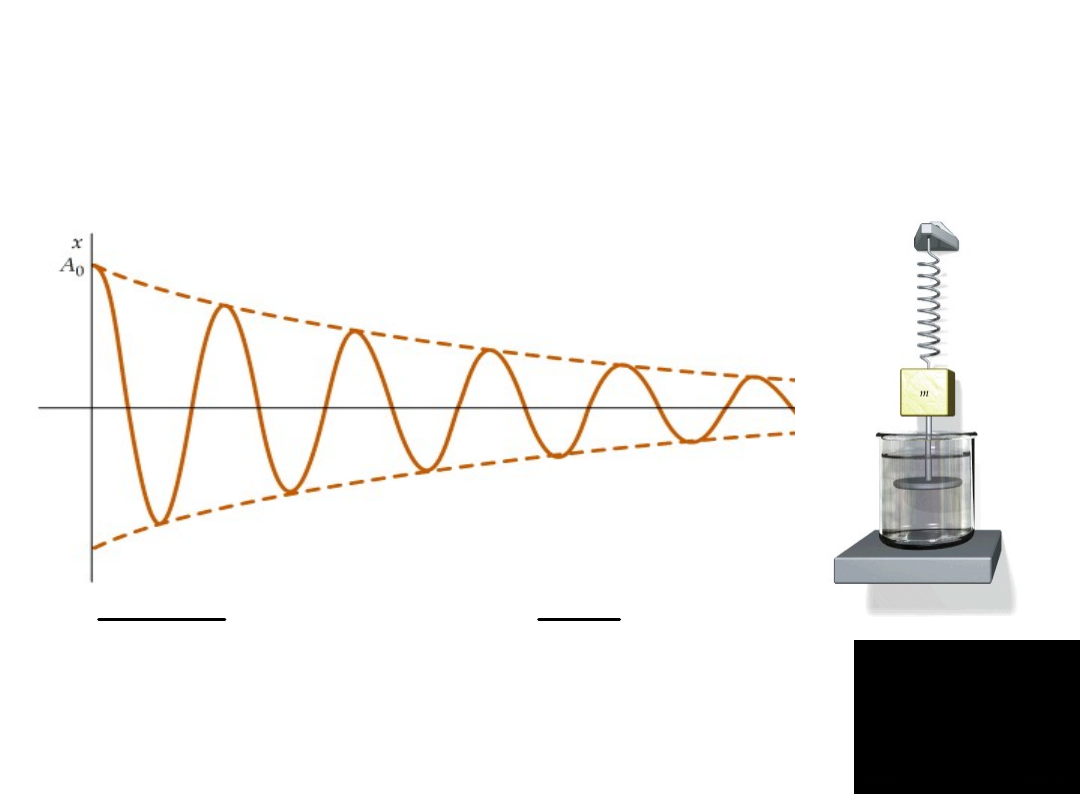
Oscylator tłumiony

otrzymamy

gdy oprócz
siły sprężystości F = - kx pojawi się
dodatkowa siła

stanowiąca opór proporcjonalny do

prędkości F = -bv

dt

dx

b

kx

dt

x

d

m







2

2

Oscylator tłumiony nie jest harmoniczny bo ma de facto wiele czestotliwości











































t

e

A

t

e

A

x

t

t

m

b

'

cos

'

cos

2

0

2

0

b

m





Rozwiązanie ma postać

0

-Ae

-



t

Ae

-



t

Ae

-



t

cos



t

-A

A

t

x

)

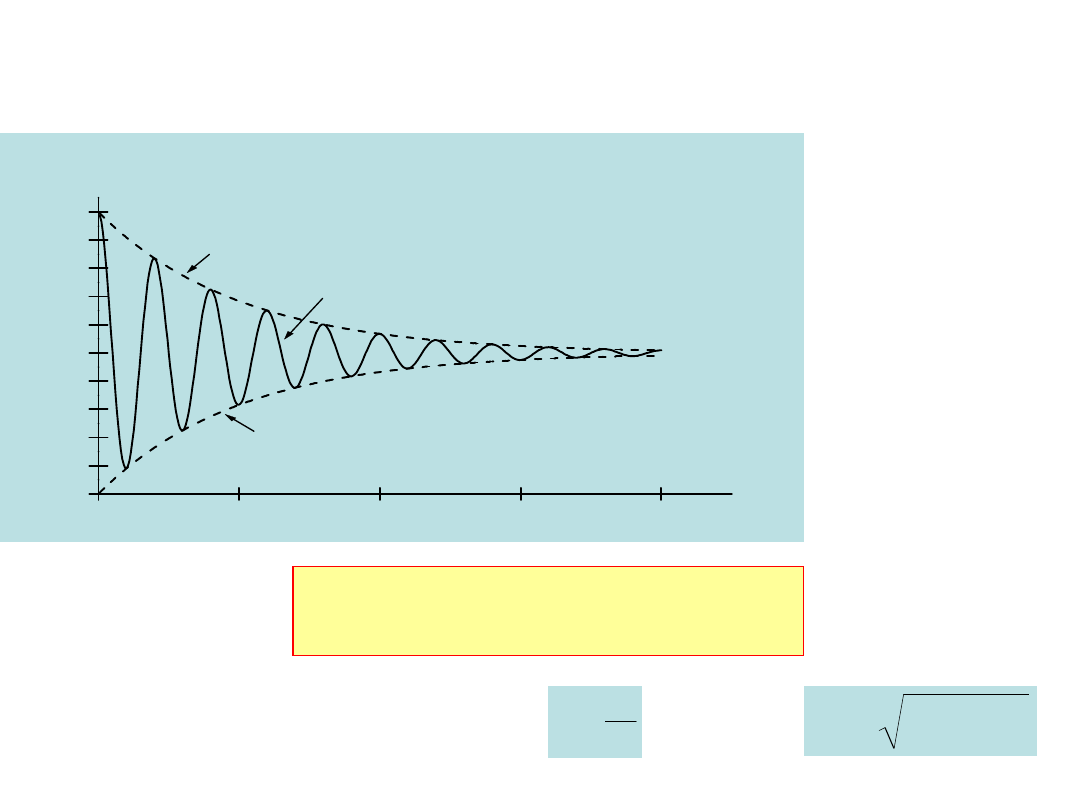
t

cos(

e

A

)

t

(

x

t









0

-A e

- t

A e

- t

A e

- t

cos



t

-A

A

t

x







2

1

:

2

2

0











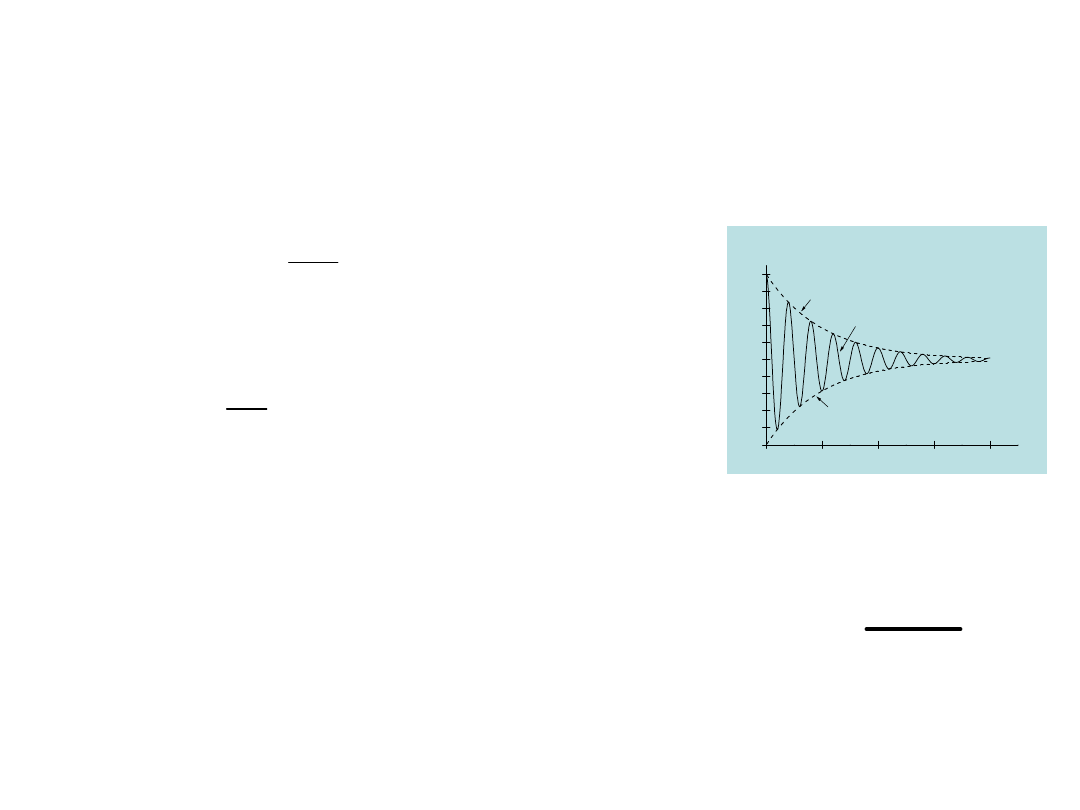
Oscylacje tłumione

Ruch pełzający

Tak to wygląda jeżeli przyjmiemy β
= b/2m:

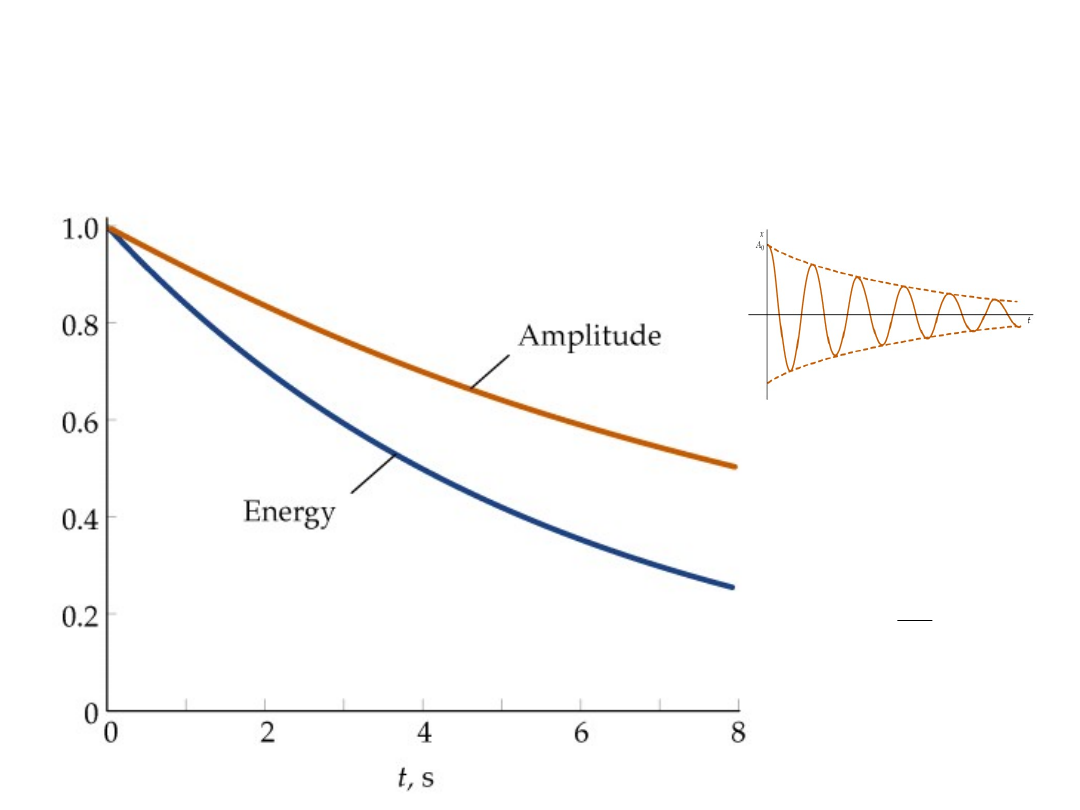
Zanik drgań

energia zanika „z

kwadratem

amplitudy” a więc szybciej

b

m





Wygląda na to, że
energia
zanika z kwadratem
amplitudy czyli

Na skutek tłumienia drgań maleje także
ich częstość

2

0

0

2

2

0

2

1

2

'









































m

b

m

b

dt

dx

b

kx

dt

x

d

m







2

2

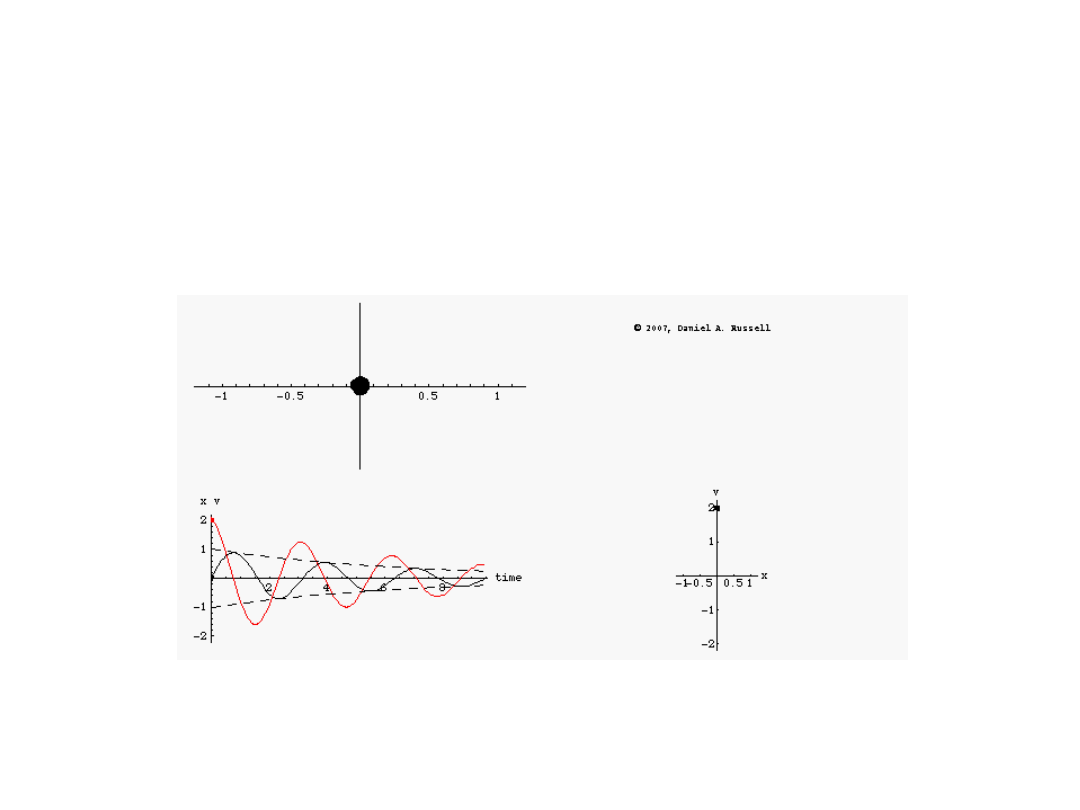
Ruch harmoniczny
tłumiony c.d.

40

Animacja ruchów harmonicznych tłumionych w zależności od czasu:

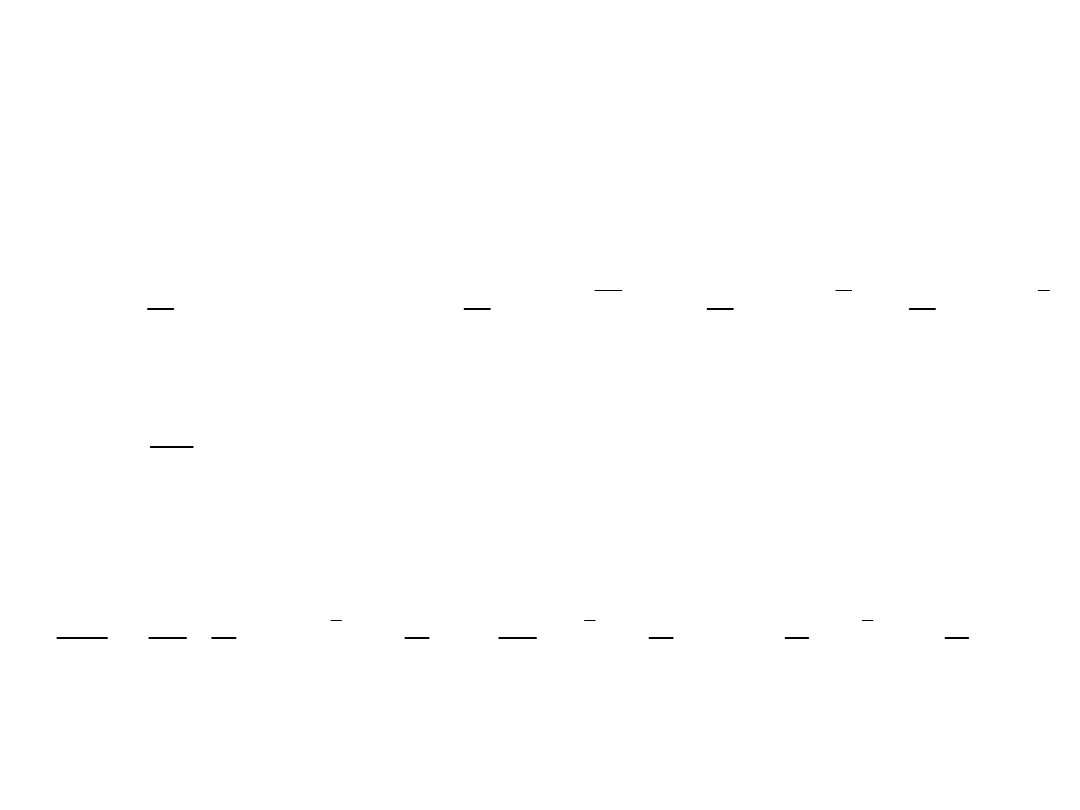
Ruch harmoniczny
tłumiony c.d.

41

Energia

w ruchu tłumionym:

 





 







t

m

m

e

kA

e

kA

Ae

k

amplituda

k

t

E

t

t















2

2

2

2

2

1

2

1

2

1

2

1

2





m



Jest to tzw.

czas relaksacji

, czyli czas po

którym energia układu maleje „e” razy

Szybkość zmian energii

:

 

E

e

kA

e

dt

d

kA

e

kA

dt

d

dt

dE

t

t

t











1

1

2

1

2

1

2

1

2

2

2















 

























Układ tłumiony traci tyle samo energii w jednakowych odstępach czasu.

Poniżej kilka slajdów dla spragnionych widoku matematycznych sztuczek

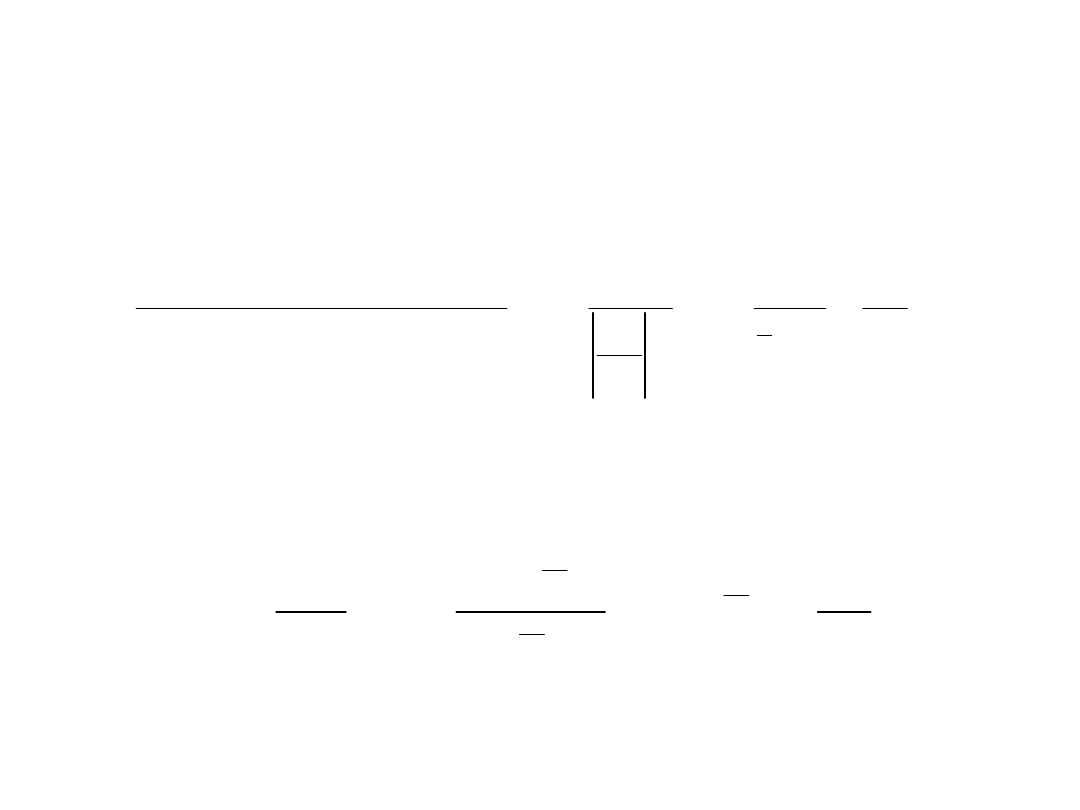
Ruch harmoniczny
tłumiony

42

Dobroć oscylatora

definiujemy następująco:

























T

ET

E

T

dt

dE

E

kresie

w jednym o

energia

oscylatora

energia

Q

2

2

2

2

1

Logarytmiczny dekrement tłumienia

definiujemy:





 

T

m

e

Ae

Ae

A

A

T

T

t

t

T

t

t

m

m

m

2

ln

ln

ln

2

2

2





















































Jest to logarytm stosunku dwóch kolejnych maksymalnych wychyleń (dla

wychylenia w jednakową stronę) . Wielkość ta nie zależy od czasu.

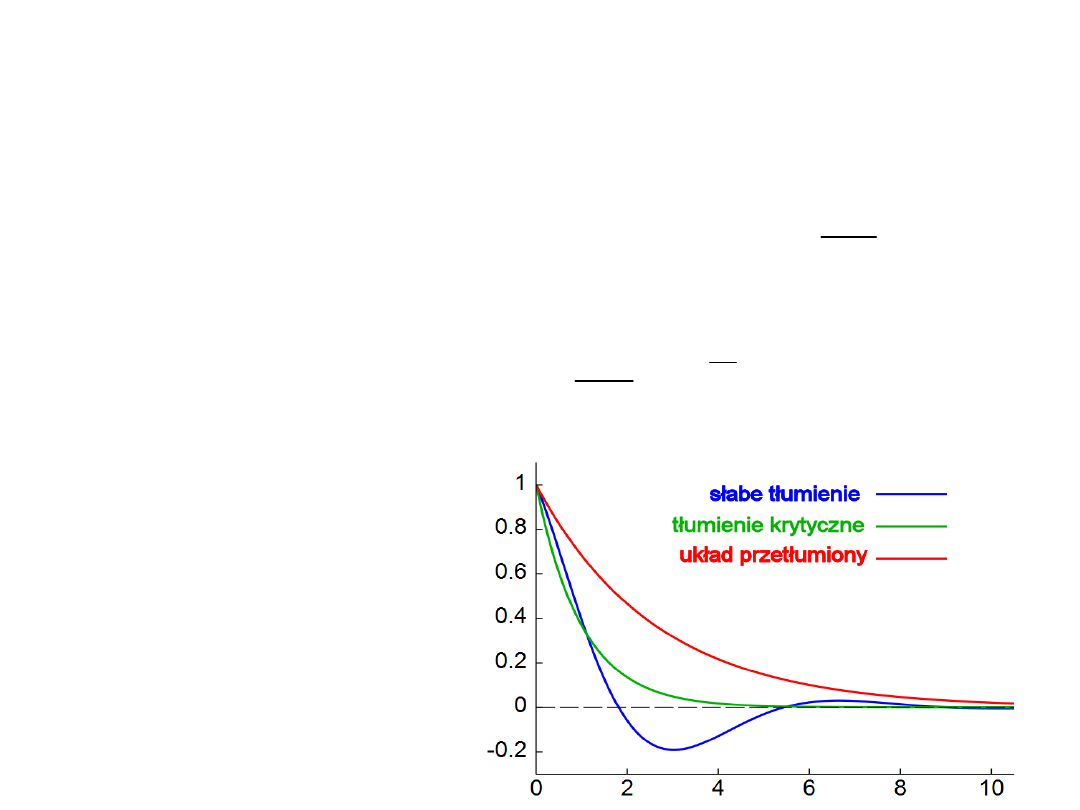
Ruch harmoniczny
tłumiony

43

Tłumienie krytyczne

zachodzi gdy:

Rozwiązaniem równania ruchu tłumionego krytycznie jest funkcja
postaci:

2

2

0

2















m





 

t

m

e

t

m

b

B

A

t

x

2

2















 



Równanie powyższe nie
opisuje ruchu drgającego.
Ciało (cząstka) tłumiona
krytycznie nie przechodzi
przez punkt równowagi
lecz stopniowo się do
niego zbliża.

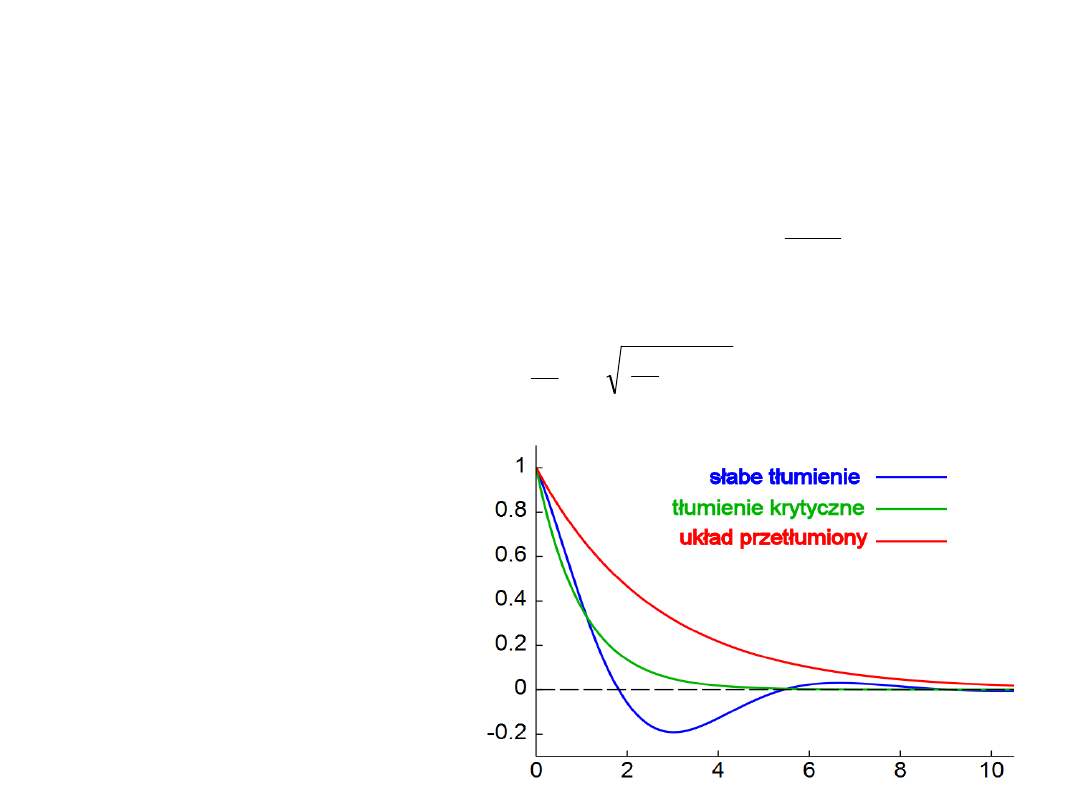
Ruch harmoniczny
tłumiony

44

Przetłumienie

zachodzi gdy:

Rozwiązaniem równania dla układu przetłumionego jest funkcja
postaci:

2

2

0

2















m





 

 

t

t

m

m

e

Ae

t

x

2

0

2

2

2















Równanie powyższe nie
opisuje ruchu drgającego.
Układ przetłumiony
dochodzi do położenia
równowagi dłużej niż
układ tłumiony
krytycznie.

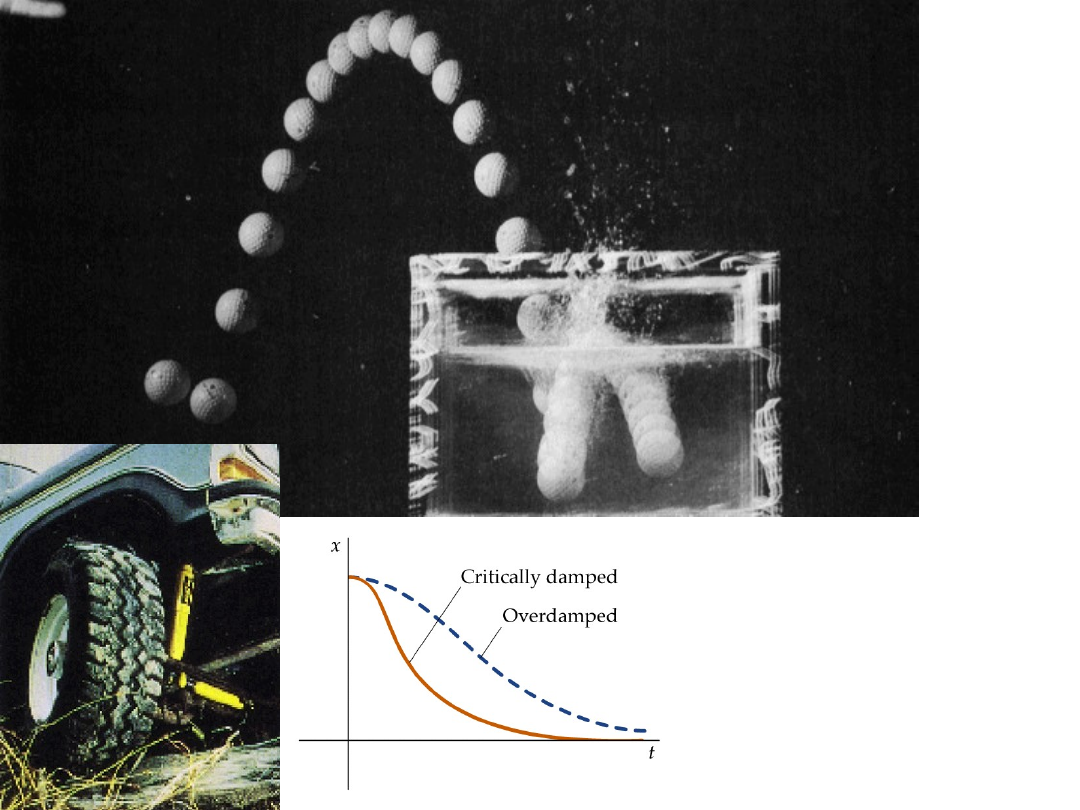
• Na fotografii pokazano 400-tonowe bloki służące do tłumienia

drgań. Są one poprzez układ sprężyn połączone z budowlą tak
by wykonywały oscylacje w przeciwnej fazie (przesunięcie o 180
stopni) w stosunku do fazy naturalnych drgań wzbudzanych
wiatrem (Citicorp Building, New York).

Sposób na tłumienie drgań
Wieżowca w Nowym Yorku

Drgania

wymuszone

Oscylator wymuszony

Drga z częstością wymuszającą ale niezbyt zgodnie bo
pojawia się

przesunięcie fazowe

Równanie oscylatora

wymuszonego

t

F

x

b

kx

dt

x

d

m

ma

x



cos

0

2

2













t

m

F

x

m

k

x

m

b

x



cos

0











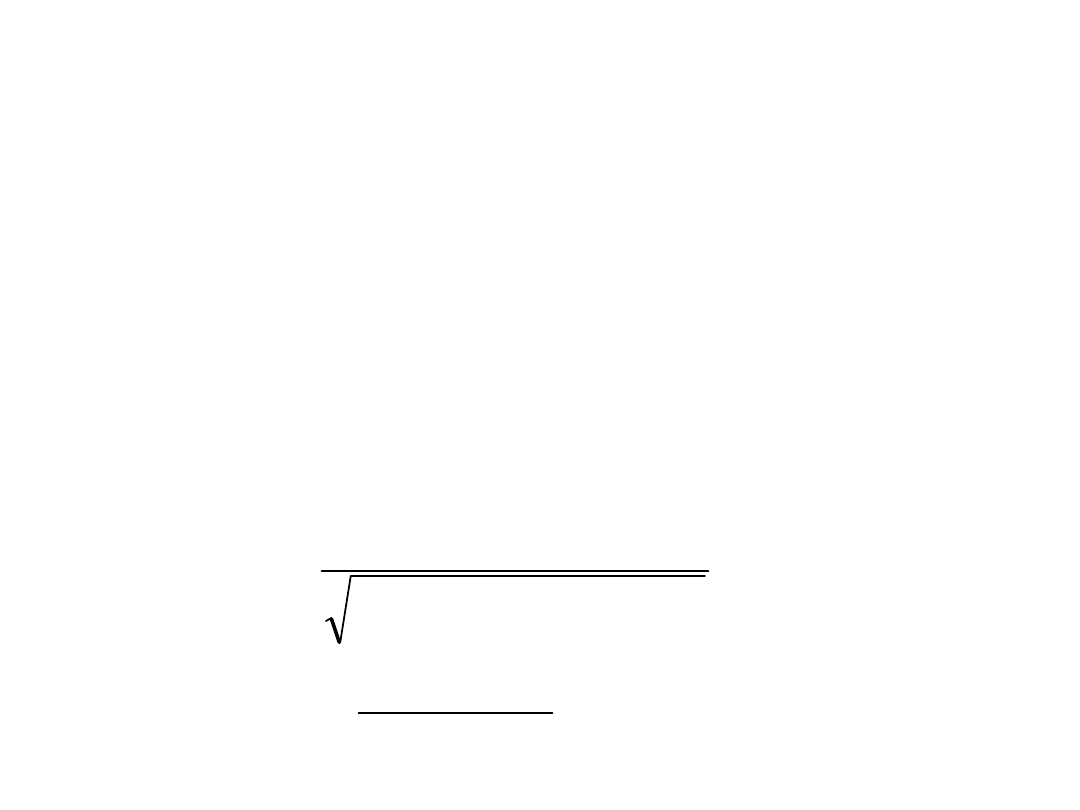
W efekcie oscylator drga z

częstością, która zostaje na nim

wymuszona ale w innej fazie

Amplituda drgań i przesunięcie fazowe

zależą od różnicy częstości
wymuszającej i częstości własnej

rezonatora













t

A

x

cos









2

2

0

2

2

2

2

2

0

2

0

tg

























m

b

b

m

F

A

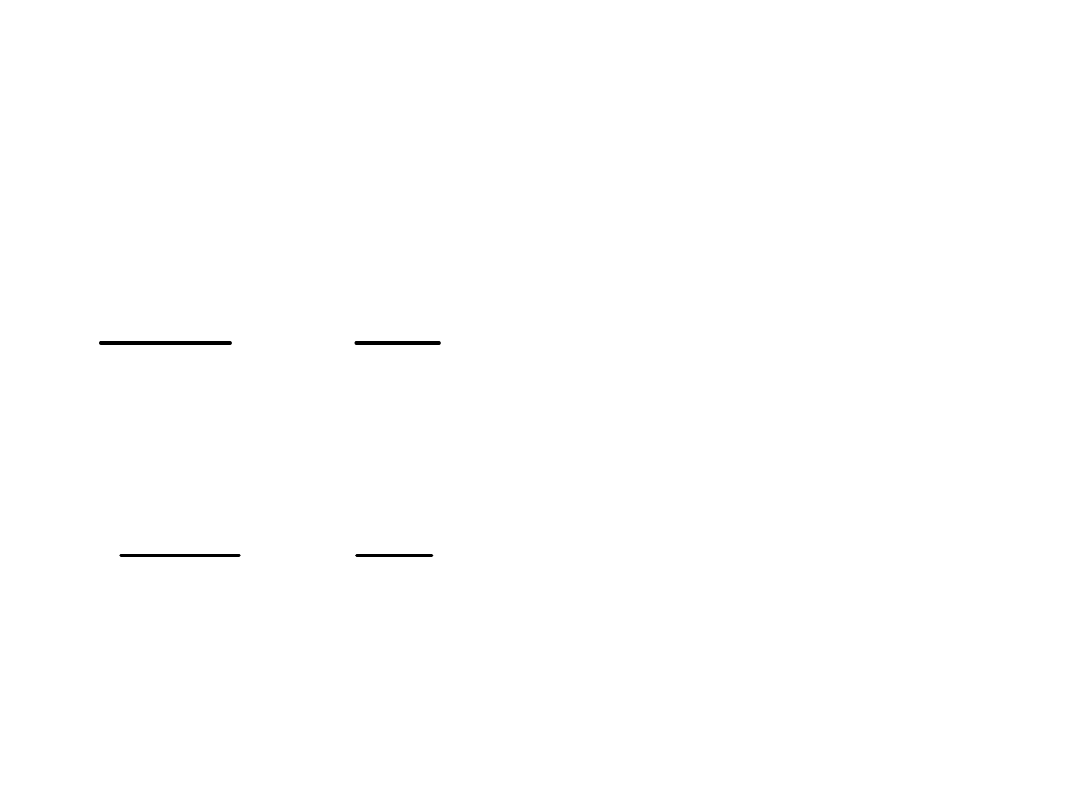
Drgania wymuszone

harmoniczne

t

F

x

m

dt

dx

b

dt

x

d

m





cos

0

2

0

2

2







t

i

e

F

z

m

dt

dz

b

dt

z

d

m





0

2

0

2

2







Część rzeczywista funkcji zespolonej z(t) będzie rozwiązaniem
dla równania pierwszego













































2

2

0

2

/

1

2

2

2

2

0

0

/

arctg

t

sin

]

)

/

(

)

[(

)

t

(

x

poszukiwane rozwiązanie ma postać:

poszukiwane rozwiązanie ma postać:



0

A





4



3



2



1



0

= 0

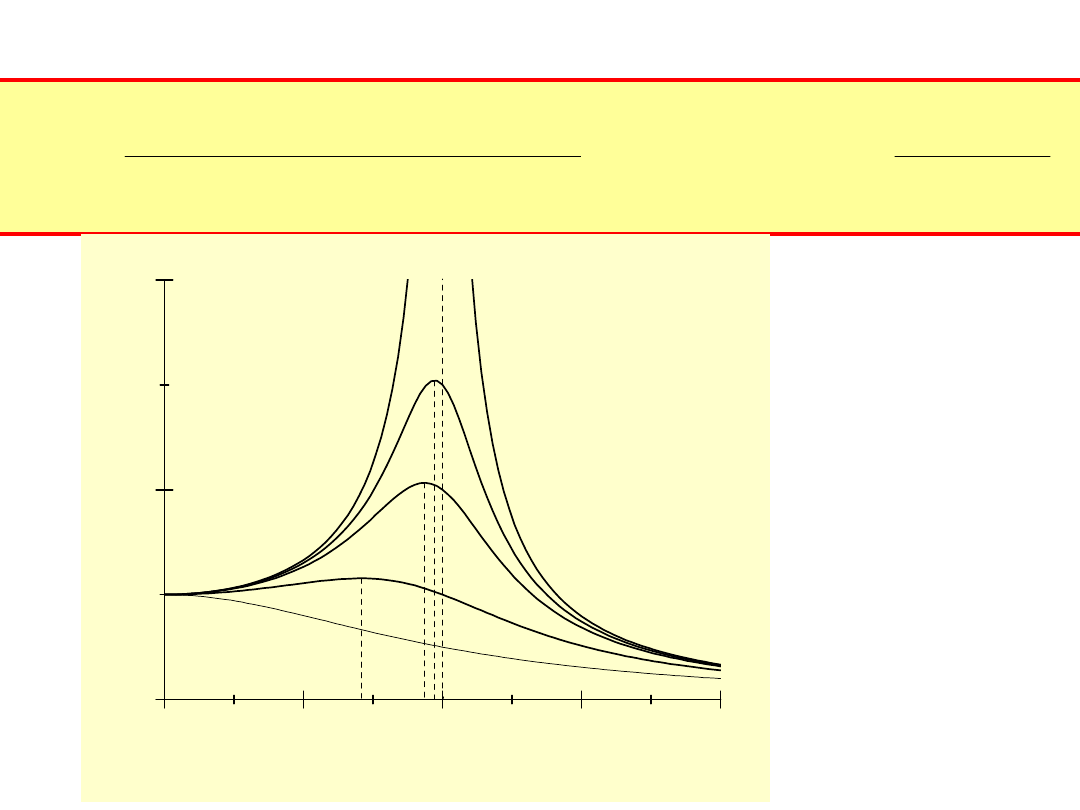
Wykres przedstawia

Wykres przedstawia

rezonansowy wzrost

rezonansowy wzrost

amplitudy drgań w

amplitudy drgań w

funkcji częstości siły

funkcji częstości siły

wymuszającej

wymuszającej





dla

dla

różnych wartości

różnych wartości

współczynnika

współczynnika

tłumienia

tłumienia

  



  



.

.

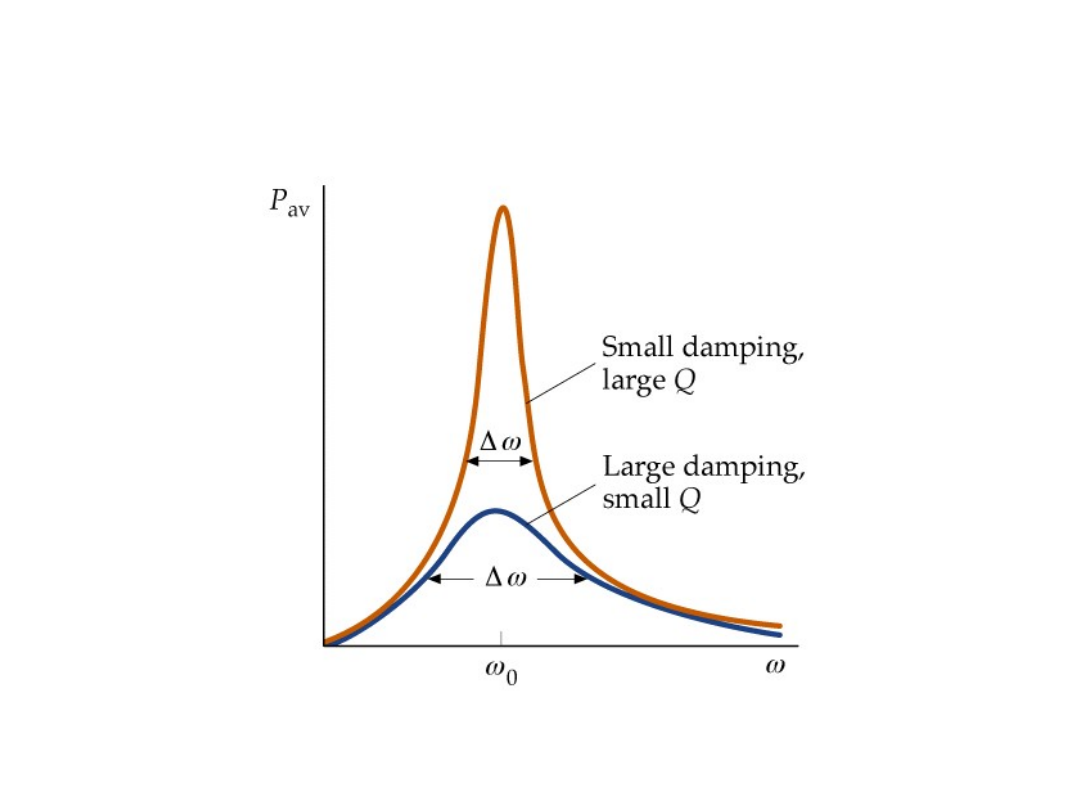
Tłumienie zależy od

częstości

Jeżeli częstość wymuszająca zbliża się do częstości własnej
układu dochodzi do rezonansu

Uwaga!! - może dojść do rezonansów

Tak było w

Takomie,

tyle, że

bardziej skomplikowanie

1940

1950

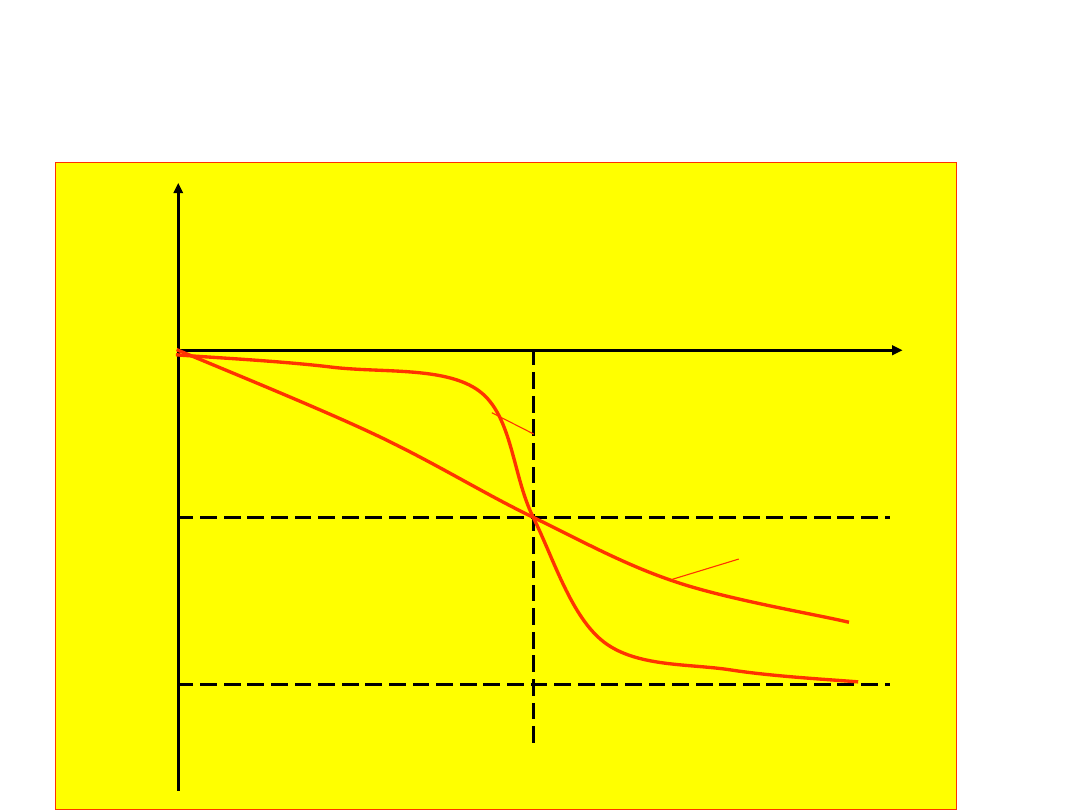
Zmiana fazy będzie zależeć od

częstotliwości wymuszającej

0

-90

0

-180

0







0



0

 = 100



0

 = 1

Z tych wszystkich slajdów trzeba zestawić

trzy podstawowe równania dla

oscylatorów:

1.

harmonicznego

2.

tłumionego i ..

3.

wymuszonego

oraz podać rozwiązania tych równań.

Zrozumienie tego zestawienia

przypieczętuje na egzaminie ocenę 3.5 i

otworzy drogę do oceny dobrej i więcej

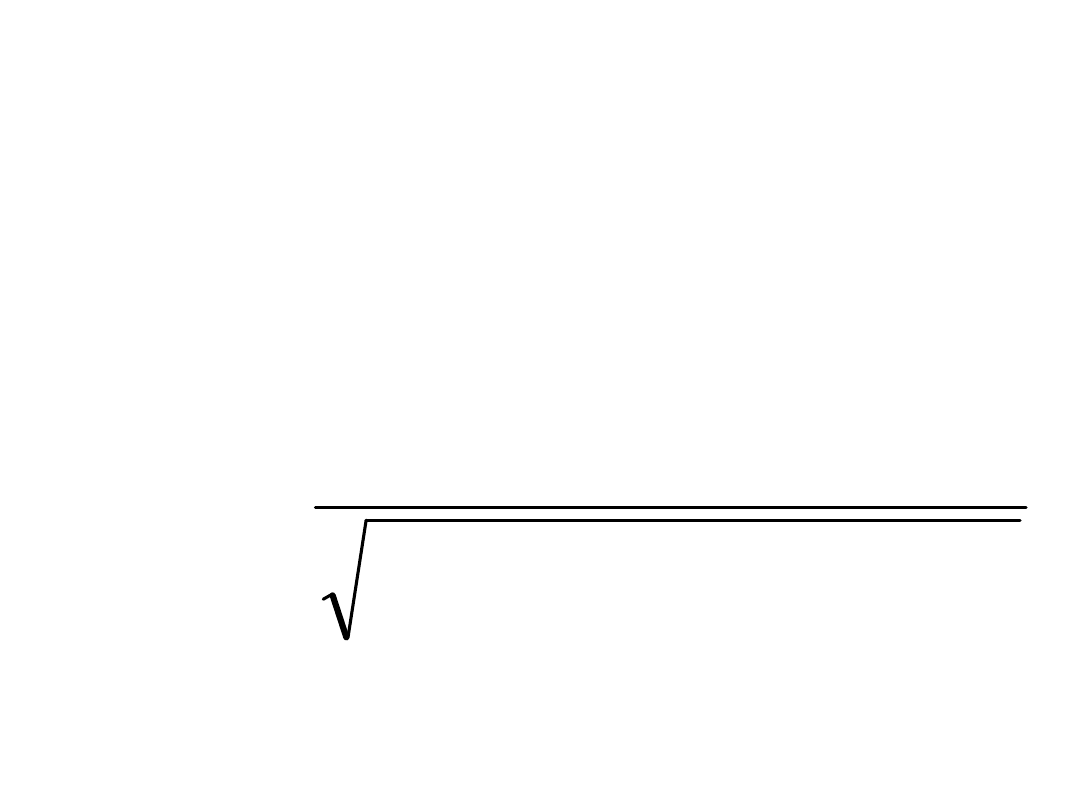
Rozwiązanie w postaci

zespolonej





.

2

2

2

2

2

0

2

0

)

(











b

m

F

A

Ae

z

t

i











Oscylatory - zwłaszcza tłumiony i wymuszony – dobrze jest opisywać przy pomocy
liczb zespolonych. Główną zaletą ich stosowania jest jednoczesny opis amplitudy
i fazy.

Część rzeczywistą

rozwiązania

już znamy





.

cos









t

A

x

Postać zespolona

i

z





















sin

cos

sin

cos

i

r

ir

r

z













i

re

z 























tg

z

r

,

2

1

2

2

Dwa klocki symbolizują ruch
materii „góra” „dół”. Fala może
przemieszczać się w „lewo” lub
„w prawo” a klocki tego nie robią
: )

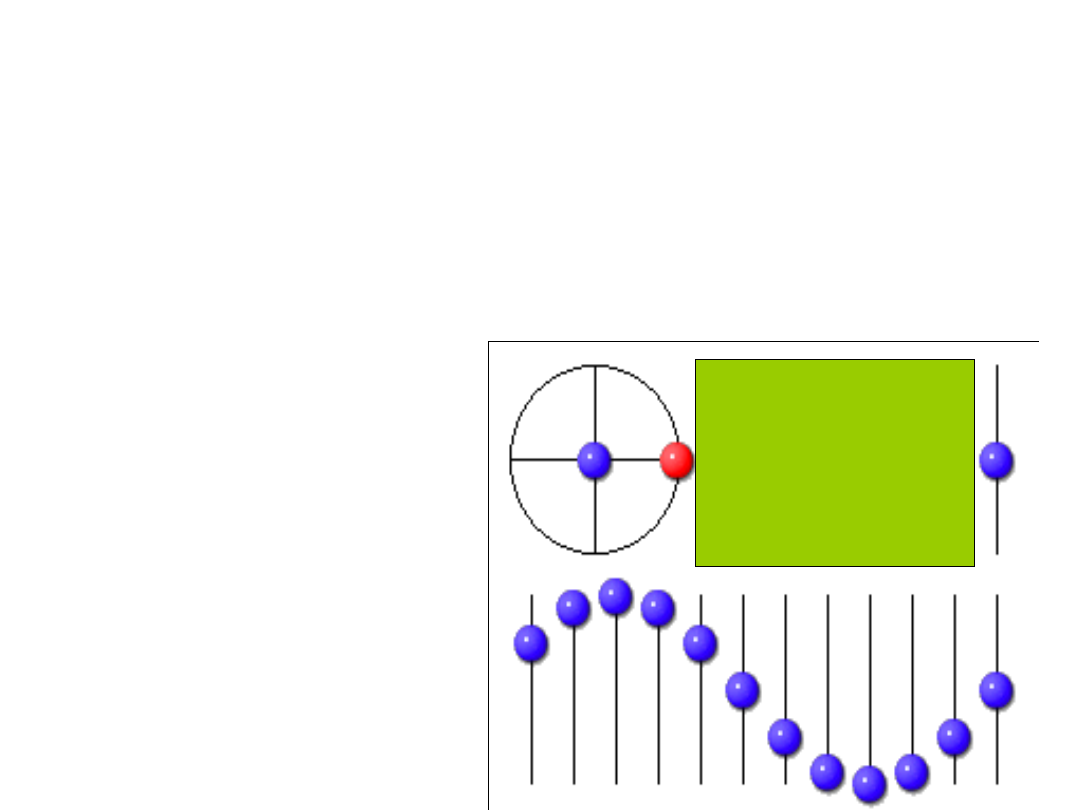
Ruch
harmoniczny

Ruch harmoniczny jest szczególnym
przykładem ruchów periodycznych. Są nimi
przykładowo:

•

wahadło matematyczne i fizyczne

• ciężarek na sprężynie

• drgania drobiny dwuatomowej (model to dwa ciężarki
na sprężynie)

Rozważmy animację
przedstawiającą ruch
punktu po okręgu i
rzut tego ruchu na
jedną z osi.

 : przemieszczenie

kątowe
 : prędkość kątowa

t : czas
 = t

r : promień koła,
amplituda
y(t) = r sin() =r

sin(t)

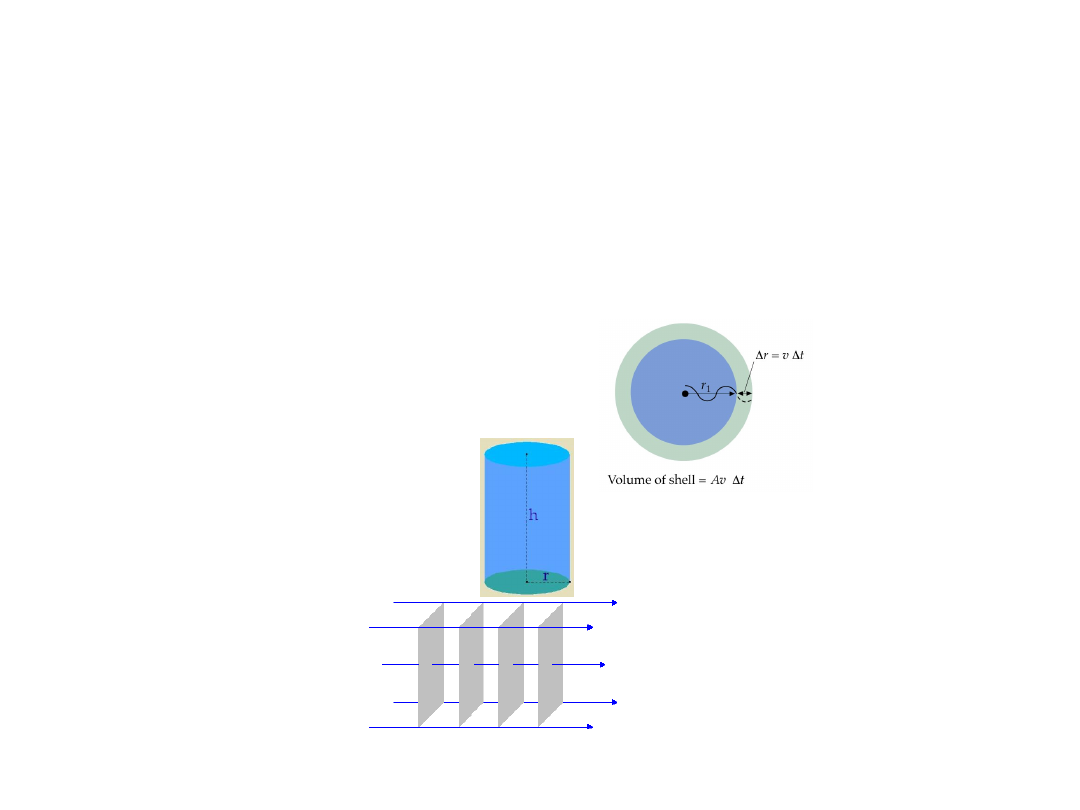
Rodzaje fal

Ze względu na zależność wychyleń

cząstek ośrodka od ich położenia

w przestrzeni

– Kuliste

– Walcowe

– płaskie

63

Równanie fali

f(x,t) = A sin (ω t - k x + φ

o

)

(fala płaska)

f(x,t) = A sin (ω t - k r + φ

o

)

(fala kulista)

Minus „ -” przy kx oznacza, że fala porusza

się „w prawo”

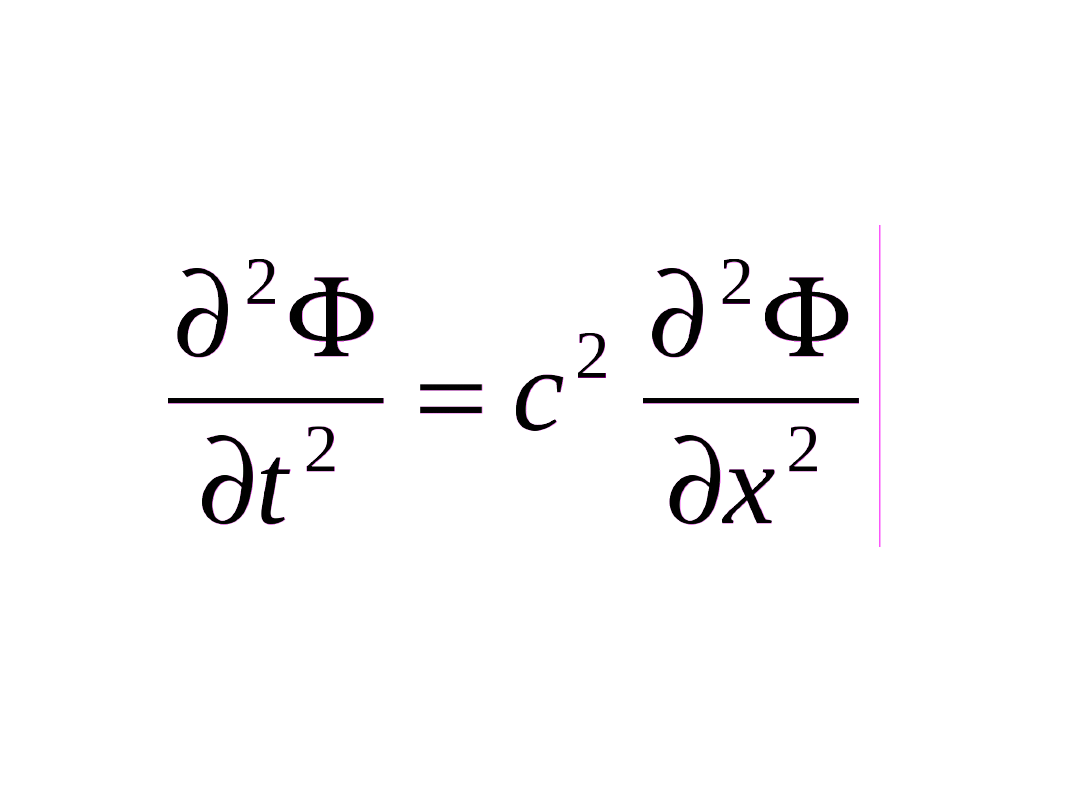
Równanie falowe

Każde równanie fali musi spełniać równanie
falowe
Zad: Sprawdź, że rzeczywiście fynkcja opisująca falę
płaską f(x,t) = A sin (ω t - k x + φ

o

)

spełnia równanie

falowe

długość fali – droga pokonywana przez powierzchnię falową

w czasie jednego okresu

liczba falowa –

liczbowo równa ilości długości fal mieszczących się

w długości 2

(okresowość przestrzenna)

Pulsacja, częstość kołowa

(okresowość czasowa)

ω = 2π/T

T

c









2



k

66

k może być zapisane jako wektor ale
wtedy współrzędne x,y,z, lub r zapisujemy
Wraz z odpowiednimi wersorami

Podstawowe parametry fali

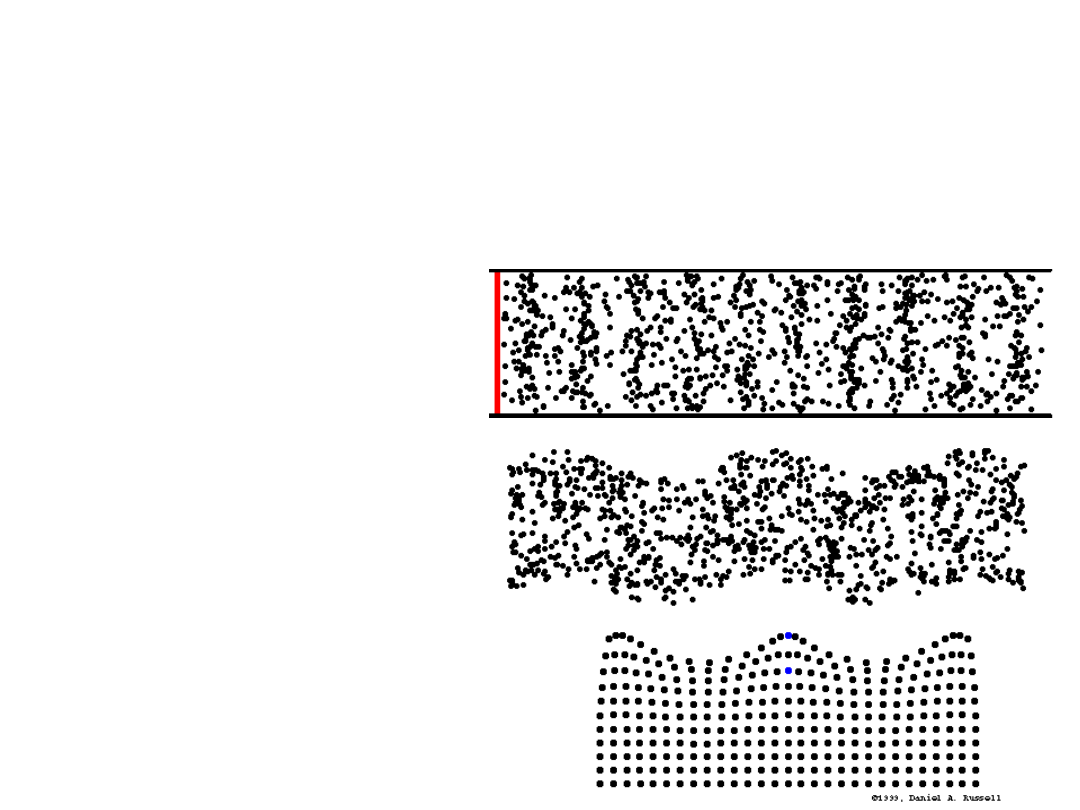
Rodzaje fal

Ze względu na kierunek wychyleń

(drgań) cząstek ośrodka

– podłużne

– poprzeczne

– mieszane

67

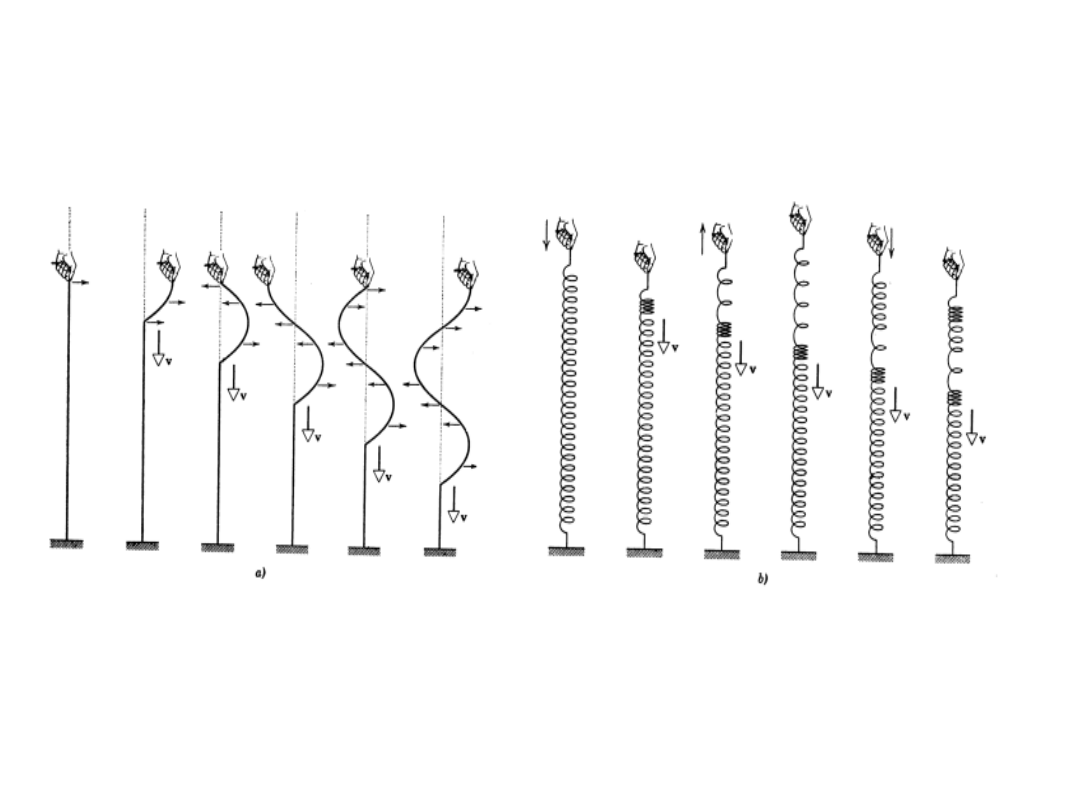
Rodzaje fal

W przypadku fali poprzecznej cząstki ośrodka (napiętej liny)
drgają w kierunku prostopadłym do kierunku rozchodzenia się
samej fali.

W przypadku fali podłużnej punkty materialne ośrodka
(rozciągniętej sprężyny) drgają w tym samym kierunku, w jakim
rozchodzi się fala.

68

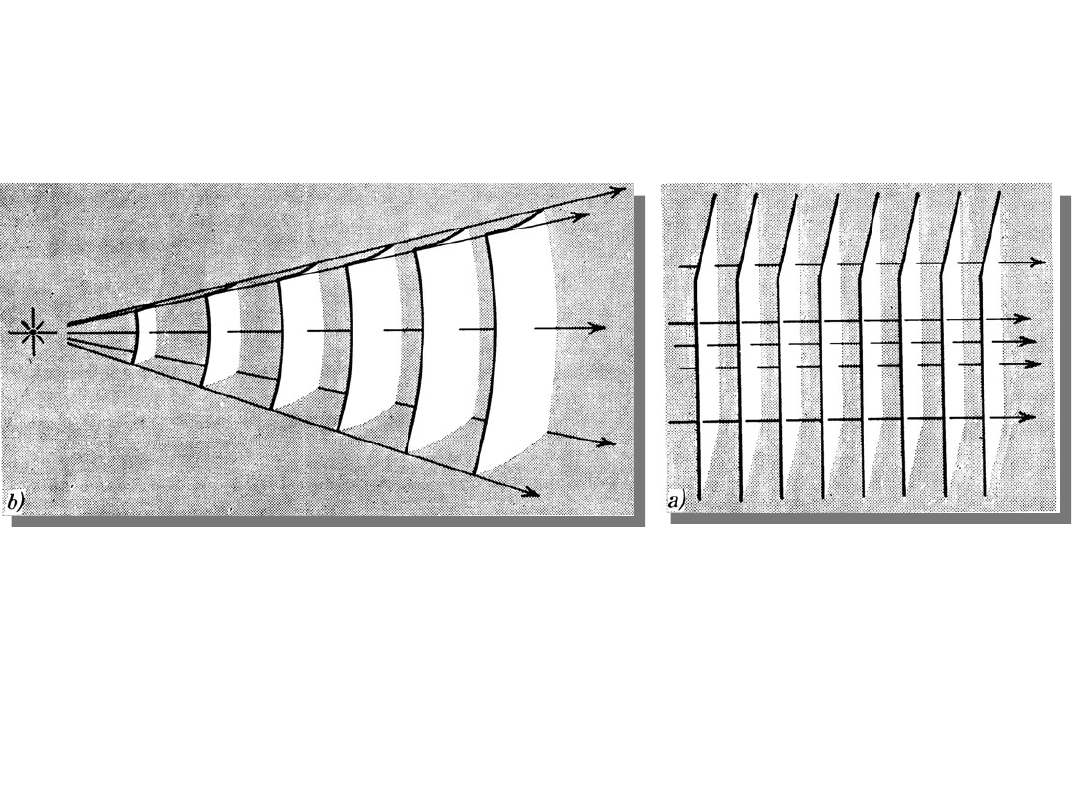
Rodzaje fal

(b) Fala kulista. Promienie fali układają się radialnie, a powierzchnie
falowe, odległe od siebie o długość fali, tworzą wycinki powłok
sferycznych. Daleko od źródła małe fragmenty powierzchni falowych
można traktować jako płaskie.

(a) Fala płaska. Płaszczyzny reprezentują powierzchnie falowe (czoła
fali) odległe od siebie o długość fali. Strzałkami oznaczono promienie
fali.

69

Fala kulista

Fala
płaska

Fale - definicje

Fala – zaburzenie lub zespół zaburzeń

rozchodzących się w przestrzeni ze skończoną

prędkością i niosące ze sobą energię.

Zaburzenie może mieć postać impulsu lub

drgań. Opisuje je tzw. funkcja falowa



=



o

(x,t) –

równanie fali płaskiej



=



o

(r,t) –

równanie fali kulistej.



=



o

(x,y,t)

– to mogła by być fala walcowa

jak ją zapisać?

W ogólnym przypadku  może być dowolną wielkością,

(ciśnieniem dla fali akustycznej, natężeniem E lyb H dla

fali EM

70

Fale - definicje

fala podłużna – kierunek drgań równoległy do kierunku

rozchodzenia się fali

fala poprzeczna – kierunek drgań prostopadły do kierunku

rozchodzenia się fali

fala kulista – powierzchnie falowe są wycinkami sfer

współśrodkowych (radialnych)

fala płaska – powierzchnie falowe są wycinkami

równoległych do siebie płaszczyzn

powierzchnia falowa – zbiór punktów przestrzeni

będących w tej samej fazie drgań

promień falowy (promień fali) – półprosta

rozpoczynająca się w źródle i przechodząca przez dany

punkt ośrodka (jest zawsze prostopadła do pow. falowych)

czoło fali – powierzchnia falowa najbardziej oddalona od

źródła

71

Fale - definicje

faza drgań – stan drgań danego punktu

ośrodka opisywany przez

, d/dt,

d

2

/dt

2

w przypadku fali harmonicznej liczba z

przedziału od 0 do 2)

prędkość (fazowa) fali – prędkość

przemieszczania się dowolnej powierzchni

falowej (jest to jednocześnie prędkość

przenoszenia energii przez falę)

częstość fali –

f=1/T

okres fali – najmniejszy odstęp czasu po

którym w danym punkcie ośrodka fala

ponownie będzie miał tą samą fazę drgań

72

natężenie fali – energia

przenoszona przez falę przez

jednostkową powierzchnię w

jednostce czasu

t

S

E

I









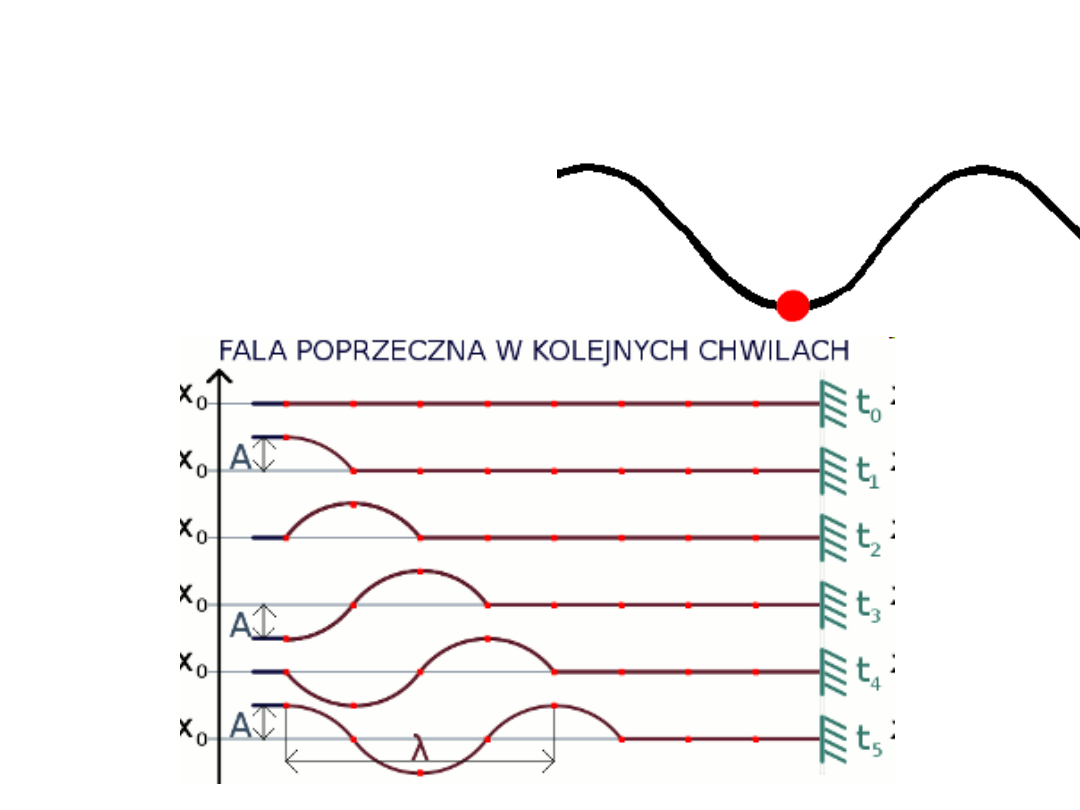
fale poprzeczne

fale poprzeczne

–

–

gdy kierunek drgań jest prostopadły do kierunku

gdy kierunek drgań jest prostopadły do kierunku

rozchodzenia się fali, np. fale rozchodzące się

rozchodzenia się fali, np. fale rozchodzące się

w strunach instrumentów muzycznych ,

w strunach instrumentów muzycznych ,

(do fal poprzecznych zaliczamy również

(do fal poprzecznych zaliczamy również

fale elektromagnetyczne);

fale elektromagnetyczne);

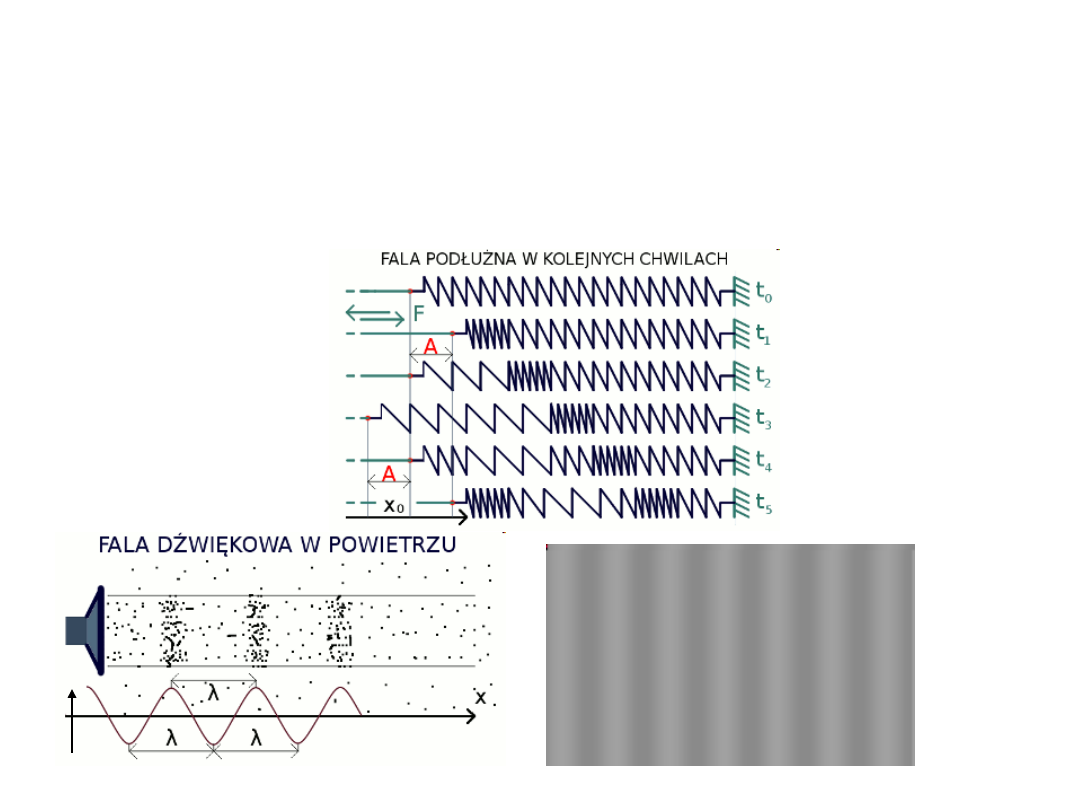
fale podłużne

fale podłużne

- jeśli cząstki ośrodka poruszają się równolegle

- jeśli cząstki ośrodka poruszają się równolegle

do kierunku

do kierunku

rozchodzenia się fali, np. fale dźwiękowe.

rozchodzenia się fali, np. fale dźwiękowe.



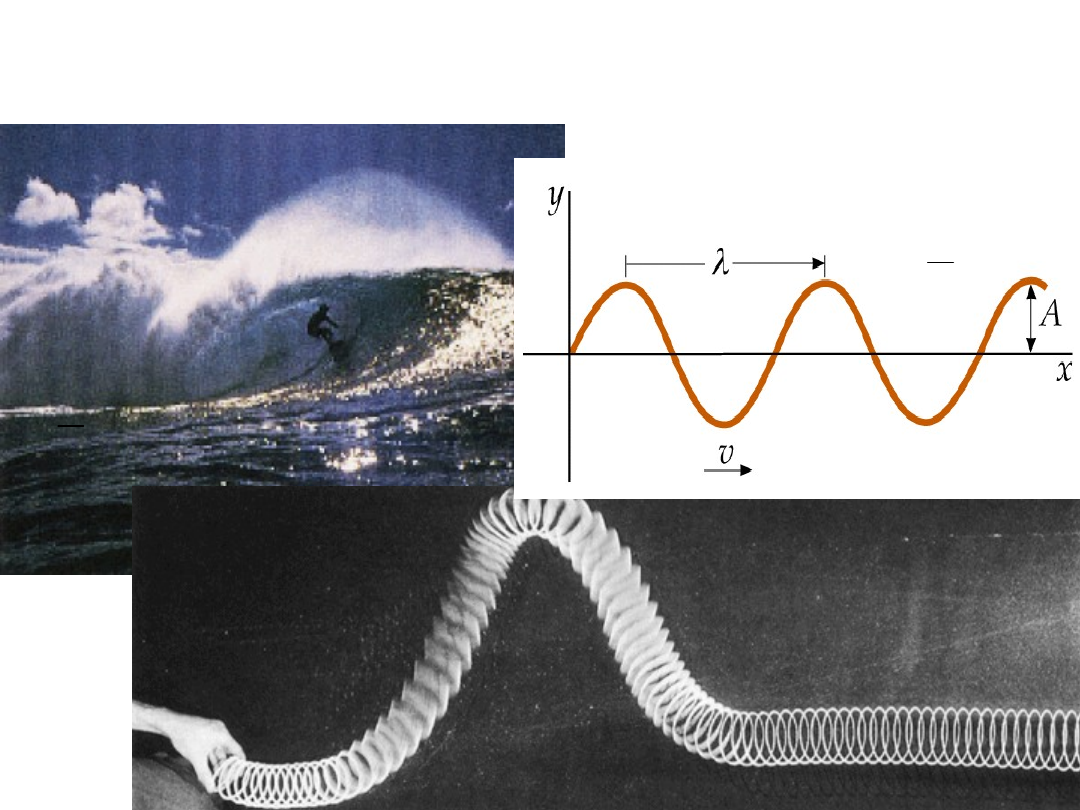
Ruch falowy

musi być opisany

zarówno w czasie jak

i w przestrzeni

f

v

f

v











f

v

f











v

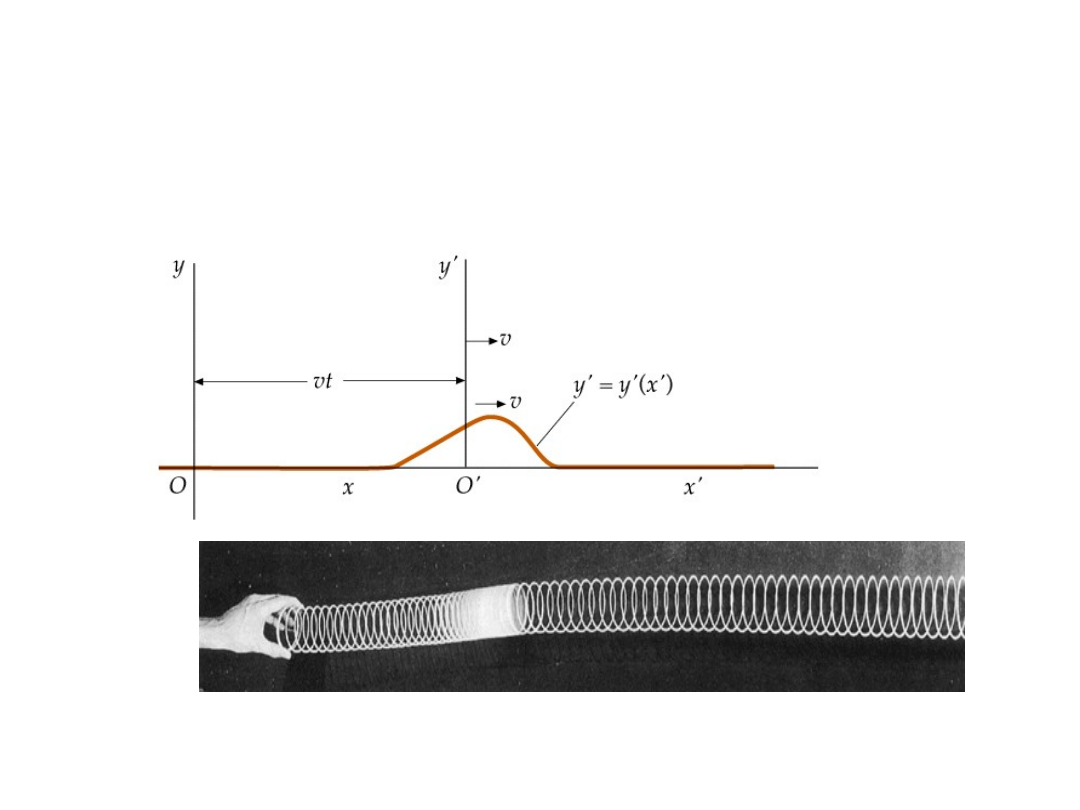
Impuls falowy

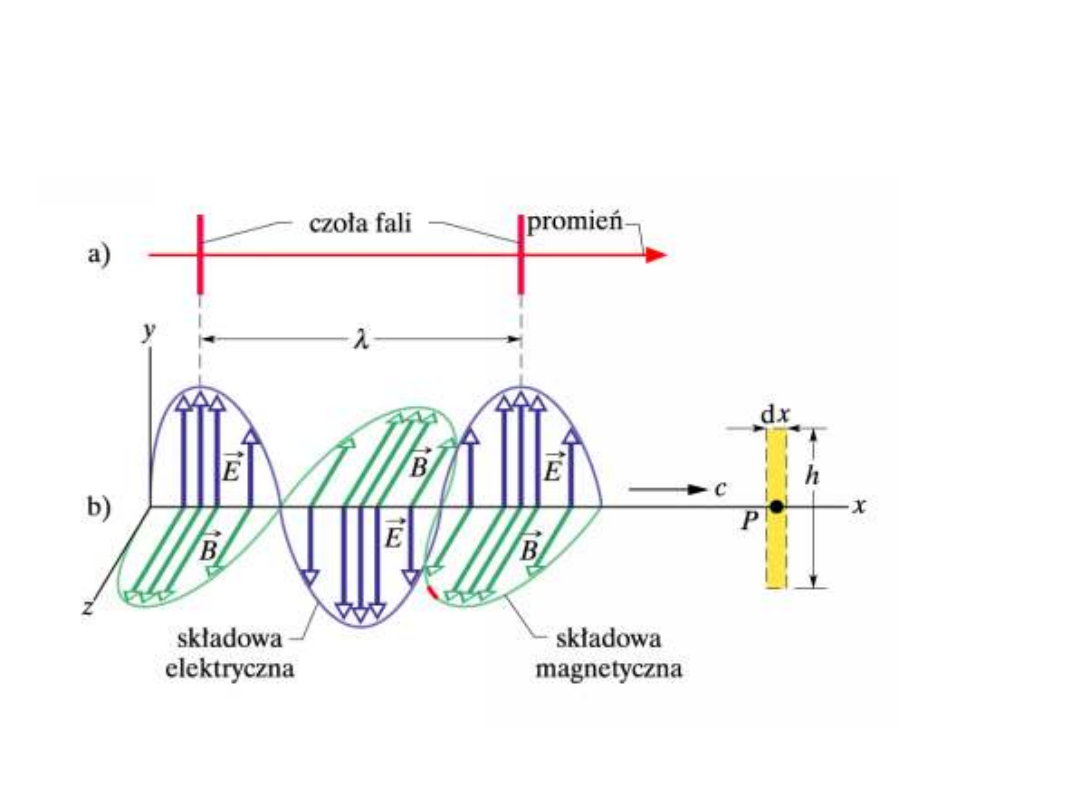
Fala poprzeczna

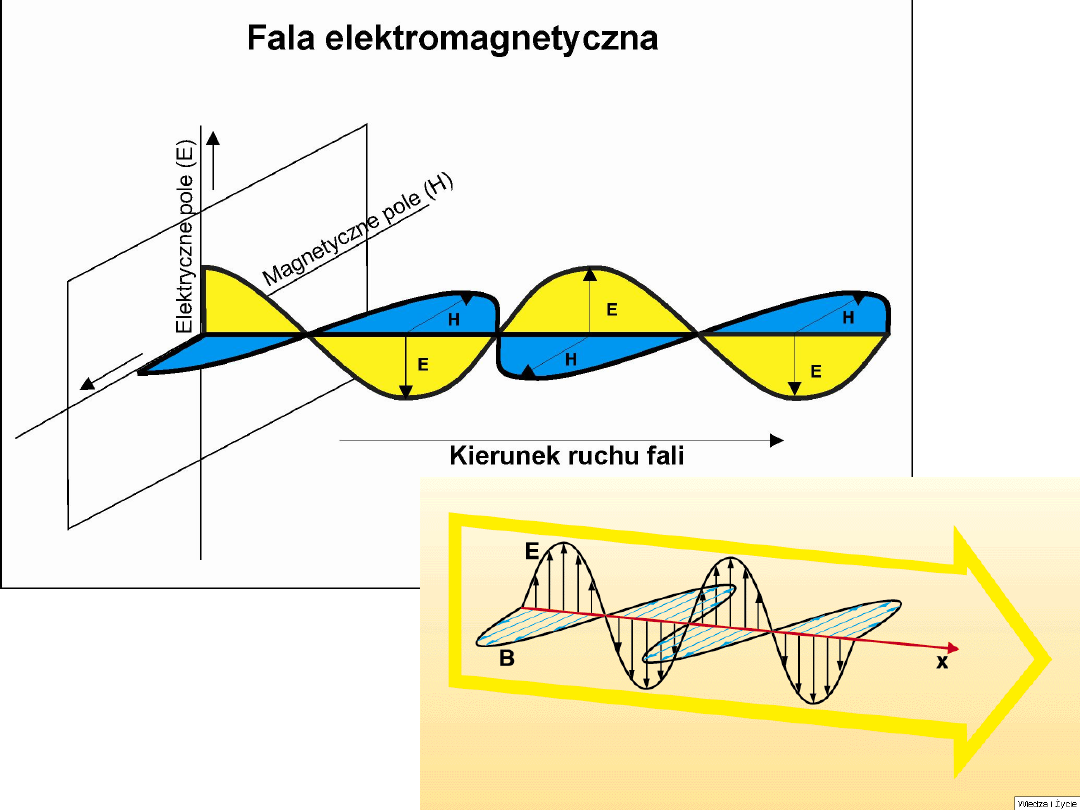
Przykład
rozchodzenia się
Fali poprzecznej

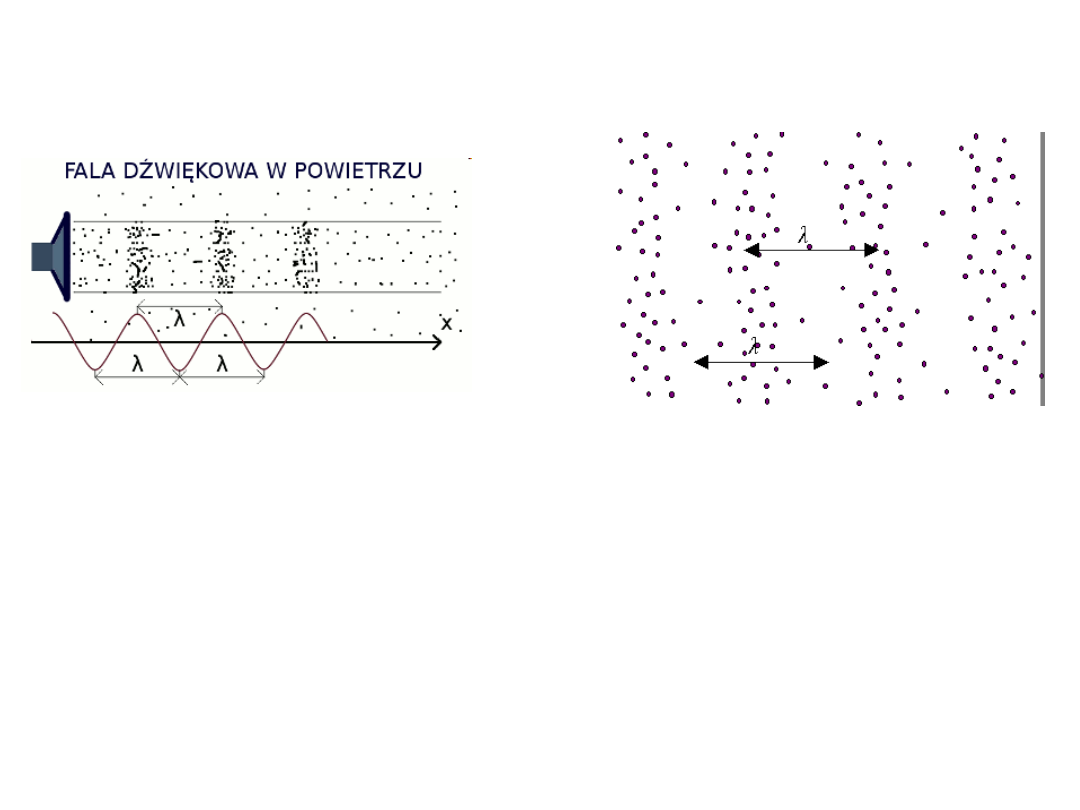
Fala akustyczna jest falą podłużną

Przeciętne ucho słyszy dźwięki o częstości od 16 Hz do 20 kHz.

Fale o częstości poniżej 16 Hz nazywamy infradźwiękami,

a powyżej 20 kHz ultradźwiękami.

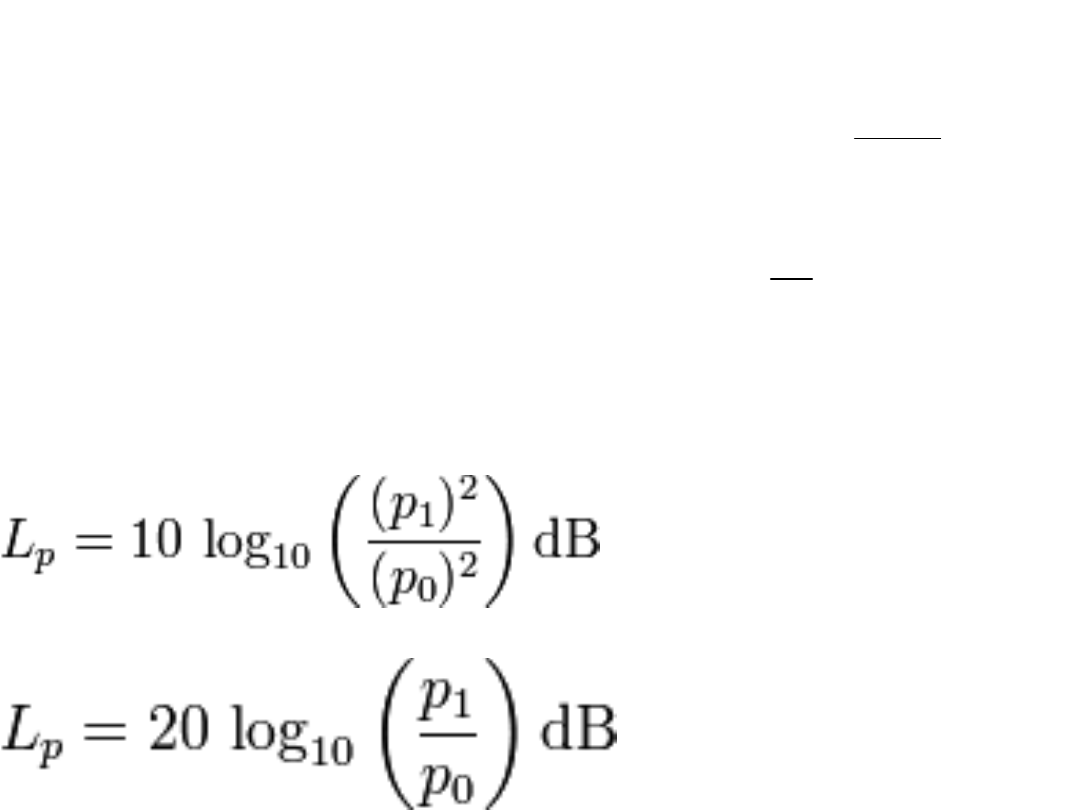
Natężenie fali akustycznej
zależy od kwadratu ciśnienia

I ~ p

2

RT

p







2

12

0

/

10

m

W

I





t

S

E

I









p

o

= 10

-5

Pa

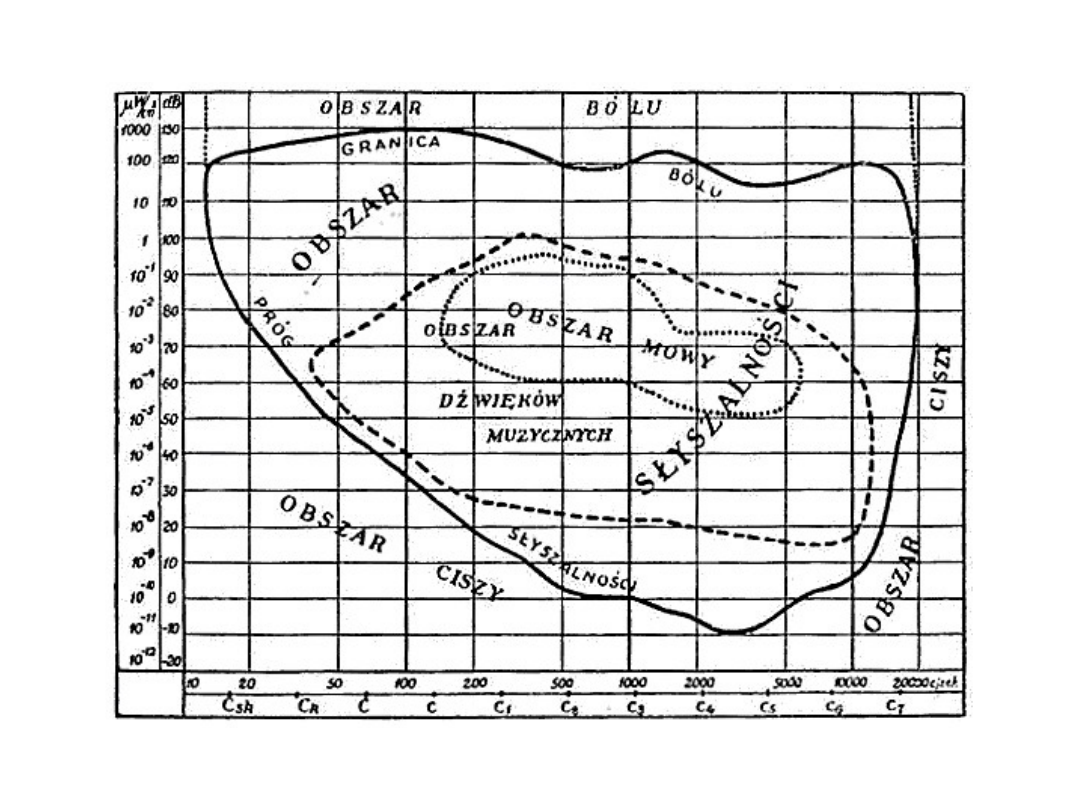
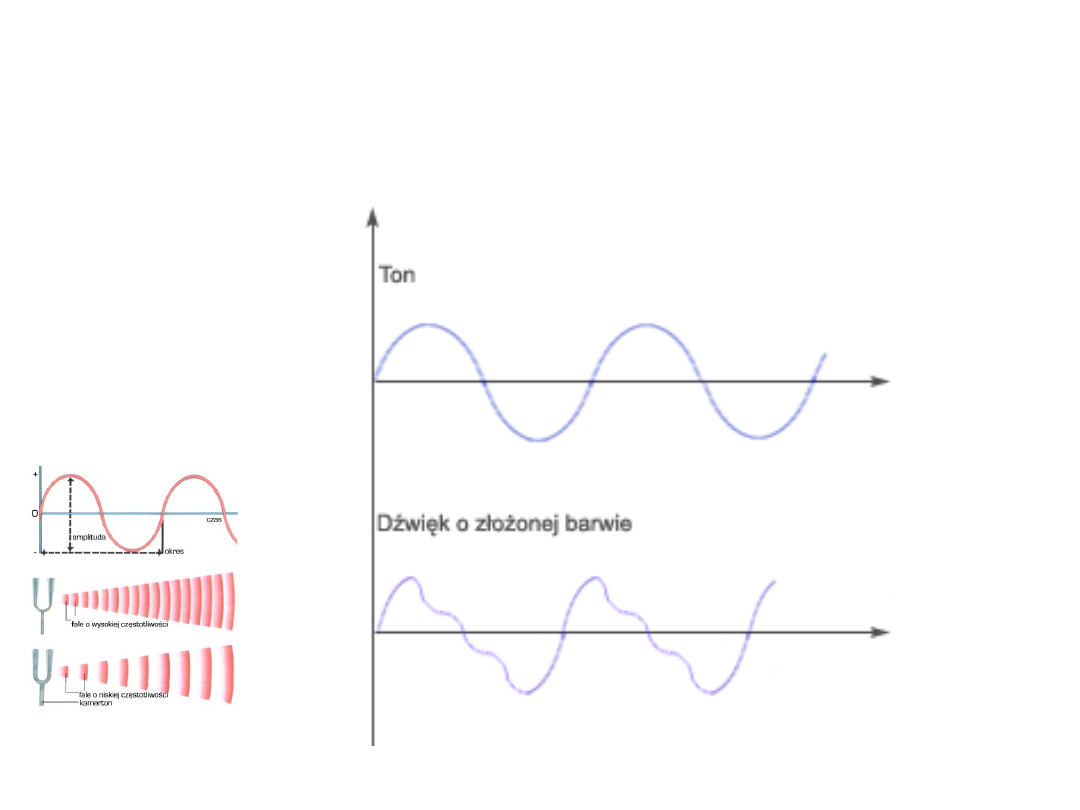
Dźwięki słyszalne charakteryzujemy podając tzw. znamiona dźwięku:
1. Wysokość (częstość drgań),
2. Głośność lub natężenie (amplitudę drgań),
3. Barwa (widmo akustyczne)

Największą czułość ucho przejawia w zakresie częstości 2-3 kHz.

Za głośność wzorcową przyjmujemy głośność
dźwięku o częstości 1 kHz i natężeniu
odpowiadającemu progowi słyszalności przy tej
częstości.

2

12

0

/

10

m

W

I





Głośność dźwięku o tej samej częstości i innym natężeniu :

I

0

lg

I

I

L 

Jednostkami głośności są bele lub częściej używane decybele .

 

B

 

dB

np. zwykła rozmowa ma głośność około ,
tzn. jej natężenie dźwięku jest razy
większe od progu słyszalności.

B

dB 4

40 

4

0

10

10

/





L

I

I

Dla dźwięków o innej częstości niż wzorcowa 1 kHz
głośność podajemy w fonach (nie decybelach), gdy
dźwięk wydaje się być tak samo głośny jak dźwięk o
częstości wzorcowej i danej liczbie decybeli.

10 dB - szmer liści przy łagodnym wietrze
20 dB - szept, cichy ogród
30 dB - bardzo spokojna ulica bez ruchu
kołowego
40 dB - szmery w mieszkaniu,
50 dB - szum w biurach
60 dB-90 dB - odkurzacz
70 dB - wnętrze głośnej restauracji
80 dB - głośna muzyka w pomieszczeniach,
100 dB - motocykl bez tłumika
120 dB - śmigło helikoptera w odległości 5 m
160 dB - wybuch petardy

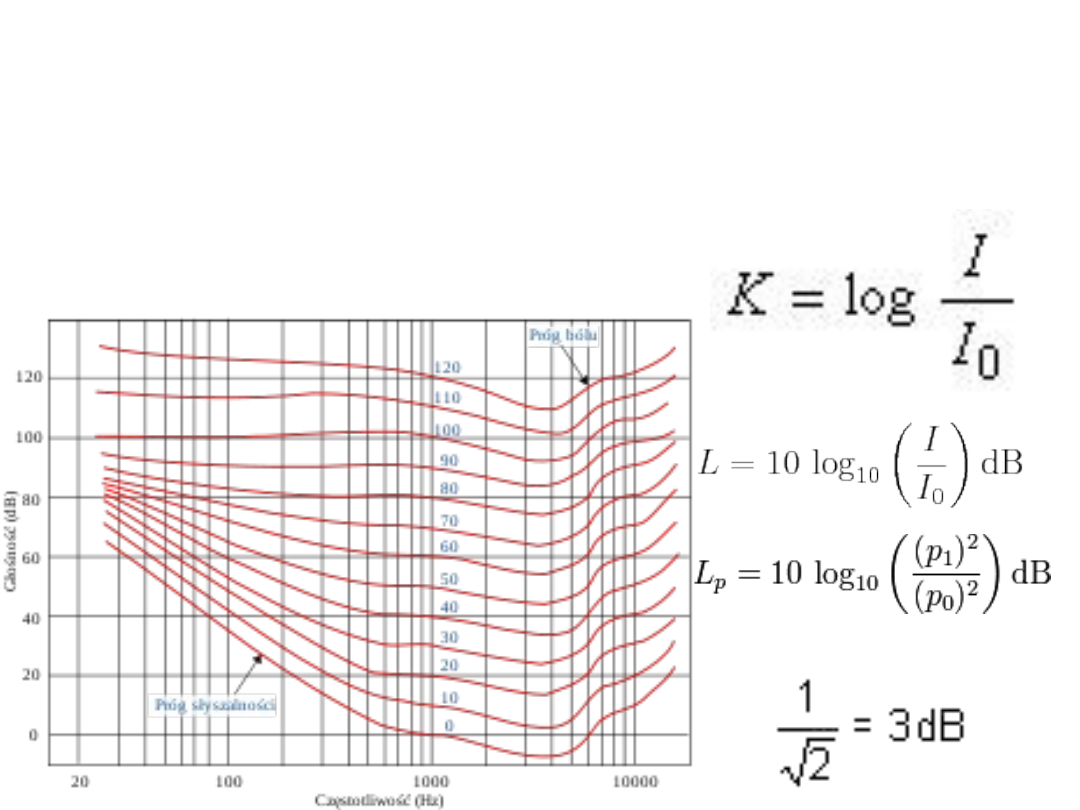
Natężenie dźwięku

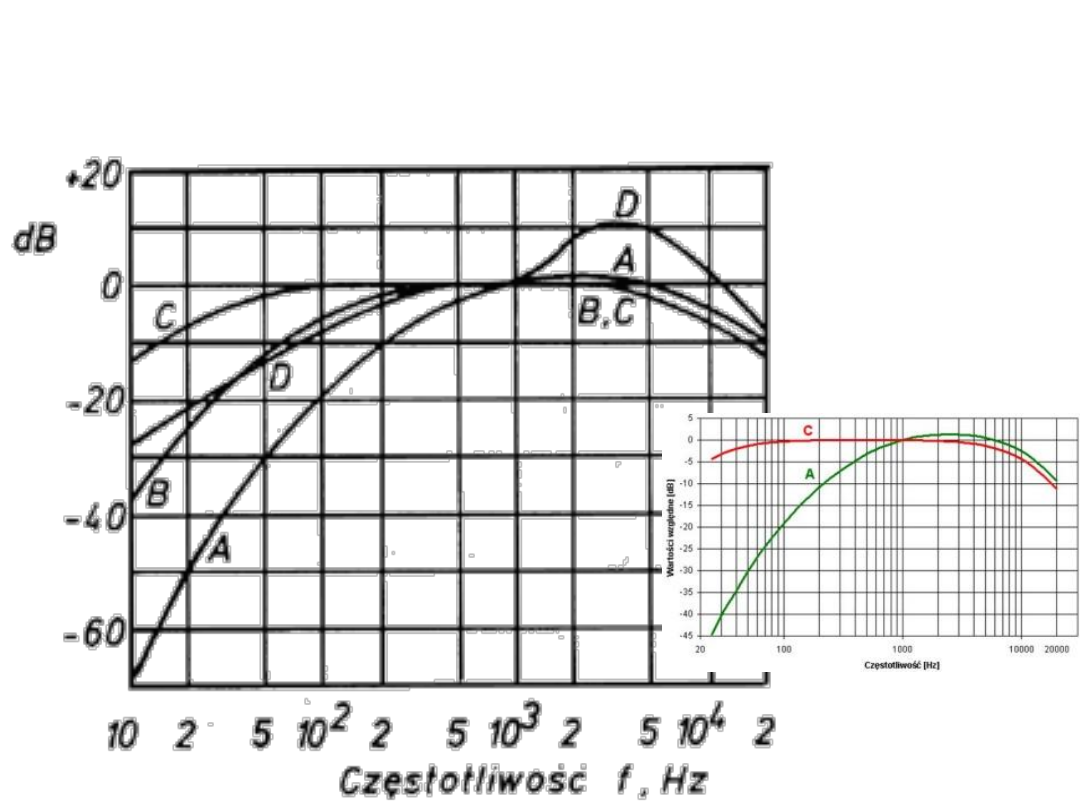
Charakterystyki
pomiarowe

Przy podawaniu
natężenia dźwięku
w decybelach
podajemy zawsze
jaka była
charakterystyka
pomiarowa np.

L

AdB

lub

L

CdB

W przypadku odkształceń objętościowych lub
postaciowych analogiczne wyprowadzenia dają
prędkość:



K

v

1





G

v 

lub

K

– moduł ściśliwości

G

– moduł sztywności

Rozchodzenie się fali głosowej w gazach odpowiada w
przybliżeniu przemianom adiabatycznym (bez
wymiany ciepła z otoczeniem):

const

pV 



V

P

c

c /





Po zróżniczkowaniu:

0

1







dV

V

p

dp

V







stąd:

V

dV

p

dp







z prawa Hooke’a:

dp

K

V

dV





Po podstawieniu:

p

K

dp

pK

dp





1







Prędkość dźwięku w gazie:





p

v 

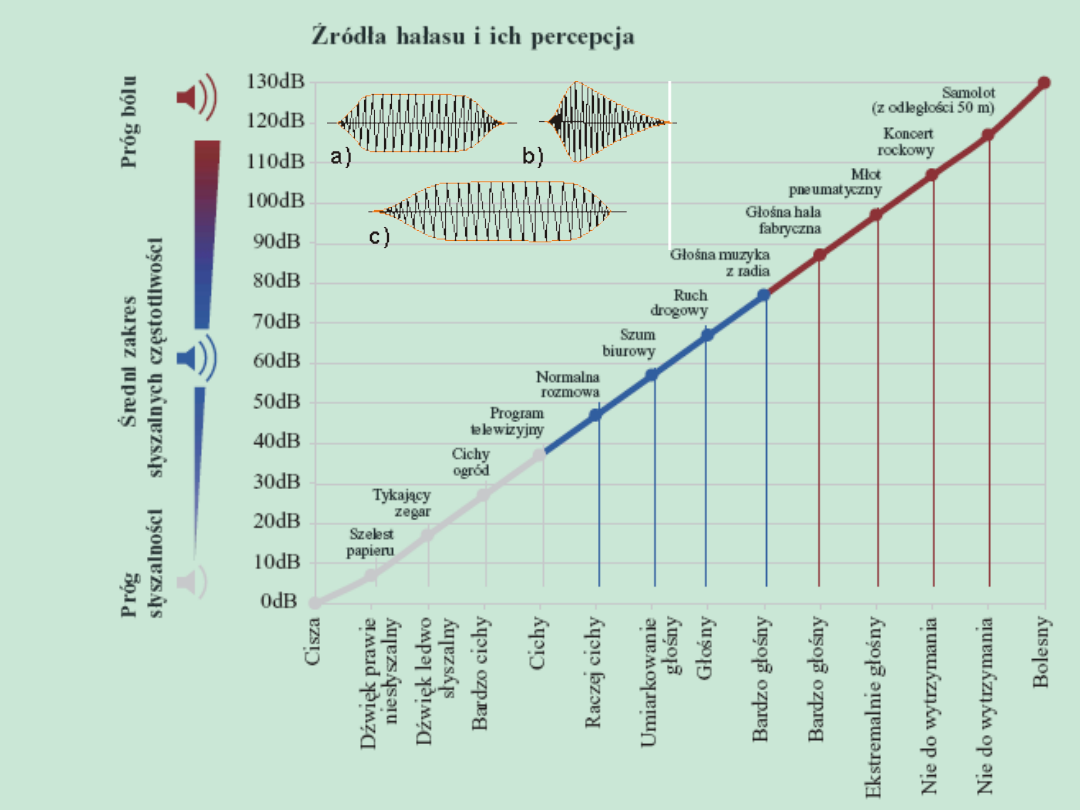
Należy dążyć do obniżenia
hałasu co najmniej poniżej
65 dB

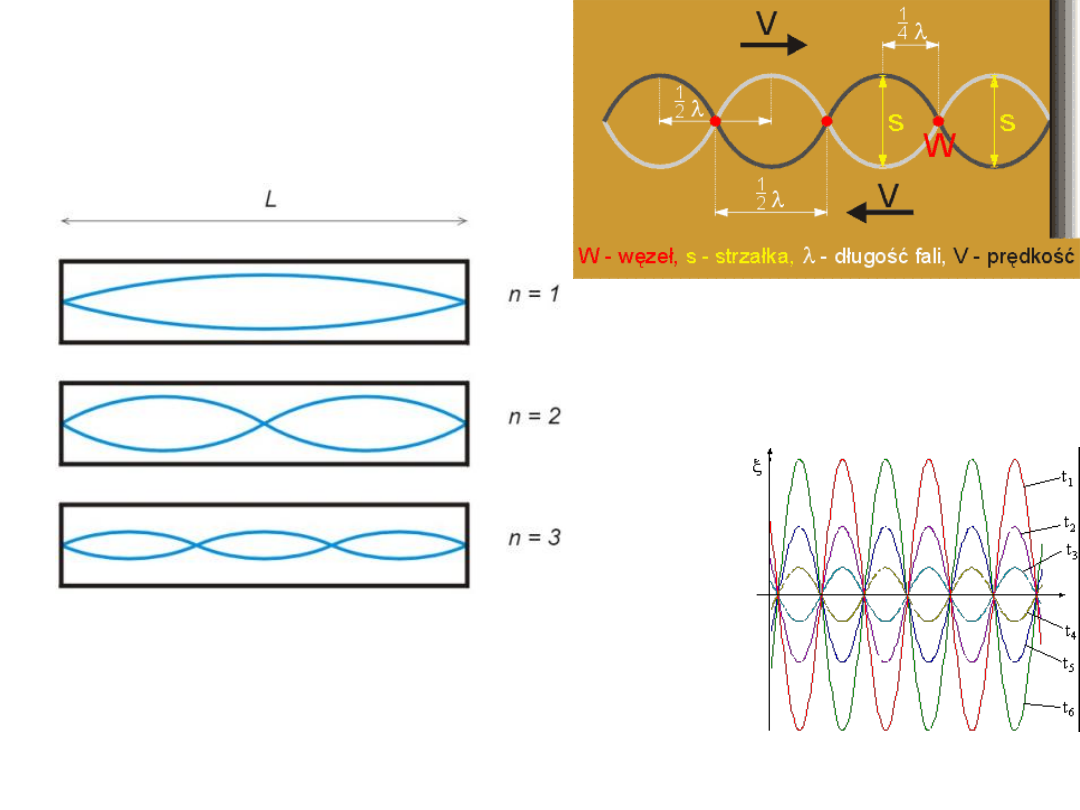
Fala stojąca

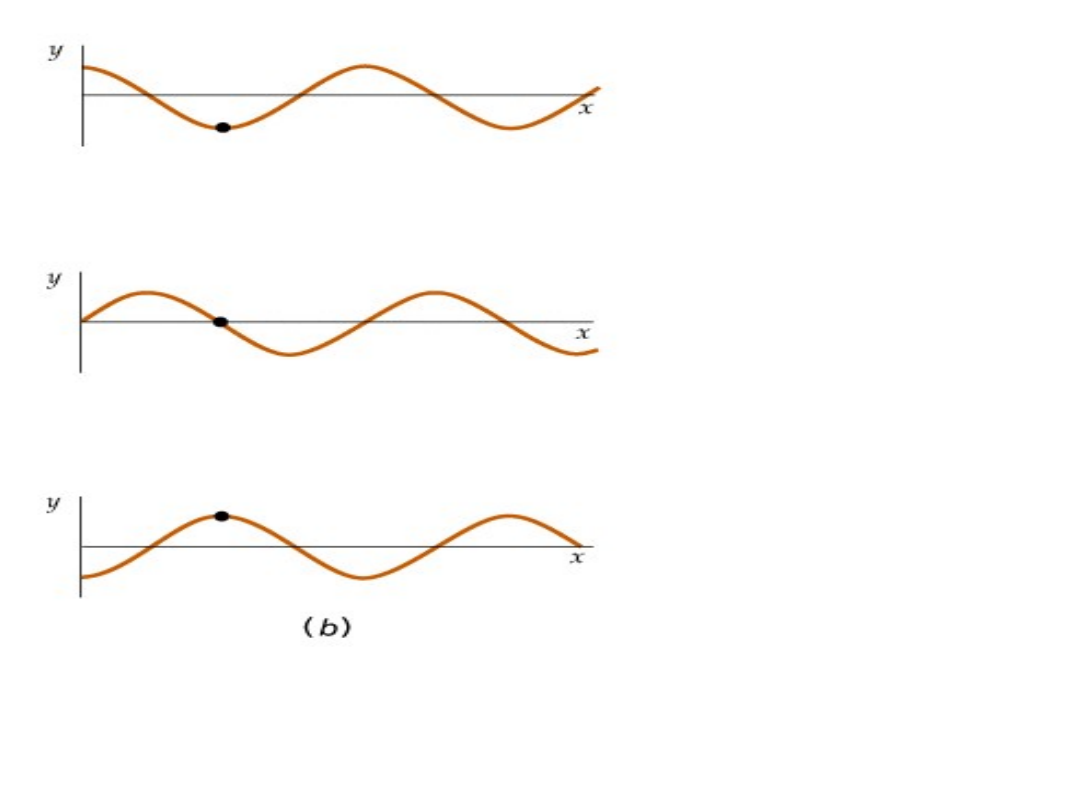
Zasada SUPERPOZYCJI

Zasada SUPERPOZYCJI

W ośrodkach liniowych podczas jednoczesnego rozchodzenia się

W ośrodkach liniowych podczas jednoczesnego rozchodzenia się

kilku fal

kilku fal

wypadkowe zaburzenie w dowolnym punkcie tego ośrodka jest sumą

wypadkowe zaburzenie w dowolnym punkcie tego ośrodka jest sumą

zaburzeń,

zaburzeń,

jakie wywołałyby poszczególne fale. Taki sposób dodawania

jakie wywołałyby poszczególne fale. Taki sposób dodawania

zaburzeń nazywamy

zaburzeń nazywamy

superpozycją (lub nakładaniem się) fal

superpozycją (lub nakładaniem się) fal

.

.

Dwie fale nazywamy

Dwie fale nazywamy

spójnymi (koherentnymi)

spójnymi (koherentnymi)

jeśli

jeśli

różnica ich faz nie zależy od

różnica ich faz nie zależy od

czasu

czasu

. Spójnym falom odpowiadają spójne drgania cząstek ośrodka.

. Spójnym falom odpowiadają spójne drgania cząstek ośrodka.

A więc fale harmoniczne o

A więc fale harmoniczne o

jednakowych częstościach

jednakowych częstościach

są zawsze spójne.

są zawsze spójne.

)

kx

sin(

A

)

0

t

,

x

(

y

)

kx

sin(

A

)

0

t

,

x

(

y

2

2

2

2

2

1

1

1

1

1

















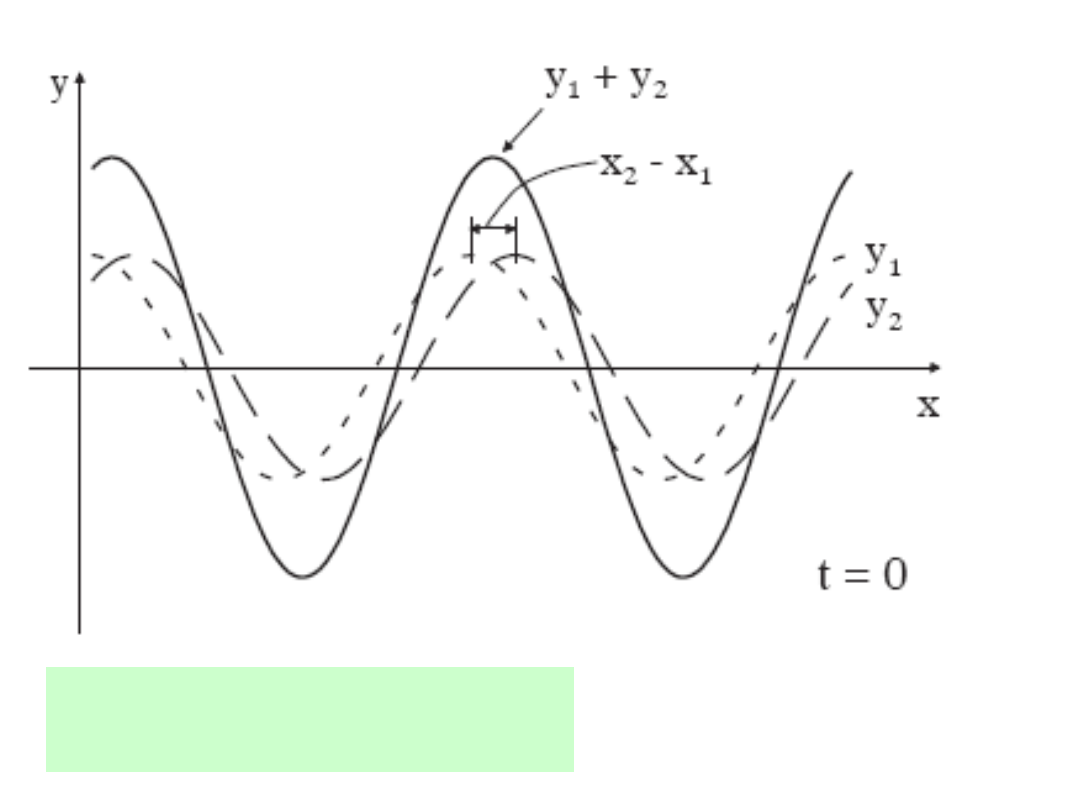
Przykład sumowania (interferencji)

Przykład sumowania (interferencji)

dwóch fal spójnych.

dwóch fal spójnych.

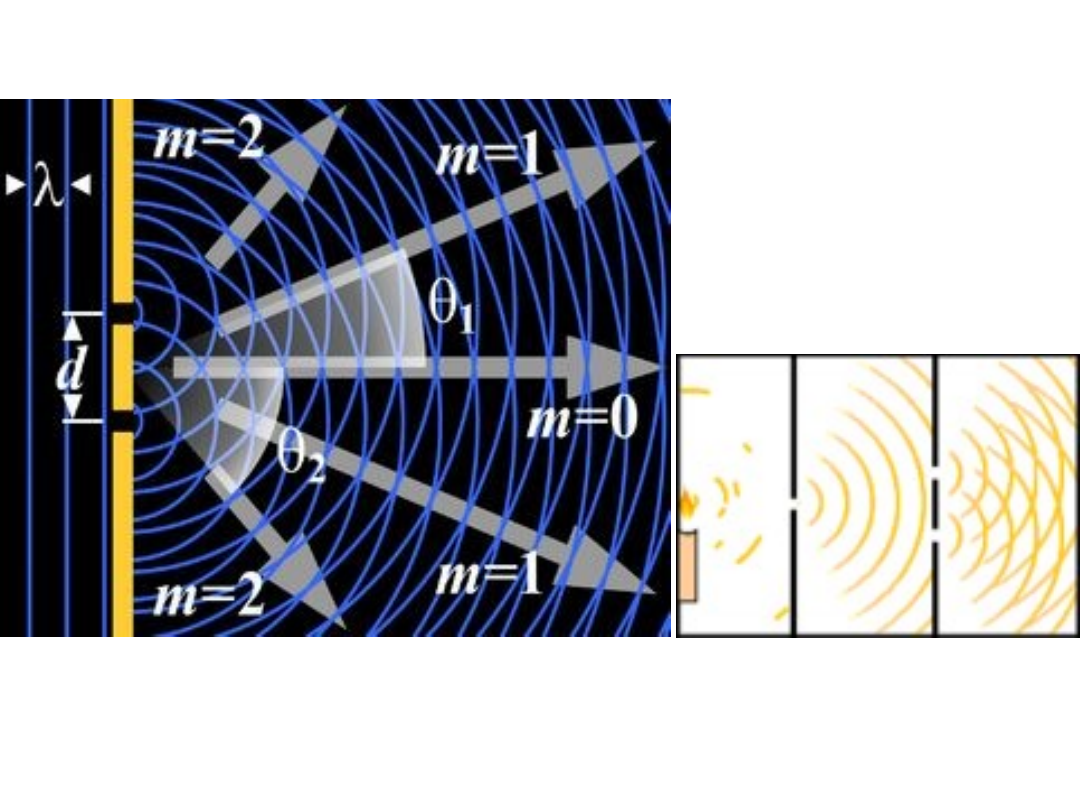
Interferencja dwóch spójnych fal wychodzących z

Interferencja dwóch spójnych fal wychodzących z

dwóch szczelin

dwóch szczelin

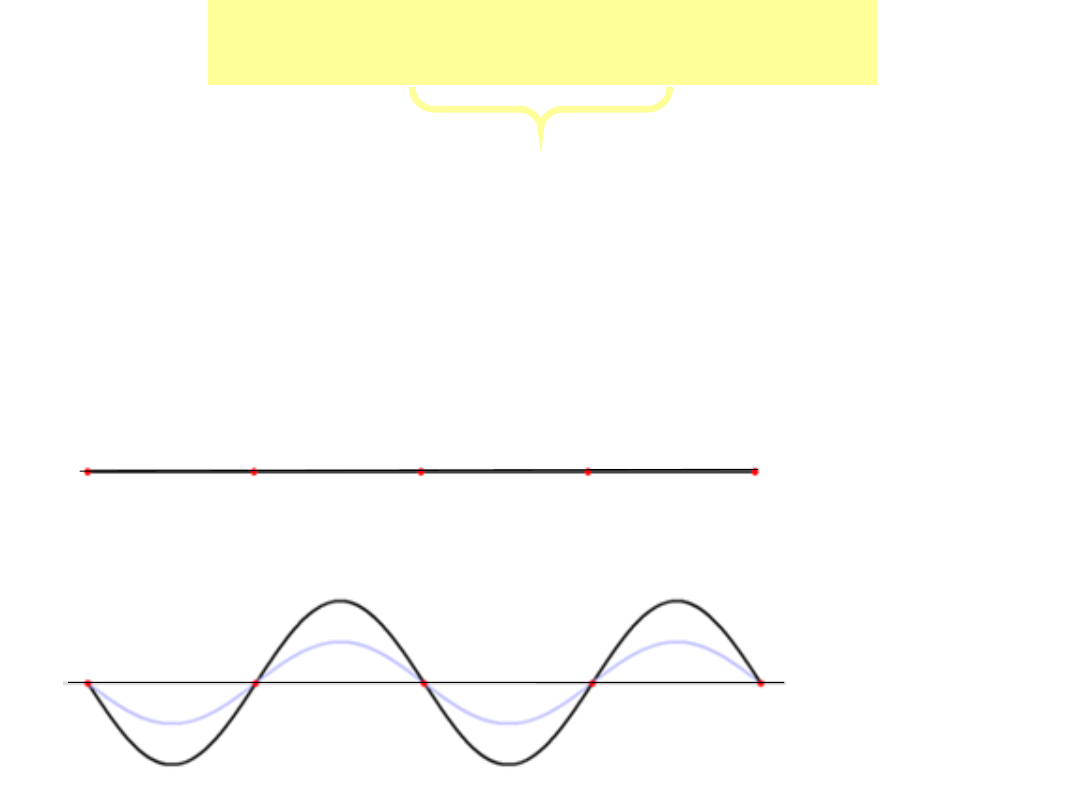
Jak widać amplituda drgań wypadkowych jest okresową funkcją współrzędnej

Jak widać amplituda drgań wypadkowych jest okresową funkcją współrzędnej

przestrzennej

przestrzennej

x

x

, a więc jest różna w różnych punktach ośrodka.

, a więc jest różna w różnych punktach ośrodka.

Fala nie przemieszcza się w przestrzeni, dlatego nazywamy ja

Fala nie przemieszcza się w przestrzeni, dlatego nazywamy ja

falą stojącą

falą stojącą

.

.

Punkty ośrodka, których amplituda drgań jest maksymalna i wynosi 2A nazywamy

Punkty ośrodka, których amplituda drgań jest maksymalna i wynosi 2A nazywamy

strzałkami fali stojącej, natomiast punkty pozostające w spoczynku nazywamy

strzałkami fali stojącej, natomiast punkty pozostające w spoczynku nazywamy

węzłami fali stojącej.

węzłami fali stojącej.

   

t

sin

kx

cos

A

2

)

t

,

x

(

y





AMPLITUDA WYPADKOWA

AMPLITUDA WYPADKOWA

Figury Chladniego

Figury Chladniego

–

figury tworzone przez piasek lub opiłki korka, gromadzące się w

figury tworzone przez piasek lub opiłki korka, gromadzące się w

węzłach fali stojącej

węzłach fali stojącej

na drgającej sprężystej płytce. Kształt i ilość obszarów węzłów i

na drgającej sprężystej płytce. Kształt i ilość obszarów węzłów i

strzałek zależy od częstotliwości siły wymuszającej drgania i od częstości drgań

strzałek zależy od częstotliwości siły wymuszającej drgania i od częstości drgań

własnych płytki.

własnych płytki.

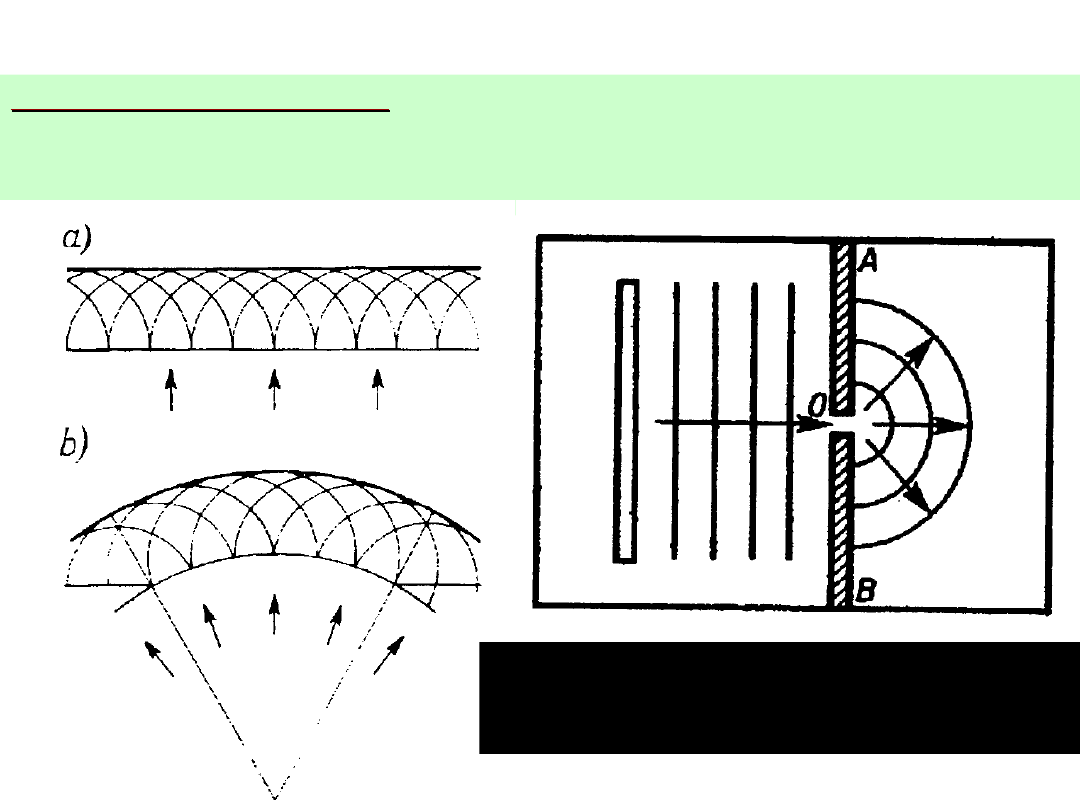
DYFRAKCJA (UGIĘCIE) FAL

DYFRAKCJA (UGIĘCIE) FAL

Zasada Huygensa (1690)

Zasada Huygensa (1690)

Każdy punkt ośrodka sprężystego po dojściu do niego zaburzenia

Każdy punkt ośrodka sprężystego po dojściu do niego zaburzenia

(czoła fali)

(czoła fali)

staje się źródłem wtórnej fali (płaskiej, kolistej, kulistej)

staje się źródłem wtórnej fali (płaskiej, kolistej, kulistej)

Ugięcie fali występuje tym wyraźniej, im mniejsze są wy-

Ugięcie fali występuje tym wyraźniej, im mniejsze są wy-

miary szczeliny w stosunku do długości padającej fali;

miary szczeliny w stosunku do długości padającej fali;

jeżeli otwór jest bardzo szeroki zjawisko praktyczne nie

jeżeli otwór jest bardzo szeroki zjawisko praktyczne nie

występuje.

występuje.

W zależności od tego, jaka jest szerokość

W zależności od tego, jaka jest szerokość

szczeliny d w porównaniu z długością fali λ,

szczeliny d w porównaniu z długością fali λ,

zjawisko dyfrakcji będzie mniej lub bardziej

zjawisko dyfrakcji będzie mniej lub bardziej

wyraźne.

wyraźne.

Obserwujemy je wyraźnie zawsze wtedy, gdy

Obserwujemy je wyraźnie zawsze wtedy, gdy

d < λ lub d = λ

d < λ lub d = λ

Dyfrakcja fal na wodzie.

Dyfrakcja fal na wodzie.

Pierścienie dyfrakcyjne;

Pierścienie dyfrakcyjne;

Efekt dyfrakcji światła na otworze

Efekt dyfrakcji światła na otworze

kołowym.

kołowym.

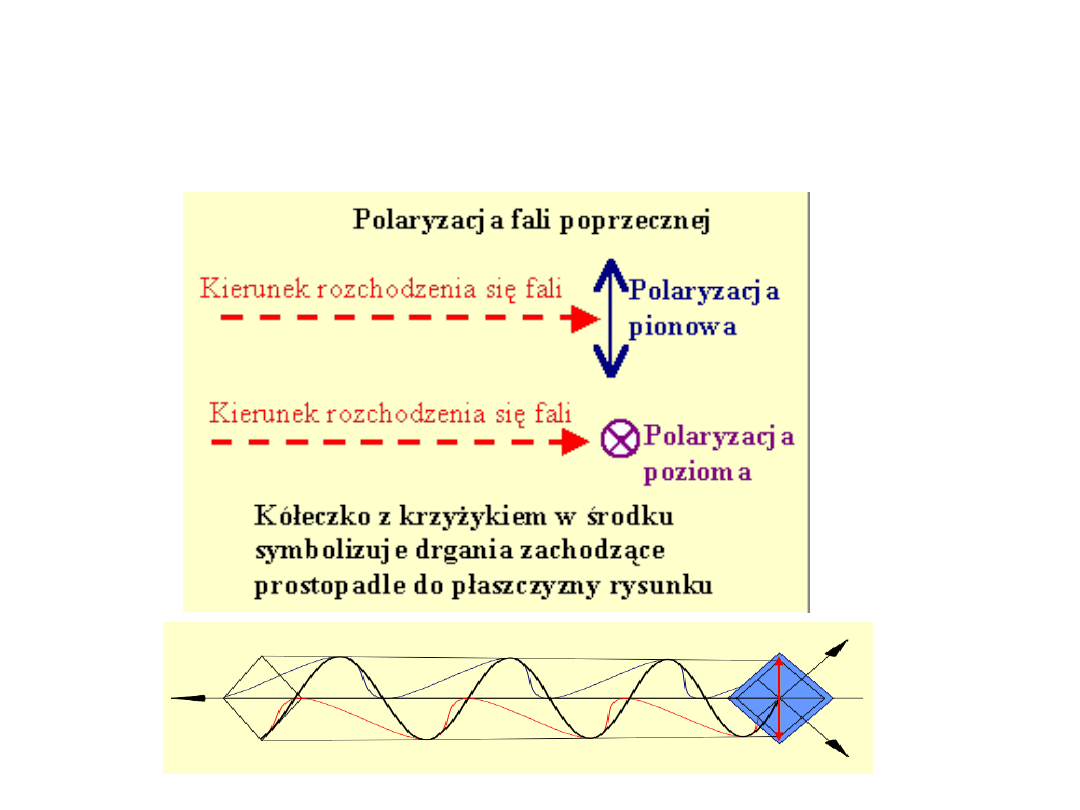
Polaryzacja fali poprzecznej

Polaryzacja fali poprzecznej

Drgania poprzeczne mają dodatkową uzupełniającą właściwość zwaną polaryzacją.

Drgania poprzeczne mają dodatkową uzupełniającą właściwość zwaną polaryzacją.

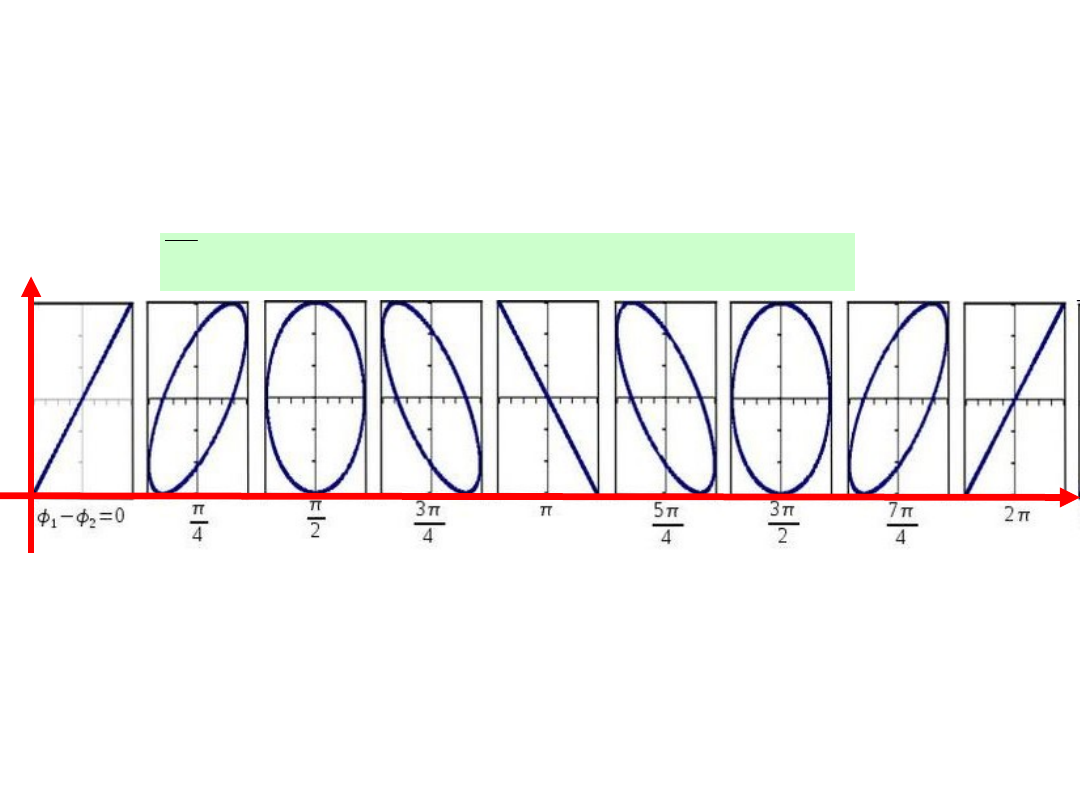
Polaryzacja eliptyczna (lub kołowa) jako superpozycja dwóch fal

Polaryzacja eliptyczna (lub kołowa) jako superpozycja dwóch fal

ogólnie o niejednakowych amplitudach i przesunięciach fazowych

ogólnie o niejednakowych amplitudach i przesunięciach fazowych

Weźmy dwie fale poprzeczne o jednakowej częstotliwości kołowej ω i o niejedna-

Weźmy dwie fale poprzeczne o jednakowej częstotliwości kołowej ω i o niejedna-

kowych amplitudach, A, oraz różnych fazach f, biegnące w kierunku osi ‘z’

kowych amplitudach, A, oraz różnych fazach f, biegnące w kierunku osi ‘z’

(prostopadłej do rysunku), których superpozycja jest opisywana 5równaniem:

(prostopadłej do rysunku), których superpozycja jest opisywana 5równaniem:

)

t

cos(

A

y

)

t

cos(

A

x

)

t

(

2

2

1

1























(gdy obie amplitudy A

(gdy obie amplitudy A

1

1

i A

i A

2

2

są równe to dla Df = p/2 oraz 3p/2 otrzymamy

są równe to dla Df = p/2 oraz 3p/2 otrzymamy

polaryzacje kołowe)

polaryzacje kołowe)

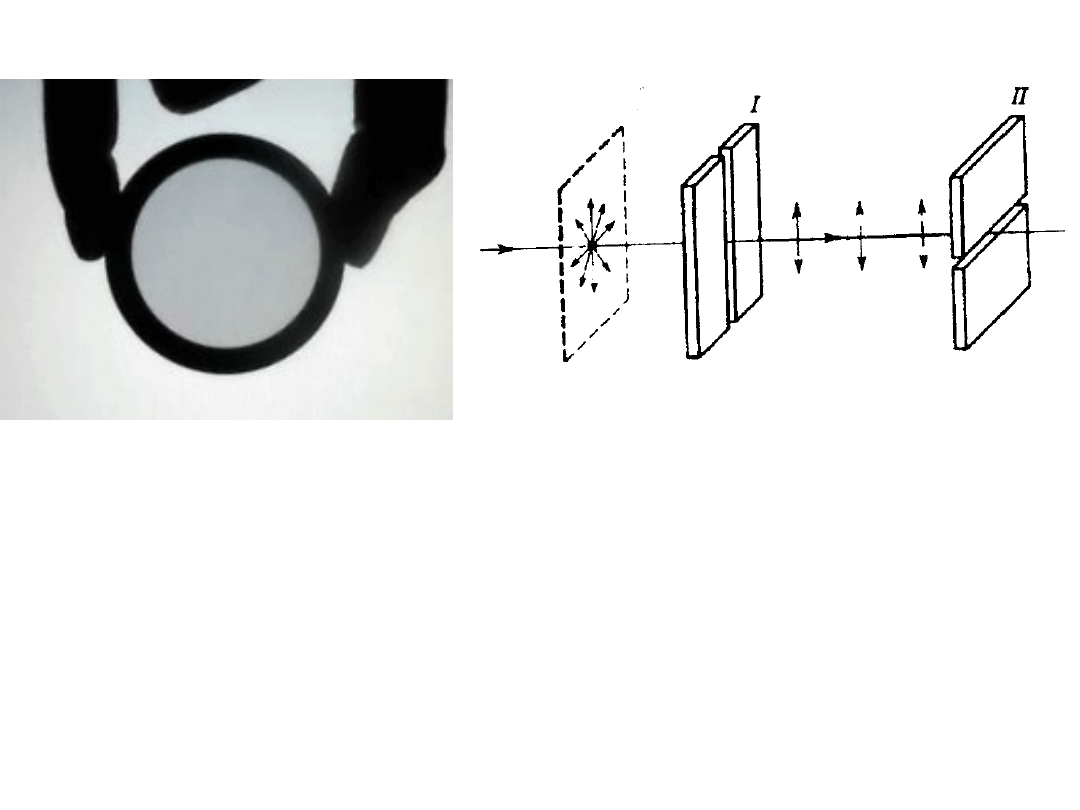
Ilustracja efektu polaryzacji światła – FILTR POLARYZACYJNY

Ilustracja efektu polaryzacji światła – FILTR POLARYZACYJNY

Kiedy dwa filtry polaryzacyjne są ustawione tak, że przepuszczają tylko fale oscylujące

Kiedy dwa filtry polaryzacyjne są ustawione tak, że przepuszczają tylko fale oscylujące

w prostopadłych płaszczyznach, to światło nie przechodzi. Jeżeli płaszczyzny polaryzacji

w prostopadłych płaszczyznach, to światło nie przechodzi. Jeżeli płaszczyzny polaryzacji

są takie same, to efekt jest taki jak dla jednego filtra.

są takie same, to efekt jest taki jak dla jednego filtra.

Filtry polaryzacyjne są stosowane np. w okularach przeciwsłonecznych, gdzie

Filtry polaryzacyjne są stosowane np. w okularach przeciwsłonecznych, gdzie

zmniejszają jasność nieba w słoneczny dzień, blokują spolaryzowane światło odbite

zmniejszają jasność nieba w słoneczny dzień, blokują spolaryzowane światło odbite

od poziomych płaszczyzn (szyb, luster itp.)

od poziomych płaszczyzn (szyb, luster itp.)

Filtr polaryzacyjny

Filtr polaryzacyjny

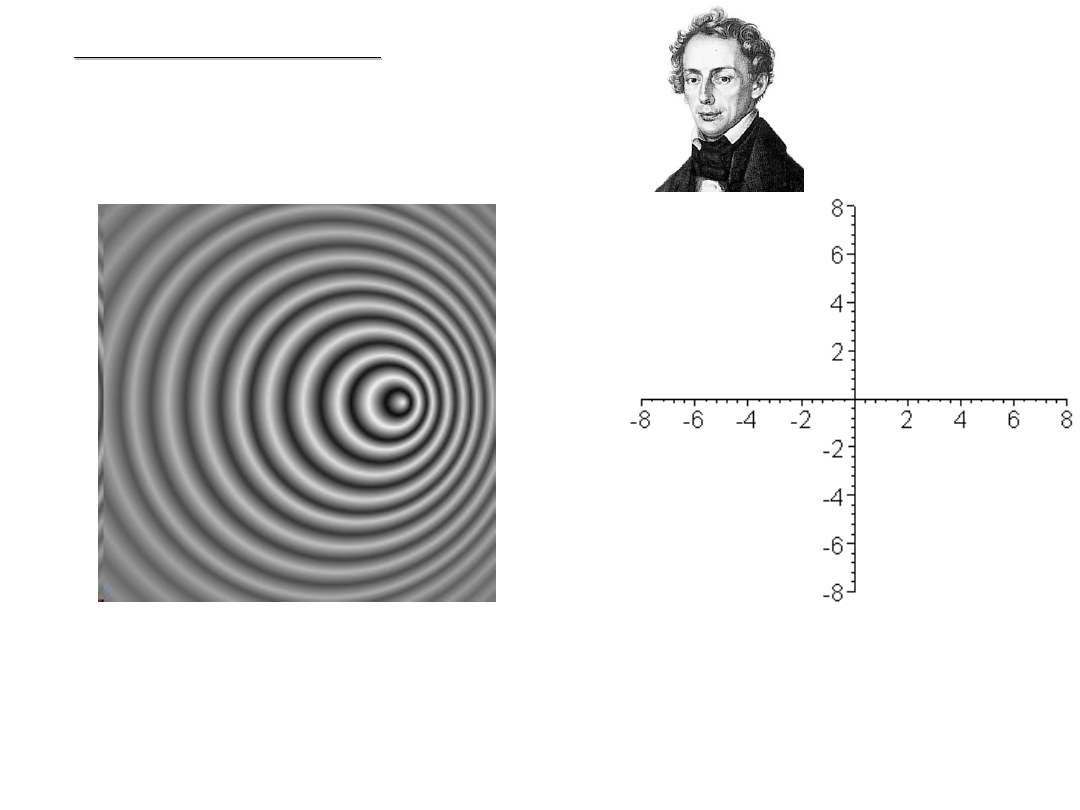
EFEKT DOPPLERA

EFEKT DOPPLERA

(1842)

(1842)

(DLA FAL MECHANICZNYCH)

(DLA FAL MECHANICZNYCH)

Źródło fal poruszające się w prawo.
Odbierana długość fali jest mniejsza
po prawej, a większa po lewej stronie od źródła.

Źródło fal porusza się względem ośrodka,

Źródło fal porusza się względem ośrodka,

w którym fale propagują.

w którym fale propagują.

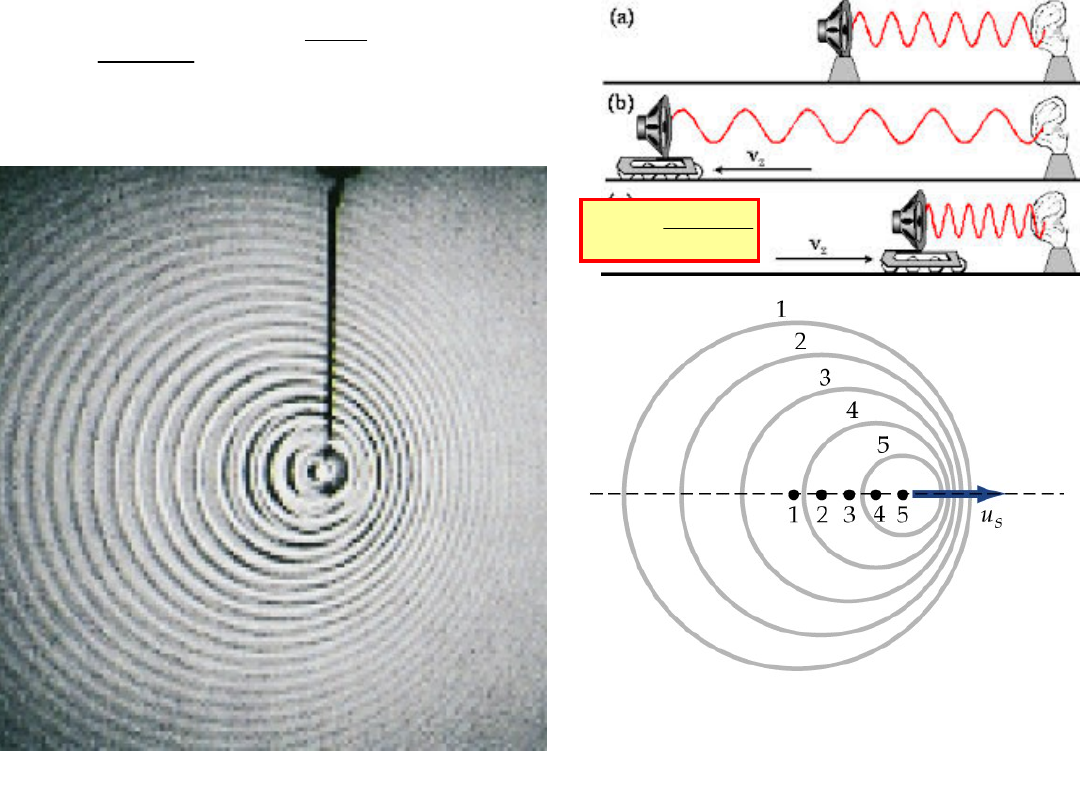
Z przodu źródła długość fali maleje
z tytułu rośnie
.

0

f

u

v







0

f

u

v







fali

obs

fali

em

odb

V

v

V

f

f





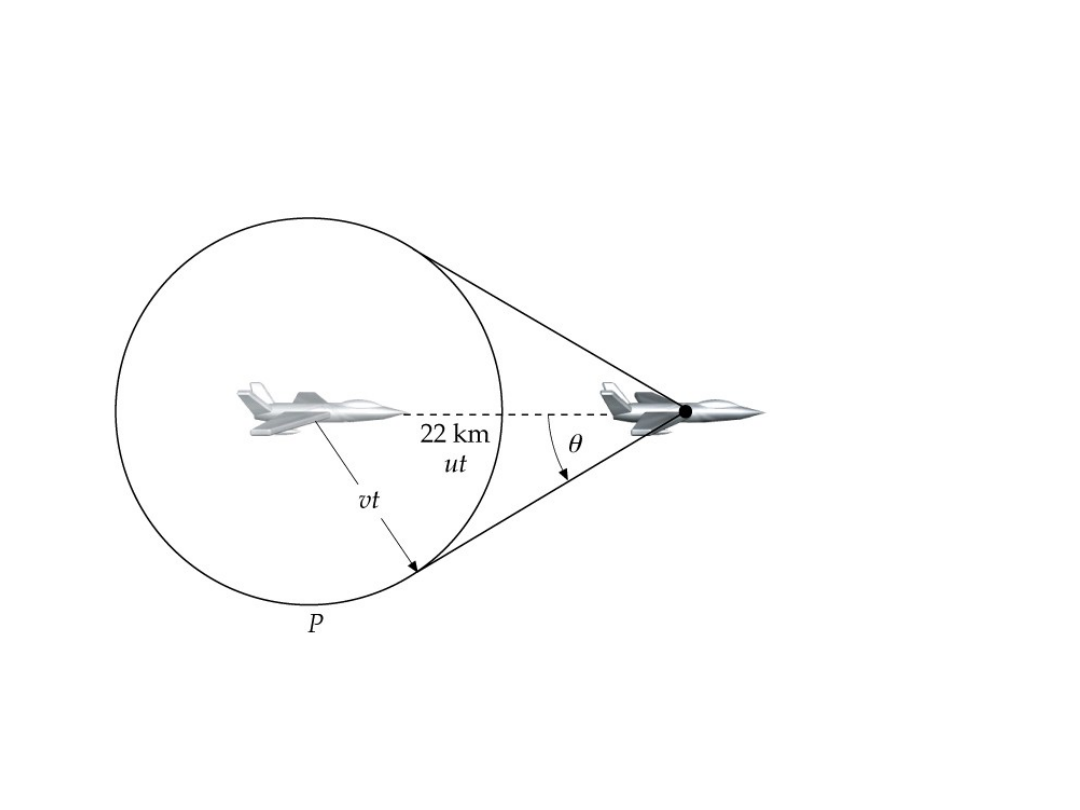
Bariera dźwieku

(2)Fala mechaniczna emitowana przez nieruchome źródło
i odbierana przez ruchomego obserwatora

W przypadku spoczywającego źródła odległości między kolejnymi grzbietami fali są

W przypadku spoczywającego źródła odległości między kolejnymi grzbietami fali są

stałe i niezależne od kierunku, ale zmienia się częstość ich spotykania przez porusza-

stałe i niezależne od kierunku, ale zmienia się częstość ich spotykania przez porusza-

jącego się obserwatora.

jącego się obserwatora.

Jeśli obserwator zbliża się do źródła, to względna prędkość obserwatora i ruchu

Jeśli obserwator zbliża się do źródła, to względna prędkość obserwatora i ruchu

falowego jest równa

falowego jest równa

v

v

wz

wz

= V

= V

fali

fali

+ v

+ v

obs

obs

wobec tego czas między obserwacjami kolejnych

wobec tego czas między obserwacjami kolejnych

frontów (czyli obserwowany okres fali

frontów (czyli obserwowany okres fali

T

T

’) jest równy:

’) jest równy:

obs

fali

zr

v

V

'

T







Stąd częstość odbierana:

Stąd częstość odbierana:

fali

obs

fali

em

odb

V

v

V

f

f





(3)

(3)

Źródło fali oraz obserwator jednocześnie

Źródło fali oraz obserwator jednocześnie

poruszają się

poruszają się

względem ośrodka.

względem ośrodka.

Z połączenia poprzednich dwóch wzorów szczególnych wynika, wzór opisujący

Z połączenia poprzednich dwóch wzorów szczególnych wynika, wzór opisujący

zjawisko gdy zarówno źródło jak i obserwator poruszają się:

zjawisko gdy zarówno źródło jak i obserwator poruszają się:

Górne znaki oznaczają przypadek gdy źródło lub odbiorca poruszają się

Górne znaki oznaczają przypadek gdy źródło lub odbiorca poruszają się

względem ośrodka zbliżając się do siebie, a dolne przy oddalaniu.

względem ośrodka zbliżając się do siebie, a dolne przy oddalaniu.

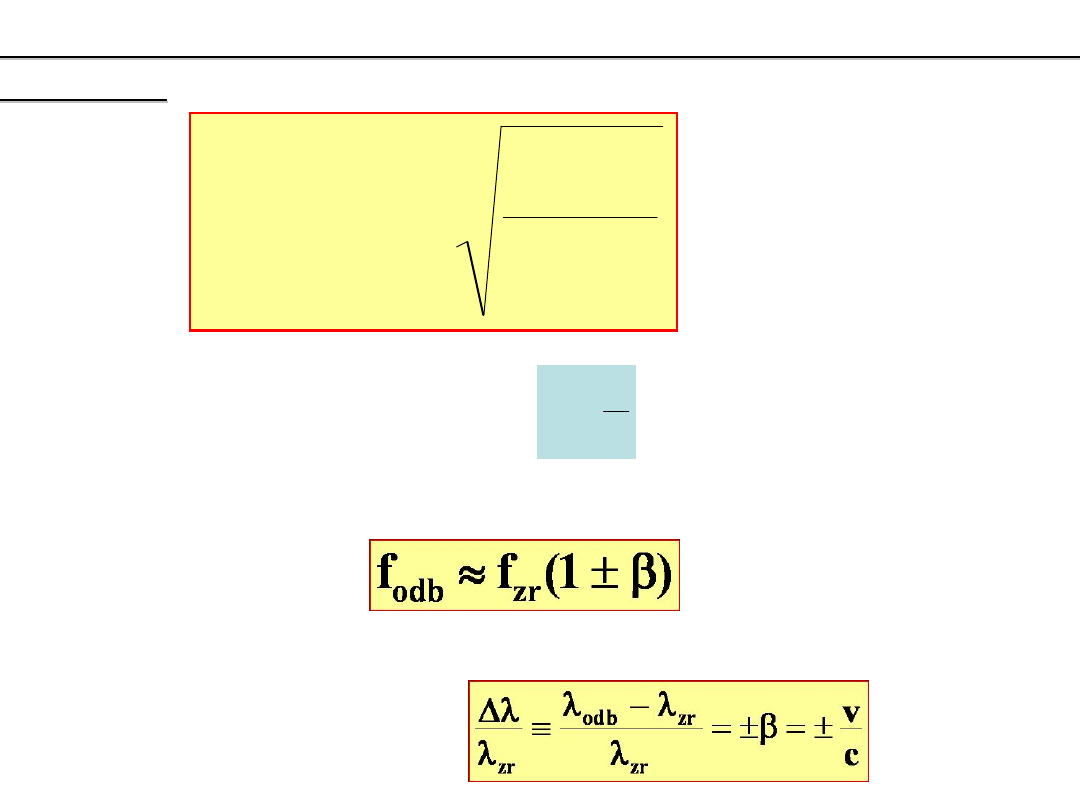
EFEKT DOPPLERA DLA FAL ELEKTROMAGNETYCZNYCH

EFEKT DOPPLERA DLA FAL ELEKTROMAGNETYCZNYCH

(w próżni)

(w próżni)











1

1

f

f

zr

odb

c

v





gdzie

gdzie

Dla małych wartości prędkości (

Dla małych wartości prędkości (





<< 1 ) z powyższego wzoru otrzymamy przybliżenie

<< 1 ) z powyższego wzoru otrzymamy przybliżenie

Jest to tzw nierelatywistyczne przybliżenie efektu Dopplera, które można też zapisać dla

Jest to tzw nierelatywistyczne przybliżenie efektu Dopplera, które można też zapisać dla

zmiany odbieranej długości fali:

zmiany odbieranej długości fali: