WŁASNOŚCI ŚWIATŁA

1. Optyka geometryczna i falowa

•zasady i prawa optyki geometrycznej

•całkowite wewnętrzne odbicie; światłowody

2. Oddziaływanie fali z materią

•dyfrakcja promieni X na sieci krystalicznej i techniki badania
struktury

•oddziaływanie mikrofal z materią

3. Oddziaływanie światła z materią: zjawisko fotoelektryczne

4. Dwoista natura światła: foton i jego własności

5. Idea de Broglie: dualizm cząstkowo-falowy

a=10 

l

a=5

l

a= 

l

10

5

10

5

w

zg

lę

d

n

e

n

a

tę

że

n

ie

q (deg)

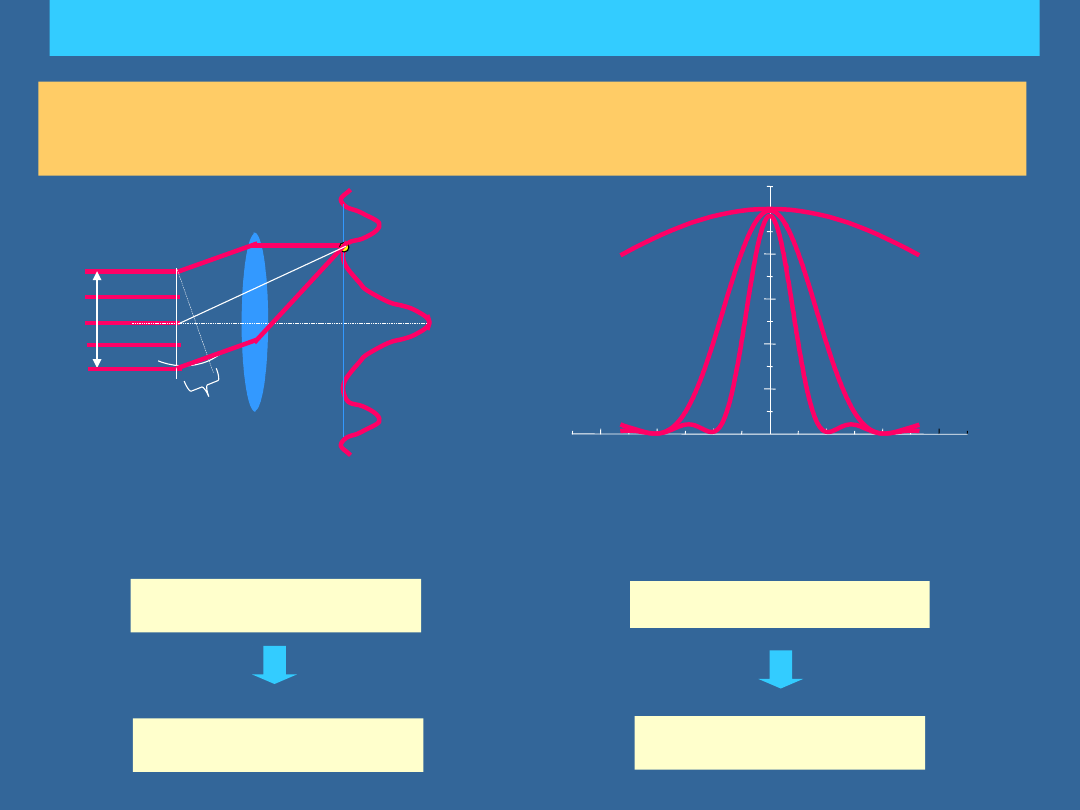
Jeśli przeszkody mają duże rozmiary w porównaniu z długością fali, to można
powiedzieć, że promieniowanie rozchodzi się po liniach prostych i efekty falowe
nie grają roli

OPTYKA

a





r

 <<rozmiar

przeszkody

 ~rozmiar przeszkody

optyka geometryczna

optyka falowa

OPTYKA GEOMETRYCZNA: WSPÓŁCZYNNIK

ZAŁAMANIA

Zasady optyki geometrycznej:
1. światło rozchodzi się po liniach prostych, prostopadłych do czoła fali
(promienie światła).
2. Światło w ośrodku przeźroczystym rozchodzi się z mniejszą prędkością niż
w próżni, v=c/n, gdzie n jest współczynnikiem załamania światła.

WSPÓŁCZYNNIK ZAŁAMANIA

Ośrodek

współcz. zał.

powietrze

1.003

woda

1.33

alkohol

1.36

kwarc

1.46

szkło

1.52

polietylen

1.52

szafir

1.77

diament

2.42

n=c/V

PRAWA OPTYKI GEOMETRYCZNEJ

Jeżeli światło pada na powierzchnię
zwierciadła, to odbija się od niego tak, że
promień padający i odbity leżą w jednej
płaszczyźnie, oraz że kąt padania równy
jest kątowi odbicia.

PRAWA ODBICIA

kąt padania


kąt odbicia
’

PRAWA ZAŁAMANIA (SNELLIUSA)

Na granicy dwóch ośrodków światło załamuje
się tak, że :

gdzie n

21

jest współczynnikiem załamania

ośrodka 2 względem 1.

1

2

1

2

21

2

1

n

n

V

c

V

c

n

V

V

)

sin(

)

sin(













kąt padania


kąt
załamania


CAŁKOWITE WEWNĘTRZNE ODBICIE; ŚWIATŁOWODY

Jeśli światło przechodzi z ośrodka optycznie
gęstszego (duże n) do rzadszego (małe n), to
dla pewnego kata krytycznego może nastąpić
całkowite wewnętrzne odbicie: światło nie
może wyjść z ośrodka gęstszego optycznie

Na granicy dwóch ośrodków światło załamuje
się tak, że :

Ale n

2

>n

1

, czyli

może więc  być 90

0

, nawet jeśli  jest

mniejsze.
Jeśli  =90

0

, to następuje całkowite wewnętrzne

odbicie





ośrodek

1;

n

1

ośrodek

2;

n

2

n

1

> n

2

1

2

n

n

)

sin(

)

sin(







odbicie

światłowód

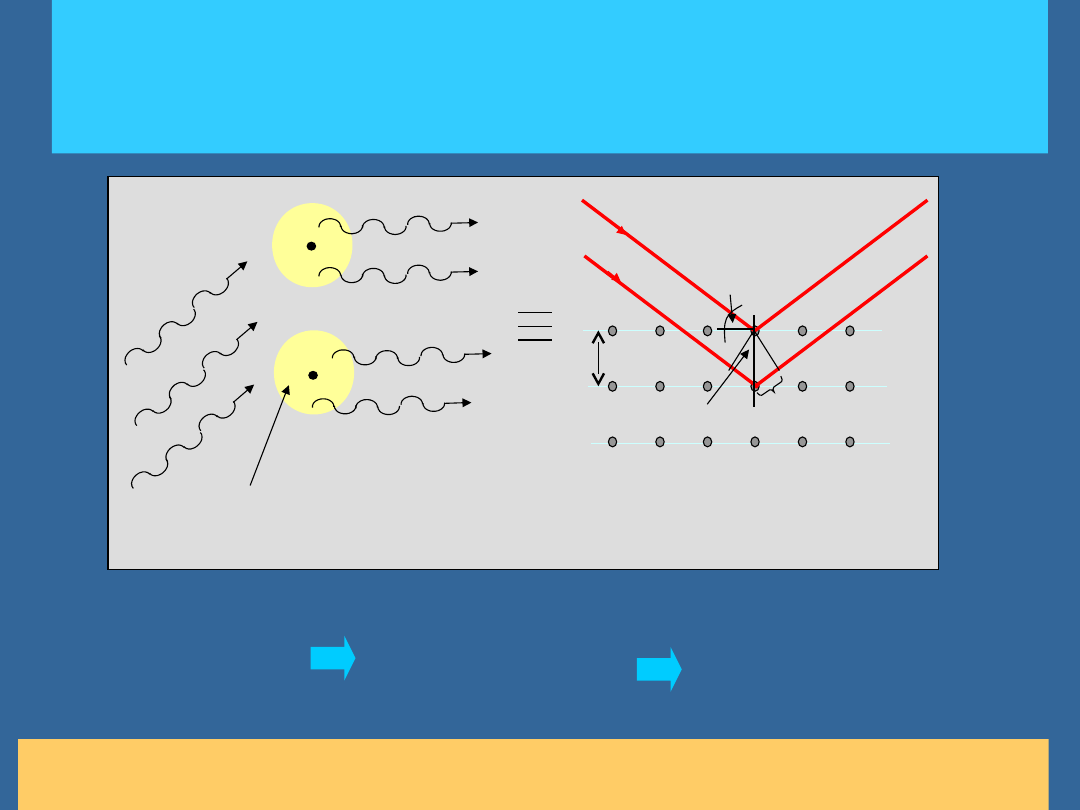
FALOWA NATURA PROMIENIOWANIA

ELEKTROMAGNETYCZNEGO: ROZPROSZENIE

PROMIENI RENTGENA NA SIECI KRYSTALICZNEJ

wiązka
padająca

d

hk

l





x

wiązka rozproszona

elektrony
wokół jądra

wiązka
padająca

Wiązka promieni
X pada na
materiał

Elektrony
atomów drgają i
promieniują

Wypadkowe natężenie
pola E jest wynikiem
interferencji tych fal

Ponieważ w krysztale atomy ułożone są regularnie, dlatego promieniujące elektrony
(też ułożone regularnie) zachowują się jak układ wielu szczelin: atomowa siatka
dyfrakcyjna

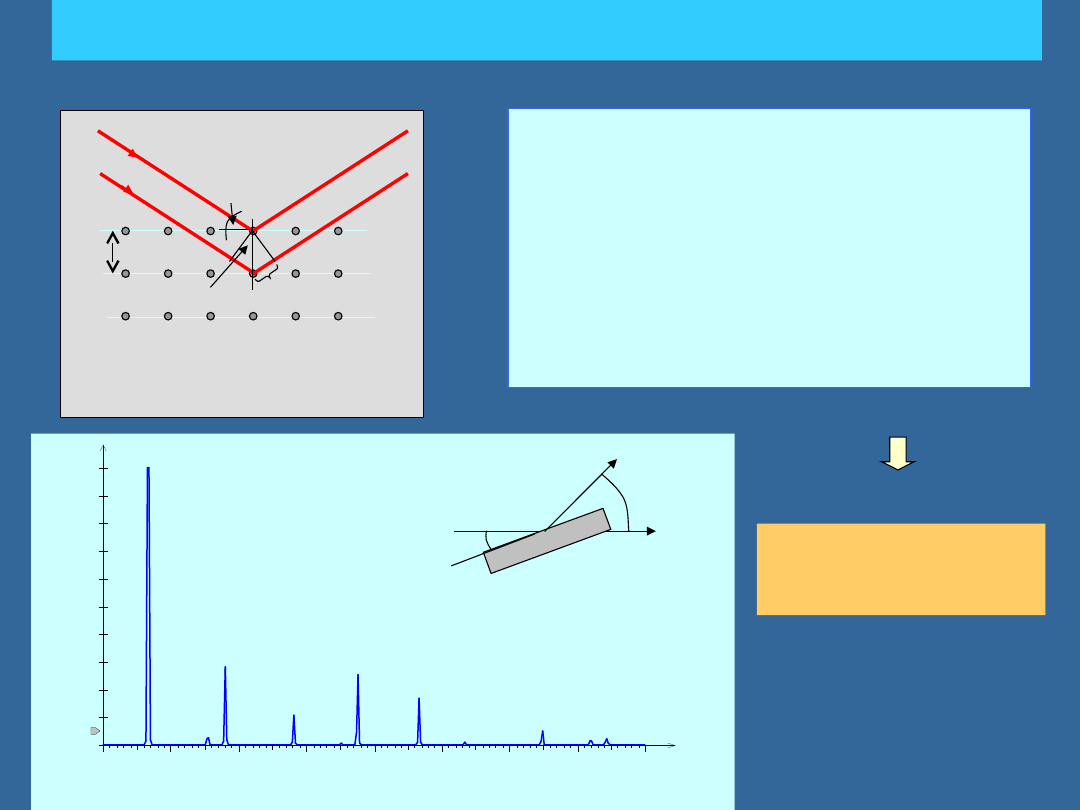
PRAWO BRAGGA

ANALIZA BRAGGA

Różnica dróg optycznych między
promieniami odbitymi na sąsiednich
płaszczyznach:
=2x

ale x/d

hkl

= sin   x=d

hkl

sin 

=2x = 2 d

hkl

sin 

Promienie się wzmacniają, jeśli  równa

jest wielokrotności długości fali:

d

hk

l





x

wiązka
padając
a

prawo Bragga

n = 2 d

hkl

sin 

Intensity (%)

 

2

40

50

60

70

80

90

100

110

120

0

10

20

30

40

50

60

70

80

90

100

o

(1.540562 Ĺ)
20°,60°]

B = 2.0 Ų

2





2,2,0

2,2,2

4,0,0

4,2,0

4,2,2

4,4,2

lampa Cu, =1.54562Ĺ



2

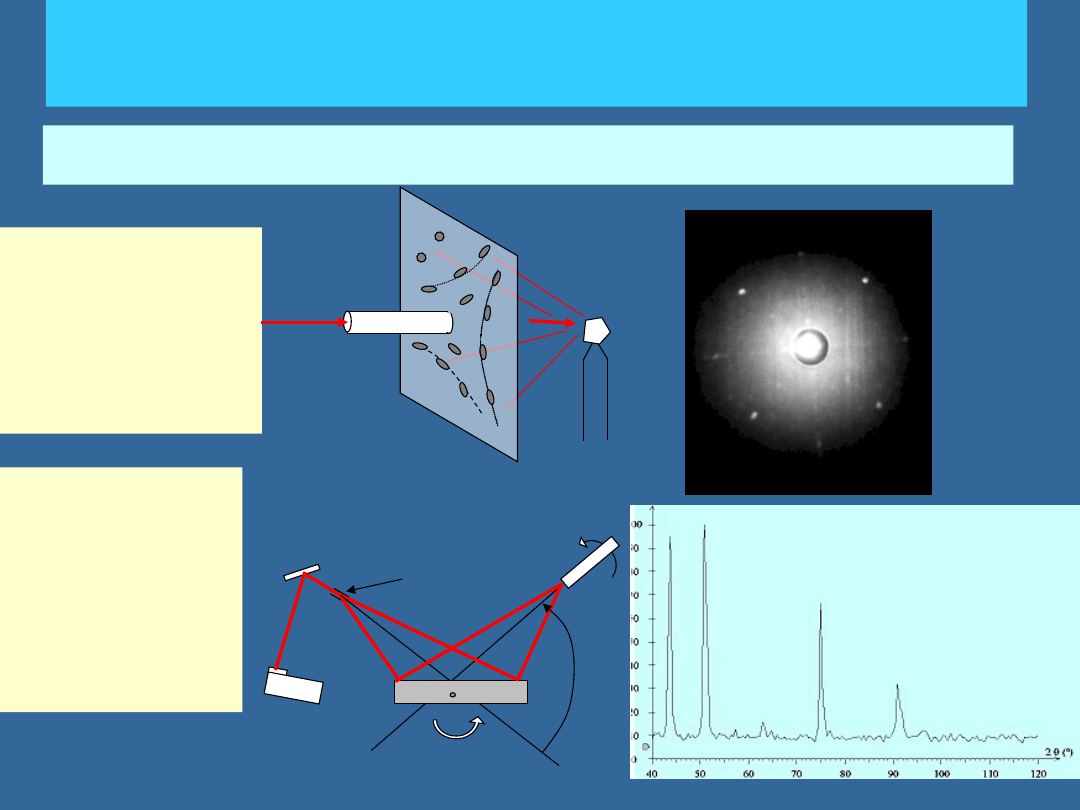
RÓŻNE METODY OBSERWACJI STRUKTUR

KRYSTALICZNYCH

Aby doprowadzić do spełnienia warunku Bragga n = 2 d

hkl

sin  trzeba zmienić

 lub 

Metoda Lauego:

•monokryształ

•białe
promieniowanie

•zastosowanie:orie
ntacja
monokryształów

Metoda
Debye'a-
Scherrera

•polikryształy

•promieniowanie
monochromatycz
ne

•zastosowanie:an
aliza fazowa

kolimato
r

lampa
rentgenowska

monochromator

próbka

obrót 

obrót 2

2

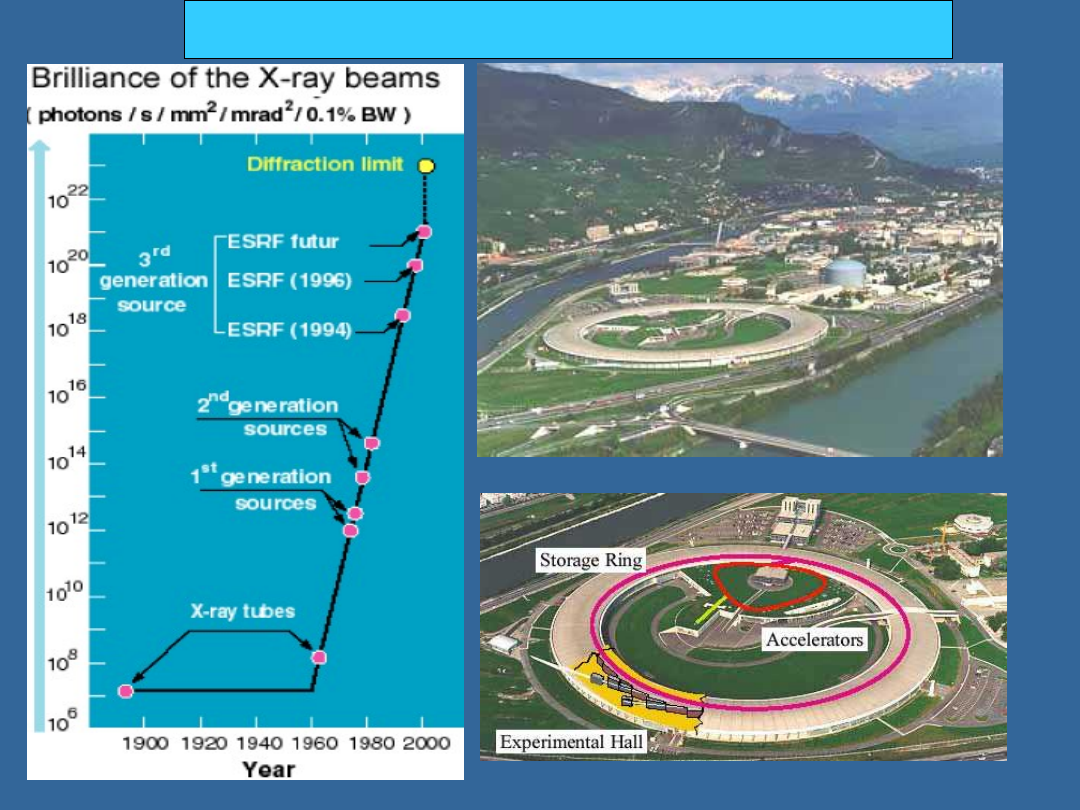
PROMIENIOWANIE SYNCHROTRONOWE

SYNCHROTRON: CO MOŻNA MIERZYĆ

Wiele własności materiału może być zrozumiane w powiązaniu z ich strukturą
mikroskopową, a ta może być zbadana techniką dyfrakcji promieni X, czasami na
bardzo małych próbkach i przeprowadzaną w czasie ruchu
Zastosowanie: Medycyna, Biologia, Fizyka, Mechanika i Nauka o materiałach

Materiałoznawstwo: polimery (pajęczyna)

Rezultat: Znaleziono związek własności
elastycznych z ułożeniem łańcuchów
atomów

Badanie zmęczenia materiałów

materiał bez
naprężeń

materiał z
naprężenie
m

pękanie

ODDZIAŁYWANIE MIKROFAL Z MATERIĄ

Mikrofale (= cm ) mają

częstość bliską częstości drgań

molekuł

Mikrofale mogą pobudzić

niektóre molekuły do drgań,

szczególnie te, które są

dipolami

Woda podlega drganiom pod wpływem padającego promieniowania

elektromagnetycznego z zakresu mikrofalowego

drgania

wody

drgania

wody

Ta własność wykorzystana

jest w kuchniach

mikrofalowych

ODDZIAŁYWANIE CZĄSTECZEK WODY:

PODGRZEWANIE

Cząsteczki wody oddziałują na siebie.

Bezpośrednie zderzenia

Przyciąganie dipoli (wiązanie

wodorowe)

Ruch drgający cząsteczek wody jest tłumiony: z powodu oddziaływania między

cząsteczkami energia fali zostaje zamieniona na wszystkie rodzaje drgań, co

powoduje zwiększenie temperatury

tarcie

Polega na tym, że jeśli powierzchnię metalu
oświetla się światłem, to z metalu wybijane
są elektrony.
http://webphysics.ph.msstate.edu/ccp/27-5/

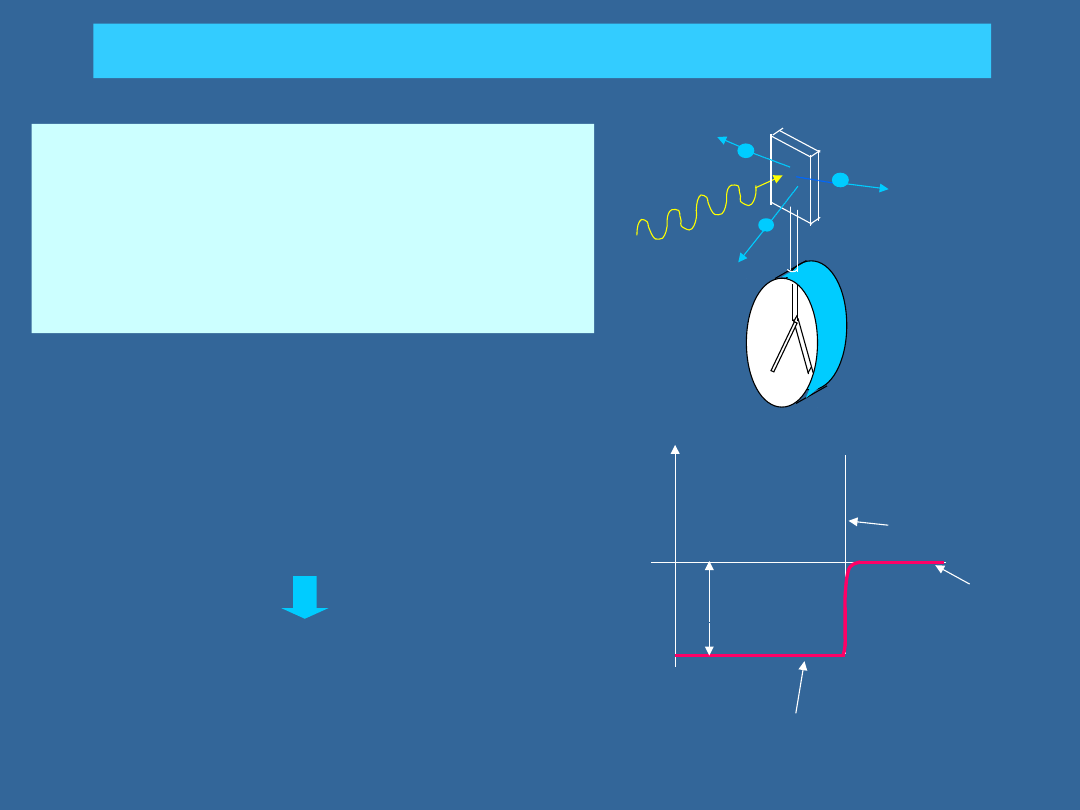
światło

płyta
metalowa

naładowan
y
elektroskop

elektro
ny

energia
elektronów
wewnątrz metalu

Energia elektronu w metalu:
elektron jest w metalu związany  jego

energia będzie ujemna względem energii
elektronu daleko od metalu przyjmowanej
jako energia odniesienia.

Aby elektron z metalu wyrzucić konieczne
jest wykonanie pracy:

pracy wyjścia

.

metal

zewnętrze
metalu

energia
elektronów
na zewnętrz
metalu

W

E

powierzchnia
metalu

ZJAWISKO FOTOELEKTRYCZNE

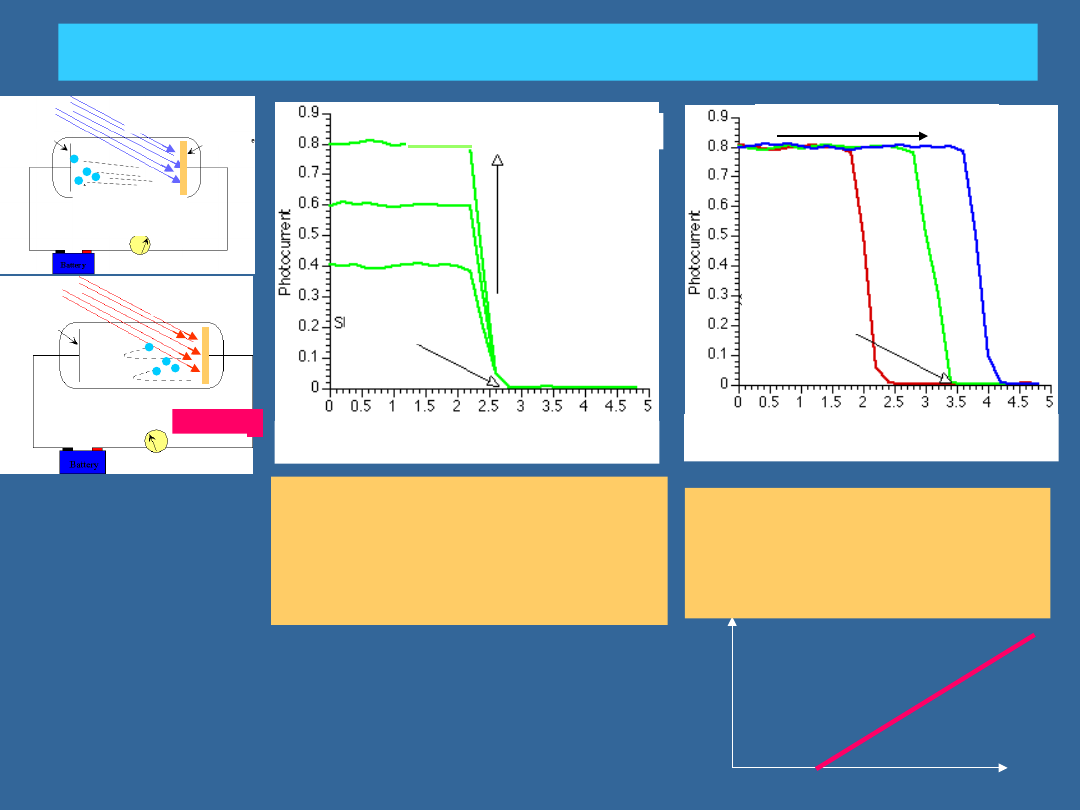
ZJAWISKO FOTOELEKTRYCZNE: EKSPERYMENT

energia
kinetyczna
elektronów

f

0

częstość

fotoefekt

-

- +

+

światło

elektron

y

1)brak jest progu natężenia
światła; liczba elektronów
zależy od natężenia.
2)energia elektronów nie
zależy od natężenia

wzrastające natężenie

napięcie opóźniające

napięcie

odcięcia

3)istnieje próg f

0

poniżej

którego brak jest wybitych
e, natomiast powyżej f

0

energia elektronów rośnie z
f.

napięcie opóźniające

wzrastająca częstość

napięcie

odcięcia

ZJAWISKO FOTOELEKTRYCZNE: WYJAŚNIENIE

EINSTEINA

elektron pochłonie foton wychodząc na
zewnątrz tylko wtedy, gdy energia
fotonu przynajmniej wyniesie W

0

, a

nadwyżka energii fotonu ponad W

0

będzie energią kinetyczną elektronu:

hf=W

0

+E

K

metal

zewnętrze
metalu

energia
elektronów
na zewnętrz
metalu

W

0

E

powierzchnia
metalu

E

K

energia elektronów wewnątrz metalu

WYJAŚNIENIE EINSTEINA

Einstein: światło jest zbiorem porcji energii:

kwantów

o energii E=hf :

fotonów

Fotony zachowują się jak cząstki. Jeśli foton
zderza się z elektronem to może mu
przekazać całą swoją energię. Część energii
kwantu potrzebna jest do wyjścia elektronu z
metalu, pozostała część zwiększa jego
energię kinetyczną (już elektronu
swobodnego)

Nie jest możliwe wyjaśnienie zjawiska fotoelektrycznego w
oparciu o elektrodynamikę klasyczną

ŚWIATŁO: CZĄSTKI, CZY FALE?

Światło-fotony nie można sklasyfikować jako wyłącznie fale, albo wyłącznie
cząstki. Światło jest czymś do czego opisu konieczny jest inny język

Zjawisko fotoelektryczne:
Zjawisko Comptona:
Promieniowanie ciała doskonale czarnego

CZĄSTKI

E

K

= hf-W

0

E = hf

FALE

Ulega
interferencji

WŁASNOŚCI FOTONU

Przykład:

Obliczyć energię czerwonego światła emitowanego przez wodór =656nm

E = hc/ =(6.63*10

-34

Js*3*10

8

m/s)/656*10

-9

m=3.03*10

-19

J=1.89eV

ENERGIA







hc

hf

E

DŁUGOŚĆ FALI

 jest określona eksperymentem dyfrakcyjnym

Jaką prace trzeba wykonać, aby elektron
przesunąć między punktami o różnicy
potencjałów 1V

Elektronowolt: inna jednostka energii

V= 1V

W=eV= 1.6*10

-19

C* 1V= 1.6*10

-19

CJ/C= 1.6*10

-

19

J=1eV

1eV= 1.6*10

-19

J

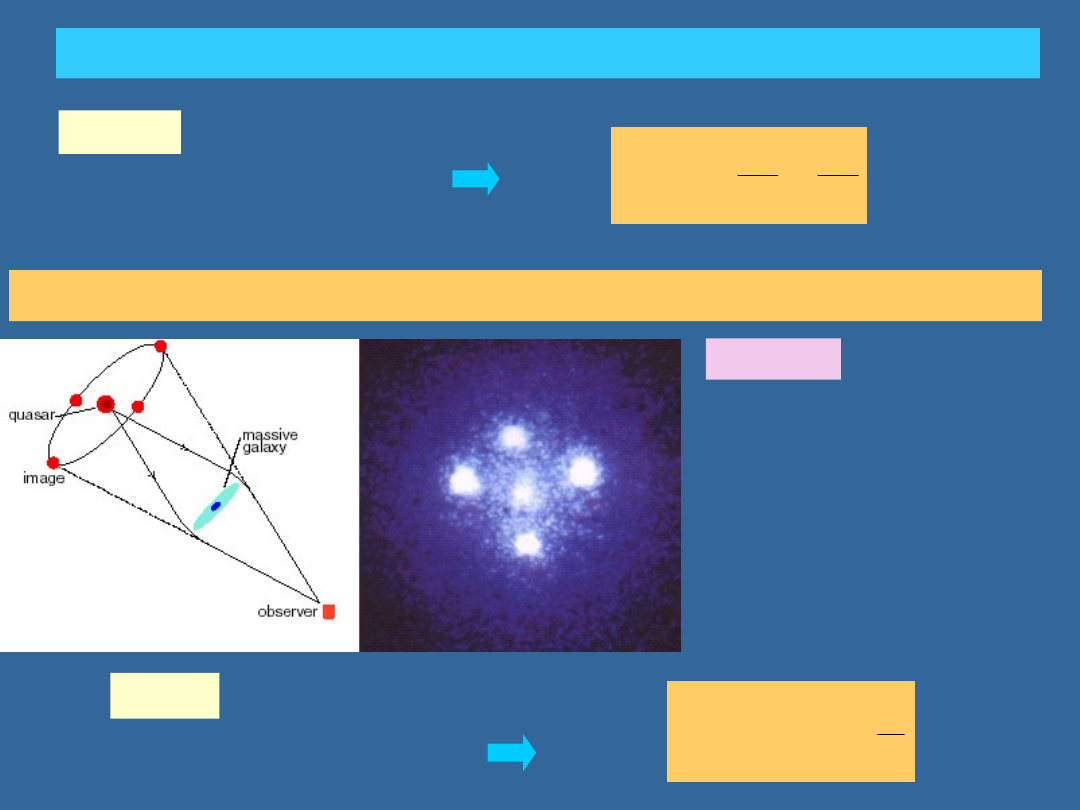
WŁASNOŚCI FOTONU

PĘD

p=mc







h

c

m

p

foton

E =
hf=mc

2







c

h

c

hf

m

2

foton

MASA

Ponieważ foton ma energię, to także ma masę, chociaż jego masa
spoczynkowa=0

soczewkowanie grawitacyjne:
ponieważ masa przyciąga
grawitacyjnie fotony, to
możliwa jest obserwacja
obiektu znajdującego się za
masywną galaktyką

Galaktyka, działając
jak soczewka, może
dać wielokrotne
obrazy odległego
kwazara

Przykład:

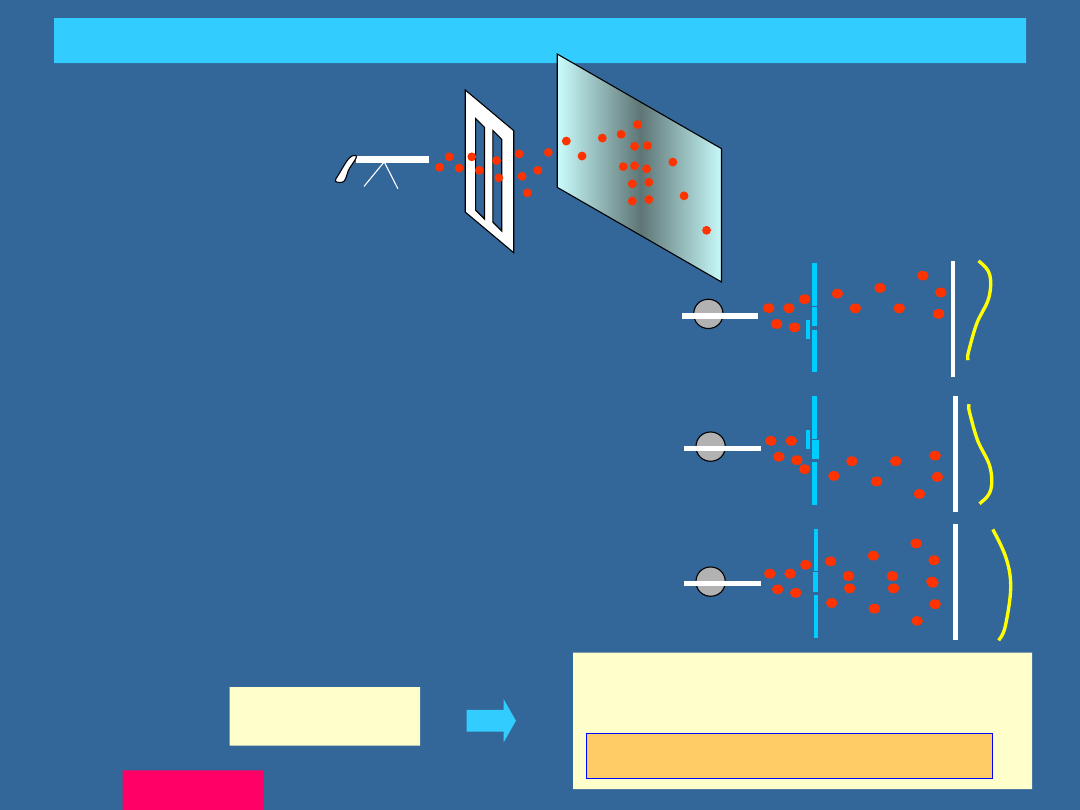
EKSPERYMENT Z DWIEMA SZCZELINAMI: CZĄSTKI

karabin

Prawdopodob. dojścia kuli do miejsca x
ściany tylko przez szczelinę 1: P

1

Prawdopodob. dojścia kuli do miejsca x
ściany tylko przez szczelinę 2: P

2

Prawdopodob. dojścia kuli do miejsca x
ściany przez szczelinę 1 i 2: P=P1+P2

•cała kula przybywa do ekranu,
•brak interferencji

natężenieprawdop. ~P

1

+P

2

CZĄSTKI

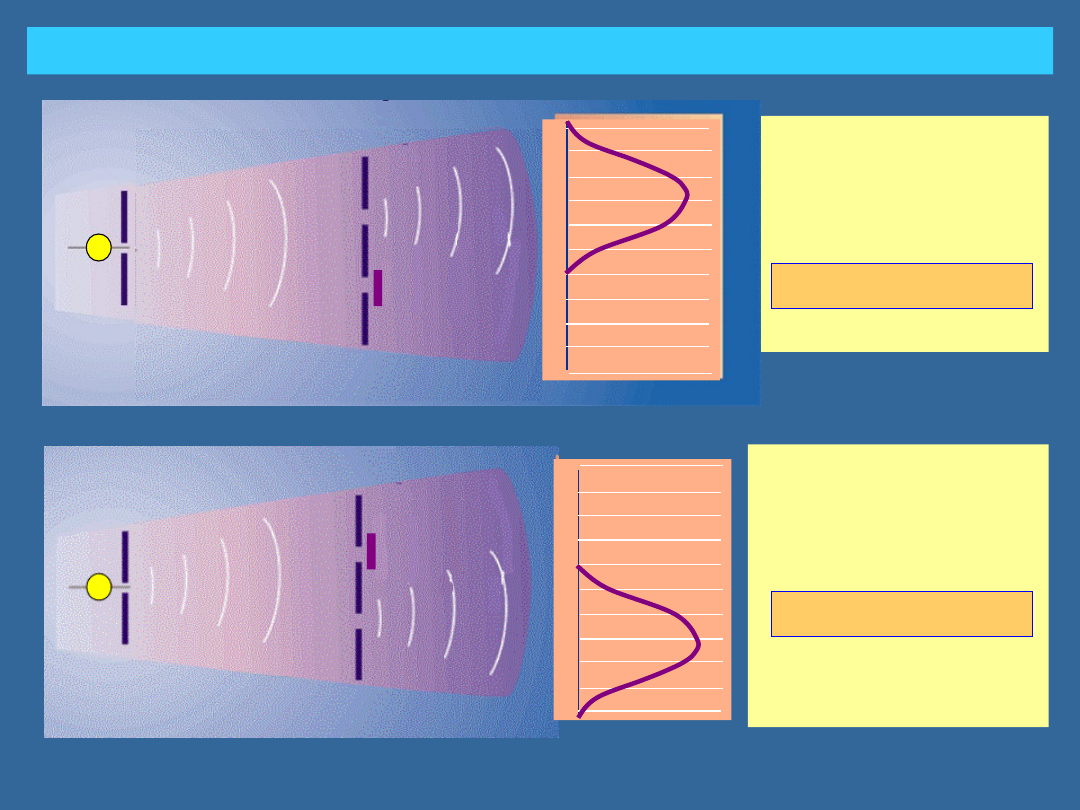
EKSPERYMENT Z DWIEMA SZCZELINAMI: ŚWIATŁO

natężenie~(E

1

)

2

t)

(kx

sin

E

E

0

1







natężenie
światła

natężenie~(E

1

)

2

t)

(kx

sin

E

E

0

2







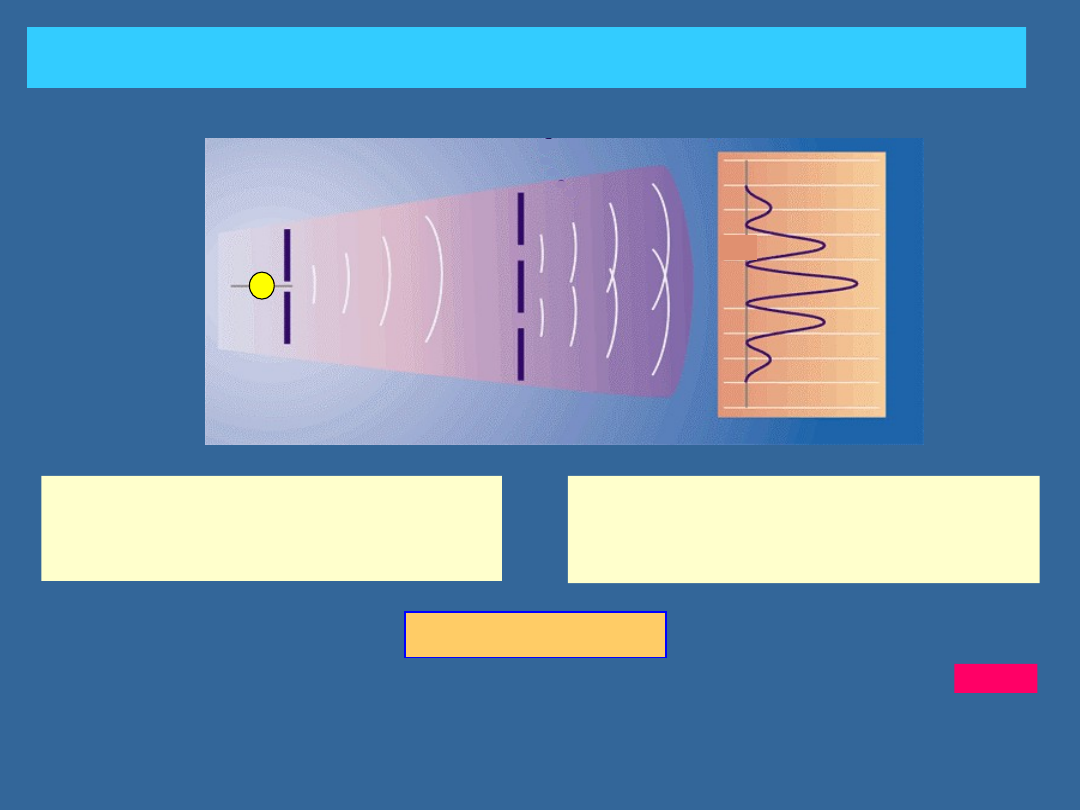
natężenie
światła

EKSPERYMENT Z DWIEMA SZCZELINAMI: ŚWIATŁO

DETEKTOR: oko

•tylko część energii w punkcie
ekranu,

•interferencja

natężenie~(E

1

+E

2

)

2

swiatło

Gdyby pierwszym eksperymentem ze światłem było zjawisko fotoelektryczne,
lub zjawisko Comptona, to wynik interferencji na 2 szczelinach byłby zupełnie
niezrozumiały

DETEKTOR: zjaw. fotoelektryczne

•światło dochodzi grudkami,

•interferencja

Wszystkie „cząstki” mikroświata mają tę własność,
że czasem, w niektórych eksperymentach zachowują
się jak fale, a czasem jak zwykłe cząstki. Wzory

obowiązują zawsze

IDEA DE BROGLIE’A





h

p

hf

E 

Potrzebny jest nowy język i nowy aparat matematyczny do opisu takich
tworów

MECHANIKA KWANTOWA