W fizyce klasycznej obowiązują zasady
zachowania;
Oto jak można je skomplikować
energii, pędu i momentu pędu
.
Te trzy zasady można traktować jako konsekwencje
pewnych symetrii.
Zasada zachowania energii
wynika więc z
niezmienniczości
względem przesunięcia w czasie. Inaczej mówiąc,
jeżeli w każdej chwili czasu
zasada wariacyjna
najmniejszego działania,
oraz równania ruchu
opisujące układ nie zmieniają się , to energia
układu w tych chwilach jest taka sama.
i …..Zasada jedności Przyrody
Jeżeli coś ma się stać to się stanie : )
zasady zachowania mają zastosowanie także dla
reakcji jądrowych
Zasada zachowania energii
zabrania aby zachodziły reakcje jądrowe takie, że
masy spoczynkowe produktów byłyby większe od
mas spoczynkowych substratów.
Zasada zachowania pędu
wymaga aby wskutek anihilacji elektronu i pozytonu
powstawały dwa fotony.
Spełniona musi być także
Zasada zachowania momentu pędu.
moment pędu przed rozpadem i po powinien być
stały
Czwartą zasadą ograniczającą możliwe reakcje
jest
Zasada zachowania ładunku.
Sumaryczny ładunek przed reakcją musi być taki
sam jak po reakcji lub rozpadzie.
• A teraz kawał
• Rozważmy rozpad
• Ten rozpad jest zgodny z zasadami
zachowania ładunku, energii, pędu i
momentu pędu a jednak nigdy nie
zachodzi. !!!!
Działanie
, wielkość fizyczna mająca wymiar
iloczynu
energii i czasu
lub
pędu i
położenia
(jak kręt). Charakteryzuje ruch
układu mechanicznego, ale pojęcie to
wykorzystuje się również w
elektrodynamice, termodynamice i
mechanice kwantowej.
Najmniejszy kwant działania to stała
Plancka h[J
*
s]
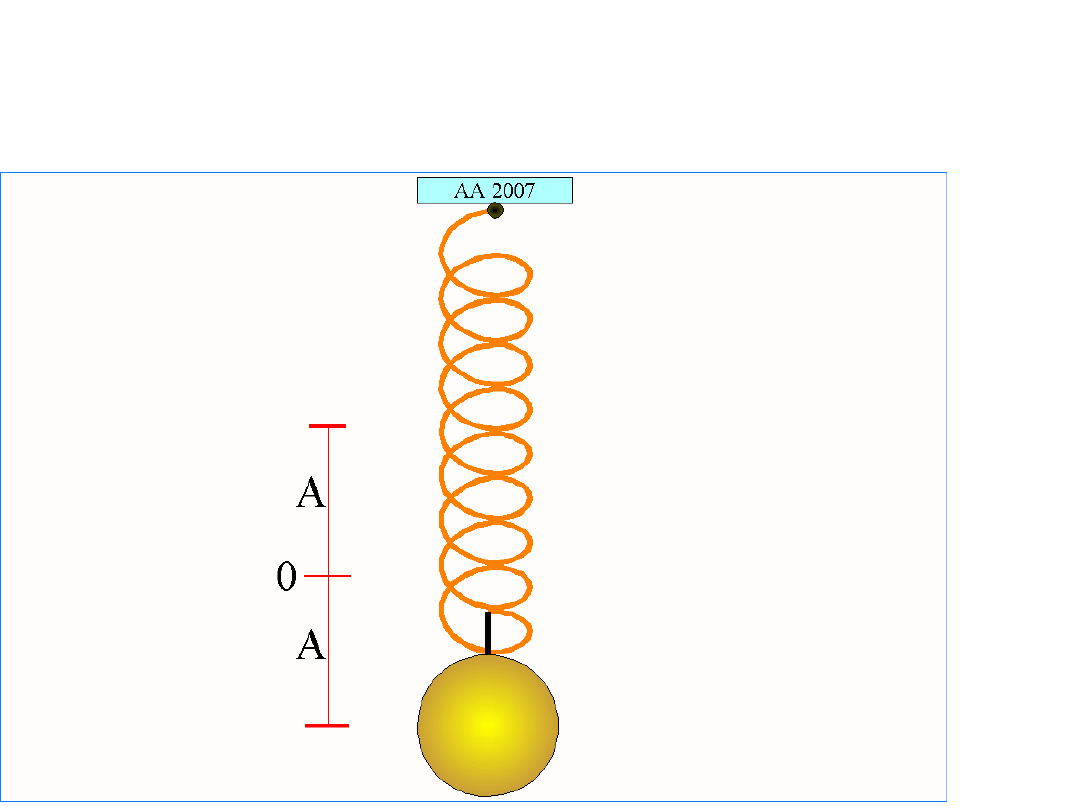
Praca i energia potencjalna
przy podnoszeniu ciężaru
Jeśli podniesiemy masę
m
wbrew sile
grawitacji na wysokość
h
(niewielkiej
względem promienia Ziemi), wymaga to
wykonania pracy zwiększającą energię
potencjalną masy m ;
p
E
mgh
Jeśli pozwolimy masie
m
spaść z wysokości
h
,
wzrasta jej prędkość, a tym samym energia
kinetyczna, równocześnie spada energia
potencjalna masy m. Jednak sumaryczna
energia pozostaje niezmieniona.
2
2
2
m
v
mgh
v
gh
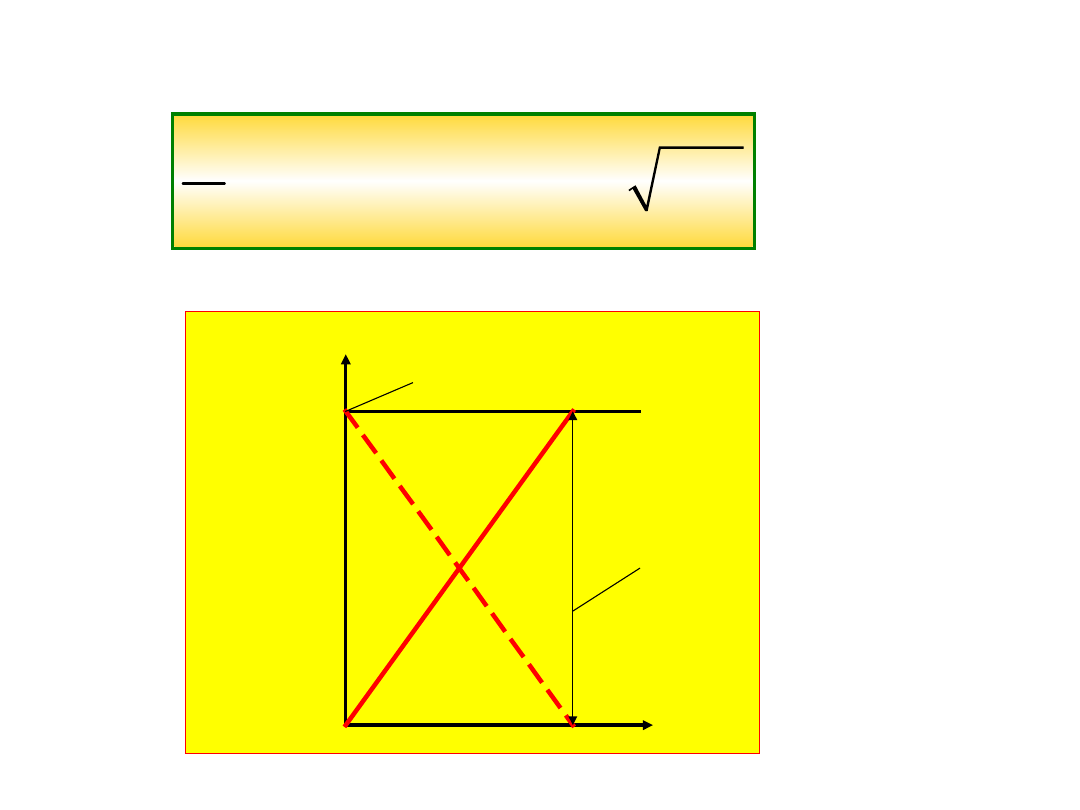
Energia
h
E
k
E
p
E=mgh
E
pmax
=E
kin
.
Energia kinetyczna po spadku masy z wysoko
ś
ci h wynosi;
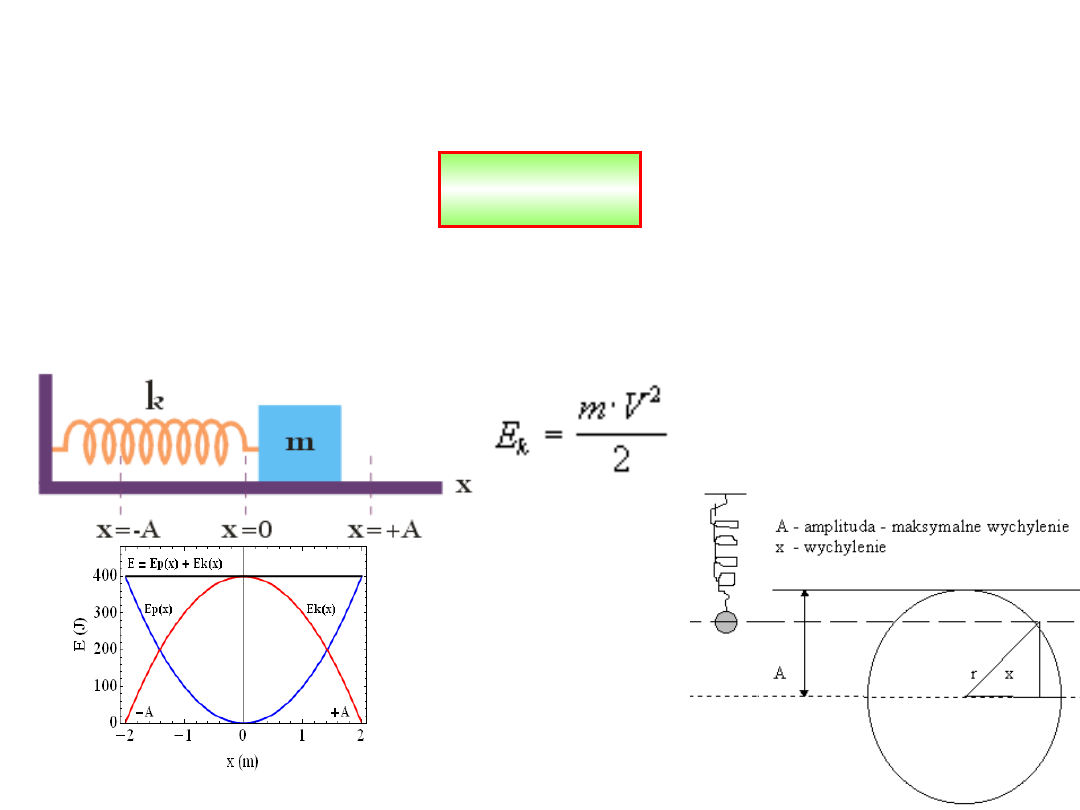
Energia, którą zmagazynowała sprężyna przy
wydłużaniu
nazywamy
energią potencjalną
.
p
E
W
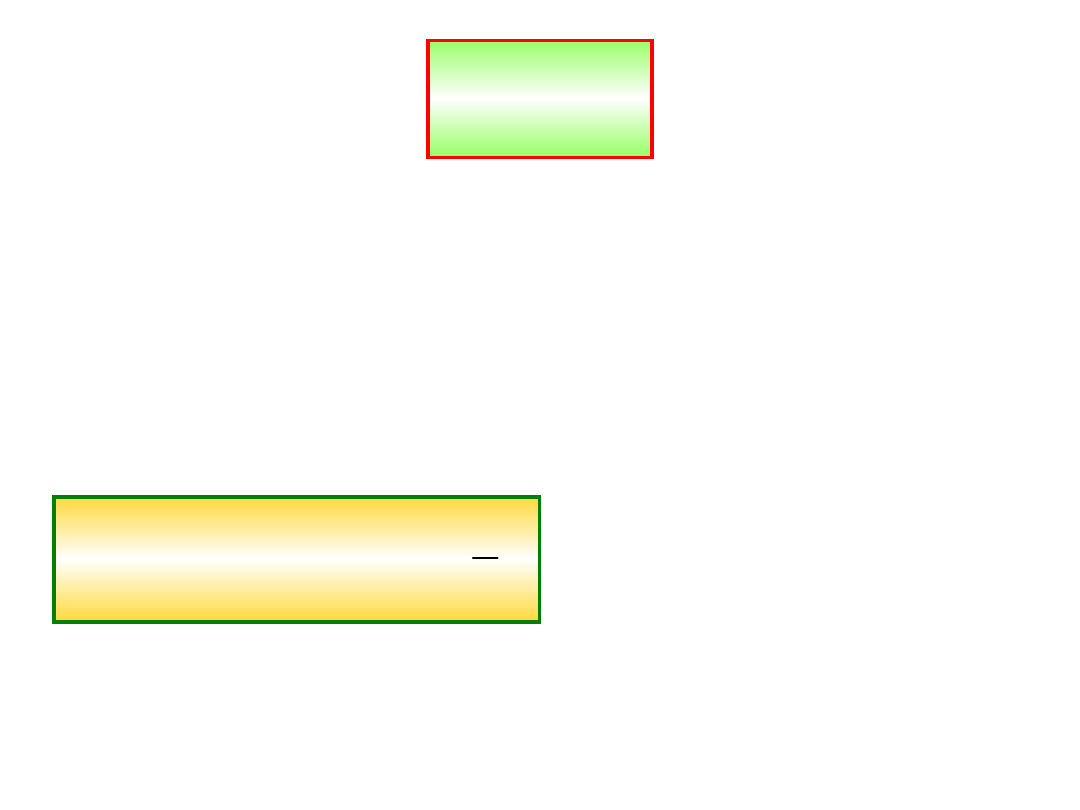
Dla
sprężyny:
W = - ½ k x
2
B
A
W
F dr
r
r
.
Z równania tego widzimy również, że praca
może być wykonana tylko przez składową siły
styczną do drogi.
Jaką pracę musimy wykonać wydłużając
sprężynę z położenia równowagi o x. Zgodnie z
prawem Hooke’a sprężyna sprzeciwia się
rozciąganiu z siłą
F=-kx. Wobec tego
2
0
0
2
x
x
c
W
Fdx
c xdx
x
Gdzie k = stała sprężystości w [N/m]
W = - ½ k x
2
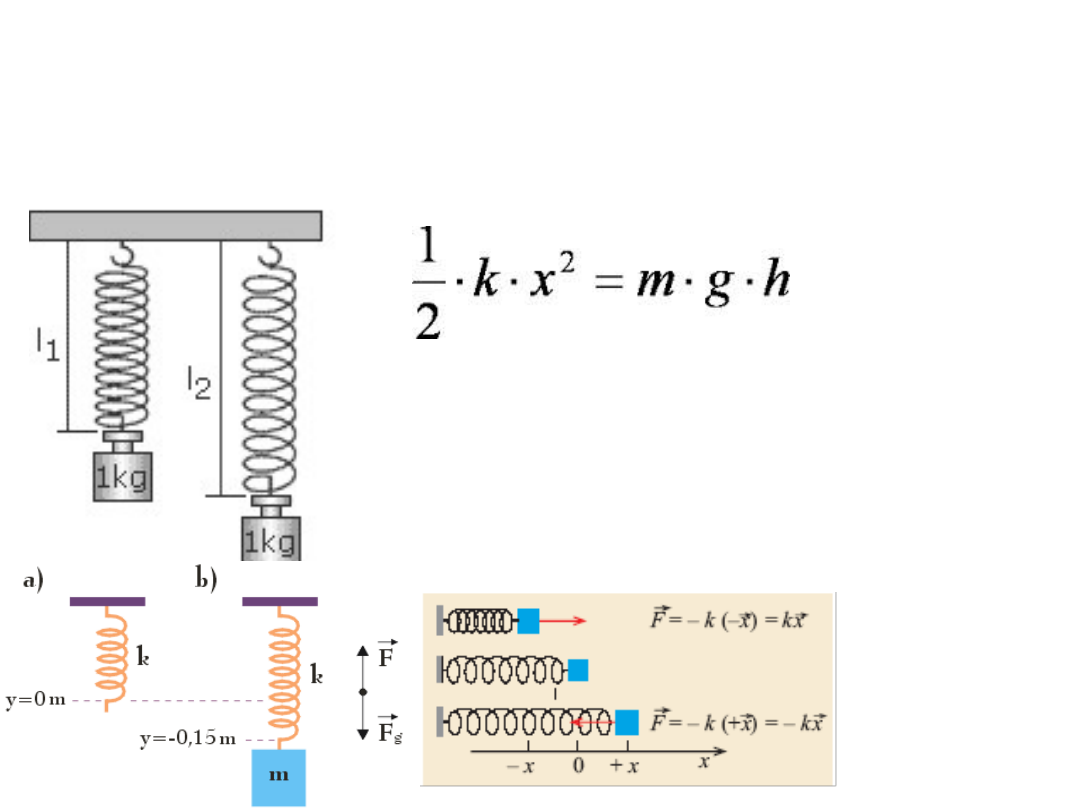
Jak obliczyć stałą
sprężystości?
h = l
2
– l
1
k = mg/h = mg/x
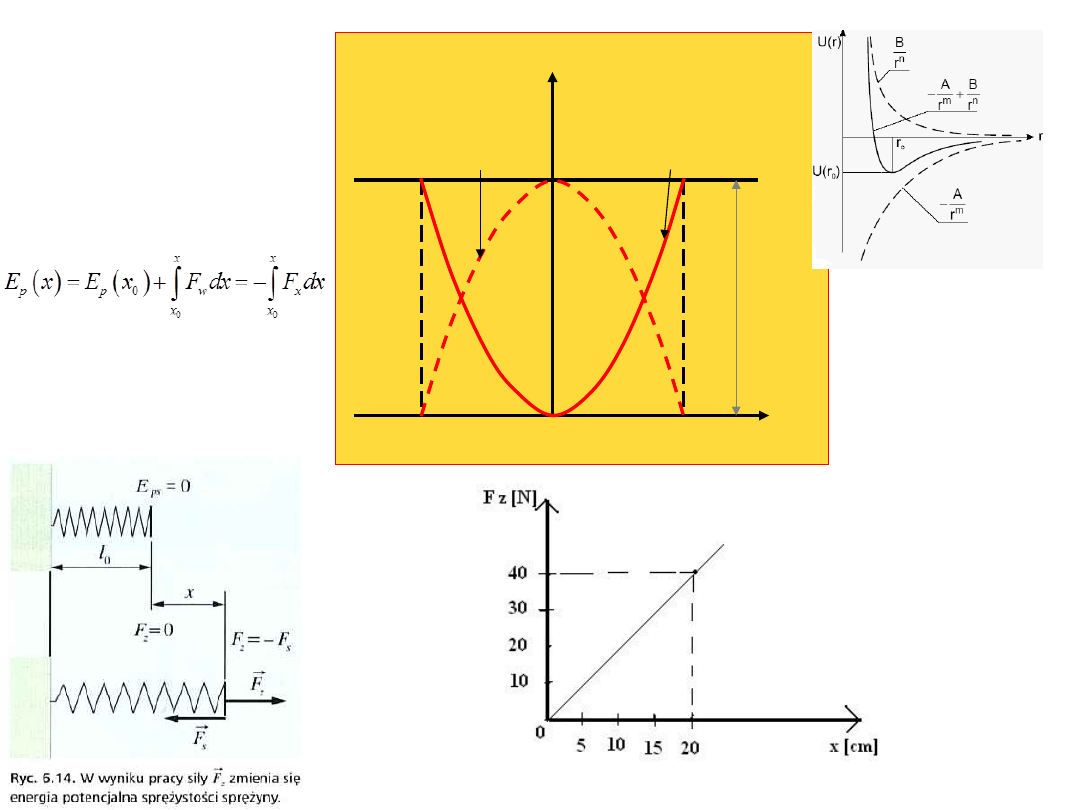
energia
x
E
k
=E-E
p
E
kmax
=E
E
p
=c/2x
1
2
E
p
=c/2x
2
E
pmax
E
k
=0
-x
1
x
1
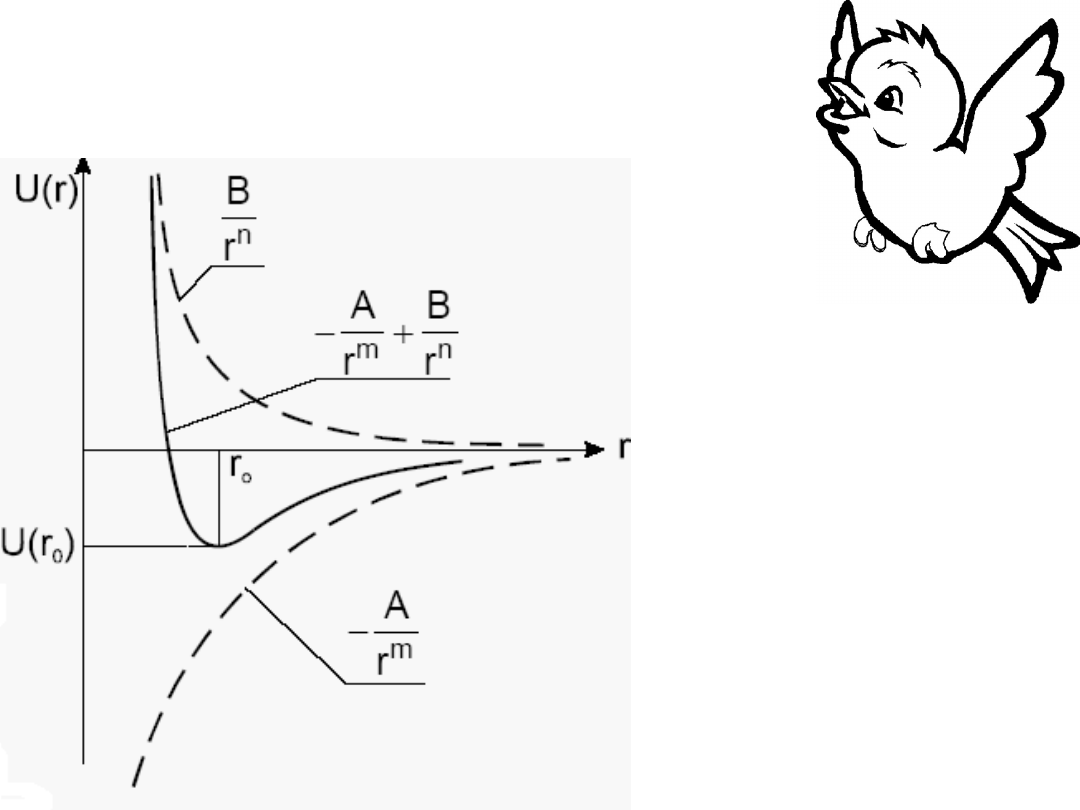
Rozkład potencjału
dla drobiny dwuatomowej
Zasada zachowania pędu
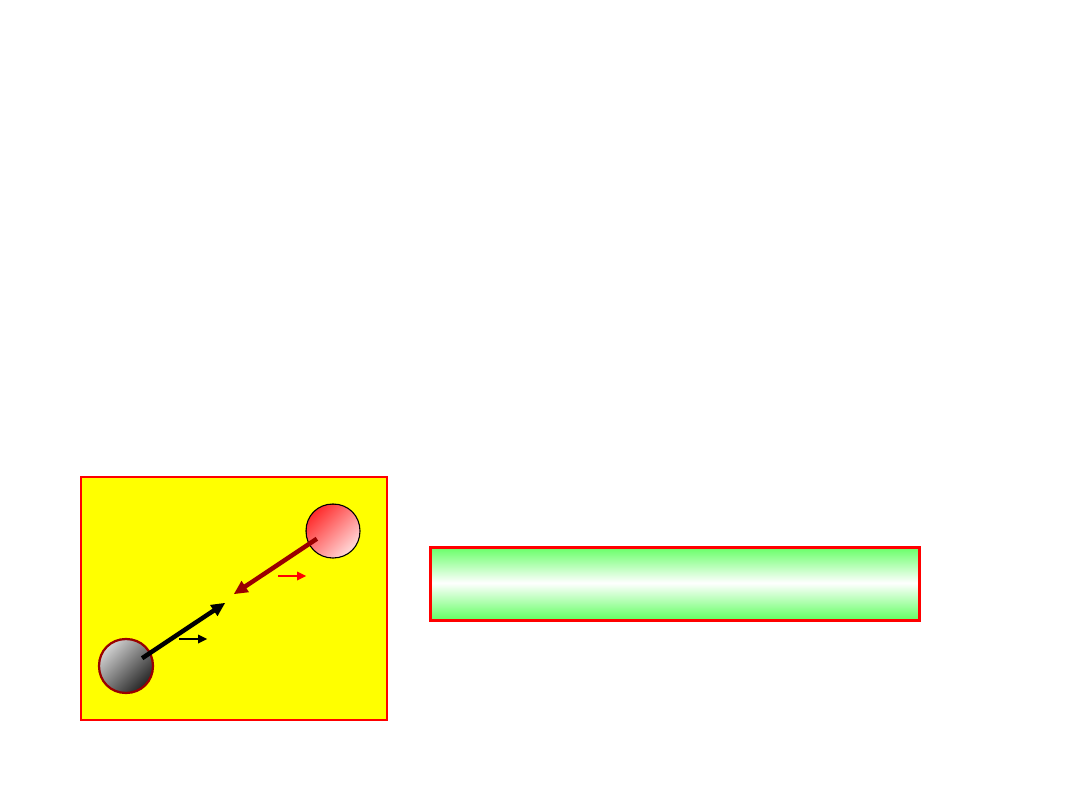
Zasada zachowania pędu
korzystając z 3 zasady dynamiki Newtona
znajdziemy dodatkową regułę dotyczącą
oddziaływania pomiędzy ciałami, która
podobnie jak zasada zachowania energii jest
ważna dla wszystkich sił niezależnie od tego,
czy siły te szczegółowo znamy czy nie.
zasada akcji i reakcji
F
2
1
F
12
Wiemy, że,
12
21
12
21
0
F
F
F
F
r
r
r
r
Zasadę akcji i reakcji da się uogólnić
na wiele ciał.
1 1
2 2
mv mv
p const
r
r
r
Całkowity pęd p układu dwóch ciał nie
zmienia się pod wpływem działania sił
wewnętrznych
.
Równanie to możemy uogólnić dla układu
N
ciał oddziaływujących tylko przez siły
wewnętrzne.
1
N
i i
i
mv
p const
r
r
Równanie
to
stanowi zapis
zasady
zachowania pędu
dla układu N izolowanych ciał.
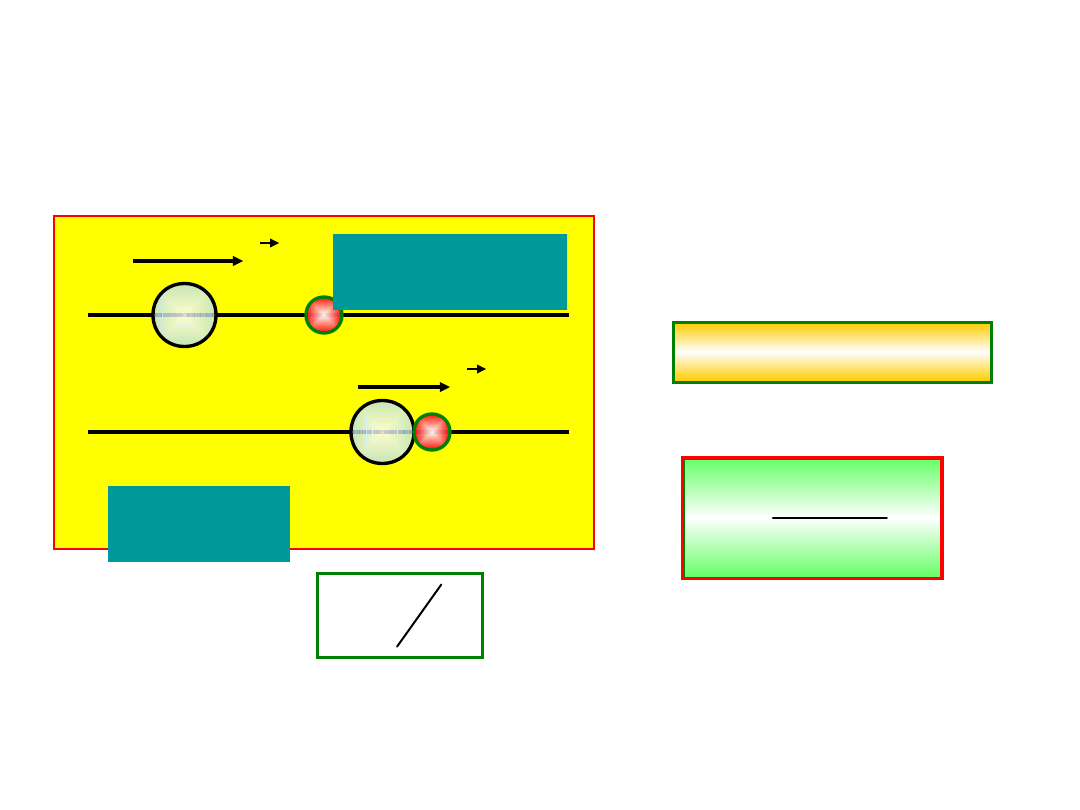
Zderzenie
niesprężyste
Mamy następujące zderzenie, kulka o masie
m
1
wpada na
spoczywającą
kulkę o masie m
2
.
m
1
m
2
m
1
+
m
2
v
1
v
1
’
przed
zderzeniem
po
zderzeniu
W oparciu o zasadę
zachowania pędu
mamy;
2
'
1 1
1
1
0 (
)
mv
m m v
r
r
Stąd mamy:
'
1
1
1
1
2
m
v
v
m m
r
r
Dla m
1
= m
2
.
'
1
1
1
2
v
v
r
r
Policzmy czemu równa się zmiana energii
kinetycznej
E
K
dla tego zderzenia
Pod wpływem działania siły F ciało zmienia w czasie dt swój pęd,
dp F dt
r
r
oraz położenie
dr v dt
r r
Eliminując z tych równań dt otrzymujemy;
0
v dp F dr
r
r r
r
To ostatnie równanie możemy napisać jako:
0
p dp
F dr
m
r
r
r
r
Wykorzystując fakt, że
(
)
2
d p p
dp p p dp
p dp
r r
r r
r r
r
,
Możemy równanie zapisać jako;
2
0
2
p
d
F dr
m
r r
Znaleźliśmy więc dwie wielkości zawierające
charakterystyczne dla ruchu parametry – pęd,
masę, siłę i pozycję, których suma podczas
ruchu pozostaje stała.
Wyrażenie
p
2
/2m
nazywa się energią kinetyczną
.
2
2
2
2
k
p
mv
E
m
Wyrażenie oznacza więc
zmianę energii kinetycznej wzdłuż drogi dr.
2
(
)
2
k
p
dE
d
m
Drugi człon w równaniu
(4.5)
nazywamy
pracą.
Zderzenia sprężyste ciał –
Zasada
zachowania
Energii kinetycznej i zasada zachowania pędu
Zasadę zachowania pędu dla dwóch
zderzających się cząstek o masach
m
1
i
m
2
,
możemy zapisać następująco:
'
'
1 1
2 2
1 1
2 2
mv mv
mv mv
r
r
r
r
W układzie kartezjańskim otrzymujemy trzy
równania;
'
'
1
2
1
2
1
2
1
2
'
'
1
2
1
2
1
2
1
2
'
'
1
2
1
2
1
2
1
2
dx
dx
dx
dx
m
m
m
m
dt
dt
dt
dt
dy
dy
dy
dy
m
m
m
m
dt
dt
dt
dt
dz
dz
dz
dz
m
m
m
m
dt
dt
dt
dt
2
2
'2
'2
'
1
2
1
2
1
2
1
2
2
2
2
2
p
p
p
p
T
T
m
m
m
m
2
2
'2
'2
1
2
1
2
1
2
1
2
2
2
2
2
p
p
p
p
Q
m
m
m
m
2
2
2
2
k
p
mv
E
m
Jeżeli zderzenie nie jest całkowicie sprężyste będziemy
musieli uwzględnić ciepło Q, które powstaje w czasie zderzenia
Zasadę zachowania energii możemy także zapisać
używając
zamiast kwadratu prędkości kwadratu pędu
wtedy:
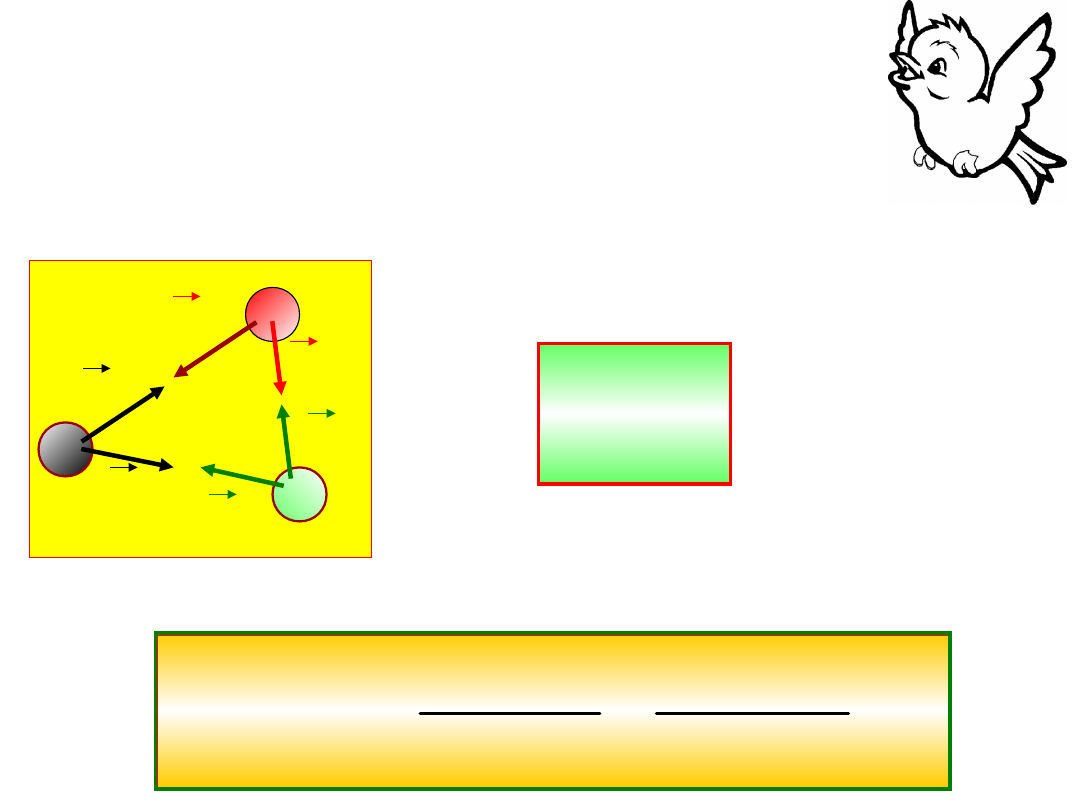
Suma wszystkich sił działających pomiędzy tymi ciałami jest równa
zero. Siły takie nazywamy siłami wewnętrznymi i ich suma jest równa
0, gdyż siły te się znoszą parami.
F
2
1
F
32
F
13
F
31
F
23
F
12
1
0
N
ik
i k
i k
F
r
Z zasady tej obowiązującej tylko
dla sił wewnętrznych znajdziemy
ważną regułę.
1 1
2 2
12
21
(
)
(
)
0
d mv
d mv
F
F
dt
dt
r
r
Zderzenia wielu ciał
• momentu pędu,
• ładunku elektrycznego
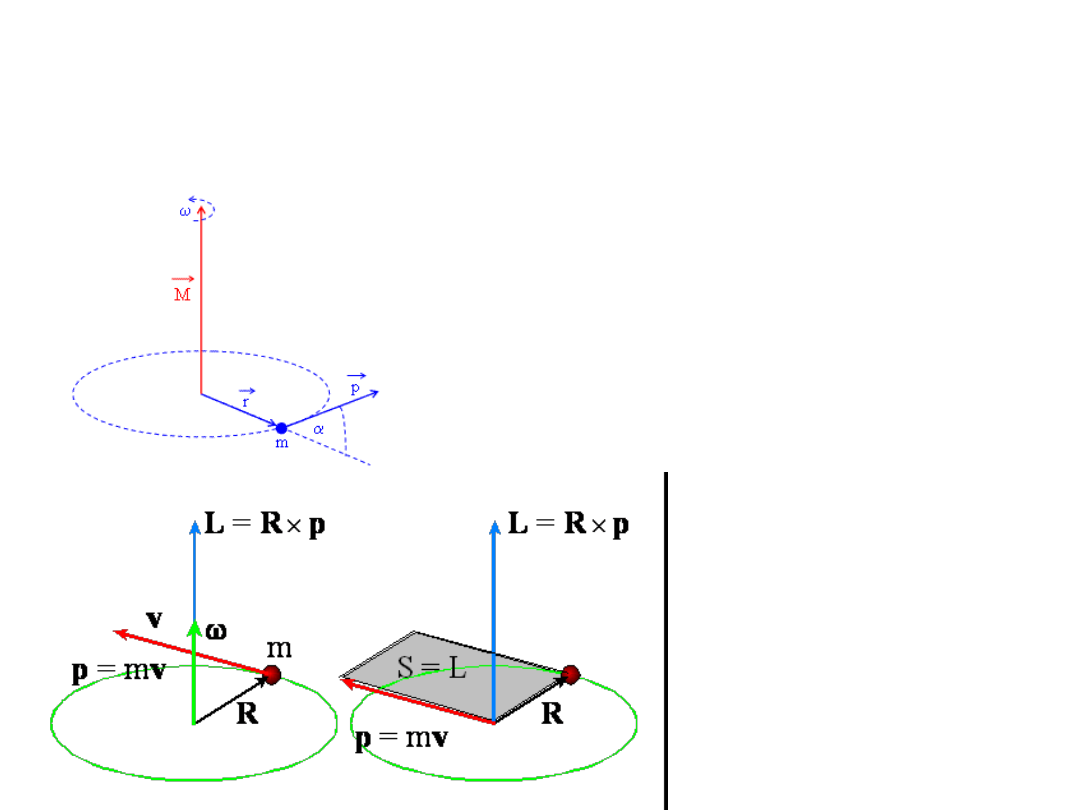
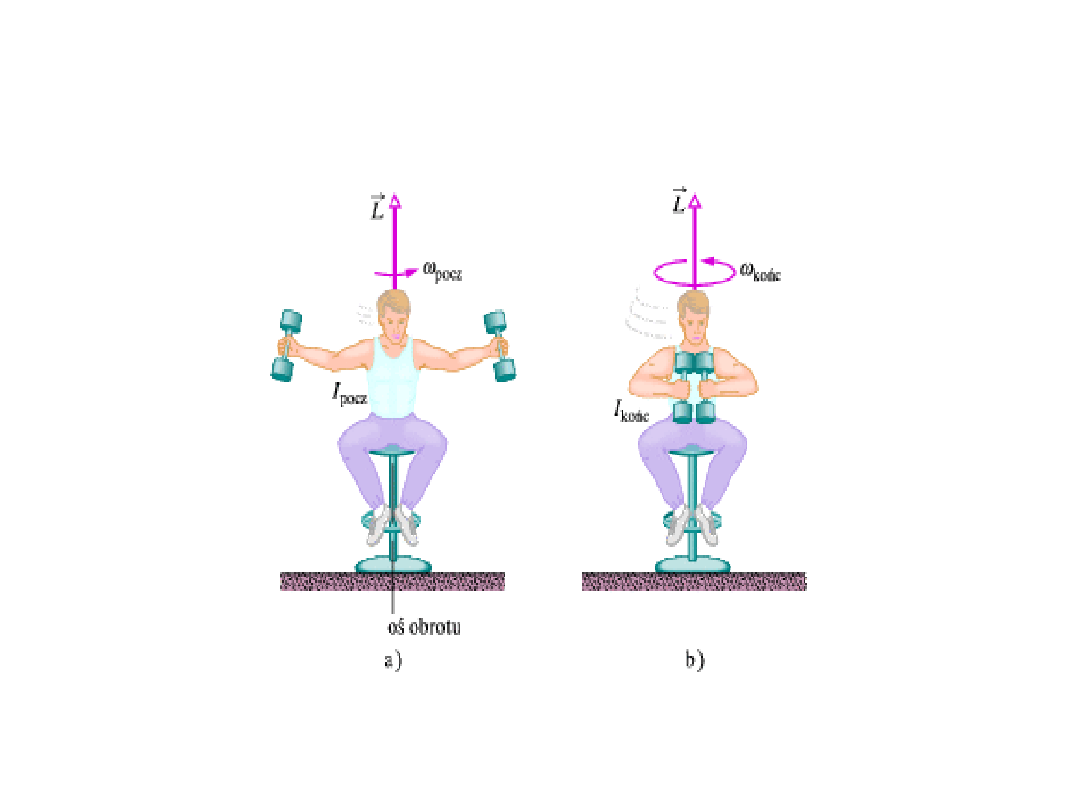
Moment pędu
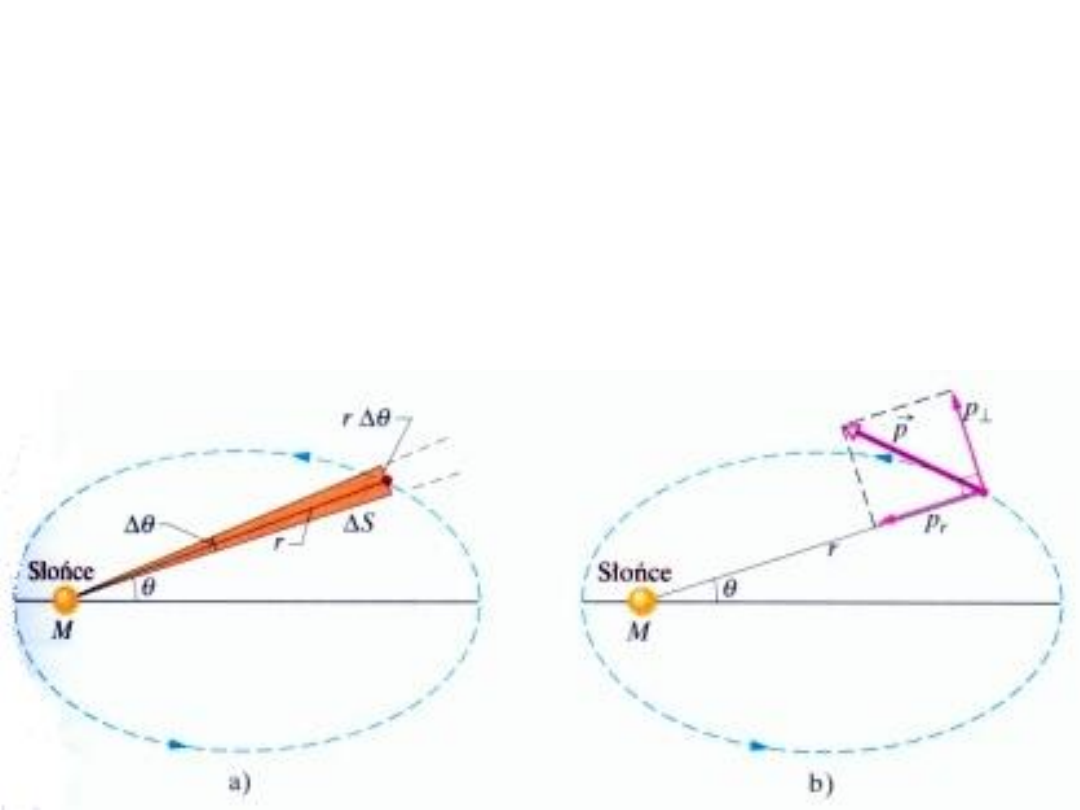
Zasada zachowania
momentu pedu
Energia w polu
Pole jako przestrzeń w której
określone są wielkości fizyczne. Mogą
to być wielkości skalarne lub
wektorowe. Mamy więc np.. Pole sił,
pole potencjału, pole natężeń,
temperatur, ciśnienia, itd.
Zacznijmy od pola grawitacyjnego
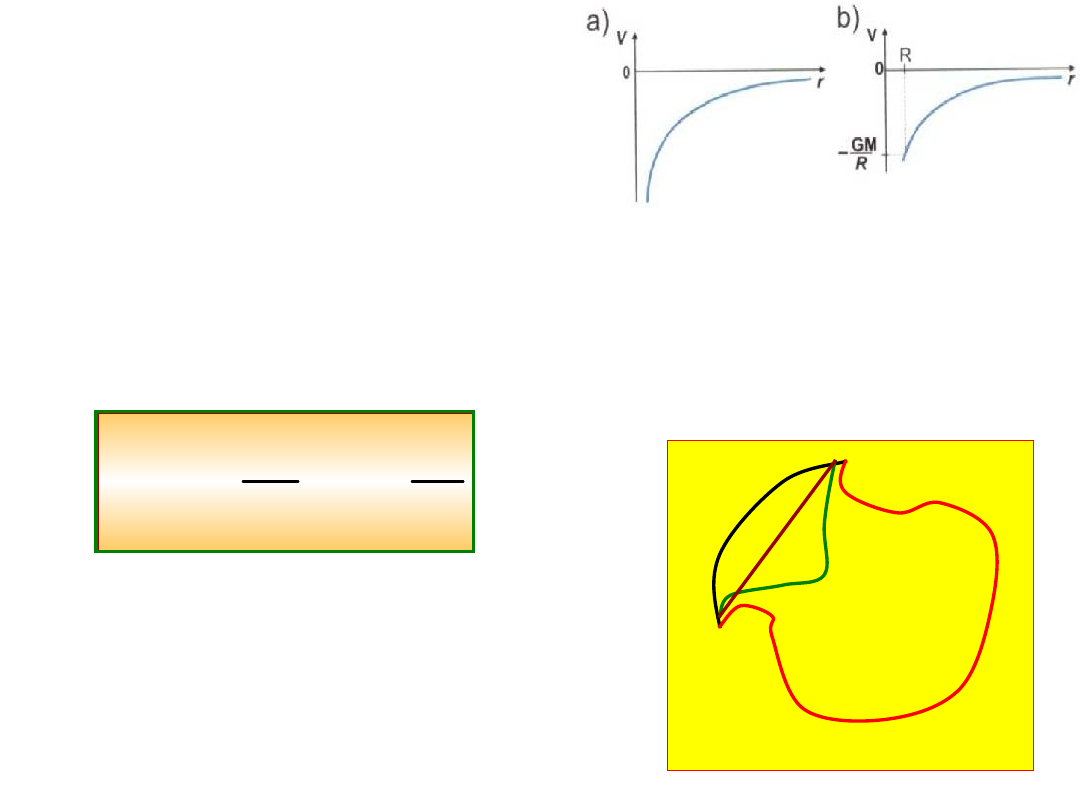
Pole grawitacyjne
Jest polem potencjalnym co oznacza, że
posiada potencjał a to z kolei oznacza, że
praca sił przy przejściu z punktu A do B nie
zależy od obranej drogi ale tylko od różnicy
potencjału
B
A
p
1
2
E
m
V(r )
G
m
r
V(r) = V(x,y,z,)
Potencjał jest skalarem
Działają siły zachowawcze
B
A
F ds const
r r
niezależnie od drogi pomiędzy A i B.
B
A
Siły są zachowawcze,
jeśli w czasie ruchu pod
wpływem tych sił
spełniona jest
zasada
zachowania energii
mechanicznej.
Możemy również
stwierdzić, że
Zależność pomiędzy energią a
potencjałem
Trzeba zwrócić uwagę, że naprawdę potrafimy tylko policzyć
E
p
a nie samą E
p
(r) ,
.
ponieważ E
p
=E
p
(r) –E
p
(r
0
). Żeby
znaleźć E
p
(r) trzeba nie tylko znać siłę ale jeszcze wartość E
p
(r
0
)
Punkt określony przez promień wodzący r
0
jest zwykle tzw.
punktem odniesienia.
Wygodnie jest wybrać go tak, ażeby
energia potencjalna w tym punkcie była równa zero!
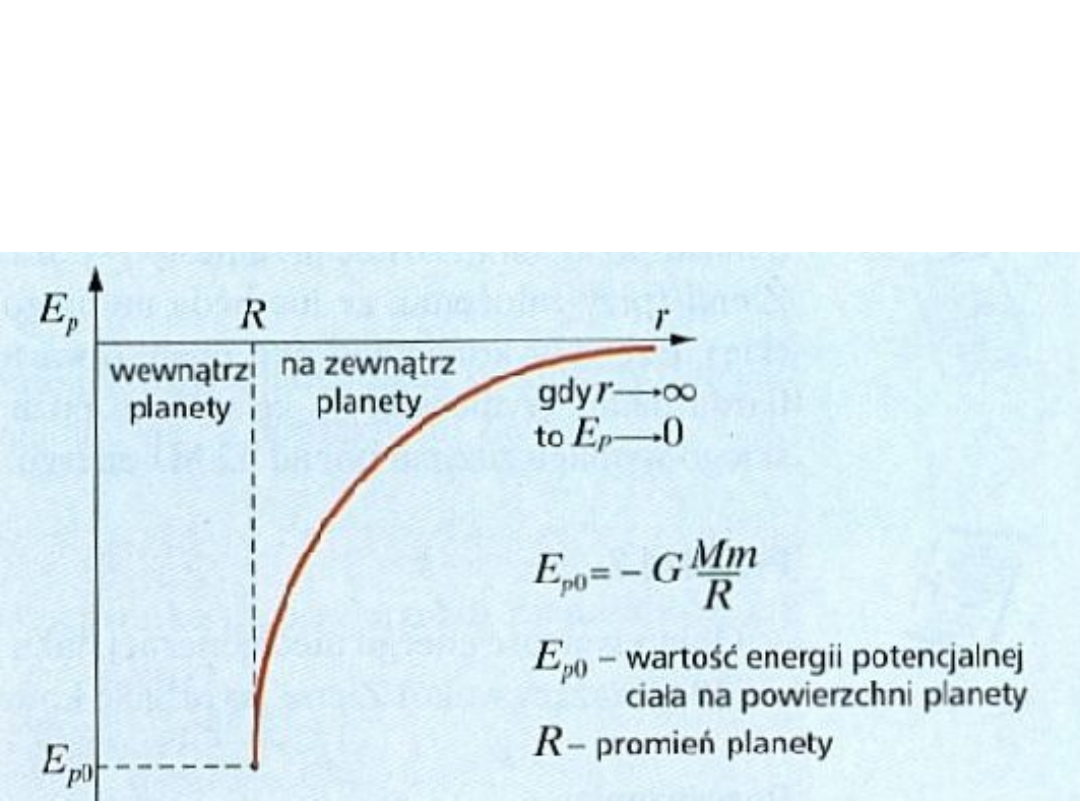
Na stronie 10 poprzedniego wykładu uzyskaliśmy dla energii
potencjalnej masy m
2
punkcie r wartość
0
0
( )
( )
r
p
p
p
r
E
E r
E r
F ds
r
r
Pamiętamy, że zmianę energii potencjalnej
definiowaliśmy jako:
1 2
( )
p
Gmm
E r
r
.
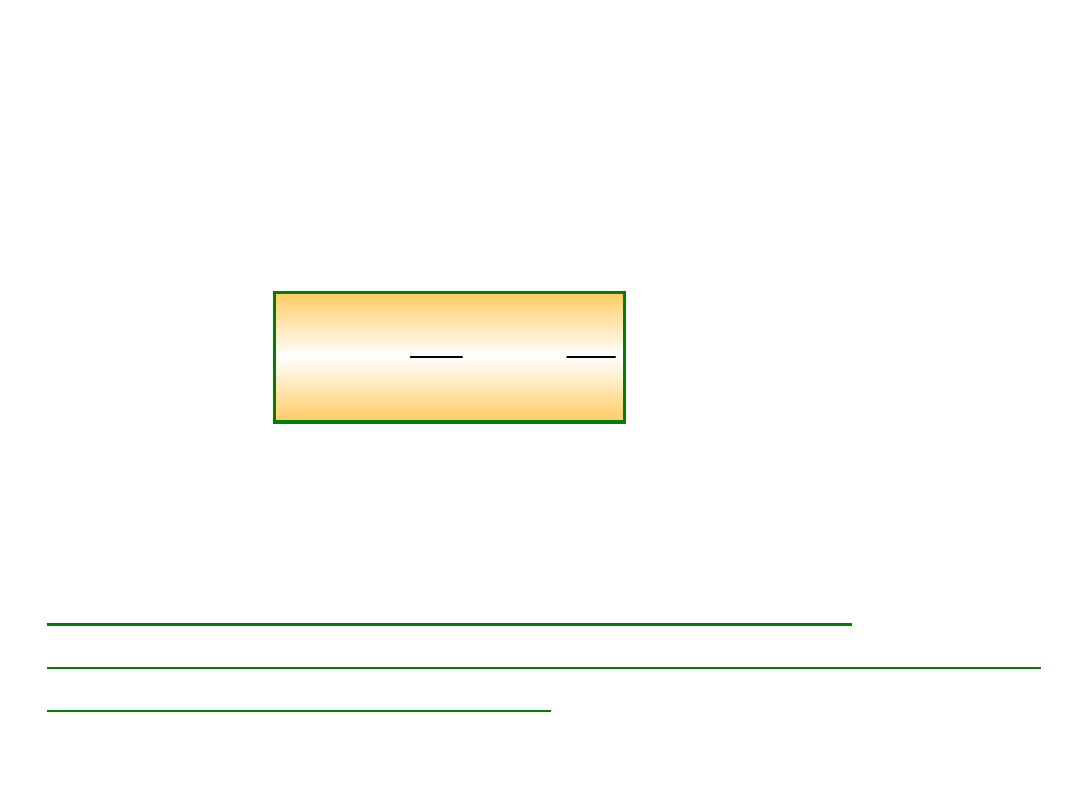
Widzimy, że wokół masy m
1
istnieje
przestrzeń, w której na dowolną dowolną masę
m
2
działa siła dana poprzednim wzorem.
Wprowadźmy wielkość charakteryzującą
przestrzeń roztaczającą się wokół masy m
1
w
postaci funkcji ;
p
1
2
E
m
V(r )
G
m
r
Funkcję V(r) w omawianym przypadku nazywamy
potencjałem
pola grawitacyjnego.
Potencjał ten definiujemy jako stosunek
grawitacyjnej energii potencjalnej dowolnej masy
m do wielkości tej masy .
Podobnie postąpimy już niedługow przypadku pola elektrycznego.
Siły zachowawcze i niezachowawcze
Ogólnie dzielimy siły na dwie klasy, siły
zachowawcze i siły niezachowawcze.
Rozróżnienie pomiędzy nimi jest oparte na
wielkości pracy jaką siła wykonuje na drodze
zamkniętej.
Siły zachowawcze są to takie siły dla których
praca po drodze zamkniętej jest równa zero.
0
F ds
r r
�
Siły tarcia są siłami niezachowawczymi.
Ogólnie biorąc siłami niezachowawczymi są
siły zależne od czasu i siły zależne od
prędkości.
Należy podkreślić, że suma energii
potencjalnej i kinetycznej jest stała tylko dla
sił zachowawczych.
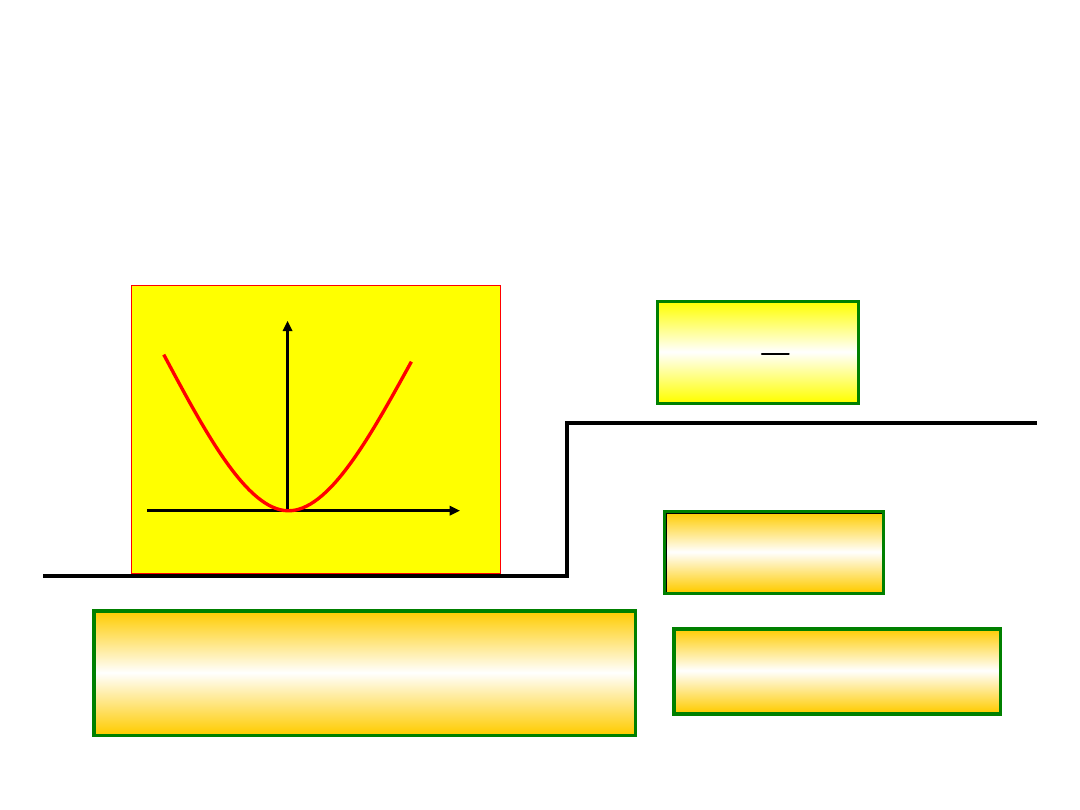
Przykłady energii potencjalnych sił zachowawczych
1. Energia potencjalna sprężyny
Energię potencjalną sprężyny omówiliśmy
już poprzednio.
Otrzymaliśmy na energię potencjalna
wartość:
2
1
2
p
E
cx
E
p
x
2. Energia Potencjalna stałej siły
ˆ
x
F
mgi
r
0
ˆ ˆ
(
)
x
p
x
x
E
mgi i dx
mgx
( )
p
E x
mgx
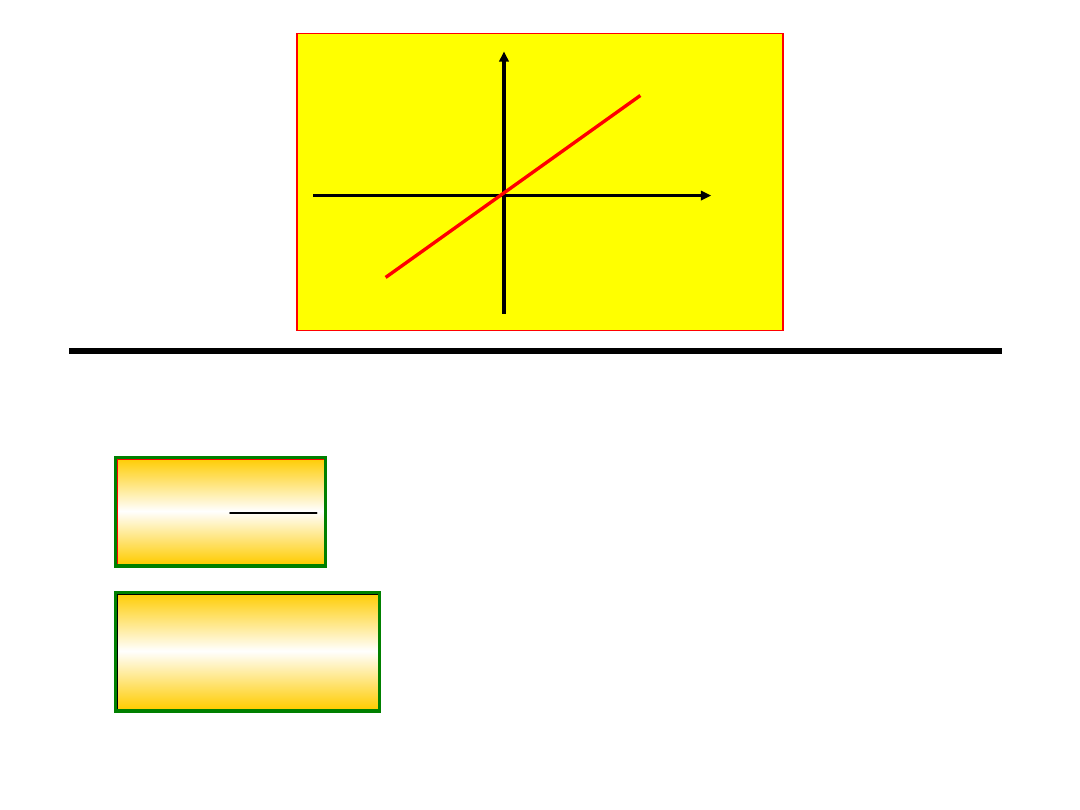
E
p
x
3 Energia potencjalna uniwersalnej siły
grawitacji
1 2
2
mm
F G
r
r jest odległością masy m
1
od
masy m
2
.
0
r
p
r
E
F ds
r
r
Załóżmy, że liczymy zmianę energii
przy przesunięciu masy m
2
z
nieskończoności do r.
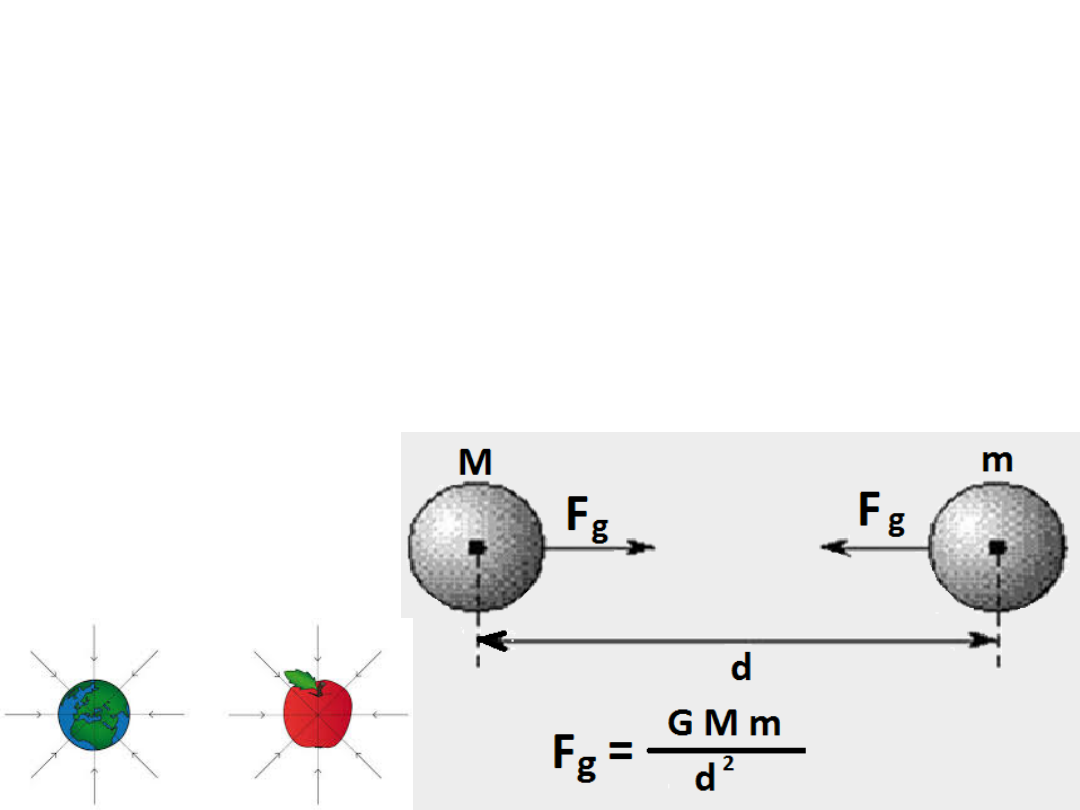
W przypadku pola grawitacyjnego lub
elektrostatycznego wygodnie jest przyjąć
potencjał i energię potencjalną
umieszczonego w tym polu ciała lub
ładunku w odniesieniu do
nieskończoności gdzie
przyjmujemy potencjał równy zero
Siły oddziałują za pośrednictwem pola.
Inaczej mówiąc wokół mas i ładunków mamy pole
sił.
W polu, które ma potencjał są to siły zachowawcze
Potencjał to stosunek energii potencjalnej do
masy lub ładunku. Potencjał jest określony dla
każdego punktu pola w którym działają siły a
więc możemy powiedzieć, że mamy pole
potencjału … np. dla układu współrzędnych Oxyz
potencjał zapiszemy jako V(x,y,z). Potencjał jest
skalarem a pole potencjału polem skalarnym
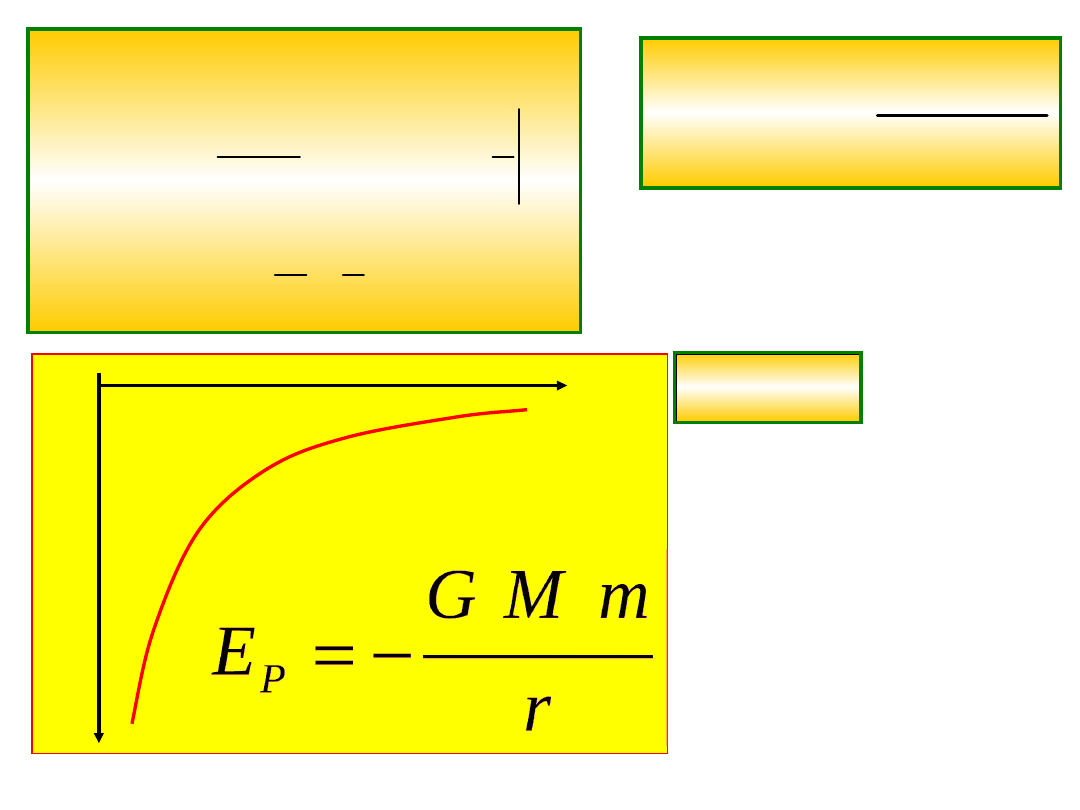
1 2
1 2
2
1 2
( )
( )
1
1 1
p
p
p
r
r
E
E r
E
mm
G
dr Gmm
r
r
Gmm
r
( ) 0
p
E
1 2
( )
p
Gmm
E r
r
r
E
p
Potencjał w polu
grawitacyjnym
jest ujemny, bo trzeba
wykonać
pracę aby masę Δm
przenieść
do nieskończoności gdzie
(jak się
umówiliśmy) potencjał
wynosi zero.
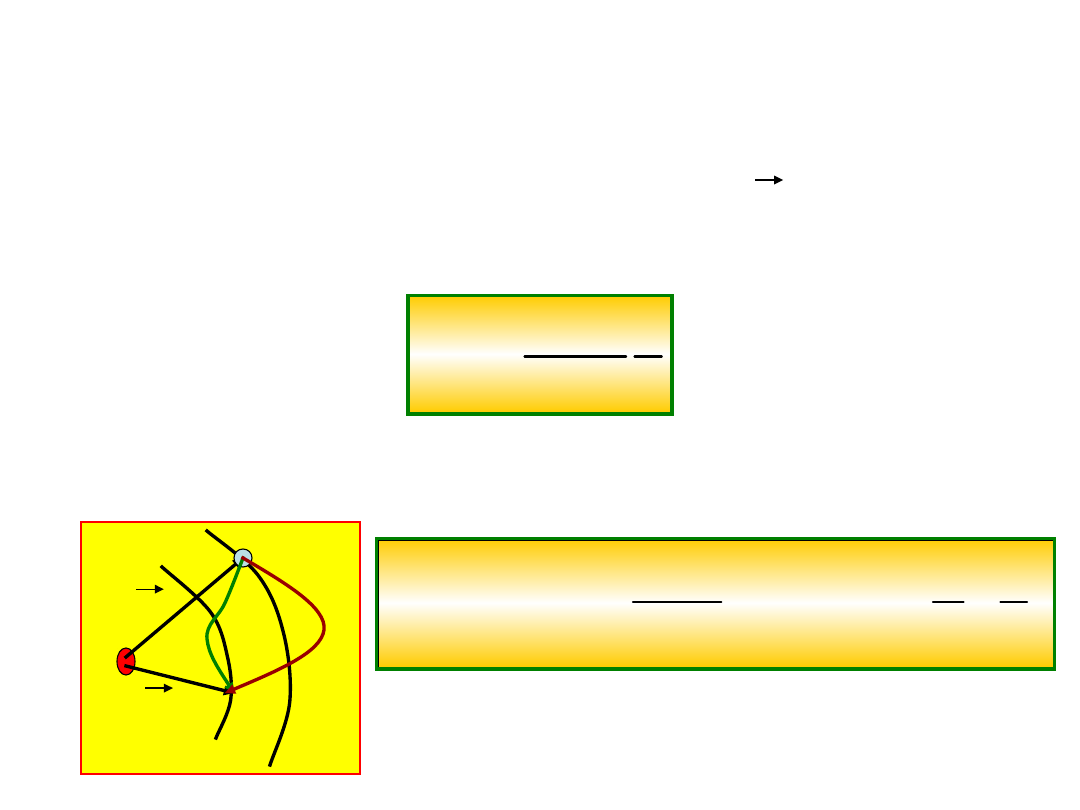
Praca i energia potencjalna dla sił
elektrostatycznych
Pomiędzy dwoma ładunkami q
1
i q
2
umieszczonymi w odległości r od siebie działa
wzdłuż wektora r siła elektrostatyczna zgodnie z
prawem Coulomba,
1
2
2
q q r
F k
r
r
r
r
Jaką pracę wykona ta siła, jeśli ładunek q
2
przesuniemy z punktu P
1
do punktu P
2
.
2
2
1
1
1
2
1 2
2
2
1
1 1
r
r
r
r
q q
W
Fdr
k
dr
kqq
r
r
r
q
1
q
2
P
2
P
1
r
1
r
2
.
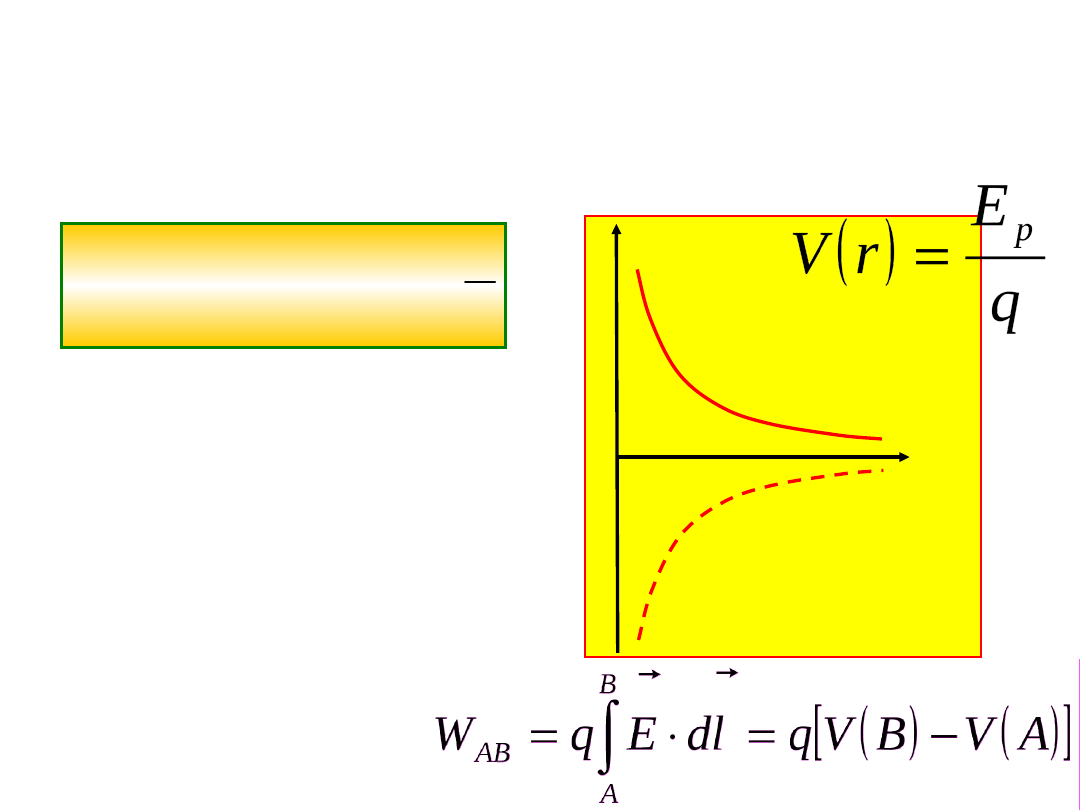
Oznacza to, że energia potencjalna E
p
= -W
zależy tylko od r
1
i r
2
. Często interesuje nas
pytanie jaką prace należy wykonać, aby
ładunek z nieskończoności przesunąć do
punktu P
2.
2
2
1 2
2
1
P
r
E
W
F dr kqq
r
r
E
p
q
1
·q
2
> 0
q
1
·q
2
< 0
przyciąganie
odpychanie
Kształt energii
potencjalnej
oddziaływania
elektrostatycznego
jest opisany taką samą
funkcją f(r) jak dla
oddziaływania
grawitacyjnego. Może
ona jednak być
również dodatnia, czyli
odpychająca.
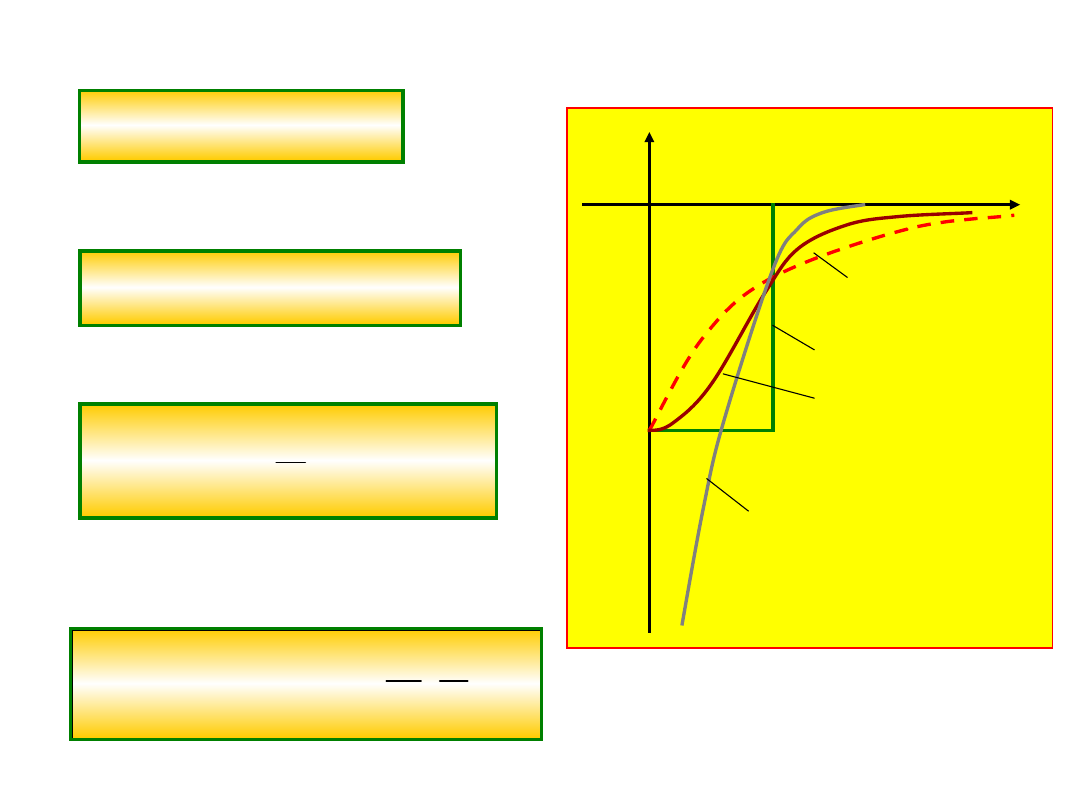
2. Potencjał wykładniczy
0
0
( )
exp( / )
p
E r
V
r r
3. Potencjał Gaussa
2
2
0
0
( )
exp(
/ )
p
E r
V
r r
0
0
0
( )
( )exp( / )
p
r
E r
V
r r
r
4. Potencjał Yukawy
5. Potencjał
oscylatora
harmonicznego
2
2
0
0
2
0
0
( )
(
)
(
1)
p
V r
E r
r r
r r
E
p
(r)/V
0
r/r
0
p. Yukawy
p. Gaussa
p. jamy prostokątnej
p. wykładniczy
Jak wyglądają te potencjały?
Związek pomiędzy siłą a energią
potencjalną
Pokazaliśmy, że energia potencjalna ciała może
być w prosty sposób obliczona w dowolnej
odległości od niego jako iloczyn masy lub
ładunku oraz potencjału pola.
Miejsca o tej samej energii potencjalnej dane
są przez równanie:
( , , )
p
E x y z const
.
Jest to równanie powierzchni, którą nazywamy
powierzchnią ekwipotencjalną.
W atomie powierzchnie ekwipotencjalne
elektronów znajdujących się w zasięgu
oddziaływania dodatnich protonów mają
równanie;
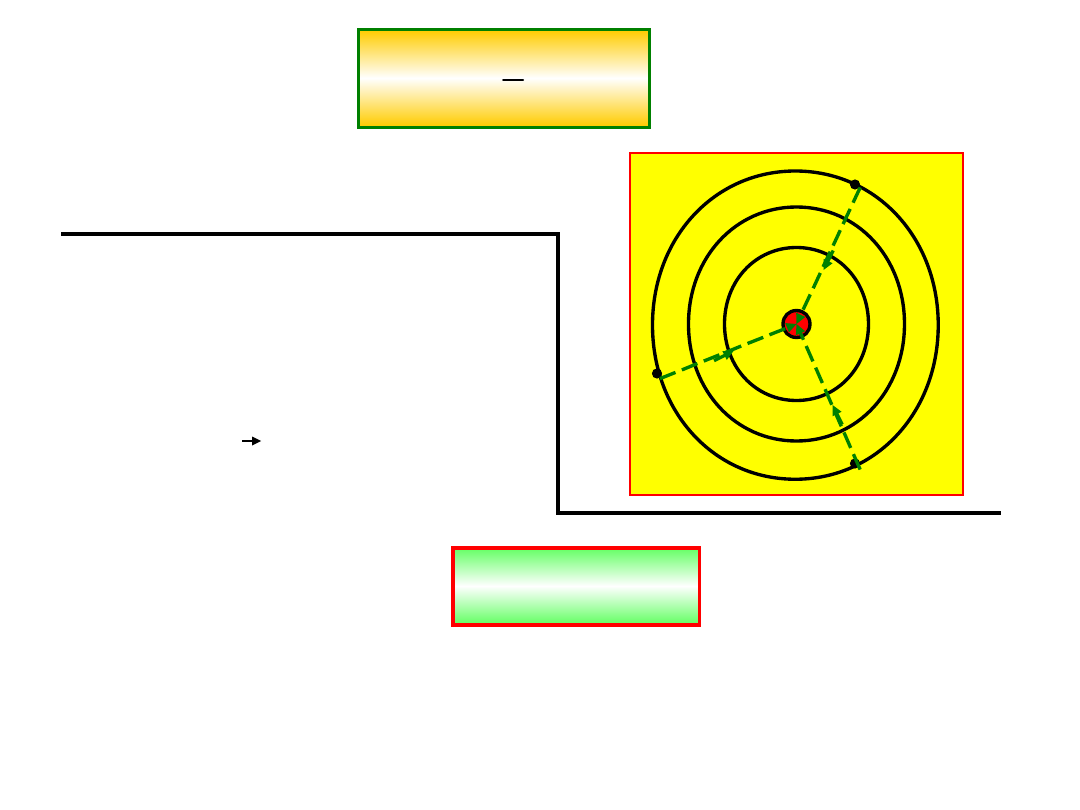
1
p
E
k
const
r
,
są powierzchniami kul.
W jaki sposób można
policzyć
wielkość siły
działającej na elektron
w dowolnym miejscu.
Jeśli przesuniemy
elektron o dr, to
energia potencjalna
zmieni się o
p
dE
F dr
r r
Jeśli przesuniemy elektron po powierzchni
ekwipotencjalnej,
dE
p
= 0, czyli nie została wykonana praca.
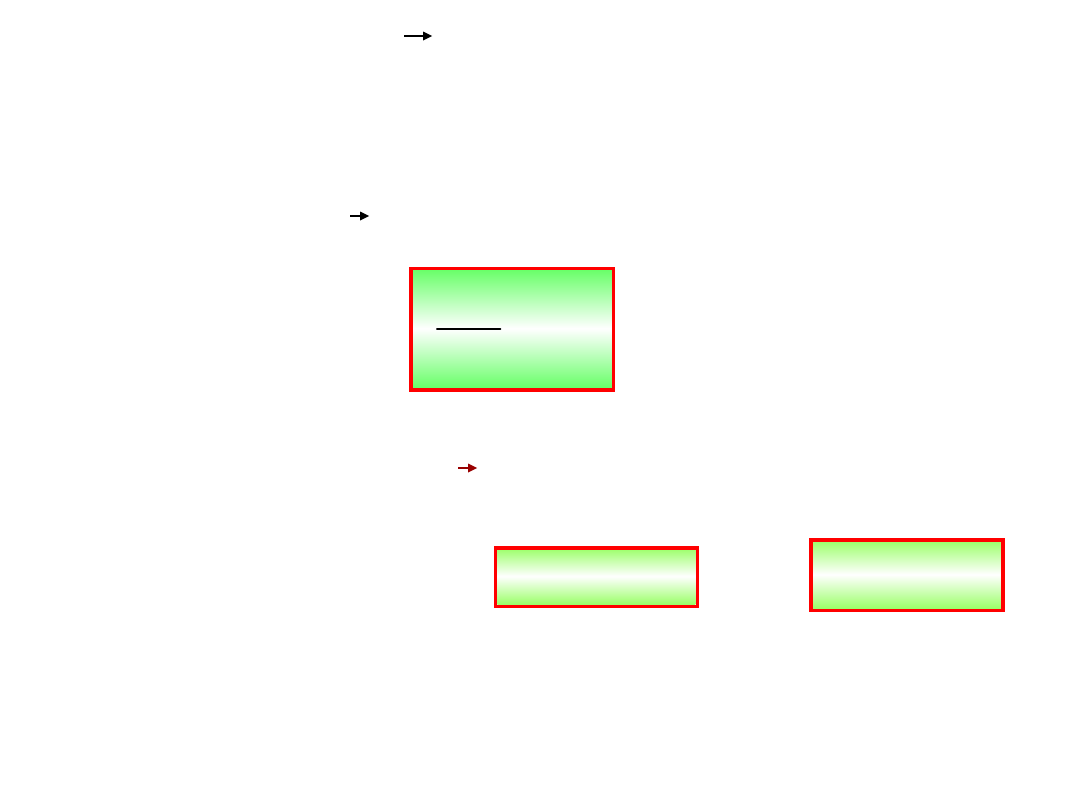
Wynika z tego, ze siła F może być skierowana
tylko prostopadle do powierzchni
ekwipotencjalnej. Kierunek siły jest więc dany
przez „linie sił”, które są prostopadłe do
powierzchni ekwipotencjalnych. Przesuwając
elektron wzdłuż linii sił o odcinek dr
równoległy do linii sił, otrzymujemy,
p
dE
F
dr
.
Możemy więc powiedzieć,
że siła jest pochodną
energii potencjalnej w kierunku r, czyli tzw.
pochodną kierunkową
.
dW F dr
r r
p
E
W
W oparciu o równania
i
możemy napisać;
( , , )
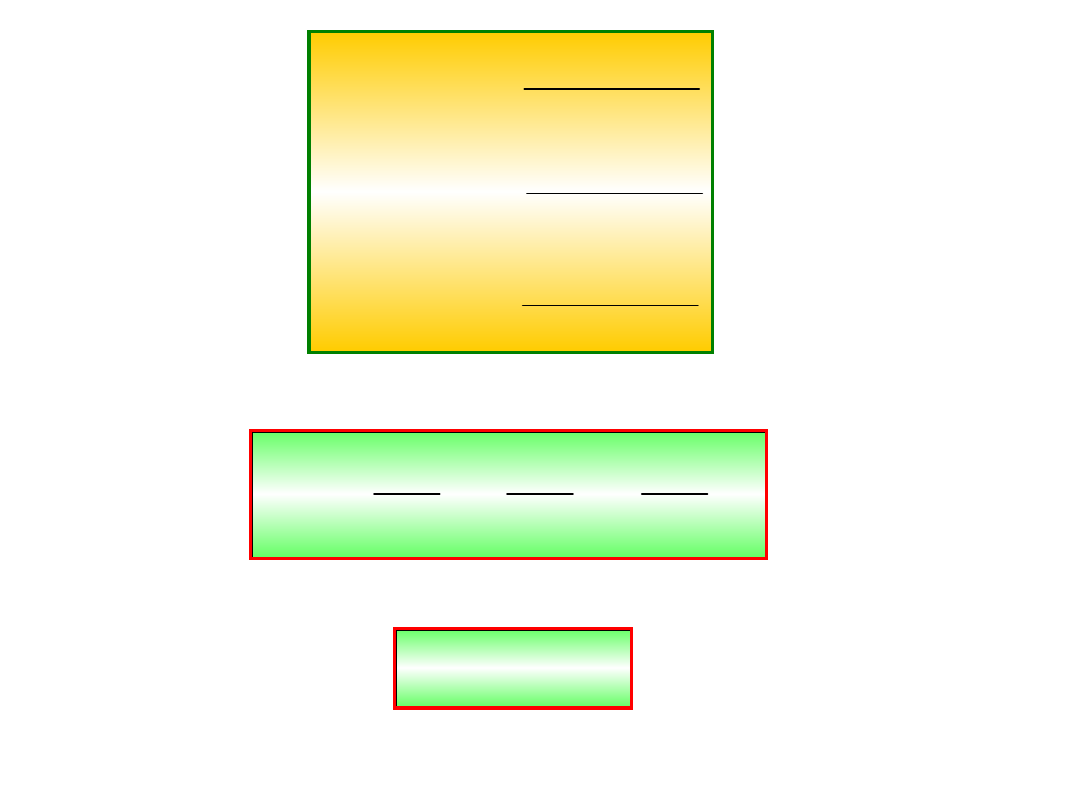
ˆ
( , , )
ˆ
( , , )
ˆ
p
x
x
p
y
y
p
z
z
E x y z
F
F i
x
E x y z
F
F i
y
E x y z
F
F i
z
r
r
r
.
Podany układ równań jest równoważny
równaniu:
ˆ
ˆ
ˆ
p
p
p
x
y
z
E
E
E
F
i
i
i
x
y
z
r
.
Inaczej piszemy, że
p
F
gradE
r
.
Document Outline
