Metodologia badań
Metodologia badań
i statystyka
i statystyka
Wojciech Grabowski
wgrabowski@aps.edu
.pl
spotkanie szóste
Metodologia badań
Metodologia badań
i statystyka
i statystyka
Wojciech Grabowski
wgrabowski@aps.edu
.pl
spotkanie szóste
Prezentacja danych
ilościowych
Pomiar
wykonany na
niewielkiej
próbie
ujmujemy jako
szereg danych
indywidualnych
.
Gdy danych jest
więcej, a cecha
ma charakter
skokowy, to
można je
pogrupować w
szereg
rozdzielczy
punktowy.
Gdy danych jest
dużo, a cecha
ma charakter
ciągły, to można
je pogrupować
w szereg
rozdzielczy
klasowy.
Bez względu na to,
czy liczymy wskaźniki
z szeregu
indywidualnego, czy
punktowego, to ich
wartości będą
identyczne.
Wartości wskaźników liczone z
szeregu klasowego są tylko
przybliżone. Dlatego często
rezygnuje się z takiego
przedstawienia danych, a
obliczenia wykonuje się
komputerowo z zapisu
indywidualnego
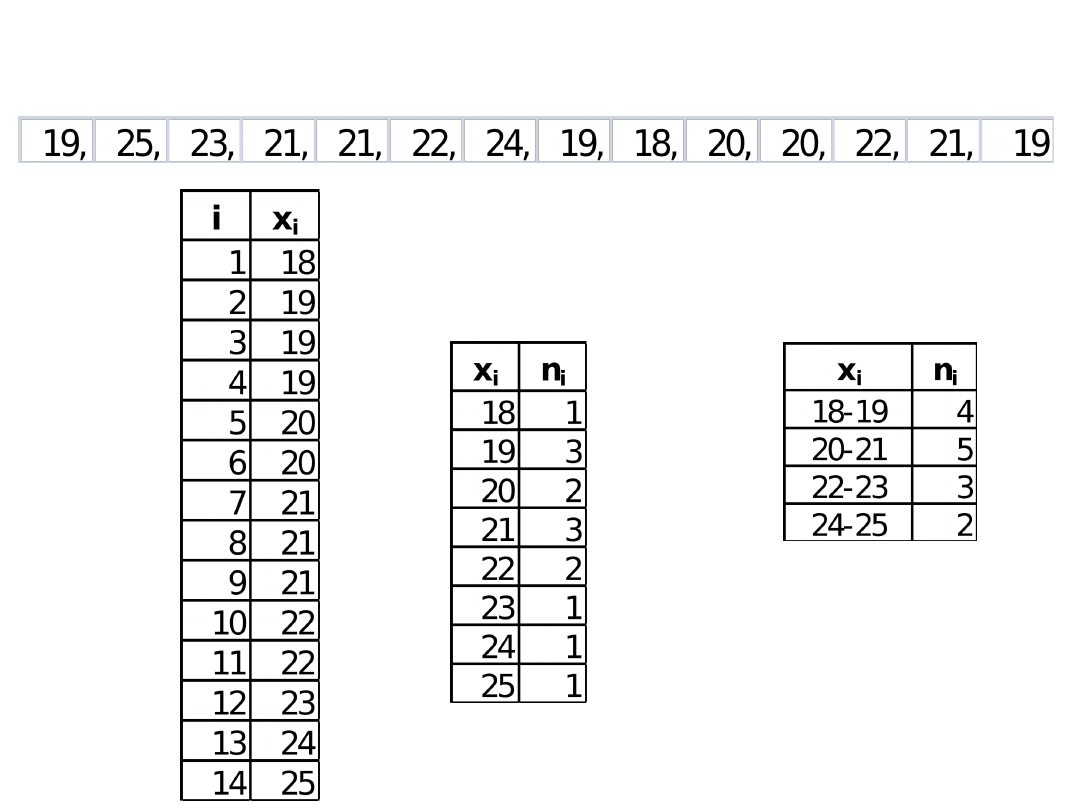
Przykłady prezentacji
danych
Dane
indywi
-
dualn
e
Dane punktowe
Dane klasowe
Wskaźniki
dla indywidualnych danych ilościowych
Przykład:
Zapytano grupę studentów ile książek
przeczytali w ciągu ostatniego roku.
Odpowiedzi: 6, 2, 0, 1, 7, 2.
1. Zestawiamy posortowane
dane w tabelce.
2. Określamy liczebność
próby.
N
=
3. Wskazujemy dominantę.
Dominanta to najliczniejsza
kategoria.
D
=
Interpretacja:
Typowe dla grupy
jest
przeczytanie
dwóch
książek.
x
i
0
1
2
2
6
7
2
6
x
i
0
1
2
2
6
7
N = 6
D = 2
4. Liczymy pozycję
mediany i wskazujemy
medianę.
poz. Me
=
N + 1
2
=
6
+
1
2
=
7
2
=
3,5
Me
=
1
2
3
3,
5
2
Interpretacja:
Połowa grupy
przeczytała nie więcej niż
2
książki
i
połowa
przeczytała co najmniej 2
książki.
5. Liczymy średnią.
18
18
=
6
= 3
Interpretacja:
Przeciętnie
na osobę przypadają
trzy
przeczytane
książki.
x =
x
i
N
N = 6
D = 2
x
i
0
1
2
2
6
7
18
Me =
2
6. Wskazujemy rozstęp.
rozstęp
:
0
–
7
7. Liczymy wariancję
s
2
i odchylenie standardowe
s
.
x
i
–x
0 – 3
1 – 3
2 – 3
2 – 3
6 – 3
7 – 3
–3
–2
–1
–1
3
4
!
0
(x
i
–x)
2
(-3)
2
9
(-2)
2
4
(-1)
2
1
(-1)
2
1
3
2
9
4
2
16
40
=
40
6
– 1
=
40
5
=
8
x = 3
s =
s
2
=
8
=
2,8
Interpretacja:
Liczba
książek
przeczytanych przez poszczególne
osoby odchyla się przeciętnie o
2,8 książki w górę lub w dół od
średniej.
Interpretacja:
W ciągu ostatniego
roku
poszczególni
studenci
przeczytali pomiędzy 0 a 7
książek.
s
2
=
(x
i
–x)
2
N –
1
N = 6
D = 2
Me =
2
x
i
0
1
2
2
6
7
18
x
i
–x
–3
–2
–1
–1
3
4
!
0
(x
i
–x)
2
9
4
1
1
9
16
40
x = 3
8. Wyznaczamy obszar przeciętnej
zmienności.
x ± s
3
0,2
x
typ
5,8
Interpretacja:
Wyniki typowe
dla
grupy
zawierają
się
pomiędzy
0,2
a
5,8
przeczytanej książki.
rozstęp: 0 –
7
s =
2,8
±
2,8
9. Do oceny wielkości
zróżnicowania liczymy
współczynnik zmienności.
v =
s
x
.
100
2,8
3
=
.
100
= 93,3
%
v
zróżnicowan
ie
0
> 0 – 20%
>20 – 40%
>40 – 60%
>60 – 80%
>80 –
100%
> 100%
brak
bardzo
słabe
dość słabe
umiarkowan
e
dość silne
bardzo silne
ekstremalnie
silne
Interpretacja:
Grupa
jest
bardzo
silnie
zróżnicowana
pod względem
liczby
przeczytanych
książek.
N = 6
D = 2
Me =
2
x
i
0
1
2
2
6
7
18
x
i
–x
–3
–2
–1
–1
3
4
!
0
(x
i
–x)
2
9
4
1
1
9
16
40
x = 3
10.
Oceniamy skośność danych.
rozstęp: 0 –
7
s =
2,8
a) wstępne
oszacowanie
0,2 x
typ
5,8
v =
93,3%
• jeżelix = D = Me,
to mamy rozkład
typowy.
• jeżelix D > Me,
to mamy rozkład
dodatni,
czyli
z
przewagą wyników
niższych.
• jeżelix D < Me,
to mamy rozkład
ujemny,
czyli
z
przewagą wyników
wyższych.
3
2
2
x D
Me
>
>
=
=
Metoda
ta
nie
przyniosła
rozstrzygnięcia, choć
możemy
podejrzewać rozkład
dodatni.
N = 6
D = 2
Me =
2
x
i
0
1
2
2
6
7
18
x
i
–x
–3
–2
–1
–1
3
4
!
0
(x
i
–x)
2
9
4
1
1
9
16
40
x = 3
rozstęp: 0 –
7
s =
2,8
b) współczynnik
skośności
0,2 x
typ
5,8
v =
93,3%
W
sk
=
x –
Ds
=
3
–
2
2,
8
=
2,
8
1
=
+
0,36
W
sk
skośnoś
ć
brak
nikła
słaba
umiarkowan
a
dość silna
bardzo
silna
0,01 –
0,2
0
0,21 –
0,4
0,41 –
0,6
0,61 –
0,8
0,81 –
1
> 1
ekstremaln
ie
silna
Interpretacja:
Występuje słaba
skośność
dodatnia, czyli
słaba przewaga
mniejszej od
średniej liczby
przeczytanych
książek.
• Nie można policzyć wskaźnika
W
sk
,
jeżeli
nie
występuje
dominanta.
• Gdy
dominanta
jest
mało
wyrazista, wskazania W
sk
mogą
być dość przypadkowe.
N = 6
D = 2
Me =
2
x = 3
rozstęp: 0 –
7
s =
2,8
0,2 x
typ
5,8
v =
93,3%
W
sk
=
+
0,36
c) współczynnik asymetrii
-3
.
9
-2
.
4
-1
.
1
-1
.
1
3
.
9
4
.
16
(x
i
–x)
3
x
i
0
1
2
2
6
7
18
x
i
–x
–3
–2
–1
–1
3
4
!
0
(x
i
–x)
2
9
4
1
1
9
16
40
–27
–8
–1
–1
27
64
54
Jeżeli
zależy
nam
na
dokładnym
wyznaczeniu
skośności,
stosujemy
współczynnik asymetrii A.
Najpierw liczymy tzw.
trzeci moment
centralny.
m
3
=
(x
i
–x)
3
N – 1
5
4
6
=
= 10,8
– 1
Następnie możemy
policzyć A.
A =
m
3
s
3
10,
8
2,8
3
=
=
10,8
21,95
2
A =
0,49
N = 6
D = 2
Me =
2
x = 3
rozstęp: 0 – 7
s =
2,8
0,2 x
typ
5,8
v =
93,3%
W
sk
=
+
0,36
(x
i
–x)
3
x
i
0
1
2
2
6
7
18
x
i
–x
–3
–2
–1
–1
3
4
!
0
(x
i
–x)
2
9
4
1
1
9
16
40
–27
–8
–1
–1
27
64
54
A =
0,49
A =
0,49
A
asymetri
a
0,01 –
0,4
0,41 –
0,8
0,81 –
1,2
1,21 –
1,6
1,61 – 2
0
> 2
brak
nikła
słaba
umiarkowan
a
dość silna
bardzo silna
ekstremaln
ie
silna
Interpretacja:
Występuje
słaba
skośność
dodatnia,
czyli słaba przewaga
mniejszej od średniej
liczby przeczytanych
książek.
Wskaźniki
dla punktowych danych ilościowych
Przykład:
Sprawdzono, ile długopisów przynieśli na
zajęcia studenci z pewnej grupy
ćwiczeniowej.
1. Zestawiamy dane w
tabelce.
2. Określamy liczebność
próby.
39
N =
n
i
39
3. Wskazujemy dominantę.
D
=
1
Interpretacja:
Typowe dla
tej grupy
było
przyniesieni
e na zajęcia
po jednym
długopisie.
x
i
0
1
2
3
n
i
10
20
8
1
=
4. Liczymy pozycję mediany i wskazujemy
medianę.
n
cum
x
i
.
n
i
N =
39
D =
1
poz. Me
=
N + 1
2
39
=
+
1
2
=
40
2
= 20
Me
=
1
10
30
38
39
Interpretacja:
Połowa
grupy
przyniosła
co
najwyżej 1 długopis i połowa przyniosła nie
mniej niż 1 długopis.
5. Liczymy średnią
ważoną.
Interpretacja:
Przeciętnie na osobę przypada
jeden przyniesiony długopis.
x
=
N
(x
i
.
n
i
)
0
.
10
0
1
.
20
20
2
.
8
16
3
.
1
3
39
=
3
9
3
9
=
1
x
i
0
1
2
3
n
i
10
20
8
1
39
6. Wskazujemy
rozstęp.
(x
i
–x)
2 .
n
i
N =
39
D =
1
Me = 1
x =
1
rozstęp:
0
–
3
Interpretacja:
Każdy ze studentów przyniósł
na zajęcia od 0 do 3 długopisów.
7. Liczymy wariancję
s
2
i odchylenie
standardowe
s
.
s
2
=
(x
i
–x)
2 .
n
i
N –
1
(-1)
2 .
10
10
0
2 .
20
0
1
2 .
8
8
2
2 .
1
4
22
=
22
3
9
– 1
=
2
2
3
8
=
0,579
s =
s
2
s =
0,579
s =
0,76
Interpretacja:
Liczba długopisów przyniesionych przez
poszczególne osoby odchyla się przeciętnie o 0,76
sztuki w górę lub w dół od średniej.
x
i
–x
n
cum
x
i
.
n
i
x
i
0
1
2
3
n
i
10
20
8
1
39
10
30
38
39
0
20
16
3
39
0–1
–1
1–1
0
2–1
1
3–1
2
(dla danych skokowych można zaokrąglić
do 1)
8. Wyznaczamy obszar przeciętnej
zmienności.
N =
39
D =
1
Me = 1
x =
1
(x
i
–x)
2 .
n
i
10
0
8
4
22
x
i
–x
n
cum
x
i
.
n
i
x
i
0
1
2
3
n
i
10
20
8
1
39
10
30
38
39
0
20
16
3
39
–1
0
1
2
rozstęp: 0 –
3
x ± s
1
±
0,76
s =
0,76
0,24
x
typ
1,76
Interpretacja:
Wyniki typowe dla grupy zawierają się
pomiędzy
0,24
(0)
a
1,76
(2)
przyniesionego długopisu.
9. Badamy wielkość
zróżnicowania.
v =
s
x
.
100
0,76
1
=
.
100
= 76
%
v
zróżnicowan
ie
0
> 0 – 20%
>20 – 40%
>40 – 60%
>60 – 80%
>80 –
100%
> 100%
brak
bardzo
słabe
dość słabe
umiarkowan
e
dość silne
bardzo silne
ekstremalnie
silne
Interpretacja:
Grupa jest dość silnie
zróżnicowana pod względem
liczby
przyniesionych
długopisów.
0
x
typ
2
Dla danych
skokowych można
zaokrąglić:
10.
Oceniamy skośność
danych.
N =
39
D =
1
Me = 1
x =
1
(x
i
–x)
2 .
n
i
10
0
8
4
22
x
i
–x
n
cum
x
i
.
n
i
x
i
0
1
2
3
n
i
10
20
8
1
39
10
30
38
39
0
20
16
3
39
–1
0
1
2
rozstęp: 0 –
3
s =
0,76
1
1
1
x D
Me
=
=
=
=
a) wstępne
oszacowanie
b) współczynnik
skośności
W
sk
=
x –
Ds
=
1
–
1
0,7
6
=
0,7
6
0
=
0
W
sk
skośnoś
ć
brak
nikła
słaba
umiarkowan
a
dość silna
bardzo
silna
0,01 –
0,2
0
0,21 –
0,4
0,41 –
0,6
0,61 –
0,8
0,81 –
1
> 1
ekstremaln
ie
silna
Interpretacja:
W badanej grupie brak
jest skośności ze względu
na liczbę przyniesionych
długopisów.
0,24 x
typ
1,76
v =
76%
Interpretacja:
Rozkład danych
jest
symetryczny.
(x
i
–x)
3 .
n
i
N =
39
D =
1
Me = 1
x =
1
(x
i
–x)
2 .
n
i
10
0
8
4
22
x
i
–x
n
cum
x
i
.
n
i
x
i
0
1
2
3
n
i
10
20
8
1
39
10
30
38
39
0
20
16
3
39
–1
0
1
2
rozstęp: 0 –
3
s =
0,76
c) współczynnik asymetrii
0,24 x
typ
1,76
v =
76%
W
sk
=
0
m
3
=
(x
i
–x)
3 .
n
i
N – 1
6
39
=
=
0,158
– 1
(-1)
3 .
10
–10
0
3 .
20
0
1
3 .
8
8
2
3 .
1
8
6
A =
m
3
s
3
0,15
8
0,76
3
=
=
0,158
0,43
9
=
0,36
=
3
8
6
A
asymetri
a
0,01 –
0,4
0,41 –
0,8
0,81 –
1,2
1,21 –
1,6
1,61 – 2
0
> 2
brak
bardzo
słaba
dość słaba
umiarkowan
a
dość silna
bardzo silna
ekstremalnie
silna
Interpretacja:
Występuje bardzo słaba
asymetria dodatnia, czyli bardzo
słaba przewaga mniejszej od
średniej liczby przyniesionych
długopisów.
Wskaźniki
współzależności
cech ilościowych
Najprostszym wskaźnikiem współzależności dla
cech ilościowych jest współczynnik korelacji liniowej
r
Pearsona. Można go wyznaczyć posługując się
jednym z dwóch równoważnych wzorów:
r =
cov
x
y
s
x
.
s
y
gdzie
:
(x
i
– x)(y
i
–
y)
(x
i
– x)
2 .
(y
i
–
y)
2
r =
cov
xy
=
(x
i
– x)(y
i
–
y)
N – 1
s – odchylenie
standardowe danej
cechy
lub
bezpośrednio:
Warunki liczenia
r:
1. Obie cechy muszą być
ilościowe. Zaleca się, by
były
co
najmniej
w
przybliżeniu ciągłe.
2. Zależność musi być
uzasadniona logicznie.
3. Zależność musi być liniowa
lub w przybliżeniu liniowa.
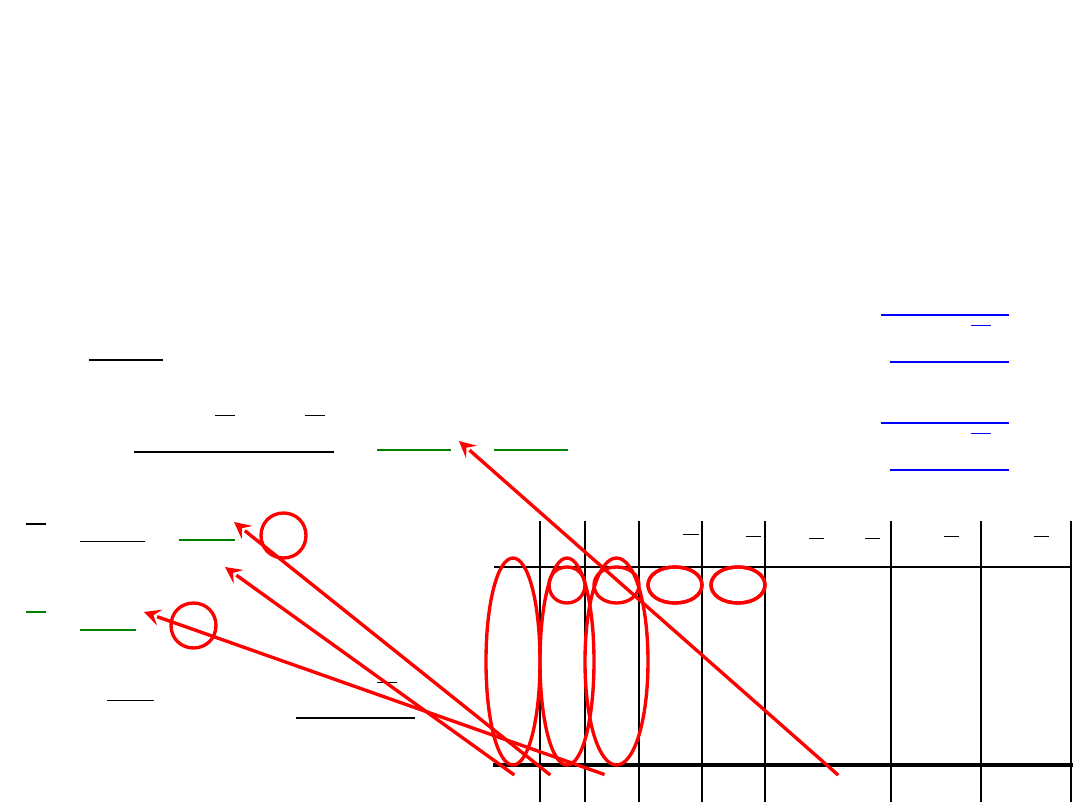
Liczenie współczynnika r
Pearsona
r =
cov
x
y
s
x
.
s
y
cov
xy
=
(x
i
– x)(y
i
–
y)
N – 1
Przykład:
Badano zależność pomiędzy liczbą dni
„zabierania się” do nauki a wynikiem
egzaminu.
(x
i
–x)(y
i
–
y)
(x
i
– x)
2
(y
i
– y)
2
x
x
i
–
y
y
i
–
N=
7
3
5
x
i
y
i
l.p.
1
2
3
4
5
6
7
1
8
5
5
2
9
5
30
8
11
20
27
5
18
119
Liczbę dni „zabierania się” oznaczmy
przez x.
Liczbę punktów z egzaminu oznaczmy
przez y.
s = s
2
s
2
=
(x
i
–
x)
2
N – 1
x
=
x
i
N
35
=
7
=
5
y
=
11
9
7
=
17
1-5
– 4
8-5
3
5-5
0
5-5
0
2-5
– 3
9-5
4
5-5
0
!
0
30-
17
13
8-
17
– 9
11-
17
– 6
20-
17
3
27-
17
10
5-
17
– 12
18-
17
1
!
0
-4
.
13
– 52
3
.
(-9)
– 27
0
.
(-6)
0
0
.
3
0
-3
.
10
– 10
4
.
(-12)
– 48
0
.
1
0
– 157
=
–
157
7
– 1
=
–
157
6
=
–
26,167
(-
4)
2
16
3
2
9
0
2
0
0
2
0
(-
3)
2
9
4
2
16
0
2
0
s
x
=
(x
i
–
x)
2
N – 1
s
y
=
(y
i
–
y)
2
N – 1
50
13
2
(-
9)
2
16
9
81
(-
6)
2
36
3
2
9
10
2
10
0
(-12)
2
14
4
1
2
1
540
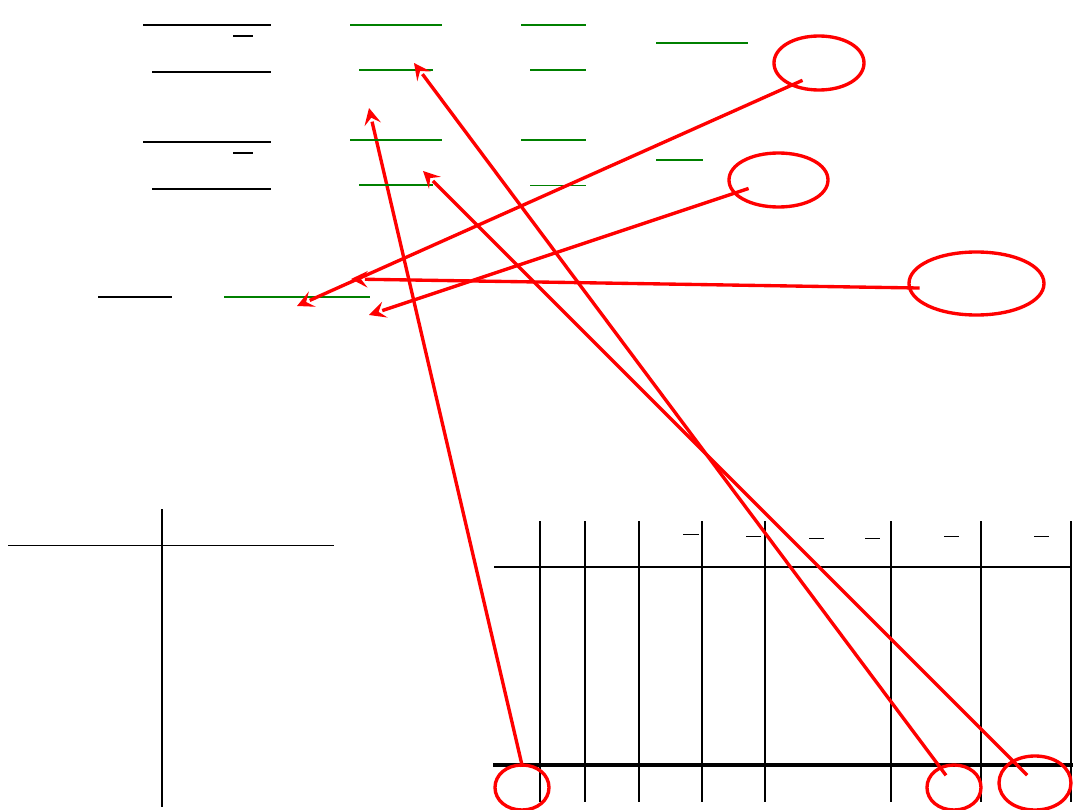
r =
cov
x
y
s
x
.
s
y
cov
xy
= –
26,167
s
x
=
(x
i
–
x)
2
N – 1
s
y
=
(y
i
–
y)
2
N – 1
(x
i
–x)(y
i
–
y)
(x
i
– x)
2
(y
i
– y)
2
x
x
i
–
y
y
i
–
N=
7
3
5
x
i
y
i
l.p.
1
2
3
4
5
6
7
1
8
5
5
2
9
5
30
8
11
20
27
5
18
119
– 4
3
0
0
– 3
4
0
!
0
13
– 9
– 6
3
10
– 12
1
!
0
– 52
– 27
0
0
– 10
– 48
0
– 157
16
9
0
0
9
16
0
50
16
9
81
36
9
10
0
14
4
1
540
=
50
7
– 1
=
50
6
= 8,333
=
2,89
=
540
7
– 1
=
540
6
= 90
=
9,49
=
–
26,167
2,89
.
9,49
=
–
0,95
r
zależność
0,01 –
0,10
0,11 –
0,30
0,31 –
0,60
0,61 –
0,90
0,91 –
0,99
1
0
brak
nikła
słaba
umiarkowan
a
silna
bardzo
silna
pełna
Interpretacja:
Występuje bardzo silna zależność ujemna
polegająca na tym, że im krócej student
„zbierał się” do nauki, tym wyższy osiągał
wynik z egzaminu.
Współczynnik
determinacji
Możemy
również
wyznaczyć
współczynnik
determinacji
r
2
, który informuje nas w jakim
stopniu zmienna zależna (skutek) zależy od
zmiennej niezależnej (przyczyny).
r = –0,95
r
2
= (
-0,95
)
2 .
100
= 0,9025
.
100
= 90,25
%
Interpretacja:
Wynik
punktowy
z
egzaminu
zależy
w
90,25%
od
czasu
„zbierania się” studenta
do nauki, a w 9,75% od
wszystkich
innych
czynników
towarzyszących.
100,00%
– 90,25%
9,75%