Potencjał grawitacyjny Ziemi

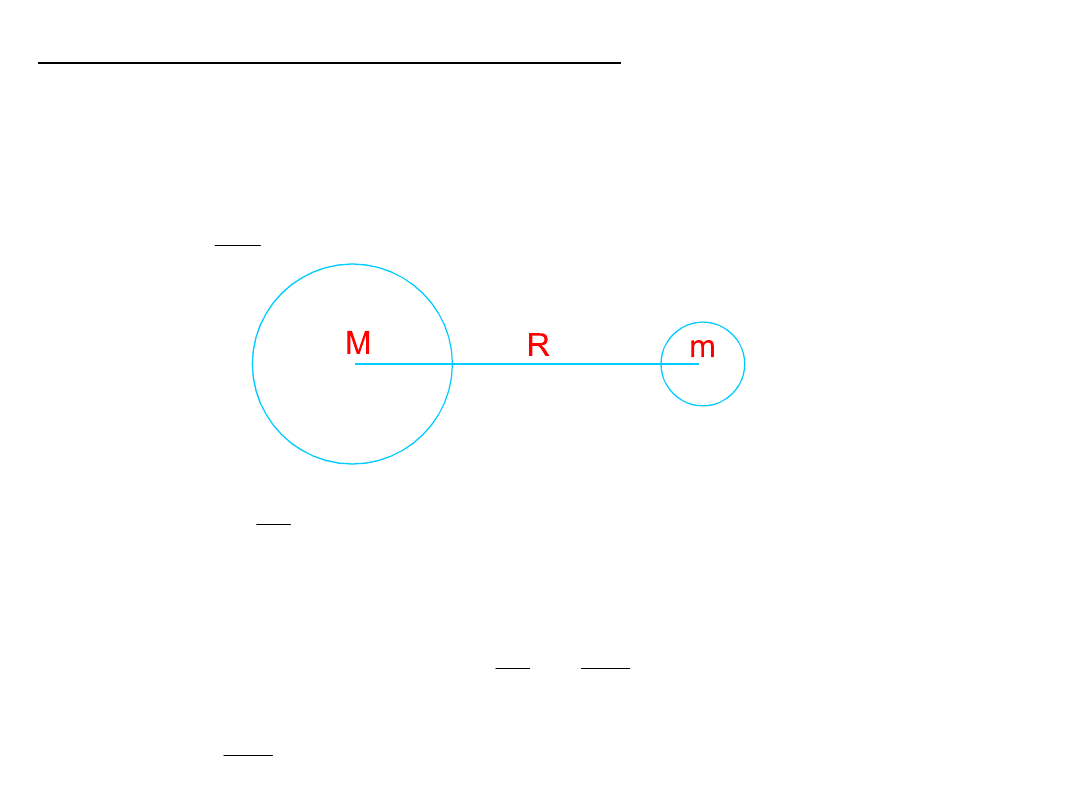
Przesunięcie jednorodnej masy kulistej w polu siły
przyciągania masy M również jednorodnej i kulistej o
wartość dR wymaga wykonania pracy:

dR

F

dL





gdzie:

2

r

Mm

G

F 

zaś:





2

R

dR

GMm

L

Jeżeli masę będziemy oddalać z odległości R do nieskończoności wówczas:

mV

R

GM

m

R

dR

GMm

L

R











2

gdzie:

2

R

GM

V 

Rozpatrując jak wyżej pracę przeciwko sile odśrodkowej w
płaszczyźnie prostopadłej do osi obrotu

r

m

F

2





gdzie:

 – prędkość kątowa
r – odległość od osi obrotu

Otrzymamy:

u

m

r

m

rdr

m

L

r











2

2

2

0

2





gdzie:

2

2

2

r

u 



- potencjał siły odśrodkowej

Potencjał siły ciężkości = potencjał siły przyciągania + potencjał siły odśrodkowej

Oznaczając przez W potencjał siły ciężkości otrzymamy:

2

2

r

R

dM

k

W

V









Bezpośrednie całkowanie po objętości V Ziemi jest
niemożliwe, ponieważ nie znamy ani rozkładu mas ani też
dokładnego kształtu Ziemi. Przybliżony wzór z
wykorzystaniem informacjo o głównych momentach
bezwładności przyjmuje postać:





T

U

T

GMK

GM

W



























2

2

2

2

3

cos

2

sin

3

1

2

gdzie:

 

AB

C

MK

2

1





A, B, C – główne momenty bezwładności Ziemi
T – potencjał zakłócający
U – potencjał normalny

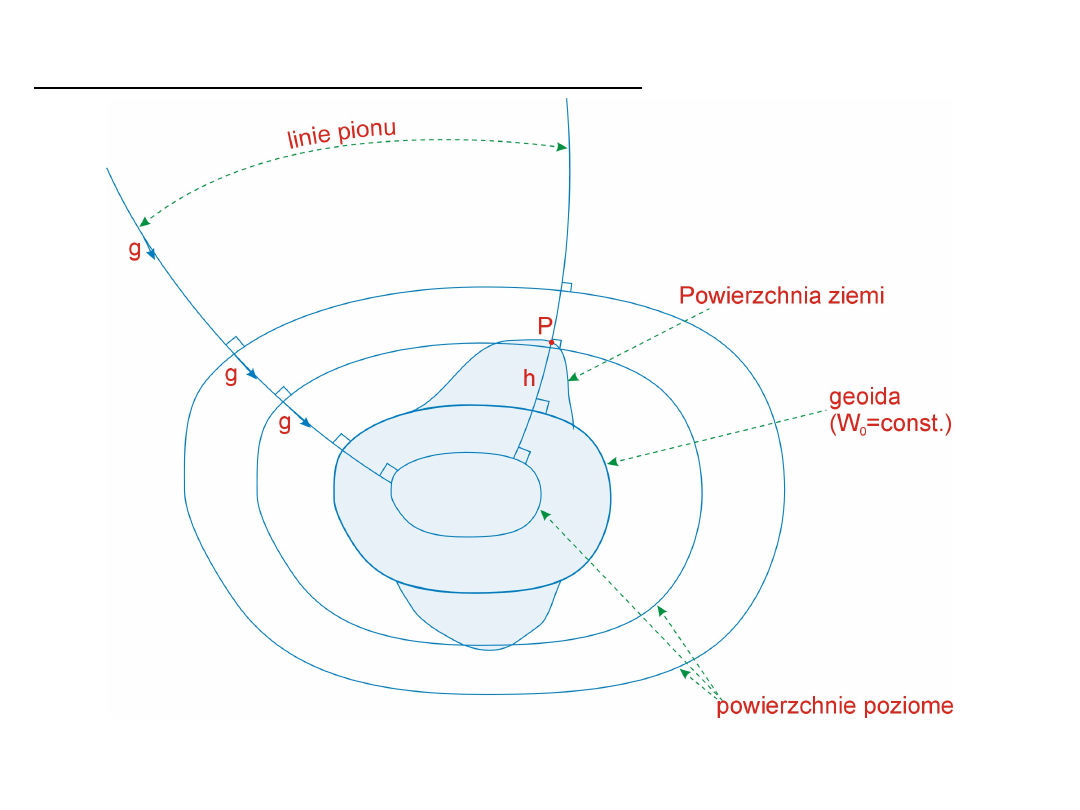
Powierzchnie ekwipotencjalne

Powierzchnie poziome, linie pionu, geoida

Rozwinięcie potencjału w szereg funkcji kulistych

Całkowanie wzoru na potencjał siły ciężkości możemy
wykonać po jego rozwinięciu w szereg funkcji kulistych.

Potencjał siły ciężkości możemy zapisać w postaci:



































1

0

sin

sin

cos

n

nm

n

m

nm

nm

n

P

m

S

m

C

r

a

R

GM

R

GM

V







gdzie:



– szerokość geocentryczna

a – duża półoś elipsoidy ziemskiej



– długość geodezyjna

C

nm

i S

nm

– są współczynnikami harmonicznych sferycznych

P

nm

– stowarzyszony wielomian Legendre’a

Odrzucając pierwszy człon czyli wpływ jednorodnej sfery otrzymamy:

Potencjał wywołujący perturbacje w ruchu sztucznych satelitów:

































1

1

sin

sin

cos

n

n

m

nm

nm

nm

P

P

m

S

m

C

R

a

R

GM

V







Jest to potencjał przyciągania minus potencjał jednorodnej kuli.

Ruch perturbowany sztucznych satelitów Ziemi

Równania ruchu 2.7 w postaci

w przypadku ruchu zakłóconego (perturbowanego) siłą
powodującą przyśpieszenie przyjmą postać

W przypadku perturbacji wywołanych niecentralnością pola
grawitacyjnego Ziemi przyspieszenie perturbujące przyjmie
postać:

p

a

r

r

r





3





p

a

0

3





r

r

r





z

V

k

y

V

j

x

V

i

V

grad

a

p

p

p

p

p



















