Testowanie hipotez

Hipotezy

 Hipoteza – dowolna wypowiedź o 

rozkładzie zmiennej losowej



parametryczna (mówi o wartościach 
parametrów rozkładu)



nieparametryczna

 Hipoteza parametryczna



prosta (jedna wartość)



złożona (zbiór wartości, np. przedział)

Hipotezy - przykłady

 AUC nie ma rozkładu normalnego.
 Wartość oczekiwana t

max

 wynosi 2h.

 Odchylenie standardowe C

max

 nie 

przekracza 3 mg/l.

 

2

max



t

E

2

max



t



lub:





9

max



C

V

albo:

3

max



C



Cel testowania

 Zadaniem testu jest obalenie hipotezy 

zerowej (H

0

) na rzecz hipotezy alterna-

tywnej (H

1

).

 Obalenie hipotezy polega na 

wykazaniu, że gdyby była ona 
prawdziwa, to uzyskanie takich 
wyników pomiarów jak otrzymane 
byłoby mało prawdopodobne.

Weryfikacja

 Na podstawie wyniku badania (próby) 

obliczamy tzw. statystykę testową T. 
Wybór T zależy od H

0

 i H

1

, planu 

eksperymentu i przyjętych założeń o 
rozkładzie wyników pomiarów.

 W oparciu o H

0

 i H

1

, ew. inne, niejawne 

założenia i (nieraz głęboką) wiedzę 
statystyczną konstruujemy dla T 
obszar krytyczny K.

Weryfikacja

 Jeśli T znajdzie się w tym obszarze, 

H

0

 odrzucamy i twierdzimy, że 

prawdziwa jest H

1

 W przeciwnym razie słuszność 

hipotez H

0

 lub H

1

 pozostaje 

nierozstrzygnięta.

Błędy

 Błąd I rodzaju – odrzucenie słusznej 

hipotezy. Prawdopodobieństwo tego 
błędu oznaczamy  i nazywamy 

poziomem istotności.

 Z reguły =0,05, czyli 5%.











0

H

K

T

P

Błędy

 Błąd II rodzaju – niepowodzenie 

obalenia H

0

, mimo że prawdziwa jest H

1

 Prawdopodobieństwo błędu II rodzaju 

oznaczamy . Nie jest ono zwykle 

równe 1- (i na ogół trudno je obliczyć).

 Prawdopodobieństwo udanej weryfikacji 

nazywa się mocą testu, jest ona 

równa 1-.











1

H

K

T

P

Moc i liczebność próby

 Ocena mocy, choć trudna, jest 

ważnym elementem planowania 
badań.

 Moc testu wzrasta z liczebnością 

próby.

 Staramy się tak dobrać liczbę 

pomiarów, aby uzyskać 
spodziewaną moc co najmniej 80%.

Testy parametryczne dla 

rozkładów ciągłych

 test równości wartości oczekiwanych



test t-Studenta i jego modyfikacje



analiza wariancji z porównaniami post 
hoc

 test równości wariancji



test F-Fishera-Snedecora

 testy dla współczynnika korelacji

Testy parametryczne dla 

rozkładów dyskretnych

 Test frakcji (proporcji)

Testy nieparametryczne

 Testy zgodności rozkładów



U - Manna-Whitneya-Wilcoxona



Kruskalla-Wallisa i Friedmana



   - Pearsona

 Testy normalności



Lillieforsa, Shapiro-Wilka, 
Kołmogorowa-Smirnowa

2



Test t-Studenta

 Dwie grupy pomiarów:



na tych samych podmiotach, np. przed i po 

posiłku (zmienne połączone)



na różnych podmiotach, np. ♀ i 

♂

♂

 

 (zmienne 

niepołączone)

 Zakładamy, że pomiary podlegają 

rozkładowi normalnemu.

 Dla zmiennych niepołączonych 

dodatkowo zakładamy równość 

wariancji w grupach.

Test t-Studenta

 Hipoteza zerowa:
 Hipotezy alternatywne



test jednostronny



test dwustronny

2

1

0

:







H

2

1

1

:







H

2

1

1

:







H

Przykład – test t-

Studenta, zmienne 

połączone

 Czy dieta (np. sok grejpfrutowy) 

wpływa na DB?  Y – wielkość będąca 
miarą DB.

 Przeformułowanie problemu:

 

 

B

A

Y

E

Y

E

H



:

0

 

 

B

A

Y

E

Y

E

H



:

1

B

A

Y

Y

D





 

 

0

:

0

:

1

0





D

E

H

vs

D

E

H

test t-Studenta (cd)

 Wykonujemy eksperyment i 

wyznaczamy dla każdego osobnika 
D

i

.

 Wyznaczamy estymaty 

(oszacowania) wartości oczekiwanej 
i odchylenia standardowego 
zmiennej losowej D









n

i

i

D

D

1

ˆ







1

ˆ

2

1

ˆ











n

D

D

n

i

i





test t-Studenta (cd)

 Odchylenie standardowe średniej 

jest       razy mniejsze:  

 Jeśli D ma rozkład normalny              

       to statystyka

 ma rozkład t-Studenta z n-1 

stopniami swobody.





D

N

D



,

0

~

n

D

t





ˆ

ˆ



n

D

D







n

D

D





ˆ

ˆ



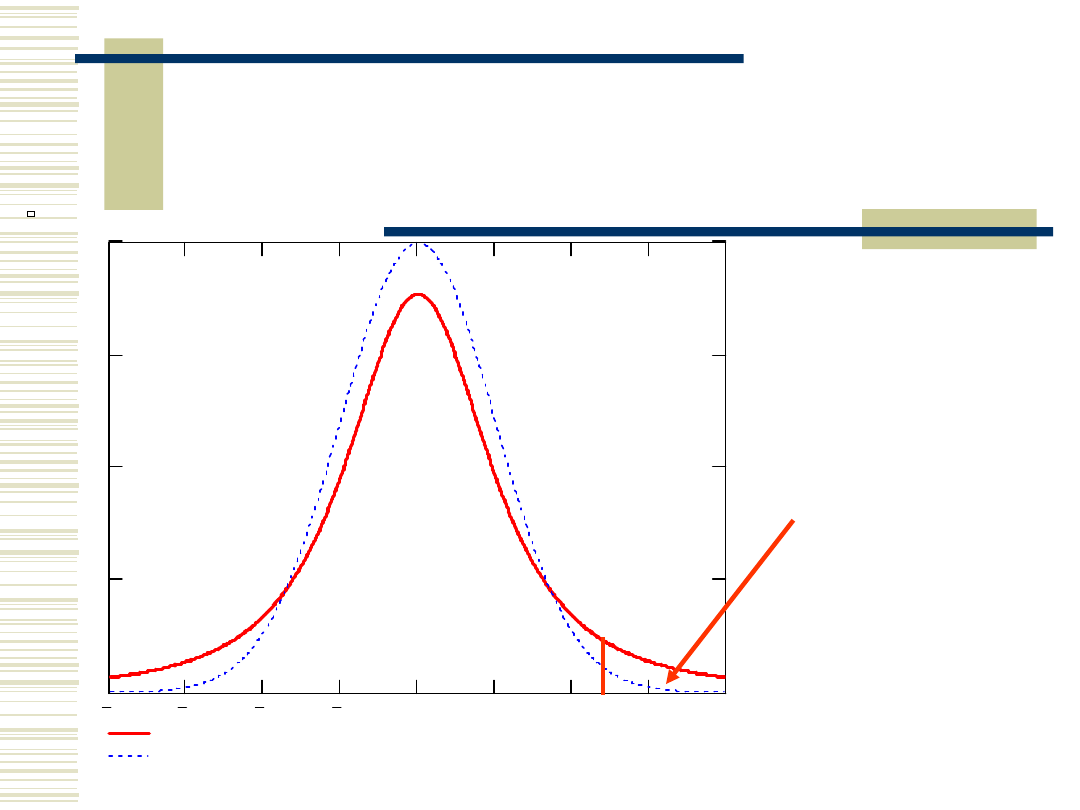
test t-Studenta (cd)











t

t

P

4

3

2

1

0

1

2

3

4

0

0.1

0.2

0.3

0.4

Student

Gauss





t

Test t-Studenta – moc 

 W przedstawionym teście H

0

 była 

hipotezą prostą, a jej alternatywa – 
hipotezą złożoną.

 Weźmy jeden ze składników 

alternatywy:

 

0

:

1

1







D

E

h

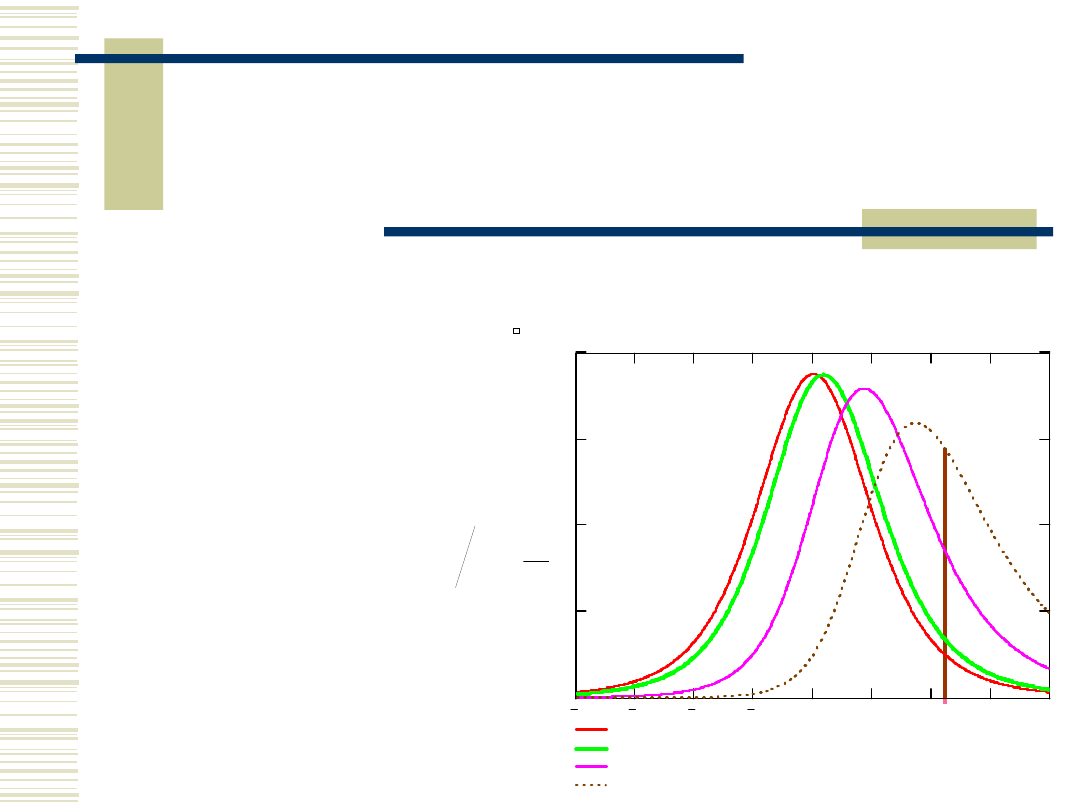
Test t-Studenta – moc 

 Wtedy                      

     a rozkład 
zmiennej t jest 
nieco inny (nazy-wa 
się niecentralnym 
rozkładem t ).

 Ze wzrostem            

  maleje  , a więc 

zwiększa się moc 
testu.









,

~

1

N

D

4

3

2

1

0

1

2

3

4

0

0.1

0.2

0.3

0.4

t-Studenta
Niecentralny t 0.2

Niecentralny t 1.0

Niecentralny t 2.0

D





1

Test t-Studenta – moc 

 Moc zwiększa się ze wzrostem 

liczebności próby.

 Dokładne określenie mocy testu nie 

jest możliwe, gdyż nie znamy 
dokładnie potrzebnych parametrów.

Test t-Studenta, 

jedno- i dwustronny

 W teście jednostronnym porównujemy 

wartość t z fraktylem     .

 W teście dwustronnym porównujemy      

   |t| z

 Jeśli są przesłanki przemawiające za 

tes-tem jednostronnym, warto go 
stosować. Postawą tej decyzji nie może 
być jednak bieżący eksperyment.



t

2

/



t

Test t-Studenta, 

zmienne niepowiązane

 Test dla zmiennych niepowiązanych 

zawiera istotne założenie o równości 
wariancji w obu grupach 
(jednorodność wariancji).

 Jeśli założenie to nie jest spełnione, 

należy stosować przybliżony wariant 
opracowany przez Satterthwaite’a. 
Spotyka się też nazwę test Welcha.

Test równoważności

 Test t-Studenta pozwala udowodnić 

istnienie różnic między grupami.

 W celu udowodnienia braku tych 

różnic chciałoby się w teście 
dwustronnym zamienić role 
hipotezy zerowej i alternatywnej:

                             vs

2

1

0

:







H

2

1

1

:







H

Test równoważności

 Niestety, moc takiego testu byłaby 

równa dokładnie 0.

 Test równoważności ma udowodnić, 

że różnica wartości oczekiwanych 
nie przekracza z góry zadanego 
zakresu.

1

2

1

2

2

1

0

lub

:





















H

2

2

1

1

1

:















H

Test równoważności

 Taki test, opracowany przez 

Schuirmanna, używany bywa do 
wykazywania równoważ-ności 
postępowania terapeutycznego. 

 Określenie granic      i       należy do 

ekspertów z zakresu nauk 
medycznych, a nie do statystyków.

1



2



Test równości wariancji

 Test F-Fishera-Snedecora pozwala 

porównać wariancje (a więc i odchylenia 

standardowe) w dwu grupach pomiarów.

 Zakłada się w nim rozkład normalny w 

obu grupach.

 Test może być jednostronny lub 

dwustronny.

 Dla wielu wariancji używamy testu 

Levene’a.

Analiza wariancji

 Analiza wariancji (ANOVA) stanowi 

rozszerzenie testu t-Studenta w 

przypadku porównywania większej 

liczby grup.

 Podział na grupy (czyli klasyfikacja) 

dokonywany jest na podstawie 

jednego lub kilku czynników. Mówimy 

więc o jednoczynnikowej (one-way) lub 

wieloczynnikowej analizie wariancji.

Analiza wariancji

 Czynnik może przybierać pewną 

liczbę wartości, zwanych poziomami.

 Np. czynnik płeć ma tylko dwa 

poziomy   (♀,♂), czynnik grupa krwi – 

cztery poziomy (0,A,B,AB).

 Należy odróżniać liczbę czynników od 

liczby poziomów danego czynnika.

 Jeszcze ważniejsze jest odróżnianie 

wyniku od czynnika.

Analiza wariancji

Założenia

 Podobnie jak w teście t-Studenta 

zakłada się, że wyniki podlegają 
rozkładowi normalnemu, a wariancje 
we wszystkich grupach są takie 
same.

 Procedury analizy wariancji są dość 

odporne na naruszenie tych założeń.

Jednoczynnikowa

analiza wariacji

 Hipoteza zerowa: wartość oczekiwana 

w każdej grupie jest taka sama.

 Hipoteza alternatywna: nie wszystkie 

wartości oczekiwane są jednakowe.

k

H















2

1

0

:

Jednoczynnikowa

analiza wariancji

 Weryfikacja hipotezy polega na estymacji 

wariancji na dwa niezależne od siebie 
sposoby: 



uśredniając wyniki uzyskane dla każdej grupy



badając zmienność średnich między grupami

 O ile H

0

 jest słuszna, obie wariancje 

powinny być jednakowe.

 Sprawdzamy to jednostronnym testem F.

Jednoczynnikowa

analiza wariancji

 Wyniki przedstawia się w postaci 

tabeli analizy wariancji:

Źródło 

zmienności

Sumy 

kwadratów

St. 

swobody

Średni 

kwadrat

F

Pomiędzy 
grupami

k-1

Wewnątrz 
grup (błąd)

n-k

Całkowita

n-1

1

2





k

Q

s

p

p

k

n

Q

s

w

w





2

2

2

w

p

s

s

F 













k

i

i

p

x

x

Q

1

2







 





k

i

n

j

i

ij

w

i

x

x

Q

1

1

2













k

i

ij

x

x

Q

1

2

Jednoczynnikowa

analiza wariancji

 Pozytywny wynik testu (odrzucenie 

hipotezy zerowej) nie daje odpowiedzi 
na pytanie, które wartości 
oczekiwane różnią się między sobą.

 Odpowiedzi takiej udzielają testy po 

analizie wariancji, zwane 
porównaniami post-hoc.

Testy po analizie 

wariancji

 Porównania post-hoc są w istocie 

równoczesnym wykonaniem wielu 
testów. 

 Jeśli pojedynczy test miałby poziom 

istotności    , to poziom istotności 
wszystkich porównań mógłby być 
znacznie wyższy.



Testy po analizie 

wariancji

 Wybór testu post-hoc zależy od 

porównań, jakie zamierzamy 

przeprowadzić.

 Jeśli porównujemy grupy z kontrolą, 

możemy użyć testu Dunnetta.

 Gdy chcemy dokonać porównań typu 

każdy z każdym przyda się nam test 

Tukeya (lub Tukeya-Kramera dla 

niejednakowo licznych grup).

Testy post-hoc

 Wymienione testy zapewniają 

poziom istotności     dla całego 
zbioru porównań.



Test frakcji (proporcji)

 Test służy sprawdzeniu, czy 

prawdopo-dobieństwa dwu zdarzeń 
są jednakowe.

 Istnieje też wariant pozwalający 

sprawdzić, czy prawdopodobieństwo 
zdarzenia ma określoną z góry 
wartość (np. czy P(♂)=0,5).

Testy nieparametryczne

Testy zgodności 

rozkładów

 Test dla zmiennych połączonych – 

test rang Wilcoxona. Zmienna losowa 
nie musi być zmienną ciągłą, ale 
może być zmienną porządkową.

 Dla zmiennych niepołączonych 

analogicznym testem jest test rang    
       U – Manna-Whitney’a.

Testy zgodności

 Rozszerzenia tych testów na 

porównanie większej liczby grup to:

 Test Kruskala-Wallisa dla zmiennych 

niepołączonych.

 Test Friedmana dla zmiennych 

połączonych.

Testy normalności

 Do badania, czy pomiary podlegają 

rozkładowi normalnemu służą testy:



Lillieforsa



Shapiro-Wilka



D-Kołmogorowa-Smirnowa

Test zgodności 

z rozkładem 

teoretycznym

 Test zgodności
 Test zgodności Kołmogorowa 

2



Test niezależności

 Jest to rozszerzenie testu proporcji na 

więcej niż dwie grupy. Używany jest 
często do oceny skuteczności 
zabiegów terapeutycznych.

 Test ten przeznaczony jest dla 

zmiennych losowych dyskretnych, nie 
mających charakteru porządkowego. 
Wrócimy do tego tematu.

2



Test Q-Dixona

 Test Q-Dixona służy do eliminacji 

pomiarów, co do których 
spodziewamy się błędu grubego. 
Może być źródłem nadużyć.

 Można go użyć do odrzucenia tylko 

jednego pomiaru w danej próbie.