Wykład 2: Prezentacja danych

Biometria i

Biostatystyka

Analiza danych



Strategie



Niezależna analiza każdej ze zmiennych



Poszukiwanie relacji między zmiennymi



Analiza wielowymiarowa



Statystyki opisowe oraz reprezentacje
graficzne są najlepszym sposobem
prezentacji danych

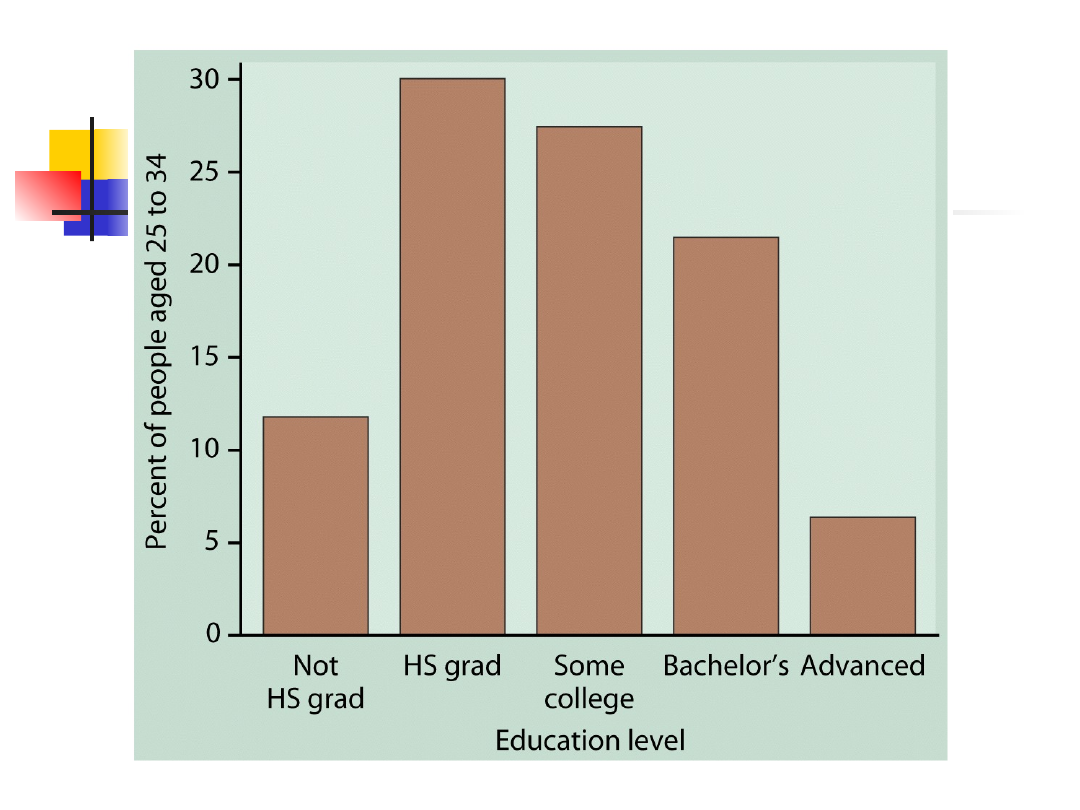
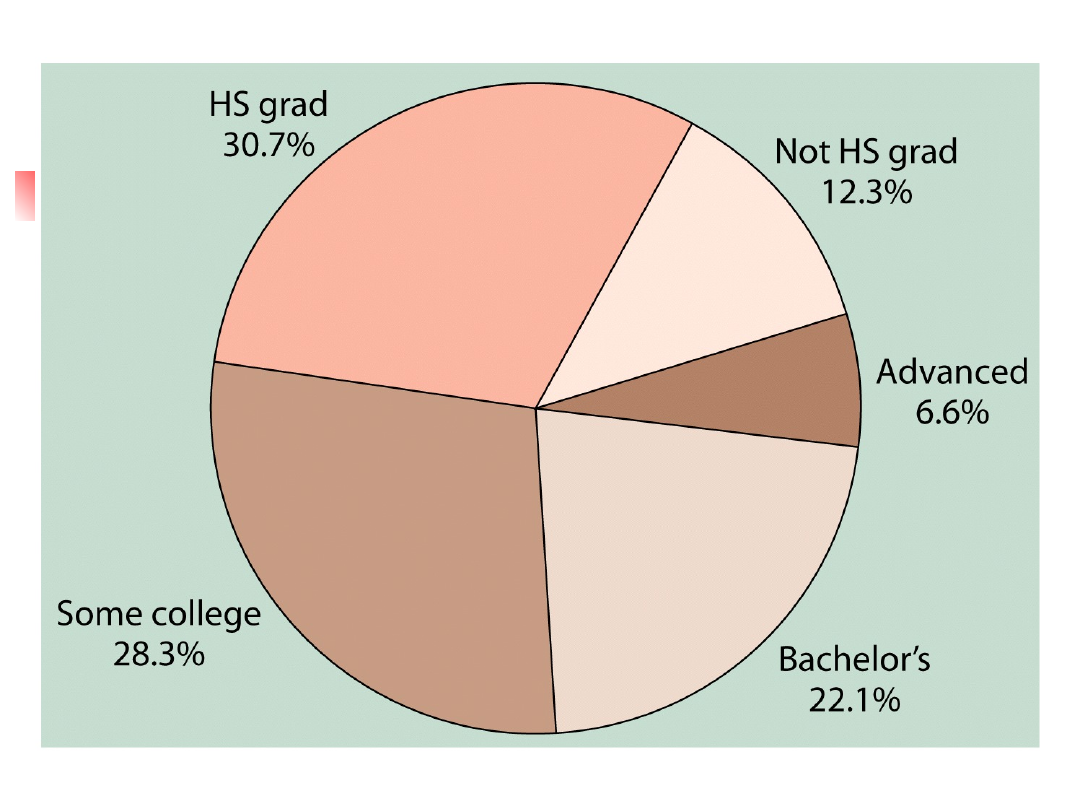
Wykresy zmiennych typu
kategorie



Dystrybucja zmiennych typu
kategorie



Prezentacja:



Ilościowa



Procentowa



Wykresy słupkowe



Wykresy kołowe

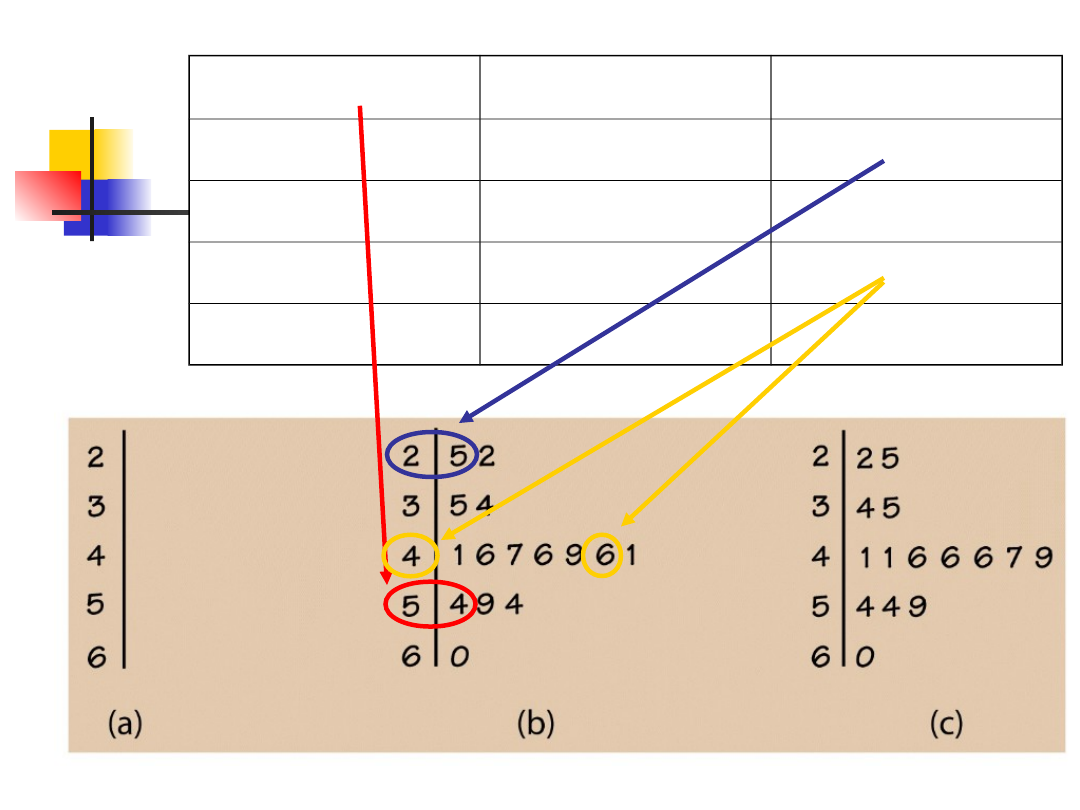
Wykresy „łodygowe” (stem-
leaf)



Obrazują kształt rozkładu,
jednocześnie ukazując na wykresie
wartości numeryczne.



Są najbardziej odpowiednie dla
niewielkiej liczby dodatnich
obserwacji.

Rysowanie wykresu
łodygowego



Podziel każdy wynik na łodygę (stem) i

listek (leaf).



Łodyga: tyle cyfr ile potrzeba



Listek: pojedyncza cyfra



Wypisz łodygi w pionowej kolumnie

rosnąco w dół. Narysuj pionową linię po

prawej stronie.



Wypisz każdy listek w wierszu po prawej

stronie od jego łodygi, w porządku

rosnącym.

Liczba odwiedzin dziennie

54

59

35

41

46

25

47

60

54

46

49

46

41

34

22

54

59

35

41

46

25

47

60

54

46

49

46

41

34

22

Porównywanie dwóch
rozkładów



Wykresy o
wspólnym
pniu

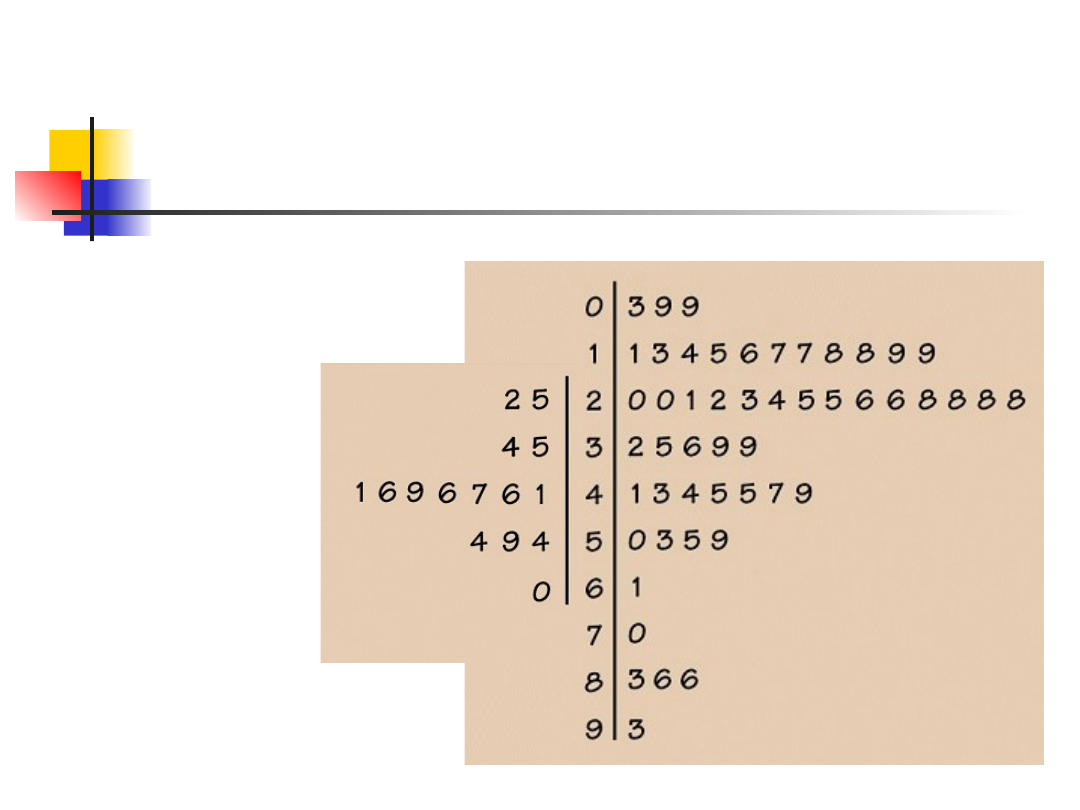
Wykresy „łodygowe”, cd.



Są nieodpowiednie dla dużych zestawów

danych



Każda łodyga musi zawierać dużą ilość listków



Warianty:



Podzielić każdą łodygę na dwie, np.:



Jedna z liśćmi od 0 do 4



Druga z liśćmi od 5 do 9



Zadanie: zobrazować kształt rozkładu



Zasady:



dzielić jeśli jest mniej niż 5 łodyg



łączyć jeśli wiele łodyg ma po 1 liściu (lub wcale)

Badanie rozkładu



Należy zwrócić uwagę na ogólny wzorzec

oraz na odstępstwa od niego.



Pomocne określenia



Kształt



Środek



Rozrzut



Ważnym rodzajem odstępstwa jest

wielkość odstająca - niezależna wartość,

która wyraźnie odstaje od ogólnego

wzorca.

Badanie rozkładu, cd.



Punkt środkowy



Opisuje środek rozkładu



Połowa obserwowanych wartości jest mniejsza
od niego, druga połowa ma wartości większe



Zakres - różnica największej i
najmniejszej wartości



Opisuje rozrzut/zmienność rozkładu



Wykres łodygowy



Obrazuje kształt rozkładu

Badanie rozkładu, cd.



Moda



Szczyt wykresu dystrybuanty



Unimodalne rozkłady mają jeden szczyt



Rozkład symetryczny



Wartości po jednej stronie mediany są
lustrzanym odbiciem wartości po drugiej
stronie



Rozkład skośny



Jeden koniec wykresu jest dłuższy niż drugi

Histogramy



Nie mają takich ograniczeń jak
wykresy łodygowe



Dzielą zakres obserwowanych wartości
na przedziały, pokazując jedynie
liczności lub udział procentowy
obserwacji w danym przedziale



Można wybrać dowolną liczbę
przedziałów równej szerokości

Rysowanie histogramu

1.

Podziel zakres zmienności danych
na przedziały o równej szerokości.

2.

Zlicz liczbę obserwacji w każdym
przedziale. Zrób tabelę częstości
wystąpień.

3.

Narysuj histogram.

Histogramy, cd.



Częstości względne



Ułamek lub procent obserwacji, które
przypadają na poszczególne przedziały



Poprawnie oznacz „liczba” lub „procent”.



Właściwy wybór przedziałów:



Za mało: wszystkie wartości tylko w kilku
przedziałach



Za dużo: dużo przedziałów ma 1 lub mniej
wyników

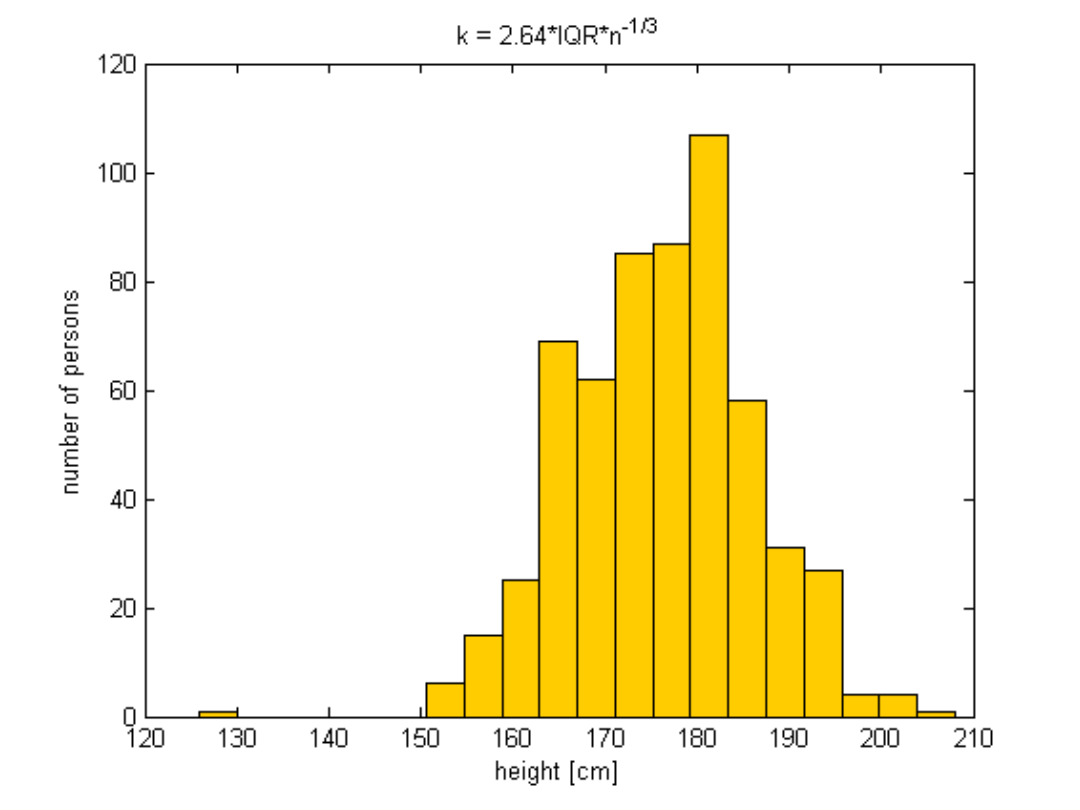
Histogramy, cd.



Wzór heurystyczny do oszacowania szerokości

przedziału:



Jeśli szerokość przedziału jest za mała lub za

duża, można ją skorygować przez pomnożenie

lub podzielenie przez a = 1.2 ÷1.5



Sprawdza się przy rozkładach zbliżonych do

rozkładu normalnego oraz przy względnie

dużych n (liczność próby)

3

1

n

IQR

64

.

2

h

0









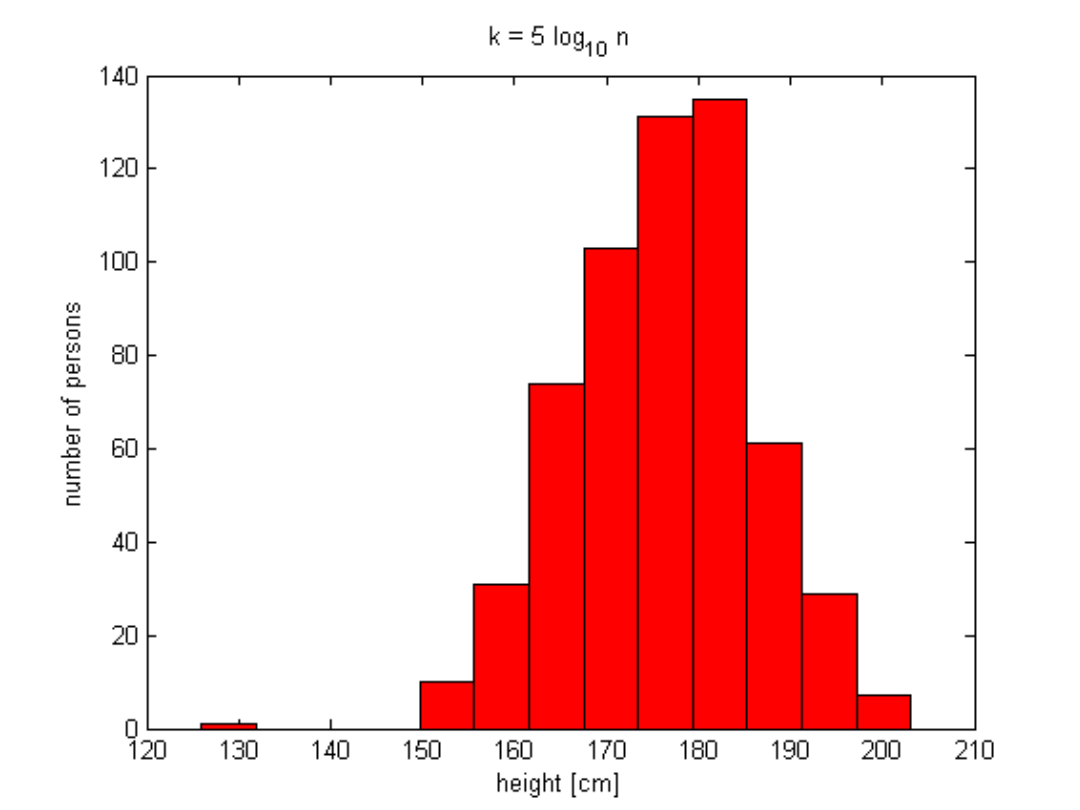
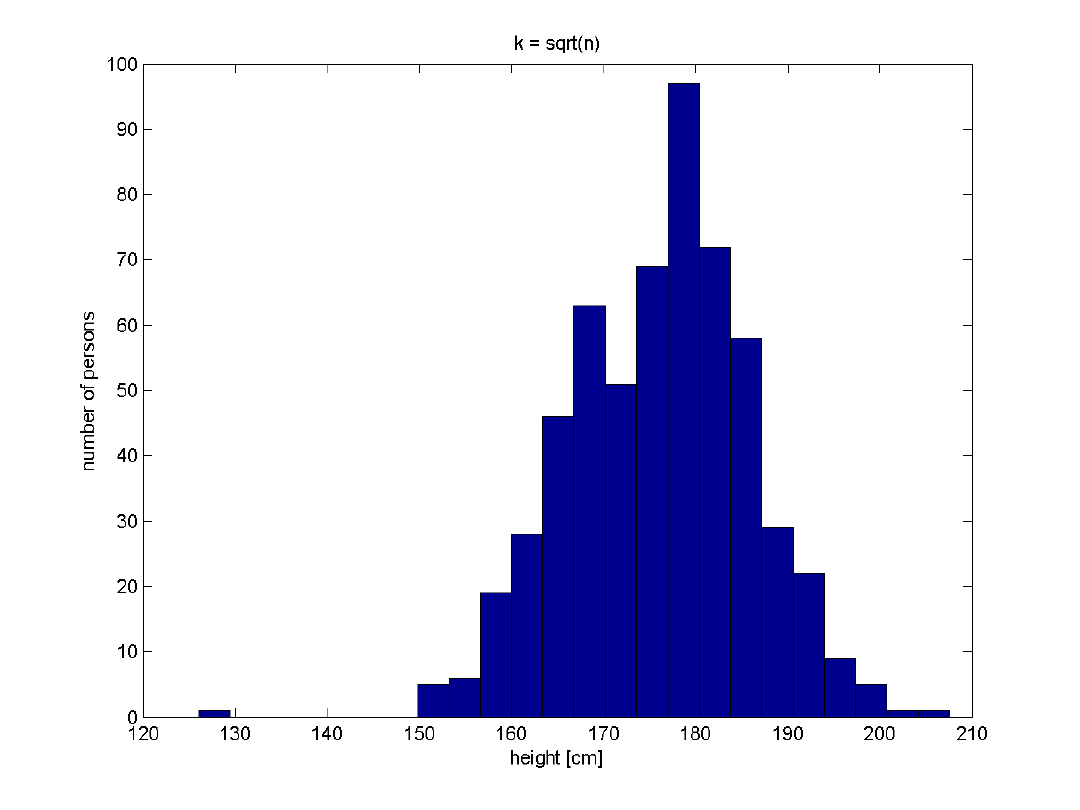
Histogramy, cd.



Jest kilka innych wzorów pomocnych
przy poszukiwaniu liczby przedziałów.
Kilka przykładów:



Żeby znaleźć szerokość, wystarczy
podzielić zakres przez k.

)

n

(

log

3

.

3

1

k

n

k

)

n

(

log

5

k

10

10













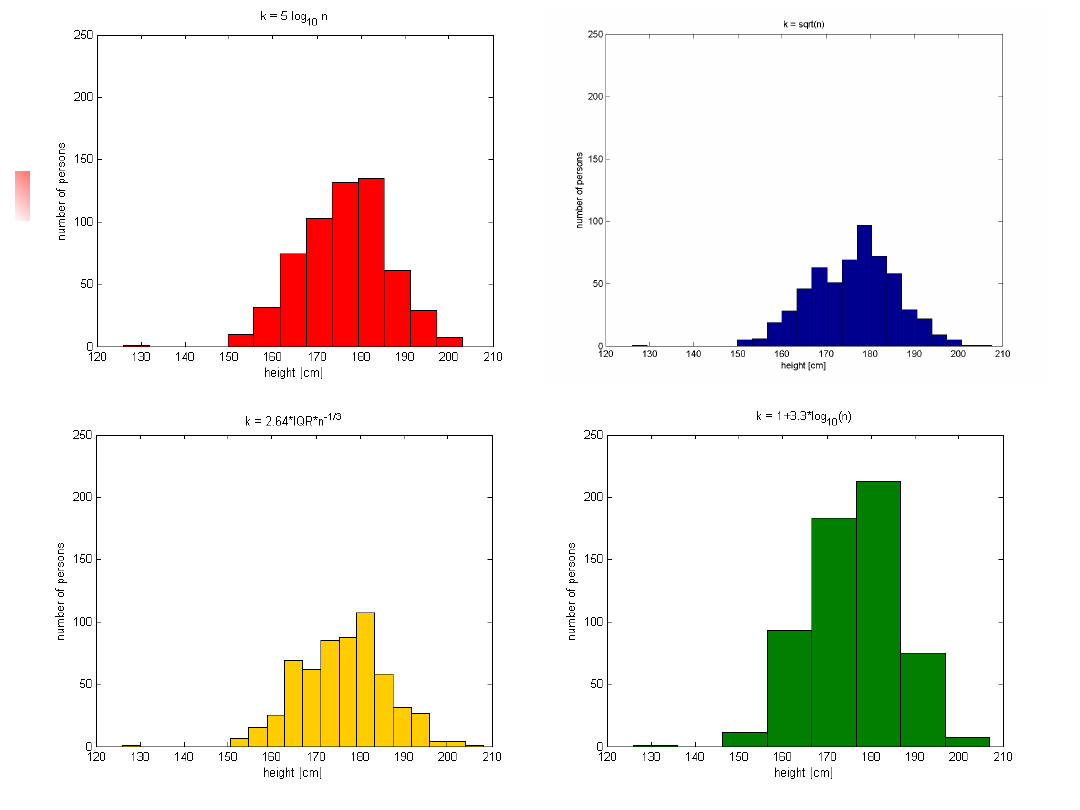
Histograms, cont.

93

.

5

h

14

k

0





Histograms, cont.

40

.

3

h

24

k

0





Histograms, cont.

11

.

4

h

20

k

0





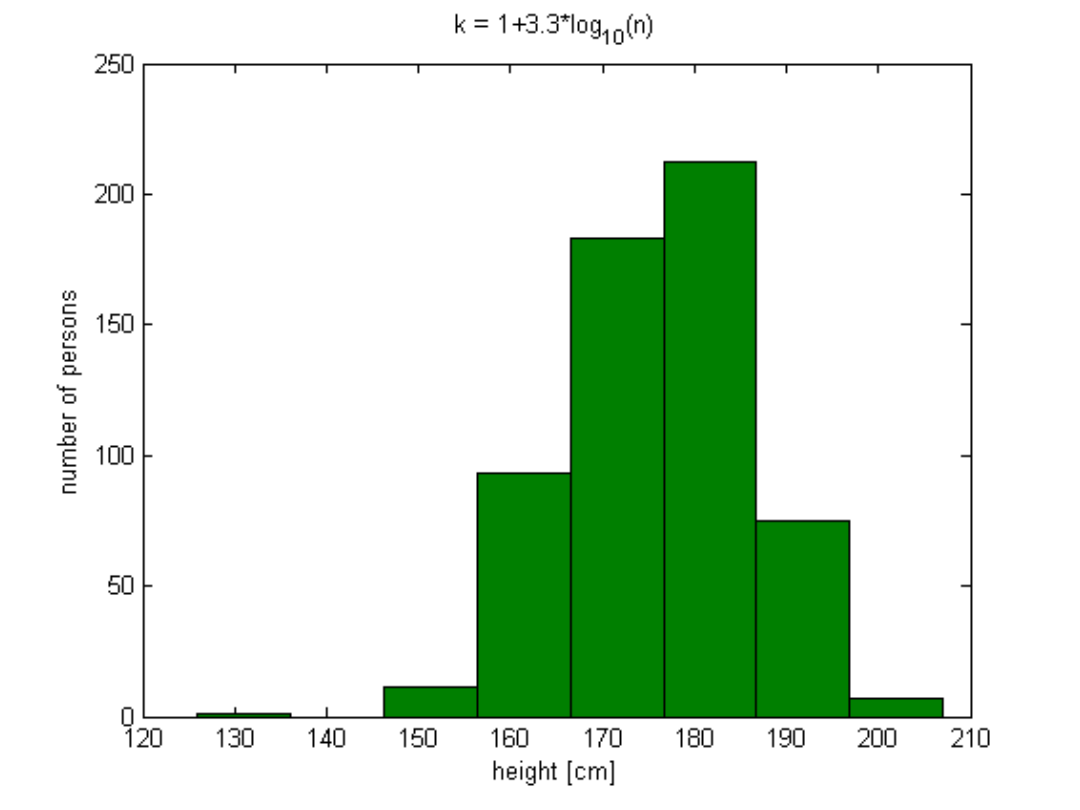
Histograms, cont.

12

.

10

h

8

k

0





Histograms, cont.

Histogramy, cd.



Wiele zależy od Twojej decyzji odnośnie
szerokości przedziałów.



Pole pod krzywą zmienia się w zależności od h i
jest równe:



Żeby otrzymać eksperymentalną funkcję gęstości
prawdopodobieństwa, musimy sprowadzić pole
powierzchni S do 1. Ponieważ h nie może być
zmienione, musimy skorygować jednostkę na osi
OY.

n

*

h

S

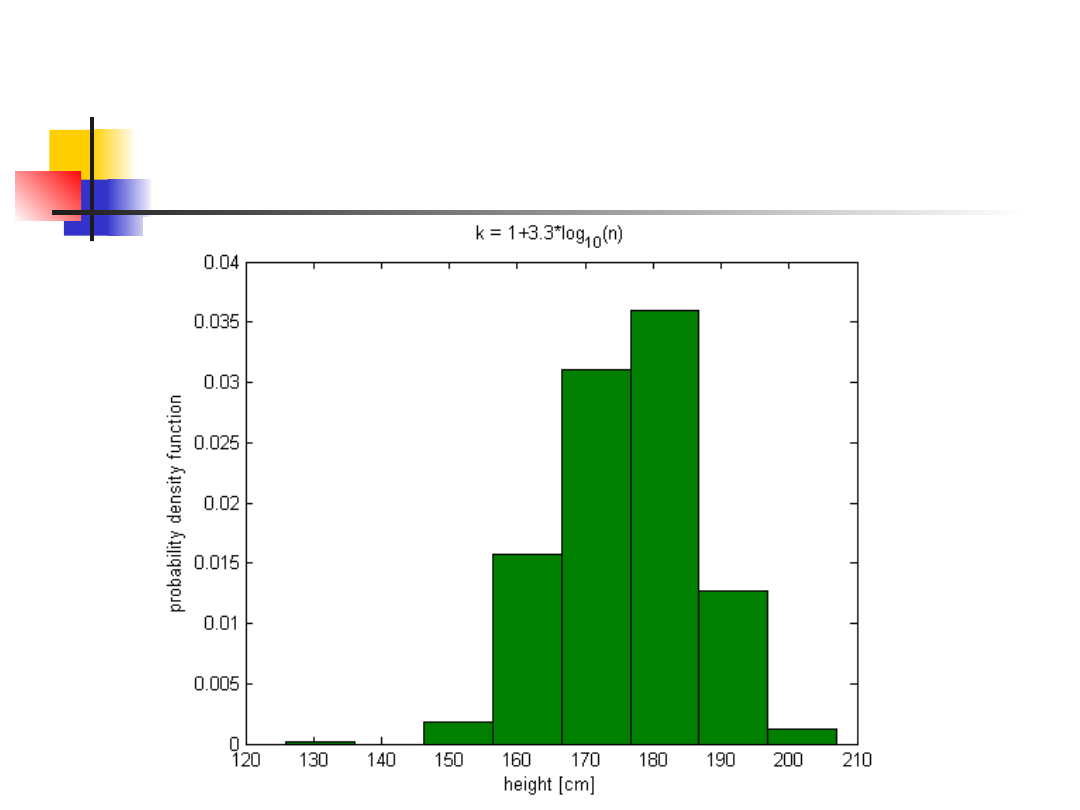
Histogramy, cd.

Opisywanie rozkładów
liczbami



Miary położenia



Wartość średnia



Mediana



Miary rozrzutu



Odchylenie standardowe



Kwartyle



Metoda pięciu liczb



Wykresy ramkowe



Poszukiwanie wielkości odstających

Opisywanie rozkładów



Krótki opis



Kształt (np.: symetryczny, skośny)



Określony dzięki



Wykresom stem-leaf



Histogramom



Miary liczbowe



Środek



Rozrzut

Przykład - wzrost



Średni wzrost = 176,13 cm



Czy widać wielkości odstające?



Wady średniej jako miary położenia:



Dla małych prób - wrażliwość na
wielkości odstające



Dla dużych prób - słabo reaguje na
zmiany w kilku wynikach, nieważne jak
wielkie zmiany to są.

Miary położenia, cd.



Mediana



Formalne określenie punktu
środkowego, ze specyficzną metodą
obliczania



M



Punkt środkowy: taka wartość, że
połowa wyników jest od niego
mniejsza, a druga połowa większa

Obliczanie mediany

1.

Uporządkuj wszystkie pomiary
rosnąco

2.

Jeśli n (liczba pomiarów) jest
nieparzyste, M to środkowy
pomiar na liście

3.

Jeśli n jest parzyste, M jest średnią
dwóch środkowych pomiarów

Przykład



Znajdź medianę liczby mil na galon
benzyny samochodów klasy kabriolet



Uporządkuj dane w rosnącym
porządku

13 13 16 19 21 21 23 23 24 26
26 27 27 27 28 28 30 30 68

•

Nieparzyste n, więc mediana jest
środkiem listy, czyli 26

Mediana



Jeśli N jest parzyste, wynik powyżej
mógłby nie być liczbą całkowitą. To
wskazuje na to, że nie ma jednej
wartości środkowej, za to są dwie
takie, a medianę definiuje się jako
średnią z tych dwóch:

2

/

)

(

1

2

2







N

N

X

X

M

Mediana



Kiedy wyniki obserwacji się
powtarzają, mogą się pojawić
problemy w szukaniu mediany.
Obliczanie mediany jest
trudniejsze, ponieważ wiele
wartości leży w tym samym
przedziale (klasie) co mediana i
mają to samo oznaczenie klasy.

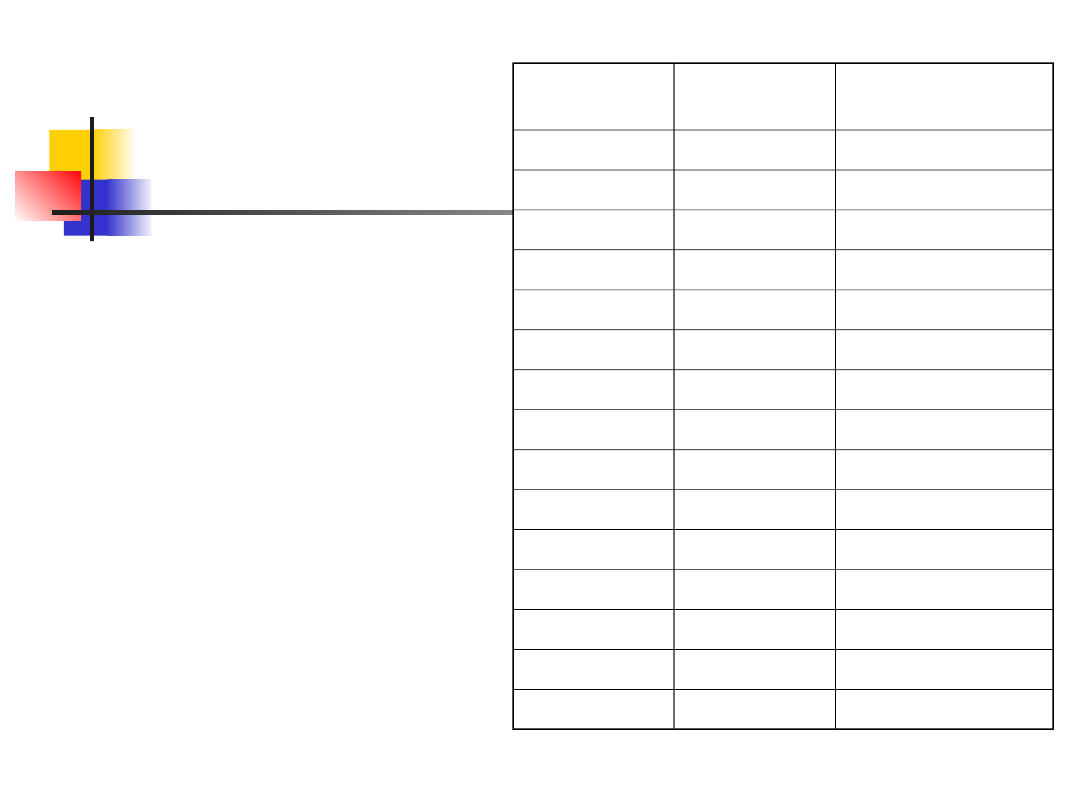
Przykład



Dane są w formie rozkładu
częstości z powodu dużej
ilości obserwacji w
doświadczeniu



Mediana dla zestawionej
tabeli jest (n+1)/2 wartością.
Tutaj n=9465 więc szukamy
4733-ciej obserwacji.



4733-ci wynik jest w klasie
107.5, czyli gdzieś między
103.5 a 115.5. Ta klasa
zawiera 2240 wyników, a
wynik 4733 jest 4733-
3049=1684-tym wynikiem w
klasie.

Klasa

wagowa

Częstość f

Kumulatywne f

59.5

2

2

67.5

6

8

75.5

39

47

83.5

385

432

91.5

888

1320

99.5

1729

3049

107.5

2240

5289

115.5

2007

7296

123.5

1233

8529

131.5

641

9170

139.5

201

9371

147.5

74

9445

155.5

14

9459

163.5

5

9464

171.5

1

9465

Wagi chińskich noworodków w
uncjach

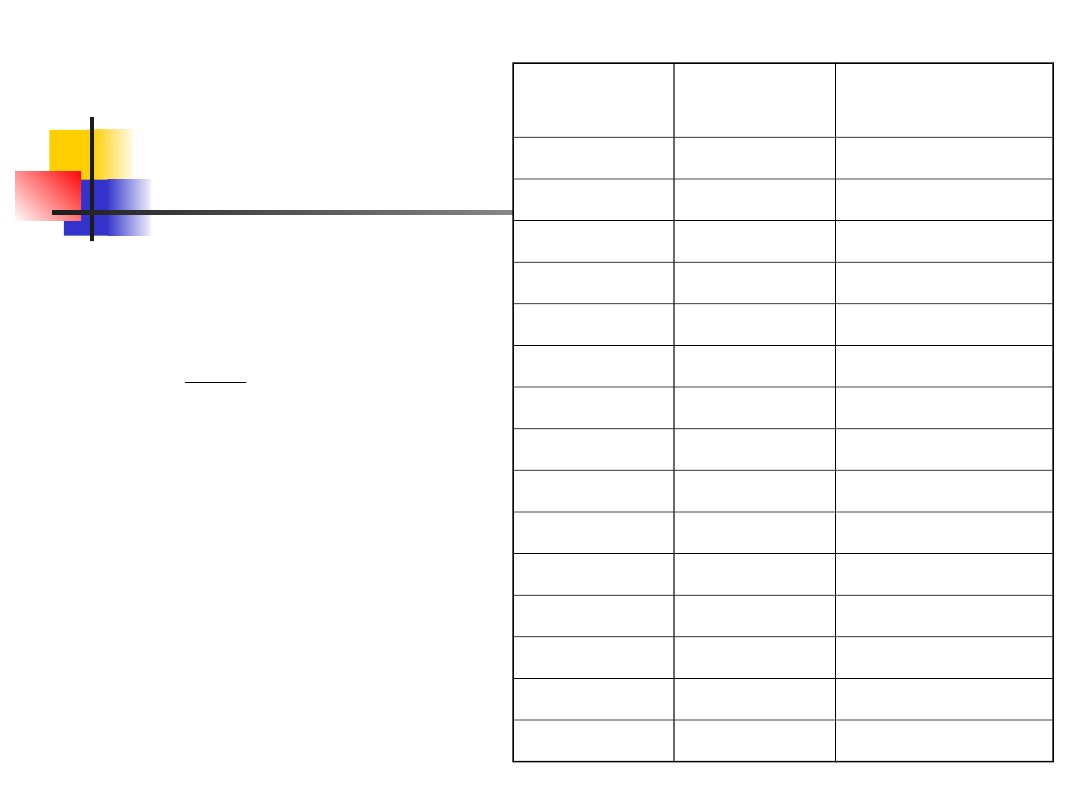
Przykład



Przyjmując rozkład
równomierny w klasie,
wartość nr 4733 będzie w:

całego przedziału klasy lub w
75.18% odległości między
dolną a górną granicą
przedziału.



Ponieważ przedział każdej
klasy to 8 oz, wartość
medianowa to 0.7518 x 8.0
= 6.014 oz powyżej dolnej
granicy klasy (103.5 oz); czyli
mediana wag noworodków
wynosi 103.5 + 6.014 =

109.514

oz.

Klasa

Licznosc f

Licznosc

skumulowana F

59.5

2

2

67.5

6

8

75.5

39

47

83.5

385

432

91.5

888

1320

99.5

1729

3049

107.5

2240

5289

115.5

2007

7296

123.5

1233

8529

131.5

641

9170

139.5

201

9371

147.5

74

9445

155.5

14

9459

163.5

5

9464

171.5

1

9465

Wagi chińskich noworodków w
uncjach

7518

.

0

2240

1684



Porównanie średniej i
mediany



Mediana jest bardziej odporna niż
średnia.



Rozkłady symetryczne



Mediana i średnia są blisko siebie



Rozkłady skośne



Obie są na dłuższym końcu, ale
średnia jest nieco dalej od szczytu niż
mediana

Punkty odstające



Mogą być wynikiem błędu
aparatury albo błędu pomiarów



Możemy wyeliminować obserwacje
z błędem aparatury



Możemy poprawić błędy pomiarów



Kiedy nie znamy powodu, musimy
osądzić sami

Detekcja punktów
odstających

1.

Znajdź punkty odstające i zbadaj
dlaczego istnieją.

2.

Użyj takich metod, żeby punkty
odstające miały mały wpływ na
wnioski z doświadczenia.

Miary rozrzutu: Kwartyle



podanie jedynie miary położenia może być
niewystarczające i mylące.



Najprostsze opisy liczbowe rozkładów
składają się z miar zarówno położenia jak i
rozrzutu.



p-ty percentyl: wartość, poniżej której jest
jest dokładnie p procent innych wartości



Najbardziej popularna: Mediana = 50-ty percentyl



Drugie popularne: Kwartyle

Inne kwartyle



Mediana to tylko jedna z rodziny
statystyk porządkowych, dzielących
wyniki na części. Dzieli zbiór na dwie
równoliczne części. Z kolei

kwartyle

to

punkty w 25%, 50%, i 75% zbioru –
które dzielą rozkład na pierwszą,
drugą, trzecią i czwartą ćwiartkę. Są
zwykle opisywane symbolami Q

1

(dolny kwartyl), M (mediana), Q

3

(górny kwartyl).

Inne statystyki
porządkowe



Istnieją także kwintyle, decyle i
percentyle, dzieląc rozkład na
odpowienio 5, 10, i 100 równych
części.



Ogólny termin dla tych wszystkich
to

kwantyle

.

Przykład



Znajdź Q1, M, i Q3.
13 13 16 19 21 21 23 23 24

26 26 27 27 27 28 28 30 30



Znajdź Q1, M, i Q3.
13 13 16 19 21 21 23 23 24

26 26 27 27 27 28 28 30

Metoda pięciu liczb



Obejmuje najmniejszą obserwację,
pierwszy kwartyl, medianę, trzeci
kwartyl i największą obserwację,
napisane od najmniejszego do
największego:

Minimum Q1 M Q3
Maksimum

Metoda pięciu liczb, cd.



Dostarcza w miarę pełnej informacji
o położeniu i rozrzucie.



Położenie



Mediana



Rozrzut



rozrzut środkowej połowy pomiarów
(od 25% do 75%) ukazują kwartyle



Min i max pokazują pełny rozrzut

Wykresy ramkowe



Wykres metody pięciu liczb



Centralna ramka obejmuje Q1 i Q3



Linia w pudełku to M



Linie wychodzące z ramki dochodzą
do największej i najmniejszej wartości
wśród pomiarów

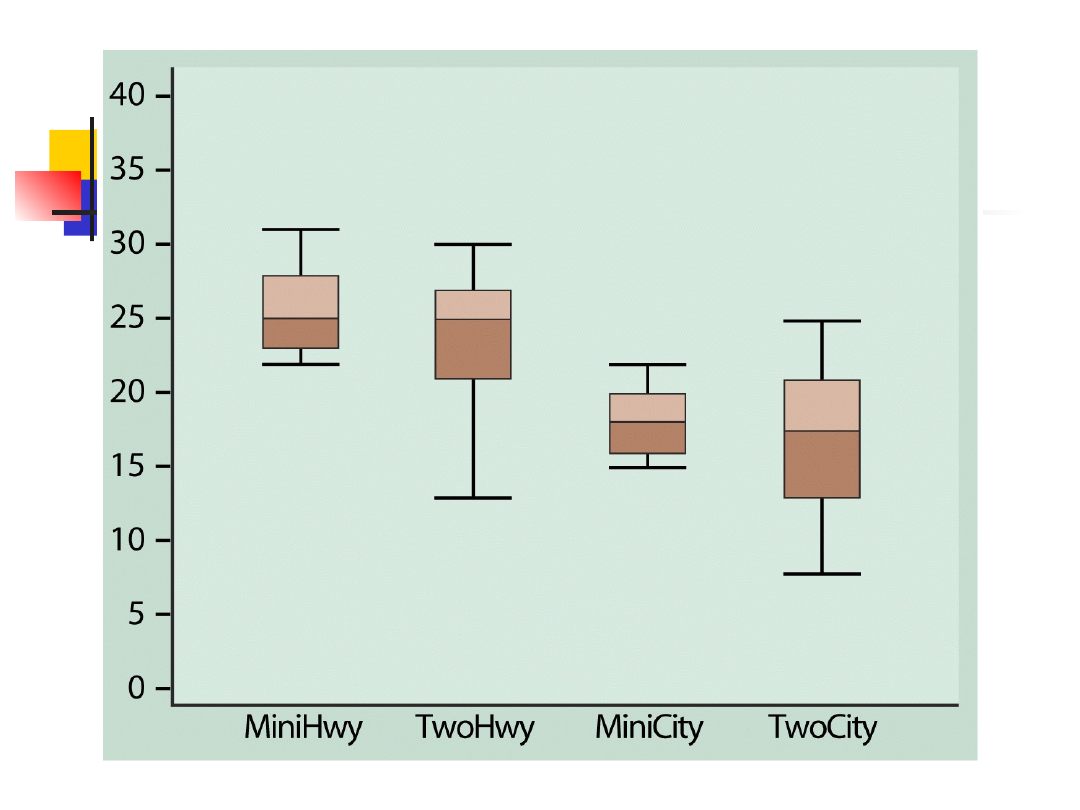
Wykresy ramkowe, cd.



Przedstawiają mniej informacji niż

histogramy i wykresy łodygowe



Używane do porównania więcej niż

jednej serii pomiarów



Analiza wykresu



Znajdź medianę (środek)



Określ rozrzut (między Q1 i Q3;

między min i max)

Co z punktami
odstającymi?



Odległość między kwartylami = zakres
połowy danych = przedział
międzykwartylowy = IQR



IQR = Q3 – Q1



IQR jest odporny na zmiany na końcach
dystrybucji zmiennej losowej.



Wynik może być punktem odstającym,
jeśli ma wartość powyżej Q3+1.5 x IQR
lub poniżej Q1-1.5 x IQR.

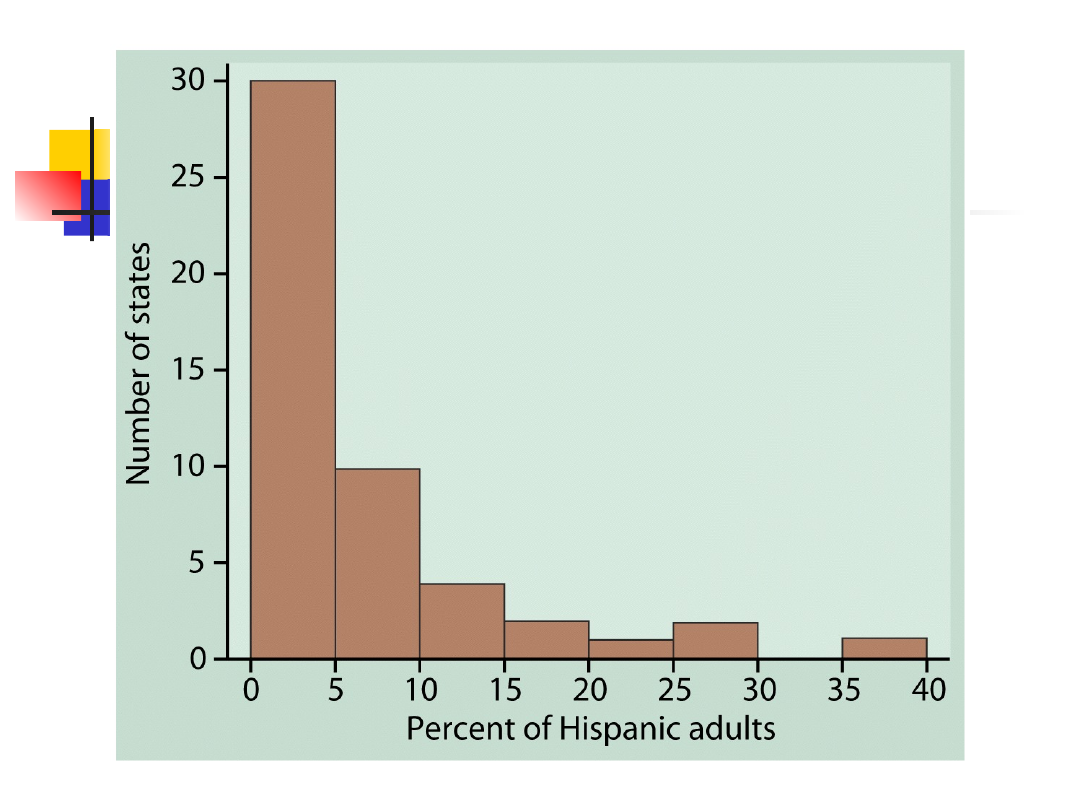
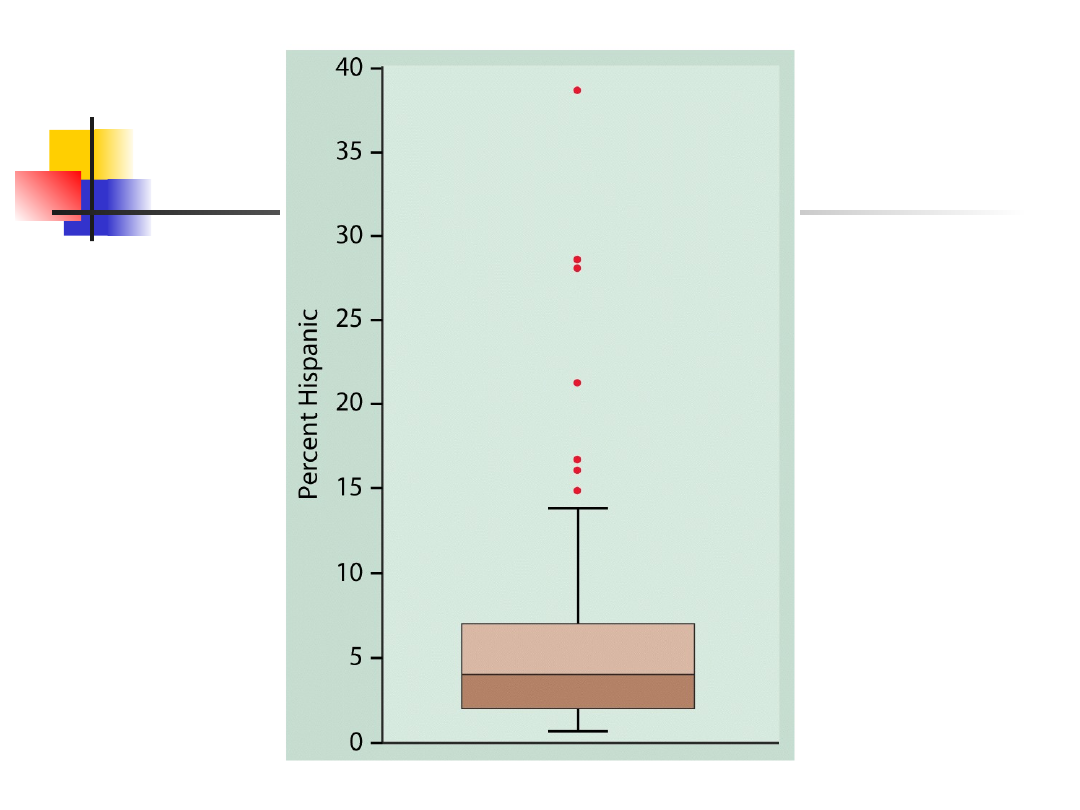
Example: % Hispanics
data



Q1 = 2.0, Q3 = 7.0



IQR = 7.0 – 2.0 = 5.0



Wszystkie wartości poniżej 2.0 – 1.5*5.0 = -5.5 lub

ponad 7.0 + 1.5*5.0 = 14.5 są oznaczone jako

możliwe punkty odstające. Jest 7 takich obserwacji.



To nie zwalnia od własnego osądu – trzeba zerknąć

na dystrybucje i podjąć decyzję o pozostawieniu lub

usunięciu pomiaru z dalszej analizy.



Wygodne narzędzie do oceny dużych zbiorów

danych.

Zmodyfikowany wykres
ramkowy



Zaznacz każdy punkt odstający osobno
używając symboli typu ‘*’ lub ‘o’.



Linie od „pudełka” prowadzą tylko do
największych i najmniejszych pomiarów,
które pozostały po usunięciu punktów
odstających.

Przykład - wzrost



Liczność próbki N = 582



Wartość średnia = 176.16 cm



Mediana = 177 cm



Zakres = 82 cm



Q1 = 170 cm; Q3 = 183 cm



IQR = 13 cm



Odchylenie standardowe = 9.86 cm

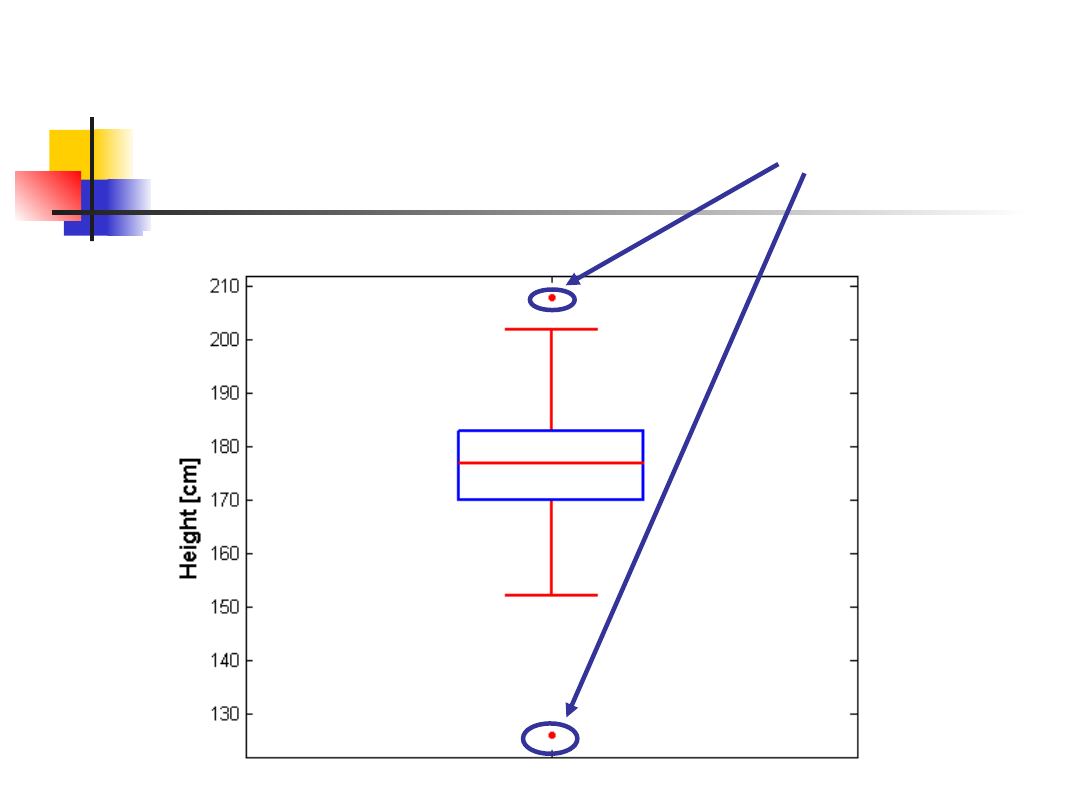
Przykład - wzrost

Dwie wielkości odstające
210 cm i 125 cm

Kształt histogramu



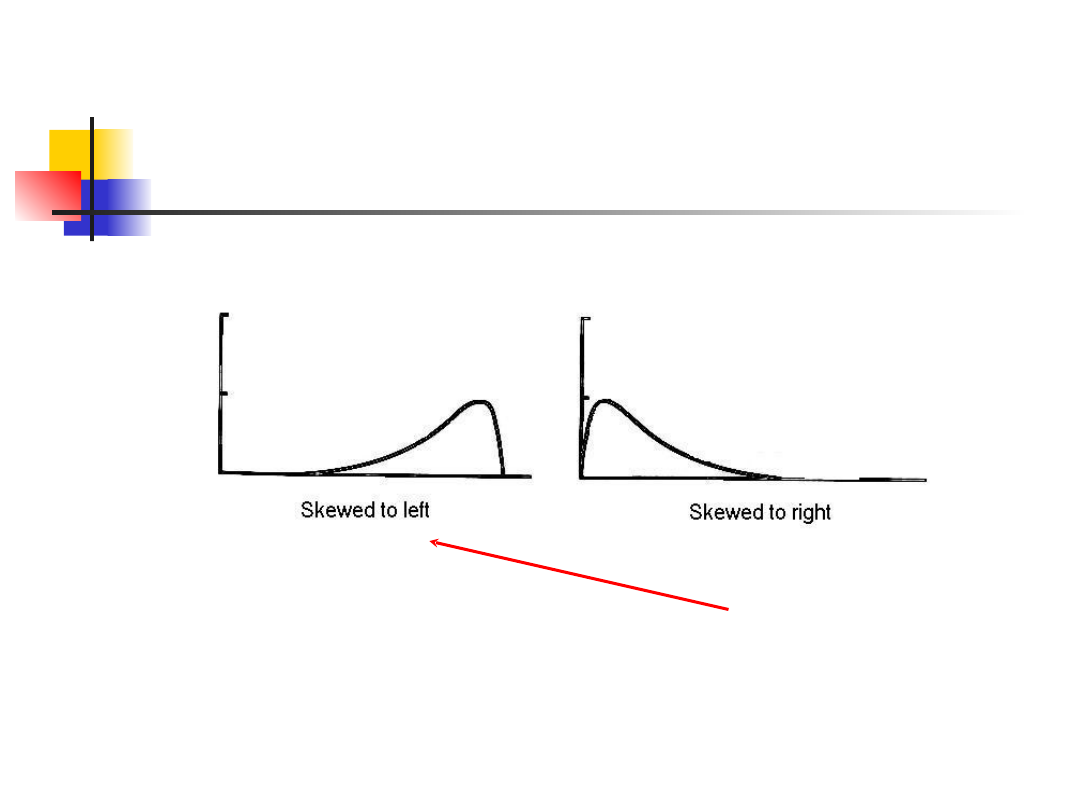
Skośność (asymetria) oznacza że jeden koniec

jest dłuższy niż drugi.



Możemy obliczyć skośność przez:



Krzywe nazywamy skośnymi w prawo (g1>0)

lub w lewo (g1<0), zależnie od tego, który

koniec jest dłuższy.

3

3

i

i

1

s

*

)

2

n

)(

1

n

(

)

X

X

(

n

n

g











Kształt histogramu

Przykład - wzrost: skośność =
-0.26

Kształt histogramu



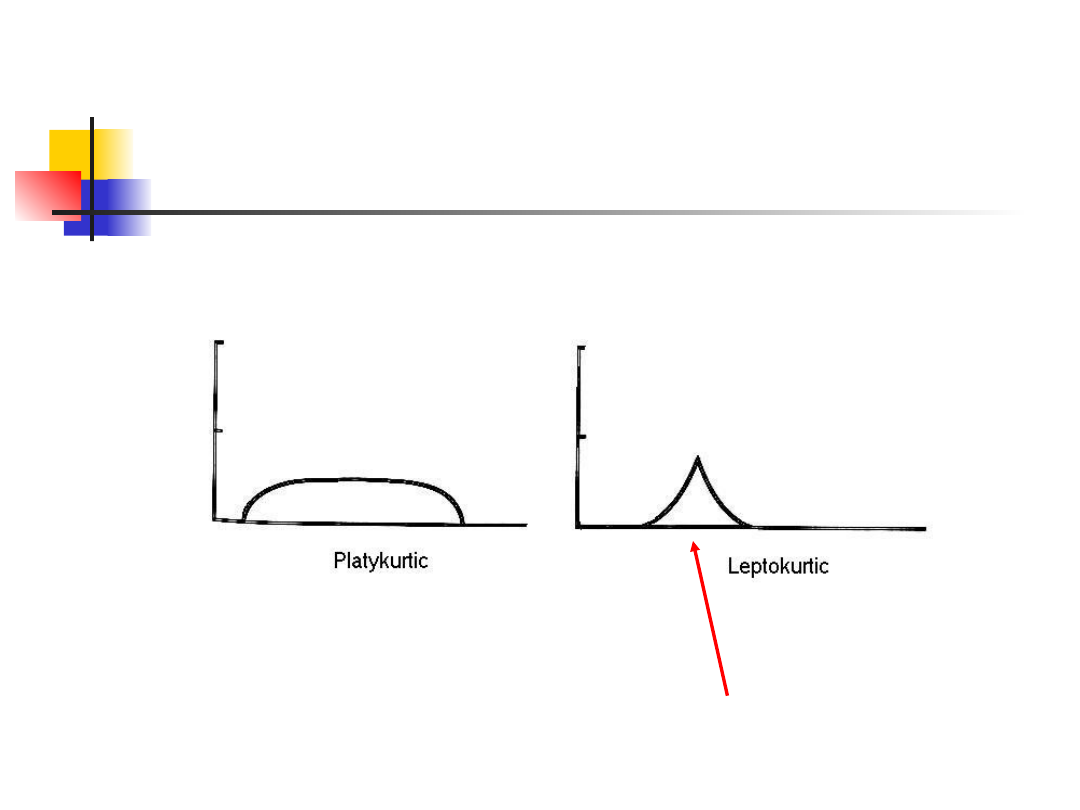
Inny rodzaj odstępstwa od normalności to kurtoza, jest to

bardziej skomplikowana zmiana w kształcie dystrybucji.



Jeśli symetryczny rozkład ma środek, dwa ramiona i dwa

końce, kurtoza opisuje stosunek między częścią środkową

i końcami w odniesieniu do ramion.



O leptokurtozie mówimy, gdy krzywa ma więcej

obserwacji blisko środka i na końcach a mniej w

ramionach w porównaniu do rozkładu normalnego, z tą

samą średnią i wariancją.



Platykurtoza - ma mniej elementów w środku, za to

więcej w ramionach.

Kształt histogramu



Możemy obliczyć kurtozę ze wzoru:



Ujemne g

2

wskazuje na platykurtozę,

zaś dodatnie g

2

mówi leptokurtozie.





4

2

2

4

1

)

1

(

2

)

3

)(

2

(

)

(

3

)

(

s

n

n

X

X

X

X

g

i

i

n

n

n





















Kształt histogramu

Przykład - wzrost: kurtoza = 3.65

Ocena skośności i kurtozy za
pomocą kwantyli



Oznaczając i-ty kwartyl jako Q

i

, możemy

zdefiniować współczynnik skośności
Bowley’a (Bowley, 1920):

1

3

2

1

3

2

Q

Q

Q

Q

Q

skewness









wartość, która może przyjmować wartości od
-1 dla rozkładu ekstremalnie lewoskośnego,
przez 0 dla rozkładu symetrycznego, do 1 dla
rozkładu prawoskośnego

Ocena skośności i kurtozy za
pomocą kwantyli



Pomiar kurtozy (wyostrzenia) na podstawie
oktyli O

i

(12.5%, 25%, 37.5% itd.) został

zaproponowany przez Moors’a w 1988

1

3

1

3

5

7

)

(

)

(

Q

Q

O

O

O

O

kurtosis













Dla skrajnie spłaszczonego rozkładu ta
wartość wynosi 0; 1.233 dla normalnego;
nieskończoność dla skrajnie wyostrzonego.

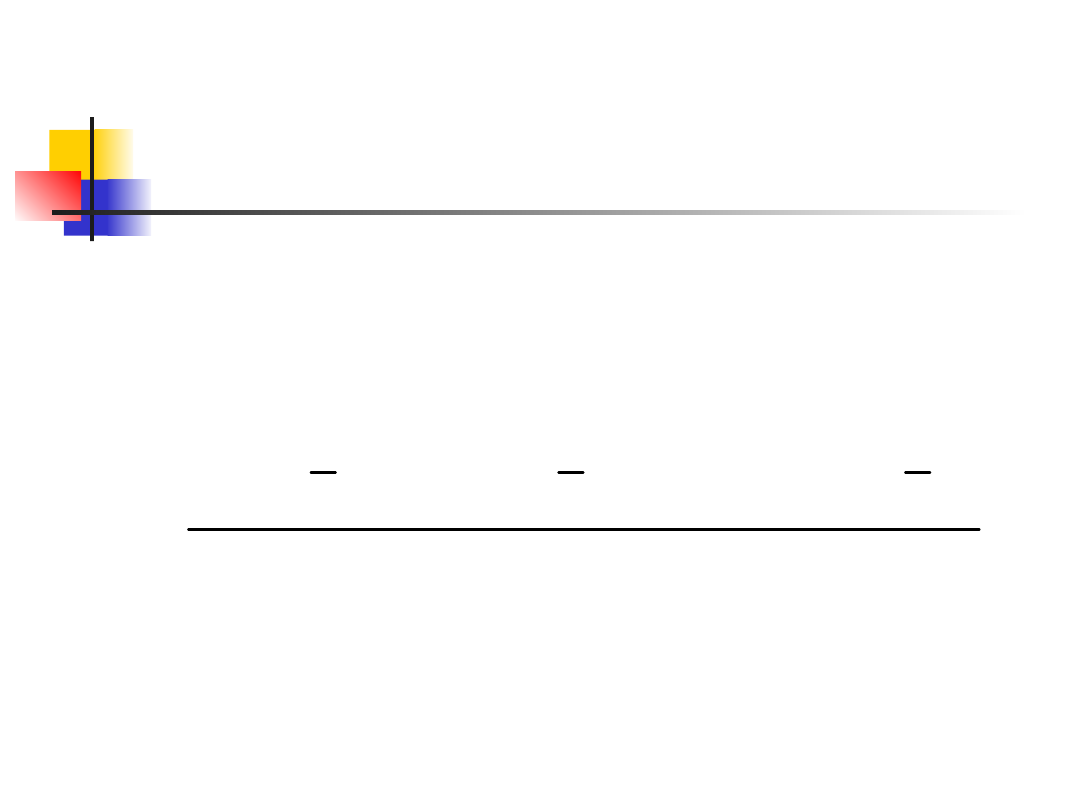
Pomiar rozrzutu:
odchylenie standardowe



Najpopularniejszy opis liczbowy
rozkładu składa się ze średniej i
odchylenia standardowego



Odchylenie standardowe s mówi,
jak obserwacje są oddalone od ich
średniej

Odchylenie standardowe



Wariancja s

2

to suma kwadratów

odchyleń obserwacji od ich średniej
podzielona przez n-1.



Odchylenie standardowe s to dodatni
pierwiastek kwadratowy z wariancji s

2

.

1

)

(

)

(

)

(

2

2

2

2

1

2

















n

x

x

x

x

x

x

s

n



Odchylenie standardowe,
cd.



Duże, jeśli obserwacje są mocno

rozrzucone wokół średniej; Małe, jeśli

wszystkie obserwacje są blisko średniej



Własności



Mierzy rozproszenie i i powinno być używane

tylko wtedy, gdy jako miara położenia jest

wybrana średnia



Równe 0, gdy zupełnie nie ma rozrzutu

(wszystkie obserwacje mają tą samą wartość)



Nie jest odporne - kilka punktów odstających

może diametralnie zwiększyć s.

Wybór miar położenia i
rozrzutu



Stosuj średnią i odchylenie
standardowe dla symetrycznych
rozkładów, bez punktów
odstających



Stosuj przedstawienie w postaci 5
liczb (Min Q1 M Q3 Max) kiedy
opisujesz rozkłady silnie skośne z
dalekimi punktami odstającymi.

Rozkłady normalne



Krzywe gęstości



Miary położenia i rozrzutu



Rozkłady normalne



Właściwości



Standardowy rozkład normalny



Obliczenia



Wykresy kwantylowe



Standaryzowanie obserwacji

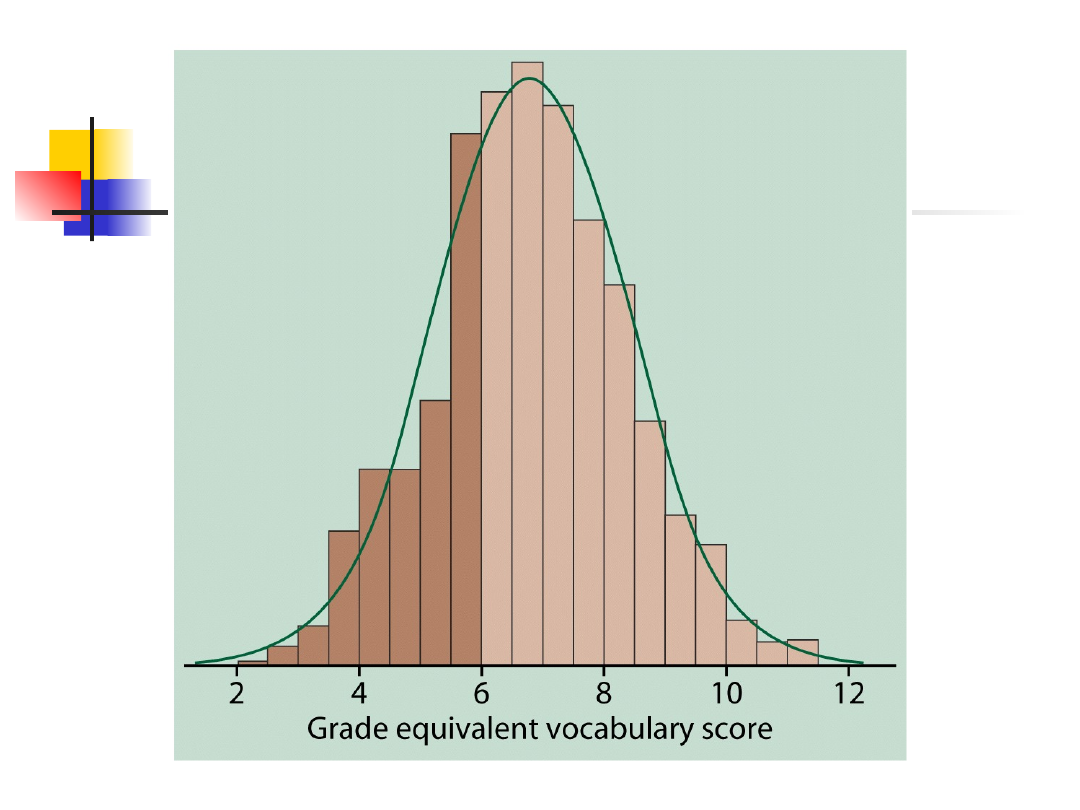
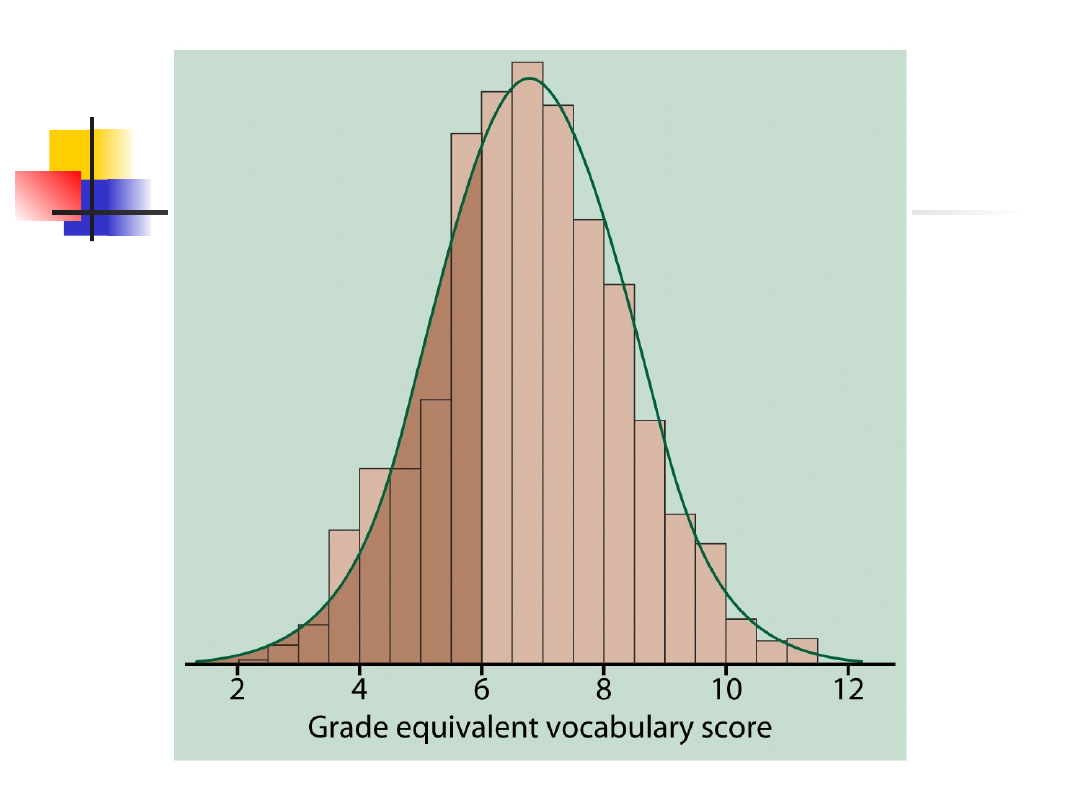
Krzywe gęstości



Krzywe, które



Są zawsze na lub nad osią poziomą



Mają pole pod sobą równe dokładnie 1



Opisują cały kształt rozkładu



Pole pod krzywą, powyżej

dowolnego zakresu wartości, jest

relatywną częstością wszystkich

obserwacji z tego zakresu.

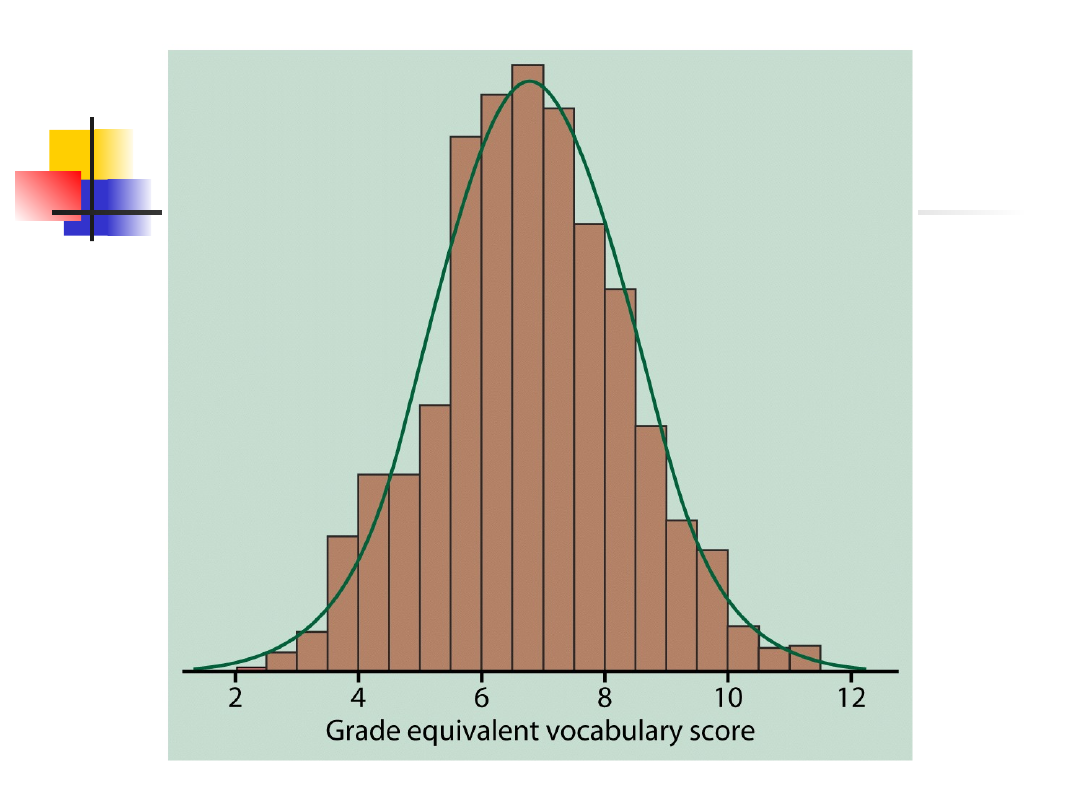
Miary położenia i rozrzutu
dla krzywych gęstości



Moda



Punkt szczytowy krzywej



Miejsce gdzie krzywa jest najwyższa



Mediana krzywej gęstości



Punkt, który dzieli pole pod krzywą na dwie
połowy



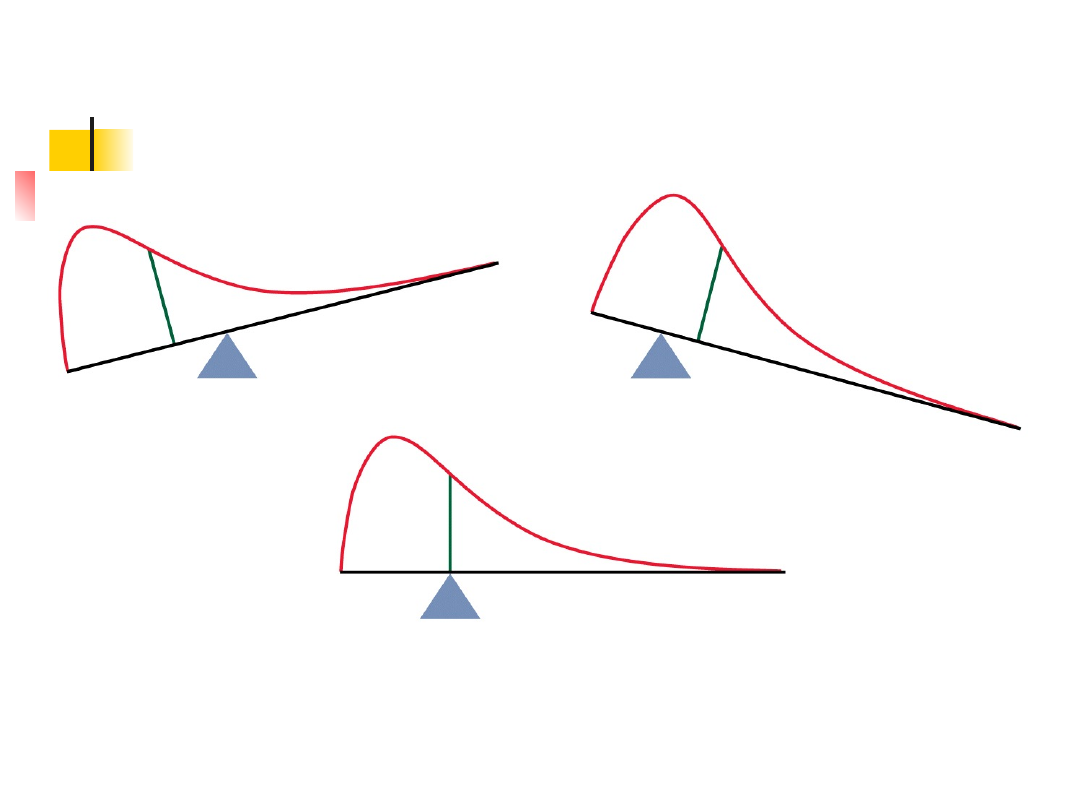
Średnia krzywej gęstości



Gdyby wykonano kształt z litego materiału zgodny
z obserwowanym rozkłądem, średnia byłaby
punktem podparcia, dla którego bryła balansuje.

Miary położenia i rozrzutu
dla krzywych gęstości



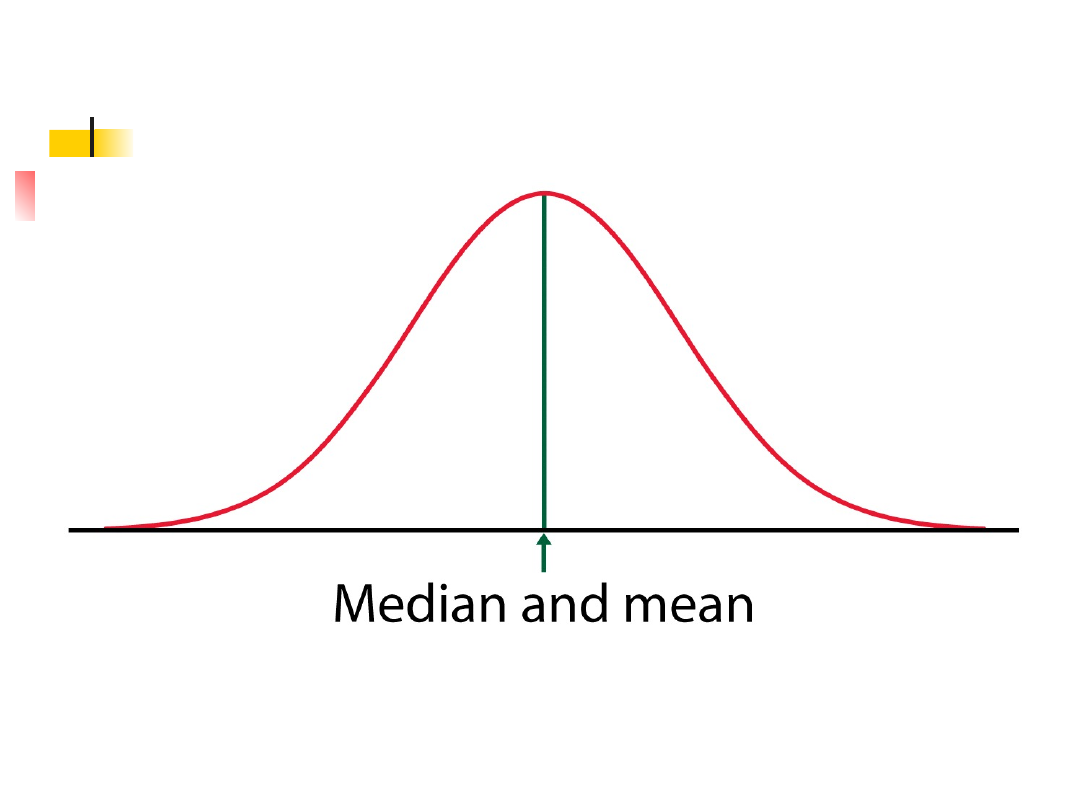
Dla symetrycznych krzywych gęstości,

średnia = mediana (są na środku)



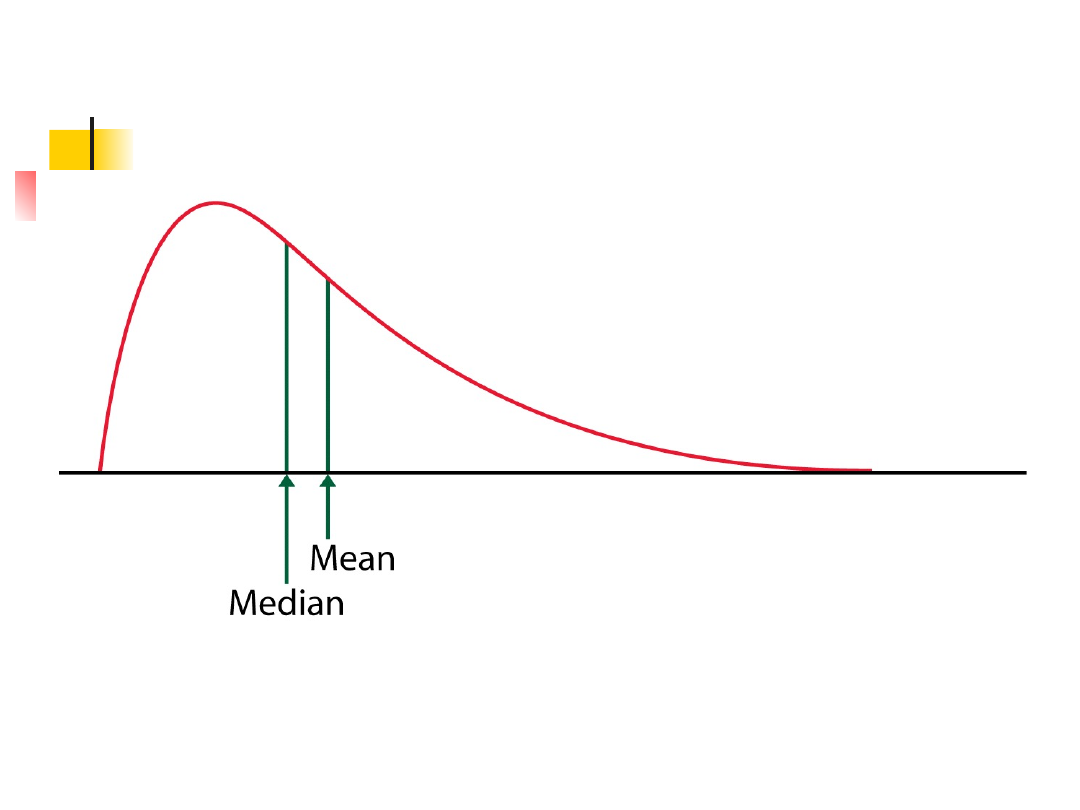
Dla skośnych krzywych, średnia jest

odsunięta dalej od mediany, w stronę

dłuższego ogona.



Kwartyle



Można je znaleźć przez dzielenie powierzchni pod

krzywą na ćwiartki



IQR



Odległość (rozstęp) między pierwszym i trzecim

kwartylem

- średnia

Krzywe gęstości



Wyidealizowany matematyczny
model rozkładu danych



Symetryczny



Teoretyczny vs. empiryczny



i s



μ i σ

x

Rozkłady normalne



Krzywe normalne to takie krzywe
gęstości, które:



Są symetryczne



Są jednomodalne



Mają dzwonowaty kształt



Opisują rozkłady normalne



Rozkłady normalne mają ten sam kształt



Odpowiednia krzywa opisana przez średnią i
odchylenie standardowe.

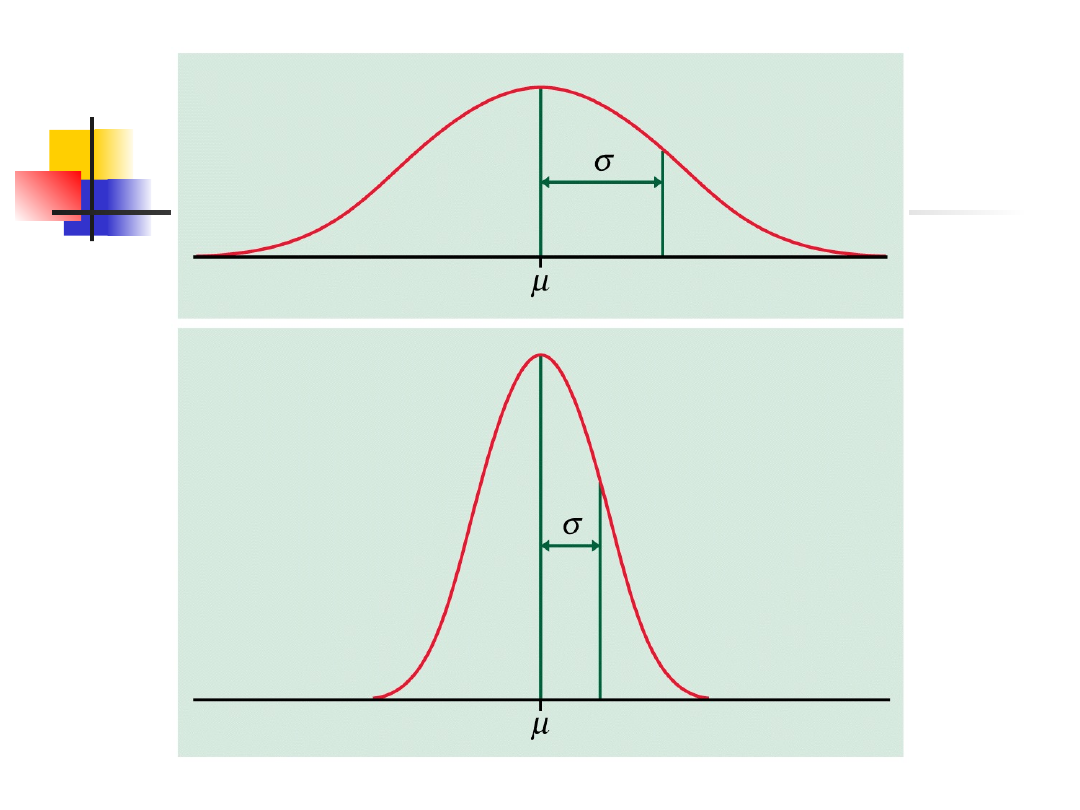
Odchylenie standardowe
dla krzywych normalnych



Kontroluje rozrzut



Lokalizacja odchylenia
standardowego



punkt przegięcia ramion krzywej

Rozkłady normalne, cd.



Wysokość krzywej gęstości



Znaczenie w statystyce



Dobry opis niektórych rozkładów danych

rzeczywistych



Dobre przybliżenie dla różnych oszacowań

prawdopodobieństw obserwowanych wyników



Wiele z procedur wnioskowania statystycznego

stworzonych przy założeniu normalności

rozkładów, jest odpowiednich również dla innych,

w przybliżeniu symetrycznych, rozkładów.

2

2

1

2

1























x

e

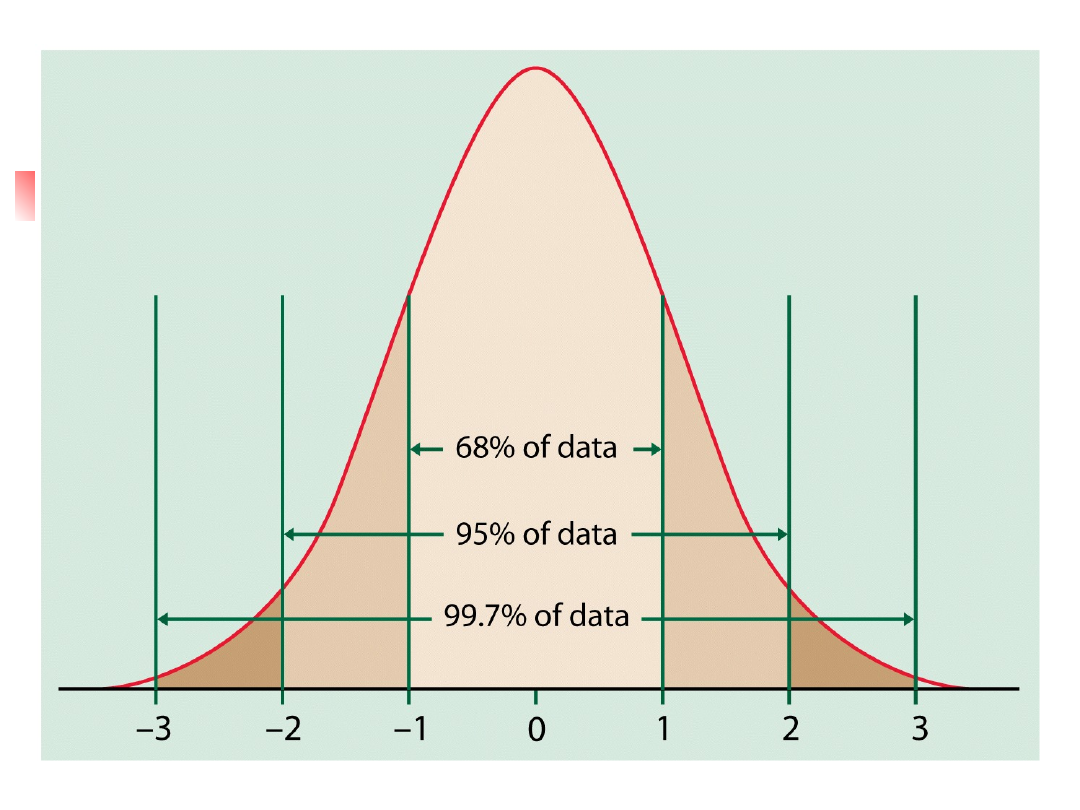
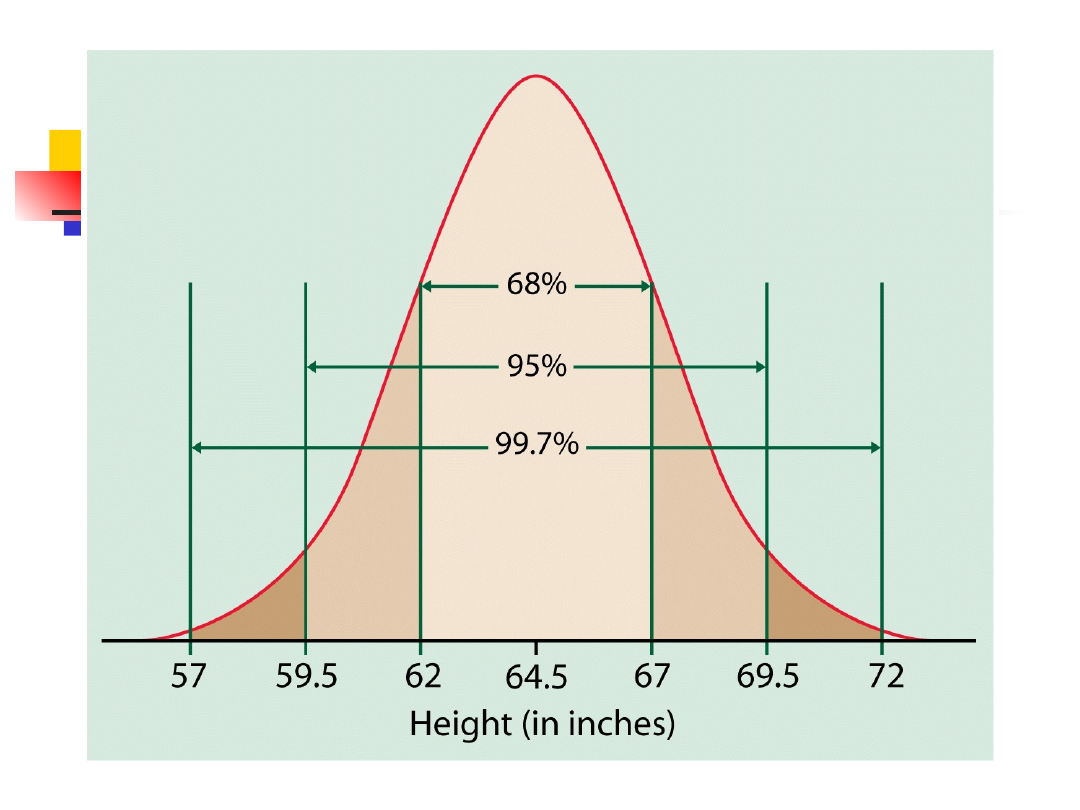
Reguła trzech sigm 68-95-
99.7



W rozkładzie normalnym z wartością

oczekiwaną μ i odchyleniem

standardowym σ



Około 68% obserwacji leży w odległości

mniejszej lub równej σ od średniej μ.



Około 95% obserwacji leży w odległości

mniejszej lub równej 2σ od średniej μ.



Około 99.7% obserwacji leży w odległości

mniejszej lub równej 3σ od średniej μ.

Oznaczenie rozkładów
normalnych



Rozkład normalny ze średnią μ i
odchyleniem σ zapisujemy
skrótowo jako N(μ, σ).

Standaryzacja obserwacji



Standaryzując pomiar, odejmij
średnią i podziel przez odchylenie
standardowe



Jeśli x jest obserwacją z rozkładu o
średnią μ i odchyleniu
standardowym σ,
standardyzowaną wartością x jest









x

z

Z-scores



Mówią nam ile krotności
odchylenia standardowego
obserwacje leżą od średniej i w
którym kierunku



Mogą być dodatnie lub ujemne



Kiedy?

Standardowy rozkład
normalny



N(0,1)



Średnia = 0



Odchylenie standardowe = 1



Jeśli zmienna X ma dowolny rozkład
normalny N(μ, σ), wtedy zmienna losowa

ma standardowy rozkład normalny N(0,1).









X

Z

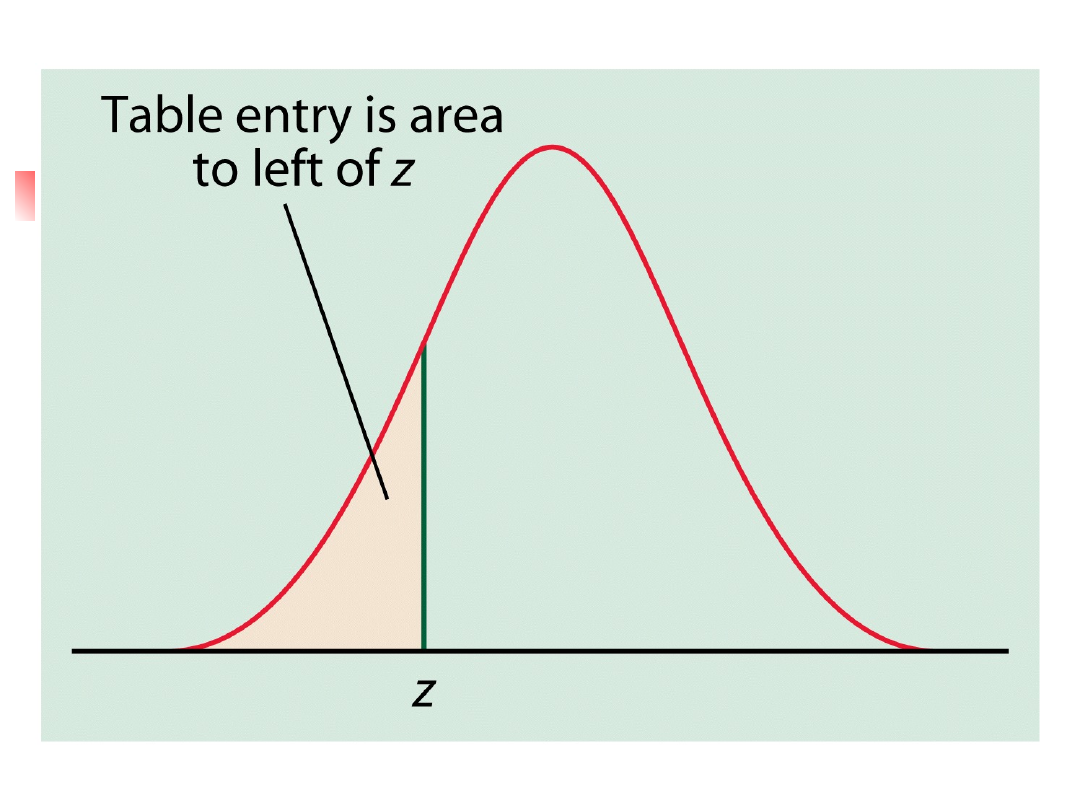
Dystrybuanta standardowego
rozkładu normalnego – tabela.
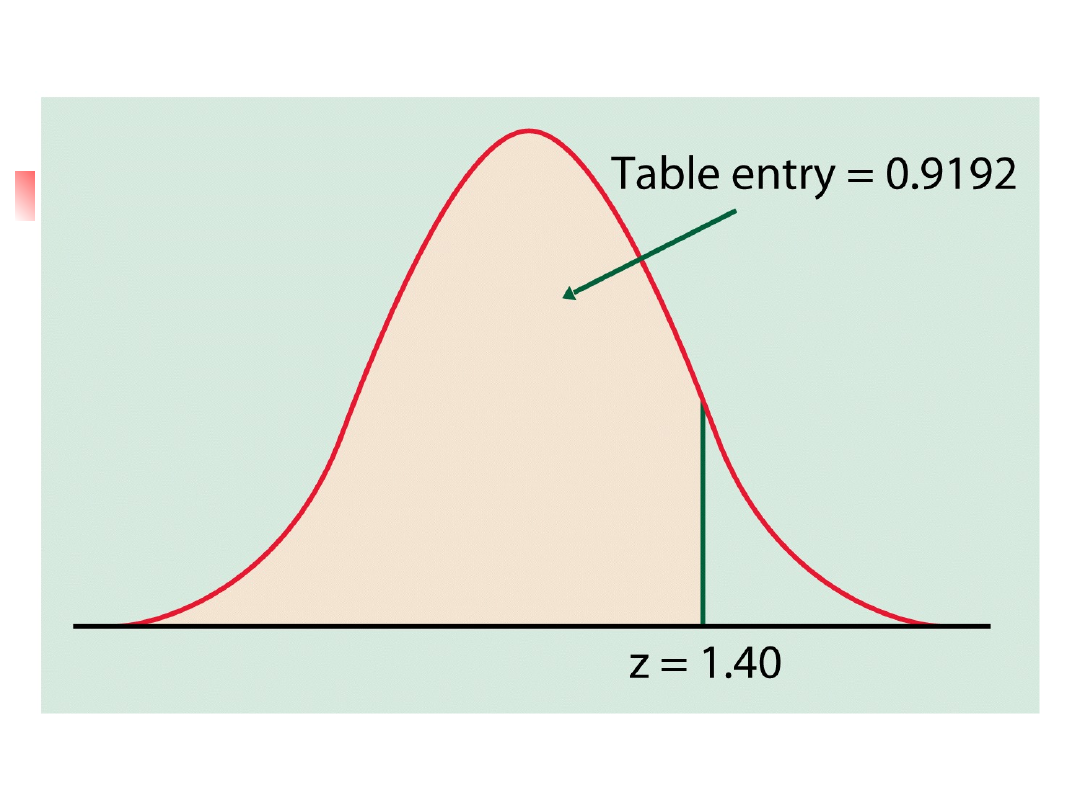
Przykład 1



Jaka część obserwacji
standardowej zmiennej normalnej
Z przyjmuje wartości mniejsze niż
1.4?



Znajdź część obserwacji ze
standardowego rozkładu
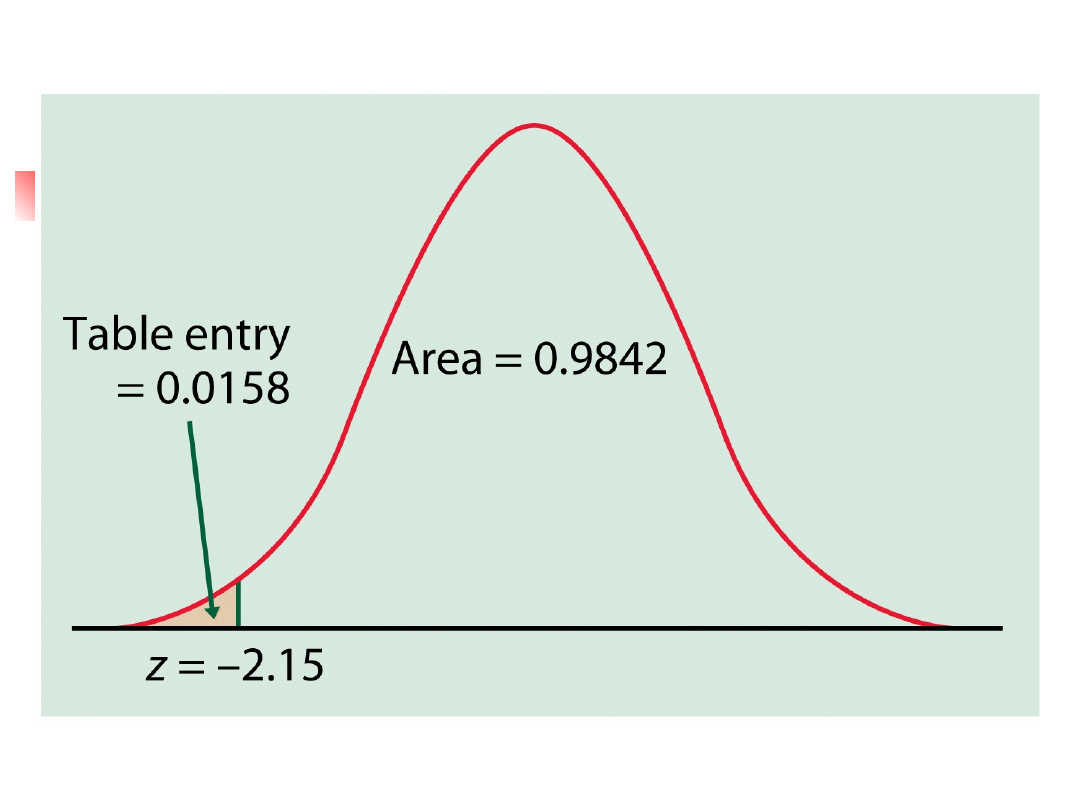
normalnego które są większe niż –
2.15.

Dystrybuanta standardowego
rozkładu normalnego – tabela.
Przykład 2

Rozkłady normalne –
przykład obliczeniowy



NCAA wymaga 820 punktów zdobytych w

trakcie egzaminu SAT. Rozkład liczby

punktów w 2000r był w przybliżeniu

rozkładem N(1019, 209).

Jaki procent wszystkich studentów miał

liczbę punktów SAT co najmniej 820?



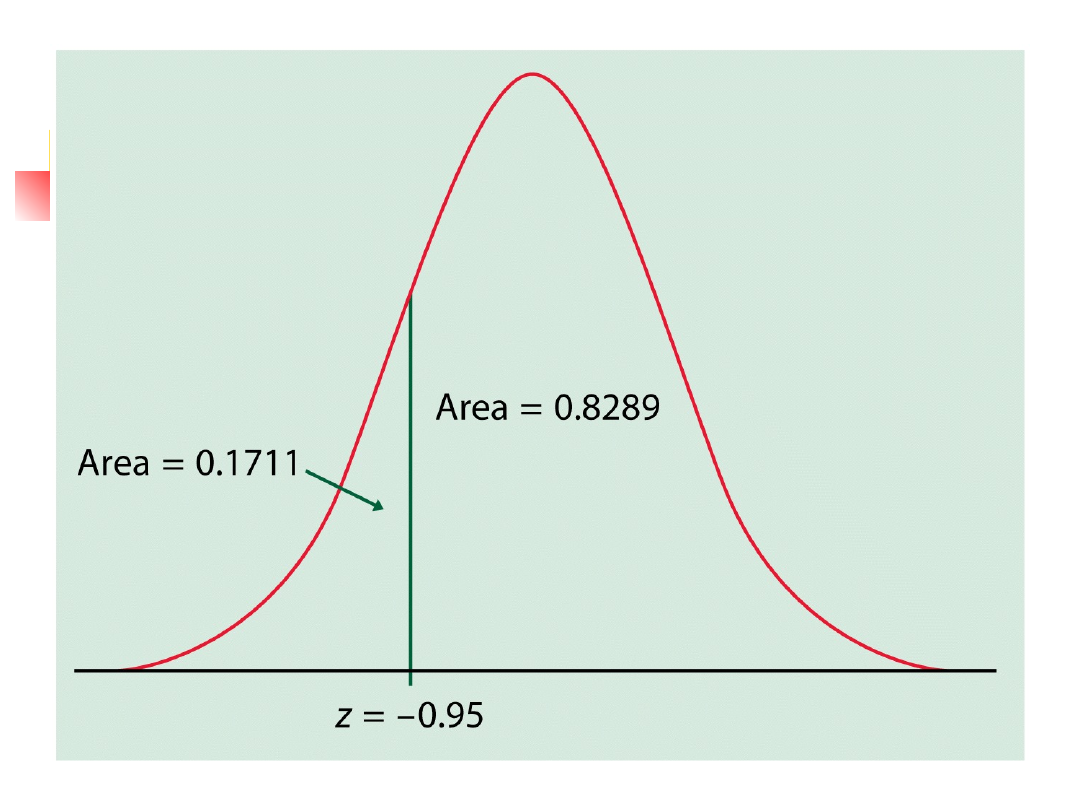
X = punkty z egzaminu SAT



X należy do rozkładu N(1019, 209)



Znajdź Z (standardowe).



Z = (820 – 1019)/209 = -0.95



P(Z > -0.95) = 1 – 0.1711 = 0.8289

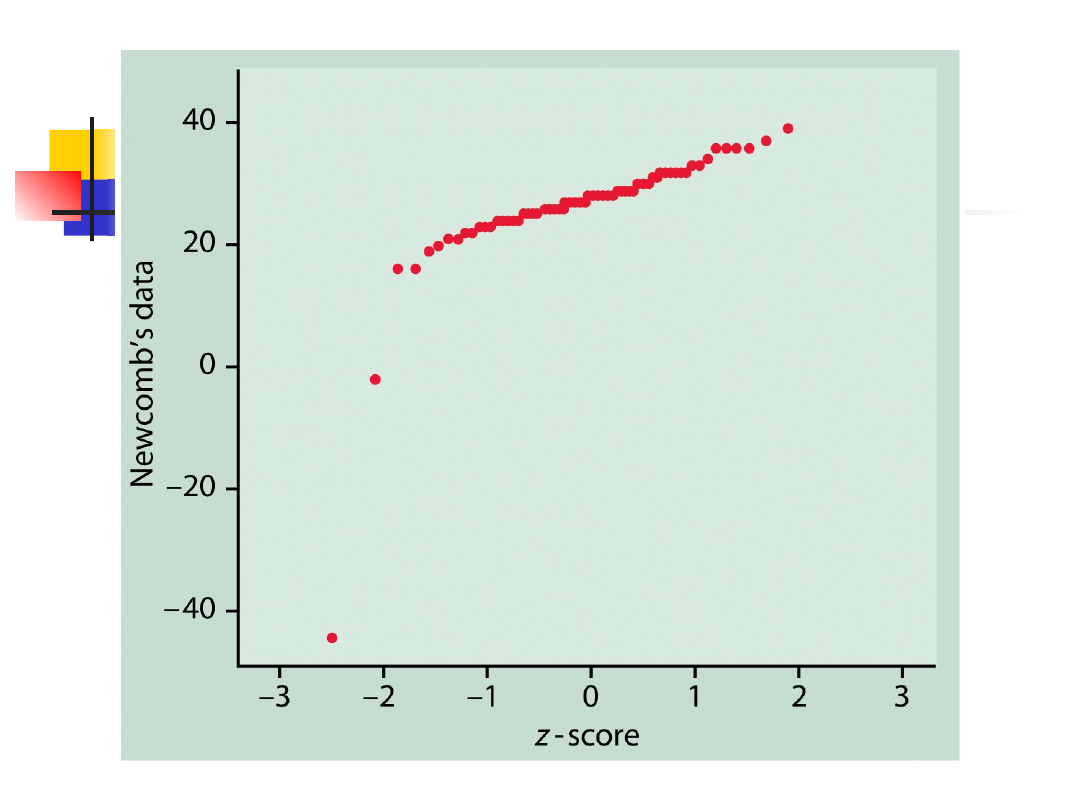
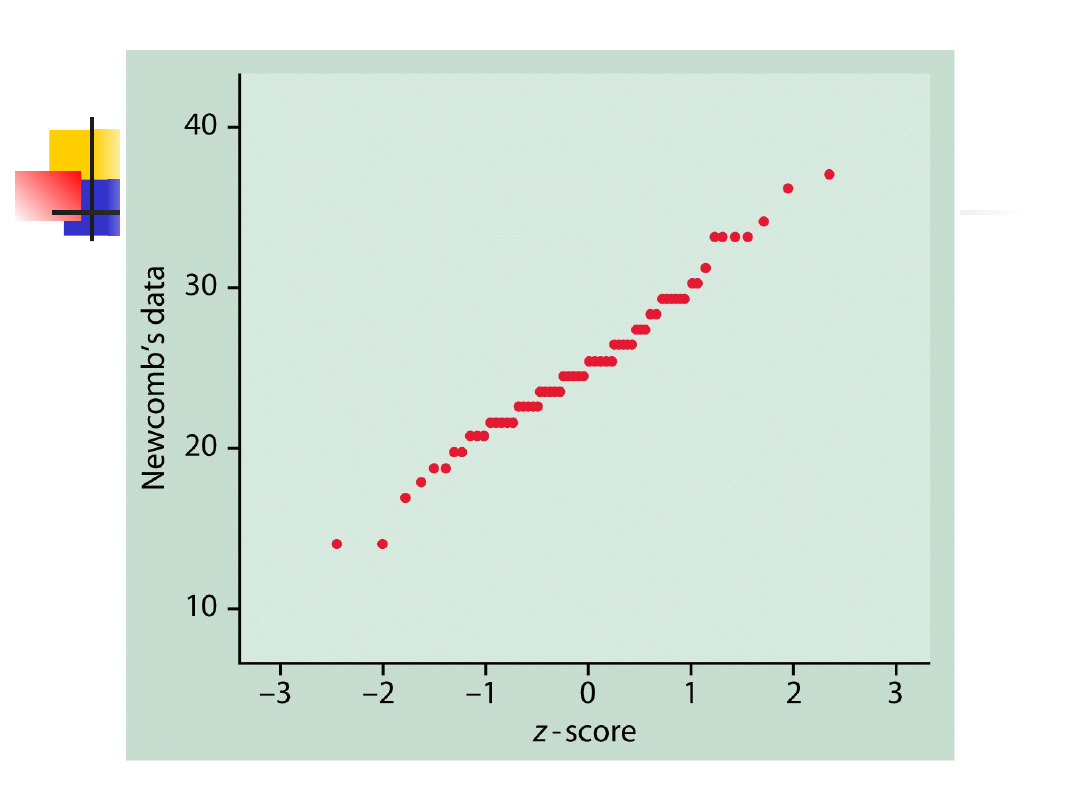
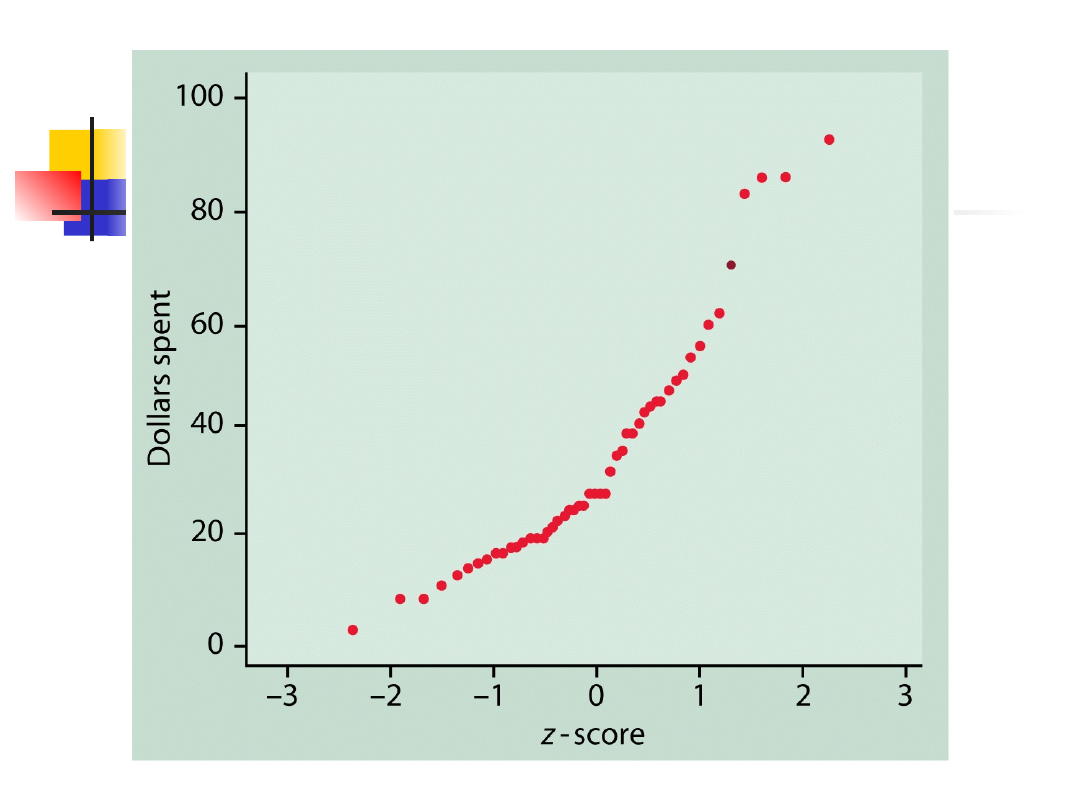
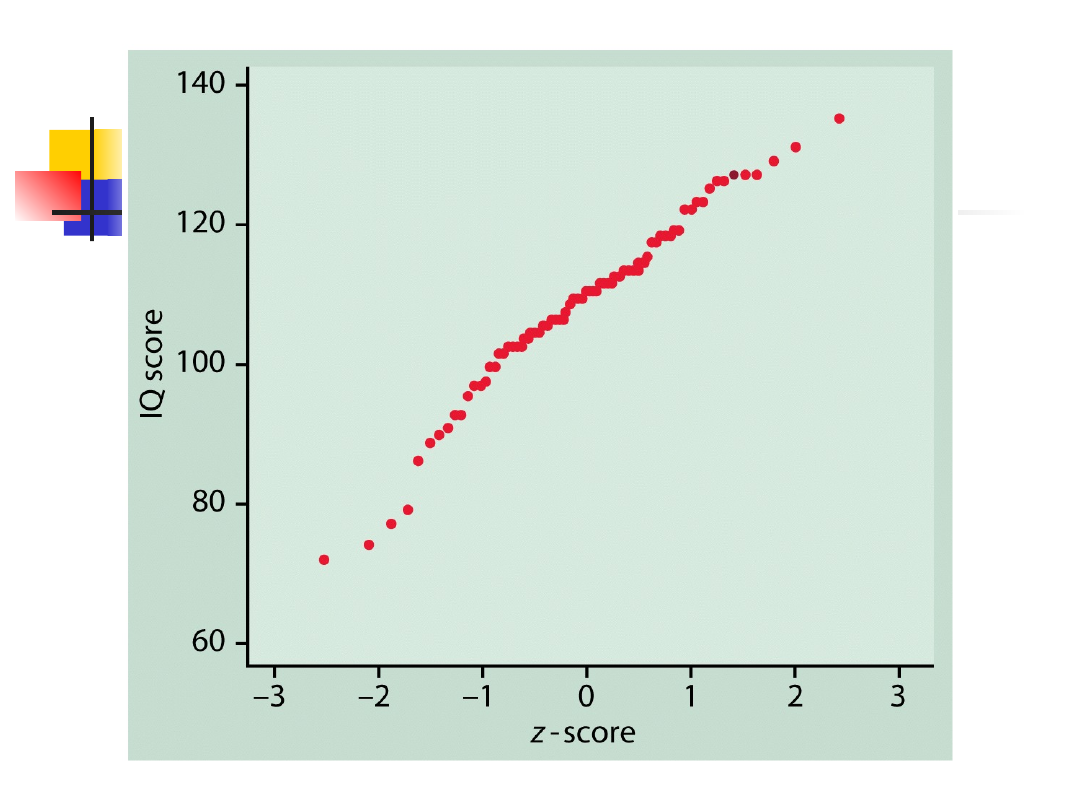
Normalny wykres
kwantylowe



Rozkłady normalne



Dobre modele dla niektórych rozkładów

rzeczywistych danych



Rozkłady niektórych zmiennych są skośne i

dalekie od normalnych



Należy przejrzeć dane!



Sposoby sprawdzenia normalności



Histogramy



Wykresy łodygowe



Normalne wykresy kwantylowe

Konstrukcja normalnego wykresu
kwantylowego

1.

Uporządkuj zaobserwowane dane w porządku

malejącym. Zapisz jakim percentylem danych

jest każda wartość.

2.

Przeprowadź obliczenia dla normalnego rozkładu

żeby znaleźć punkty standardowe z tych

percentyli.

3.

Zaznacz każdy punkt x w zależności od z. Jeśli

rozkład danych jest w przybliżeniu standardowy

normalny, narysowane punkty będą leżały blisko

prostej x=z. Jeśli rozkład danych jest bliski do

innego dowolnego rozkładu normalnego, punkty

będą leżały blisko innej linii, także prostej.

Normalny wykres
kwantylowy



Linia prosta



Dane pochodzą z rozkładu normalnego



Systematyczne odchylenia od linii

prostej



Dane nie pochodzą z rozkładu

normalnego



Punkty odstające ujawniają się jako

punkty leżące daleko od ogólnego

kształtu wykresu.