2. Znajdujemy punkt

1. Startujemy z dowolnego punktu

.

k

P

m

P

, który leży na sferze o środku

k

P

i nie zawiera w swoim wnętrzu innych punktów.

3. Znajdujemy punkt

m

P

taki, że sfera przechodząca przez punkty

n

m

k

P

P

P

,

,

nie zawiera w swym wnętrzu

innych punktów z P.

4. Szukamy punktu

,

s

P

tak aby sfera przechodząca przez

s

n

m

k

P

P

P

P

,

,

,

nie zawierała innych punktów z P.

5. Budujemy czworościan o wierzchołkach

.

,

,

,

s

n

m

k

P

P

P

P

Konstrukcja

triangularyzacji

Delaunay’a N=3

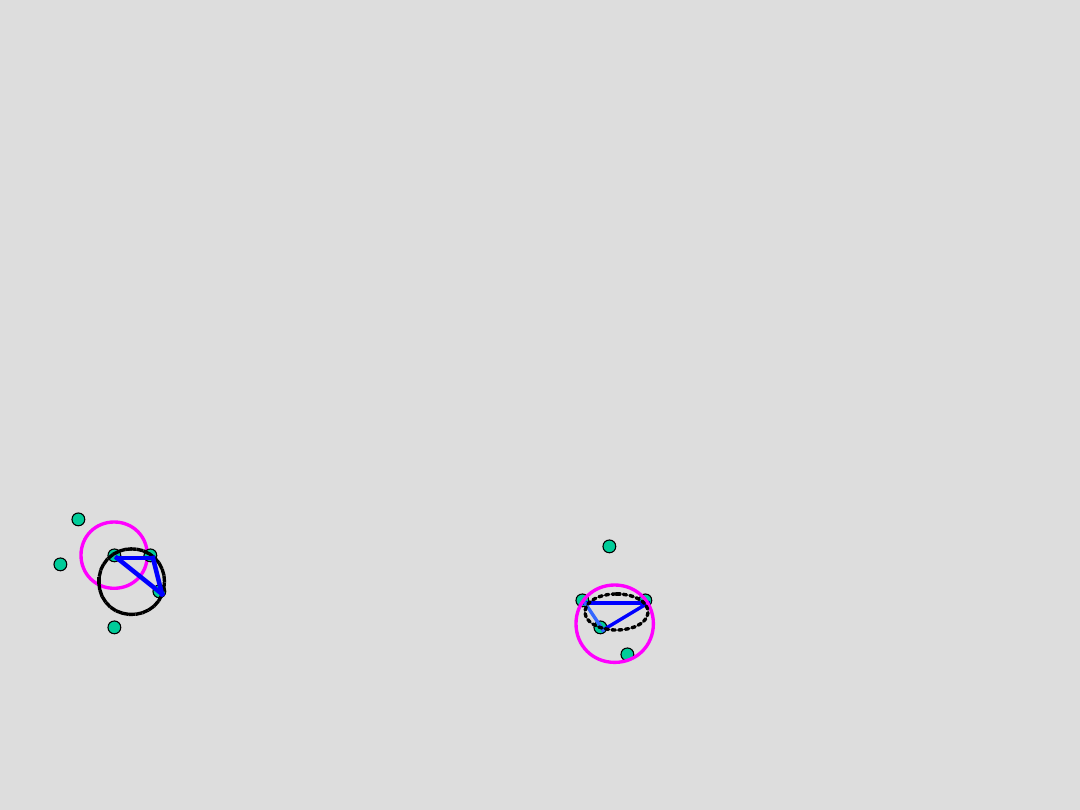
6. Startujemy z dowolnie wybranej ścianki
utworzonego czworościanu i szukamy punktu z
P tak, aby utworzyć nowy czworościan
przechodzący przez wierzchołki tej ścianki oraz
ten punkt.

Konstrukcja triangularyzacji
Delaunay’a N=3 c.d.

7. Proces kontynuujemy aż do wyczerpania punktów.

Twierdzenie (II

Delaunay’a)

}

,

,

1

:

{

)









i

T

T

Z

i

rodzina sympleksów,

,

,

)

(













j

i

j

i

T

T

j

i

T

T

T

i

,

)

(

1

_

N

i

i

T

ii











},

,

,

1

:

{









i

P

P

i

},

,

,

1

:

{









i

V

V

i

},

,

,

1

:

{









i

Q

Q

i

.

#

},

:

{

i

k

i

k

i

W

L

V

Q

V

W







zbiór wierzchołków sympleksów,

zbiór wielokątów Voronoi,

zbiór wierzchołków wielokątów
Voronoi,

P – nieosobliwy,

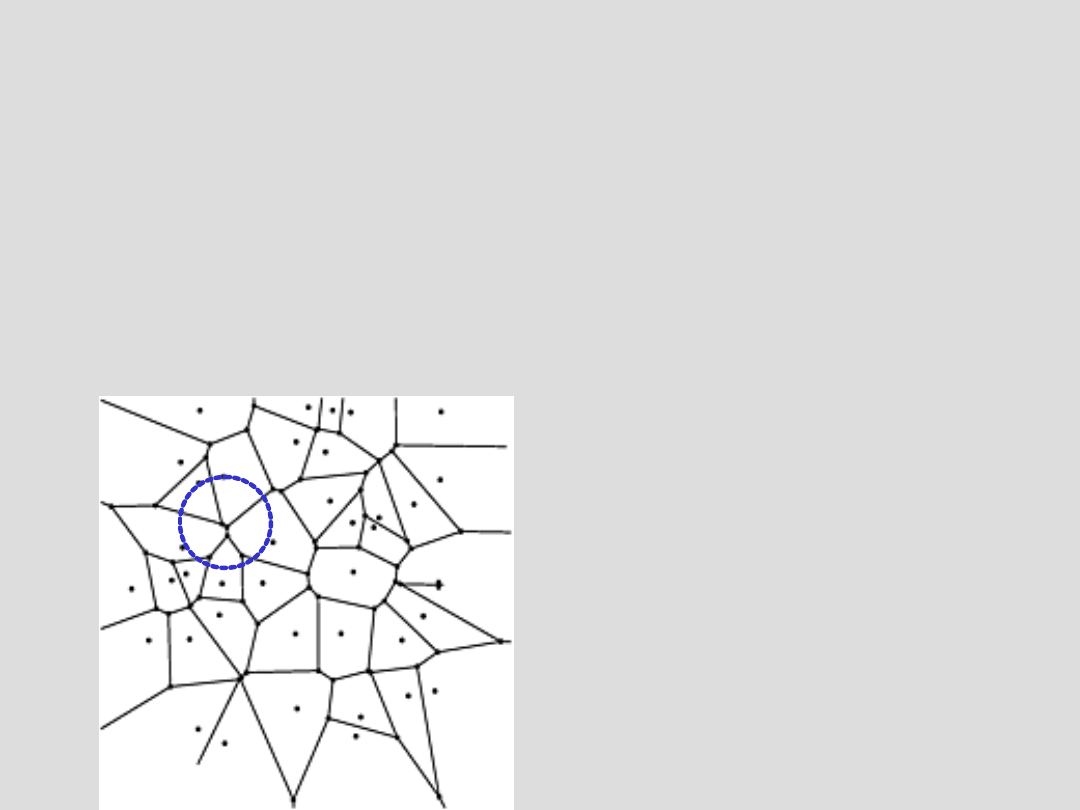
Twierdzenie (II

Delaunay’a) c.d.

T) a) Zbiór

,

}

{

1

P

P

L

k

k





które są w środkach leżą

i

W

na „sferze pustej” o środku w

.

i

Q

b) L=N+1 oraz punkty

L

k

k

P

1

}

{



określają sympleks
Delaunay’a.

i

Q

j

P

k

P

m

P

||

||

||

||

||

||

m

i

k

i

j

i

P

Q

P

Q

P

Q











1



N

L

ponieważ układ P
jest nieosobliwy

Gdyby

1



 N

L

wówczas

„wędrująca kula” znalazłaby kolejny
punkta to oznaczałoby, że ten punkt
nie jest w

.

i

W

Problem monitorowania

galerii

sztuki (obiektów

chronionych)

W celu ochrony galerii sztuki ustawiane są kamery, tak aby
każdy punkt był monitorowany. Zakładamy, że rzut galerii na
płaszczyznę poziomą jest wielokątem (ewentualnie z otworami).
Ponadto przyjmujemy:

• Kamery wiszą zawieszone na suficie,

• Kamery obracają się wokół pionowej osi,

• Liczba kamer powinna być minimalna z możliwością monitorowania
każdego zakamarka.

Problem monitorowania galerii sztuki można sprowadzić do

następujących punktów:
1. Jaka liczba kamer jest niezbędna ?,
2. Jak te kamery rozmieścić?.

Problem monitorowania

galerii

sztuki (obiektów

chronionych)

Modelujemy galerię jako wielokąt płaski.

P wielokąt, dokonujemy
triangularyzacji wielokąta

Tw. Każdy wielokąt prosty można striangularyzować. Każda taka
triangularyzacja składa się z n-2 trójkątów.

Dowód:
n=3 n=4

n-2=2

Problem monitorowania

galerii

sztuki (obiektów

chronionych)

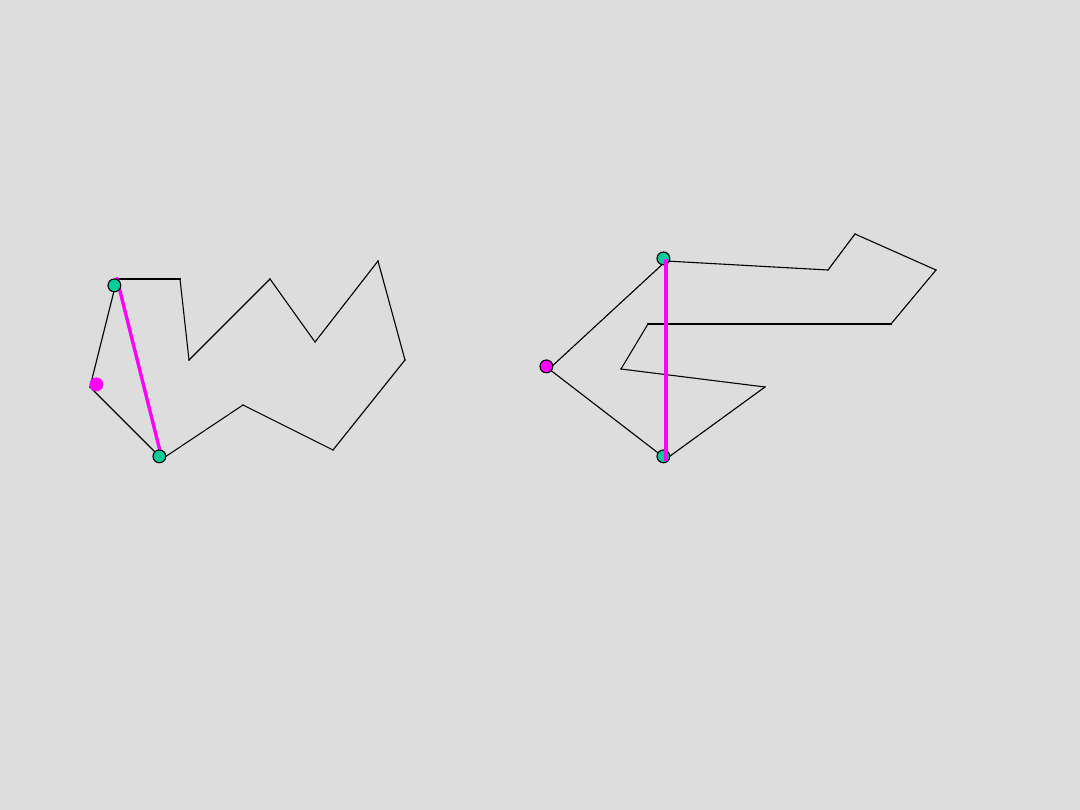
Niech n>2, zakładamy, że twierdzenie jest prawdziwe dla każdego
m<n. Niech P będzie wielokątem z n wierzchołkami.
Wykażemy, że istnieje przekątna P.

Zakładamy, że twierdzenie jest prawdziwe dla każdego m<n.
Niech P będzie wielokątem z n wierzchołkami. Wykażemy, że
istnieje przekątna wielokąta P. Niech będzie najbardziej na lewo
wysuniętym wierzchołkiem P. Niech oznaczają dwa sąsiednie
wierzchołki w stosunku do na brzegu P. Jeśli odcinek
leży w środku P mamy przekątną.

m

P

j

i

P

P,

]

,

[

j

i

P

P

m

P

Problem monitorowania

galerii

sztuki (obiektów

chronionych)

m

P

i

P

j

P

Przekątna zawiera
się w wielokącie

j

i

P

P,

m

P

j

P

i

P

Odcinek nie zawiera
się w wielokącie

j

i

P

P,

s

P

Problem monitorowania

galerii

sztuki (obiektów

chronionych)

Jeśli odcinek zawiera się w P mamy przekątną.
W przeciwnym razie istnieje przynajmniej jeden wierzchołek leżący
wewnątrz lub na odcinku . Niech będzie
najbardziej na lewo wysuniętym punktem leżącym w
. wówczas

j

i

P

P,

j

i

m

P

P

P



j

i

P

P,

]

,

[

s

m

P

P

Odcinek nie może przecinać brzegu P,
taki punkt przecięcia byłby na lewo od co przeczy temu, że
jest najbardziej oddalonym na lewo punktem leżącym w

s

P

s

P

a to oznacza, że

]

,

[

s

m

P

P

jest przekątną.

Jeśli istnieje przekątna to dzieli ona wielokąt na dwa podwielokąty

.

2

1

W

W

W





Wprowadźmy następujące oznaczenia:

j

i

m

P

P

P



s

P

.

j

i

m

P

P

P



Problem monitorowania

galerii

sztuki (obiektów

chronionych)

1

m

- liczba wierzchołków

,

1

W

2

m

- liczba wierzchołków

,

2

W

.

,

2

1

n

m

m



Z założenia indukcyjnego

,

1

W

2

W

dadzą się striangularyzować

A to oznacza, że P można striangularyzować.
Pozostaje wykazać, że P ma n-2 trójkąty.
Rozważmy dowolną triangularyzację wielokąta P. Weźmy pod uwagę
dowolną przekątną w tej triangularyzacji, ta diagonala dzieli W na

.

,

2

1

2

1











W

W

W

W

W

Problem monitorowania

galerii

sztuki

,

2

2

1







n

m

m

ponieważ dwa wierzchołki powtarzają się,

2

4

2

4

2

1















n

n

m

m

posiada

P

1

P

ma

2

1



m

trójkątów,

2

P

ma

2

2



m

trójkątów,

Z powyższego twierdzenia wynika, że wystarczy n-2 kamer.
Ale każdy wierzchołek należy do przynajmniej dwóch trójkątów
z czego wynika, że wystarczy kamer.







 

2

2

n

Problem monitorowania

galerii

sztuki

Czy istnieje lepsze rozmieszczenie kamer?
Niech będzie triangularyzacją zbioru punktów

P

T

.

P

Oznaczmy przez V najmniejszy podzbiór zbioru węzłów taki, że
każdy trójkąt ma przynajmniej jeden wierzchołek z V, wówczas
wystarczy rozmieszczać kamery w punktach zbioru V.

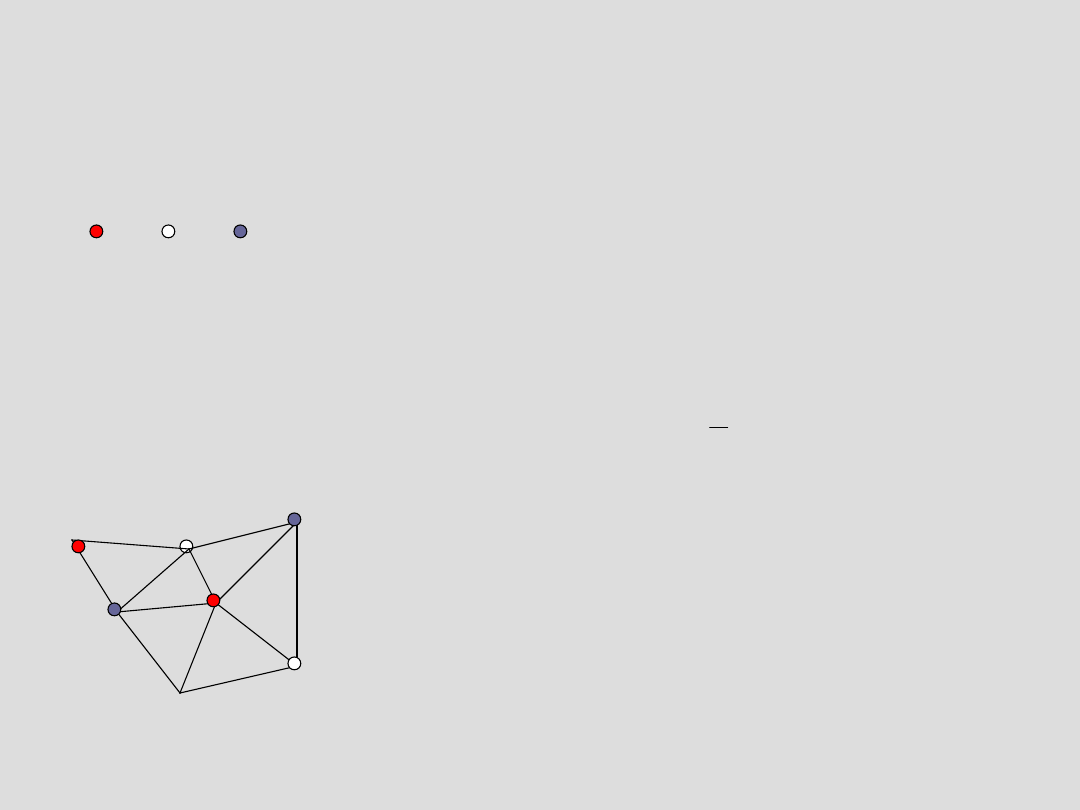
Zasada trójkoloryzacji

Mając do dyspozycji trzy kolory kolorujemy wierzchołki tak, aby
każdy trójkąt miał wierzchołki w trzech różnych kolorach. Po takim
pokolorowaniu wystarczy umieszczać kamery w wierzchołkach
jednego koloru. Wynika stąd, że wystarczy kamer.









3

n

GRAFY

Def. Grafem nazywamy trójkę {X,U,f}, gdzie
X – nazywamy zbiorem wierzchołków,
U – nazywamy zbiorem krawędzi,
f: U XX.,

f(u)=(x,y), x,yX.

Przykład

).

,

(

)

(

),

,

(

)

(

),

,

(

)

(

),

,

(

)

(

},

,

,

,

,

{

},

,

,

,

,

{

4

5

4

5

3

3

3

2

2

2

1

1

5

4

3

2

1

4

3

2

2

1

x

x

u

f

x

x

u

f

x

x

u

f

x

x

u

f

u

u

u

u

u

U

x

x

x

x

x

X













GRAFY

Def. Graf nazywamy kompletnym, jeśli każde dwa węzły są
połączone przez dokładnie jedną krawędź.

Def. Ścieżką nazywamy ciąg krawędzi w którym każde dwie
kolejne mają wspólny węzeł każdy inny dla kolejnych krawędzi.

Def. Graf (X,U,f) nazywamy spójnym, jeśli dwa dowolne węzły
można połączyć ścieżką złożoną z krawędzi.

Def. Ścieżkę nazywamy zamkniętą, jeśli węzeł początkowy
pokrywa się z końcowym.

GRAFY

Def. Graf nazywamy drzewem, jeśli nie ma w nim żadnej
ścieżki zamkniętej.

W striangularyzowanym trójkącie pokolorujemy węzły
każdego trójkąta trzema różnymi kolorami.
Do dozorowania „galerii sztuki” wystarczy [n/3] kamer.

Czy istnieje taka 3-koloryzacja?

}}

{

},

{{

)

(

:

)

(

,

}

,

,

1

:

{

ij

i

P

P

P

T

i

P

E

V

T

G

graf

oznacza

T

G

niech

T

yzacja

triangular

N

i

T

T

Niech









Graf ten nazwiemy grafem dualnym

.

GRAFY

Gdzie,

i

V

- środek ciężkości i-tego trójkąta

ij

E

-krawędź łacząca i-ty i j-ty trójkąt, które mają wspólny

- bok.

Tw.

}}

{

},

{{

)

(

ij

i

P

E

V

T

G



jest drzewem.

Krawędzie

)

(

P

T

G

przecinają przekątne, wobec usunięcie
takiej krawędzi dzieli graf na pół, to znaczy
jest on drzewem.
c.n.d.

GRAFY

}}.

{

},

{{

)

(

},

},

{

},

{{

)

(

j

i

ij

ij

i

P

V

V

E

f

f

E

V

T

G





Startujemy z dowolnego trójkąta T. Wierzchołki tego trójkąta
oznaczamy kolorem białym, czarnym i szarym. Następnie
znajdujemy trójkąt R mający wspólną przekątną z T.
Dwa wierzchołki R mają już kolory, trzeci oznaczamy „wolnym”
kolorem. Proces ten kontynuujemy. Ponieważ

)

(

P

T

G

jest drzewem to kolejny trójkąt nigdy wcześniej nie był
Koloryzowany, czyli zawsze mamy wolny kolor.
c.n.d.

Program triangularyzacji

P[2][N} – tablica punktów,
POLY[NPOL][INDVER] – tablica podwielokątów,
TRIAN[3][NTRIAN] – tablica trójkątów,
# define MAXPOINTS 1000
# define MAXPOLYGONS 1000
# define MAXTRIANGLES 1000
# define MAXINDVER 1000double P[2][MAXPOINTS];
long POLY[MAXPOLYGONS][MAXINDVER];
longTRIAN[3][MAXTRIANGLES];
void main()
{
long point1,point2,N,firstfree,nod1,nod2,NTRIAN,K,pom,k1,k2;

Program triangularyzacji

c.d.

printf(„\n Number of points \n”);
scanf(„ %ld”,N);
for(i=0;i<=N;i++)
scanf(„%lf%lf”,&P[0][i],&P[1][i]);
/*initialize array POLY*/
NPOL=1;
firstfree=0;
NTRIAN=0;
POLY[NPOL][0]=N;
for(i=0;i<=N;i++) POLY[NPOL][i+1]=i;
/* LOOP OVER ALL SUBPOLYGONS*/
for(i=0;i<=NPOL;i++)
if(POLY[i][0]==2)

Program triangularyzacji

c.d.

{for(j=0;j<=2;j++) TRIAN[j][NTRIAN]=POLY[i][j];
NTRIAN=NTRIAN++;
firstfree=i;
NPOL=NPOL-1;}
else
{/*split polygon into two*/
finddiag(i,nod1,nod2);
if(nod1>nod2) {pom=nod1;nod1=nod2;nod2=pom};
/*find k1,k2 such that POLY[i][k1]=nod1, POLY[i][k2]=nod2 */
for(j=1;POLY[i][j]==nod1;j++) k1=j;
for(j=1;POLY[i][j]==nod2;j++) k2=j;
for(j=1;j<=k1;j++) POLY[firstfree][j]=POLY[i][j];
For(j=k2;j<=POLY[i][0];j++)
POLY[firstfree][j-k2+k1+1]POLY[i][j];
POLY[firstfree][0]=POLY[i][0]-k2+k1+1;

Program triangularyzacji

c.d.

firstfree=NPOL+1;
NPOL=NPOL+1;
/*second subpolygon */
For(j=k1;j<=k2;j++) POLY[i][j-k1+1]=POLY[i][j];
POLY[i][0]=k2-k1+1;
firstfree=i;
}
/* printing of triangulation */
printf(„NUMBER of triangles = %ld\n”,NTRIAN);
printf(„Numbers of nodes of triangles\n”);
For(i=0;i<=NTRIAN;i++)
printf(„\n %ld %ld”,NTRIAN[0][i], NTRIAN[1][i], NTRIAN[2][i]);
}

Triangulacja wielokąta

1. Znajdź przekątną
2. Podziel przekątną
3. W sposób rekursywny znajdź przekątne podwielokątów.

.

2

1

P

P

P





Poszukiwanie przekątnej
Znajdujemy najbardziej oddalony na lewo punkt v z P,
łączymy punkty u, w sąsiadujące z v,
jeśli [u, w] zawiera się w P się mamy przekątną,
w przeciwnym razie znajdujemy
najbardziej oddalony na lewo punkt q z uvw.

[v,q] jest przekątną P.

finddiag(i,nod1,nod2)

long i,nod1,nod2;
{double amx,
Long np,j,left,ind1,ind2,j1;
/* find the most left point*/
amx=P[0][POLY[i][1]];
np=POLY[i][0];
for(j=1;j<=np.;j++)
if(P[0][POLY[i][j]<amx)
{amx=P[0][POLY[i][j]];
left=j;
/* find neighboring point to most left */

If(left>0 && left < np )
{ind1=left-1;
ind2=left+1;
}
else
if(left==0}
{ind2=1; ind1=np-1}
else
ind1=np-1; ind2=0}
/*check intersections with boundary segments */
ind=0;
for(j=0;j<=np; && ind==0;j++)
{
j1=j%np+1;
ind=inters(P[0][POLY[i][j]],P[1][POLY[i][j]],
P[0][POLY[i][j1]],P[1][POLY[i][j1]]);
}

if(ind==0)
{nod1=POLY[i][ind1];
nod2=POLY[i][ind2];
return 0;
}
/* find the most distant point from the segment nod1, nod2
in the triangle left,nod1,nod2 */
amx=0.;
for(j=1;j<=np;j++)
{if(intriangle(P[0][POLY[i][j]],P[1][POLY[i][j]],
P[0][left],P[1][left], P[0][nod1],P[1][nod1], P[0][nod2],P[1][nod2])
{zp=distPSEG(P[0][POLY[i][j]],P[1][POLY[i][j]],
P[0][nod1],P[1][nod1], P[0][nod2],P[1][nod2]);
If(zp>amx) {amx=zp;j1=j}}
nod1=POLY[i][left];
nod2=POLY[i][j1];
return 1}