„Temu, kto nie zna

matematyki, trudno

spostrzec głębokie piękno

przyrody.”

Richard Feynman

TRÓJKĄTY PROSTOKĄTNE W

UKŁADZIE WSPÓŁRZĘDNYCH

Prostokątny (kartezjański) układ
współrzędnych jest najpopularniejszym
narzędziem służącym do określania położenia
punktu na płaszczyźnie, czy też w przestrzeni.
Dzięki własnością trójkątów prostokątnych w
łatwy sposób możemy obliczyć długość
odcinka narysowanego w układzie
współrzędnych w oparciu o współrzędne jego
końców.

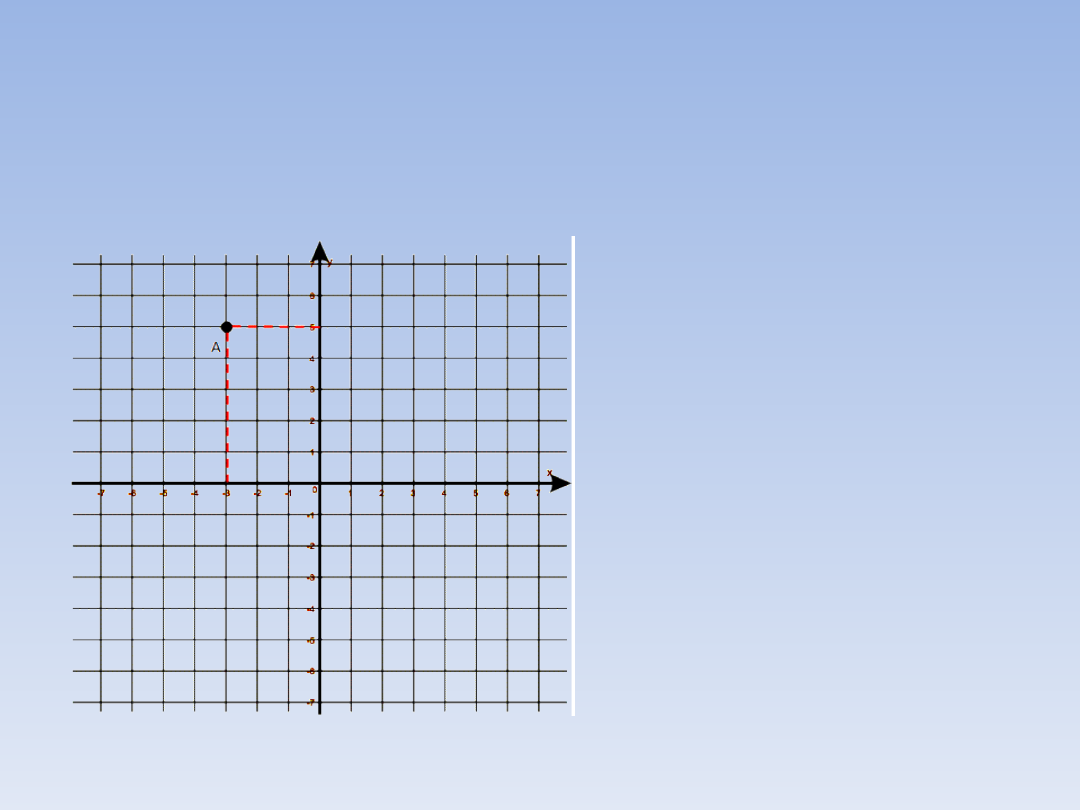
UKŁAD WSPÓŁRZĘDNYCH.

Przypomnijmy sobie jak odczytujemy dane z
układu współrzędnych:

 

Punkt A ma
współrzędne (-3; 5).
W skrócie
zapisujemy to tak:
A = (-3; 5) .
W nawiasie
podajemy
współrzędne
zawszę w tej samej
kolejności: najpierw
oś X, potem oś Y.

Punkt = (x; y)

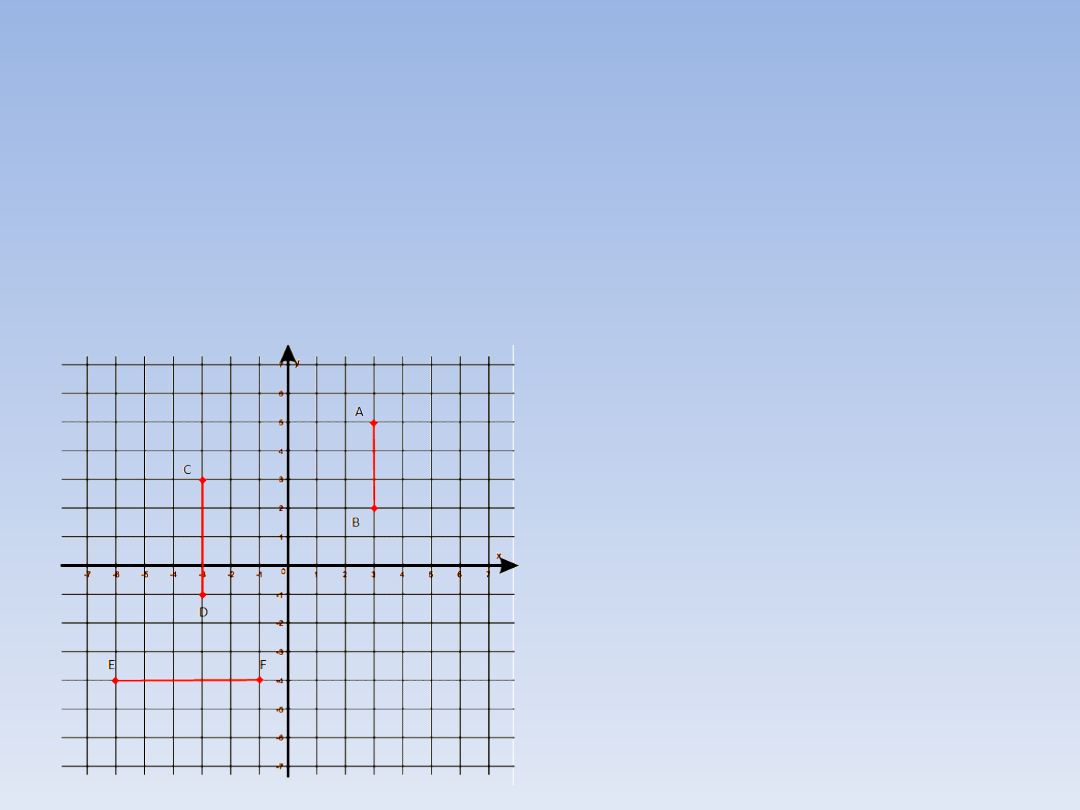
DŁUGOŚĆ ODCINKA W

UKŁADZIE WSPÓŁRZĘDNYCH.

Łatwo jest podać długość odcinka
równoległego do którejś z osi układu –
wystarczy policzyć ile kratek zajmuje (przez
ile podziałek przechodzi)

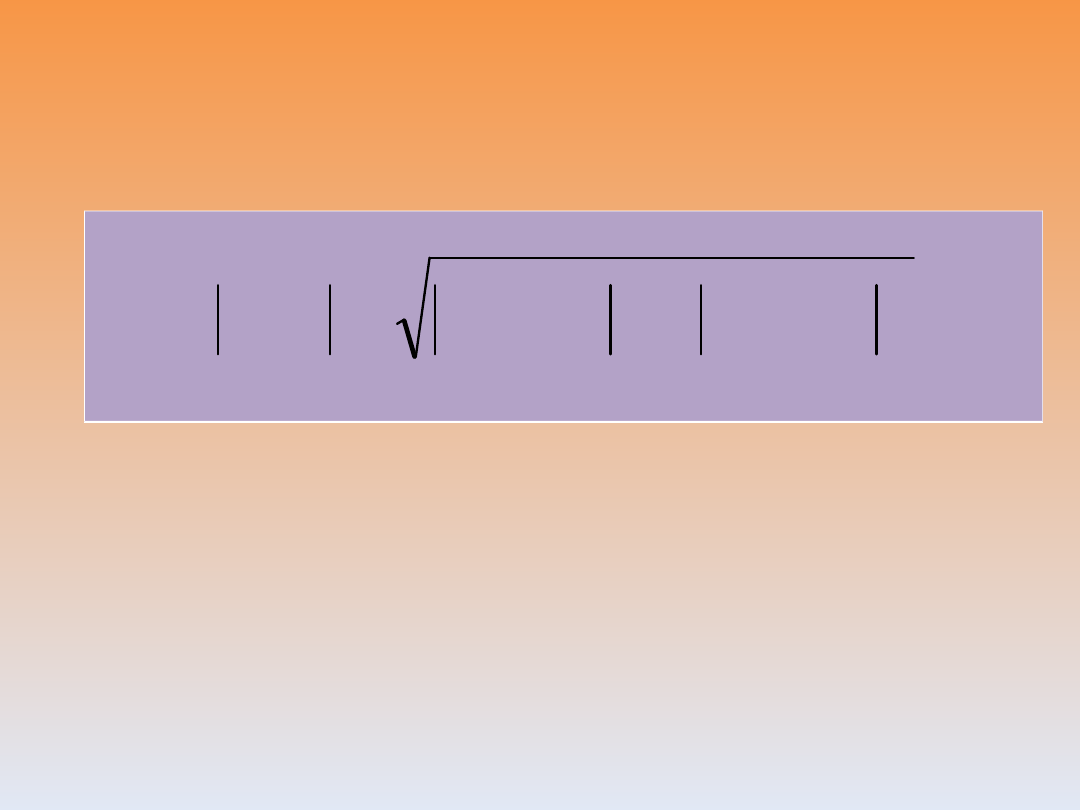
Długość odcinka
oznaczamy pionowymi
kreskami:
|AB| = 3
|CD| = 4
|EF| = 5

DŁUGOŚĆ ODCINKA W

UKŁADZIE WSPÓŁRZĘDNYCH.

Możemy także obliczyć długość na
podstawie współrzędnych końców.
A = (

3

; 5) , B = (

3

; 2)

|AB| = |5 – 2| = 3

UWAGA

Te same współrzędne osi X świadczą o tym,

że odcinek jest równoległy do osi Y. Te same

współrzędne osi Y świadczą o tym, że

odcinek jest równoległy do osi X.

DŁUGOŚĆ ODCINKA W

UKŁADZIE WSPÓŁRZĘDNYCH.

C = (

-3

; 3) , D = (

-3

; -1)

|CD| = |3 – (-1)| = |3 + 1|= 4

E = (-6;

-4

) , F = (-1;

-4

)

|EF| = |-6 – (-1)| = |-6 + 1| = |-5| = 5

W obliczeniach symbol |…| oznacza wartość
bezwzględną. Długość nie może być ujemna.

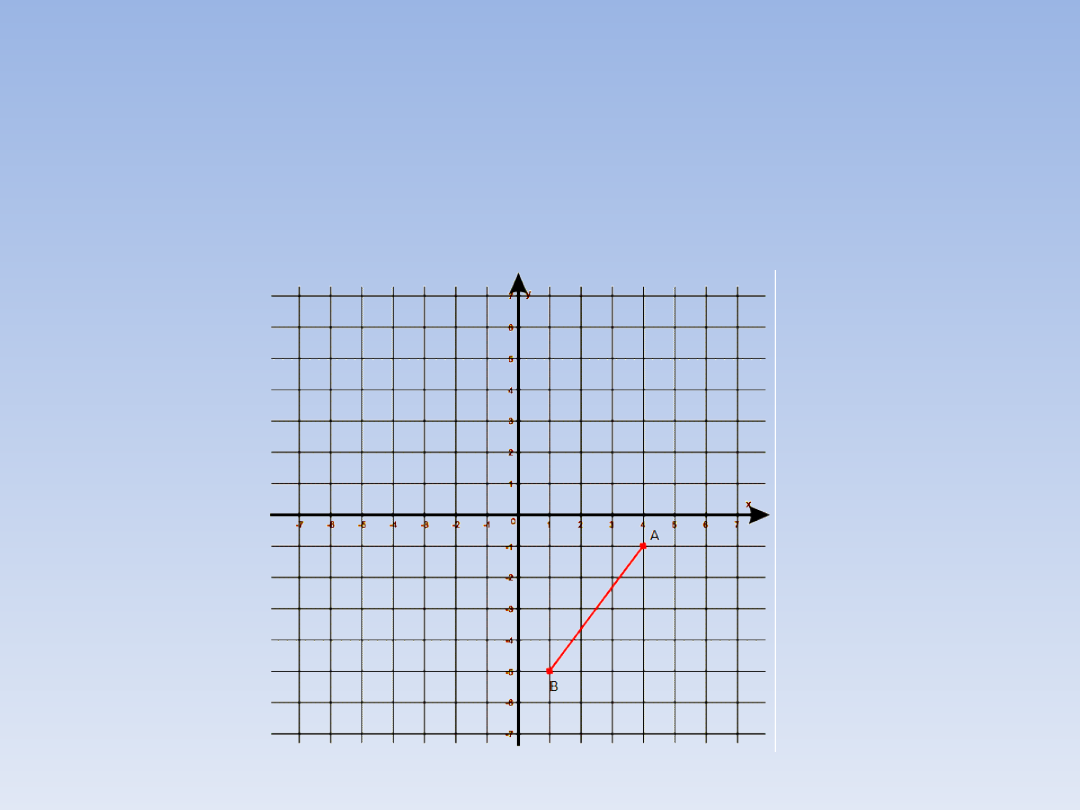
DŁUGOŚĆ ODCINKA W

UKŁADZIE

WSPÓŁRZĘDNYCH.

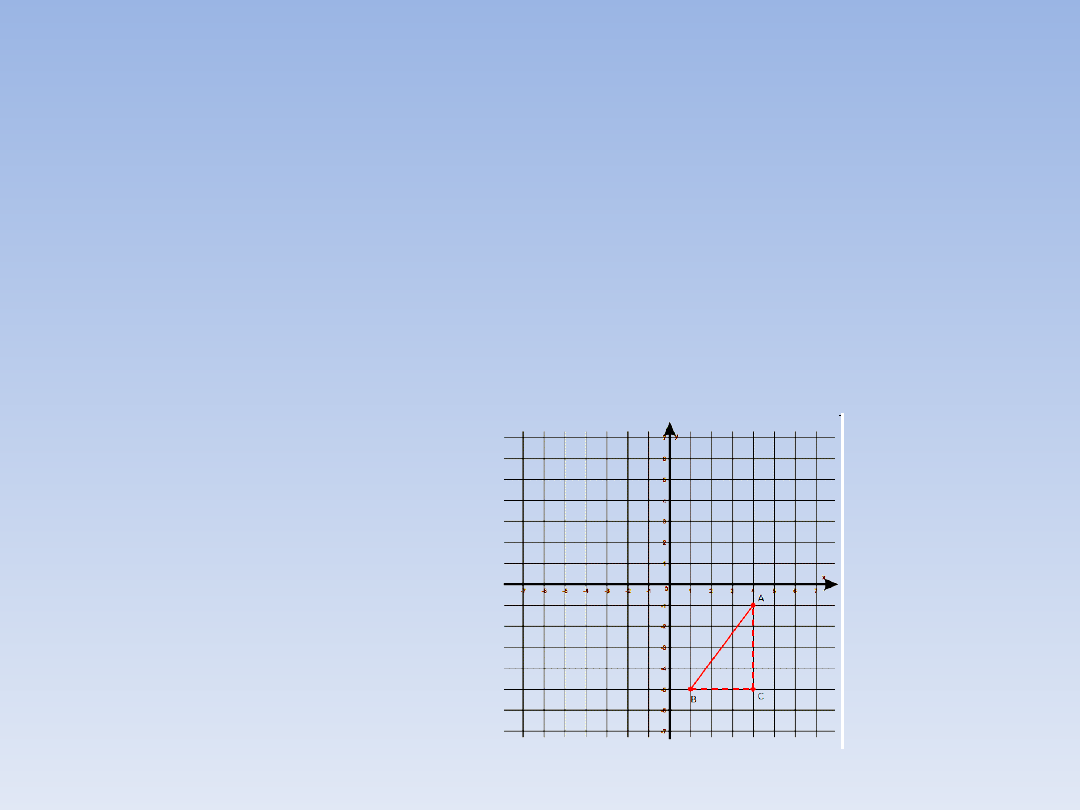
A jak obliczyć długość tego odcinka?

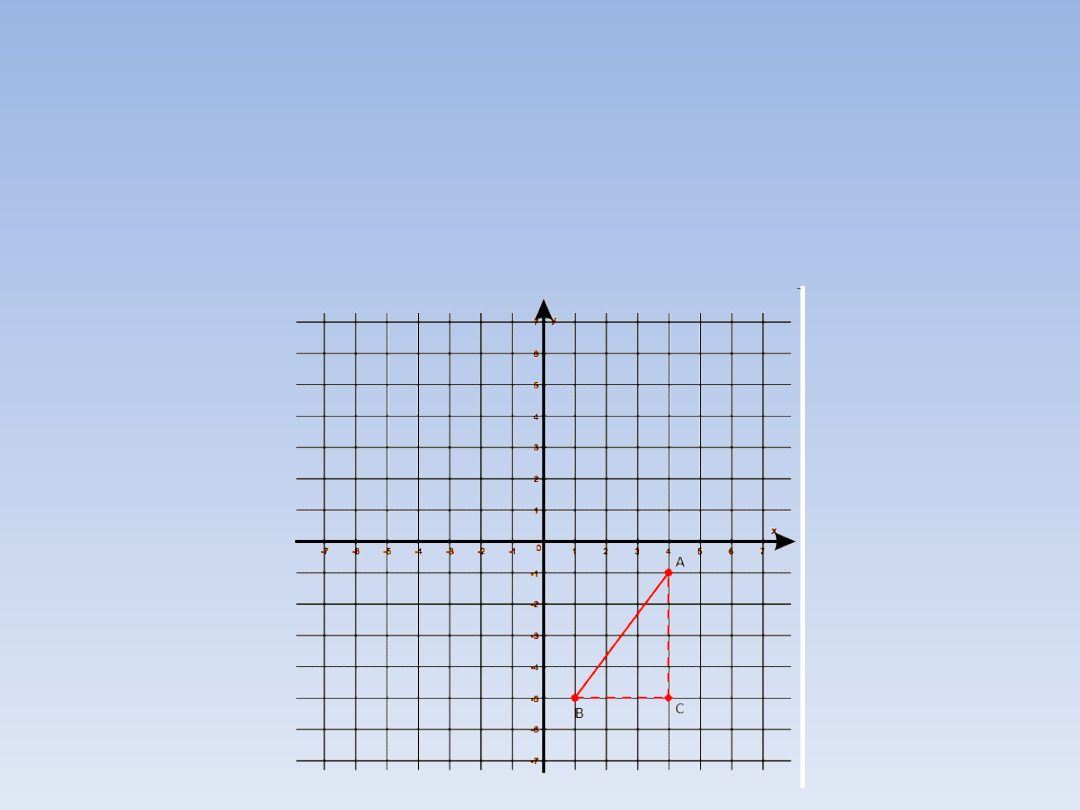
DŁUGOŚĆ ODCINKA W

UKŁADZIE

WSPÓŁRZĘDNYCH.

Wystarczy umiejętnie skorzystać z
twierdzenia Pitagorasa. A gdzie tu trójkąt
prostokątny? A tutaj: 

DŁUGOŚĆ ODCINKA W

UKŁADZIE

WSPÓŁRZĘDNYCH.

Oznaczmy sobie:
x = |BC| = 3

– odcinek równoległy do osi X

y = |AC| = 4

- odcinek równoległy do osi Y

Zgodnie z twierdzeniem Pitagorasa mamy więc:
|AB|

2

= x

2

+ y

2

|AB|

2

= 3

2

+ 4

2

|AB|

2

= 9 + 16

|AB|

2

= 25

|AB| = 5

DŁUGOŚĆ ODCINKA W

UKŁADZIE

WSPÓŁRZĘDNYCH.

Pytanie: jak sobie poradzić gdy nie mamy
rysunku? Spójrzmy inaczej na bieżący przykład.
Współrzędne punktów A i B to: A = (

4

;

-1

) , B =

(

1

,

-5

). Aby obliczyć długość odcinka

oznaczonego przez nas przez x, wystarczy
odjąć od siebie współrzędne „iksowe” i
wyciągnąć z nich wartość bezwzględną:

x

= |

4

–

1

| = 3

Analogicznie możemy obliczyć y, z tym, że
odejmujemy współrzędne „igrekowe”:

y

= |

-1

– (

-5

)| = |-1 + 5| = 4

Dalsze obliczenia są takie same jak wcześniej.

PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Oblicz długość odcinka którego końcami są

punkty:
A = (2; -3) , B = (-1; -7).

Postępujemy zgodnie ze wskazówkami z

poprzedniej planszy.
x = |2 – (-1)| = |2 + 1| = 3

y = |-3 – (-7)| = |-3 + 7| = 4

|AB|

2

= 3

2

+ 4

2

|AB|

2

= 9 + 16 = 25

|AB| = 5

PRZYKŁADOWE

ZADANIA.

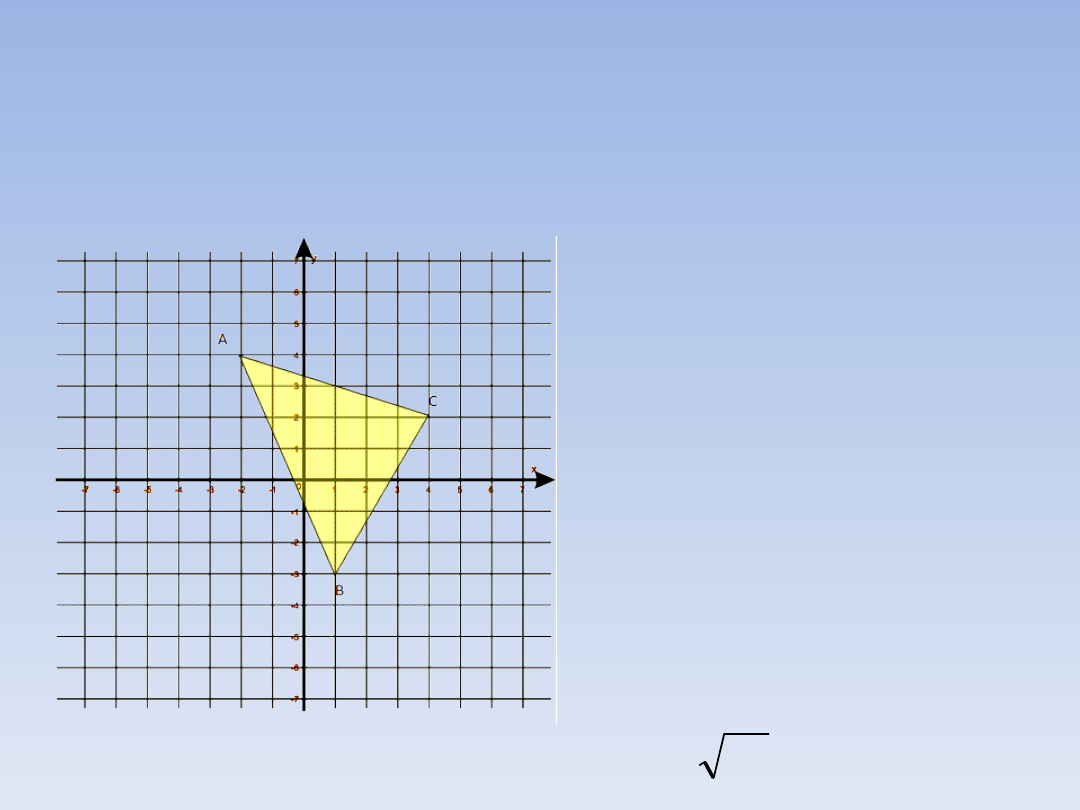
ZADANIE 1.
Oblicz długości boków narysowanego trójkąta.

Wypiszmy najpierw
współrzędne
punktów:
A = (-2; 4) , B = (1;
-3) ,
C = (4; 2).
Dla boku AB mamy:
x = |-2 – 1| = |-3| = 3
y = |4 – (-3)| = |4 +
3| = 7
|AB|

2

= 3

2

+ 7

2

|AB|

2

= 9 + 49 = 58

|AB| =

58

PRZYKŁADOWE ZADANIA.

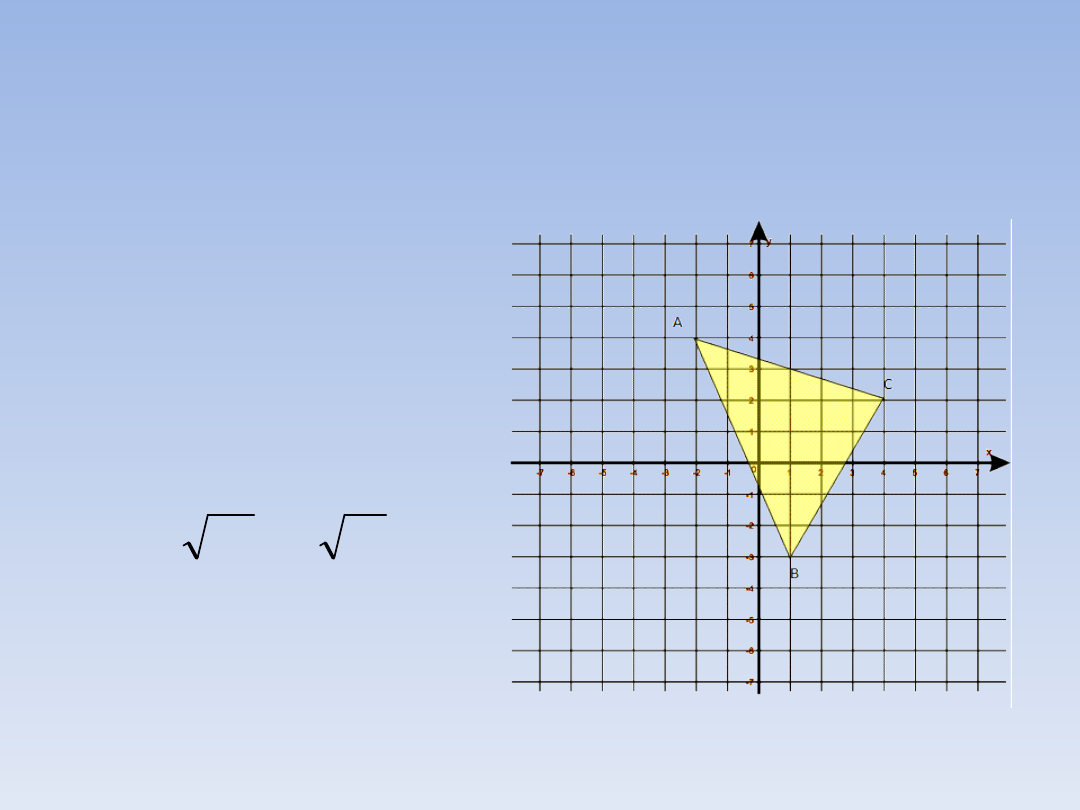
ZADANIE 1 – ciąg dalszy.
Dla boku AC mamy:
x = |-2 – 4| = |-6| = 6
y = |4 – 2| = 2
|AC|

2

= 6

2

+ 2

2

|AC|

2

= 36 + 4 = 40

|AC| = = 2

40

10

PRZYKŁADOWE ZADANIA.

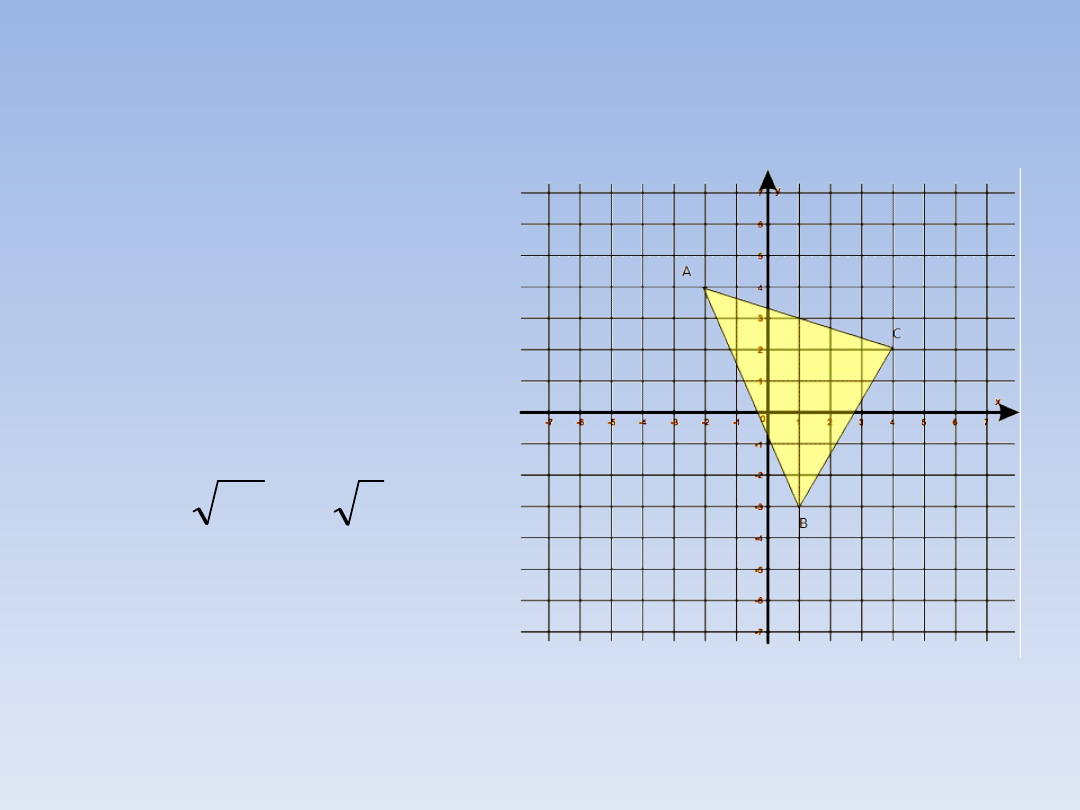
ZADANIE 1. – ciąg dalszy
Dla boku BC mamy:
x = |1 – 4| = |-3| = 3
y = |-3 – 2| = |-5| = 5
|BC|

2

= 3

2

+ 5

2

|BC|

2

= 9 + 25 = 24

|BC| = 6

2

24

PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Oblicz odległość punktu A = (12; -5) od

początku układu współrzędnych.

Początek układu współrzędnych to punkt O =

(0; 0) mamy więc dla odcinka AO:

x = |12 – 0| = 12

y = |-5 – 0| = |-5| = 5

– do obliczeń wystarczy więc

wziąć wartość

bezwzględną ze współrzędnych

|AO|

2

= 12

2

+ 5

2

|AO|

2

= 144 + 25 = 169

|AO| = 13

PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Czy punkt A = (-6; 8) leży na okręgu o
promieniu 10 i początku w układzie
współrzędnych?
Aby punkt leżał na takim okręgu jego odległość
od początku układu współrzędnych musi
wynosić 10. Sprawdźmy dla punktu A:
x = |-6| = 6
y = |8| = 8
|AO|

2

= 6

2

+ 8

2

|AO|

2

= 36 + 64 = 100

|AO| = 10
A więc ten punkt leży na danym okręgu.

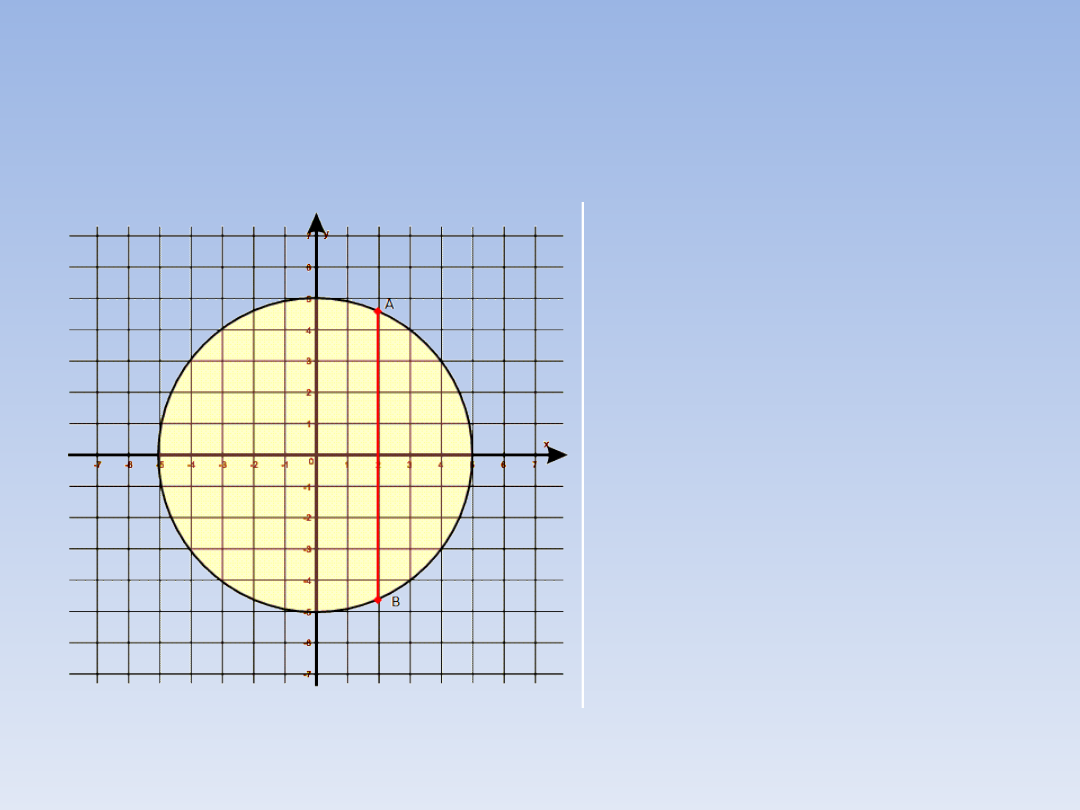
PRZYKŁADOWE ZADANIA.

ZADANIE 4.
Znajdź współrzędne punktów z rysunku.

Z rysunku można
odczytać
współrzędne x oraz
promień koła. Mamy:
r = 5
A = (2; …) , B = (2;
…)
Współrzędną y
znajdziemy
korzystając z tego,
że:
|AO| = r = 5
|BO| = r = 5

PRZYKŁADOWE ZADANIA.

ZADANIE 4 – ciąg dalszy.
Mamy więc:
5

2

= 2

2

+ y

2

25 = 4 + y

2

25 – 4 = y

2

y

2

= 21

W takim razie y = dla punktu A i y = -

dla punktu B. Zatem:

A = (2; )
B = (2; - )

21

21

21

21

WZÓR

Jeśli ktoś woli mieć gotowy przepis na
obliczanie długości odcinków w układzie
współrzędnych w oparciu o podane już
informacje może wyprowadzić wzór.
Oznaczmy współrzędne dwóch punktów:
P

1

= (x

1

; y

1

) , P

2

= (x

2

; y

2

)

Wtedy długości odcinków oznaczonych przez
nas przez x i y obliczymy tak:
x = |x

1

- x

2

|

y = |y

1

- y

2

|

A więc :
|P

1

P

2

|

2

= x

2

+ y

2

= |x

1

- x

2

|

2

+ |y

1

- y

2

|

2

WZÓR

P

1

= (x

1

; y

1

) , P

2

= (x

2

; y

2

)

Wzór ten można nieco udoskonalić. Wiesz

jak?

2

2

1

2

2

1

2

1

y

y

x

x

P

P







