WYKŁAD 8. Siła spójności

• Wierzchołek v nazywamy

wierzchołkiem

cięcia

grafu G, gdy podgraf G-v ma więcej

składowych spójności niż G.

• Krawędź e nazywamy

krawędzią cięcia

grafu G, gdy podgraf G-e ma więcej
składowych spójności niż G.

Cięcia

• Mówimy, że zbiór X

wierzchołków

(

krawędzi

) grafu G jest cięciem

wierzchołkowym

(

krawędziowym

)

grafu G, gdy podgraf G-X jest
niespójny.

• Jeśli wierzchołki u i v należą do

różnych składowych spójności

podgrafu G-X, to mówimy, że

cięcie X

rozspójnia u i v w G

.

Wierzchołki i krawędzie

cięcia

• Jeśli X={v} rozspójnia dwa wierzchołki

tej samej składowej grafu G, to v jest

wierzchołkiem cięcia

.

• Krawędź, która rozspójnia swoje końce,

to

krawędź cięcia

.

• Wierzchołek

(

krawędź

) cięcia stanowi

1-elementowe cięcie

wierzchołkowe

(

krawędziowe

), ale odwrotnie być nie

musi (

podać kontrprzykład

).

k-Spójność

• Dla k



0, graf G jest

k-spójny

, gdy |

V(G)|>k i G nie ma cięcia
wierzchołkowego mocy mniejszej niż
k.

• Każdy graf jest 0-spójny.

• Każdy spójny graf oprócz K_1 jest 1-

spójny.

• Spójny graf G jest

2-spójny

, gdy |

V(G)|>2 i G nie ma wierzchołka
cięcia.

Charakteryzacja grafów 2-

spójnych

Tw

. Graf G jest 2-spójny

wgdy

można go

otrzymać z cyklu przez sukcesywne

dodawanie ścieżek zaczepionych

obydwoma końcami w

dotychczasowym grafie,

tzn.

istnieje ciąg grafów H_1,...,H_l, gdzie

H_1 jest cyklem, H_l=G i dla każdego

i=2,...,l graf H_i jest sumą H_{i-1} i

ścieżki P_i o końcach u_i i v_i takiej, że

}

,

{

)

(

)

(

1

i

i

i

i

v

u

H

V

P

V







Dowód na ćw.

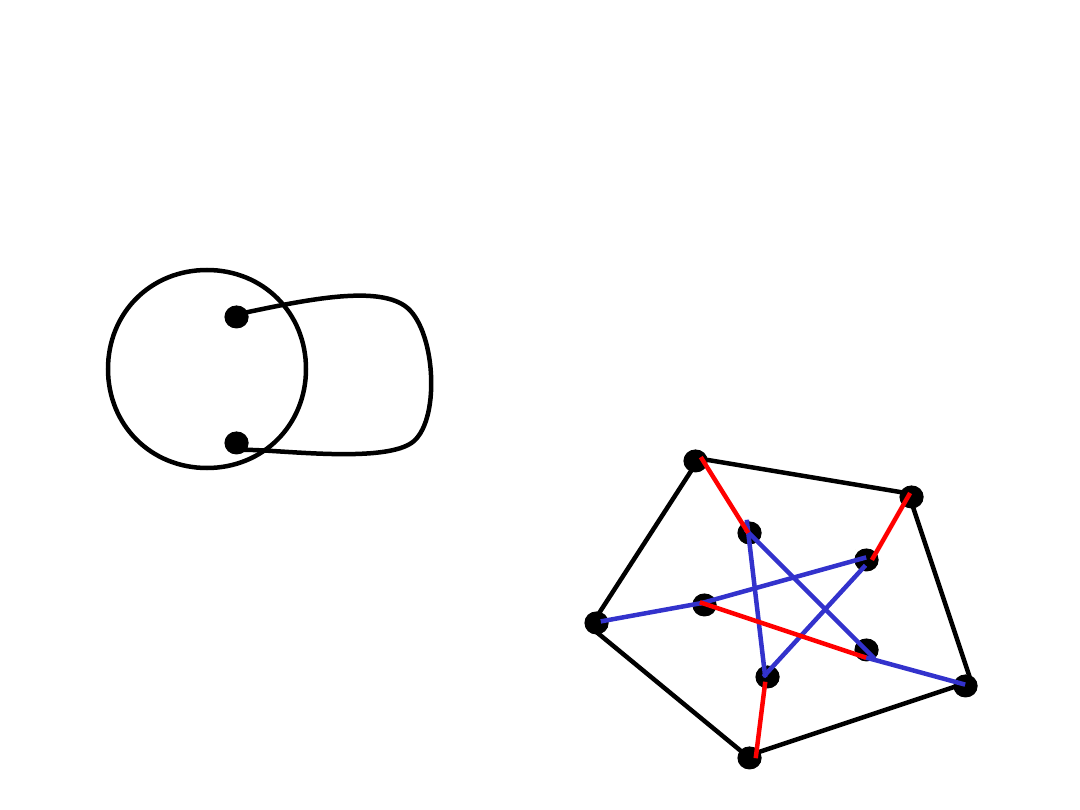
Ilustracja

H_{i-1}

P_i

Stopień spójności

• Dla k



0, graf G jest

k-spójny

, gdy |V(G)|

>k i G nie ma cięcia

wierzchołkowego mocy mniejszej niż k.

• Stopień spójności κ(G)

to

największa

liczba całkowita k taka, że G jest k-spójny.

• Np. κ(G)=0 gdy G jest niespójny;

κ(K_n)=n-1 dla n=1,2,…

• Jeśli G nie jest grafem pełnym, to

κ(G)

jest mocą

najmniejszego

cięcia

wierzchołkowego w G.

Krawędziowa k-spójność

• Graf G jest

k-krawędziowo-spójny

,

gdy |V(G)|>1 i G nie ma cięcia

krawędziowego mocy mniejszej niż k.

• Stopień spójności krawędziowej κ’(G)

to największa liczba całkowita k taka,

że G jest k- krawędziowo-spójny.

• Równoważnie,

κ’(G)

to moc

najmniejszego cięcia krawędziowego

w G.

Krawędziowa k-spójność a

RRD

• Jeśli G ma k RRD

(rozłącznych,

rozpiętych drzew),

to G jest k-

krawędziowo-spójny

(oczywiste).

• Jeśli G jest 2k-krawędziowo-spójny, to

G ma k RRD

(dowód na ćwiczeniach)

κ(G), κ’(G), δ(G)

Twierdzenie (Whitney, 1932)

)

(

'

G

(G)

κ

κ(G)







Dowód:

Prawa nierówność:

Krawędzie incydentne z dowolnym

wierzchołkiem stanowią cięcie

krawędziowe.

Lewa nierówność

:

Jeśli G=K_n, to κ(G)=κ’(G)=n-1.

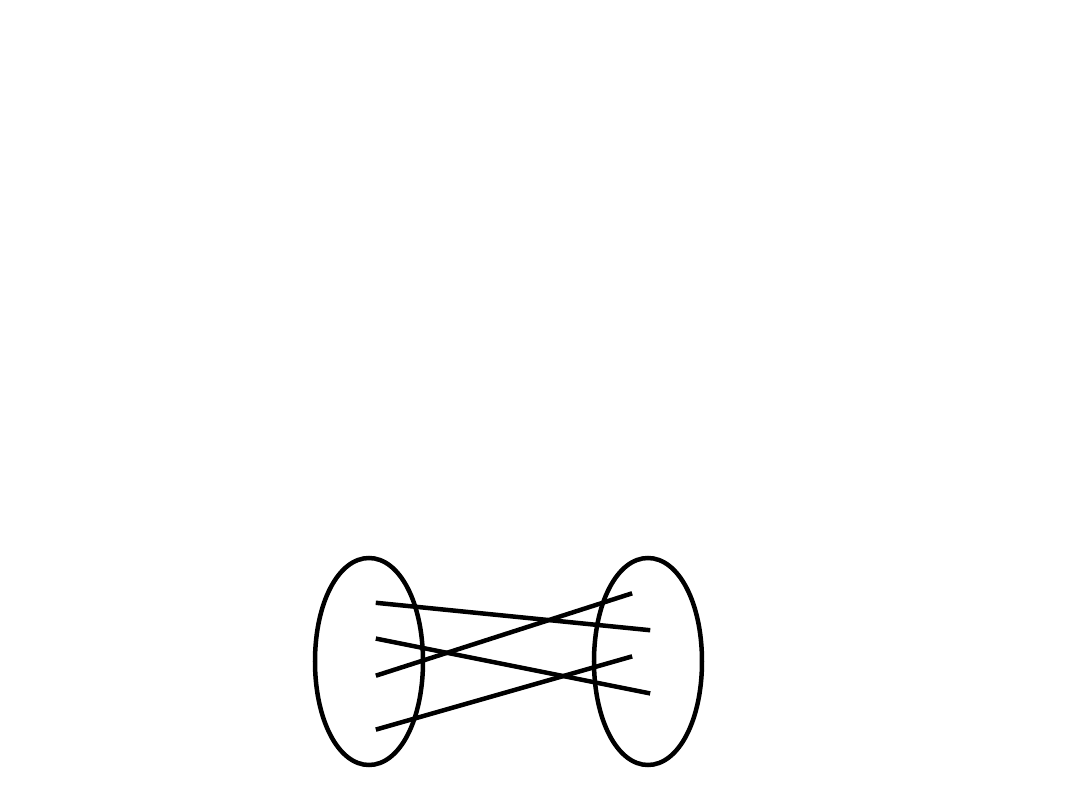
Lewa nierówność – c.d.

• W grafie G nie będącym grafem pełnym niech

X będzie najmniejszym cięciem krawędziowym.

• X można traktować jako zbiór krawędzi

dwudzielnego podgrafu grafu G z 2-podziałem

V_1, V_2=V(G)-V_1.

• Każda krawędź grafu G pomiędzy V_1 i V_2

należy do X.

V_1

V_2

X

Lewa nierówność –

dokończenie

• Ponieważ

G

nie jest pełny a

|X| =

κ’(G)



δ(G)

, to istnieją

u

w

V_1

i

v

w

V_2

takie, że

uv

nie jest krawędzią w

G

.

(ćw.)

• Biorąc po 1 końcu każdej krawędzi

zbioru X, ale tak by ominąć u i v,
otrzymujemy cięcie wierzchołkowe
(rozspójniające u i v) mocy nie większej
niż |X|.

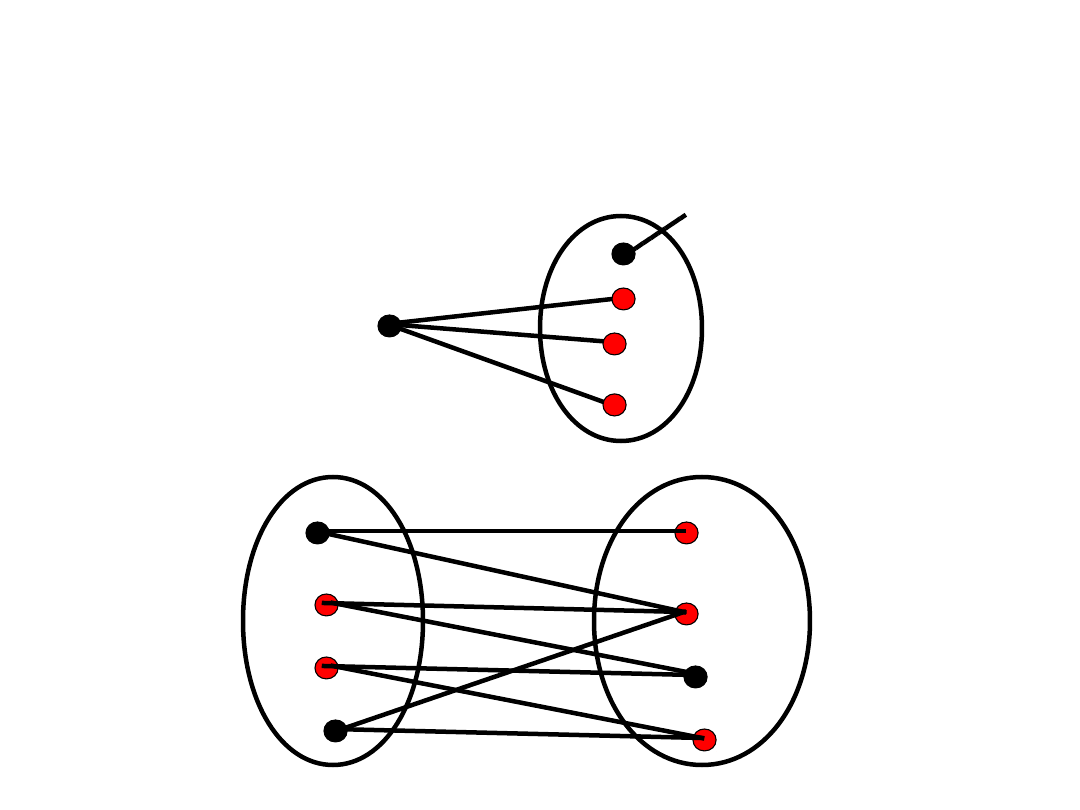
Ilustracja

v

u

d(u)=δ

V_1

V_2

X

Niezależne ścieżki

• Dwie u-v ścieżki (czyli ścieżki z u do

v) nazywamy

niezależnymi

, gdy ich

jedynymi wspólnymi wierzchołkami
są ich końce u i v.

• Jeśli istnieje k parami niezależnych

u-v ścieżek, to każde cięcie
wierzchołkowe rozspójniające u i v
musi mieć moc co najmniej k.

Tw. Mengera dla pary

wierzchołków

Tw.1 (Menger, 1927).

Niech a i b będą

wierzchołkami grafu G.

(i) Jeśli a i b

nie są połączone krawędzią

,

to moc

najmniejszego

cięcia

wierzchołkowego, rozspójniającego a

i b, jest równa mocy

największego

zbioru niezależnych a-b ścieżek.

(ii) Moc

najmniejszego

cięcia

krawędziowego rozspójniającego a i b

jest równa mocy

największego

zbioru

krawędziowo rozłącznych a-b ścieżek.

Globalne Tw. Mengera

Tw 2. (Menger, 1927)

(i) Graf jest k-spójny

(tzn.|V(G)|>k i G nie ma

cięcia wierzchołkowego mocy mniejszej niż k)

wgdy zawiera co najmniej k parami

niezależnych

ścieżek pomiędzy każdą parą

wierzchołków.

(ii) Graf jest k-krawędziowo-spójny

(tzn. |V(G)|

>1 i G nie ma cięcia krawędziowego mocy

mniejszej niż k)

wgdy zawiera co najmniej k

parami

krawędziowo rozłącznych

ścieżek

pomiędzy każdą parą wierzchołków.

Dowód Tw. 2(i)



Jeśli G ma k niezależnych ścieżek między

każdą parą wierzchołków, to |V(G)|>k i G nie

może mieć cięcia wierzchołkowego mocy

mniejszej niż k.

Zatem G jest k-spójny

.

 Przypuśćmy, że k-spójny graf G zawiera

wierzchołki a i b nie połączone k

niezależnymi ścieżkami.

.

Dowód Tw. 2(i)  c.d.

• Z Twierdzenia 1(i), ab jest krawędzią.

• Podgraf G’:=G-ab ma co najwyżej k-2

niezależne a-b ścieżki

.

• Ponownie z

Twierdzenia 1(i),

istnieje

cięcie wierzchołkowe X mocy |X|



k-

2 rozspójniające a i b w G’.

• Ponieważ |V(G)|



k+1, to istnieje w

G wierzchołek v taki, że

}

,

{ b

a

X

v





Dowód Tw. 2(i) 

dokończenie

• X rozspójnia w G’ wierzchołki v i a

lub b (powiedzmy a).

• Wtedy zbiór X powiększony o b

rozspójnia w G v i a, co przeczy k-
spójności G.



Dowód Tw. 2 (ii) – ćwiczenia!

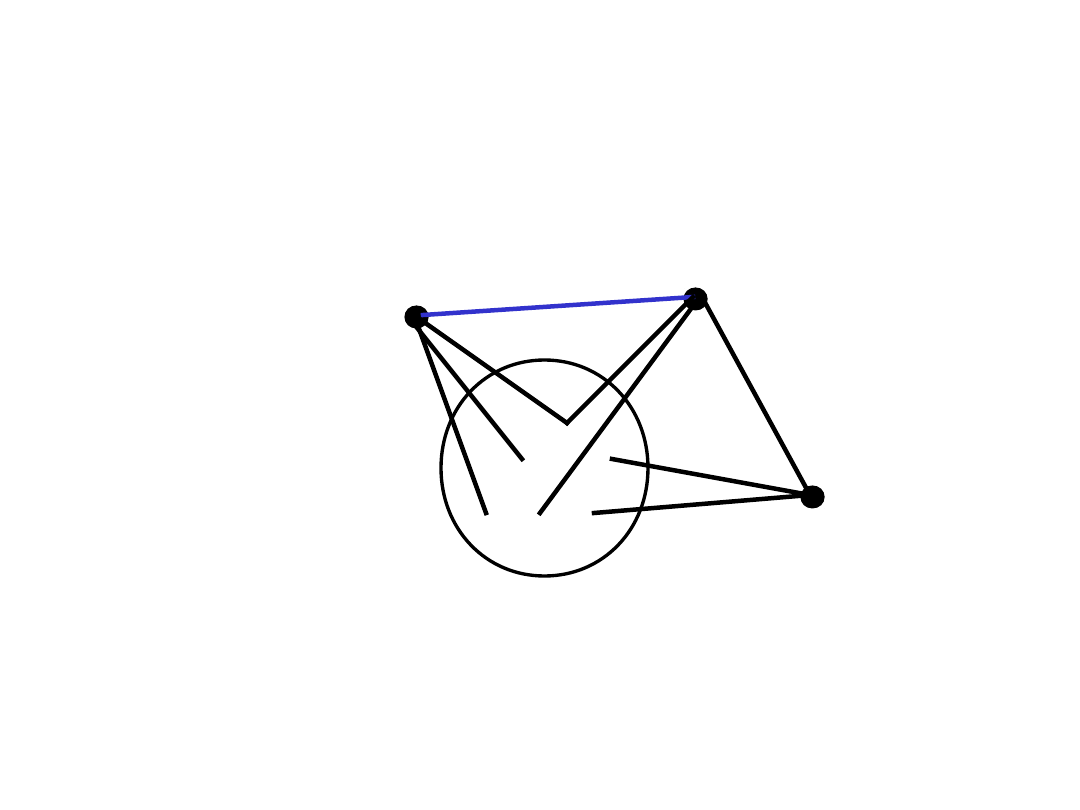
Ilustracja

a

b

X

v

A-B ścieżki

i zbiory

rozdzielające

• A,B – dowolne podzbiory V(G)
• Ścieżkę P w grafie G o końcach a i b

nazywamy

A-B ścieżką

, gdy

}

{

)

(

},

{

)

(

b

B

P

V

a

A

P

V









• Mówimy, że zbiór wierzchołków X
grafu G

rozdziela A i B

, gdy każda A-B

ścieżka zawiera wierzchołek z X.

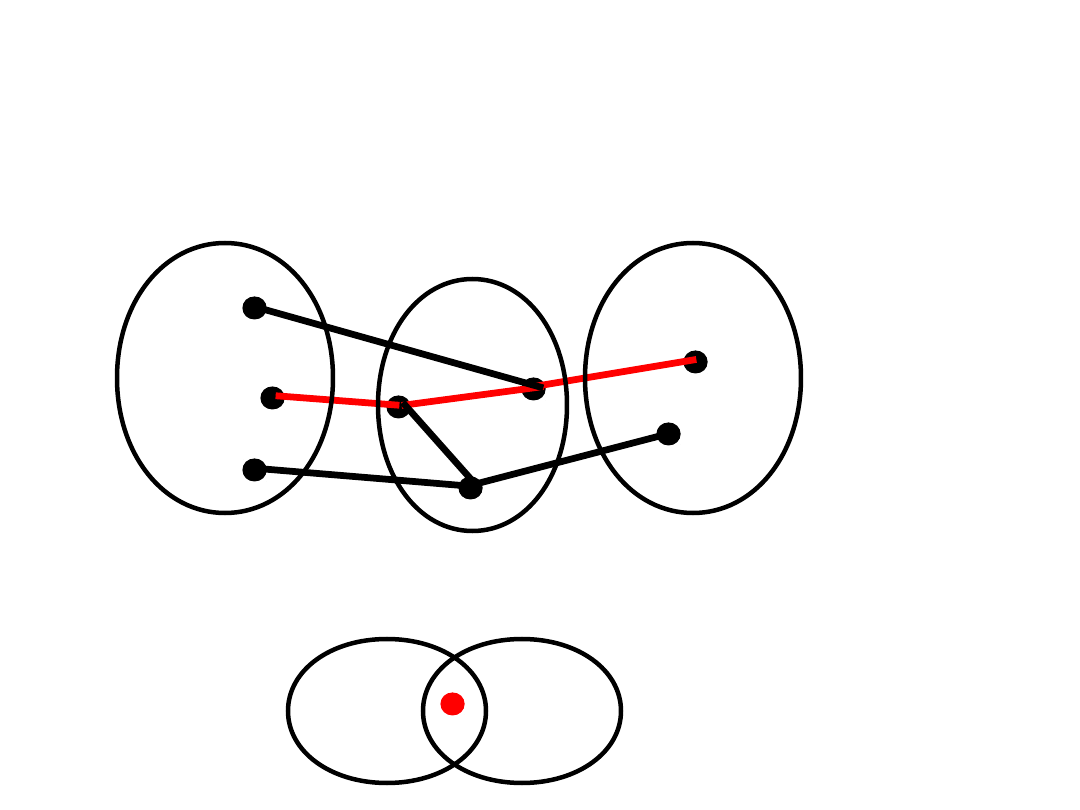
Ilustracja

A

B

X

Tw. Mengera (1927)

Tw 3.

Niech A,B będą dowolnymi

podzbiorami V(G). Wtedy moc

najmniejszego

zbioru

rozdzielającego A i B równa się mocy

największego

zbioru rozłącznych A-B

ścieżek.

Bez dowodu

.

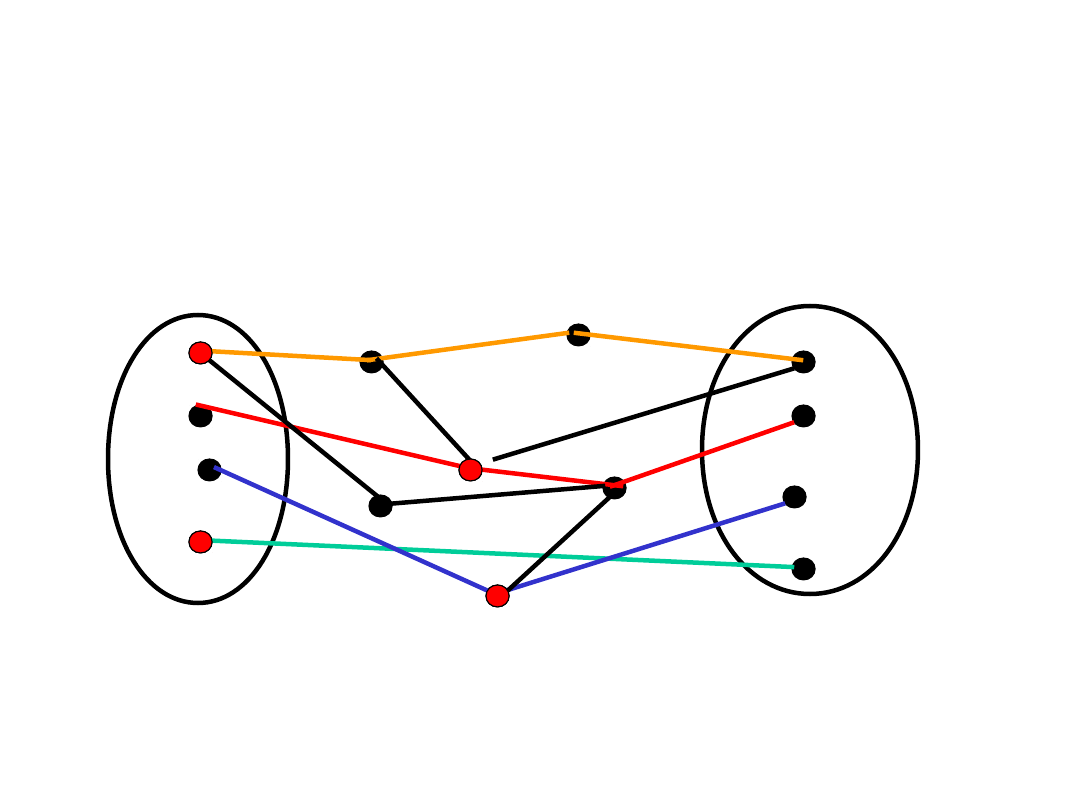
Ilustracja

V_1

V_2

Tw. Mengera dla pary

wierzchołków

Tw.1 (Menger, 1927).

Niech a i b będą

wierzchołkami grafu G.

(i) Jeśli a i b

nie są połączone krawędzią

,

to moc

najmniejszego

cięcia

wierzchołkowego, rozspójniającego a

i b, jest równa mocy

największego

zbioru niezależnych a-b ścieżek.

(ii) Moc

najmniejszego

cięcia

krawędziowego rozspójniającego a i b

jest równa mocy

największego

zbioru

krawędziowo rozłącznych a-b ścieżek.

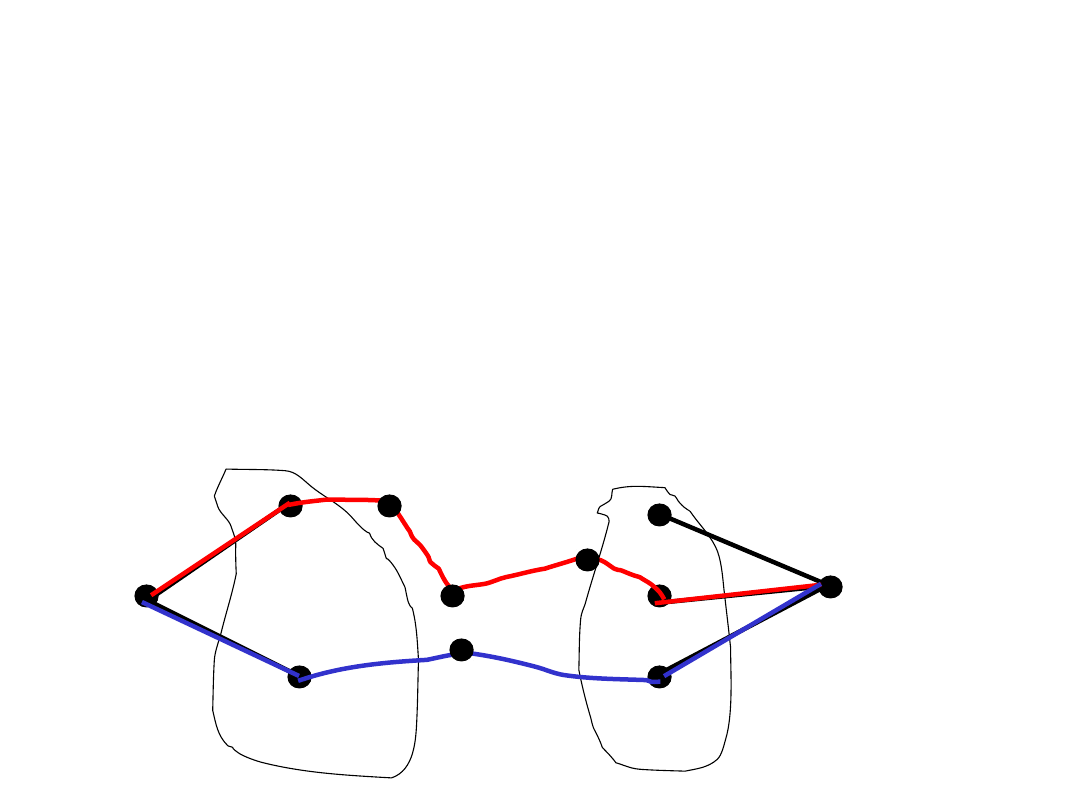
Dowód Tw. 1

(ćw.)

(i) Zastosuj Tw. 3 do A=N(a) i B=N(b) 

(ii)

Zastosuj Tw. 3 do grafu krawędziowego

L(G), A=E(a), B=E(b)



a

b

A

B

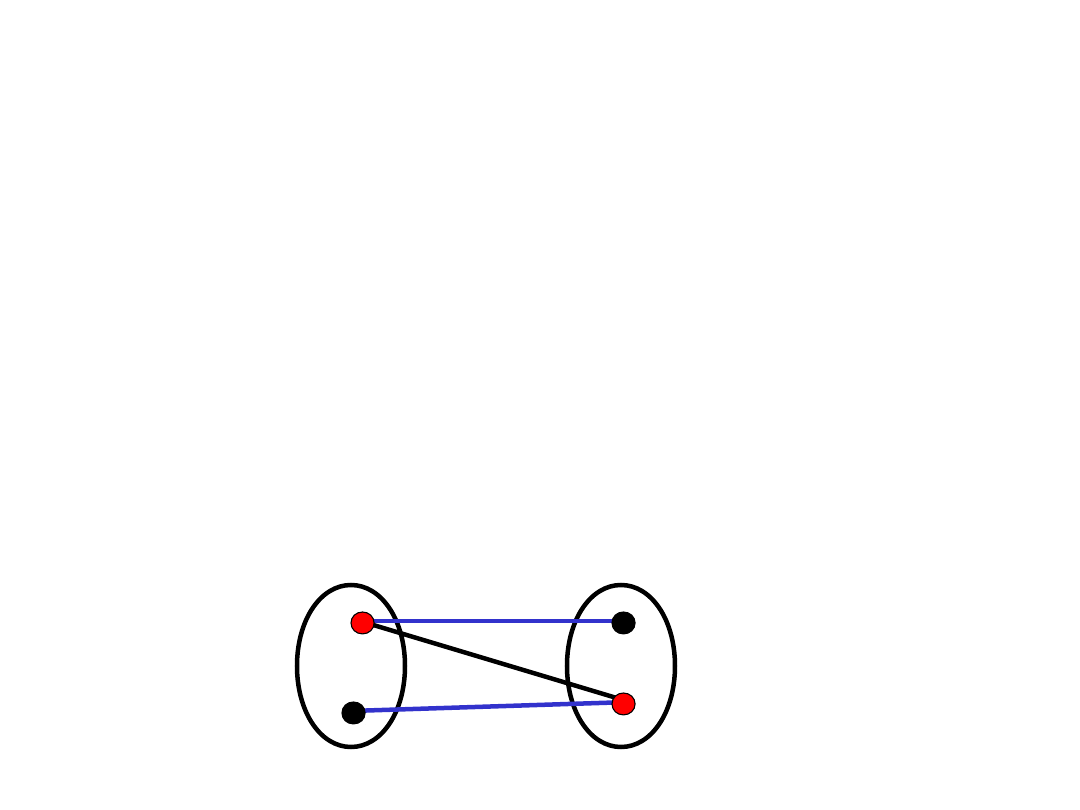
Tw. Königa raz jeszcze

Wniosek 1 : Tw. Königa

Dowód:

Niech G będzie grafem 2-dzielnym

o 2-podziale (A,B). Zbiór rozdzielający to
pokrycie wierzchołkowe. Rozłączne A-B
ścieżki to skojarzenie. 

A

B