Ruch falowy

Ruch falowy



Fale mechaniczne

Fale mechaniczne

•

Rodzaje fal

Rodzaje fal

•

Rozchodzenie się fal

Rozchodzenie się fal

•

Superpozycja fal

Superpozycja fal

•

Interferencja

Interferencja

•

Fale stojące

Fale stojące

•

Rezonans

Rezonans



Fale dźwiękowe

Fale dźwiękowe

•

Charakterystyki dźwięku

Charakterystyki dźwięku

•

Fale podłużne

Fale podłużne

•

Dudnienia

Dudnienia

•

Zjawisko Dopplera

Zjawisko Dopplera

Wykład

Wykład

7

7

Fale mechaniczne

Fale mechaniczne

Wykład

Wykład

7

7

Falami mechanicznymi nazywamy fale powstające w ośrodkach

sprężystych.

Powstają one w wyniku wychylenia się jakiegoś fragmentu ośrodka

sprężystego z położenia równowagi. Dzięki sprężystym właściwościom

ośrodka drgania te przekazywane są do dalszych jego części i fala

przechodzi przez cały ośrodek. Ośrodek jako całość nie przesuwa się

wraz z falą.

Energia fali to kinetyczna i potencjalna

energia cząstek materii.

Ruch falowy jest związany z dwoma

procesami: z transportem energii przez

ośrodek od cząstki do cząstki i z ruchem

drgającym poszczególnych cząstek dokoła

ich położeń równowagi. Ruch falowy nie

jest związany z ruchem materii jako

całości.

Do rozchodzenia się fal mechanicznych

niezbędny jest ośrodek materialny.

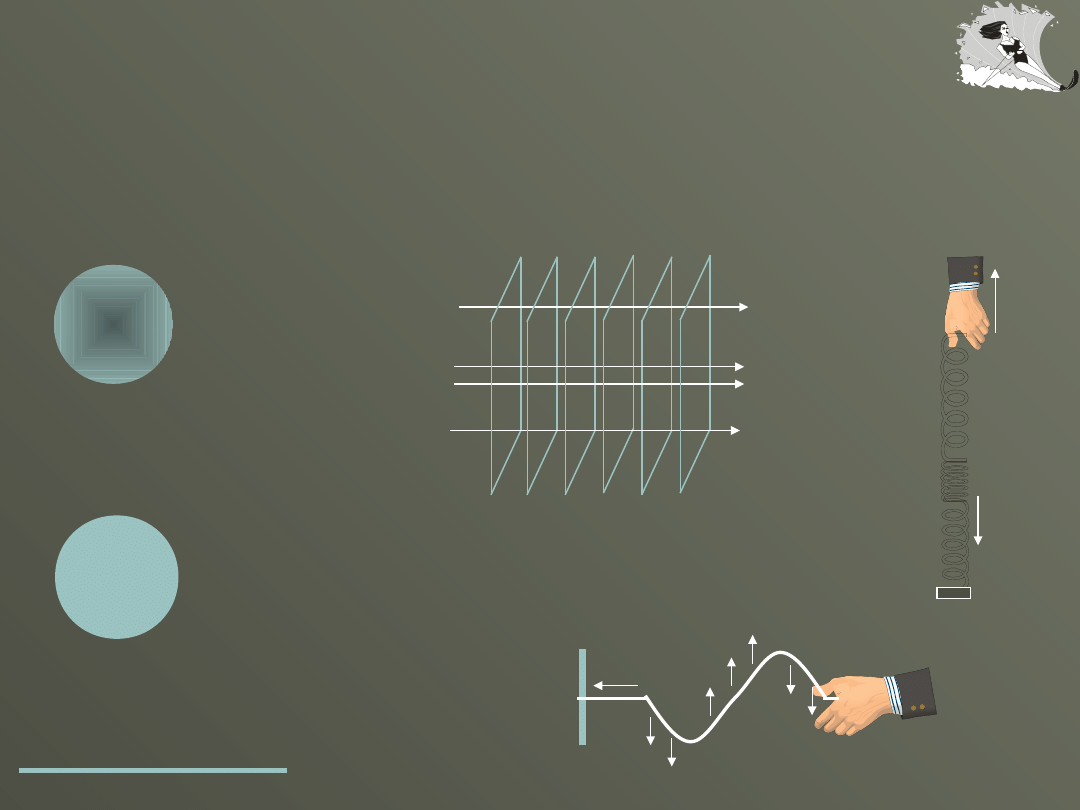
Rodzaje fal

Rodzaje fal

Wykład

Wykład

7

7

Powierzchnia falowa

kulista

Fala trójwymiarowa – powietrze

w otoczeniu drgającej kuli

Fala dwuwymiarowa –

powierzchnia wody w postaci

okręgów

Powierzchnia falowa

kołowa

Fala jednowymiarowa – punkty

materialne cienkiej struny

Powierzchnia falowa

jeden punkt

Fale płaskie

Fale poprzeczne

v

tylko w ciałach stałych

Fale podłużne

v

we wszystkich
ośrodkach
sprężystych

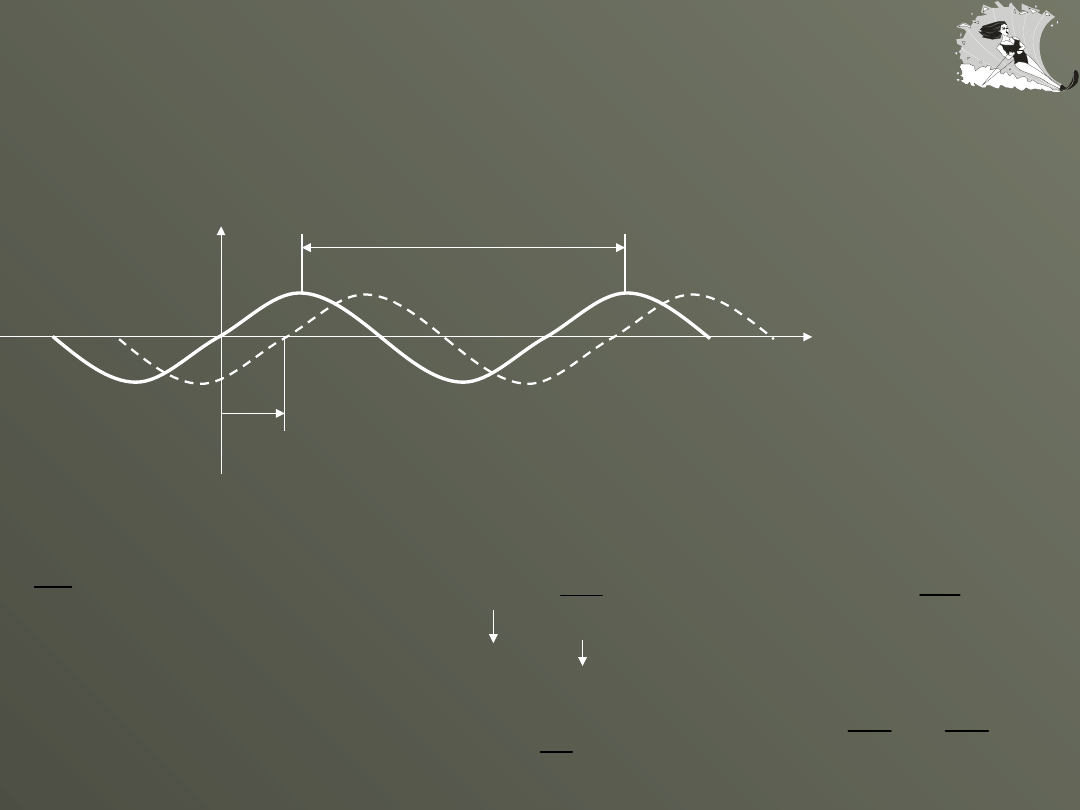
Rozchodzenie się fal

Rozchodzenie się fal

Wykład

Wykład

7

7

x

y

t=0 t=t

vt



Na podstawie równania można zbadać zachowanie się w czasie
określonej wartości zmiennej y np. szczytu fali – matematycznie
oznacza to, że badamy jak zmienia się w czasie x przy zachowaniu
ustalonej wartości dla (x-vt).

.

x vt const

dx

v

dt

- =

=

(

)

y f x vt

=

-

dla fali biegnącej

w prawo

prędkość fazowa fali

2

sin

A

y y

x

p

l

=

długość fali

amplituda fali

po czasie t

(

)

2

sin

A

y y

x vt

p

l

=

-

Okres dla fali jest czasem, w którym

fala przemieszcza się na odległość

równą jednej długości fali:

T

v

l

=

2

2

sin

A

y y

x

t

T

p

p

l

�

�

=

-

�

�

�

�

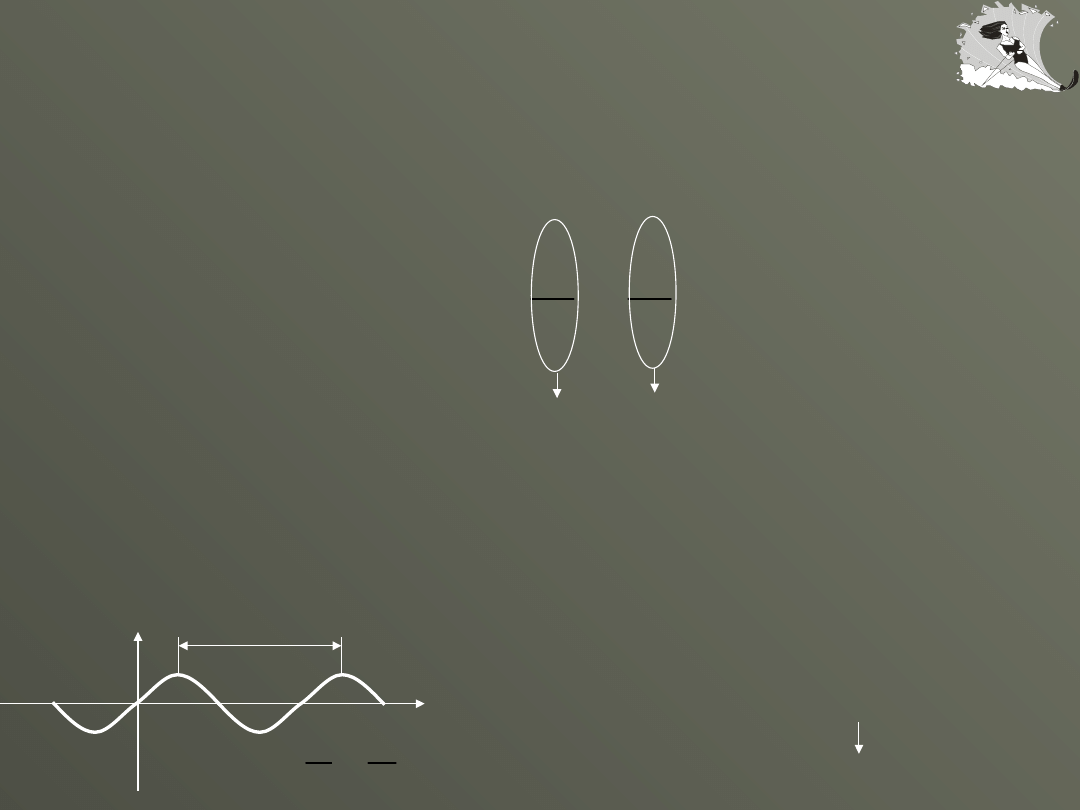
Rozchodzenie się fal

Rozchodzenie się fal

równanie fali

równanie fali

Wykład

Wykład

7

7

(

)

sin

A

y y

kx

t

w j

=

-

-

(

)

(

)

sin
sin

A

A

y y

kx

t

y y

kx

t

w

w

=

-

=

+

2

2

sin

A

y y

x

t

T

p

p

l

�

�

=

-

�

�

�

�

liczba falowa

częstość kołowa

x

y



v

T

k

l

w

= =



faza początkowa

równanie fali sinusoidalnej przesuwającej się w prawo

równanie fali sinusoidalnej przesuwającej się w lewo

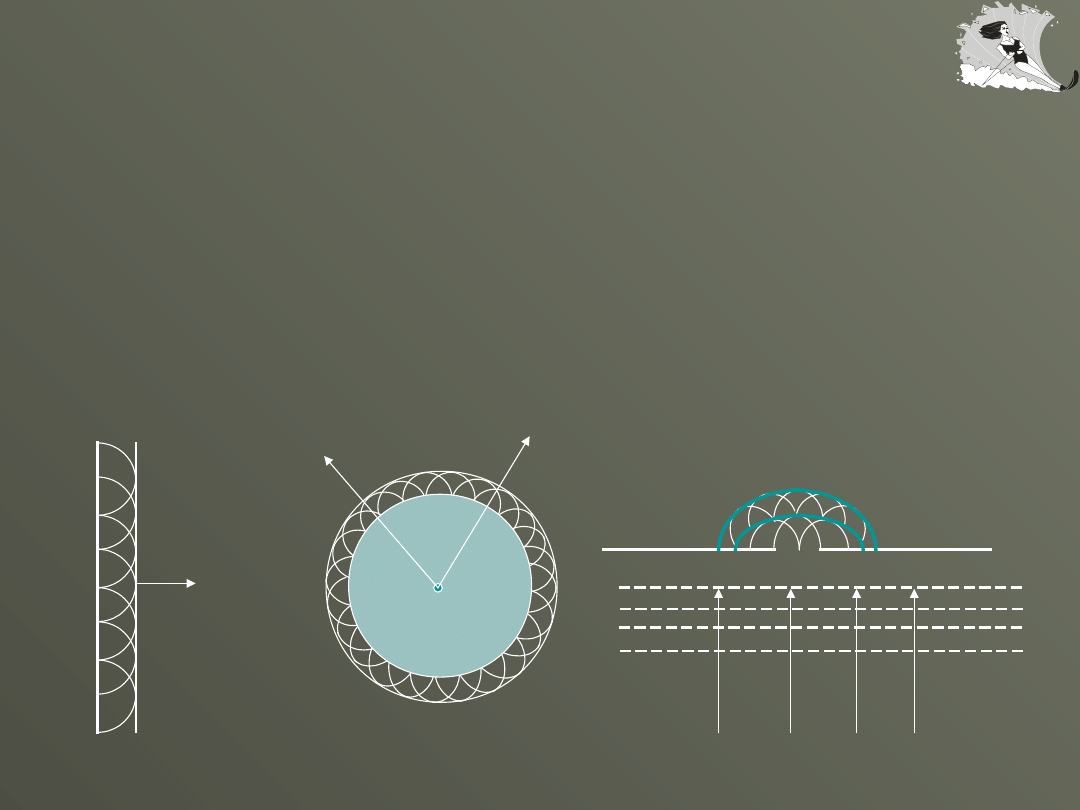
Rozchodzenie się fal

Rozchodzenie się fal

zasada Huygensa

zasada Huygensa

Wykład

Wykład

7

7

Każdy punkt ośrodka, do którego dociera czoło fali staje się

samodzielnym źródłem wysyłającym fale kuliste cząstkowe.

Powierzchnia styczna do wszystkich fal kulistych cząstkowych stanowi

nowe czoło fali.

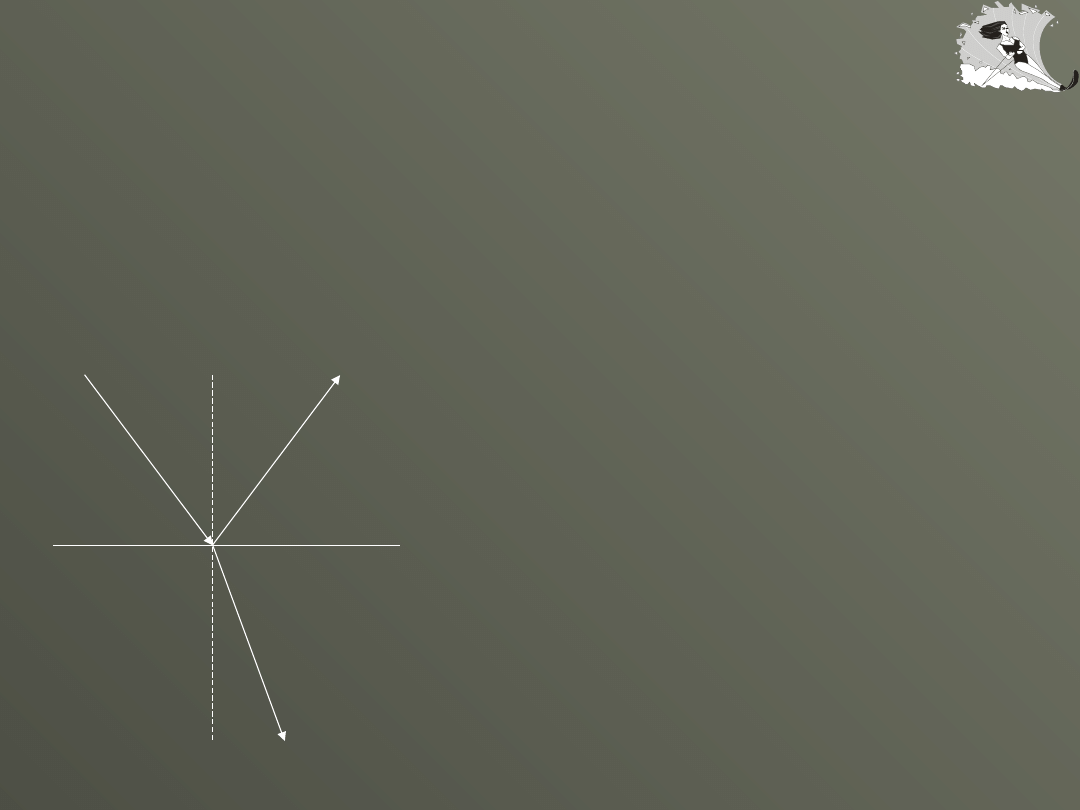
Rozchodzenie się fal

Rozchodzenie się fal

prawo odbicia i załamania

prawo odbicia i załamania

Wykład

Wykład

7

7

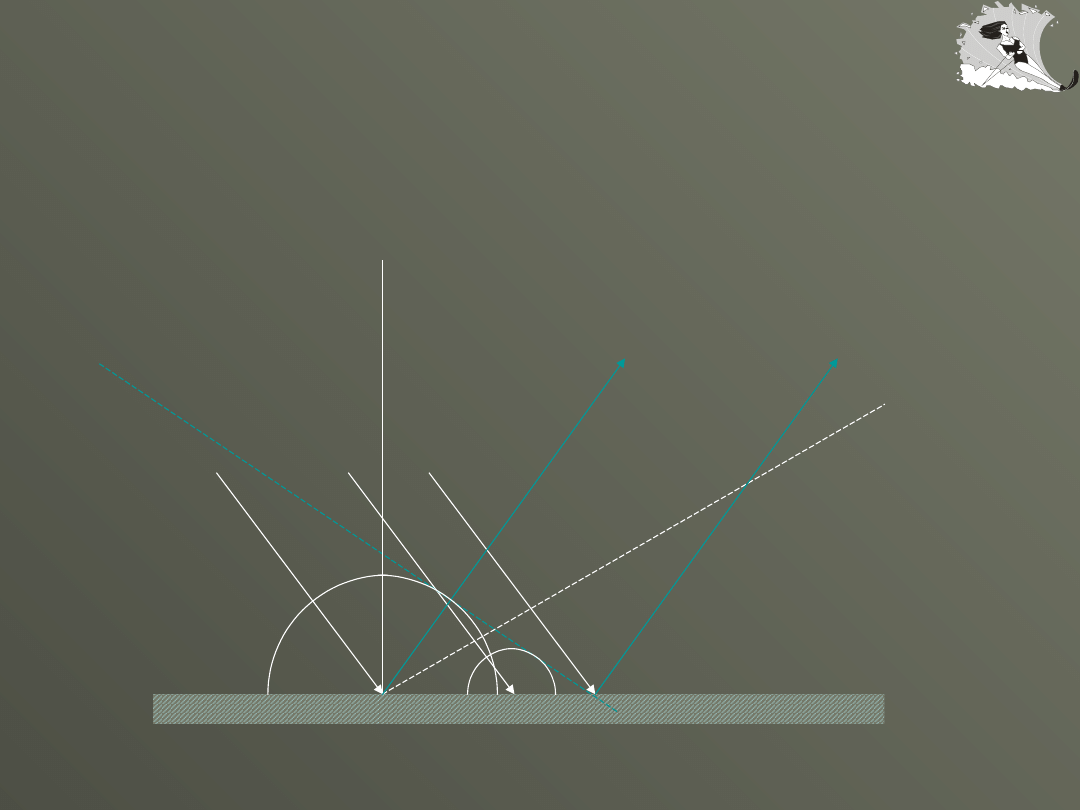
Prawo odbicia

1. Promień fali padającej, fali odbitej i
normalna wystawiona w punkcie padania
leżą w jednej płaszczyźnie.

2. Kąt padanie równy jest kątowi odbicia

Prawo załamania

1. Promień fali padającej, fali załamanej i
normalna wystawiona w punkcie padania
leżą w jednej płaszczyźnie.

2. Stosunek sinusa kąta padania do
sinusa kąta załamania równa się
stosunkowi prędkości rozchodzenia się
fali w ośrodku pierwszym do prędkości
rozchodzenia się fali w ośrodku drugim.

fala
płaska

fala
płaska

fala
płaska

kąt
padania

kąt
odbicia

kąt
załamania

Rozchodzenie się fal

Rozchodzenie się fal

zasada Huygensa – prawo odbicia

zasada Huygensa – prawo odbicia

Wykład

Wykład

7

7

czo

ło

fal

i p

ad

ają

ce

j

czo

ło fa

li o

dbit

ej

N









v

2

t

Rozchodzenie się fal

Rozchodzenie się fal

zasada Huygensa – prawo

zasada Huygensa – prawo

załamania

załamania

Wykład

Wykład

7

7

czo

ło

fal

i p

ad

ają

cej

N









czo

ło f

ali

zał

am

ane

j

v

1

v

2

v

1

t

P

1

sin

vt

P

a =

2

sin

v t

P

b =

1

2

sin

sin

v

v

a

b

=

1

2,1

2

v

n

v

=

współczynnik załamania
ośrodka drugiego
względem pierwszego

1

2

v

v

a

b

>

>

przejście z ośrodka

rzadszego do gęstszego

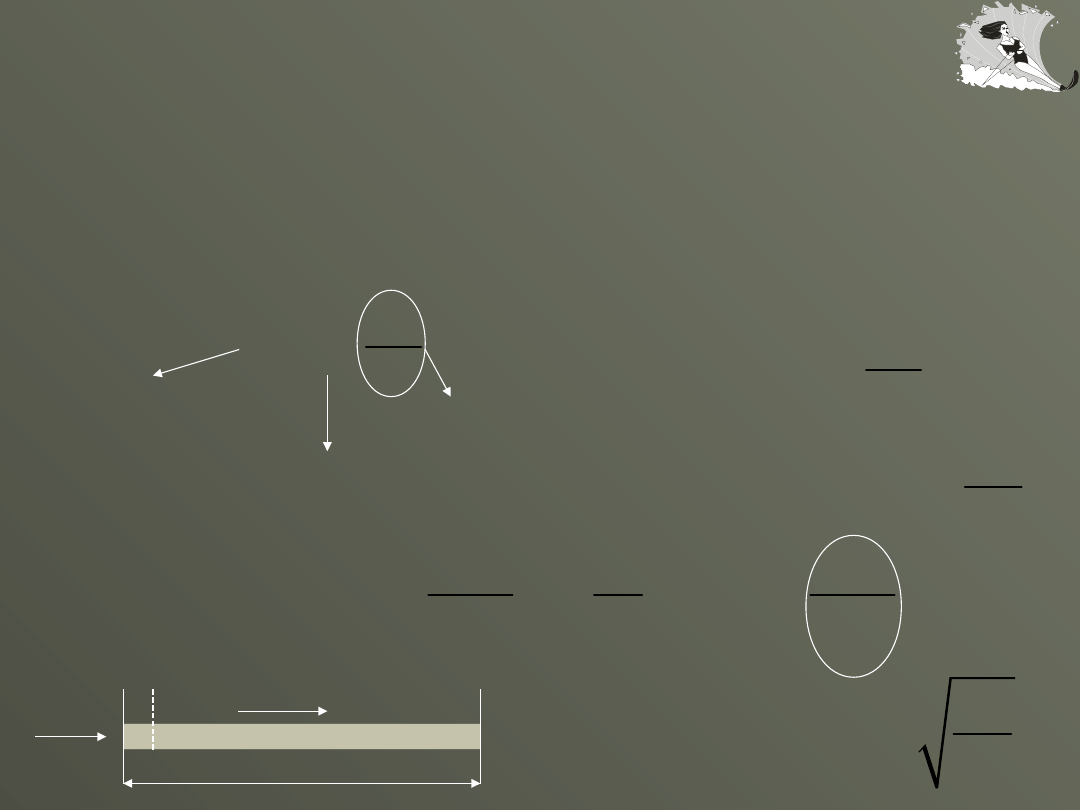
Rozchodzenie się fal

Rozchodzenie się fal

prędkość fali w ośrodku

prędkość fali w ośrodku

sprężystym

sprężystym

Wykład

Wykład

7

7

M

e

s

e

D

=

Prawo Hooke’a

naprężenie powodujące
odkształcenie w ośrodku
sprężystym

moduł
sprężystości
ośrodka

odkształcenie
względne

Druga zasada dynamiki Newtona

v

m

t

s

D

=

D

m

v

t

e

r e

D

=

D =

D

( )

( )

2

2

2

M

M

t

t

e

e

e

r e

r

e

D

D

=

=

D

D

M

v

r

=

prędkość
rozchodzenia się
zaburzenia

l

l

v

F

S

Superpozycja fal

Superpozycja fal

Wykład

Wykład

7

7

Doświadczalnie ustalono, że kilka fal może przebiegać ten sam obszar

przestrzeni niezależnie od siebie. Oznacza to, że przemieszczenie

dowolnej cząstki w ustalonej chwili czasu jest sumą przemieszczeń,

który wywołałyby poszczególne fale.

Proces wektorowego dodawania przemieszczeń nazywamy

superpozycją.

Ważną konsekwencją zasady superpozycji jest możliwość rozłożenia

skomplikowanych ruchów falowych na kombinację prostych fal.

Francuski matematyk J. Fourier wykazał, że dowolny periodyczny ruch
cząstki może być przedstawiony w postaci kombinacji liniowej ruchów

harmonicznych prostych.

( )

0

1

2

3

1

2

sin

sin2

sin3

cos

cos2

y t

A A

t A

t A

t

B

t B

t

w

w

w

w

w

= +

+

+

+ +

+

+

K

K

Interferencja fal

Interferencja fal

Wykład

Wykład

7

7

(

)

1

sin

A

y

y

kx

t

w j

=

-

-

(

)

2

sin

A

y

y

kx

t

w

=

-

(

)

(

)

1

2

sin

sin

A

y y

y

y

kx

t

kx

t

w

j

w

= +

=

�

-

-

+

-

�

�

�

2sin

cos

2 cos sin

2

2

2

2

A

A

y y

kx

t

y

kx

t

j

j

j

j

w

w

�

�

�

� �

�

=

-

-

=

-

-

�

�

�

� �

�

�

�

�

� �

�

(

)

(

)

1

1

sin

sin

2sin

cos

2

2

A

B

B A

B A

+

=

+

-

Zjawisko interferencji jest szczególnym przypadkiem superpozycji.

Zjawisko to polega na nakładaniu się (superpozycji) dwóch lub więcej

ciągów falowych harmonicznych o jednakowej częstotliwości i nie

zależnych od czasu różnicach faz wywołujących wychylenie cząstek od

położenia równowagi skierowane wzdłuż tej samej prostej.

nowa amplituda

zależna od różnicy faz

dwóch fal składowych

Interferencja fal

Interferencja fal

Wykład

Wykład

7

7

(

)

1

sin

A

y

y

kx

t

w j

=

-

-

(

)

2

sin

A

y

y

kx

t

w

=

-

1

sin

A

y

y

k x

t

k

j

w

�

�

�

�

=

-

-

�

�

�

�

�

�

�

�

w porównaniu z falą 2 fala 1 jest przesunięta wzdłuż

osi x o /k

w ustalonym punkcie przestrzeni fale 1 i 2 wywołują

drgania harmoniczne proste przesunięte w czasie o /

1

sin

A

y

y

kx

t

j

w

w

�

�

�

�

=

-

+

�

�

�

�

�

�

�

�

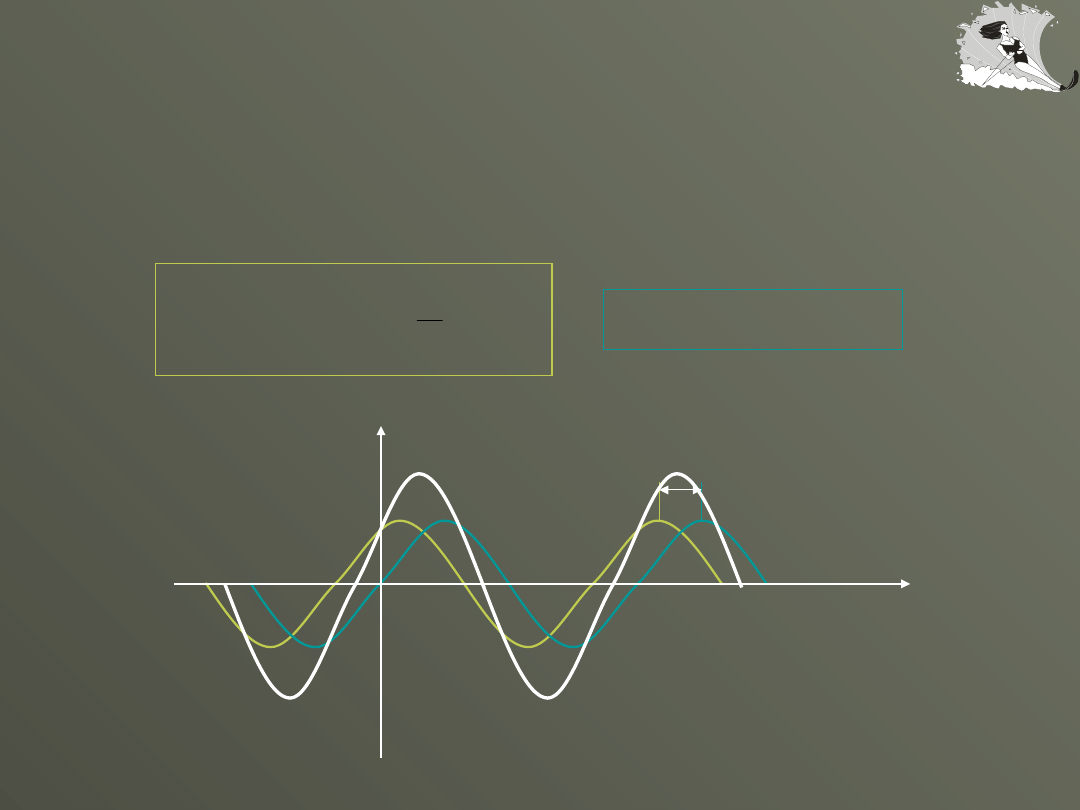
1

sin

A

y

y

k x

t

k

j

w

�

�

�

�

=

-

-

�

�

�

�

�

�

�

�

(

)

2

sin

A

y

y

kx

t

w

=

-

Interferencja fal

Interferencja fal

Wykład

Wykład

7

7

x

y

/k

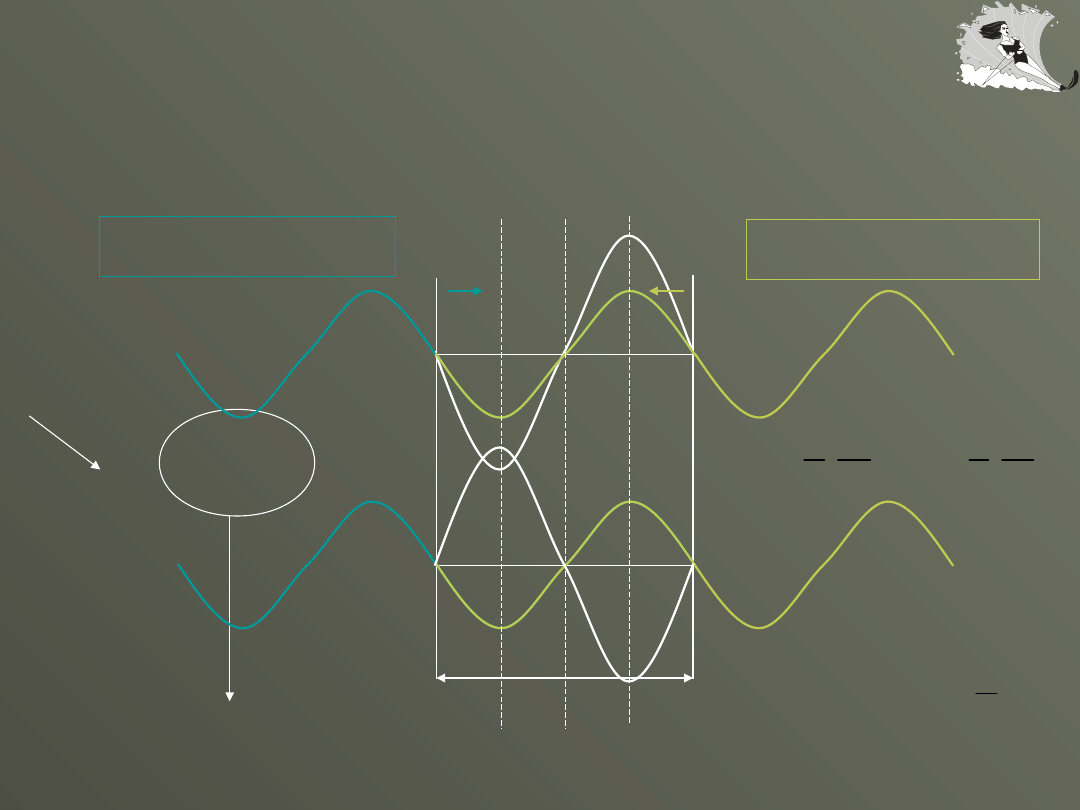
Fale stojące

Fale stojące

Wykład

Wykład

7

7

(

)

2

sin

A

y

y

kx

t

w

=

+

(

)

1

sin

A

y

y

kx

t

w

=

-

2 sin cos

A

y

y

kx

t

w

=

amplituda zmienia się z

położeniem cząstki



amplituda jest ekstremalna dla:

3

3

,

,

,

,

2 2

4 4

kx

x

p

p

l

l

=

=

K

K

równanie fali stojącej

amplituda jest minimalna (zero) dla:

,2 ,

, ,

2

kx

x

l

p p

l

=

=

K

K

t=1/4T

t=3/4T

t=1/2T

1/4

1/2

3/4

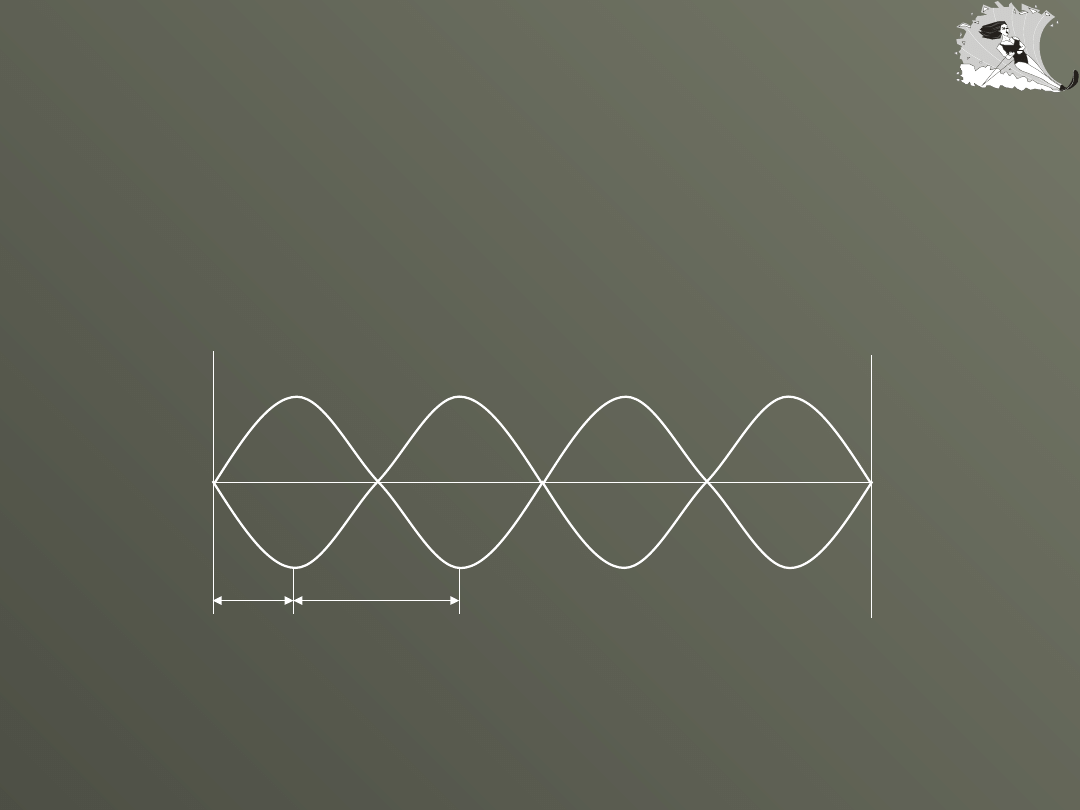
Fale stojące

Fale stojące

Wykład

Wykład

7

7

/4

strzałka

węzeł

Obwiednia fali stojącej

/2

węzeł

węzeł

węzeł

węzeł

strzałka

strzałka

strzałka

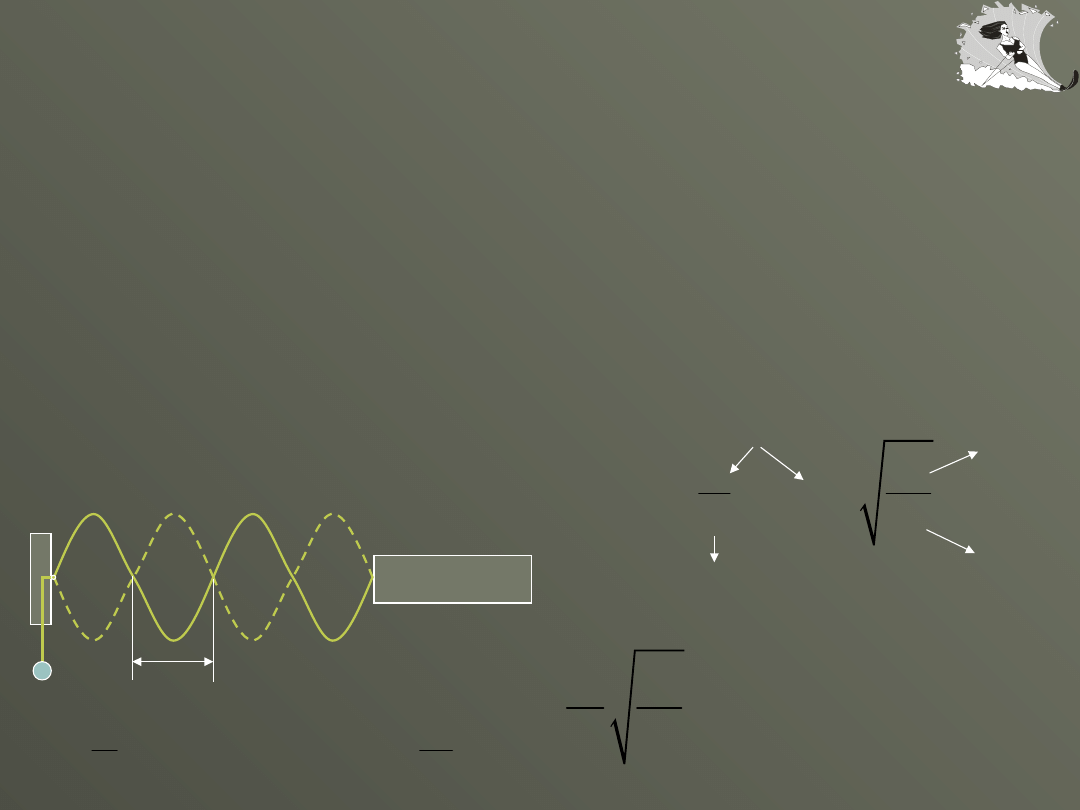
Rezonans

Rezonans

Wykład

Wykład

7

7

v

M

v

l

w

r

=

=

Zjawisko rezonansu polega na tym, że gdy układ fizyczny zdolny

do wykonywania drgań pobudzany jest periodyczną serią impulsów o

częstości równej lub prawie równej częstości własnej układu to układ

ten zostaje wprawiony w drgania o dużej amplitudzie. Mówimy wtedy,

że układ znajduje się w rezonansie z przykładanymi impulsami.

impulsy

wymuszające

2

1,2,3,

2

l

l n

n

n

l

l

=

=

=

K

/2

sznur o długości l

częstość

moduł

sprężystości

prędkość

fazowa

gęstość

2

n M

l

w

r

=

Istnieje wiele częstości własnych

rozpatrywanego układu.

Jeżeli częstość wymuszająca jest

bliska jednej z częstości własnych

to sznur drga z tą częstością i

bardzo dużą amplitudą

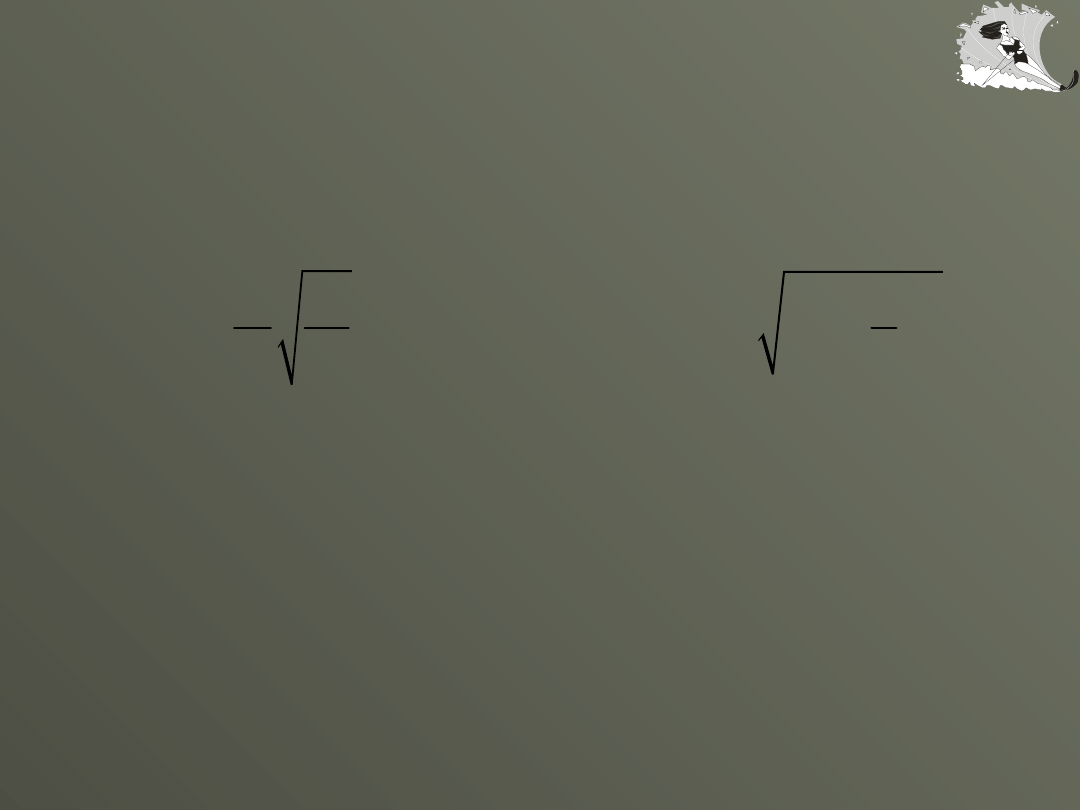
Rezonans

Rezonans

Wykład

Wykład

7

7

2

2

0

1

2

r

b

w

w

=

-

2

n M

l

w

r

=

Drgający sznur - wiele częstości

rezonansowych.

Każdy element sznura ma zarówno

bezwładność jak i sprężystość.

O układach tego typu mówimy, że mają

elementy rozłożone.

W napiętym sznurze elementy podobne do

masy i sprężyny są rozłożone

równomiernie wzdłuż sznura. Istnieje wiele

sposobów wymiany pomiędzy kinetyczną i

potencjalną formą energii w czasie drgań,

odpowiednio do różnych dopuszczalnych

wartości parametru n.

Drgająca masa - jedna częstość

rezonansowa.

Bezwładność koncentruje się w jednym

elemencie układu – masie, a sprężystość

ma tylko drugi element – np. sprężyna.

O układach tego typu mówimy, że mają

elementy skupione.

Istnienie tylko jeden sposób wymiany

energii – energia kinetyczna związana

jest z ruchem masy a energia

potencjalna z deformacją sprężyny.

Fale dźwiękowe

Fale dźwiękowe

Wykład

Wykład

7

7

Fale dźwiękowe są podłużnymi falami mechanicznymi.

Mogą się rozchodzić w ciałach stałych, cieczach i gazach. Zakres

częstości mechanicznych fal podłużnych obejmuje zakres słyszalny

(20 Hz – 20000 Hz) oraz zakres infradźwiękowy (częstości niższe od

częstości słyszalnych) i zakres ultradźwiękowy (częstości wyższe od

częstości słyszalnych).

Fale słyszalna powstają w wyniku drgań strun, słupów powietrza oraz

płyt i membran. Wszystkie te elementy drgające na przemian

zgęszczają i rozrzedzają otaczający je ośrodek.

obszar słyszalności

I

 [Hz]

10

-1

10

-5

10

-9

10

-13

10

2

10

3

10

4

próg bólu

dolny próg słyszalności

Charakterystyki dźwięku

Charakterystyki dźwięku

Wykład

Wykład

7

7

Wysokość dźwięku – wielkość związana z częstotliwością drgań

źródła. Małym częstotliwościom odpowiadają dźwięki niskie a dużym

wysokie.

Natężenie dźwięku – wielkość związana z ilością energii

przenoszonej w jednostce czasu przez jednostkę powierzchni

ustawionej prostopadle do promienia fali. Natężenie jest

proporcjonalne do kwadratu amplitudy źródła.

Barwa dźwięku – wielkość związana ze złożonością fali dźwiękowej.

O barwie decydują: liczba składowych tonów harmonicznych i

stosunki ich natężeń.

Fale podłużne

Fale podłużne

Wykład

Wykład

7

7

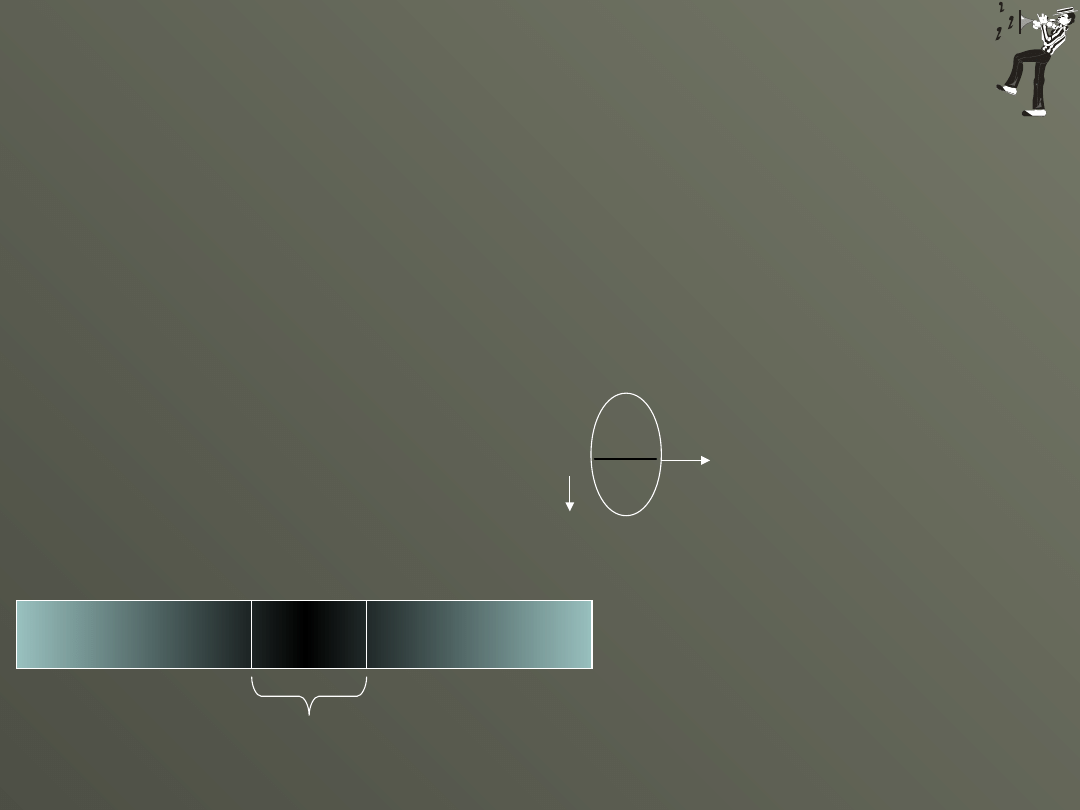
Propagacja fali podłużnej polega na przemieszczaniu się zagęszczenia

ośrodka i dlatego wygodniej jest w tym przypadku zajmować się

zmianami ciśnienia a nie jak do tej pory chwilowymi

przemieszczeniami cząstek przenoszących falę.

V

p

B

V

D

D =-

odchylenie od ciśnienia niezaburzonego

moduł ściśliwości

względna zmiana objętości

strefa

zagęszczenia

p+p

A

( )

V A x

= D

objętość warstwy płynu

gdy wszystkie cząstki

znajdują się w położeniach

równowagi

( )

V A y

D = D

zmiana objętości warstwy płynu gdy

cząstki wychylą się z położenia

równowagi pod wpływem zmiany

ciśnienia

Fale podłużne

Fale podłużne

( )

( )

A y

y

p

B

B

A x

x

D

�

D =-

=-

D

�

Wykład

Wykład

7

7

Zakładamy, że wychylenie cząstki w obszarze zagęszczenia
można opisać za pomocą funkcji harmonicznej:

(

)

cos

A

y y

kx

t

w

=

-

(

)

sin

A

y

ky

kx

t

x

w

�

=-

-

�

(

)

sin

A

p Bky

kx

t

w

D =

-

amplituda ciśnienia

Falę podłużną można traktować jako falę przemieszczeń
albo jako falę ciśnieniową. Gdy pierwsza opisana jest
funkcję cosinus to drugą wyraża sinus i odwrotnie.

Dudnienia

Dudnienia

cos

cos

2cos

cos

2

2

A B

A B

A

B

-

+

+

=

Wykład

Wykład

7

7

Dudnienie powstaje w wyniku superpozycji fal, które przebiegają ten

sam obszar przestrzeni w jednym kierunku ale posiadają różne

częstości.

( )

( )

1

1

2

2

cos

cos

A

A

y

y

t

y

y

t

w

w

=

=

(

)

1

2

cos

cos

A

y y

t

t

w

w

=

+

1

2

1

2

2

cos

cos

2

2

A

y

y

t

t

w

w

w

w

-

+

�

� �

�

=

�

�

�

�

�

� �

�

częstość drgania

wypadkowego

amplituda

drgania

wypadkowego

Dudnienia a fale stojące

Dudnienia a fale stojące

1

2

1

2

2 cos

cos

2

2

A

y

y

t

t

w w

w w

-

+

�

� �

�

=

�

�

�

�

�

� �

�

2 sin cos

A

y

y

kx

t

w

=

Wykład

Wykład

7

7

Dudnienia – interferencja w czasie

Fale stojące – interferencja w przestrzeni

amplituda zmienia się w
czasie z częstością:

1

2

2

amp

w w

w

-

=

amplituda zmienia się z
położeniem cząstki

Zjawisko Dopplera

Zjawisko Dopplera

Wykład

Wykład

7

7

Doppler, w pracy z roku 1842

zwrócił uwagę na fakt, że barwa

świecącego ciała musi się zmienić z

powodu względnego ruchu ciała i

obserwatora.

Zjawisko to nazwane zjawiskiem

Dopplera występuje dla wszystkich

fal, w tym dla fali dźwiękowej.

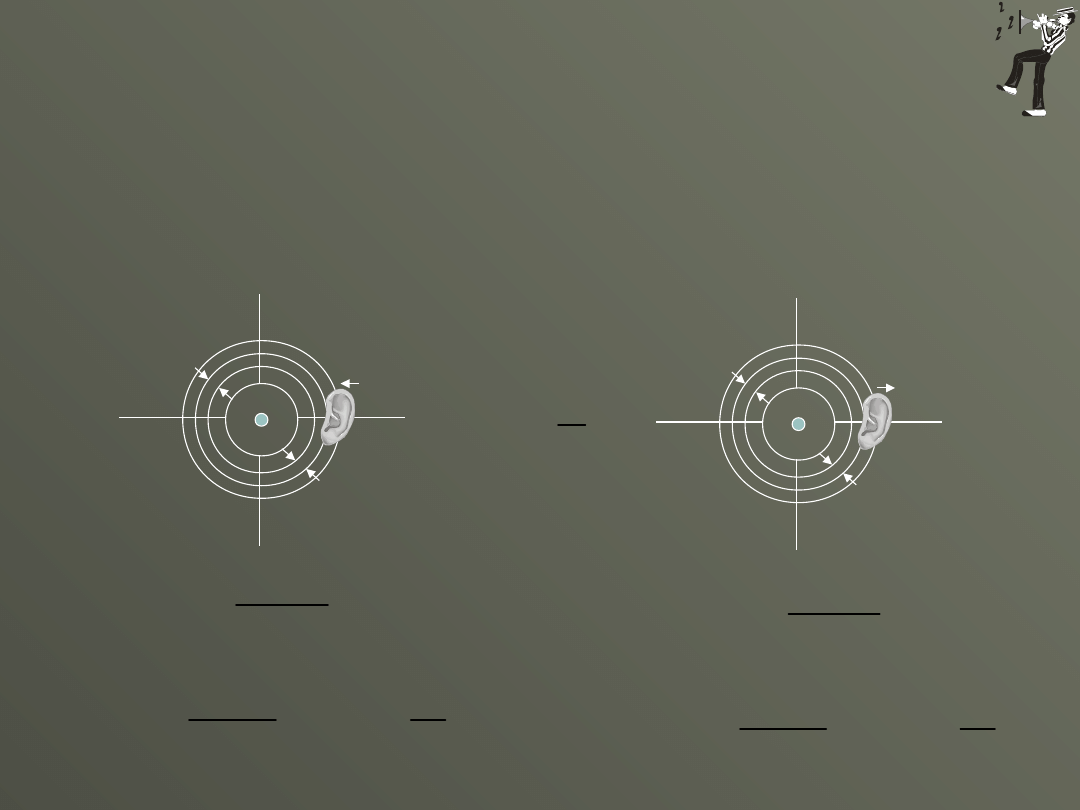
Zjawisko Dopplera dotyczy rozbieżności między częstością fali wysyłanej i

odbieranej w przypadku gdy nadajnik i odbiornik (lub jeden z nich)

poruszają się względem ośrodka przenoszącego falę.

Christian Johann Doppler (1803 – 1853)

0

0

1

v v

v

v

v

w w

w

-

�

�

�

=

=

-

�

�

�

�

0

v v

w

l

-

�=

Zjawisko Dopplera

Zjawisko Dopplera

0

0

1

v v

v

v

v

w w

w

+

�

�

�

=

=

+

�

�

�

�

Wykład

Wykład

7

7

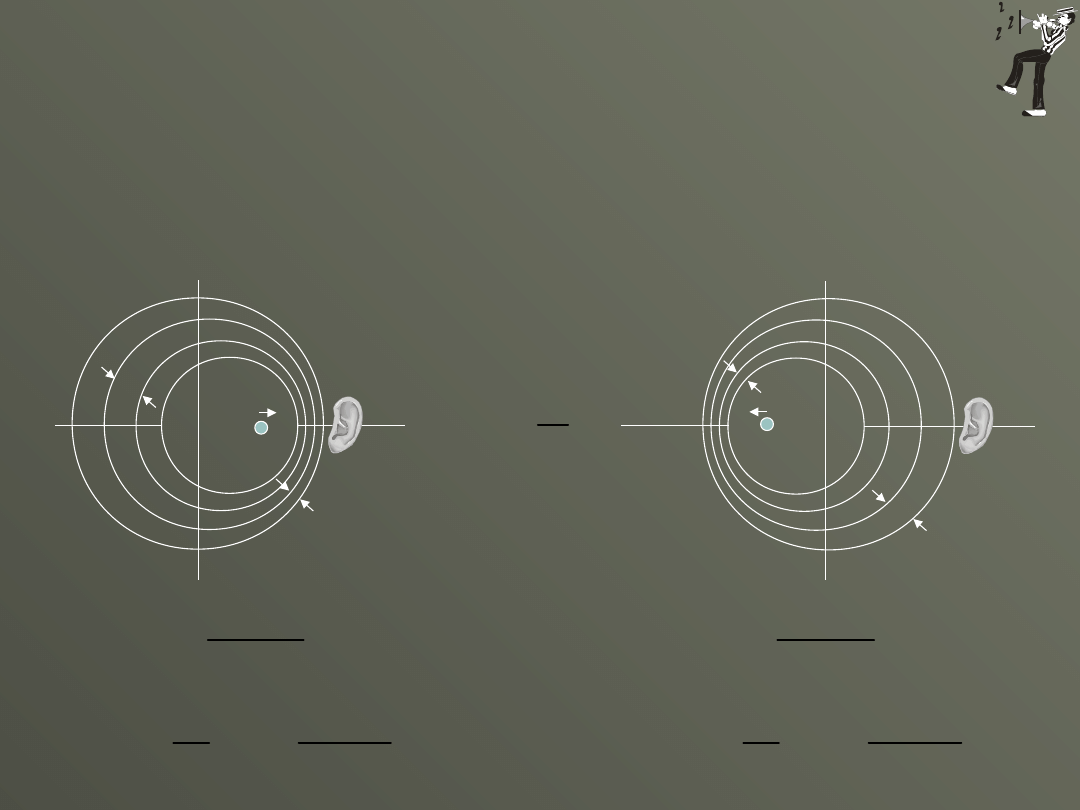
Rozpatrzymy przypadek gdy odbiorca fal dźwiękowych porusza się

wzdłuż prostej łączącej go ze źródłem.

0

v v

w

l

+

�=



v

0

v

Z

=0

x

y



v

w

l

=

dla obserwatora

w spoczynku

v

0



v

Z

=0

x

y



v

Z

v

0

=0

x

y

’

’’

Zjawisko Dopplera

Zjawisko Dopplera

Z

v

v

v v

w

w

l

�

�

�

= = �

�

�

-

�

�

Wykład

Wykład

7

7

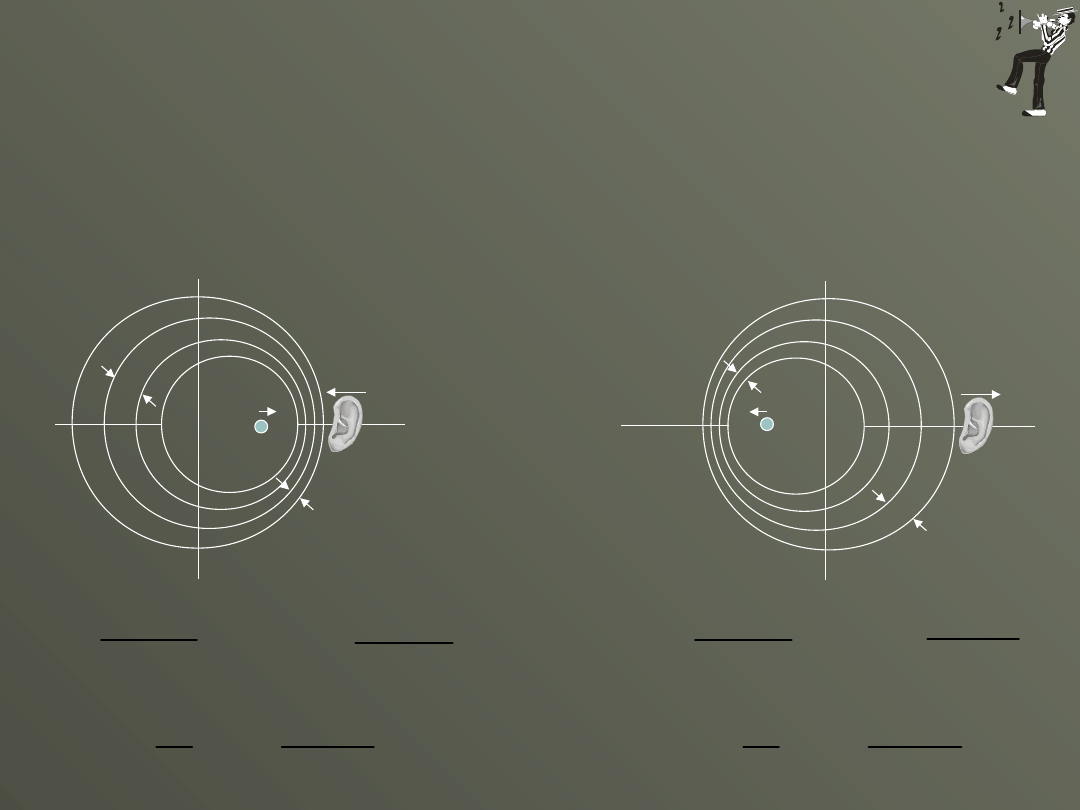
Rozpatrzymy przypadek gdy źródło fal dźwiękowych porusza się

wzdłuż prostej łączącej je z obserwatorem.

Z

v v

l

w

-

�=

v

l

w

=

dla źródła w

spoczynku

v

Z

v

0

=0

x

y

’

’’

Z

v

v

v v

w

w

l

�

�

�= = �

�

�

+

�

�

Z

v v

l

w

+

�=

Zjawisko Dopplera

Zjawisko Dopplera

0

Z

v v

v

v v

w

w

l

�

�

+

�= = �

�

�

-

�

�

Wykład

Wykład

7

7

Rozpatrzymy przypadek gdy źródło i odbiorca fal dźwiękowych

poruszają się wzdłuż łączącej ich prostej.

0

Z

v v

v

v v

w

w

l

�

�

-

�= = �

�

�

+

�

�

v

Z

v

0

x

y

’

’

v

Z

x

y

’

’

v

0

Z

v v

l

w

-

�=

0

v v

w

l

+

�=

�

Z

v v

l

w

+

�=

0

v v

w

l

-

�=

�