Podstawy teorii gier
1. Podstawowe pojęcia teorii gier
Teoria gier
to jest rozdział badań operacyjnych, który zajmuje się opracowaniem
metod podejmowania decyzji w warunkach sytuacji konfliktowych i warunkach
niepewności.
Zbiór reguł definiujących jednoznacznie kolejność działalności jednej ze stron
(jednego z graczy) w sytuacji konfliktowej nazywa się
strategią
.
„
Grą
” nazywa się zbiór omówionych wcześniej graczami reguł i warunków.
Jeśli n gracze G
1
, G
2
, ... , G
n
, przejmują udział w grze, wtedy podstawowe zadanie
teorii gier brzmi: jak powinien postępować gracz z numerem j (j=1, 2, ... , n)
dla osiągnięcia swojego celu – maksymalizacji wygranej?
Przepuśćmy dalej, że w końcu gry każdy gracz G
j
otrzymuje kwotę v
j
, którą
nazywamy wygranej w tej grze. Jeżeli
v
j
>0
, to gra jest
wygrana
graczem G
j
, jeśli
v
j
<0
, to
przegranej
graczem G
j
, a jeśli
v
j
= 0
, to gra skończyła się
remisem
.
W dużej ilości przypadków mamy
gry o sumie zero
: v
1
+ v
2
+ ... + v
n
= 0. W
takich grach suma wygranej przechodzi od jednego gracza do drugiego, bez
wykorzystania zewnętrznych źródeł.
W takich zadaniach suma wygranej jest stała, zmienia się tylko suma wygranej
każdego gracza. W przeciwnym przypadku mamy grę o sumie niezerowej.
W grze może brać udział dwóch lub więcej graczy lub koalicji.
Poniżej rozważamy:
— gry dwuosobowe o sumie zero, w tym tzw. gry z naturą,
— gry dwuosobowe o sumie dowolnej, niekooperacyjne i kooperacyjne,
— gry wieloosobowe, niekooperacyjne i kooperacyjne.
Podstawa matematycznej teorii gier jest schemat gry dwuosobowej z sumą zero. Jest to gra
ściśle konkurencyjna, nie ma w niej miejsca na negocjacje między graczami — co jeden z nich
wygrywa, co drugi przegrywa. Jeżeli w grze ściśle konkurencyjnej każdy z graczy dysponuje
jedynie skończoną liczbą strategii, to nazywa się grą macierzową. Optymalne postępowanie
obu graczy określone przez teorię gier ma charakter zasady stabilności: każdemu z graczy
niewygodnie jest zmieniaé swoja strategie, jeżeli jego przeciwnik pozostawi swoją strategię nie
zmieniona.
W grach dwuosobowych o sumie dowolnej wypłaty dla graczy określa się przy każdym
podjęciu decyzji, przy czym interesy obu graczy nie są (nie musza być) dokładnie przeciwne,
bardzo często obaj mogą nawet zyskać przez współpracą. Ponieważ zyski jednego gracza nie
muszą być równe stratom drugiego, to wypłaty każdego z nich zapisujemy w osobnej macierzy
(tablicy), skąd bierze się nazwa gry dwumacierzowe.
Rozróżnią się dwa rodzaje gier dwumacierzowych: 1) niekooperacyjne oraz 2) kooperacyjne.
W grach dwumacierzowych niekooperacyjnych jakiekolwiek porozumienie (np.
skorelowane strategie czy wypłaty uboczne) jest zabronione.
W przypadku dwumacierzowych gier kooperacyjnych różnego rodzaju współpraca między
obu graczami jest dozwolona.
Teoria wieloosobowych gier niekooperacyjnych niewiele różni się od teorii dwuosobowych
gier niekooperacyjnych o sumie dowolnej. W przypadku wieloosobowych gier kooperacyjnych
występuje pojęcie koalicji, która może powstać i utrzymać się przez pewien czas tylko pod
warunkiem, że poszczególni jej członkowie powinni osiągnąć pewnego rodzaju równowagę lub
stabilność.
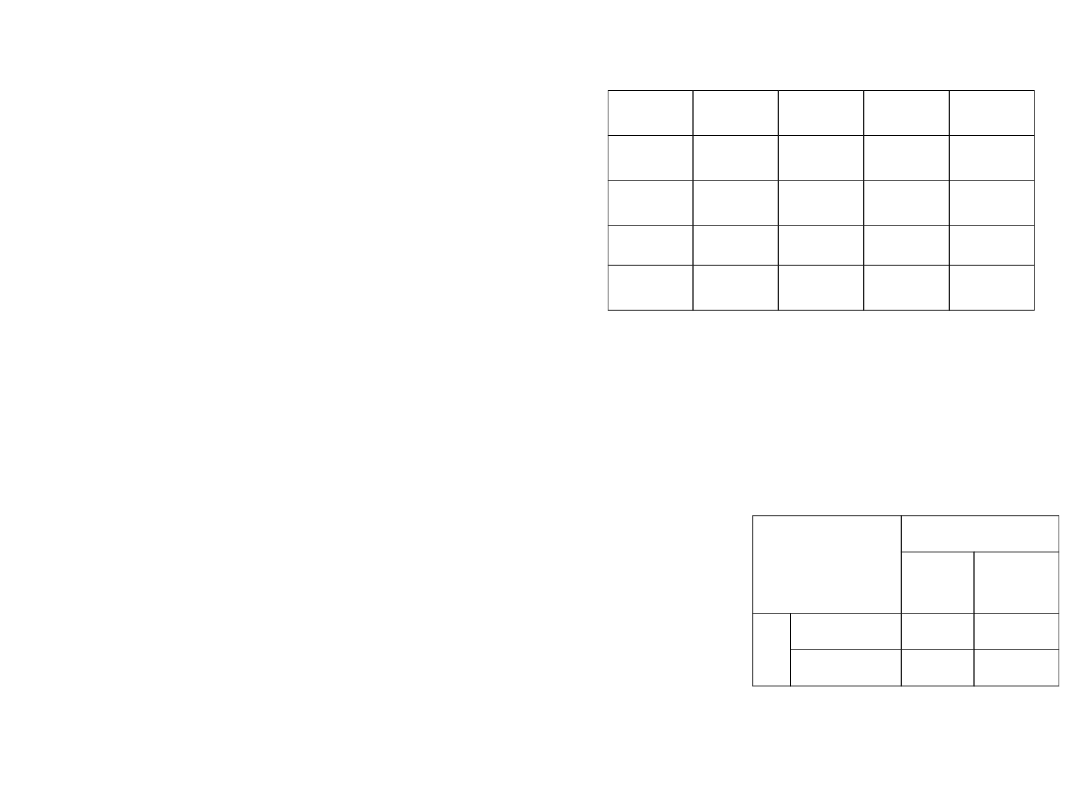
2. Gry macierzowe o sumie zero
W ogólnym przypadku gra macierzowa
definiuje się przez prostokątną macierz
wymiaru m x n. Numer i wiersza macierzy
odpowiada numeru strategii A
i
gracza P, oraz
numer kolumny B
j
odpowiada numeru
strategii gracza D.
11
12
1
21
22
2
1
2
...
...
...
... ... ...
...
n
n
m
m
mn
a
a
a
a
a
a
A
a
a
a
B
1
B
2
...
B
n
A
1
a
11
a
12
...
a
1n
A
2
a
21
a
22
...
a
2n
...
...
...
...
...
A
m
a
m1
a
m2
...
a
mn
Elementy macierzy a
ij
są wartości rzeczywiste i
odpowiada sumie, wygranej przez graca P u gracza
D, jeśli P wybiera strategie A
i
, oraz D wybiera
strategie B
j
. Macierz A zwykle nazywa się macierzą
wypłat.
Przykład. Rzucanie monety. Pierwszy gracz P
wybiera jedną z dwóch stron monety. Drugi gracz D
nie znając wyboru pierwszego, też wybiera jedną ze
stron monety. Reguły gry są następujące: gracz D
zapłaci 1 zł graczowi P, jeśli po jednoczesnym rzucaniu
monet graczami P i D wypadli takie same stronę
(orzeł-orzeł lub reszka-reszka), w przeciwnych
przypadkach (orzeł-reszka lub reszka-orzeł) 1 zł płaci
gracz P graczowi D (gracz P wygrywa (–1) zł). Przy
takim przypuszczeniu mówimy, że gracz D gra na
minimum, oraz gracz P – na maksimum.
Strategii
graczy
D
orzeł
reszk
a
P
orzeł
1
-1
reszka
-1
1
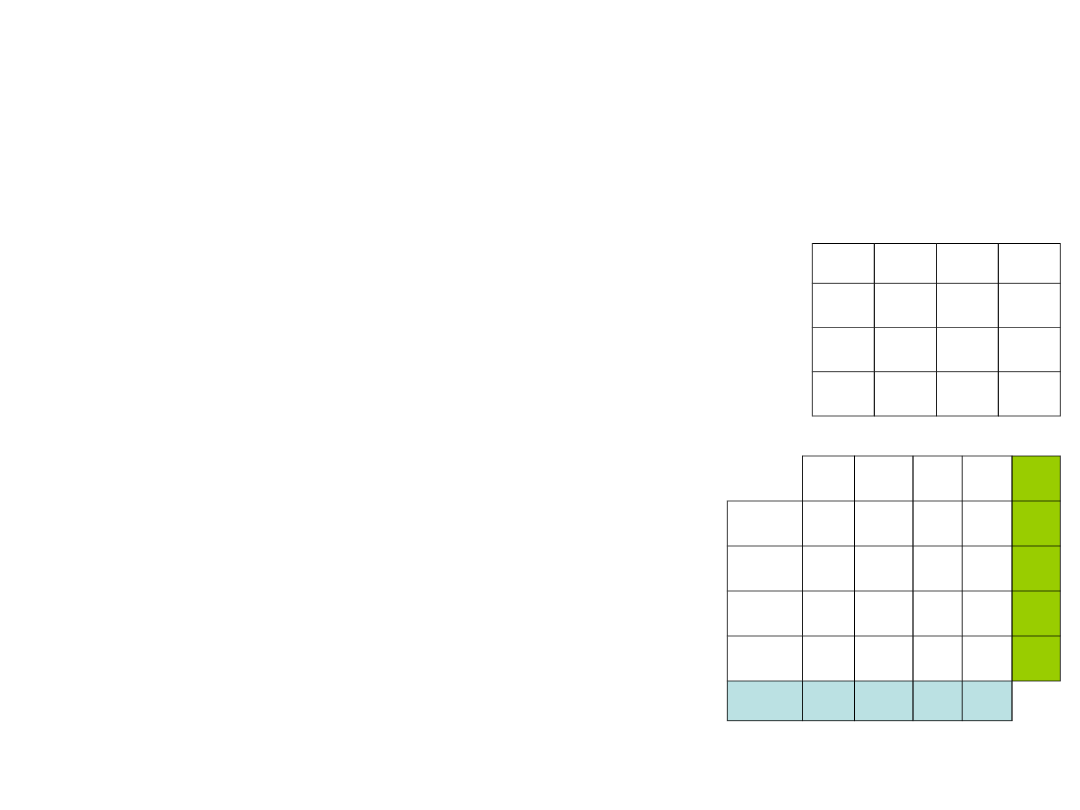
maxmin
ij
j
i
a
a
minmax
ij
i
j
b
a
Dolną czystą ceną gry (maksyminem) nazywa się
wartość
Górną czystą ceną gry (minimaksem) nazywa się
wartość
Strategii graczy, odpowiadające maksyminu (minimaksu), nazywają się straregii
maksyminowymi (minimaksowymi).
Przykład. Znaleźć się strategii maksyminowe i minimaksowe w grze macierzowej:
3
-3
4
6
3
8
7
4
5
1
4
8
4
6
2
9
B
1
B
2
B
3
B
4
a
A
1
3
-3
4
6
-3
A
2
3
8
7
4
3
A
3
5
1
4
8
1
A
4
4
6
2
9
2
b
5
8
7
9
Dla każdego wiersza znajdziemy najmniejszą wartość i
zapiszemy w kolumnę a: (-3, 3, 1, 2).
To oznacza, że dla dowolnej strategii gracza D najgorsza
wygrana gracza P będzie odpowiednie (-3, 3, 1, 2). Z
drugiej strony, gracz P powinien wybrać taką strategie
(wiersz), żeby maksymalizować swoją wygraną. Wtedy a
= max(-3, 3, 1, 2) = 3 i strategią maksyminową dla gracza
P będzie strategia A2.
Analogicznie znajdziemy minimaksową strategie gracza
D. Ponieważ gracz D wybiera strategii według kolumn,
wtedy w najgorszym przypadku on może przegrać
odpowiednie 5, 8, 7, 9. Dla minimalizacji przegranej gracz
D wybiera strategię dla min(5, 7, 8, 9), tj. minmaksowi: b =
min(5, 7, 8, 9) = 5. Z macierzy wypłat widać, że strategią
minimaksową gracza D będzie B1.
Sytuacją równowagi a = b reprezentuje
punkt
siodłowy
, utworzony przez pary strategii Ai i Bj
odpowiednio graczy P i D, przy których osiągana jest
relacja:
maxmin
minmax
ij
ij
j
i
i
j
a
a
3. Czysty i mieszany strategii
Wyróżniają strategii czyste i mieszane.
Czysta strategia
Ai (i=1,2,...,m) pierwszego gracza P (czysta strategia Bj
(j=1,2,...,n) drugiego gracza D) — są to możliwa strategia pierwszego (drugiego)
gracza wybrana z prawdopodobieństwem p=1.
1
2
; ;...; ;...;
i
m
p
p p
p
p
0 ( 1,2,..., )
i
p
i
m
1
1
m
i
i
p
1
2
; ;...; ;...;
j
n
q
q q
q
q
1
1
n
j
j
q
Mieszaną strategią
pierwszego (drugiego) gracza nazywa się wektor
, gdzie
i
(wektor
, gdzie
Ponieważ gracze wybierają swoje czyste strategii losowo i niezależnie od drugiego
graczy, gra ma przypadkowy charakter i wielkość wygranej (przegranej) też będzie
wartością losową. Wtedy średnia wartość wygranej (przegranej) — wartość
oczekiwana — jest funkcją od mieszanych strategii р, q:
1
1
( , )
m
n
ij i j
i
j
f p q
a pq
Czyste strategii gracza wchodzące do jego optymalnej mieszanej strategii z
prawdopodobieństwami nie równymi zero, nazywają się aktywnymi strategiami
gracza.
Jest prawidłowe twierdzenie o aktywnych strategiach (bez dowodu).
Twierdzenie. Jeśli jeden z graczy wykorzystuje swoją optymalną mieszaną
strategię, to jego wygrana zostanie niezmiennej i równa się cenie gry niezależnie
od tego, jaką strategie stosuje inny gracz, jeżeli tylko on nie wychodzi za przedziały
swoich aktywnych strategii.
Na podstawie twierdzenia rozwiązanie gry macierzowej będzie uproszczono, jeśli
wyjaśnić dominowanie jednych strategii nad innymi.
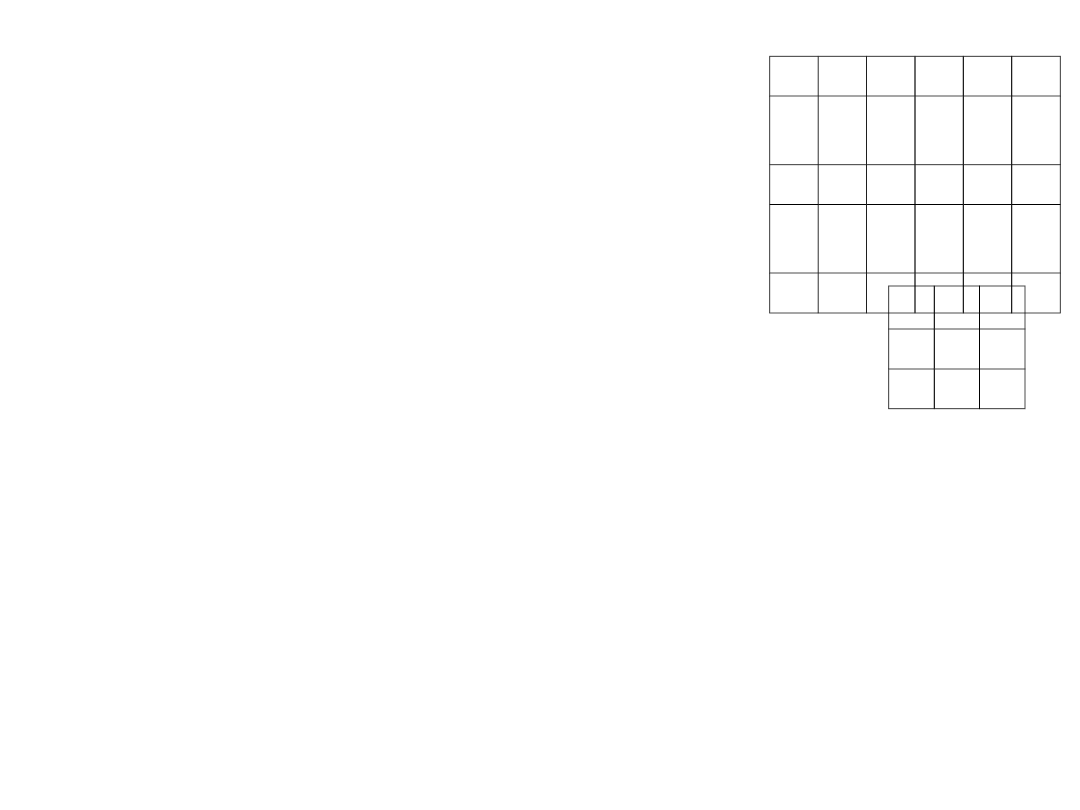
Przykład. Uprościć grę macierzową
Rozwiązanie. Ponieważ elementy drugiego i czwartego
wiersza są równe, tj. mamy dwa dublujących się wierszy.
Wyeliminujemy, na przykład, czwarty wiersz.
Porównujemy elementy wierszy. Wszystkie elementy
drugiego wierszu są mniejszy od odpowiednich elementów
trzeciego wierszu. Wtedy strategia A
2
jest niewygodna
graczowi P. Wyeliminujemy również drugi wiersz.
Porównujemy elementy kolumn. Elementy pierwszej
kolumny są dominujące nad elementami trzeciej i szóstej
kolumny (są najmniejszy). Wyeliminujemy 3-cią i 6-tą
kolumnę. Analogicznie, elementy drugiej kolumny są
dominujące nad elementami czwartej kolumny. Graczowi D
jest niewygodnie wykorzystać strategii B
3
, B
4
, B
6
.
Otrzymujemy uproszczoną macierz gry:
Jeżeli potrzebujemy macierz z dodatnimi elementami,
wystarczy dodać do wszystkich elementów, na przykład,
wartość +4.
-4 -2 2
3
5
1
2
1
5
-4 -2
5
1
2
7
1
2
4
3
0
1
0
3
5
6
7
1
9
1
2
4
3
0
1
0
2
1
3
6
5
4
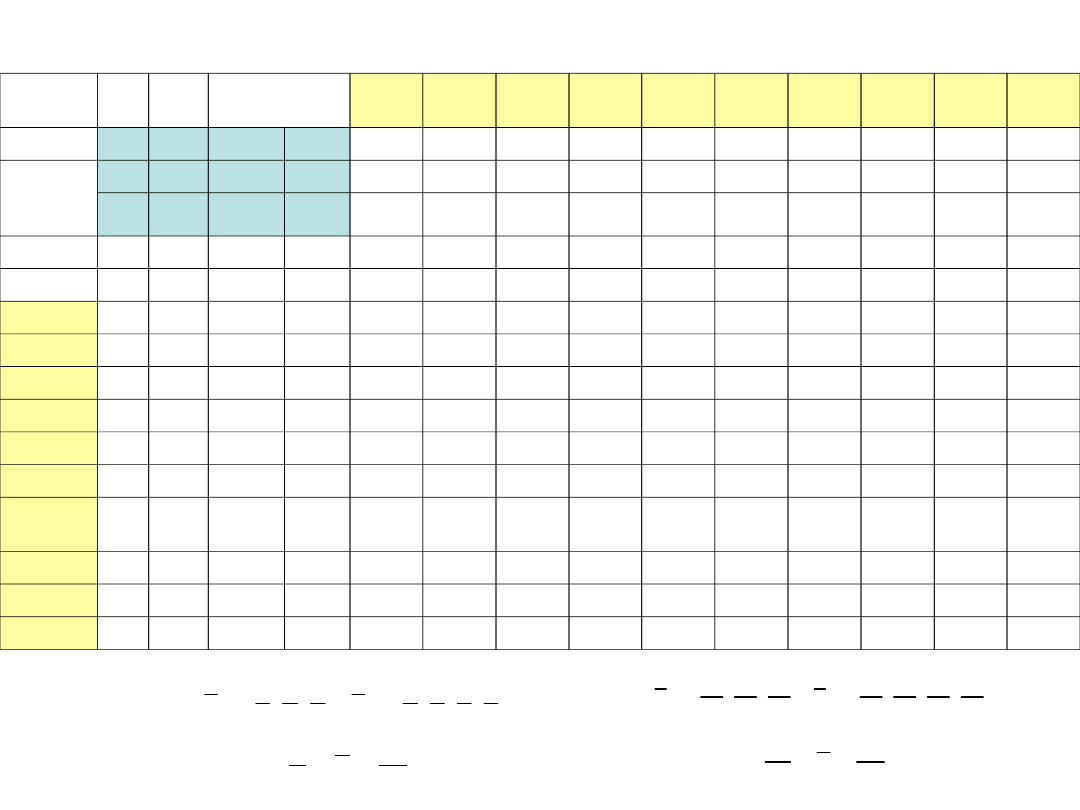
4. Metoda Brown’a rozwiązania zadań teorii gier
Krok gracza
2
1
2
3
4
5
6
7
8
9
10
2
0
9
6
9*
9
9
9
15
21*
23*
23*
23*
23
Krok
gracza
1
1
3
6
0
6
9*
12*
15*
15*
15
16
19
22
25*
4
2
1
3
1
3
5
7
10
13
17
19
21
23
9
9
12
15
15
21
23
23
23
25
max
1
5
1
4
2
1*
3
1
min
4
5
2
6
2*
10
9
2
0
0
3
7
5*
16
9
5
4
8
8*
22
9
8
5
9
11
28
9*
9
0
3
1
1
6
10
14
34
9*
9
7
12
*
14
43
15
12
8
14
14*
52
21
14
9
16
14*
61
27
14
10
18
14*
70
33
14
1
6
1
2
9
15
5
5
v
1 4 0
0 3 1 1
, ,
,
, , ,
5 5 5
5 5 5 5
x
y
14
25
10
10
v
5 5 0
1 6 1 3
,
,
,
,
,
,
10 10 10
10 10 10 10
x
y
Stopień przybliżenia do rozwiązania zależy od wyboru pierwszego kroku i od ilości
kroków. Na przykład, dla n=5
n=10
5. Zadania teorii gier a zadania planowania liniowego
Niech mamy grę rozmiarem m x n z macierzą { aij } :
11
12
1
21
22
2
1
2
...
...
...
... ... ...
...
n
n
m
m
mn
a
a
a
a
a
a
A
a
a
a
*
*
*
*
*
1
2
; ;...; ;...;
i
m
p
p p
p
p
*
*
*
*
*
1
2
; ;...; ;...;
j
n
q
q q
q
q
11 1
21 2
1
12 1
22 2
2
1
1
2
2
...
...
...
...
m
m
m
m
n
n
mn m
a p a p
a p
v
a p a p
a p
v
a p a p
a p
v
1
1,
0, 1,2,..., .
m
i
i
i
p
p
i
m
Zaznaczymy przez
i
optymalne mieszane strategii graczy P i D. Strategia р* gracza P gwarantuje
jemu wygraną nie niższą niż v niezależnie od wyboru strategii B
j
graczem D. Ten fakt
możemy zapisać w postaci:
gdz
ie
Analogicznie, strategia q* gracza D gwarantuje jemu przegraną nie wyższą niż v
niezależnie od wyboru strategii Ai graczem P. Ten fakt możemy zapisać w postaci:
11 1
12 2
1
12 1
22 2
2
1 1
2 2
...
...
...
...
n n
n n
m
m
mn n
a q a q
a q
v
a q a q
a q
v
a q a q
a q
v
gdzie
1
1,
0, 1,2,..., .
n
j
j
j
q
q
j
n
,
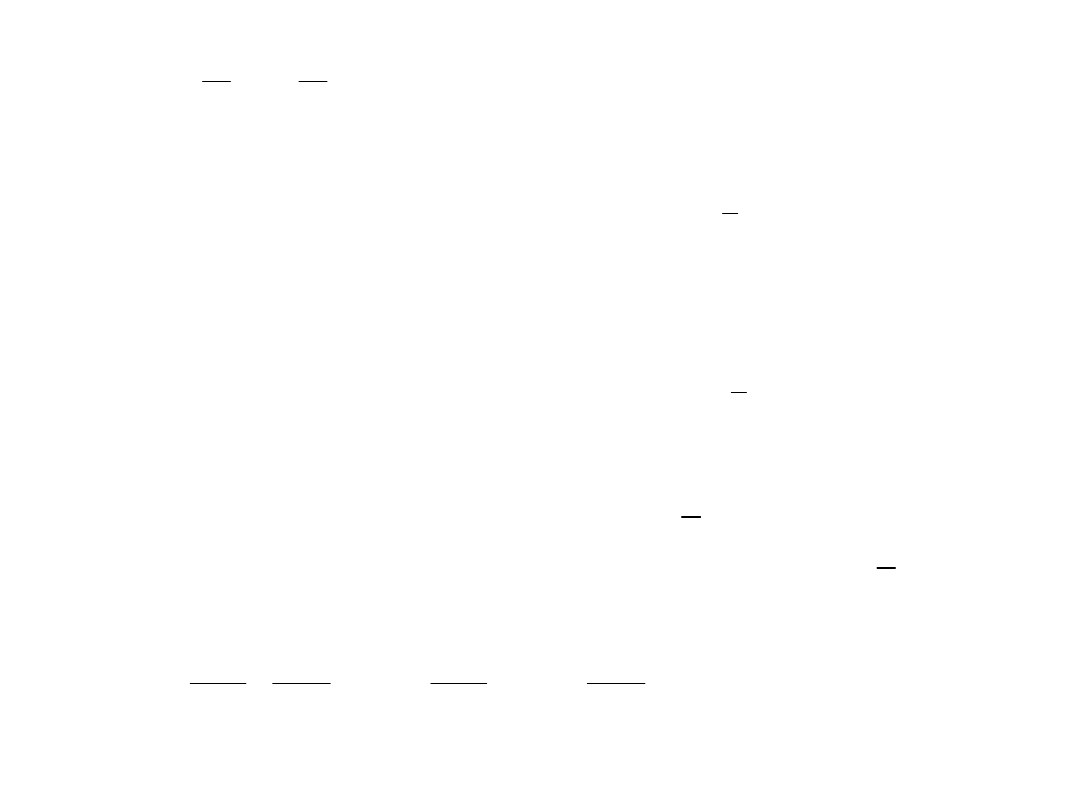
, ( 1,2,..., ; 1,2,..., )
j
i
i
j
q
p
x
y
i
m j
n
v
v
11 1
21 2
1
12 1
22 2
2
1
1
2
2
...
1
...
1
...
...
1
m m
m
m
n
n
mn m
a x a x
a x
a x a x
a x
a x a x
a x
1
1
,
0, 1,2,..., .
m
i
i
i
x
x
i
m
v
Przekształcimy układy nierówności. Dla tego podzielmy nierówności na v>0 i
wprowadzimy zaznaczenia
Otrzymuj
emy:
gdzie
11 1
12 2
1
12 1
22 2
2
1 1
2 2
...
1
...
1
...
...
1
n n
n n
m
m
mn n
a y a y
a y
a y a y
a y
a y a y
a y
gdzie
1
1
,
0, 1,2,..., .
n
j
j
j
y
y
j
n
v
v
1
v
Ponieważ gracz P dąży do maksymalizacji ceny gry
, wtedy
będzie minimalizowana
Optymalna mieszana strategia gracza D jest dualną do zadania PL dla gracza P:
1
v
będzie
maksymalizowana.
Rozwiązując parę dualnych zadań PL metodą simplex (lub graficznej dla dwóch
zmiennych), znajdziemy:
*
*
*
*
*
*
*
*
1
1
1
1
1
1
,
,
, ( 1,2,..., ; 1,2,..., )
j
i
i
j
m
n
m
n
i
j
i
j
i
j
i
j
y
x
v
p
q
i
m
j
n
x
y
x
y
Document Outline