Plan nalotów,  parametry zdjęć 

lotniczych

Katedra Fotogrametrii i Teledetekcji 

Akademia Rolnicza w Krakowie

Podstawowe parametry zdjęć lotniczych przy opracowaniu planu 

nalotu, wybór ich wartości.

1.

Ocena jakości fotogrametrycznej wykonanego nalotu.

2.

Praktyczne opracowanie planu nalotu.

Ad. 1
Podstawowe parametry :

•

skala oryginalnego zdjęcia  (m),

•

wysokość fotografowania  (W),

•

ogniskowa kamery  (f),

•

format zdjęcia (lx ly),

•

wielkość pokrycia (p i q),

•

czas otwarcia migawki (T),

•

prędkość samolotu (V),

•

interwał między dwiema kolejnymi ekspozycjami (t)

•

plamka rozmazania (σ)

Plan

 

nalotu

Wybór konkretnych wartości tych parametrów powinien być 

uzasadniony:

•

podstawowym przeznaczeniem wykonywanego nalotu, np 

wykonanie  w żądanej skali opracowania sytuacyjnego, 

sytuacyjno- wysokościowego, fotointerpretacja, specjalne 

przeznaczenie.

•

charakterem fotografowanego terenu (rzeźba, zagęszczenie 

sytuacji, rodzaj szczegółów itp).

•

przewidywaną technologią i okresem wykonania niezbędnych 

opracowań a również ich dokładnością i kosztami.

Sposoby doboru skali nalotu 

Wybór skali :

A/     według empirycznego wzoru Grubera
                        
                  
gdzie:        m

z 

- mianownik skali zdjęcia

                  M - mianownik skali opracowania,
                   C - wielkość stała, wartość której może się wahać w 

zależności od jakości technicznej sprzętu stosowanego 

zarówno do wykonania jak i opracowania zdjęć.

         Gruber przyjął c =130, obecnie w związku z postępem 

technicznym w konstrukcji sprzętu fotogrametrycznego 

wartość „ C’ dochodzi do 280 a nawet 300 .

M

C

m

z





Sposoby doboru skali nalotu 

B/       na podstawie wielkości błędów pomiaru 

fotogrametrycznego  (w skali zdjęcia lub modelu) i 

dopuszczalnych błędów opracowania końcowego       (w 

skali opracowania)

Średnie błędy położenia wyrażone w skali zdjęcia wynoszą odpowiednio:

0,04 - 0,06 mm dla metody analitycznej,

0,06 - 0,08 mm dla sposobu analogowego, autogrametrycznego

0,10 - 0,12 mm przy opracowaniu w oparciu o przetwarzanie

      Przyjmując skalę opracowania 1 : 2000 i dopuszczalny błąd położenia 0,3 

- 0,4 mm otrzymamy skalę zdjęcia odpowiednio :

1 : 14000 dla metody analitycznej             0,057 = 0,35 mm

1 : 10000 dla metody analogowej              0,075 = 0,35 mm

1 :  7000  przy przetwarzaniu                     0,113,5=0,38 mm

W przykładzie nie wzięto pod uwagę błędów graficznych nieuniknionych 

przy sporządzaniu pierworysu. Po ich uwzględnieniu otrzymamy 

odpowiednio :

 dla metody analitycznej   1 : 10000 - 1 : 11000

dla metody analogowej     1 :   8000 - 1 :   9000

przy przetwarzaniu             1 :   6000 - 1 :   7000

 

Sposoby doboru skali nalotu 

C/       na podstawie minimalnych wielkości obiektów, 

które powinny zostać odfotografowane

                          gdzie :       z - zdolność rozdzielcza oryginalnego 

zdjęcia

                                           d - minimalny wymiar obiektu w terenie

1

1

m z d





Plan nalotu

Typowe relacje między skalą zdjęć a skalą opracowania 

     1 : M  (skala mapy)               1 : m  (zakres skal zdjęć)           

             

     1:      500                                1 :  3500   - 1 :  5500

     1 :   1000                                1 :  5500   - 1 :  8000                

     1 :   2000                                1 :  8000   - 1 :  12000            

     1 :   5000                                1 : 13000 -  1 : 20000              

     1 : 10000                                1 : 19000 -  1 : 28000                

     1 : 25000                                1 : 30000  - 1 : 45000 

Plan nalotu

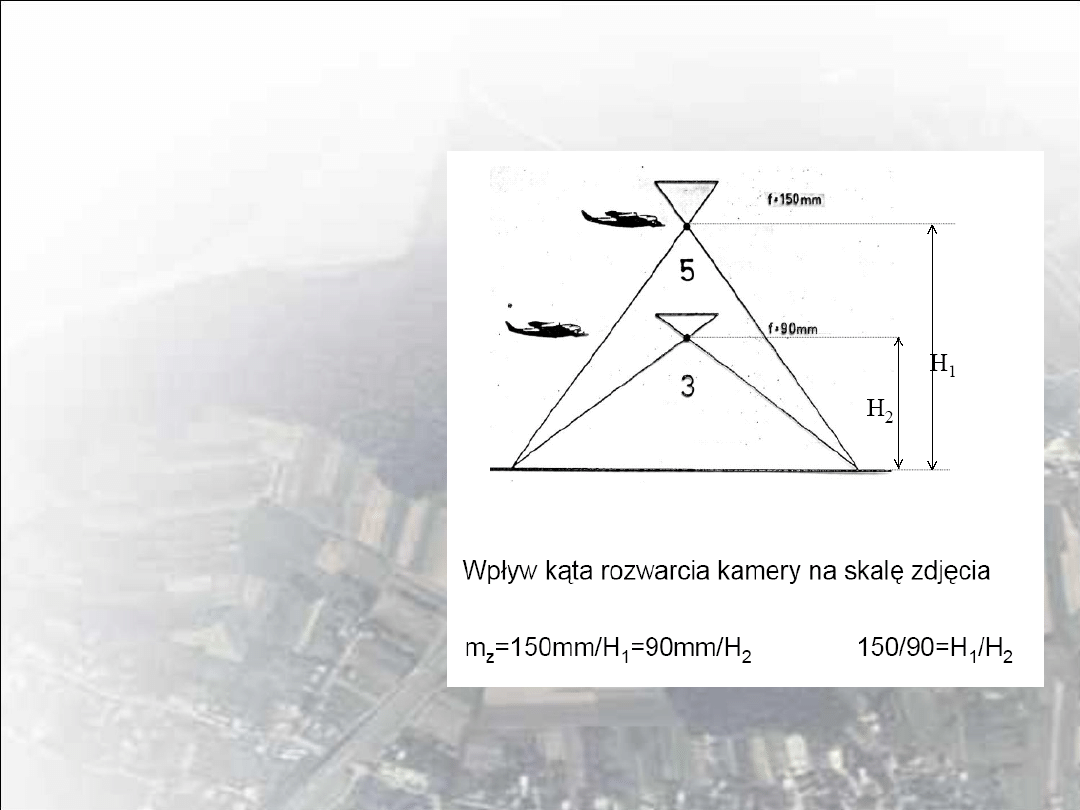
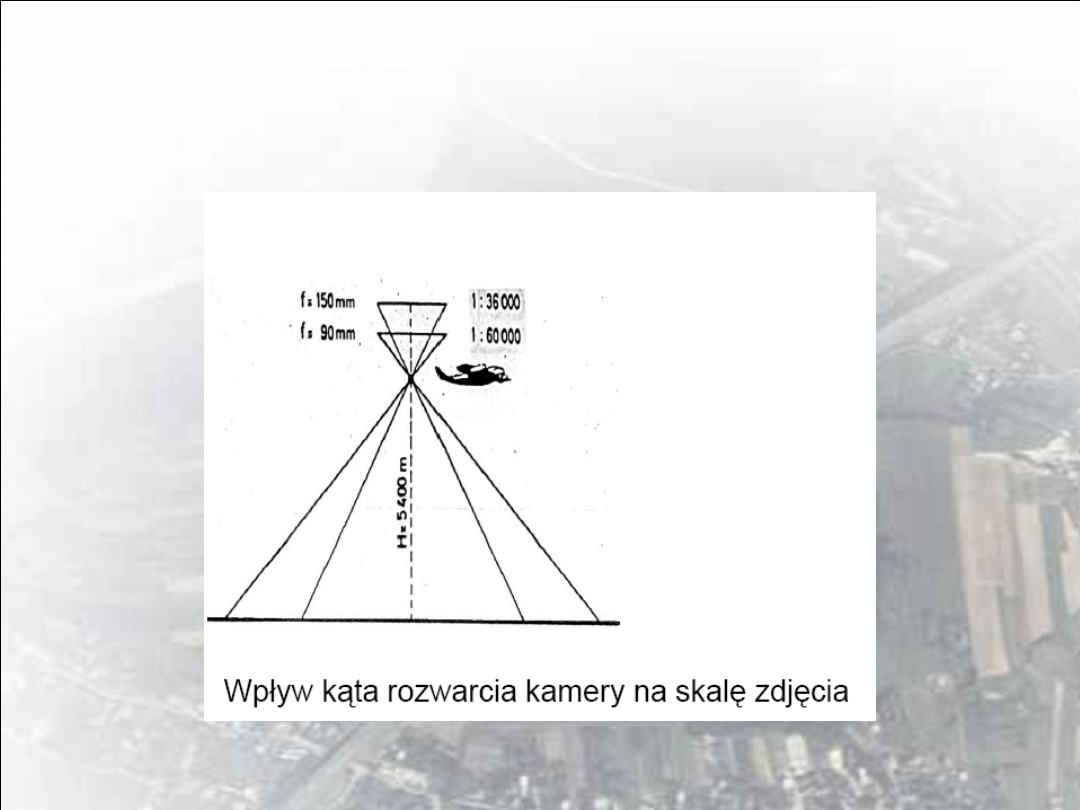
Wysokość fotografowania i ogniskowa kamery są wielkościami 

bezpośrednio zależnymi od skali zdjęcia. Konkretna wartość f jest 

uzależniona warunkami terenowymi i przeznaczeniem wykonywanego 

nalotu. Dla opracowań sytuacyjnych stosowane są zazwyczaj 

obiektywy normalnokątne, rzadziej szerokokątne przy założeniu, że 

teren jest równy lub pofałdowany. Przy opracowaniach 

stereometrycznych terenu równinnego celem zwiększenia dokładności 

określenia wysokości stosuje się obiektywy szerokokątne. W terenach 

górskich obiektywy szerokokątne raczej nie są stosowane. 

Minimalna wysokość fotografowania jest limitowana szybkością i możliwym 

najmniejszym pułapem samolotu, interwałem czasowym, 

dopuszczalnym rozmazaniem (wielkość plamki rozmazania), a w 

przypadku znacznych deniwelacji w terenie, stosunkiem h : W, którego 

wielkość powinna wynosić 1/8 do 1/10 i nie może być większa od 1/4. 

 Również stosunek B : W jest bardzo istotny szczególnie dla opracowań 

stereometrycznych. Na wartość B : W wpływa wielkość pokrycia 

podłużnego. Pokrycie podłużne zależy od przeznaczenia zdjęć i tak dla 

opracowań sytuacyjnych drogą przetwarzania wynosi 20% - 30%, 

natomiast dla stereometrycznych pokrycie powinno być większe od 

50%. 

Plan nalotu

Plan nalotu

Dla obecnie powszechnie 
używanego formatu kadru 
lotniczych kamer 
pomiarowych 
23x23 cm stosuje się 
obiektywy:

normalnokątny    f ≈ 305 
mm,     

2β = 55º

półnormalnokątny   f ≈ 210 
mm,     

2β = 70º

szerokokątny        f ≈ 153 
mm,     

2β = 90º

nadszerokokątny      f ≈   
88 mm,     

2β 

= 120º

              
1:

Plan nalotu

Plan nalotu

Plan nalotu

Plan nalotu

Plan nalotu

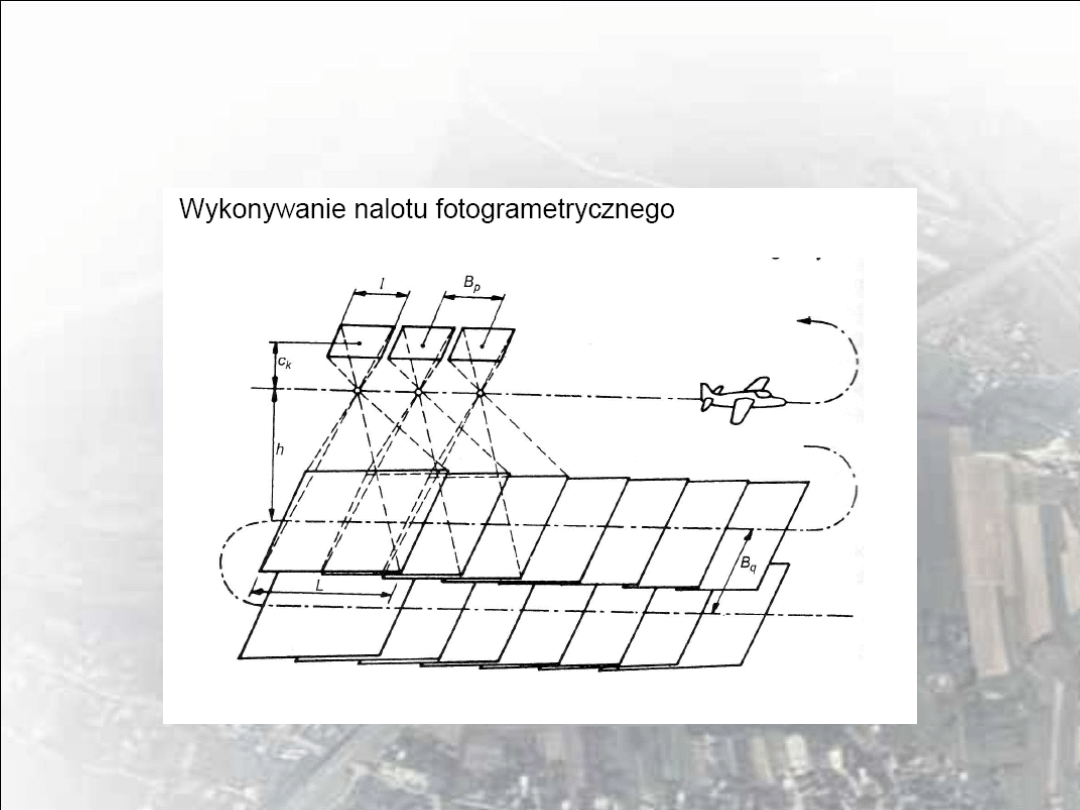
Wielkość pokrycia podłużnego (określa pokrycie między 

sąsiednimi zdjęciami w szeregu i wyrażane jest w procentach). 

Projektowane zasadnicze pokrycie podłużne zdjęć lotniczych 

dla opracowań stereoskopowych wynosi standartowo po= 60 % 

Przy fotografowaniu terenów pofałdowanych pokrycie podłużne 

należy zwiększyć o wpływ rzeźby terenu. Oblicza  się je ze 

wzoru :

p[%]  =

p

o 

– zasadnicze pokrycie (po= 60 %)

h – przewyższenie względem średniej płaszczyzny odniesienia

                    

                       

W

h





 50

[%]

p

o

Plan nalotu

Wielkość p

o

 w funkcji skali zdjęć

                                    Skala zdjęć                                        

  p

o

                          
                          1: 1000 – 1: 4999                                   65
                          1: 5000 – 1: 9999                                   64
                          1: 10000 – 1: 24999 

                                

 62

                          1: 25000 i mniejszych                                      

60

Plan nalotu

 

Pokrycie poprzeczne (określa pokrycie zdjęć między sąsiednimi 

szeregami i wyrażane jest w %). Projektowane zasadnicze pokrycie 
poprzeczne zdjęć lotniczych wynosi standartowo:

q

o

 = 30% dla fotografowania z wysokości ≤ 1500 m 

q

o

 = 25% dla fotografowania z wysokości > 1500 m 

Przy fotografowaniu terenów pofałdowanych pokrycie poprzeczne należy 

zwiększyć o wpływ rzeźby terenu.   W przybliżeniu określa je 
zależność

 

                            q[%]=    

Wielkość q

o

 w funkcji skali zdjęć

                             

Skala zdjęć                                                     q

o

                           1: 1000 – 1: 4999                                                 40
                           1: 5000 – 1: 9999 

                                              36

                          1: 10000 – 1: 24999 

                                34

                          1: 25000 – 1: 34999 

                                32

                          1: 35000 i mniejszych                                  30

W

h





 50

[%]

q

o

Plan nalotu

 

Format zdjęć

  - 

zdjęcia lotnicze wykonywane są w formatach 18 x 18 cm 

(zdjęcia archiwalne)    i 23 x 23 cm (obecnie stosowane).

 

          
 

Pomimo ustalonych parametrów zdjęć, nalot dla celów 

kartograficznych powinien dodatkowo spełniać szereg 

warunków :

•

 linie nalotu (osie szeregów) powinny być z dokładnością 0,015 m 

równoległe do zadanych linii, np. ramki sekcyjnej, linii znaków 

orientacyjnych itp.

•

szeregi powinny być prostoliniowe a odchylenie punktów głównych 

poszczególnych     zdjęć od prostej łączącej punkty główne skrajnych 

zdjęć szeregu nie powinny przekroczyć 3% długości tej prostej,

•

brzegi zdjęć powinny być w przybliżeniu równoległe (prostopadłe) do 

osi szeregu,

•

wahania wysokości nie powinny przekracza 3% W,

•

kąty odchylenia osi optycznych od linii pionu nie powinny przekraczać 

         1,5° - 2 °, a nachylenia powyżej 3 °  są niedopuszczalne,

•

osie szeregów powinny przebiegać równoleżnikowo to jest ze 

wschodu na zachód, lub być dostosowane do kształtu zdejmowanego 

obiektu (np. pokrywać się z osią obiektów liniowych),

•

linie nalotu powinny być tak zaprojektowane aby w ramach 

poszczególnych stereogramów wahania wysokości były możliwie jak 

najmniejsze.

Plan nalotu

Dla prawidłowego projektu planu nalotu istotnymi są zależności jakie 

zachodzą pomiędzy określonymi jego parametrami. W 
szczególności pomiędzy prędkością samolotu (v), czasem 
otwarcia migawki (T) a wielkością rozmazania σ (plamka 
rozmazania) oraz prędkością samolotu (v), czasem pomiędzy 
ekspozycjami (t)   a pokryciem podłużnym  (p).

Rozmazanie obrazu spowodowane ruchem samolotu w czasie 

otwarcia migawki kamery wynosi:

V - prędkość samolotu
T -  czas ekspozycji 
m - skala zdjęć 
                                       

m

T

V

W

T

V

f













Plan nalotu

Aby wielkość plamki σ nie przekroczyła żądanej wielkości      

(np. 0,04mm) należy zastosować odpowiedni czas 
ekspozycji (T) obliczony ze wzoru :

Interwał fotografowania (t) (interwał czasu między 

wykonaniem kolejnych zdjęć w szeregu) zależy od skali 
zdjęć, prędkości samolotu, pokrycia podłużnego i wynosi 

V

m

T







100

100 p

V

m

l

V

B

t

x











Plan nalotu

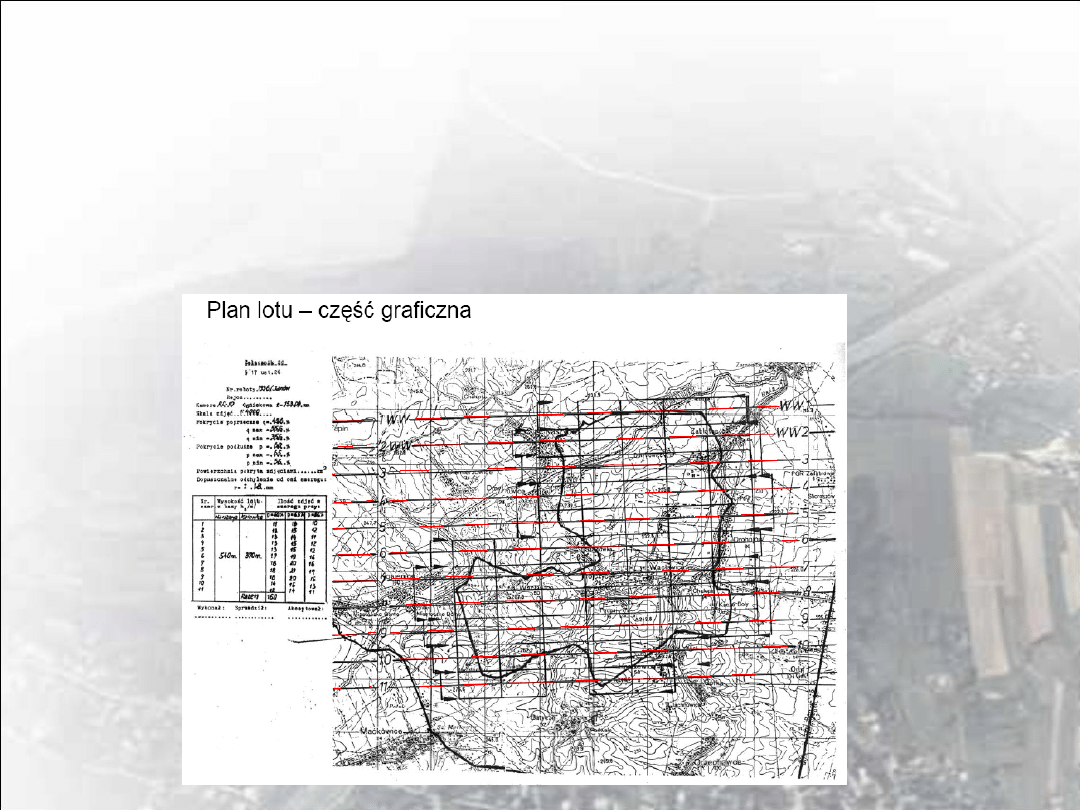
Projekt lotu składa się z części obliczeniowej i graficznej, 

opracowywany jest na istniejących mapach topograficznych w 
skali kilkakrotnie mniejszej od skali zdjęć.

Plan nalotu

Dane wejściowe
•

skala mapy (M)

•

obszar opracowania (wniesiony na mapę)

•

rodzaj opracowania fotogrametrycznego

•

typ kamery

•

prędkość  (V) i pułap samolotu 

•

wysokość bezwzględna lotniska H

lot

Na podstawie analizy danych określa się:
•

rodzaj stożka kamery (f)

•

pokrycie podłużne (p) i poprzeczne (q) zdjęć

•

skalę wykonanych zdjęć (1: m)

•

kierunek lotu

Plan nalotu

Następnie oblicza się:
•

wysokość lotu ponad poziom lotniska W

lot

•

odstęp między osiami szeregów (By)

•

długość bazy (Bx)

•

ilość szeregów (Ny)

•

ilość zdjęć w szeregach (Nx)

•

powierzchnia stereogramu (Pm)  i powierzchnia użyteczna (Pn)

•

interwał czasu między kolejnymi ekspozycjami (t)

•

maksymalny dopuszczalny czas ekspozycji (T)

•

długość błony filmowej 

Na mapę do projektu należy wnieść:
•

granicę obiektu terenu

•

granicę sekcji

•

osie szeregów

•

znaki włączenia i wyłączenia kamery

Plan nalotu

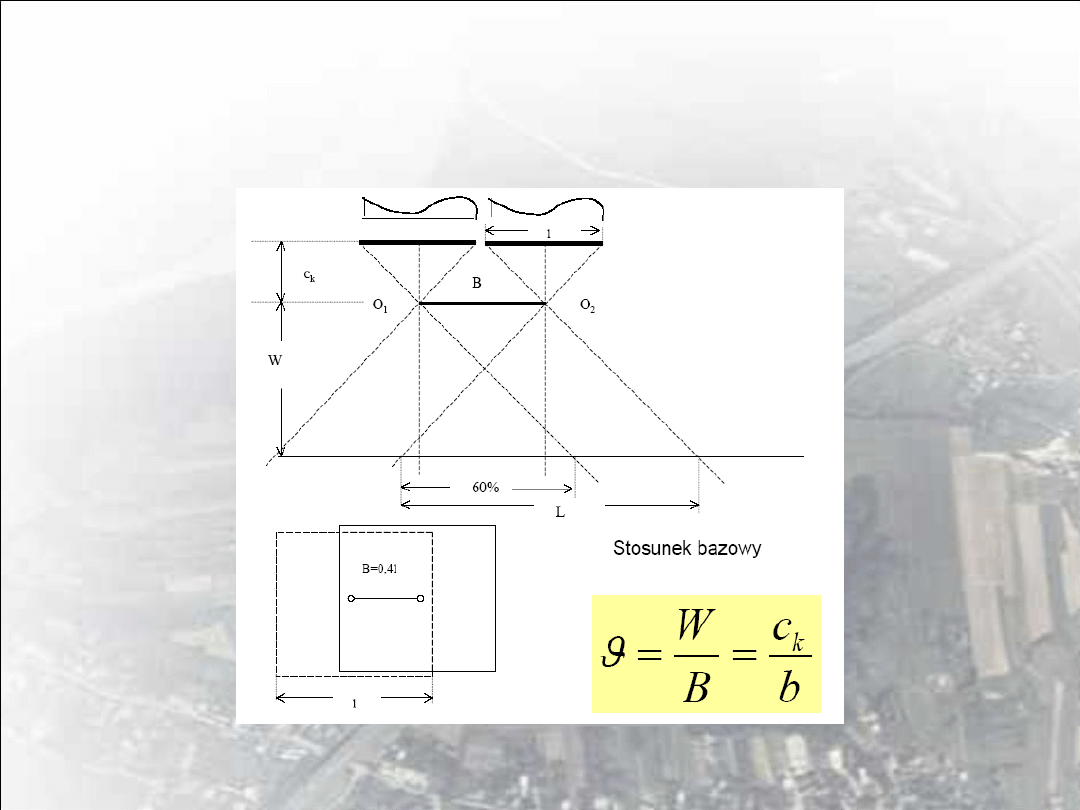
Podstawowe wzory:
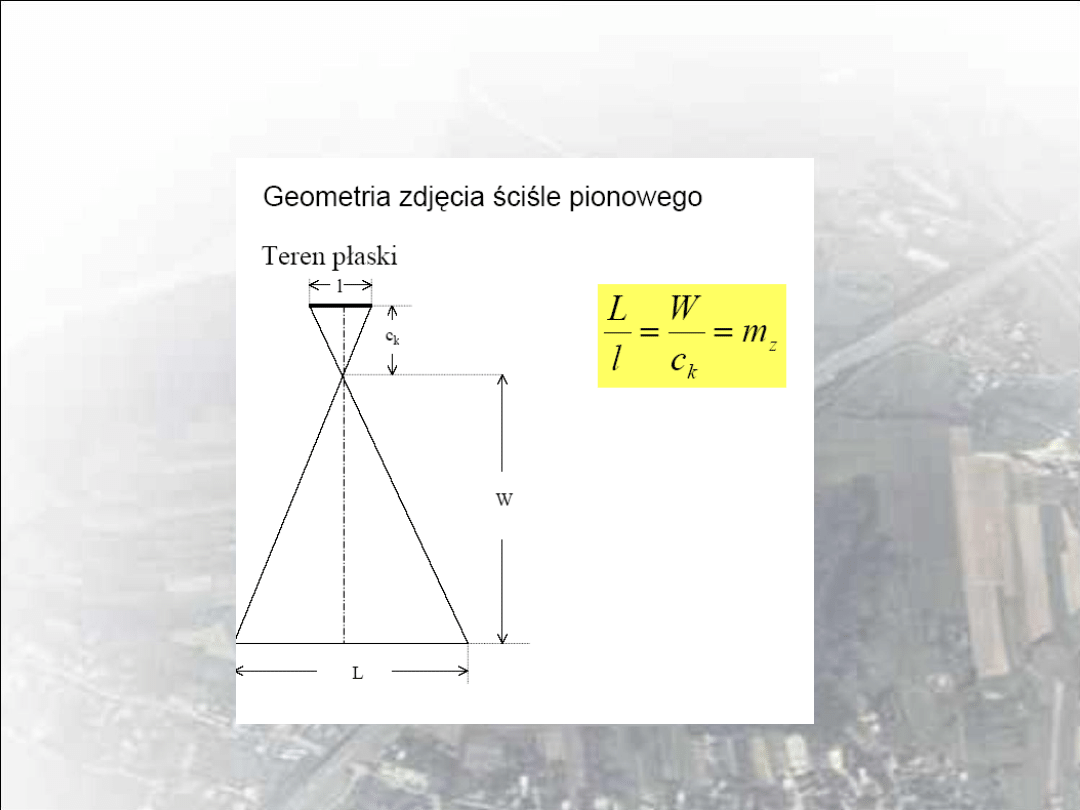
1. skala zdjęć 1: m= f :W
2. wysokość fotografowania W = mf
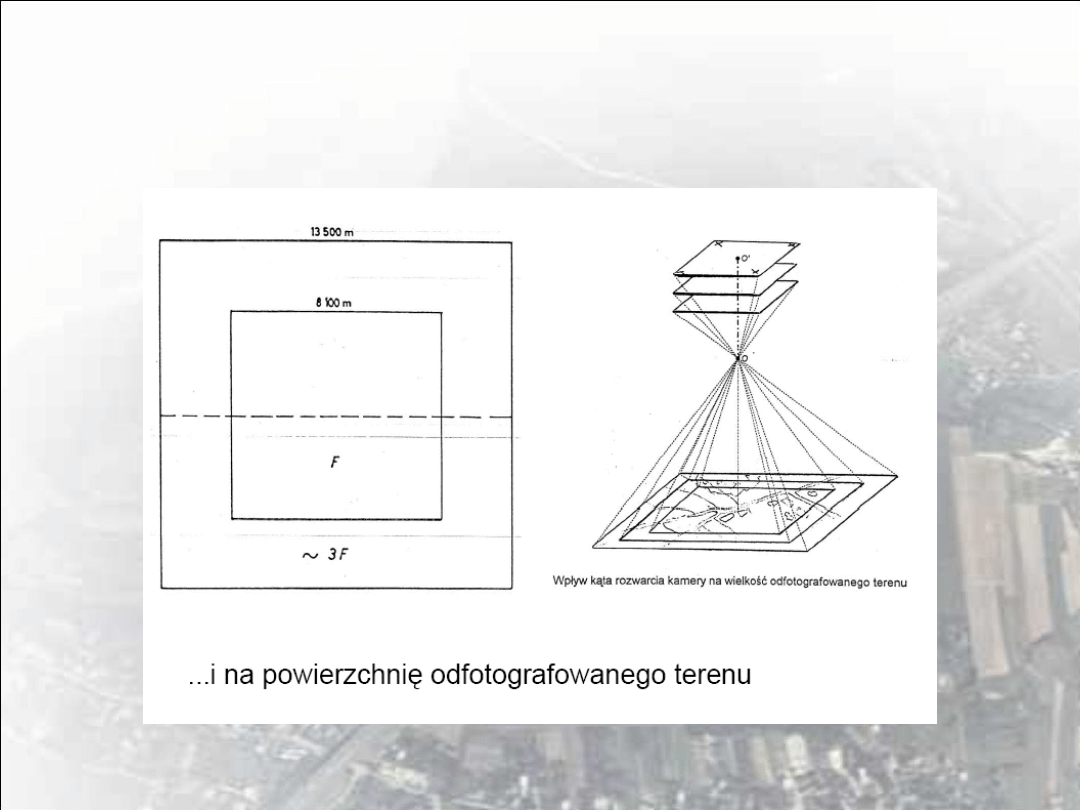
3. terenowy zasięg zdjęcia L = lm
4. baza podłużna

                                               

5. baza poprzeczna                          

6. stosunek bazowy                               

7. wysokość absolutna lotu              W

abs

= W + H

śr

8. wysokość lotu względem lotniska 

             W

lot

= W + H

śr

 

- H

lot

 

100

100 p

L

B

x







100

100 q

L

B

y







f

b

W

B

v

x

x





Plan nalotu

  9. powierzchnia zdjęcia 

P

z 

= L

2

10. powierzchnia modelu 

P

m

 = (L – B

x

) L

11. powierzchnia użyteczna modelu 

             P

n 

= B

x

By

12. liczba zdjęć w szeregu

           

                                                                          (Dx – długość obszaru fotografowania)

13. liczba szeregów

  

                          

                                                                         (Dy – szerokość obszaru 

fotografowania)

14. całkowita liczba zdjęć w rejonie     N = N

x

N

y

     

 lub 

 

      

                                                                     
                                                          

P

ob

  - powierzchnia obszaru 

fotografowania

5





x

x

x

B

D

N

y

y

y

B

D

N 

n

ob

P

P

N 

Plan nalotu

 PRZYKŁAD  OBLICZENIA 
Dx = 24 km,  Dy = 6 km, Pob = 144 km2, M = 1:2000, f = 200mm, format 

18x18cm, 

Hśr =300, h = 100m, wysokość lotniska Hlot= 200m, V=160 km/godz., 
 = 0,03mm, mk = 50000
Na podstawie podanej skali opracowania wybieramy zalecaną skalę nalotu
                                              mz = 8000
Obliczamy wysokość względną lotu
                                              W = mf = 8000200mm = 1600 m
Bezwzględna wysokość wyniesie :
                                        W = 1600 m +300 m = 1900 m
Wysokość lotu odniesiona do wysokości lotniska 

     W = 1600 m + 300 m – 200 m = 1700 m 

Plan nalotu

Z podanych powyżej zależności wyznaczamy pokrycie podłużne (p) i 

poprzeczne (q)

 p% = 64% +                       67%

 

q%  = 36% +                       39%

Zasięg pojedynczego zdjęcia w terenie bez uwzględnienia pokrycia
                                        Lx = 18cm 8000 = 1440m
                                        Ly = 18cm 8000 = 1440m
Użyteczny zasięg zdjęcia to jest po uwzględnieniu pokrycia wyniesie :
                                        Bx = 1440m(1-0,67)= 475m
                                        By = 1440m(1-0,39)= 878,4 m





1600

100

50





1600

100

50

Plan nalotu

Powierzchnia użyteczna jednego zdjęcia wyniesie :
                                      Bx  By = 41,72ha
Ilość zdjęć (N) na obiekt możemy obliczyć z zależności :

                                          

N =                            zdjęć

lub jako iloczyn zdjęć w szeregu (N

x

)  i ilości szeregów (N

y

)

                                     N = NxNy = 51* 7 = 357 zdjęć

345

72

,

41

14400



ha

ha

51

5

,

50

475

24000









m

m

B

D

N

x

x

x

7

63

,

6

4

,

878

6000









m

m

B

D

N

y

y

y

Plan nalotu

do obliczonej ilości dodajemy jeszcze 10% do 15% tak zwanego 

zapasu , otrzymując ogólną ilość zdjęć, która w naszym wypadku 
wyniesie :

                                        3571,1 = 393 zdjęć.
Mając ogólną ilość zdjęć obliczamy ilość potrzebnej błony w metrach :
                                        d = 18 cm393 = 70,74m
ponieważ odstęp pomiędzy sąsiednimi zdjęciami wynosi 1 do 2 cm, to 

przy 393 zdjęciach na odstępy należy doliczyć      

                                          3931,5cm =  5,90m
zatem łączna długość błony wyniesie:
                                         70,74m + 5,90m = 76,64m
Typowe długości błon lotniczych wynoszą 60 lub 120 m, a zatem 

należy zabrać jedną szpulę ze 120 metrami taśmy filmowej. 

Plan nalotu

Linię nalotu wykreślamy z uwzględnieniem wyżej podanych 

wymagań, przy czym skrajna linia przebiega w odległości  
       od brzegu obiektu a następne w odległości By

Pozostało jeszcze obliczenie wielkości najbardziej istotnych dla 

operatora kamery to jest t, T, ewentualnie  i V.

interwał czasowy pomiędzy dwoma kolejnymi ekspozycjami 

wyniesie :

2

y

B

sekundy

sekund

sekund

km

mm

godz

km

mm

V

m

T

185

1

160000

864

3600

160

240

/

160

8000

03

,

0

















sekund

m

sekund

m

godz

km

m

V

B

t

x

68

,

10

160000

3600

475

.

/

160

475











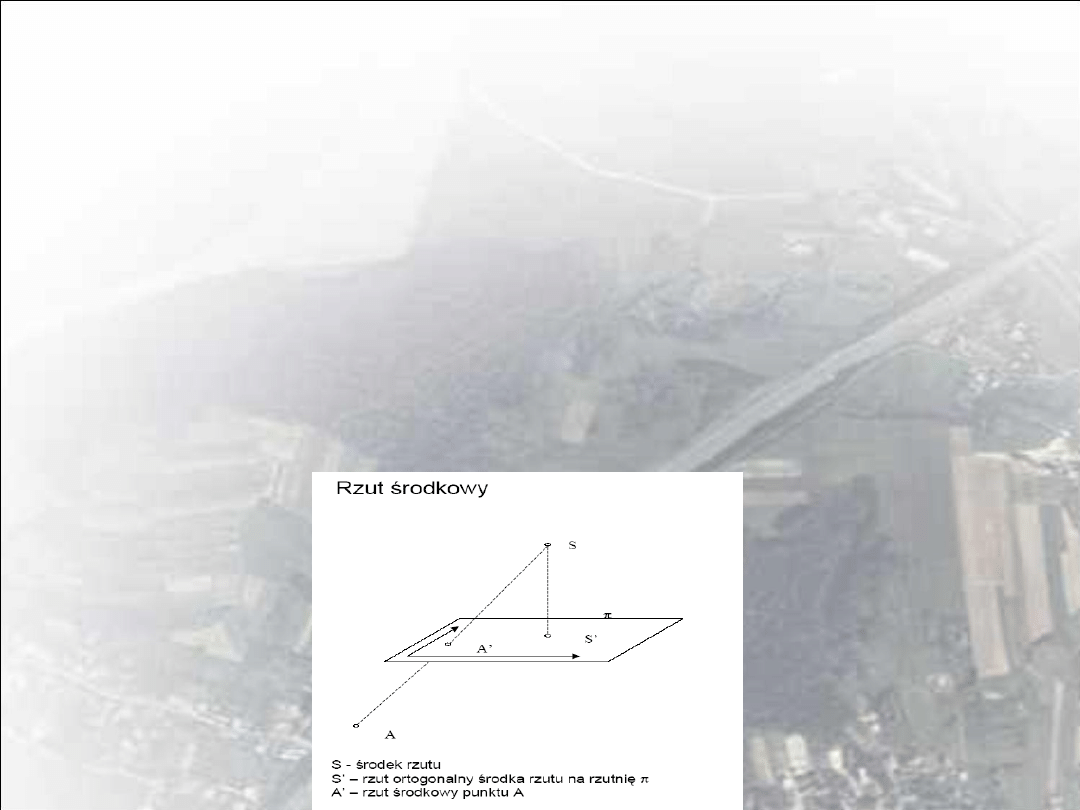
Zdjęcie będzie rzutem środkowym jeśli:

• obiektyw kamery będzie wolny od błędu dystorsji,
• w momencie ekspozycji materiał negatywowy lub matryca CCD 

będą tworzyć płaszczyznę,

• po obróbce fotochemicznej lub długim przechowywaniu obraz nie 

zostanie zdeformowany,

• migawka aparatu nie zniekształci obrazu (dlatego w kamerach 

fotogrametrycznych stosuje się migawki centralne),

• obraz nie zostanie zniekształcony przez refrakcję atmosferyczną,
• wyżej wymienione błędy zostaną usunięte w procesie 

fotogrametrycznym

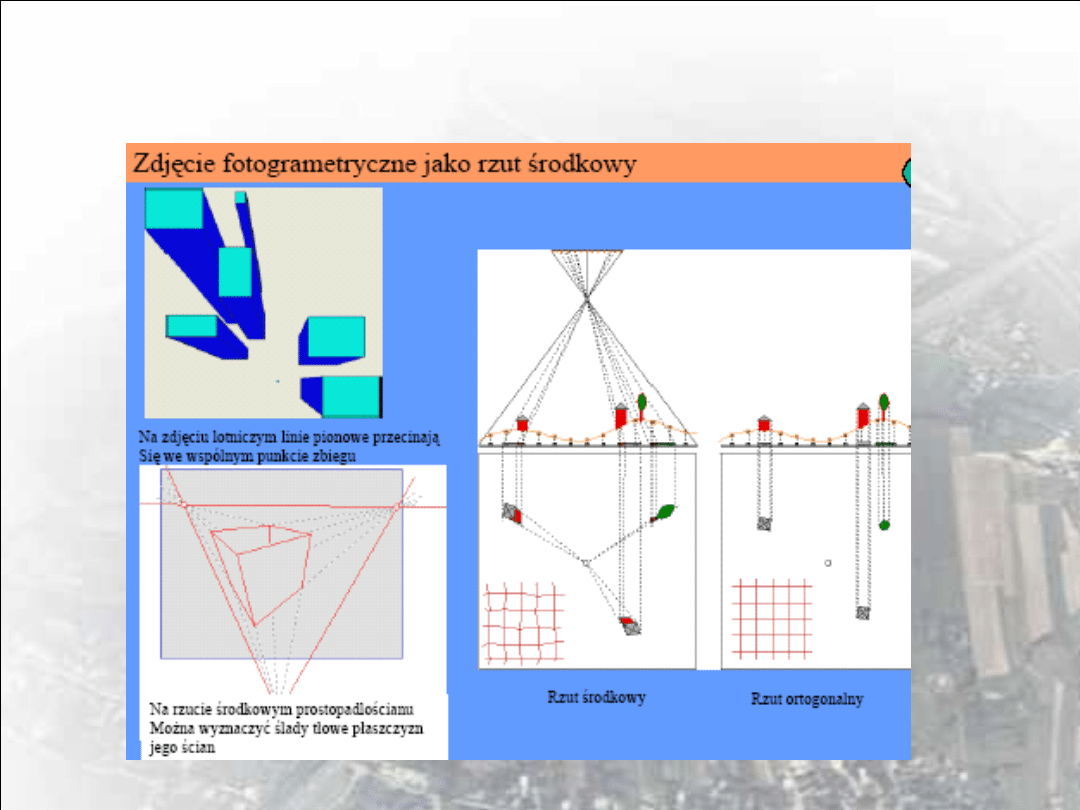
Zdjęcie lotnicze jako rzut środkowy

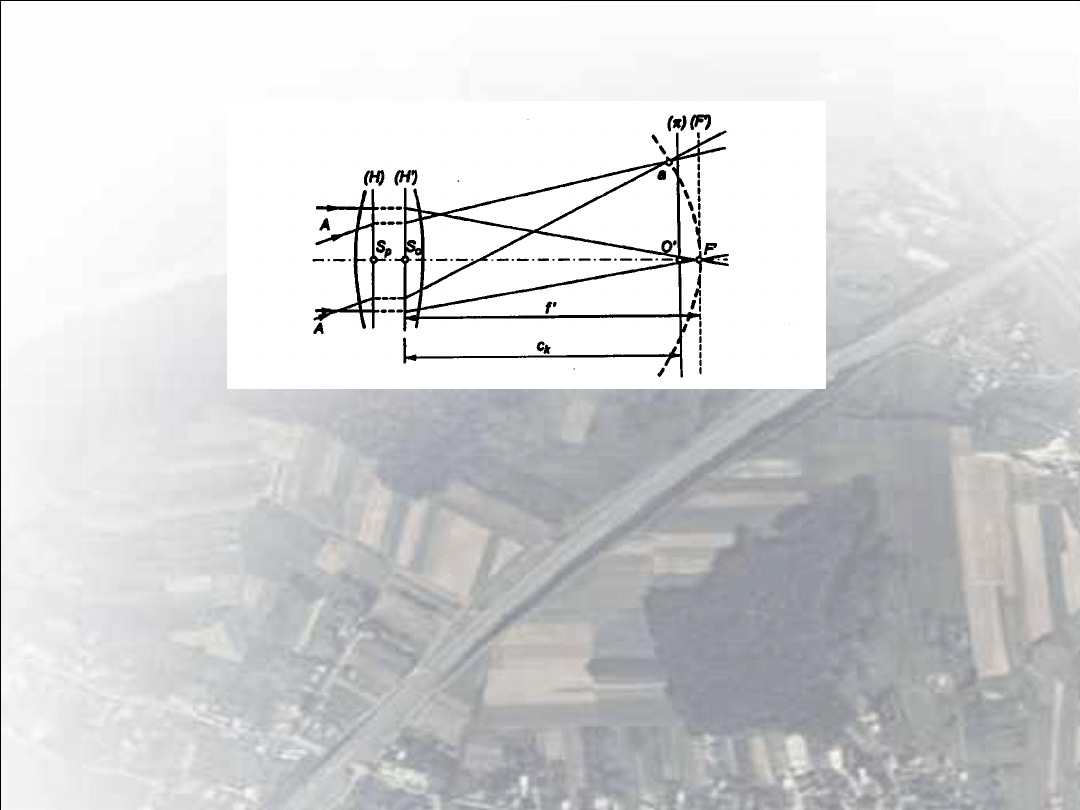
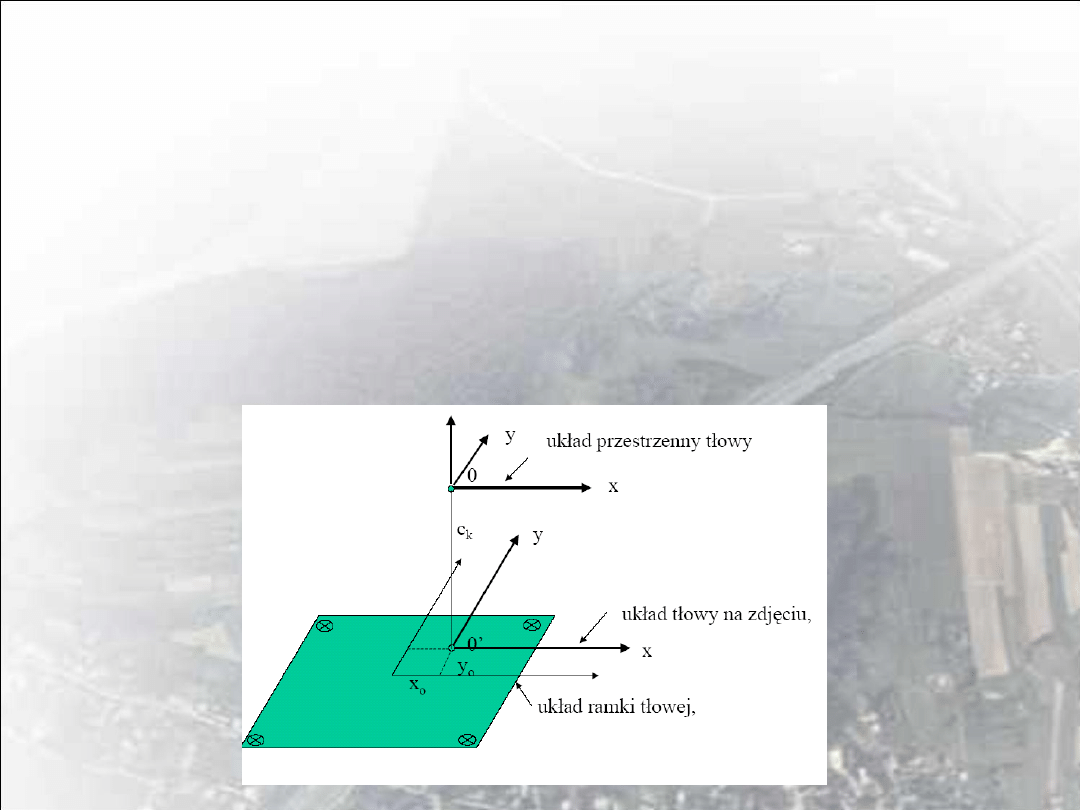
Odległość ogniskowa , a odległość obrazowa kamery c

k

 

    Rys 1  Relacje między ogniskową obiektywu a odległością obrazową 

kamery 

• Dla kamer lotniczych fotografowanym przedmiotem jest powierzchnia 

Ziemi, znajdująca się w odległości, co najmniej kilkuset metrów (dla 
obiektywu leżąca praktycznie w nieskończoności). Oznacza to, że 
obraz tworzy się w płaszczyźnie ogniskowej kamery (F’).

• W wyniku pozostałości szczątkowych błędów optycznych ostry obraz 

utworzy się nie w płaszczyźnie ogniskowej (F’), lecz na pewnej sferze, 
stycznej do płaszczyzny ogniskowej w ognisku F’. W kamerach 
lotniczych tak dobiera się położenie obiektywu względem płaszczyzny 
ramki tłowej (π), że ramka tłowa jest sieczną powierzchni „ najlepszej 
ostrości”, a rozkład ostrości na całej powierzchni zdjęcia jest 
najkorzystniejszy.

Odległość ogniskowa , a odległość obrazowa kamery c

k

 
 

Odległość ramki tłowej  (π) od obrazowego środka rzutów O jest 
odległością obrazową kamery c

K

 (inaczej stałą kamery) i jest ona 

nieznacznie mniejsza od ogniskowej obiektywu.
 
Dla obecnie powszechnie używanego formatu kadru lotniczych 
kamer pomiarowych 
23x23 cm stosuje się obiektywy:

normalnokątny                   f ≈ 305 mm,     2β = 55º
półnormalnokątny              f ≈ 210 mm,     2β = 70º
szerokokątny                      f ≈ 153 mm,     2β = 90º
nadszerokokątny                f ≈   88 mm,     2β = 120ºk

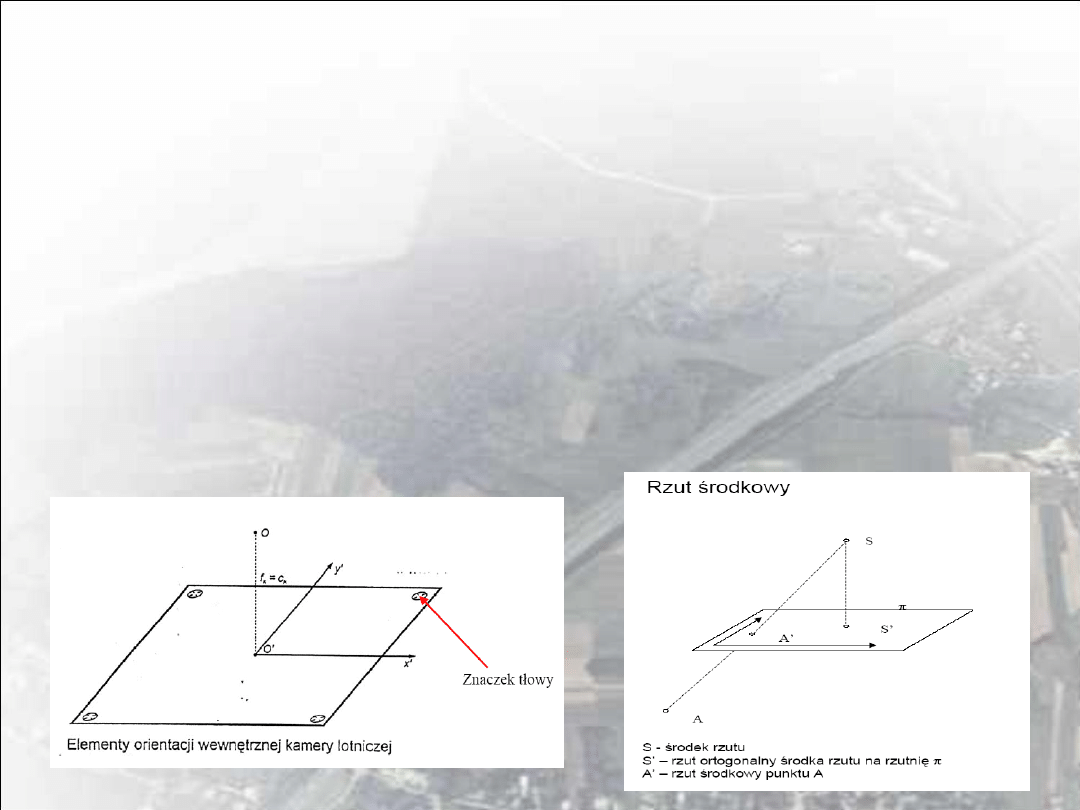
Elementy orientacji wewnętrznej kamery 

•  Obraz utworzony  „idealnym obiektywem” jest rzutem środkowym 

przestrzennego obiektu (np. powierzchni Ziemi fotografowanej z 
samolotu) na płaszczyznę obrazową.

• Z teorii rzutu środkowego wiadomo, że dla rekonstrukcji wiązki 

projekcyjnej potrzebna jest znajomość położenia środka rzutów 
względem obrazu (tj. zdjęcia). To położenie wyznaczają:

• położenie tzw. punktu głównego zdjęcia O’, tj. spodka 

prostopadłego środka rzutów (obrazowego środka rzutów S

o

) na 

płaszczyznę ramki tłowej,

• odległość środka rzutów S od płaszczyzny ramki tłowej, tzw. 

odległość obrazowa kamery c

k 

 (inaczej stała kamery)

Elementy orientacji wewnętrznej kamery 

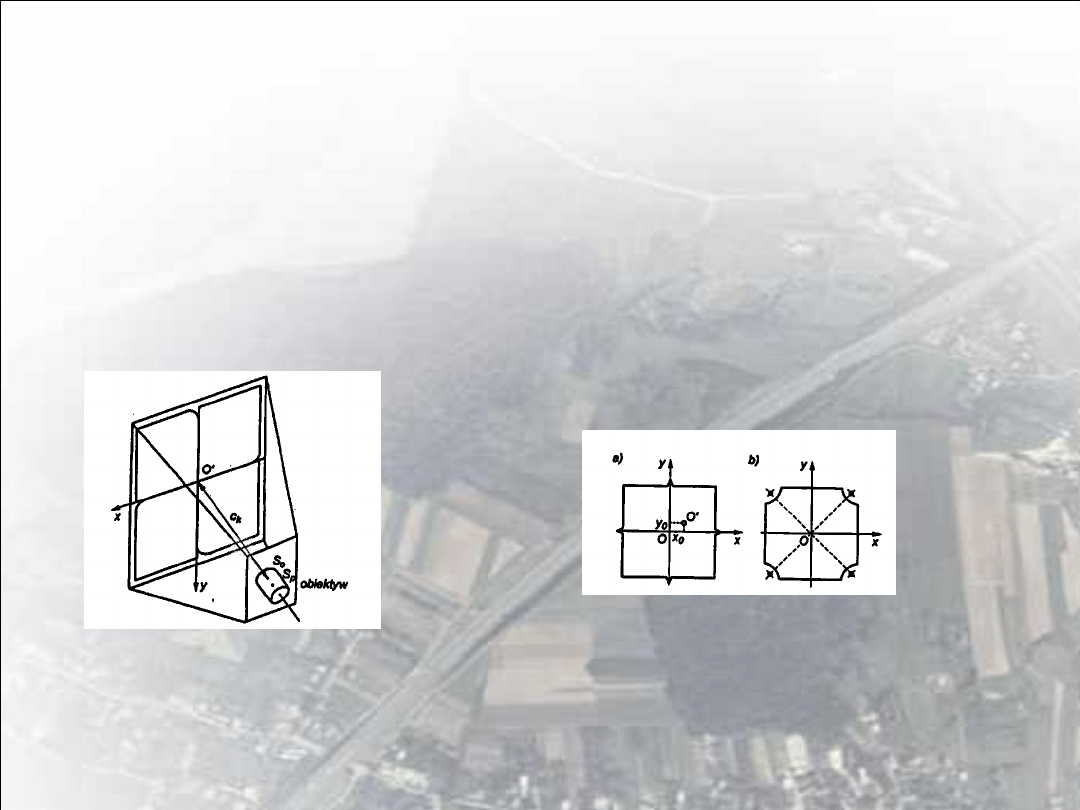
Wielkości pozwalające na rekonstrukcję wiązki projekcyjnej zdjęcia określają 

tzw. elementy orientacji wewnętrznej kamery, do których zaliczamy:

- odległość obrazową kamery c

k

- położenie punktu głównego, określone przez jego współrzędne tłowe x

o

, y

o

 
 

                                                                    

  Rys. 3 Układ współrzędnych tłowych  kamery 

Rys. 2    Elementy orientacji wewnętrznej kamery 
                                                           

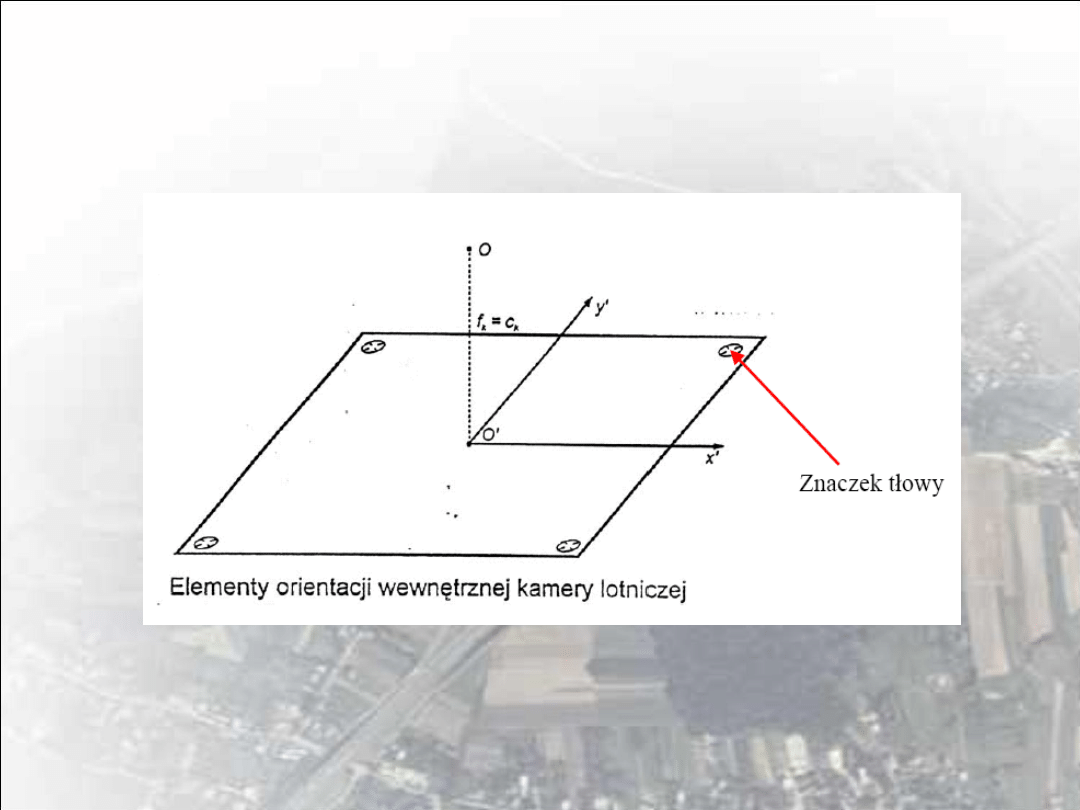
Elementy orientacji wewnętrznej kamery 

    

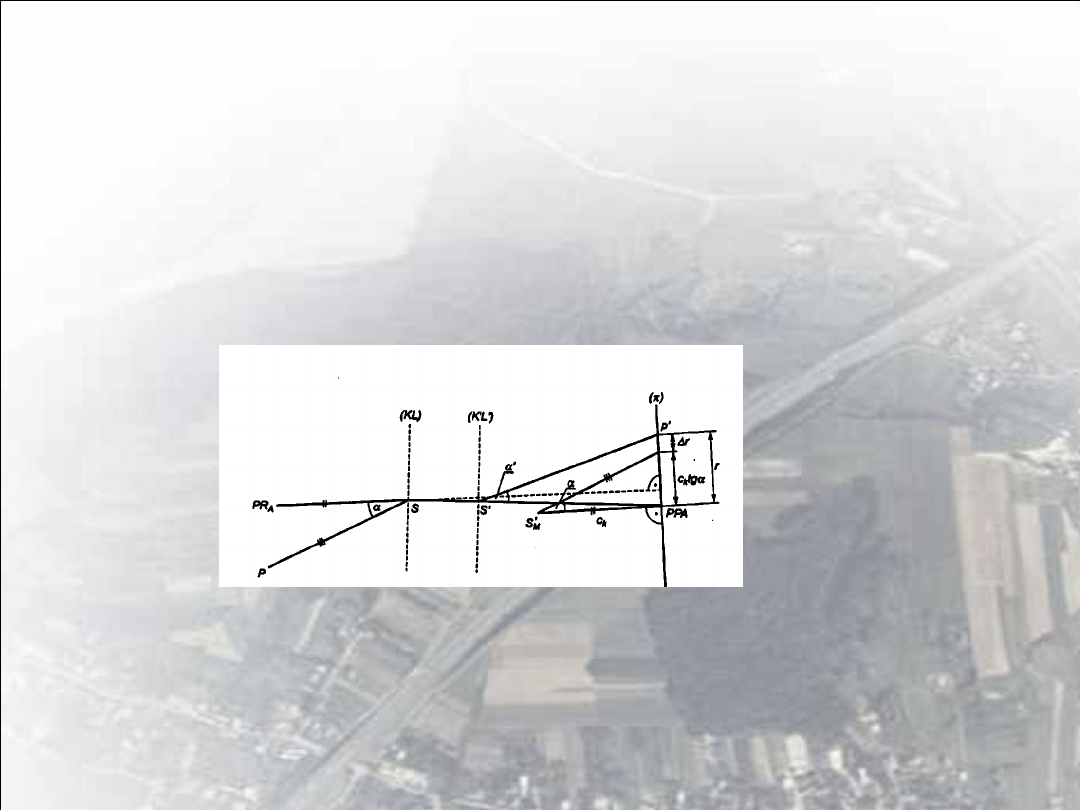
Techniczna definicja elementów orientacji wewnętrznej 

kamery

•

 Z powodu błędów rzeczywistego obiektywu „model matematyczny” 
obiektywu zastępujemy „modelem technicznym”, w którym oś 
główną obiektywu zastępuje się autokolimacyjną osią obiektywu 
PR

A

 (taką, która w przestrzeni przedmiotowej jest prostopadła do 

ramki tłowej kamery i przechodzi przez przedmiotowy punkt 
węzłowy S). Oś autokolimacyjna po przejściu przez obiektyw 
wyznacza punkt główny autokolimacji PPA.

                                 Rys. 4 Elementy orientacji wewnętrznej „realnego obiektywu    

       

                     

 PR

A 

- autokolimacyjna oś  obiektywu,

                     

 PPA - punkt główny autokolimacji,

                    

 KL, K’L’ – wejściowa i wyjściowa źrenica obiektywu, 

S, S’ – przedmiotowy i obrazowy fizyczny środek projekcji,
C

k

 – odległość obrazowa, S’

M

 – matematyczny środek projekcji

Techniczna definicja elementów orientacji wewnętrznej 

kamery 

• Ze względu na fakt, że dystorsja radialna nie jest ściśle 

symetryczna (jej wartości w danym punkcie zdjęcia zależą nie 
tylko od promienia radialnego, ale również od położenia) i jeżeli ta 
asymetria jest znacząca, to dąży się do „scentrowania” jej 
wykresów przez odniesienie ich nie do punktu głównego 
autokolimacji PPA, lecz do punktu najlepszej symetrii PPBS. 
Tak określony punktu najlepszej symetrii jest – w dalszych 
opracowaniach fotogrametrycznych – traktowany jako punkt 
główny.

Zdjęcie lotnicze w skali  1: 5000