STATYSTYKA OPISOWA

ĆWICZENIA 2

Metody opisu.

Miary przeciętne

Opis tabelaryczny

Metoda opisu statystycznego polegająca na 

ujęciu zgromadzonego materiału 

statystycznego w postaci szeregu 

statystycznego (gdy opis dotyczy jednej 

cechy) bądź w postaci tablicy statystycznej 

(gdy opis dotyczy większej liczby cech. 

Tablice statystyczne można klasyfikować na:
•  proste zwane szeregami uwzględniające 

jedną cechę
•  złożone – uwzględniające kilka cech.
Inny podział wyróżnia tablice:
•  robocze, 
•  wynikowe

Opis tabelaryczny

Wśród szeregów statystycznych można
 dodatkowo wyróżnić:
• szeregi szczegółowe (nieuporządkowane i 

uporządkowane)

• szeregi rozdzielcze

- punktowe
- przedziałowe

Mogą mieć one postać szeregów liczebności bądź 
częstości (prostej lub skumulowanej).
Uwzględniając cel wykorzystania szeregu  można wyróżnić:
• szeregi strukturalne,
• szeregi czasowe (dynamiczne
• szeregi przestrzenne

TYPY SZEREGÓW STATYSTYCZNYCH

1) Liczba wyjazdów służbowych za granicę 
pracowników firmy „Z”:
                  0,   0,    0,   1,    2,   2,   2,    3,   4,    5,

2) Ocena jakości pewnego produktu (w punktach):

Ocena 

jakości

n

i

f

i

f

i

 %

3,5

4

4,5

5

4

18
22
20

0,06
0,28
0,35
0,31

6

28
35
31

Razem

64

1,0

100

3) Wiek pracowników firmy „A”

Wiek

n

i

f

i

f

i

 %

20-25
25-30
30-35
35-40
40-45

4
9
20
8
5

0,09
0,20
0,43
0,17
0,11

9
20
43
17
11

Razem

46

1,0

100

5)  Wiek pracowników firmy „B”

Wiek

n

i

f

i

f

i

 %

mniej niż 
25
25-30
30-35
35-40
40 i więcej

4
9
20
8
5

0,09
0,20
0,43
0,17
0,11

9
20
43
17
11

Razem

46

1,0

100

Tablice i szeregi statystyczne -

szereg z przedziałami klasowymi

Tworząc szereg z przedziałami 

klasowymi należy rozstrzygnąć 

następujące kwestie:

1.ile klas winno być utworzonych?

2.jaka winna być ich wielkość 

(rozpiętość)?

3.jak winny być ustalone 

(zamknięte) granice przedziałów?

Ad.1.Liczba klas zależy od 
liczebności opisywanej zbiorowości i 
liczby wariantów cechy

Ad. 2 Wielkość (rozpiętość) klas zależy 

od obszaru zmienności badanej cechy 

oraz liczby klas. Łączna rozpiętość 

wszystkich klas – w przypadku cechy 

ciągłej – musi przekraczać obszar 

zmienności tej cechy.
Ad. 3. W przypadku cechy ciągłej każda 

z klas musi być jednostronnie 

domknięta („od dołu bądź z góry”)

Budowa tablicy 

statystycznej

Właściwie skonstruowana tablica winna składać się z tytułu, 

makiety tablicy oraz źródła danych. 

• Tytuł tablicy winien precyzyjnie określać badaną zbiorowość 

pod względem rzeczowym, czasowym i przestrzennym oraz 

zawierać ujęte w tablicy cechy statystyczne; 

• Makieta tablicy (zwana również tablicą właściwą) składa się z 

wierszy i kolumn oraz ich tytułów (tytuły wierszy określa się 

„boczkiem” tablicy, zaś tytuły kolumn „główką” tablicy).  

Wnętrze tablicy, czyli „pola” znajdujące się na skrzyżowaniach 

poszczególnych wierszy i kolumn są wypełniane 

zgromadzonym materiałem statystycznym. Należy tu 

zaznaczyć, iż każde pole tablicy musi być bezwzględnie 

wypełnione. Jeśli z różnych względów nie ma możliwości 

wypełnienia pola tablicy danymi liczbowymi wówczas 

wykorzystywane są odpowiednie znaki umowne. 

• Źródło danych wskazuje miejsce pochodzenia danych 

zawartych w tablicy (np. rocznik statystyczny, wyniki spisu, 

badania własne, sprawozdawczość firmy bądź instytucji0. 

Znaki umowne stosowane w tablicach 

statystycznych

„ – „ (kreska) -

oznacza, że zjawisko nie występuje,

„ . „ (kropka) - oznacza zupełny brak informacji lub brak informacji 
                          wiarygodnych,
„0” (zero)   -      oznacza, że zjawisko występuje w niewielkich 

ilościach 

                          (mniej niż 50% przyjętej jednostki miary),
„×” (ukośny krzyżyk) -  oznacza, że wypełnienie danego pola ze
                         względu na układ tablicy jest niemożliwe bądź 

niecelowe,

„Δ” (pusty trójkąt) -  oznacza, że nazwy zostały skrócone w 

stosunku do

                          obowiązującej klasyfikacji,
„▲” (pełny trójkąt) - oznacza, że dane nie mogą być opublikowane 

ze względu na konieczność zachowania tajemnicy statystycznej,

„w tym” -  oznacza, że nie podaje się wszystkich składników sumy

.

Opis graficzny

Metoda opisu polegająca na graficznej prezentacji 
materiału statystycznego w postaci wykresów. 
Obejmuje ona następujące typy wykresów:
- powierzchniowe (np. kołowe, wykresy słupkowe),
- bryłowe,
- liniowe (np. diagramy)
- punktowe,
- obrazkowe,
- mapowe
- kombinowane

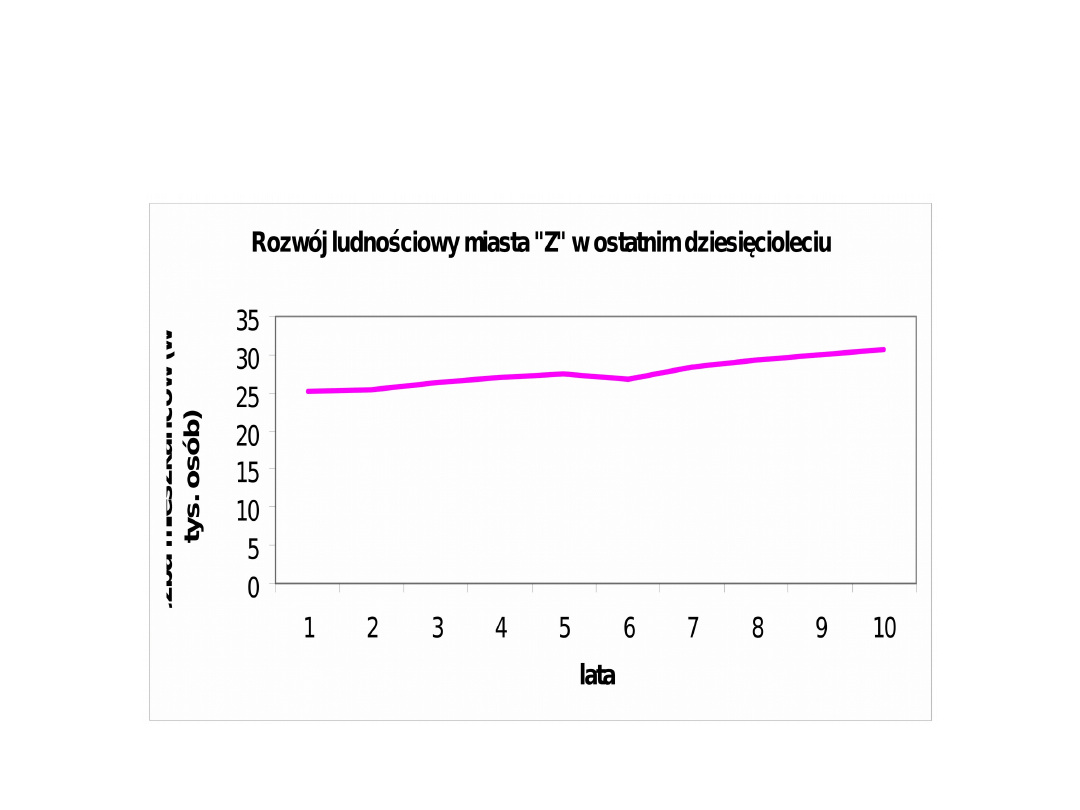
Wykres liniowy

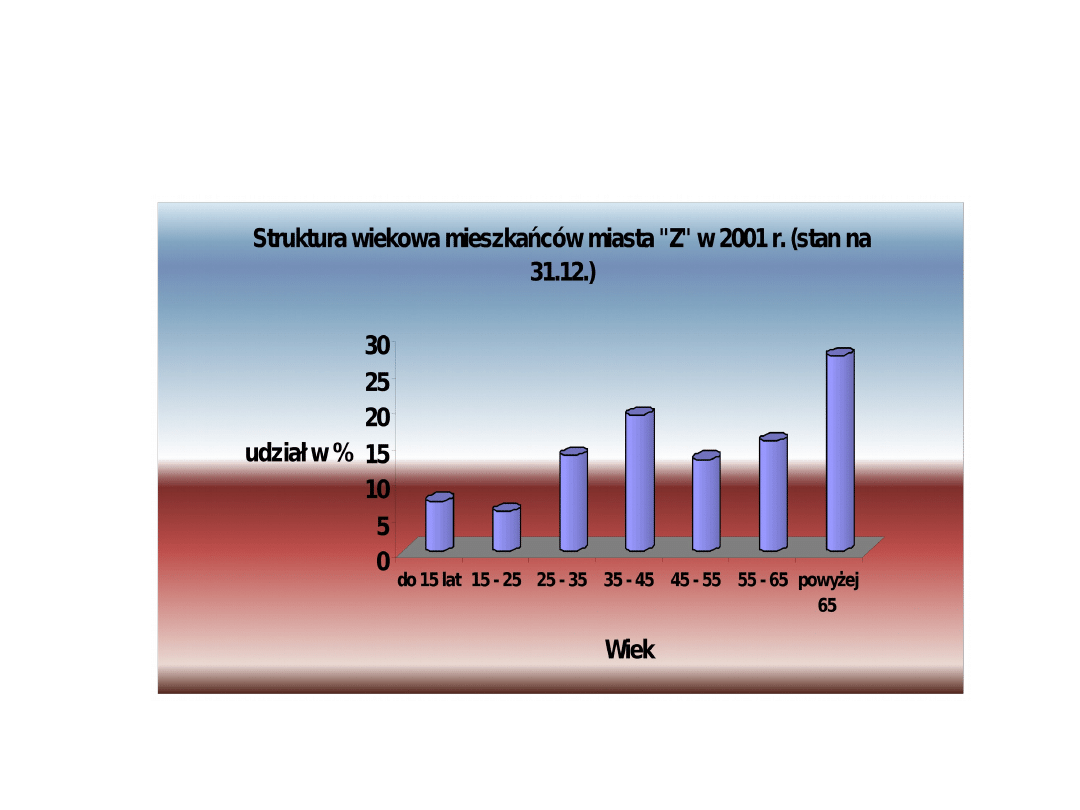
Wykres bryłowy

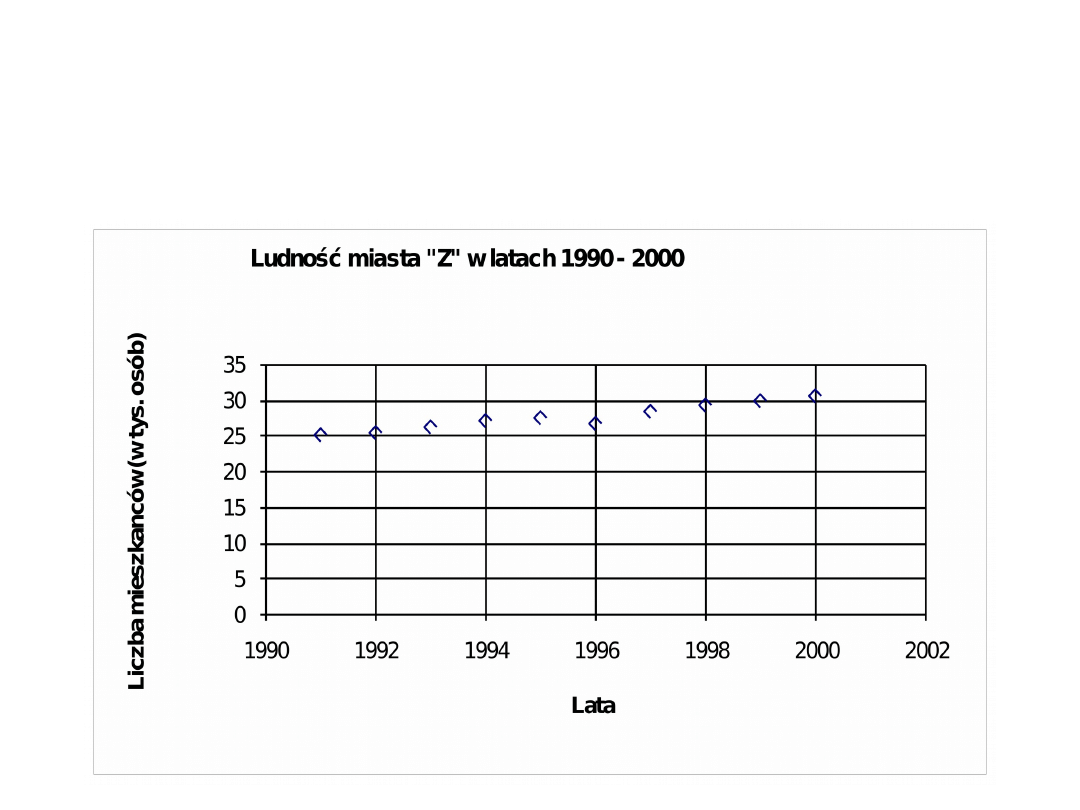
Wykres punktowy

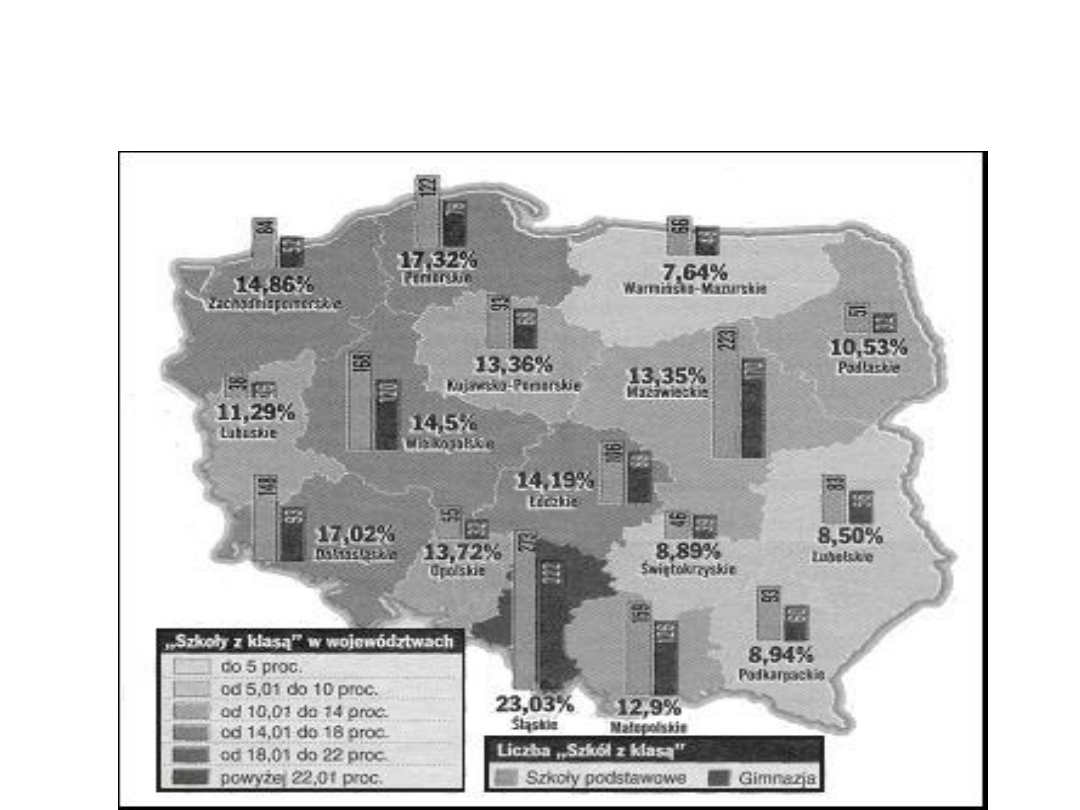
Wykres mapowy

Wykres obrazkowy

Wykres słupkowy 

(histogram)

Wykres kołowy

Opis parametryczny

Opis parametryczny stanowi jeden z 
najczęściej wykorzystywanych sposobów 
opisu rozkładu cechy statystycznej 
głównie z uwagi na jego syntetyczną i 
skróconą postać. Ta forma opisu 
wykorzystuje parametry statystyczne, 
tj. charakterystyki liczbowe opisujące 
określone właściwości rozkładu wartości 
badanej cechy w szeregu statystycznym 
oraz momenty statystyczne .

Momenty statystyczne

Momenty statystyczne są często wykorzystywanymi 

charakterystykami rozkładów cechy statystycznej. 
Wśród nich wyróżnia się dwie podstawowe grupy:

•

momenty zwykłe, które są średnimi odchyleń 
wartości cechy od punktu zerowego podniesionych 
do potęgi k; ich ogólną postać można wyrazić 
wzorem:

•

momenty centralne, które są średnimi odchyleń 
poszczególnych wartości cechy od ich średniej 
arytmetycznej podniesionych do potęgi k; ich 
ogólną postać wyraża wzór:





N

n

x

N

n

x

x

M

l

i

i

k

i

l

i

i

k

i

k















1

1

*

*

0

)

(

 





N

n

x

x

x

m

l

i

i

k

i

k









1

*

PARAMETRY STATYSTYCZNE

• Parametry przeciętne 
(średnie)

• Parametry zmienności 
(rozproszenia)

• Parametry skośności 
(asymetrii)
• Parametry 
koncentracji

PARAMETRY (MIARY) 

ŚREDNIE (PRZECIĘTNE)

służą do analizy przeciętnego 

(średniego) poziomu wartości cechy

Podział miar średnich:

klasyczne

pozycyjne

Parametry średnie

Klasyczne miary przeciętne – 

średnia 

arytmety-

  czna

, średnia geometryczna, średnia 

harmoniczna,

  średnie potęgowe, 

Pozycyjne miary przeciętne - mediana, 

dominanta

 kwartyle, centyle

ŚREDNIA ARYTMETYCZNA 

-  określa  przeciętny  poziom  wartości 
cechy  przypadający  na  jednostkę 
zbiorowości. 
tzn. 

rozkłada 

globalny 

fundusz 

wartości  cechy  równomiernie  między 
wszystkie jednostki. 
 
Średnia arytmetyczna to często 
wielkość abstrakcyjna.
 

Średnia arytmetyczna – sposoby obliczania:

- szereg szczegółowy i surowy materiał 
statystyczny

N

x

x

N

i

i







1

- szereg rozdzielczy punktowy

N

n

x

x

k

i

i

i







1

- szereg rozdzielczy przedziałowy

N

n

x

x

k

i

i

i

o







1

i

o

x

- środek przedziału

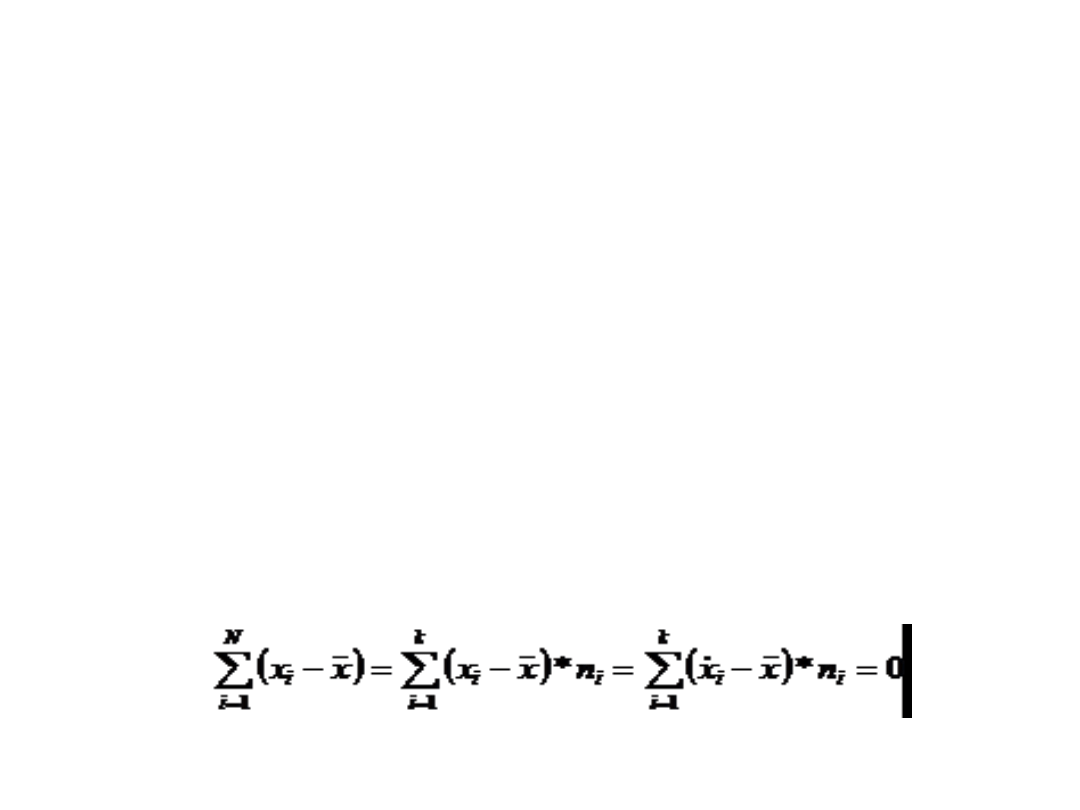
Własności średniej arytmetycznej

• jako parametr klasyczny ustalana jest na 

podstawie wszystkich wartości cechy, a 
więc 

posiada wysoką wartość poznawczą 

(w odróżnieniu np. od parametrów 
pozycyjnych),

• suma ważona odchyleń poszczególnych 

wartości cechy od ich średniej 
arytmetycznej wynosi zawsze zero, co 
wynika z faktu, że średnia ta pełni rolę 
„środka ciężkości” analizowanego zbioru 
wartości cechy. Własność tę można zapisać 
relacją:

Własności średniej 

arytmetycznej

• ważona suma kwadratów odchyleń poszczególnych 

wartości cechy od ich średniej arytmetycznej jest 
najmniejsza z możliwych, co można zapisać 
następującą zależnością:

• jeśli w szeregu rozdzielczym wszystkie wagi - w 

szczególnym przypadku będą to liczebności bądź 
częstości - pomnożymy (bądź podzielimy) przez ten 
sam czynnik q, to średnia arytmetyczna wartości 
cechy z nowym systemem wag będzie identyczna 
jak średnia liczona według pierwotnych wag .













min

*

*

2

1

1

2

2

1

























i

k

i

i

k

i

i

i

N

i

i

n

x

x

n

x

x

x

x



Własności średniej arytmetycznej

• jeśli wszystkie wartości cechy X podzielimy (bądź 

pomnożymy) przez tę samą wielkość q to średnia 
arytmetyczna tak zmienionych wartości cechy 
będzie q-krotnie mniejsza (lub q-krotnie większa) od 
średniej pierwotnych wartości cechy. 

• jeśli do wszystkich wartości cechy X dodamy (bądź 

od wszystkich wartości odejmiemy) tę samą 
wielkość q to średnia arytmetyczna tak zmienionych 
wartości cechy będzie o wielkość q większa (lub o 
wielkość q mniejsza) od średniej liczonej dla 
pierwotnych wartości cechy.

• jeśli badaną zbiorowość podzielimy na kilka 

podzbiorowości to średnia arytmetyczna dla całej 
zbiorowości będzie średnią arytmetyczną ze 
średnich tych podzbiorowości.

Średniej arytmetycznej nie 

oblicza się gdy:

• 

w szeregu występują wartości nietypowe,

• 

gdy  przedziały  skrajne  są  otwarte  i  nie 

można ich domknąć sztucznie,

• 

kiedy przedział skrajny ma maksymalną 

liczebność (rozkład jest skrajnie 
asymetryczny) – zaleca się wówczas 
stosowanie miar pozycyjnych.

Dominanta

• Dominanta, oznaczana jako D(x), 

zwana również wartością modalną 
bądź typową; jest wartością cechy 
występującą najczęściej (najliczniej) 
w badanej zbiorowości. 

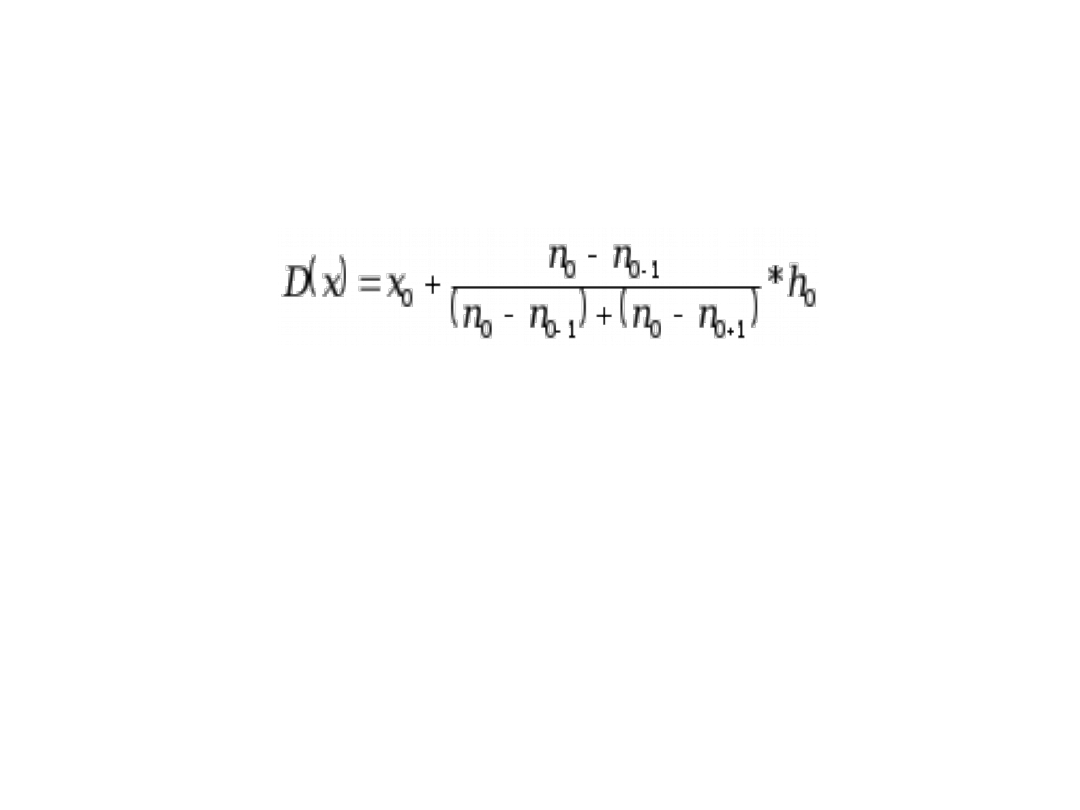
Dominanta w szeregu 

rozdzielczym przedziałowym

– dolna granica przedziału dominującego,
  – rozpiętość przedziału dominującego,
 – liczebność (częstość) przedziału dominującego,
– liczebność (częstość) przedziału poprzedzającego 
przedział dominujący,
 – liczebność (częstość) przedziału następnego po 
przedziale dominującym.

0

x

0

h

0

n

1

0

n

1

0

n

Dominanty nie oblicza się, 

gdy:

• 

w szeregu występuje więcej niż jedno 

maksimum,

• 

przedziały mają różną rozpiętość,

• 

dominanta znajduje się w przedziale 

skrajnym, a ten przedział jest otwarty i nie 
można go domknąć sztucznie

.

MEDIANA 

(KWARTYL 

DRUGI, 

WARTOŚĆ 

ŚRODKOWA)

KWARTYLE  –  wartości  cechy,  które  dzielą 
zbiorowość  na  cztery  równe  liczebnościowo 
części

Me

Q

2

Q

1

Q

3

MEDIANA  -  wartość  cechy,  która  dzieli 
zbiorowość na dwie równe liczebnościowo części. 
Połowa  jednostek  ma  wartości  cechy  nie  większe 
od  mediany  (mniejsze  lub  równe  medianie),  a 
druga  połowa  jednostek  ma  wartości  cechy  nie 
mniejsze od mediany (równe lub większe).

Q

2

  nie  można  obliczyć,  jeśli 

znajduje  się  w 

skrajnym przedziale, a przedział ten jest otwarty i 
nie można go domknąć sztucznie.

Me

Q

2

Q

1

Q

3

Mediana – obliczanie

-szereg szczegółowy i rozdzielczy 
punktowy
dla N – nieparzysta

2

1

)

(





N

x

x

Me

medianą jest wartość środkowej jednostki

dla N – parzysta

2

)

(

1

2

2







N

N

x

x

x

Me

medianą  jest  średnia  arytmetyczna  z  wartości 
dwóch środkowych jednostek

- 

szereg rozdzielczy przedziałowy 

o

o

n

o

h

n

cum

N

x

x

Me

o









 1

2

)

(

o

x

o

n

1



o

n

cum

o

h

- dolna granica przedziału mediany 

- skumulowana liczebność przedziału 
poprzedniego

- liczebność przedziału mediany 

- rozpiętość przedziału mediany 

KWARTYL  PIERWSZY  - 

wartość  cechy 

która  dzieli  zbiorowość  na  dwie  części.  25% 
jednostek  ma  wartości  cechy  nie  większe  od 
Q

1

,  a  75%  jednostek    ma  wartości  cechy  nie 

mniejsze od Q

1

.

Q

1

  nie  można  obliczyć,  jeśli 

znajduje  się  w 

skrajnym przedziale, a przedział ten jest otwarty i 
nie można go domknąć sztucznie.

Q

1

25%

75%

o

x

o

n

1



o

n

cum

o

h

- dolna granica przedziału kwartyla 
pierwszego 

- skumulowana liczebność przedziału 
poprzedniego

- liczebność przedziału kwartyla 
pierwszego 

- rozpiętość przedziału kwartyla 
pierwszego 

Kwartyl pierwszy – obliczenia

- szereg rozdzielczy przedziałowy

o

o

n

o

h

n

cum

N

x

x

Q

o









 1

4

)

(

1

KWARTYL  TRZECI  - 

wartość  cechy  która 

dzieli  zbiorowość  na  dwie  części.  75% 
jednostek  ma  wartości  cechy  nie  większe  od 
Q

3

,  a  25%  jednostek    ma  wartości  cechy  nie 

mniejsze od Q

3

.

Q

3

  nie  można  obliczyć,  jeśli 

znajduje  się  w 

skrajnym przedziale, a przedział ten jest otwarty i 
nie można go domknąć sztucznie.

Q

3

75%

25%

o

x

o

n

1



o

n

cum

o

h

- dolna granica przedziału kwartyla 
trzeciego 

- skumulowana liczebność przedziału 
poprzedniego

- liczebność przedziału kwartyla trzeciego 

- rozpiętość przedziału kwartyla trzeciego 

Kwartyl trzeci – obliczenia

- szereg rozdzielczy przedziałowy

o

o

n

o

h

n

cum

N

x

x

Q

o









 1

4

3

)

(

3