Modele komputerów, maszyna

Turinga

„…Otóż moglibyśmy skonstruować maszynę,
która wykonałaby pracę tego komputera…” A.
Turing

Sławomir Nowak

Podstawy informatyki

„computers” – ludzie którzy

liczą…

computer

http://www.digital-rights.net/?p=1640

„computers”

Komputer służy do liczenia to przecież oczywiste!

Skuteczność komputerów cyfrowych w ich liczeniu opiera się na

matematycznej idei

mówiącej, że

każdy poprawnie sformułowany problem ma

swoje rozwiązanie poprzez jego obliczenie

Maszyna Turinga - od ''komputera'' do komputera, Computerworld, 5 październik 1998, Marek Hetmański

„computers”

Obliczeniem

jest mechaniczna procedura wykonania

zadania w skończonej liczbie kroków. Inaczej

mówiąc, obliczenie jest wykonalne, jeśli istnieje dla

niego

algorytm

.

U podstaw matematyki, logiki i informatyki toczyła

się dyskusja nad

obliczalnością

problemów na

podstawie mechanicznych (algorytmicznych)

procedur.

Maszyna Turinga - od ''komputera'' do komputera, Computerworld, 5 październik 1998, Marek Hetmański

Rozstrzyganie problemów

matematycznych

Znaleźć skończony zbiór reguł i
aksjomatów, pozwalający rozstrzygnąć
dowolny problem matematyczny (idea
Hilberta)

Pewnych problemów matematycznych
nie da się rozstrzygnąć. Problem zdań
typu:
„

to zdanie jest fałszywe

”. Nie sposób

uniknąć paradoksów (twierdzenie Godla)

Alan Turing

(1912-1954),

matematyk, kryptolog,

neurolog, wizjoner, sportowiec

, prekursor sztucznej

inteligencji, twórca teorii automatów, dziedziny

stanowiącej matematyczne podstawy teorii obliczeń.

Największe znaczenie dla rozwoju informatyki miały jego

prace teoretyczne, w szczególności praca podająca

teoretyczny model komputera (

„automat Turinga”

).

TIME zaliczył Turinga do
Największych postaci XX w.

ENIGMA i COLLOSUS

• W czasie wojny Turing należał do grupy ekspertów

zaangażowanych

w odcyfrowywanie niemieckich szyfrów ENIGMA.

Niemałą rolę w tej pracy grał polski wywiad.

• Dla potrzeb deszyfracji zbudowano imponującą maszynę liczącą

o nazwie Collossus. Analizowała ona tysiące wiadomości

dziennie poszukując właściwego klucza (zmienianego trzy razy

dziennie), dzięki któremu Enigma mogła odcyfrować wiadomości.

• Jeden ze współpracowników Turinga tak powiedział komentując

jego rolę w programie łamania szyfrów:

„Nie powiem, że dzięki Turingowi wygraliśmy wojnę ale

śmiem powiedzieć, że bez niego moglibyśmy ją

przegrać”.

1954

• Samobójstwo Turinga

Źródło: http://www.egrafik.pl/tutoriale-photoshop/inne-efekty/nagryzione-jablko/

Maszyna Turinga

Turing pracował na problemem rozstrzygalności

i obliczalności zadań matematycznych;

Rozważył obliczanie od strony czynności, które

wykonuje rachmistrz, a nawet każde dziecko, gdy
na kartce papieru, etap po etapie, przeprowadza
obliczenia.

http://www.sxc.hu/pic/m/b/br/brokenarts/187211_hands_1_writing_hand_.jpg

Maszyna Turinga

Na działanie „komputera” (rachmistrza) składają się

zatem skończone instrukcje przechodzenia
między poszczególnymi kratkami (częściowymi
obliczeniami) na kartce wraz z wykonaniem
pewnych działań – odczytywaniem i
zapisywaniem.

http://www.sxc.hu/pic/m/b/br/brokenarts/187211_hands_1_writing_hand_.jpg

Maszyna Turinga

Wobec każdego problemu, wykonywanego przez

rachmistrza istnieje maszyna uniwersalna, która
może imitować jego obliczenia.

http://www.sxc.hu/pic/m/b/br/brokenarts/187211_hands_1_writing_hand_.jpg

„…Otóż moglibyśmy skonstruować maszynę,
która wykonałaby pracę tego komputera…”

A.

Turing

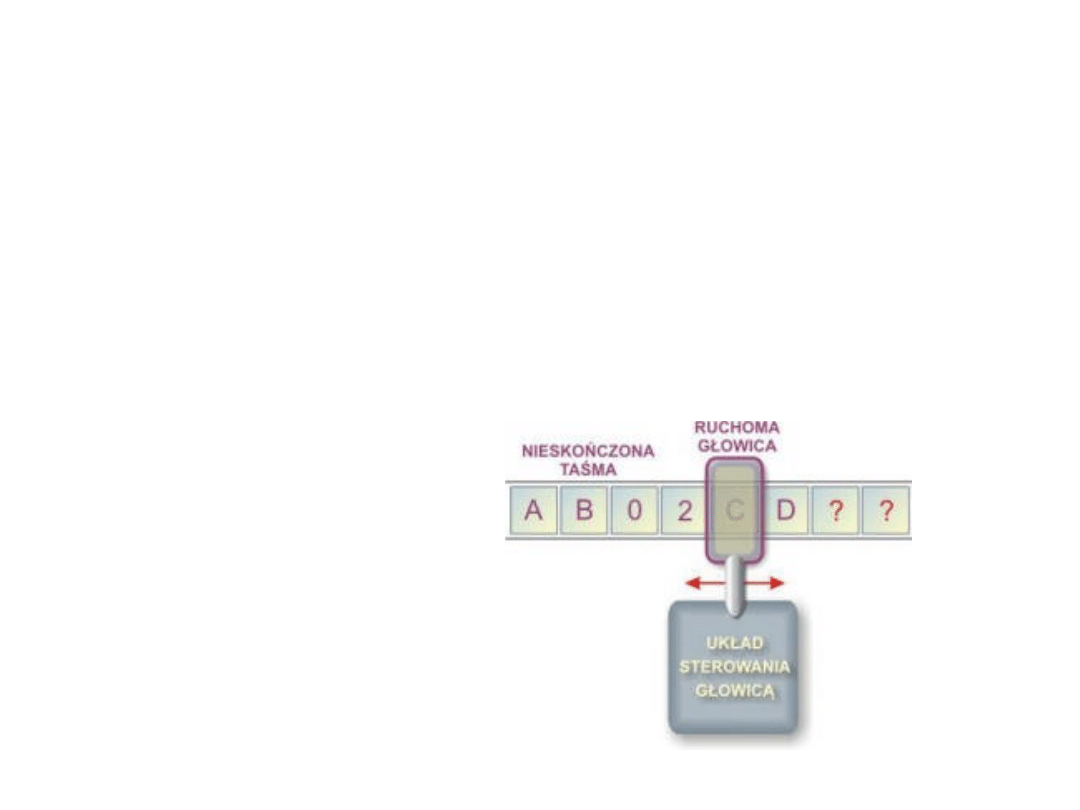
Maszyna Turinga

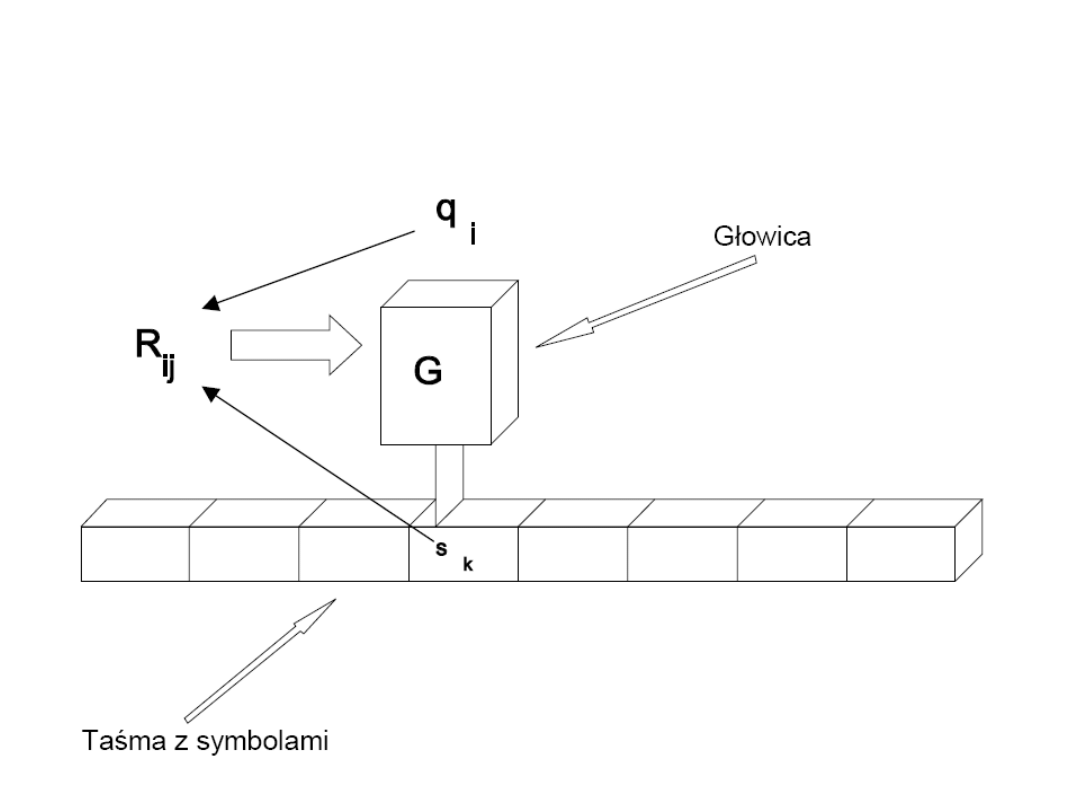
Maszyna Turinga składa się z:

• Nieskończonej taśmy zawierającej komórki z

symbolami

• Ruchomej głowicy zapisująco-odczytującej.
• Układu sterowania głowicą.

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Maszyna Turinga

Taśma

Nieskończona taśma dzieli się na komórki, w
których umieszczone zostały symbole,
(przetwarzane znaki).
MT odczytuje symbole z kolejnych komórek i
przetwarza na inne symbole. Wyniki obliczeń są
zapisywane w komórkach taśmy.

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

, Graf. taśma: wikipedia

A

A

C

C

D

1

4

A

B

…

Maszyna Turinga

Głowica

Głowica odczytuje i zapisuje symbole na taśmie.

Głowice zawsze znajduje się nad jedną z komórek
taśmy. Może ona odczytywać zawartość tej komórki
oraz zapisywać do niej inny symbol (przetwarzanie
danych). Pomiędzy odczytami głowica porusza się w
prawo i w lewo do sąsiednich komórek. W ten sposób
może się ona przemieścić do dowolnie wybranej
komórki taśmy.

Przed rozpoczęciem pracy głowica jest zawsze

ustawiana nad komórką taśmy zawierającą pierwszy
symbol do przetworzenia.

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Maszyna Turinga

Układ sterowania

(odpowiednik procesora)

Zarządza przetwarzaniem informacji. Odczytuje za

pomocą głowicy symbole z komórek taśmy,
przesyła do głowicy symbole do zapisu w
komórkach oraz steruje jej przemieszczaniem.

Podstawą działania MT są stany układu sterowania.

Stan układu sterowania określa jednoznacznie
jaką operację wykona MT gdy odczyta z taśmy
określony symbol

.

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Maszyna Turinga

Układ sterowania

Zatem operacje wykonywane przez układ sterowania

zależą od dwóch czynników:

• symbolu odczytanego z komórki na taśmie.
• bieżącego stanu układu sterującego.

Stany będziemy określać kolejnymi nazwami: q

0

, q

1

, q

2

,

... ,q

n

, gdzie q

0

jest

stanem początkowym

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Maszyna Turinga

Instrukcje MT

Instrukcje składają się z piątki symboli:

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Maszyna Turinga

Instrukcje MT

S

0

i q

i

są tzw.

częścią identyfikacyjną

instrukcji. MT

wykonuje tyle różnych instrukcji, ile zdefiniujemy
części identyfikacyjnych.

W programie nie może być dwóch różnych instrukcji

o identycznej części identyfikacyjnej.

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Maszyna Turinga

Instrukcje MT

S

z

, q

j

i L/P są tzw.

częścią operacyjną

, która określa

jakie działanie podejmuje dana instrukcja.

Części operacyjne różnych instrukcji mogą być takie

same. Oznacza to, iż instrukcje te wykonują
dokładnie to samo działanie.

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Maszyna Turinga

Przykład

Instrukcja:

(

A, q

0

, B, q

0

, P)

 
Jeżeli odczytanym przez głowicę symbolem z taśmy

będzie A, a układ sterowania znajduje się w
stanie q

0

, to głowica zamieni ten symbol na B,

stan wewnętrzny nie zmieni się (pozostanie dalej
q

0

), a głowica przesunie się do sąsiedniej komórki

po prawej stronie (P – prawo).

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Przykładowe programy MT

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

Program zamiany bitów

0,q0,1,q0,L bit 0 zamień

na 1

1,q0,0,q0,L bit 1 zamień

na 0

Przykładowe programy MT

http://edu.i-lo.tarnow.pl/inf/prg/003_mt/0001.php

…

?

1

0

1

1

0

?

…

…

?

1

0

1

1

1

?

…

…

?

1

0

1

0

1

?

…

…

?

1

0

0

0

1

?

…

…

?

1

1

0

0

1

?

…

…

?

0

1

0

0

1

?

…

symbol nierozpoznany - koniec

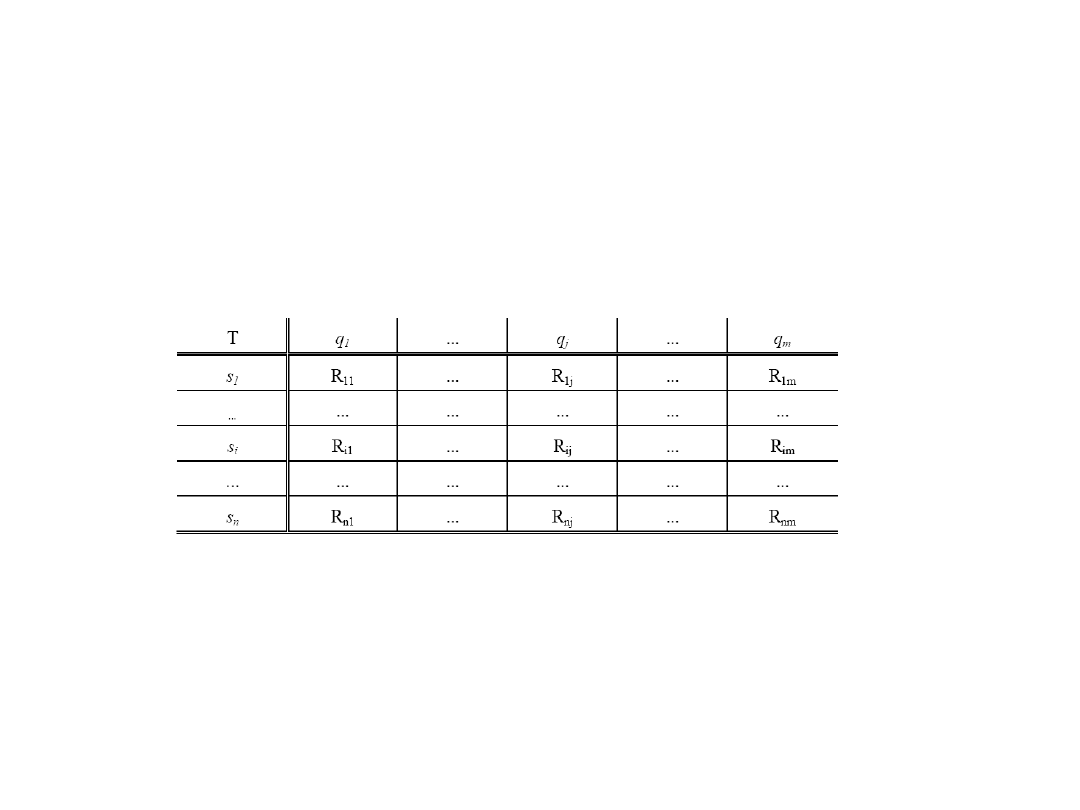
Bardziej złożone programy składają się z wielu instrukcji,

dlatego wygodniej zapisywać je w postaci tzw.

tablicy

charakterystycznej MT

, gdzie każdy ruch R (instrukcja)

związany jest z odczytanym symbolem s

i

oraz stanem q

j

,

czyli

R

ij

= (s

k

, K, q

l

)

Interpretacja tej tabeli jest następująca: Jeżeli będąc w stanie q

j

głowica odczytała symbol s

i

, to należy zapisać na taśmie

symbol s

k

, przesunąć taśmę w kierunku określonym przez K,

a głowica ma przejść do stanu q

l

.

Maszyna Turinga

Na podst. Wykłady z podstaw informatyki prof.. Stefana Węrzyna, wyd. Pol. Śl. Gliwice 2003

Maszyna Turinga

Na podst. Wykłady z podstaw informatyki prof.. Stefana Węrzyna, wyd. Pol. Śl. Gliwice 2003

Maszyna Turinga

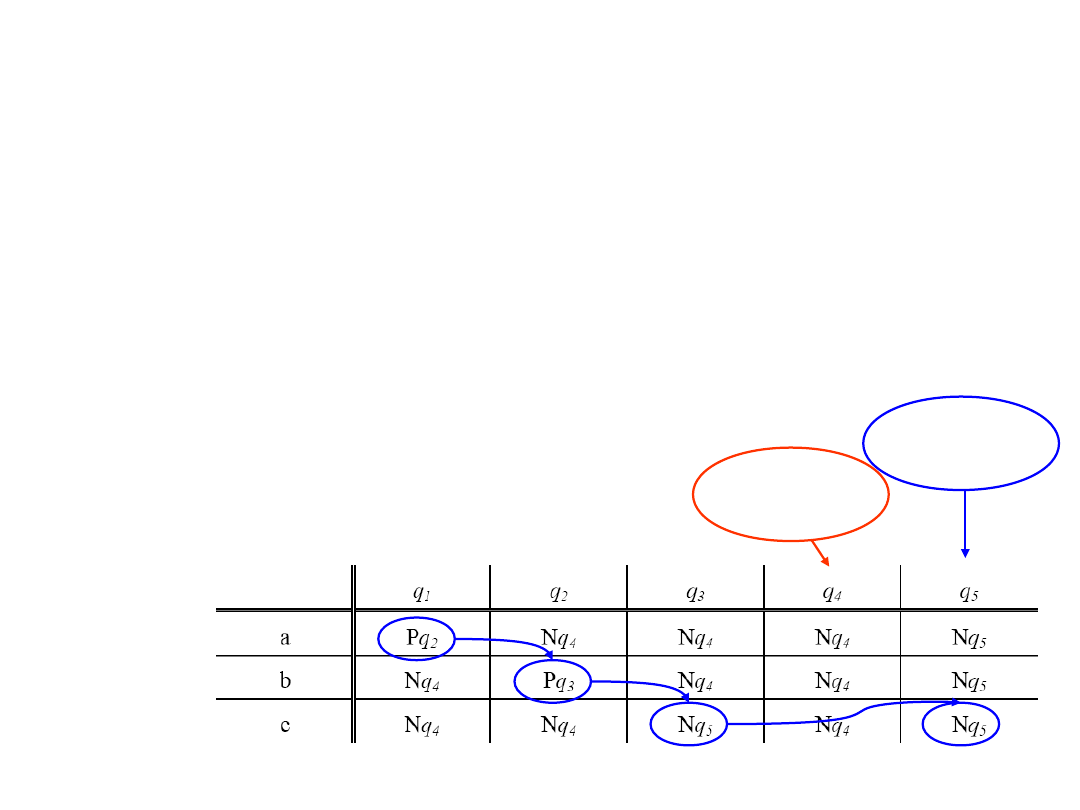
Przykład: W zbiorze napisów trójliterowych utworzonych z liter

a, b, c

tylko napis

abc

jest poprawny. Zapisać dla MT program rozpoznawanie

takiego zapisu.

Jaki jest

algorytm

?

1. Pobierz symbol. Jeżeli jest nim a, to pobierz następny

symbol i idź do 2, w przeciwnym przypadku idź do 4.

2. Jeżeli pobranym symbolem jest b, to pobierz następny

symbol
i przejdź do 3, jeżeli nie, idź do 4.

3. Jeżeli pobranym symbolem jest c, idź do 5, w przeciwnym

przypadku idź do 4.

4. Sygnalizuj nieprawidłowy napis.
5. Sygnalizuj napis poprawny.

Ciąg
poprawny

Ciąg
niepoprawny

Na podst. Wykłady z podstaw informatyki prof.. Stefana Węrzyna, wyd. Pol. Śl. Gliwice 2003

Maszyna Turinga

Przykład: Zaprojektować maszynę Turinga obliczającą sumę dowolnej
liczby zapisanej w systemie dziesiętnym i liczby 1.

Aby do dowolnej liczby dodać 1, należy przeanalizować jej

ostatnią cyfrę.

Jeżeli jest nią któraś z cyfr 0 – 8, to dodanie jedynki sprowadzi

się do zapisu w tym miejscu danej cyfry zwiększonej o
jeden, tzn. jednej
z cyfr 1 – 9.

Jeśli ostatnią cyfrą jest cyfra 9, to należy w jej miejscu

napisać cyfrę 0, a następnie dodać 1 do cyfry
przedostatniej lub napisać jedynkę, jeżeli cyfra nie
występuje.

Na podst. Wykłady z podstaw informatyki prof.. Stefana Węrzyna, wyd. Pol. Śl. Gliwice 2003

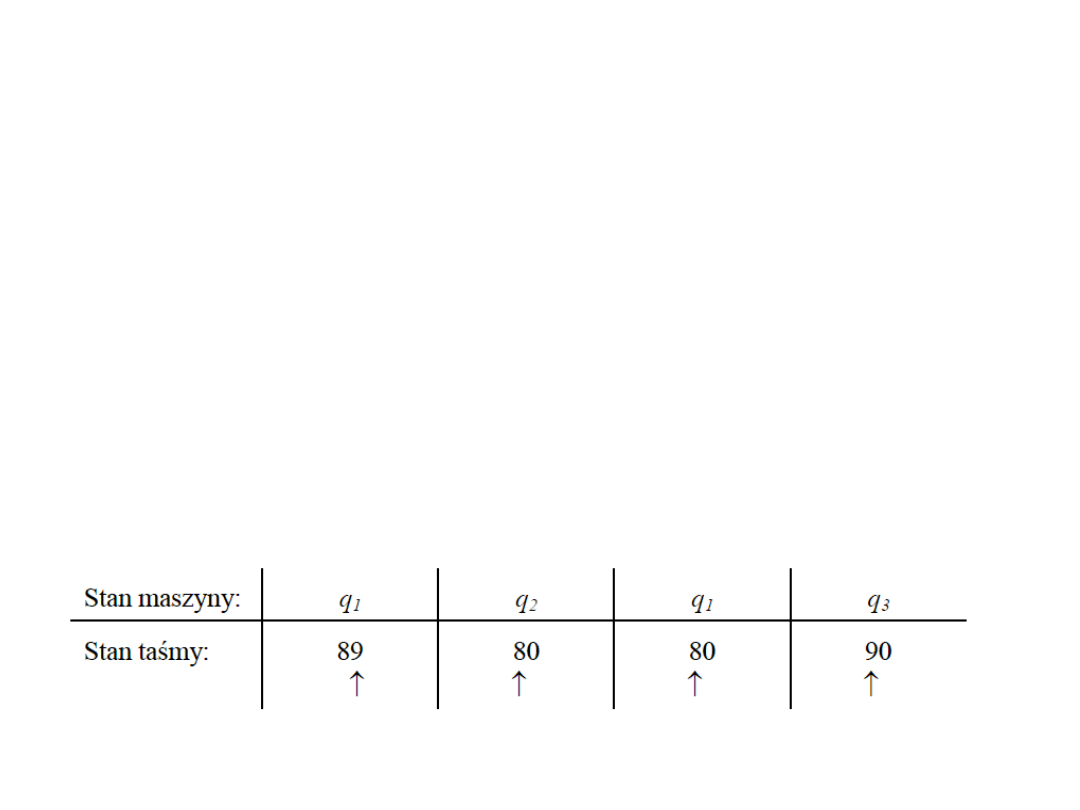
Maszyna Turinga

Przykład: Zaprojektować maszynę Turinga obliczającą sumę dowolnej
liczby zapisanej w systemie dziesiętnym i liczby 1.

Algorytm

(głowica maszyny Turinga powinna być ustawiona na ostatniej cyfrze):
1. Jeżeli cyfra z zakresu 0 – 8 pisz odpowiednio 1 – 9 i idź do 3, w

przeciwnym przypadku pisz 0, przesuń głowicę w lewo i idź do 2.

2. Jeżeli miejsce puste ∅ pisz 1, idź do 3, jeśli nie idź do 1.
3. Sygnalizuj

koniec

.

Przykład działania dla liczby 89:

Maszyna Turinga

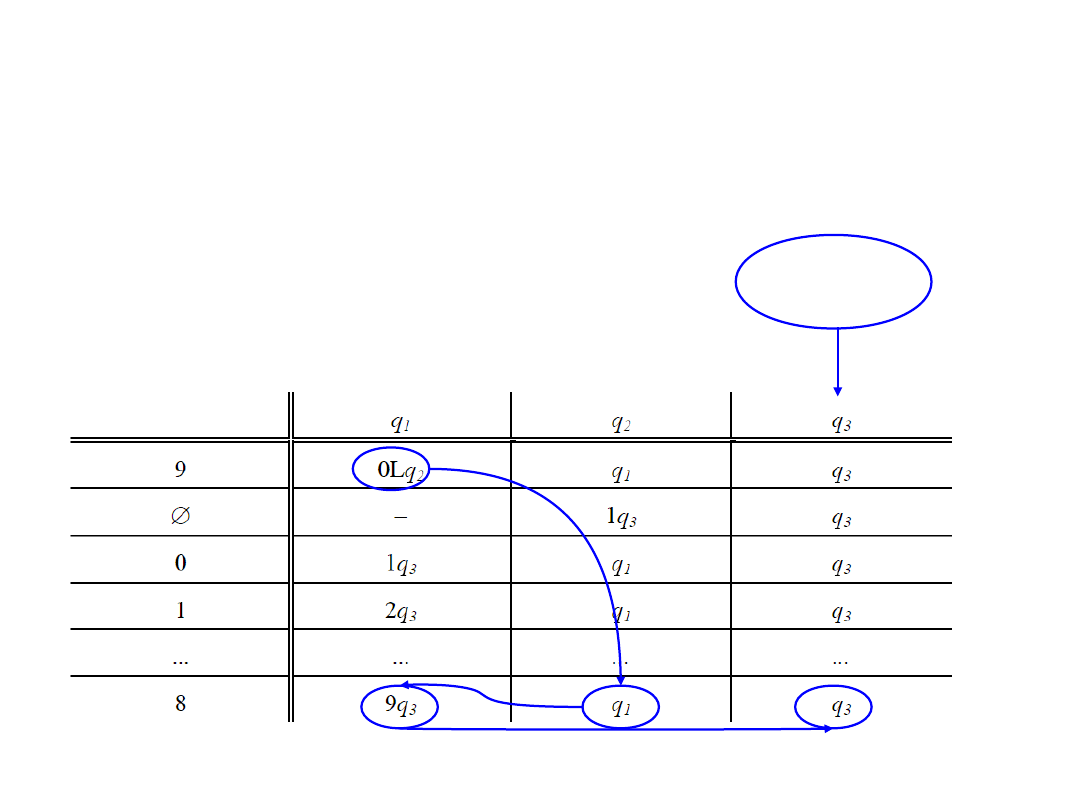
Przykład: Zaprojektować maszynę Turinga obliczającą sumę dowolnej
liczby zapisanej w systemie dziesiętnym i liczby 1.

Tablica charakterystyczna MT:

(przejścia dla liczby 89)

Koniec

Na podst. Wykłady z podstaw informatyki prof.. Stefana Węrzyna, wyd. Pol. Śl. Gliwice 2003

Podsumowanie

Jakie znaczenie ma w Informatyce maszyna Turinga?

Twierdzenie: Każdy algorytm może być

realizowany przez odpowiednio zaprogramowaną
(za pomocą tablicy charakterystycznej) maszynę
Turinga.

W postaci MT dokonało się przejście od ery

automatycznych kalkulatorów do komputerów
sterowanych algorytmami.

Podsumowanie

Można rozważać bardzo wiele różnych wariantów

maszyny Turinga. Istnieją maszyny Turinga
wielotaśmowe lub niedeterministyczne (gdzie
jednej parze (symbol, stan) może odpowiadać
kilka instrukcji).

Podsumowanie

Program dla maszyny Turinga jest

tablicą instrukcji

.

Kolejność instrukcji w tablicy jest zupełnie dowolna.
Program kończy się, jeśli program nie definiuje
działania dla bieżącego symbolu wejściowego i
stanu wewnętrznego.

Praktyczne zastosowanie koncepcji Turinga jest trudne

ze względu na słabą skalowalność programów, a
także ich nieczytelność i trudność modyfikacji.

We współczesnych komputerach program składa się

z

ciągu kolejno wykonywanych instrukcji

.

Podsumowanie

Jeden z wielu symulatorów MT:

http://www.maszynaturinga.info/

Architektura Von Neumana

Maszyna Turinga jest jednym z matematycznych

modeli komputerów.

Praktyczny model komputera podał

John von

Neuman

.

Margittai Neumann János Lajos
(ur. Budapeszt 1903)

Johann von Neumann (Niemcy)

John von Neumann (USA)
(zm. 1957 r.)

Zasady von Neumana:

1. instrukcje i dane mają być identycznie reprezentowane w

maszynie;

2. program i dane muszą mieścić się w tej samej wewnętrznej

pamięci (operacyjnej) komputera;

3. dzięki jednakowej reprezentacji danych i instrukcji maszyna

powinna móc wykonywać operacje na instrukcjach i całym
programie.

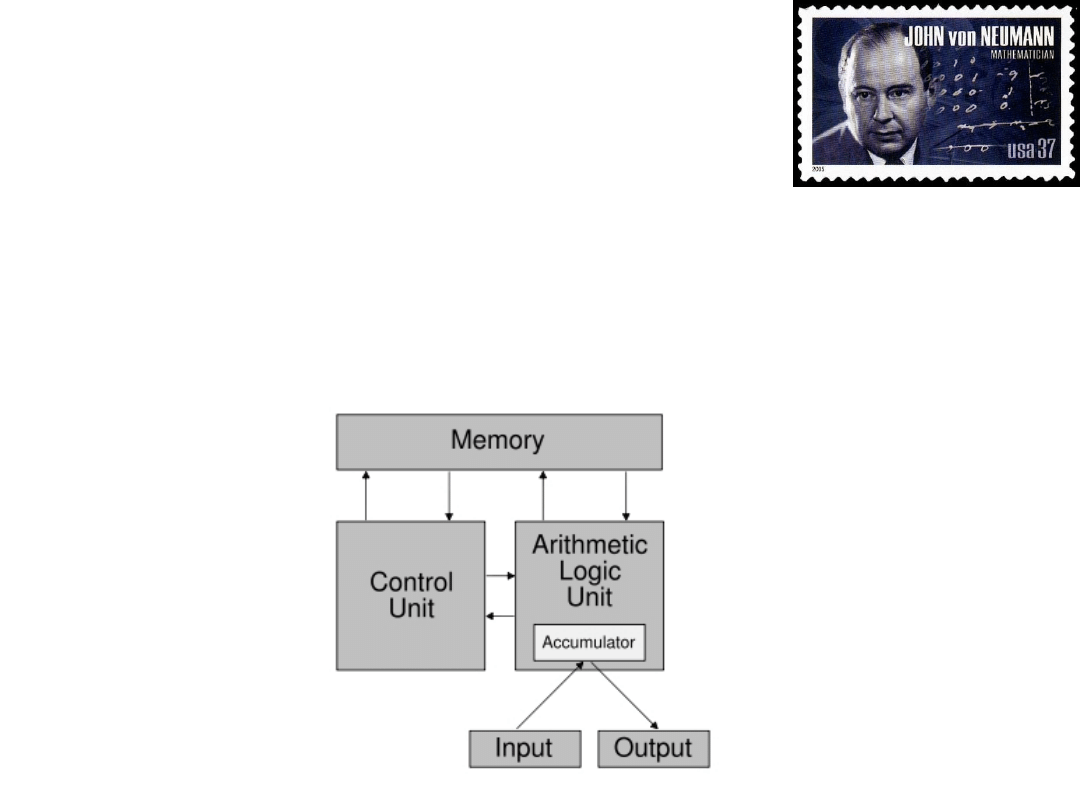
Architektura Von Neumana

W architekturze Von Neumana wyróżniamy:

Pamięć, jednostkę sterującą (procesor), jednostkę

arytmetyczno-logiczną oraz układ wejścia/wyjścia

Taką architekturę komputera nazywano

sterowaną

programem

.

Wobec tak sformułowanej definicji komputera ENIAC

wszystkie poprzedzające go maszyny nie były
komputerami wg. modelu Von Neumana.

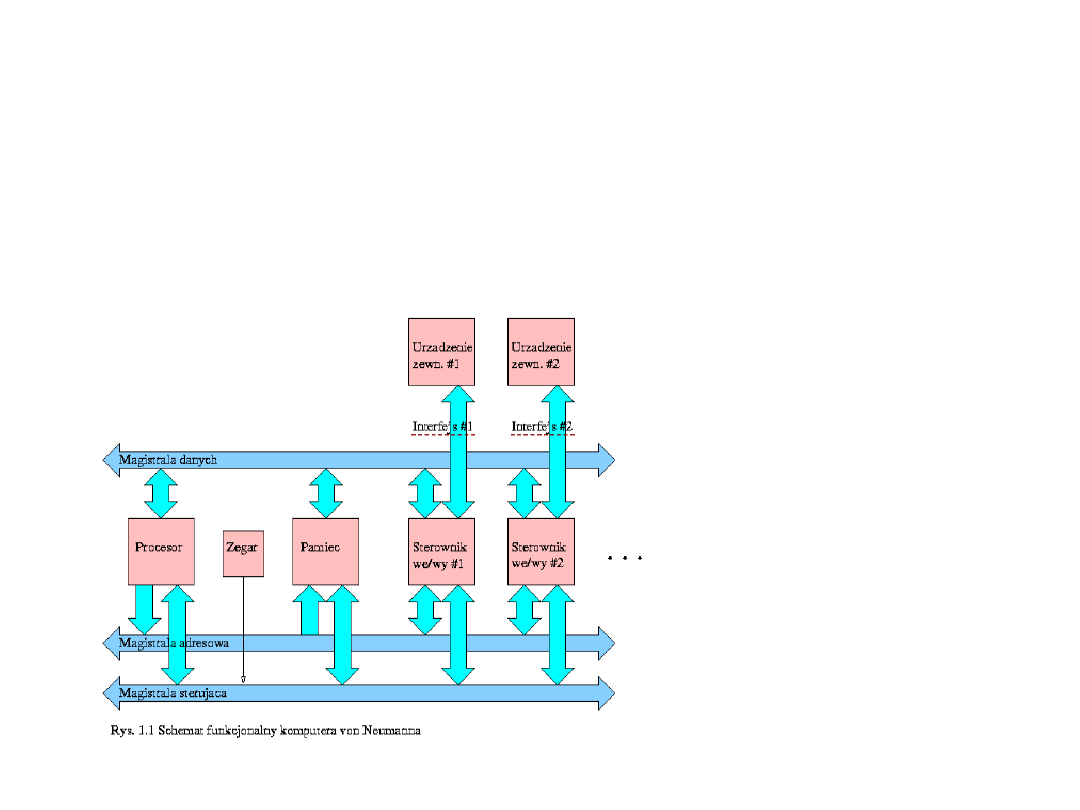
Architektura Von Neumana

We współczesnych komputerach architektura uległa pewnym

modyfikacjom. Ogólny schemat jest następujący:

Elementy

:

• procesor (wraz z
ALU)

• zegar

• magistrala danych

• magistrala adresowa

• magistrala sterująca

• pamięć

• sterowniki we/wy

Na podst: http://www.neurosoft.edu.pl/akozioro/Maszyna_Turinga.pdf

Architektura Von Neumana

Procesor

układ dokonujący operacji na danych zgromadzonych w

pamięci lub pochodzących z urządzeń we/wy, sterowany
programem, którego kod znajduje się w pamięci. Do
przechowywania swojego wewnętrznego stanu procesor
wyposażony jest w pewną ilość

rejestrów

.

Rejestry to komórki pamięci o niewielkich rozmiarach

(najczęściej 4/8/16/32/64/128 bitów) służące do
przechowywania tymczasowych wyników obliczeń,
adresów lokacji w pamięci operacyjnej itd. Większość
procesorów przeprowadza działania wyłącznie w oparciu
o wewnętrzne rejestry, kopiując do nich dane z pamięci i
po zakończeniu obliczeń odsyłając wynik do pamięci.

Na podst: http://www.neurosoft.edu.pl/akozioro/Maszyna_Turinga.pdf

Architektura Von Neumana

Zegar

odmierza cykle wykonywania instrukcji programu,

synchronizuje podzespoły komputera

Na podst: http://www.neurosoft.edu.pl/akozioro/Maszyna_Turinga.pdf

Architektura Von Neumana

Magistrale

służą do przesyłania danych i synchronizacji elementów komputera:

1. Magistrala danych służy do przesyłania danych między pamięcią,

układami we/wy, a procesorem. Ilość użytych tutaj linii
(szerokość szyny) jest równa długości słowa maszynowego i jest
równa rozmiarowi komórki pamięci, lub jest jego wielokrotnością.

2. Magistrala adresów służy procesorowi do wysyłania numerów

komórek pamięci lub rejestrów we/wy na których będzie
dokonane następne przesłanie danych. Ilość użytych tutaj linii
decyduje
o wielkości pamięci jaką można zaadresować.

3. Magistrala sterująca służy do wzajemnej synchronizacji oraz

przekazywania i potwierdzania przyjęcia/wykonania zleceń.

Na podst: http://www.neurosoft.edu.pl/akozioro/Maszyna_Turinga.pdf

Architektura Von Neumana

Pamięć

przechowuje dane i kod programu.

Jeżeli jej konstrukcja umożliwia oprócz odczytu dokonywanie w

niej modyfikacji nazywamy ją

RAM

, jeśli jej konstrukcja

pozwala jedynie na odczyt nazywana jest

ROM

.

Pamięć dzieli się na komórki, z których każda jest w stanie

przechować liczbę całkowitą z ustalonego dla danej
architektury zakresu (słowo bitowe). Każda komórka
pamięci posiada unikalny numer zwany

adresem fizycznym

,

który służy procesorowi do odwoływania się do niej.

Na podst: http://www.neurosoft.edu.pl/akozioro/Maszyna_Turinga.pdf

Podsumowanie

Maszyna von Neumanna była komputerem w pełni

automatycznym, cyfrowym i uniwersalnym,

z wczytywanym programem.

Jej wewnętrzna architektura stała się wzorem dla

komercyjnych maszyn następnej generacji i w

znacznym stopniu pozostaje aktualna do dziś.

Podsumowanie

Innym rodzajem architektury jest

architektura

harwardzka

.

W odróżnieniu od architektury von Neumanna,

pamięć danych programu jest oddzielona od pamięci

rozkazów.

Jest to podstawowa architektura komputerów zerowej

generacji i początkowa komputerów pierwszej

generacji.

Budowa ta często przekłada się na większą szybkość

działania dlatego jest często wykorzystywana

w procesorach sygnałowych oraz jednoukładowych.