ROZKŁAD

WIELOMIANU

NA CZYNNIKI

METODY ROZKŁADU WIELOMIANU NA CZYNNIKI:

I.Wyłączanie wspólnego czynnika przed nawias:

a) w(x)=x

3

+6x

2

w(x)=x

2

(x+6)

czynniki: x

2

; x+6

b) w(x)=4x

3

-6x

2

w(x)=2x

2

(2x-3)

czynniki: 2; x

2

; 2x-3

c) w(x)=x

6

+4x

4

w(x)=x

4

(x

2

+4)

czynniki: x

4

; x

2

+4

d) w(x)=x

3

+x

2

+5x

w(x)=x(x

2

+x+5)

czynniki: x; x

2

+x+5

II. Wykorzystanie wzorów skróconego mnożenia:

a) w(x)=x

3

-9x

w(x)=x(x

2

-9)

w(x)=x(x-3)(x+3)

b) w(x)=x

4

-36x

2

w(x)=x

2

(x

2

-36)

w(x)=x

2

(x-6)(x+6)

c) w(x)=x

6

-1

w(x)=(x

3

)

2

-1

2

w(x)=(x

3

-1)(x

3

+1)

w(x)=(x-1)(x

2

+x+1)(x

3

+1)=(x-1)(x

2

+x+1)(x+1)(x

2

-

x+1)

d) w(x)=x

3

+8

w(x)=x

3

+2

3

w(x)=(x+2)(x

2

-2x+4)

III. Wykorzystanie wzorów na deltę i postać

iloczynową funkcji kwadratowej:

a) w(x)=x

3

+6x

2

+5x

w(x)=x(x

2

+6x+5)

a=1 b=6 c=5
=36-20=16 delta jest większa od zera,

x

1

=-5 x

2

=-1 wykorzystujemy wzór na

postać

iloczynową:

y=a(x-x

1

)(x-x

2

)

x

2

+6x+5=(x+5)(x+1)

w(x)=x(x+5)(x+1)

b) w(x)=2x

3

-8x

2

+8x

w(x)=2x(x

2

-4x+4)

a=1 b=-4 c=4
=16-16=0 delta jest równa zero, wtedy

x

0

=2 wykorzystujemy wzór na postać

iloczynową:

y=a(x-x

0

)(x-x

0

)

w(x)=2x(x-2)

2

y=a(x-x

0

)

2

c) w(x)=-3x

3

-6x

2

-15x

w(x)=-3x(x

2

+2x+5)

a=1 b=2 c=5
=4-20=-16


<

0 - brak rozkładu na czynniki

w(x)=-3x(x

2

+2x+5)

d) w(x)=2x

3

-6x

2

-8x

w(x)=2x(x

2

-3x-4)

a=1 b=-3 c=-4
=9+16=25

x

1

=-1 x

2

=4

y=a(x-x

1

)(x-x

2

)

x

2

-3x-4=(x+1)(x-4)

w(x)=2x(x+1)(x-4)

IV. Wykorzystanie metody grupowania wyrazów:

a) w(x)=x

3

-2x

2

-9x+18 -

grupujemy po dwa wyrazy

w(x)=(x

3

-2x

2

)+(-9x+18)

w(x)=x

2

(x-2)+(-9)(x-2)

w(x)=(x-2)(x

2

-9)

w(x)=(x-2)(x-3)(x+3)

b) w(x)=4x

3

-4x

2

-x+1

w(x)=(4x

3

-4x

2

)+(-x+1)

w(x)=4x

2

(x-1)+(-1)(x-1)

w(x)=(x-1)(4x

2

-1)

w(x)=(x-1)(2x-1)(2x+1)

c) w(x)=x

3

-x

2

-4x+4

w(x)=(x

3

-x

2

)+(-4x+4)

w(x)=x

2

(x-1)+(-4)(x-1)

w(x)=(x-1)(x

2

-4)

w(x)=(x-1)(x-2)(x+2)

Zadanie: Wykorzystując odpowiednią metodę rozłóż

na czynniki wielomiany:

a) w(x)=x

4

+5x

3

+8x+40

w(x)=(x

4

+5x

3

)+(8x+40)

w(x)=x

3

(x+5)+8(x+5)

w(x)=(x+5)(x

3

+8)

w(x)=(x+5)(x+2)(x

2

-2x+4)

a=1 b=-2 c=4
=4-16=-12


<

0 - brak rozkładu na czynniki

w(x)=(x+5)(x+2)(x

2

-2x+4)

b) w(x)=x

6

+5x

4

w(x)=x

4

(x

2

+5)

a=1 b=0 c=5

=0-20=-20

 < 0 - brak rozkładu na czynniki

w(x)=x

4

(x

2

+5)

c) w(x)=x

3

+5x

2

+4x

w(x)=x(x

2

+5x+4)

a=1 b=5 c=4
=25-16=9

x

1

=-4 x

2

=-1 wykorzystujemy wzór na

postać

iloczynową:

y=a(x-x

1

)(x-x

2

)

x

2

+5x+4=(x+4)(x+1)

w(x)=x(x+4)(x+1)

d) w(x)=x

3

+3x

2

+6x+18

w(x)=(x

3

+3x

2

)+(6x+18)

w(x)=x

2

(x+3)+6(x+3)

w(x)=(x+3)(x

2

+6)

a=1 b=0 c=6

=0-24=-24

 < 0 - brak rozkładu na czynniki

w(x)=(x+3)(x

2

+6)

e) w(x)=-2x

4

-10x

3

-8x

2

w(x)=-2x

2

(x

2

+5x+4)

a=1 b=5 c=4
=25-16=9

x

1

=-4 x

2

=-1 wykorzystujemy wzór na

postać

iloczynową:

y=a(x-x

1

)(x-x

2

)

x

2

+5x+4=(x+4)(x+1)

w(x)=-2x

2

(x+4)(x+1)

f) w(x)=x

3

-9x

w(x)=x(x

2

-9)

wykorzystujemy wzory skróconego

mnożenia

w(x)=x(x+3)(x-3)

g) w(x)=x

4

-16

w(x)=(x

2

)

2

-4

2

w(x)=(x

2

-4)(x

2

+4)

w(x)=(x-2)(x+2)(x

2

+4)

a=1 b=0 c=4
=0-16=-16

 < 0 -

brak rozkładu na czynniki

w(x)=(x-2)(x+2)(x

2

+4)

h) w(x)=-4x

3

-12x

2

+x+3

w(x)=(-4x

3

-12x

2

)+(x+3)

w(x)=-4x

2

(x+3)+1(x+3)

w(x)=(x+3)(-4x

2

+1)

w(x)=(x+3)(1-4x

2

)

w(x)=(x+3)(1-2x)(1+2x)

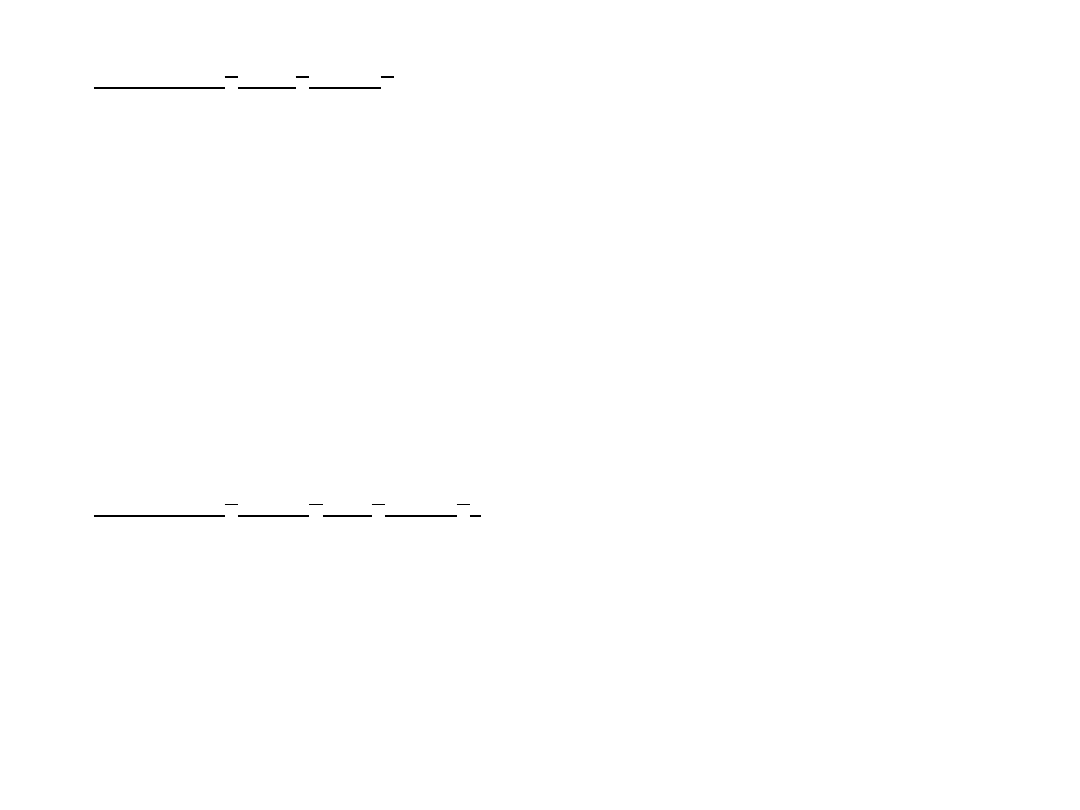
i) w(x)=x

4

-6x

3

+9x

2

w(x)=x

2

(x

2

-6x+9)

a=1 b=-6 c=9
=36-36=0

x

0

=3 wykorzystujemy wzór na postać

iloczynową:

y=a(x-x

0

)

2

x

2

-6x+9=(x-3)

2

w(x)=x

2

(x-3)

2

j) w(x)=x

5

+3x

4

+x

3

+3x

2

w(x)=x

2

(x

3

+3x

2

+x+3)

w(x)=x

2

[(x

3

+3x

2

)+(x+3)]

w(x)=x

2

[x

2

(x+3)+1(x+3)]

w(x)=x

2

(x+3)(x

2

+1)

a=1 b=0 c=1
=0-4=-4

 < 0 - brak rozkładu na czynniki

w(x)=x

2

(x+3)(x

2

+1)

k) w(x)=2x

4

+x

3

+3x

2

+x+1

w(x)=(2x

4

+x

3

+x

2

)+(2x

2

+x+1)

w(x)=x

2

(2x

2

+x+1)

+1

(2x

2

+x+1)

w(x)=(x

2

+1)

(2x

2

+x+1)

a=1 b=0 c=1

a=2 b=1 c=1

=0-4=-4

=1-8=-7

 < 0

 < 0

-

brak rozkładu na czynniki

w(x)=(x

2

+1)(2x

2

+x+1)

l) w(x)=5x

3

-6x+1

w(x)=5x

3

-5x-x+1

w(x)=(5x

3

-5x)+(-x+1)

w(x)=5x(x

2

-1)+(-1)(x-1)

w(x)=5x

(x-1)

(x+1)+(-1)

(x-1)

w(x)=[5x(x+1)-1]

(x-1)

w(x)=[5x

2

+5x-1]

(x-1)

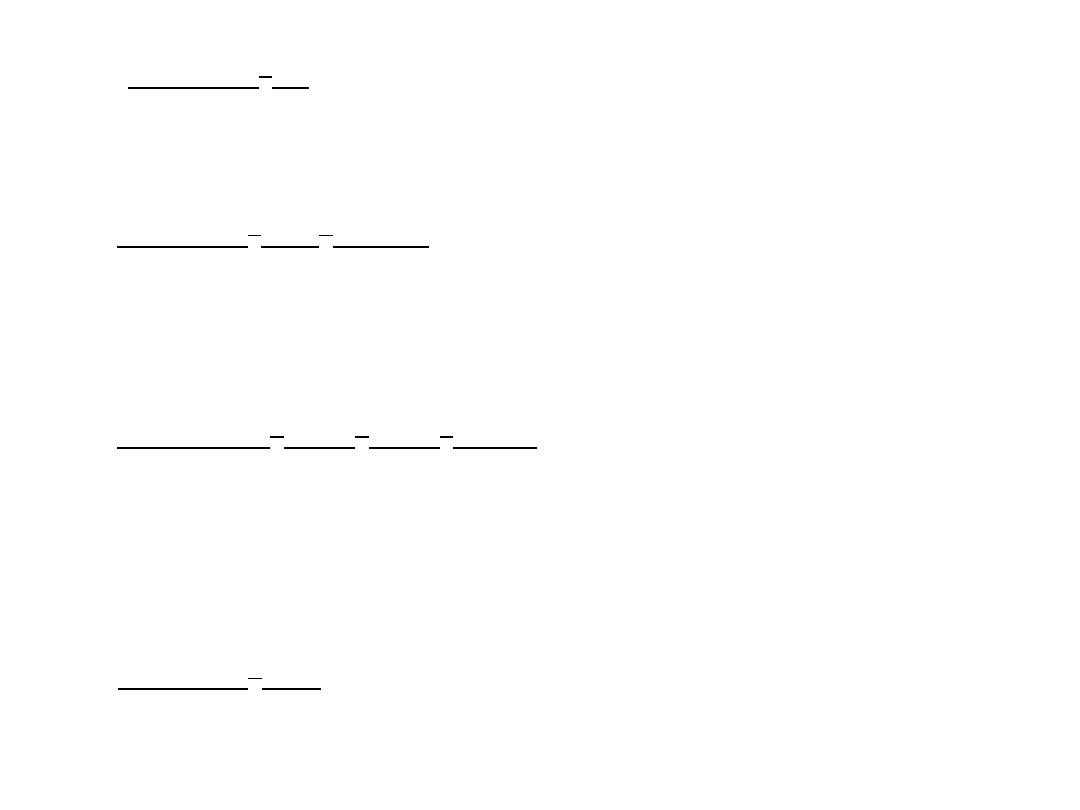
m) w(x)=x

4

-9

w(x)=(x

2

-3)(x

2

+3)

w(x)=(x-√3)(x+√3)(x

2

+3)

n) w(x)=x

3

-5x

2

+x-5

w(x)=(x

3

-5x

2

)+(x-5)

w(x)=x

2

(x-5)+1(x-5)

w(x)=(x-5)(x

2

+1)

o) w(x)=3x

4

+2x

3

+3x

2

+2x

w(x)=(3x

4

+2x

3

)+(3x

2

+2x)

w(x)=x

3

(3x+2)+x(3x+2)

w(x)=(x

3

+x)(3x+2)

w(x)=x(x

2

+1)(3x+2)

p) w(x)=x

2

-25

w(x)=(x-5)(x+5)