4. TEORIA RUCHU POJAZDÓW SZYNOWYCH

 

Dynamika pojazdu szynowego 

Ruch  postępowy  pociągu  wzdłuż  toru  odbywa  się  pod  wpływem 

działania następujących sił, a ściślej ich rzutów na kierunek biegu 

pociągu:

•

siła  pociągowa  F  [N]  –  zależna  od  działań  maszynisty  lub 

urządzeń  automatycznej  jazdy  pociągu;  w  czasie  jazdy  wywołana 

momentami  napędowymi  silników  trakcyjnych  i  przypisuje  się  jej 

wtedy  znak  „+”,  w  czasie  hamowania  wywołana  działaniem 

hamulców  lub  momentów  hamujących  silników  trakcyjnych  i 

przypisuje się jej wtedy znak „-”

•

opory  ruchu  W  [N]  –  wszystkie  inne  siły  skierowane  wzdłuż 

drogi  pociągu,  niezależne  od  woli  maszynisty;  przypisuje  im  się 

znak „+”, gdy są skierowane przeciw ruchowi pociągu i znak „-”, 

gdy są zgodne z jego kierunkiem.

Różnicę  między  siłą  pociągową  a  oporami  ruchu  nazywamy  siłą 

przyśpieszającą F

p

 [N], która może być dodatnia lub ujemna.

W

F

F

p





 

 

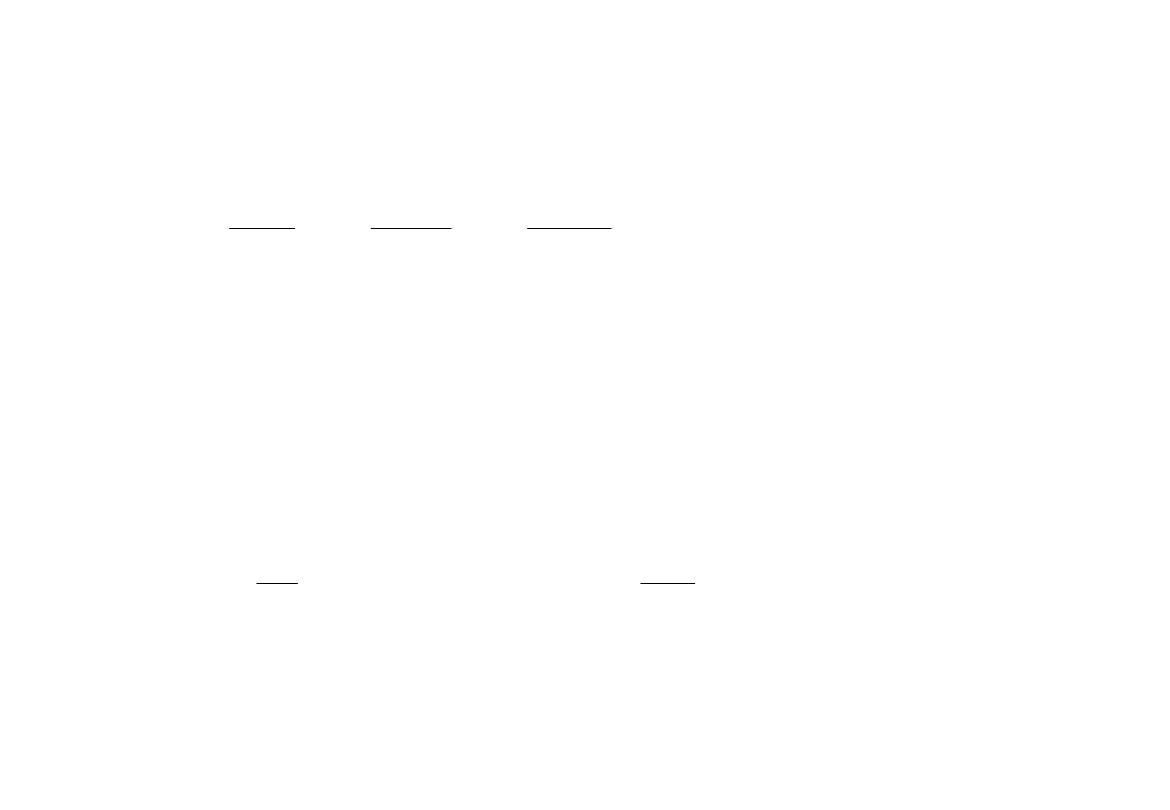
Energia kinetyczna pociągu

 

 

kwir

kp

k

E

E

E















2

2

2

2

2

2

w

w

k

k

k

I

I

mv

E





gdzie:
m – masa pociągu,
v – prędkość pociągu,
I

k

 – moment bezwładności kół wagonów lub lokomotyw,

I

w

 – moment bezwładności wirników silników trakcyjnych,

ω

k

 – prędkość kątowa kół wagonów lub lokomotyw, 

ω

w

 – prędkość kątowa wirników silników trakcyjnych. 

k

k

R

v





l

w

R

z

v





gdzie:
R

k

 – promień koła wagonu lub lokomotywy,

R

l

 – promień koła lokomotywy, 

z – przełożenie przekładni.

 

 

















































2

2

2

2

2

2

2

2

2

2

1

1

2

2

2

2

l

w

k

k

l

w

k

k

k

R

z

I

R

I

m

mv

R

z

v

I

R

v

I

mv

E























kp

kwir

kp

kwir

kp

k

E

E

E

E

E

E

1

Wielkość:  γ   wyraża stosunkowy pozorny wzrost masy pociągu 
wywołany wpływem jego mas wirujących. 





















2

2

2

1

l

w

k

k

R

z

I

R

I

m







2

2

1

2

2

v

m

v

m

E

k





















1

Uwzględniając wpływ mas wirujących, masa pozorna pociągu 
wynosi mα, gdzie α=1+γ nosi nazwę współczynnika 
bezwładności mas wirujących pociągu. 

 

 

Znając  wymiary  i  momenty  bezwładności  mas  wirujących  można 
współczynnik  α  obliczyć  osobno  dla  lokomotywy  i  wagonów,  a 
następnie dla całego składu pociągu według wzoru:

 

 

 











n

i

i

n

i

i

i

G

G

1

1





gdzie:

G

i

 – ciężar lokomotywy, wagonu,

α

i

 – współczynnik bezwładności lokomotywy, wagonu.

 

 

 

Zwykle nie ma potrzeby dokładnego obliczania wielkości wpływu 
mas wirujących, ponieważ wpływ ten jest niemal stały dla 
określonych rodzajów pojazdów. Wartości współczynnika α mogą 
być przyjmowane w następujących granicach:

lokomotywy elektryczne

1,20 

– 1,40

wagony motorowe

1,10 – 1,15

wagony osobowe

1,04 

– 1,05

wagony towarowe 4-osiowe próżne

1,07 

– 1,08

wagony towarowe 4-osiowe naładowane

1,03 

– 1,04

tramwaj – wagon motorowy

1,15 – 1,20

tramwaj 2-wagonowy

1,10 

– 1,15

trolejbus

1,25 

– 1,30

 

 

Siła przyspieszająca i przyspieszenie 

k

p

dE

ds

F





dt

dv

m

ds

dv

dt

ds

m

ds

dv

v

m

ds

dv

v

m

ds

dv

m

v

m

ds

d

ds

dE

F

k

p





































































2

2

2

2

2

2

a

m

F

p















m

F

a

p

lub





g

f

g

G

F

a

p

p









gdzie f

p

 jest jednostkową siłą przyspieszającą tj. siłą przyspieszającą 

przypadającą na jednostkę ciężaru pociągu. Taki wzór będzie 
słuszny, jeżeli f

p

 jest bezwymiarowa, to znaczy kiedy siła F

p

 oraz 

ciężar G określone są w tych samych jednostkach 

 

 

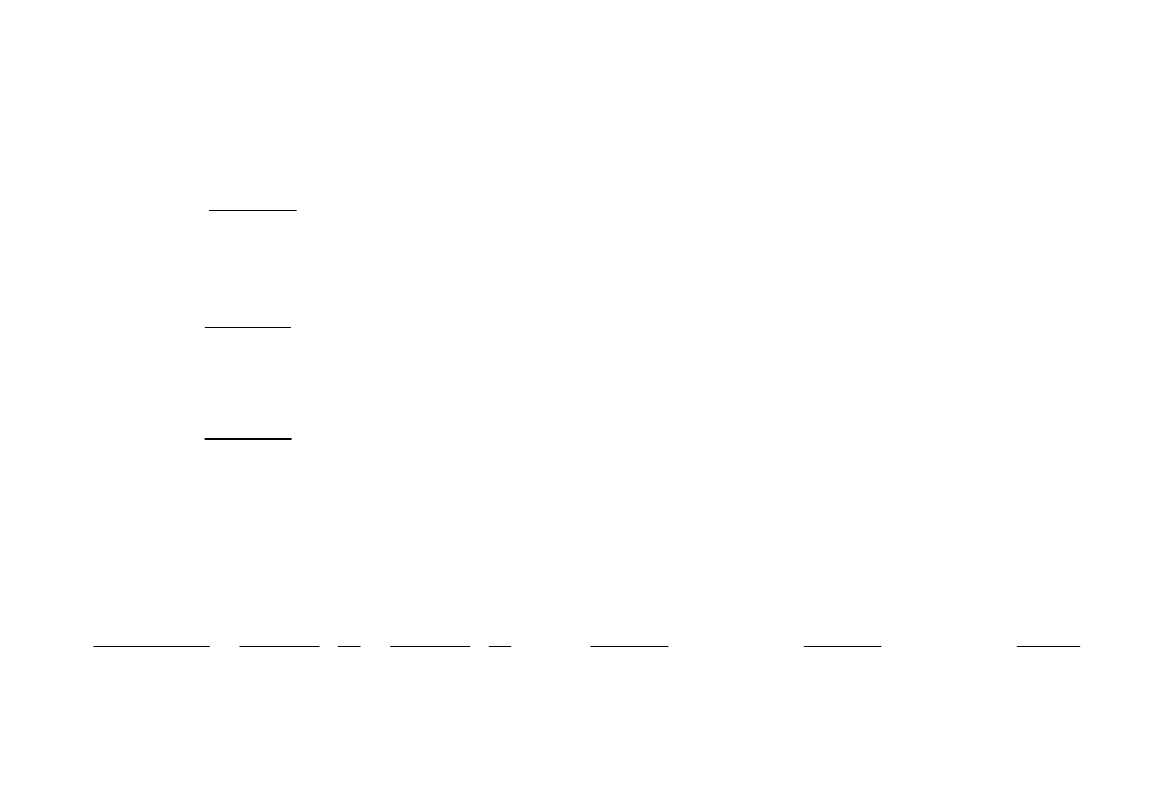
W praktyce F

p

 podaje się w [N], a G w [kN]. 

Dlatego wprowadzono jednostkową siłę określaną w promilach jako 
stosunek [N/kN]: 

]

[

]

[

]

/

[

00

0

kN

G

N

F

f

p

p



]

[

]

[

]

/

[

00

0

kN

G

N

F

f



]

[

]

[

]

/

[

00

0

kN

G

N

W

w



jednostkowa siła przyspieszająca

jednostkowa siła pociągowa

jednostkowe opory ruchu

Jeżeli: m[t], G[kN], F[N], W[N], F

p

[N], przyspieszenie oblicza się 

następująco:













102

1

)

(

1000

)

(

1000

1000

1000

1000































w

f

g

w

f

g

f

g

G

W

F

g

G

F

m

F

a

p

p

p

 

 

   Opory ruchu

Na  pociąg  będący  w  ruchu,  oprócz  siły  pociągowej,  działa 

wiele  sił  różnego  rodzaju  i  pochodzenia,  których  większość 
skierowana  jest  zwykle  przeciw  ruchowi  pociągu.  Rzuty  tych 
wszystkich  sił,  odniesionych  do  obwodu  kół  pociągu,  na 
kierunek  jego biegu nazywamy oporami  ruchu. Przypisujemy 
im  znak  „+”,  gdy  są  skierowane  przeciw  ruchowi  pociągu  i  znak 
„-”, gdy ich kierunek jest zgodny z ruchem pociągu

Wszystkie  opory  składowe  jak  i  całkowite  określa  się  jako 

siłę  w  [N]  lub  w  postaci  oporów  jednostkowych,  odniesionych  do 
1kN ciężaru pociągu, w [N/kN] lub [

0

/

00

].

Opory ruchu można podzielić na opory zasadnicze, opory 

profilu linii oraz opory dodatkowe ośrodka. 

 

 

Opory zasadnicze ruchu

Opory  zasadnicze  są  nierozłącznie  związane  z  toczeniem  się  pojazdu, 
działają stale przy jeździe pociągu po torze otwartym w linii prostej i 
poziomej, bez wiatru. Do oporów zasadniczych należą: 

•opory wewnętrzne taboru,

•opory toru,

•opory ośrodka powietrznego na czołowe i boczne ściany lokomotywy i 
wagonów.

Ze  względu  na  trudność  analitycznego  ujęcia  zjawisk,  praktyka 
kolejowa ogranicza się do pomiarów całkowitych zasadniczych oporów 
ruchu  danego  rodzaju  pociągu  w  danych  warunkach.  Na  podstawie 
dużej ilości pomiarów tworzy się odpowiednie wzory empiryczne.

Postać  większości  wzorów  na  zasadnicze  opory  ruchu  to  trójmian 
kwadratowy  będący  funkcją  prędkości.  Wpływ  niektórych  czynników 
uwzględnia się w wartości współczynników trójmianu. 

2

2

1

v

w

v

w

w

w

o







 

 

        Wzory  opracowane  dla  kolei 
rosyjskich 

•    dla  2  i  3-osiowych  wagonów 
towarowych 

v

m

w

w





















25

1

02

,

0

4

,

1

•  dla 4-osiowych wagonów 
towarowych 

w

m

v

w

55

,

0

12

65







•  dla 2 i 3-osiowych wagonów 
pasażerskich 

2

0003

,

0

017

,

0

4

,

1

v

v

w







•  dla 4 i 6-osiowych wagonów 
pasażerskich 

2

0003

,

0

012

,

0

4

,

1

v

v

w







(określają jednostkowe 
opory ruchu w funkcji 
v – prędkość pociągu w 
[km/h] )

•  dla lokomotyw 

2

0005

,

0

01

,

0

4

,

1

v

v

w







•  dla zespołów trakcyjnych 





2

0

045

,

0

1

0064

,

0

v

m

m

n

v

k

w

w

D

M

















gdzie:

m

w

 – masa wagonu w [t] 

n        –  całkowita  liczba 
wagonów
         w pociągu,
m

M

 – masa wagonów 

         motorowych [t],
m

D

 – masa wagonów

        doczepnych [t].

62

,

1

0



w

014

,

0



k

dla jazdy 
pod prądem

5

,

2

0



w

03

,

0



k

dla jazdy bez 
prądu

 

 

Wzór Francka 





2

2

10

2

1

,

1

54

,

0

10

0142

,

0

5

,

2







































v

nq

S

k

m

v

w

gdzie:
m  – całkowita masa pociągu w [t],
n   – liczba wagonów,
kS – przekrój zastępczy lokomotywy w [m

2

], przy czym S stanowi 

przekrój
        rzeczywisty i wynosi zwykle 10-12 m

2

, zaś k jest 

współczynnikiem
        uwzględniającym wpływ kształtu ściany przedniej 
lokomotywy:

k = 1,0 - dla przodu płaskiego,
k = 0,8 – dla przodu z krawędziami zaokrąglonymi,
k = 0,6 – dla przodu całkowicie zaokrąglonego,
k = 0,35 – dla przodu o kształcie opływowym,

q  – współczynnik zależny od rodzaju wagonu:

q = 0,56 – dla wagonów krytych (towarowych i 

osobowych),

q = 0,32 – dla wagonów otwartych załadowanych,
q = 1,62 – dla wagonów otwartych próżnych

 

 

Wzory opracowane dla kolei polskich przez Centrum Naukowo-
Techniczne Kolejnictwa  (

wzory określają opory w [N] w funkcji prędkości v w 

[km/h])

 

•  dla 
wagonów





2

10

5

,

2

150

10

5

,

1



































 



v

n

f

n

m

v

K

W

o

w

w

gdzie:
K – współczynnik rodzaju łożysk, który wynosi:

dla łożysk tocznych  6,5;   dla łożysk ślizgowych  9,0

m

w

 – masa wagonów w [t],

n

o

 – liczba osi w pociągu

f – współczynnik rodzaju pociągu, który wynosi:

dla wagonów pasażerskich  10
dla wagonów towarowych   8,

n – liczba wagonów w pociągu.

•  dla lokomotywy

2

10

35

150

10

5

,

1

9





























 



v

n

m

v

W

o

l

l

gdzie:
m

l

 – masa lokomotywy w [t],

n

o

 – liczba osi lokomotywy 

 

 

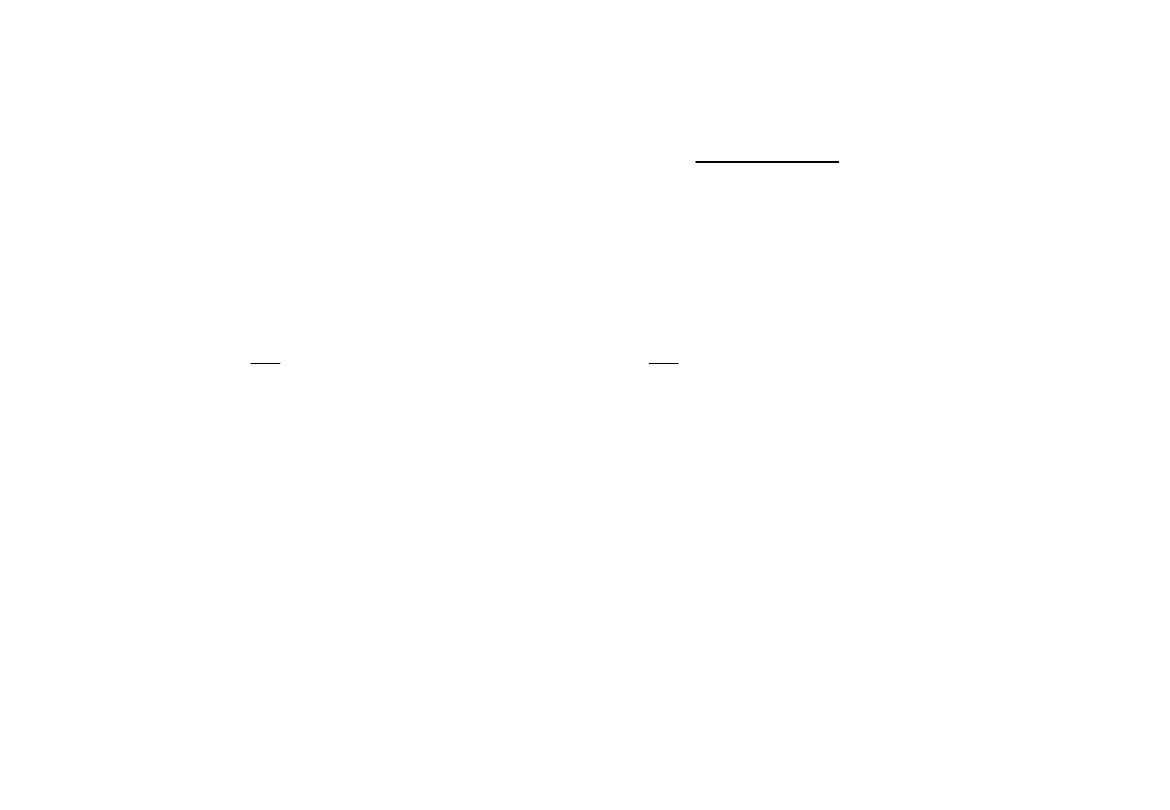
•  całkowite opory ruchu 
pociągu

   [N]

l

w

W

W

W





l

w

G

G

W

w





jednostkowe opory ruchu  
[N/kN]

•  dla zespołów elektrycznych i 
spalinowych 





2

10

7

,

2

10

150

10

5

,

1



































 



v

n

n

m

v

K

W

o

j

j

gdzie:
K – współczynnik rodzaju łożysk, jak we wzorze dla wagonów,
m

j

 – masa zespołu wraz z pasażerami [t],

n

o

 – liczba osi w zespole,

n – liczba wagonów w zespole 

 

 

W przypadku braku dokładnych danych odnośnie wartości mas 
poszczególnych pojazdów, można przyjmować następujące 
wartości średnie:

4-osiowy wagon pasażerski z obciążeniem

42 t

wagon towarowy próżny 2-osiowy

10 t

wagon towarowy próżny 4-osiowy

20 t

wagon towarowy 2-osiowy całkowicie załadowany

33 t

wagon towarowy 4-osiowy całkowicie załadowany

80 t

lokomotywa 4-osiowa

80 t

lokomotywa 6-osiowa

120 t

wagon motorowy w zespole trakcyjnym

55 t

wagon doczepny w zespole trakcyjnym

40 t

(masy dla wagonów w zespole trakcyjnym podane są bez 
pasażerów, zwykle przyjmuje się zapełnienie 150 osób o masie 70 
kg na wagon)

 

 

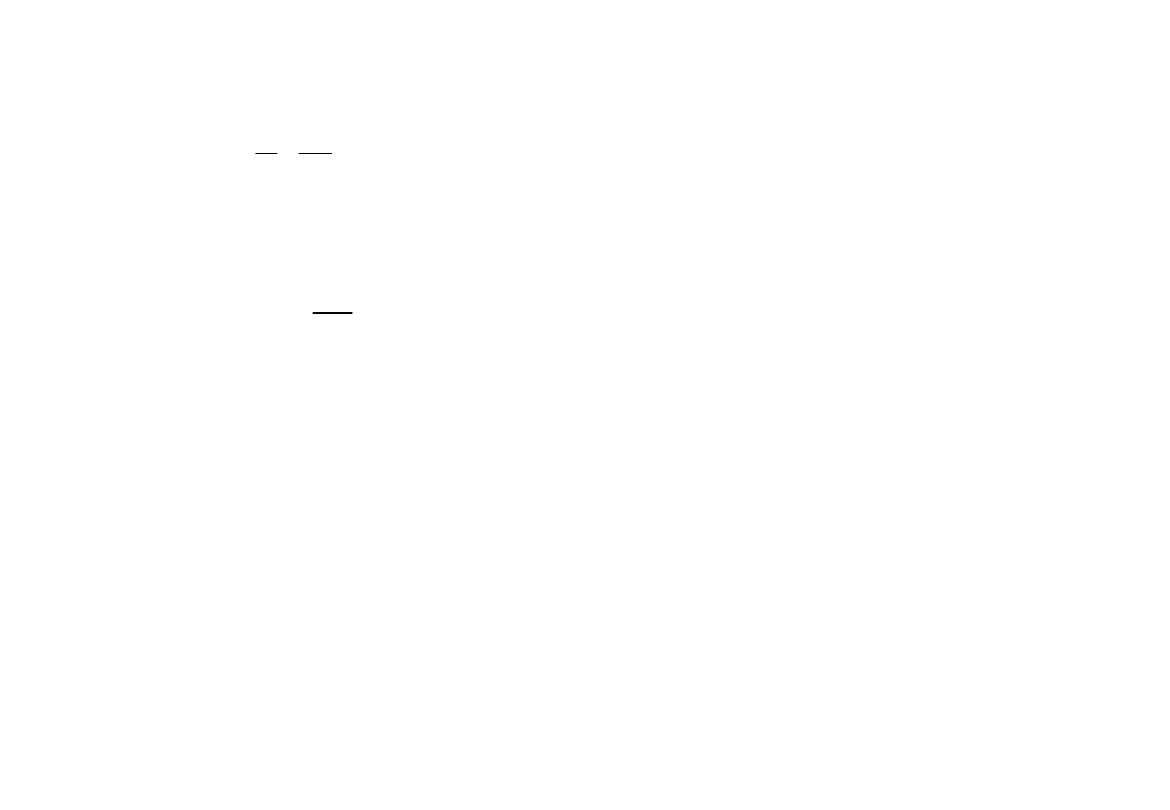
Wzór profesora Jaworskiego 

2

0

10

1

















v

k

w

w

[N/kN]

gdzie:

2

0



w











 



G

G

w

L

1

2

0

jazda pod prądem i 
hamowanie

jazda z rozpędu

0



F

0



F

G

L

– ciężar lokomotywy,

G – ciężar całego pociągu,
k – współczynnik zależny od rodzaju pociągu:

k = 40  dla ciężkich pociągów towarowych,
k = 40  dla pociągów pasażerskich z wagonami 4-

osiowymi,

k = 30  dla długich zespołów trakcyjnych,
k = 20  dla krótkich zespołów trakcyjnych,
k = 20  dla samych lokomotyw elektrycznych,
k = 15  dla samych wagonów motorowych,
k = 10  dla pociągów towarowych próżnych z 

wagonami otwartymi.

 

 

 

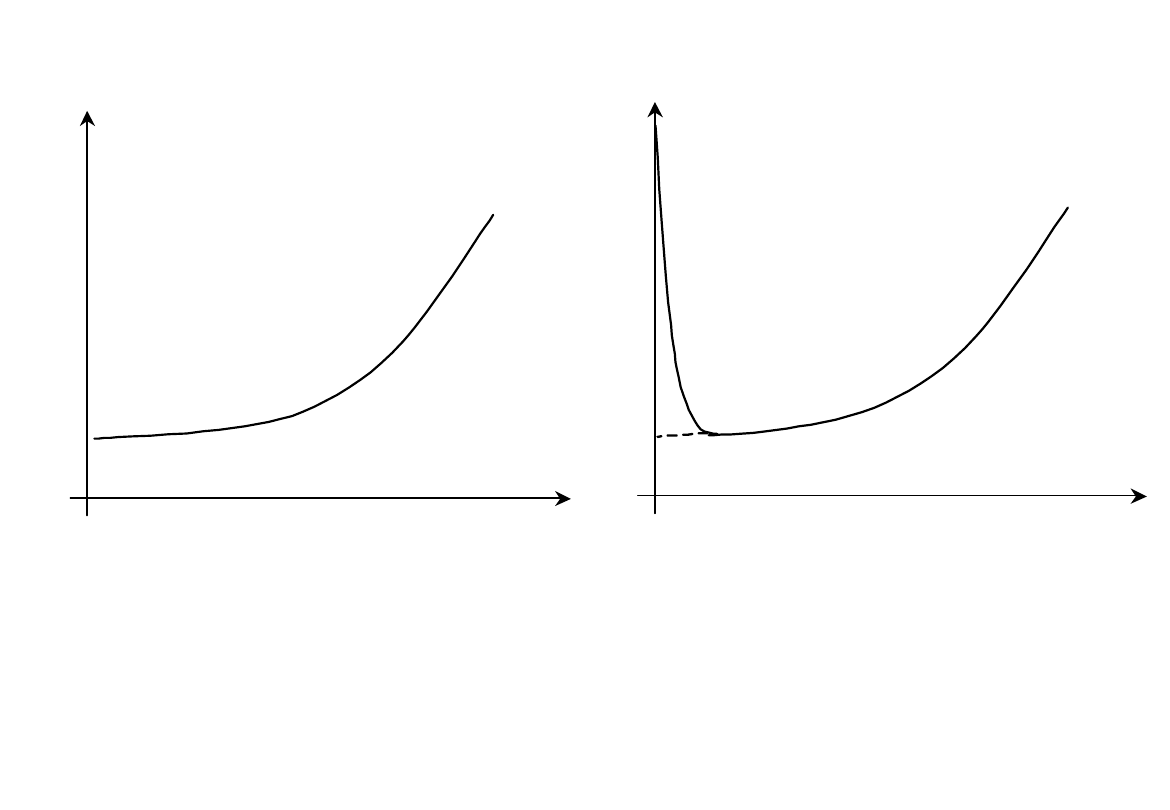
v 

w 

 

v 

w 

Jednostkowe opory ruchu w funkcji prędkości pociągu 

 

 

Opory profilu linii

Opory te dotyczą pionowego i poziomego profilu linii. Na wzniesieniach 
i na łukach pojawiają się opory dodatkowe, które dodają się do oporów 
zasadniczych.

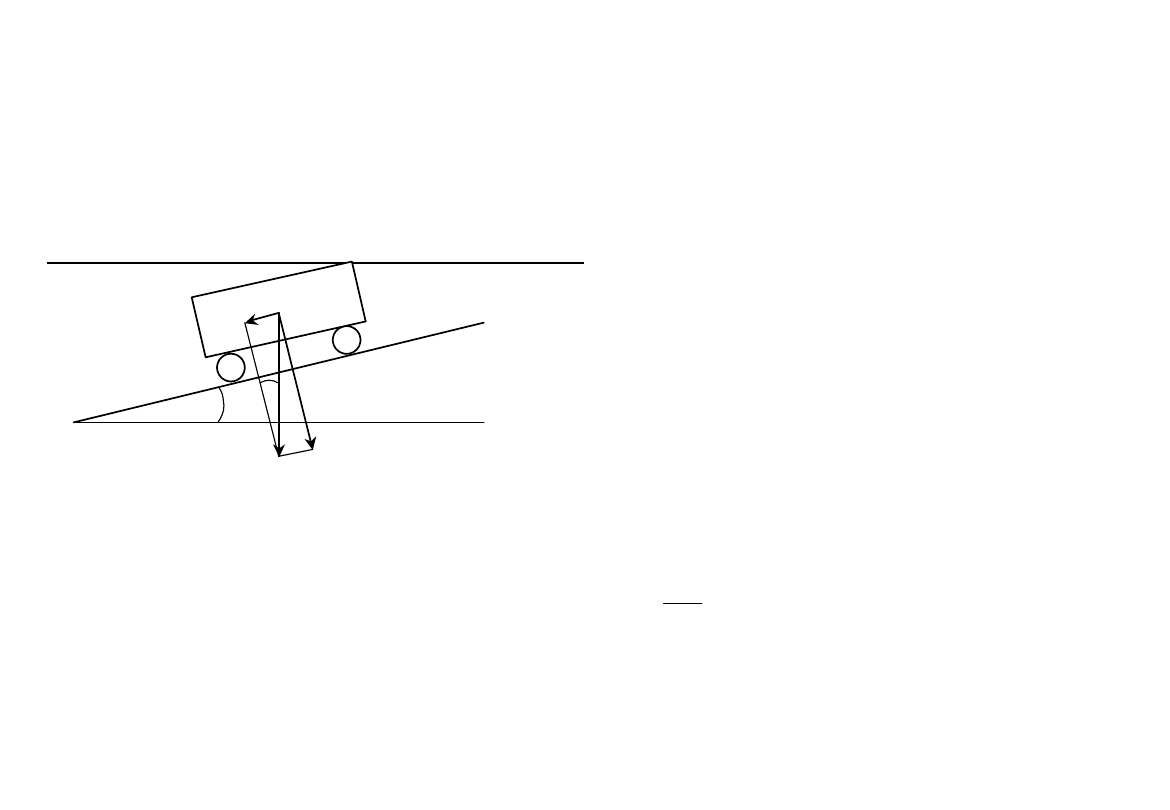
Opory na wzniesieniach i spadkach. 

 





G 

Rozkład ciężaru pociągu 
stojącego na wzniesieniu

 

Jeżeli ciężar pociągu G wyrażony 
jest w [kN], dodatkowy opór na 
wzniesieniu w [N] będzie wynosił: 



sin

1000 





G

W

i

Kąt nachylenia toru określa 
się zwykle w tysięcznych 
częściach jako stosunek 
wysokości wzniesienia w [m] 
do jego długości w [km] i 
oznacza i [

0

/

00

]. 

sin α ≈ tg α 

i

G

W

i





i

G

W

w

i

i





[N]

[

0

/

00

]

Przy wzniesieniach wartość oporu 
dodaje się do oporów 
zasadniczych, przy spadkach – 
odejmuje. 

 

 

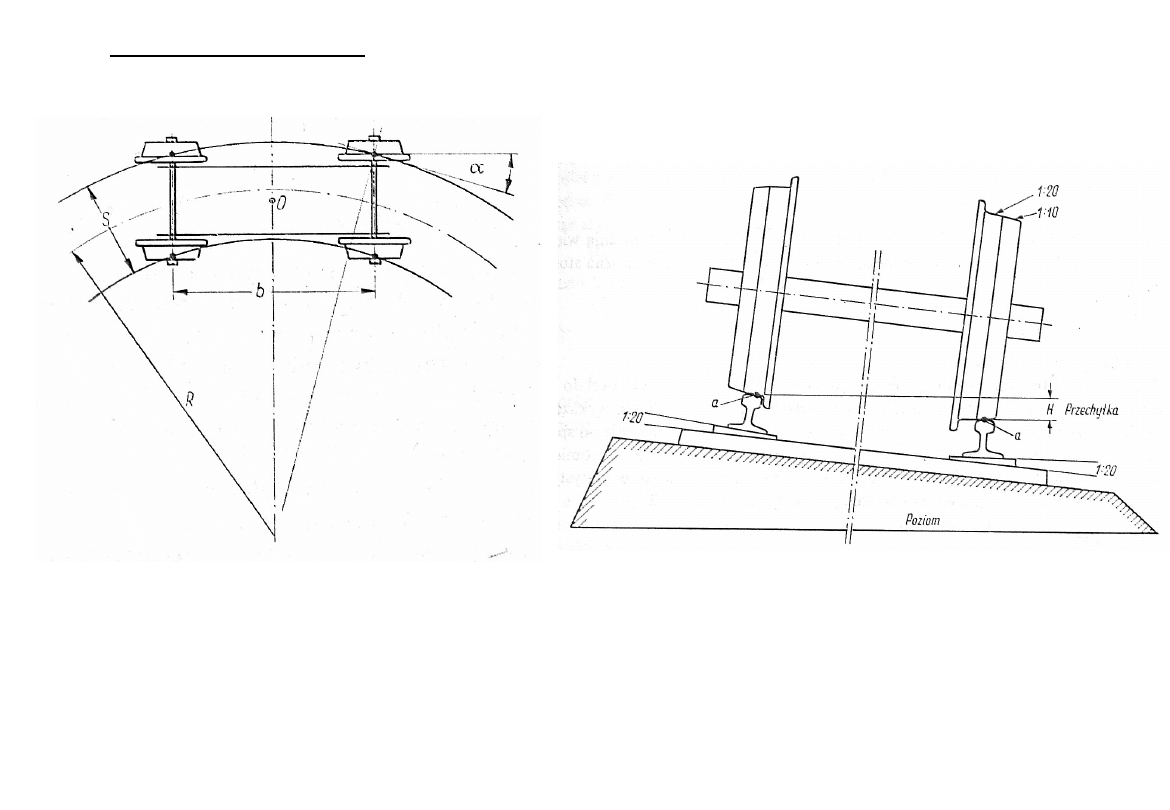
Opory krzywizny 

Wózek na łuku 

Układ kół pojazdu i szyn na 
łuku 

 

 

Opory  krzywizn  oblicza  się  zwykle  według  różnych  wzorów 
empirycznych.  Najbardziej  rozpowszechnione  są  wzory  Rőckla, 
określające jednostkowe opory w zależności od promienia łuku R:

m

R 350



m

R 350

250 



m

R 250



55

650





R

w

k

35

530





R

w

k

30

500





R

w

k

Wzory te dają niezgodne wyniki przy wartościach granicznych 
promienia łuku R. Stosować można wzór ogólny w postaci: 

20

700





R

w

k

[N/kN]

 

 

Opory dodatkowe ośrodka

Opory wiatru 

Wpływu  wiatru  na  opory  ruchu  nie  da  się  uwzględnić  zgodnie  z 
rzeczywistością,  ponieważ  ma  on  zmienną  siłę  i  kierunek  działania. 
Wpływu  tego  nie  uwzględnia  się  wcale  lub  na  trasach,  na  których 
spotyka  się  silne  wiatry,  zakłada  się,  że  prędkość  pociągu 
przyjmowana  do  obliczania  zasadniczych  oporów  ruchu  jest  o  10  do 
15 km/h większa od rzeczywistej. 

Opory w tunelach 

2

10

1

50



















v

q

L

W

t

[N]

gdzie:
L – długość tunelu w [km], dla metra długość L 
przyjmuje się
      jako odległość między dużymi i dobrze 
przewietrzanymi 
      stacjami,
q – stosunek przekroju tunelu do przekroju pociągu.

      

     Całkowite opory ruchu

Całkowite opory ruchu są sumą oporów zasadniczych, oporów 
profilu linii i ewentualnie oporów dodatkowych ośrodka





k

c

c

w

i

w

G

w

G

W













W[N],  w[

0

/

00

],  G[kN] 

 

 

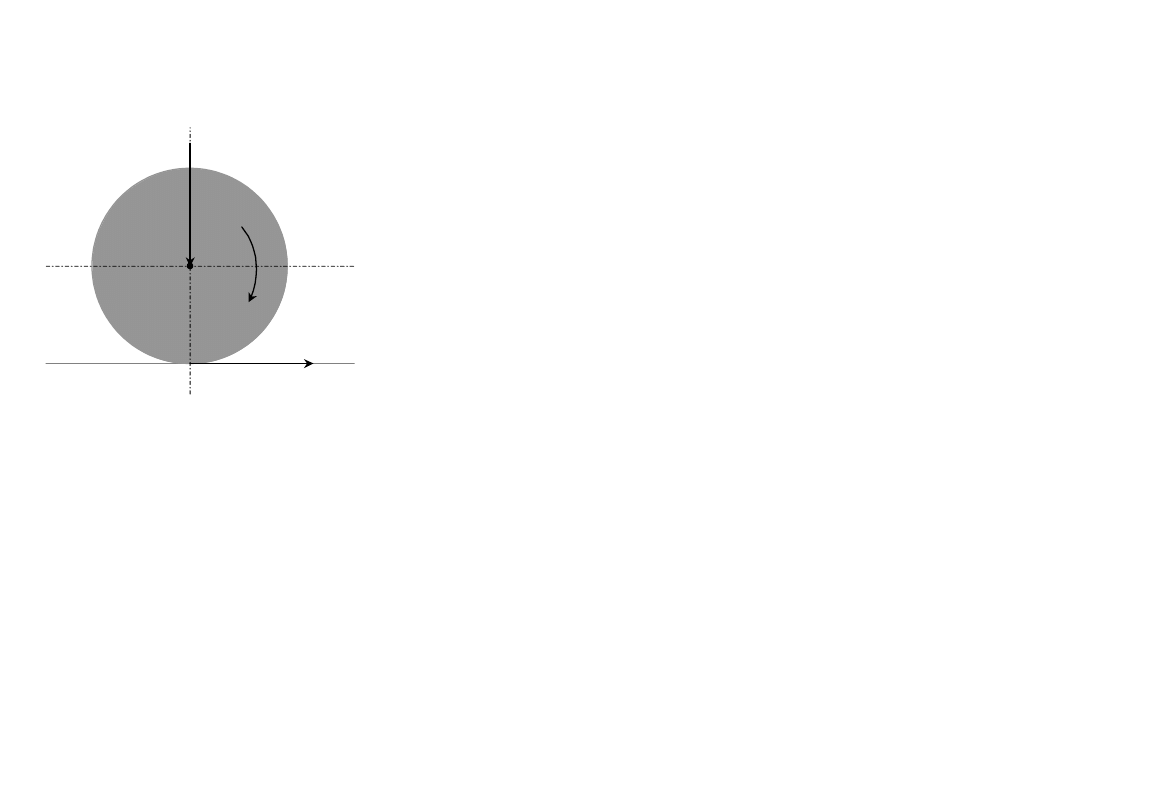
Przyczepność 

 

M 

G 

F 

Warunkiem  uzyskania  siły  pociągowej  na 
obwodzie  kół  lokomotywy  jest  sczepienie 
koła z szyną. Sczepienie występuje, jeżeli 
ciężar 

zestawu 

kołowego 

wraz 

z 

przypadającym nań ciężarem lokomotywy, 
czyli  tzw.  nacisk  osi  na  szyny  jest 
wystarczająco duży. 

Siła  działająca  na  obwodzie  koła  nie  może  być  zbyt  duża,  gdyż 
inaczej  przekroczy  wytrzymałość  powiązań  koła  z  szyną,  nastąpi 
zerwanie przyczepności,  koło zamiast toczyć się zacznie obracać się 
w miejscu i nastąpi poślizg.

Największa  siła  pociągowa,  jaką  może  rozwijać  koło  napędne, 
występująca  w  punkcie  styku  koła  napędnego  z  szyną  nosi  nazwę 
siły przyczepności i stanowi iloczyn nacisku osi napędnej na szynę i 
pewnego 

współczynnika 

zwanego 

współczynnikiem 

przyczepności.  

 

 

Prawidłowe  toczenie  koła  wymaga  w  punkcie  styczności  koła 
napędnego z szyną takiej siły pociągowej, która spełnia warunek:

 

n

G

f

F





gdzie:
F – siła działająca na obwodzie koła,
f – współczynnik przyczepności,
G

n

 = m g – ciężar części pojazdu przypadający na 

jedno koło oraz
                   ciężar tego koła (ciężar napędny).

Współczynnik  przyczepności  można  zdefiniować  jako  stosunek  siły 
pociągowej  wywołującej  zerwanie  przyczepności  między  kołem  a 
szyną do ciężaru obciążającego koło. 

Wartość  współczynnika  przyczepności  ma  bardzo  duże  znaczenie, 
ponieważ  od  niej  zależy  niezbędny  minimalny  ciężar  lokomotywy, 
potrzebny do wywołania określonej siły pociągowej.

Wartość współczynnika przyczepności zależy od wielu czynników, w 
szczególności  od  rodzaju  szyn  i  ich  stanu  (głównie  czystości),  od 
pogody  i  prędkości  pociągu.  Wartość  współczynnika  przyczepności 
spada  ze  wzrostem  prędkości.  Można  ją  powiększyć  posypując 
szyny piaskiem. 

 

 

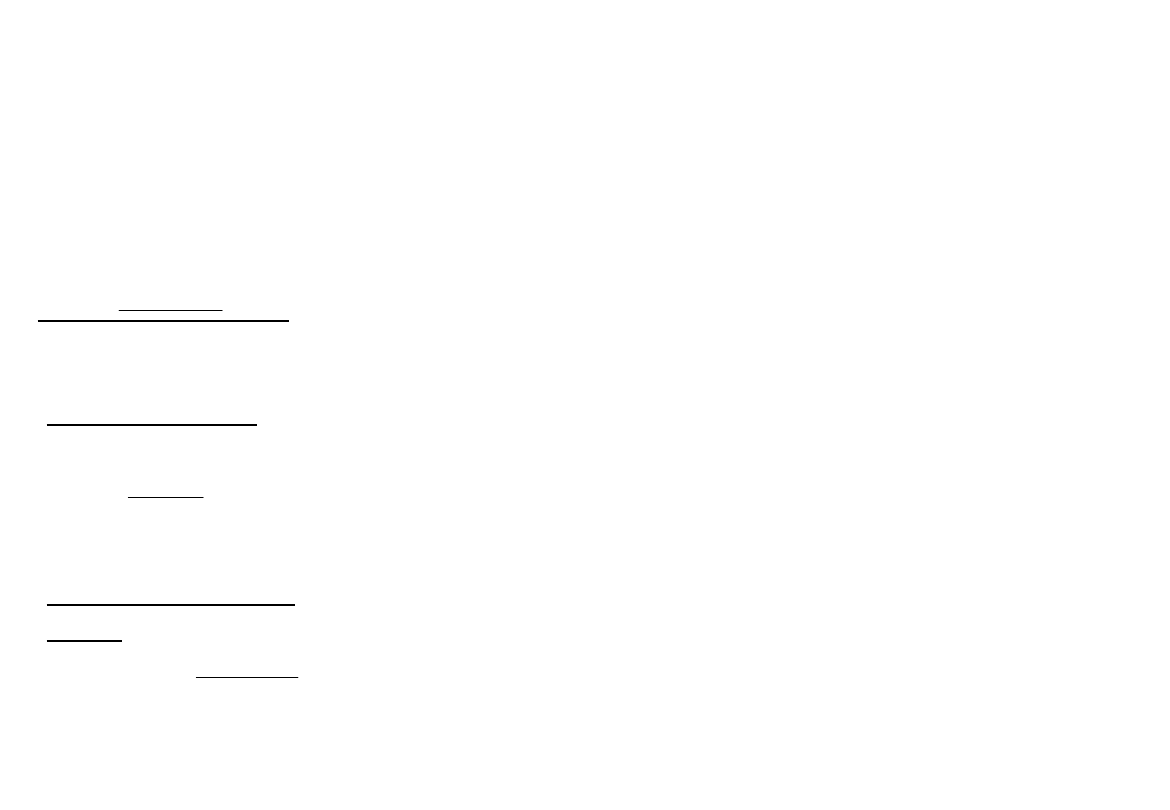
Opisując zjawisko przyczepności określa się współczynnik 
przyczepności 
całej lokomotywy f

L

. 

Analityczne ujęcie wpływu wielu różnorodnych czynników na wartość 
f

L 

nie jest możliwe. Do obliczeń stosuje się przybliżone wzory 

empiryczne.
 
Wzór Parodi’ego 

v

f

f

L

L

01

,

0

1

0





gdzie:  f

L0

 = 0,33   dla szyn suchych,

            f

L0

 =  0,27  dla szyn mokrych,

            średnio przyjmuje się   f

L0

 = 0,3.

Wzór Kothera 

v

f

L





42

9

Jest to wzór dla szyn suchych. 
Dla szyn mokrych należy wartość f

L

 

zmniejszyć 
do krotności 0,85-0,75. 

Wzór stosowany 
w PŁ 

v

v

f

f

L

L

2

100

100

0









współczynnik f

L0

 taki sam, jak we 

wzorze Parodi’ego 

 

 

Współczynnik przyczepności f

L

 maleje ze wzrostem prędkości – rys.

Tak  samo  przebiega  zależność  siły  przyczepności  F

L 

lokomotywy  , 

ograniczającej  siłę  pociągową  lokomotywy,  w  funkcji  prędkości  v. 
We  wzorze  ciężar  napędny  będzie  równy  ciężarowi  całej 
lokomotywy,  G

n

=G

L

  ,  jeżeli  wszystkie  osie  w  lokomotywie  są 

napędne.

Aby nie dopuścić do poślizgu, przyjmuje się, że maksymalna siła 
pociągowa, jaką lokomotywa może rozwijać wynosi 90% siły 
przyczepności.

 

v 

f

L

  

f

L

 (F

L

) 



Współczynnik przyczepności i 
współczynnik tarcia 
w funkcji prędkości

n

L

L

G

f

F





L

F

F



 9

,

0

 

 

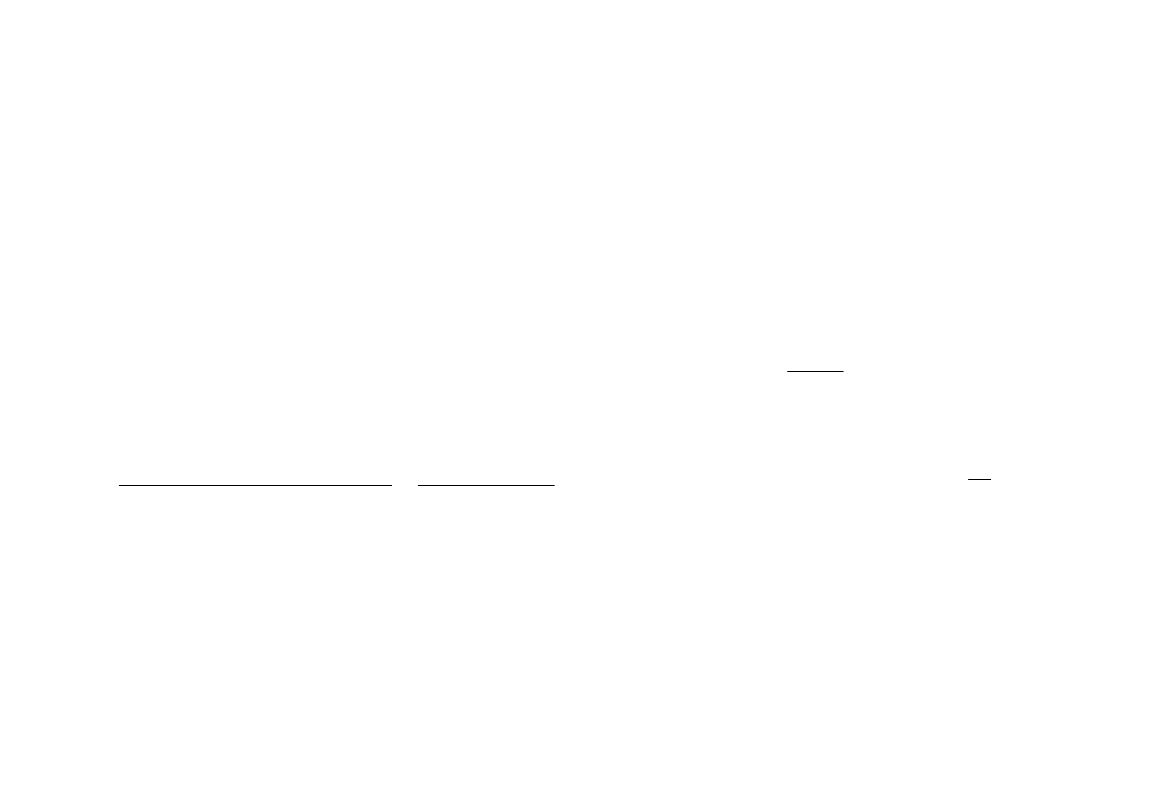
Siła  pociągowa  lokomotywy,  pochodząca  z  momentów  obrotowych 
przyłożonych  do  kół  napędnych,  musi  pokonać  opory  ruchu  samej 
lokomotywy  i  wagonów  oraz  nadać  lokomotywie  i  wagonom 
odpowiednie przyspieszenie. Jednocześnie, siła ta musi być mniejsza 
od siły przyczepności.

 

L

L

p

G

f

W

F

F

















g

m

f

w

g

m

m

a

m

m

F

L

L

w

L

w

w

L

L

































g

m

f

w

g

m

m

a

m

m

L

L

w

L

w

w

L

L



















max





































m

G

w

G

f

m

m

w

g

m

m

g

m

f

a

L

L

w

w

L

L

w

L

L

L

)

(

max

g

m

f

w

g

m

a

m

L



















L

f

w

g

a















g

w

f

a

L





max

Jeżeli pojazd lub pociąg 
ma wszystkie osie 
napędne

 

W  wyniku  ograniczenia  siły  pociągowej  lokomotywy,  przede  wszystkim 
względami  przyczepności,  ograniczona  zostaje  wielkość  przyspieszenia 
rozruchowego. 
Możliwe  do  uzyskania  przyspieszenie  będzie  większe,  jeśli  większy 
będzie  ciężar  napędny.  Konieczne  jest  zatem  nadanie  lokomotywom 
(również 

wagonom 

motorowym 

w 

zespołach 

trakcyjnych) 

wystarczającego ciężaru napędnego, z czym związane jest odpowiednie 
rozwiązanie konstrukcji podwozia lokomotywy. 

 

 

W  wyniku  ograniczenia  siły  pociągowej  lokomotywy,  przede 
wszystkim  względami  przyczepności,  ograniczona  zostaje 
wielkość przyspieszenia rozruchowego.

Przyjmując średnią siłę pociągową lokomotywy F o 10% niższą od 
maksymalnej,  wynikającej  z  warunków  przyczepności,  F=0,9  F

L

, 

otrzymuje  się  dla  pociągów  prowadzonych  lokomotywami  4-
silnikowymi,  następujące  najwyższe  wartości  przyspieszeń,  przy 
prędkości 50 km/h:

dla pociągu towarowego o masie 1800 t   0,06 m/s

2

,

dla pociągu towarowego o masie 900 t 

0,14 m/s

2

.

Dla zespołu trakcyjnego 3-wagonowego o masie 155 t

0,6 m/s

2

.

 

 

Względy ograniczające siłę pociągową, przede wszystkim 
przyczepność, powodują również ograniczenie masy pociągu. 

L

L

p

G

f

W

F







L

L

G

f

w

a

g

G





















w

a

g

G

f

G

L

L









lub

w

a

g

m

f

m

L

L









Maksymalna  masa  pociągu  jest  wprost  proporcjonalna  do  masy 
lokomotywy 

i 

współczynnika 

przyczepności, 

zależy 

od 

jednostkowych  oporów  ruchu  i  przyspieszenia  pociągu.  Zatem 
maksymalna  masa  pociągu  będzie  inna  dla  każdego  typu 
lokomotywy i profilu trasy. 

 

 

Siła pociągowa na obwodzie kół lokomotywy jest to siła F

h

 rozwijana 

„na  haku”  (sprzęgu),  czyli  siła,  z  jaką  lokomotywa  ciągnie  wagony, 
pomniejszona o siłę pociągową samej lokomotywy, stanowiącą sumę 
oporów  ruchu  lokomotywy  i  siły  nadającej  lokomotywie 
przyspieszenie. 

g

a

G

w

G

F

F

F

F

L

L

L

L

lok

h



















Wytrzymałość  sprzęgów  jest  ściśle  ograniczona  i  siła  na  haku  F

h

 

nie może być dowolnie duża. Tak więc i sama siła pociągowa F (na 
obwodzie  kół  napędnych)  jest,  prócz  przyczepności,  ograniczona 
wytrzymałością sprzęgów wagonowych.