W

OJSKOWA

A

KADEMIA

T

ECHNICZNA

Warszawa 21.4.2009

K

OMUNIKACJA CZŁOWIEK

-

KOMPUTER

S

PRAWOZDANIE Z ĆWICZENIA NR

1:

Badanie charakterystyk jakości wprowadzania informacji przez użytkownika.

Autor:
***

Prowadzący:

Lesław Mrowca

2

1 Warunki badania

1.1 Badanie I

Warunki badania pierwszego:

− tryb pracy ekranu: 80 znaków w wierszu,
− badanie bez tła,
− łańcuchy znaków wyświetlane na dole ekranu,
− duże znaki – niemigoczące,
− czas – nieograniczony,
− liczba znaków w łańcuchu N – zmienna,
− liczba łańcuchów M – zmienna, w zależności od liczby znaków N.

1.2 Badanie II

Warunki badania były zmienne, podzielone na dziewięć etapów; każdy z nich bazował na

warunkach z badania pierwszego. Wprowadzone zmiany w stosunku do badania pierwszego to N=4
znaków dla każdego etapu, oraz odpowiednio:

1. Brak innych zmian zmian.
2. Brak tła, łańcuchy w różnych miejscach.
3. Tło, łańcuchy w różnych miejscach.
4. Tło, łańcuchy w różnych miejscach, znaki migoczące.
5. Brak tła, czas dt losowany gd=0.8, gg=3.0.
6. Brak tła, łańcuchy w różnych miejscach, czas dt losowany gd=0.8, gg=3.0.
7. Tło, łańcuchy w różnych miejscach, czas dt losowany gd=0.8, gg=3.0.
8. Tło, łańcuchy w różnych miejscach, znaki migoczące, czas dt losowany gd=0.8, gg=3.0.
9. Wprowadzanie danych przy użyciu klawiatury ekranowej.

3

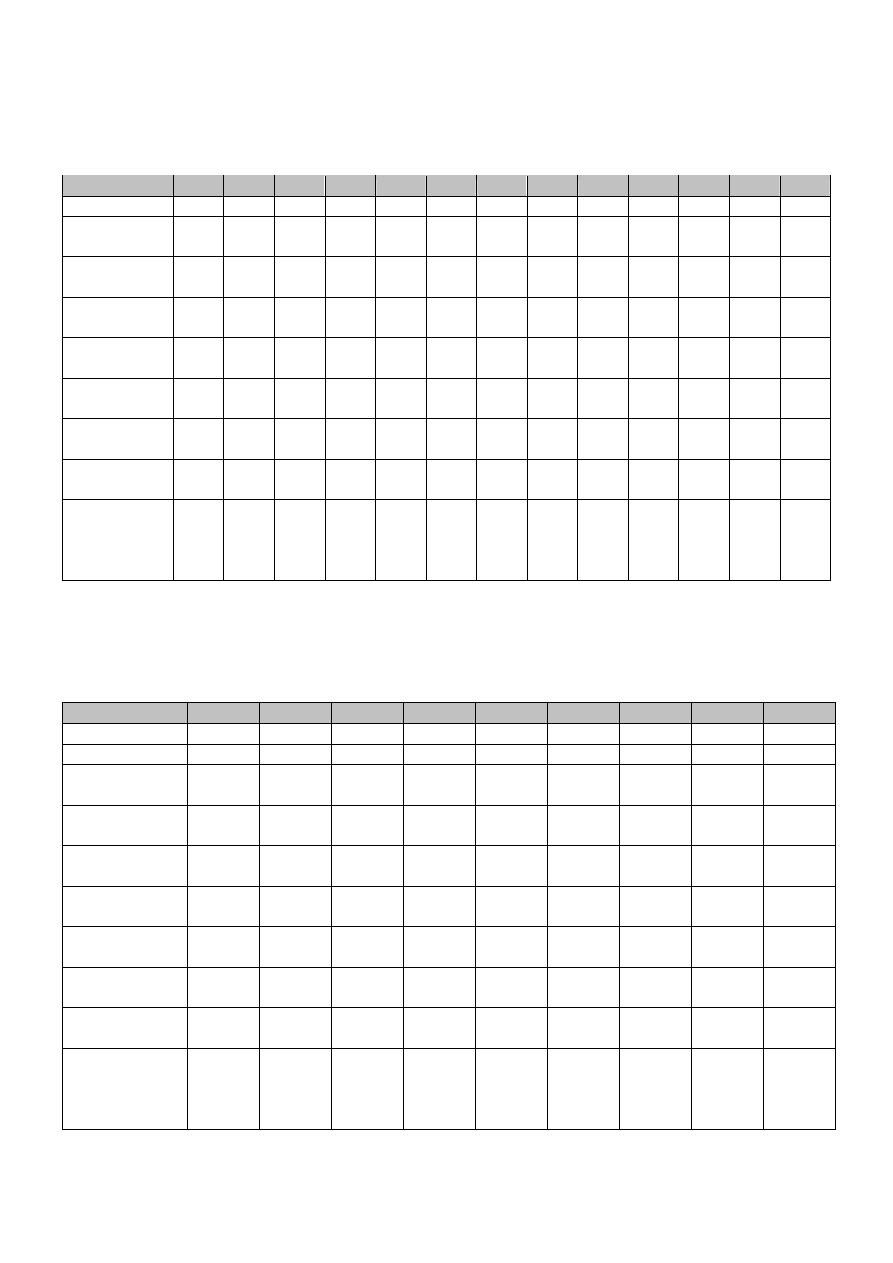
2 Zestawienie wyników

2.1 Badanie I

Dł. łańcucha N

1

2

4

6

8

10

12

14

16

18

20

22

24

Liczba łańc. M

70

70

50

50

40

30

30

30

30

30

30

30

30

DTS [s]

1,32

1,79

3,03

4,57

6,77

7,96

9,46

11,78 13,96

15,24

16,26

17,92

20,3

TSR1ZN [s]

0,66

0,6

0,61

0,65

0,75

0,72

0,73

0,79

0,82

0,8

0,77

0,78

0,81

P1

0

0,014

0,02

0,01

0,003

0,02

0,011

0,014 0,008

0,017

0,017

0,018

0,011

PN

0

0,014

0,08

0,06

0,025

0,167

0,1

0,167 0,133

0,2

0,3

0,3

0,233

Wariancja S2 [s]

0,057

0,186 0,651

1,154

2,458

3,449

3,325

13,69 5,771

5,064

8,582

8,476

13,52

Odchylenie S4 [s] 0,238

0,432 0,807

1,074

1,568

1,857

1,824

3,7

2,402

2,25

2,929

2,911

3,677

WAR1ZN [s]

0,0568 0,0466 0,0407 0,032 0,0384 0,0345 0,0231 0,0698 0,0225 0,0156 0,0215 0,0175 0,0235

ODCH1ZN [s]

0,2382 0,2159 0,2017 0,179

0,196 0,1857 0,152 0,2643 0,1501 0,125 0,1465 0,1323 0,1532

DTSUFNL [s]

1,2663 1,6845 2,8093 4,2687 6,2796 7,2941 8,8038 10,458 13,091 14,431 15,213 16,88 18,981

DTSUFNP [s]

1,378 1,8882 3,2567 4,8641 7,2514 8,6232 10,109 13,106 14,839 16,042 17,31 18,964 21,612

S1UFNL [s]

0,0418 0,1369 0,4551 0,8064 1,6538 2,1964 2,1179 8,7194 3,6501 3,2251 5,4657 5,3984 8,6108

S1UFNP [s]

0,0815 0,2685 1,0071 1,7845 4,0313 6,1806 5,9599 24,537 10,463 9,0755 15,381 15,191 24,231

PNUFNL

0

0

0,0048

0

0

0,0333

0

0,0333 0,0117 0,0569 0,136

0,136

0,082

PNUFNP

0

0,0421 0,1552 0,1258 0,0734

0,3

0,2074

0,3

0,255 0,3431 0,464

0,464 0,3847

ALFA

6,49

6,35

4,86

5,69

7,49

6,51

7,37

8,19

9,32

11,05

12,77

9,53

11,22

BETA

8,84

14,59 17,01

31,54

65,98

67,6

91,82 126,58 173,79 235,75 282,56 237,85 314,54

TM

1,303

2,192 3,243

5,238

8,52

9,93

12,027 15,018 18,229 21,003 21,857 24,424 27,592

TETA

1,362

2,296 3,498

5,543

8,814 10,378 12,455 15,453 18,639 21,342 22,121 24,951 28,023

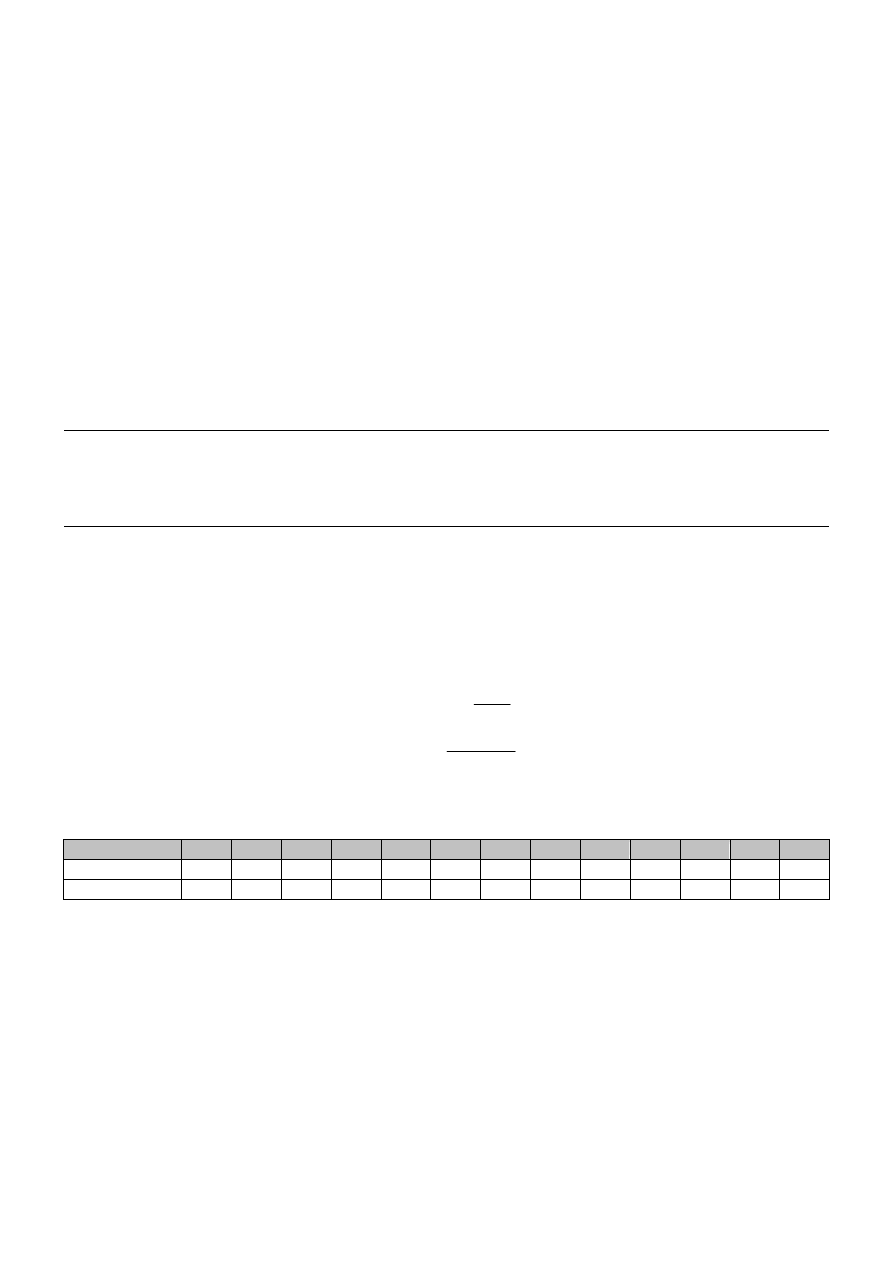
2.2 Badanie II

Nr ćwiczenia

1

2

3

4

5

6

7

8

9

Dł. łańcucha N

4

4

4

4

4

4

4

4

4

Liczba łańc. M

50

50

50

50

50

50

50

50

50

DTS [s]

3,34

3,43

3,93

3,66

4,43

4,65

4,28

3,53

4,61

TSR1ZN [s]

0,67

0,69

0,79

0,73

0,89

0,93

0,86

0,71

0,92

P1

0

0,005

0,065

0,005

0,345

0,365

0,355

0,145

0

PN

0

0,02

0,1

0,02

0,4

0,36

0,46

0,18

0

Wariancja S2 [s]

0,611

0,772

0,974

0,678

1,48

0,85

1,78

0,796

1,126

Odchylenie S4 [s]

0,782

0,879

0,987

0,824

1,217

0,922

1,334

0,892

1,061

WAR1ZN [s]

0,0382

0,0483

0,0609

0,0424

0,0925

0,0531

0,1112

0,0498

0,0704

ODCH1ZN [s]

0,1955

0,2197

0,2468

0,2059

0,3042

0,2304

0,3335

0,2231

0,2653

DTSUFNL [s]

3,1239

3,1848

3,6454

3,4363

4,0258

4,3398

3,8272

3,2627

4,3131

DTSUFNP [s]

3,5573

3,672

4,2222

3,8929

4,832

4,9687

4,724

3,79

4,9013

S1UFNL [s]

0,4273

0,5398

0,6692

0,4743

0,9718

0,5514

1,1618

0,5447

0,7872

S1UFNP [s]

0,9456

1,1944

1,5478

1,0496

2,5248

1,4758

3,0626

1,2721

1,7419

PNUFNL

0

0

0,0168

0

0,2642

0,227

0,3219

0,0735

0

PNUFNP

0

0,0588

0,1832

0,0588

0,5358

0,493

0,5981

0,2865

0

ALFA

6,19

5,99

5,34

6,49

5,14

5,17

4,18

4,93

6,29

BETA

26,76

26,29

28,45

30,33

31,61

29,11

21,68

19,65

35,53

TM

4,117

4,171

4,998

4,471

5,747

5,264

4,695

3,7

5,392

TETA

4,321

4,393

5,327

4,675

6,154

5,632

5,181

3,983

5,652

4

3 Analiza statystyczna

3.1 Test zgodności

2

χ

Hipotezy, podstawowa:

0

H (czas wprowadzania łańcucha ma rozkład normalny)

i alternatywna:

1

H (czas wprowadzania łańcucha nie ma rozkładu normalnego)

Przyjmujemy poziom istosności

0, 05

α

=

.

Liczba k odczytana z tablicy rozkładu

2

χ

dla 2 stopni swobody wynosi 5,991. Wobec tego zbiór

krytyczny przyjmuje postać:

5,991;

)

K = 〈

+∞

Obliczenie wartości krytycznej:

Nr klasy i Przedział Ilość ciągów n

a

a+1 (a-x) / s (a+1 -x) /s

F

F + 1

p

N

(n - N)^2/ N

1

do 3,4

5

3,4

-0,24284

0

0,404065 0,404065 20,20325 11,44067

2

do 4,2

11

3,4

4,2 -0,24284 -0,1494 0,404065 0,44062 0,036555 1,827747 46,02946

3

do 4,6

13

4,2

4,6 -0,1494 -0,10268 0,44062 0,45911 0,01849 0,924489 157,7282

4

do 5,8

16

4,6

5,8 -0,10268 0,037485 0,45911 0,514951 0,055841 2,792066 62,48045

5

> 5,8

5

5,8

0,037485

0,514951

1

0,485049 24,25245 15,28328

Suma

50

1

50

292,962

Wartość krytyczna zawiera się w zbiorze krytycznym więc przyjmujemy hipotezę alternatywną.

3.2 Średnia przepustowość użytkownika

Średnią przepustowość użytkownika wyznaczono przez obliczenie współczynników:

A – liczba znaków wprowadzona na sekundę,

N

A

DTS

=

B – liczba naciśnięć klawiszy na sekundę,

1

TSR1ZN

B =

Obliczenia zostały wykonane dla każdego N:

Dł. łańcucha N

1

2

4

6

8

10

12

14

16

18

20

22

24

B – klaw. na sek. 1,5152 1,6667 1,6393 1,5385 1,3333 1,3889 1,3699 1,2658 1,2195 1,25 1,2987 1,2821 1,2346
A – znak. na sek. 0,7576 1,1173 1,3201 1,3129 1,1817 1,2563 1,2685 1,1885 1,1461 1,1811 1,23 1,2277 1,1823

5

0

0,2

0,4

0,6

0,8

1

1,2

1,4

1,6

1,8

1

2

4

6

8

10

12

14

16

18

20

22

24

Dł. łańcucha N

B - klaw na sek

A - znak na sek

3.3 Porównanie DTS

Sprawdzwian wyliczany jest z zależności:

2

2

1

2

1

2

X

Y

S

S

n

n

−

+

i przyjmuje wartości:

Nr ćwiczenia

1

2

3

4

5

6

7

8

9

Dł. łańcucha N

4

4

4

4

4

4

4

4

4

Sprawdzian

-17,9869 -17,2955 -18,7669

-19,409 -18,4217 -23,8049 -16,3813

-17,721 -21,4238

Zbiór krytyczny po przyjęciu poziomu istotności

0, 05

α

=

po wykonaniu obliczeń:

( ) 1

2

k

α

Φ

= −

( )

0,975

k

Φ

=

i pod odczytaniu wartości z tablic przyjmuje postać:

(

; 1,96

1,96;

)

−∞ −

〉 ∪ 〈

+∞

Na podstawie czego można wysnuć wniosek, iż parametr DTS z badania I nie jest równy na
określonym poziomie ufności dla żadnego ćwiczenia z badania II.

6

4 Wykresy

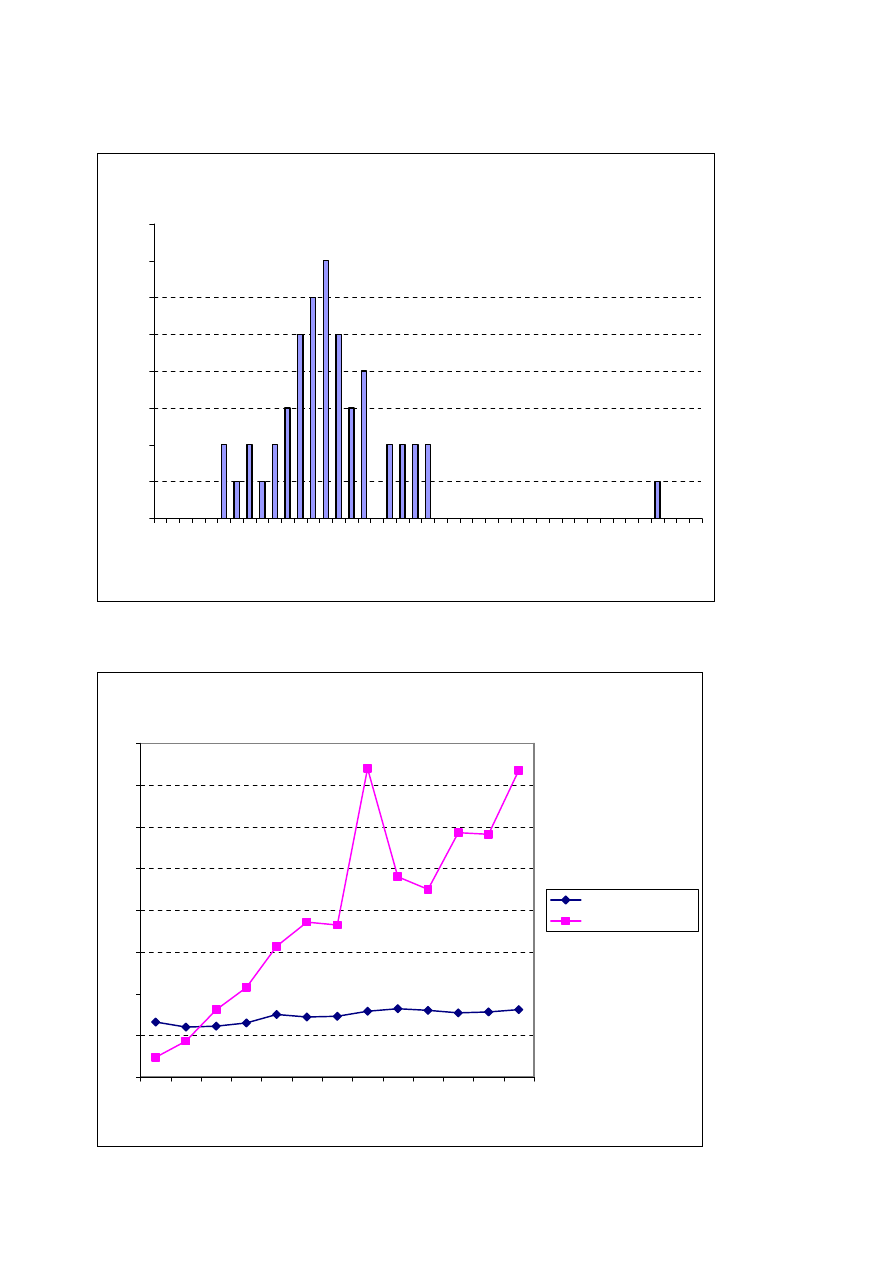
Histogram dla N=4

0

1

2

3

4

5

6

7

8

2

2,

4

2,

8

3,

2

3,

6

4

4,

4

4,

8

5,

2

5,

6

6

6,

4

6,

8

7,

2

7,

6

8

8,

4

8,

8

9,

2

9,

6

10

10

,4

Czas [s]

Il

o

ś

ć

Wykres 1 – rozkład ilości ciągów wpisanych w określonym czasie.

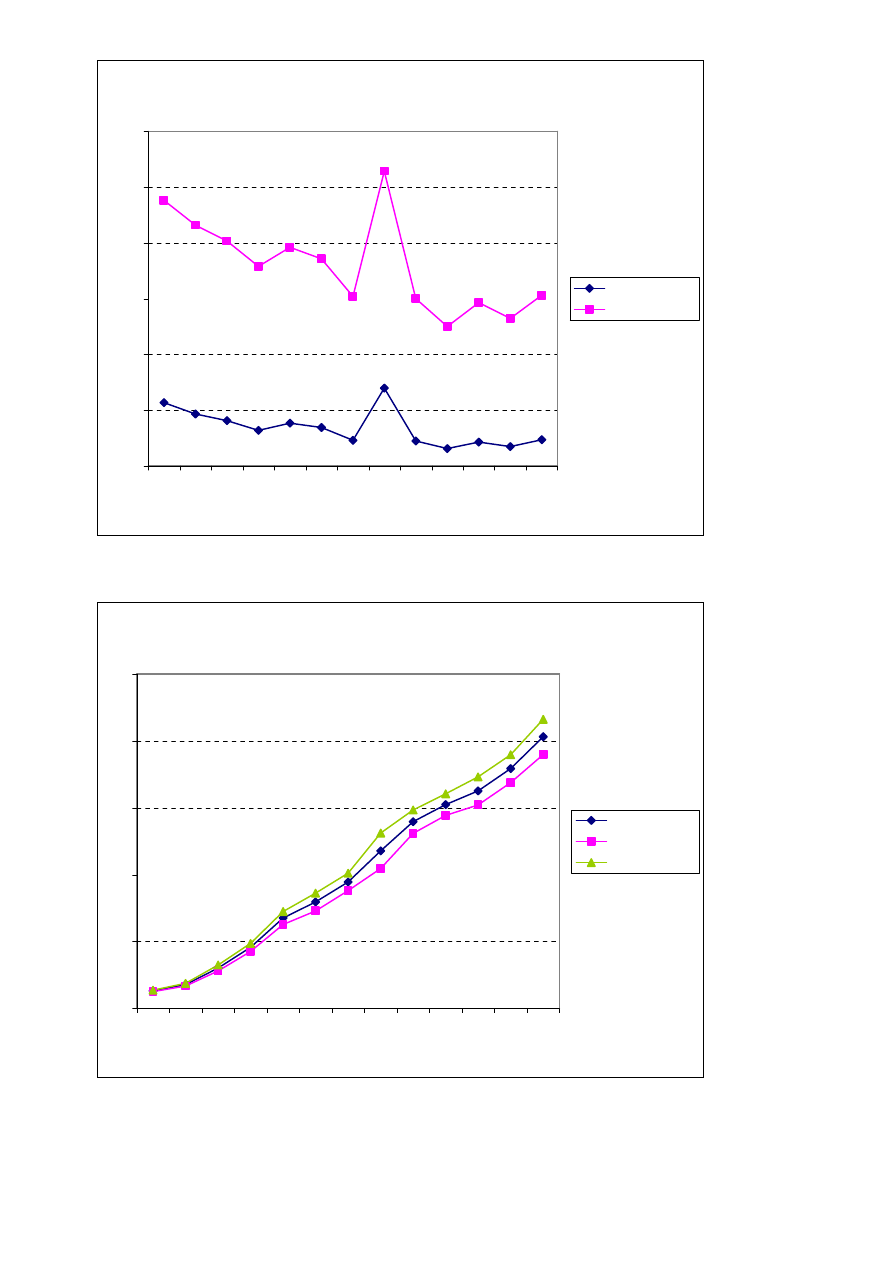
TSR1ZN i odchylenie S4

0

0,5

1

1,5

2

2,5

3

3,5

4

1

2

4

6

8

10

12

14

16

18

20

22

24

Dł. łańcucha N

TSR1ZN [s]

Odchylenie S4 [s]

Wykres 2 – średnie czasy naciśnięcia klawisza oraz odchylenia standardowe dla określonych

długości łańcucha.

7

WAR1ZN i ODCH1ZN

0

0,05

0,1

0,15

0,2

0,25

0,3

1

2

4

6

8

10

12

14

16

18

20

22

24

Dł. łańcucha N

WAR1ZN [s]

ODCH1ZN [s]

Wykres 3 – wariancje oraz odchylenia standardowe czasu wprowadzania jednego znaku

w łancuchu.

DTS i przedziały ufności [DTSUFNL, DTSUFNP]

0

5

10

15

20

25

1

2

4

6

8

10

12

14

16

18

20

22

24

Dł. łańcucha N

DTS [s]

DTSUFNL [s]

DTSUFNP [s]

Wykres 4 – średnie czasy wprowadzania łancucha wraz z przedziałami ufności.

8

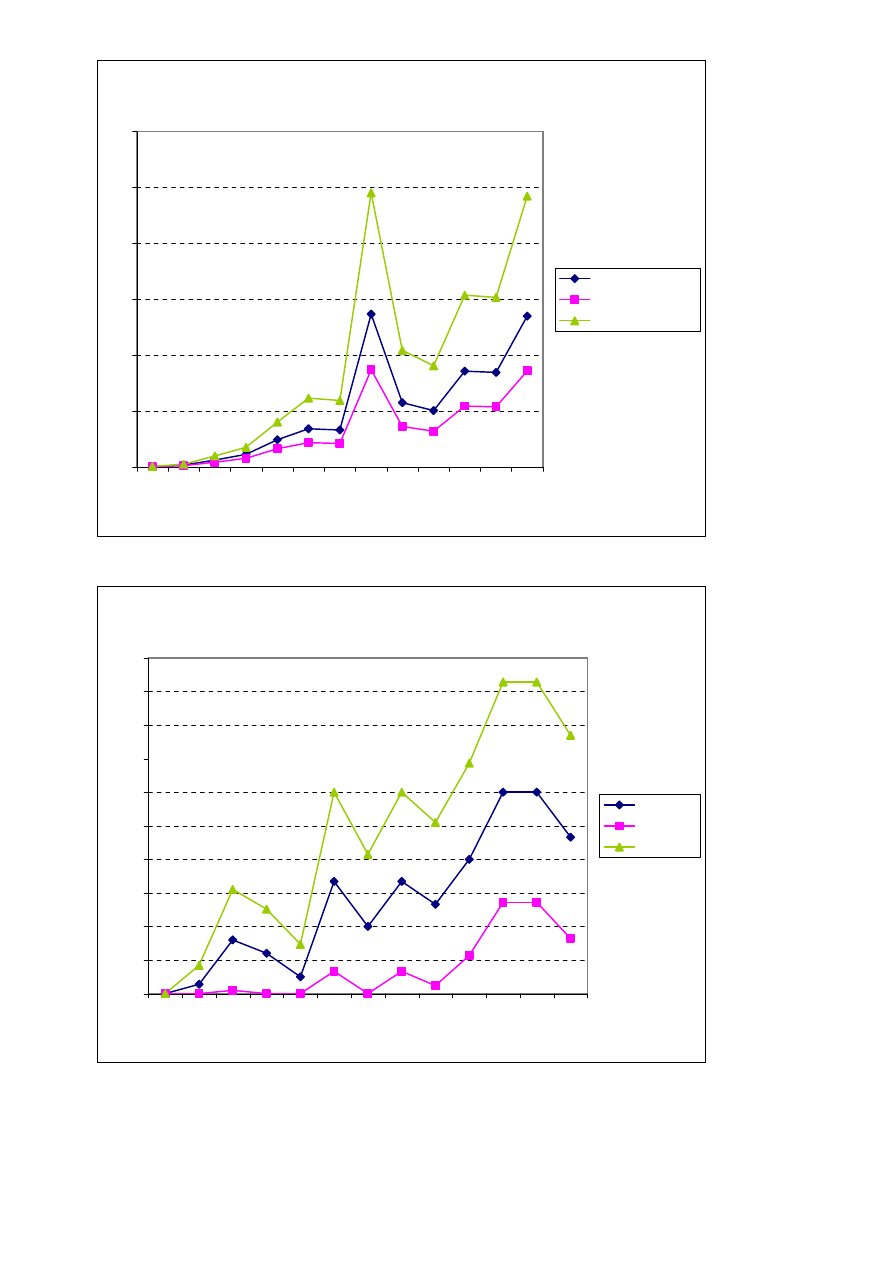
Wariancja S2 i przedziały ufności [S1UFNL, S1UFNP]

0

5

10

15

20

25

30

1

2

4

6

8

10

12

14

16

18

20

22

24

Dł. łańcucha N

Wariancja S2 [s]

S1UFNL [s]

S1UFNP [s]

Wykres 5 – wariancje czasu wprowadzania łańcucha wraz z przedziałami ufności.

PN i przedziały ufności [PNUFNL, PNUFNP]

0

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

1

2

4

6

8

10

12

14

16

18

20

22

24

Dł. łańcucha N

PN

PNUFNL

PNUFNP

Wykres 6 – prawdopodobieństwa błędnego wprowadzenia łańcucha wraz z przedziałami

ufności.

9

5 Wnioski

Test zgodności średnich przeprowadzony w punkcie 3.3 nie wykazał zgodności wartości DTS

między wprowadzaniem ciągów o tej samej długości i przy tych samych warunkach, ale
wykonywanych po dluższej przerwie – być może zadecydowało o tym samopoczucie użytkownika
podczas wprowadzania danych które mogło się różnić.

Zgodnie z oczekiwaniami wraz ze wzrostem długości wprowadzanych ciągów rośnie zarówno

prawdopodobieństwo popełnienia błedów (wykres 6) jak i średni czas wprowadzania (wykres 4).
Charakterystyka zależności DTS od N widoczna na wykresie 4 jest niemal liniowa.

Zgodne z intuicją są także wnioski płynące z wykresu 2 – czas naciśnięcia klawisza rośnie wraz z

długościa ciągów co spowodowane jest trudnością w rozpoznawianiu poszczególnych znaków w
długich napisach. Fakt, że znaki alfanumeryczne było losowe (nie tworzyły sensownych dla
człowieka wyrazów) powodował konieczność spoglądania co jakiś czas na ekran w celu odczytania
kolejnej serii znaków powodując irytujące dla użytkownika „gubienie” tekstu.

Wykres 3 pokazuje niewielką zmianę wariancji i odchylenia czasu wprowadzania jednego znaku

przy zwiększaniu długości ciągów – jest to spowodowane stałą prędkościa wpisywania znaków przez
uzytkownika, zmiana wynika ze stabilizacji wyników przy dłuższych ciągach.

Na wykresie 5 widać wzrost wariancji czasu wprowadzania łańcucha wraz ze wzrostem ilości

znaków, wykres ten może jednak być mylący ponieważ pokazuje wartości bezwzględne w
sekundach. W celu okreslenia wpływu ilości znaków na tę wartość należałoby wyliczyć wartości
względne.

W przypadku badań z ustawionym limitem czasu zauważalny jest duży stopień błędów;

spowodowane jest to niewystarczającą ilością czasu co powodowało pomyłki przy wprowadzaniu
danych – czasami użytkownik podczas kończenia wprowadzania danego ciągu nie zdawal sobie
sprawy że nastąpiła zmiana łańcucha przeznaczonego do wpisywania i naciskał klawisz ENTER.