Modelowanie konsumpcji: sta
ły dochód czy zachowanie
zgodne z zasada opart
ą na doświadczeniu?
Niniejsza praca zosta
ła oparta na artykule Dimitris’a Hatzinikolaou’a
1
pod tytu
łem „Modeling consumption:
permanent-income or rule-of-thumb behavior?”, który ukaza
ł się drukiem w grudniu 1998 roku. Ostatnimi czasy wielu
naukowców stara
ło się wyestymować stosunek procentowy zagregowanej konsumpcji odpowiadającej
konsumentom przeznaczaj
ącym cały swój dochód w każdym z okresów na bieżącą konsumpcję do konsumentów
kieruj
ących się zasadą racjonalnych oczekiwań. Ta procentowa wielkość ma ważne skutki polityczne. Istniejące
dotychczas modele dokonuj
ą pewnych przybliżeń, które mogą zaburzyć spójność estymacji jednak zaproponowany
przez autora artyku
łu model jest wolny od tego problemu.
Korzystaj
ąc z rocznych zagregowanych danych dla Grecji [z lat 1960 – 1993] model dokonuje estymacji
wielko
ści procentowych i te wyniki okazują się niższe niż dotychczas przedstawiane [jest to dobry znak]. Dane
zgromadzone przez autora pochodz
ą głównie z następujących źródeł:
OECD;
International Financial Statistics;
Bank of Greece, Demographic Yearbook – USA;
International Labor Office.
Dane te obejmuj
ą wartości takie jak dochód gospodarstw domowych, podatki, ubezpieczenia społeczne,
konsumpcja, oszcz
ędności, wydatki rządowe, transfery międzynarodowe, CPI, PKB, stopy inwestycyjne, kursy
walutowe, baza monetarna [wielko
ść podaży pieniądza], ceny w imporcie w US $, całkowite zatrudnienie, emigracja,
wysoko
ść wynagrodzenia, czas pracy, wysokość zadłużenia publicznego, poziom cen importowanych maszyn oraz
produktywno
ść pracy [productivity of labor]. Jak widać dane mają bardzo duży zakres, co sprzyja poprawności
estymacji.
W dalszej cz
ęści przedstawimy wpierw modele poprzedzające model autorski Hatzinikolaou’a, następnie
omówiony zostanie model tego
ż autora oraz poddamy analizie porównawczej wyniki estymacji dokonanych tymi
modelami.
Zaczniemy od wprowadzenia podstawowych oznacze
ń. I tak, jako C oznaczymy całkowite, krajowe prywatne
wydatki na konsumpcje dóbr nietrwa
łych, krótkotrwałych i usług podzielone przez wskaźnik cen [CPI] oraz przez
ca
łkowite zatrudnienie [N].Przez L
t
b
ędziemy rozumieli czas wolny przypadający na jednego pracownika [wyliczony
wg wzoru:
t
t
HR
L
×
−
=
50
5840
, gdzie HR
t
to liczba przepracowanych godzin tygodniowo, przy ogólnym za
łożeniu
uposa
żenia rocznego pracownika w 5840 (=365x16) godzin oraz średni okres pracy – 50 tygodni rocznie. Dalej, jako
G przyjmiemy wydatki rz
ądowe [po uszczupleniu o spłatę amortyzacji oraz odsetek zadłużenia publicznego,
ubezpieczenia socjalne, transfery zagraniczne] znormalizowane przez CPI oraz N. Jako Y oznaczymy dochód
1
The Flinders University of South Australia, School of Economics, GPO Box 2100, Adelaide, SA 5001, Australia
gospodarstw domowych [bez podatków bezpo
średnich oraz zabezpieczeń socjalnych] podobnie jak poprzednie
wska
źniki podzielony przez CPI oraz N. Średnie ważone wynagrodzenie za godzinę dla pracowników firm
zatrudniaj
ących powyżej 10 osób, dzielone przez CPI oznaczymy przez W. I dalej v stopa zwrotu z depozytów 3-12
miesi
ęcznych pomniejszona o inflacje (π) a r nominalna stopa zwrotu uszczuplona o oczekiwana inflację (π
e
).
Oczywi
ście autor modelu boryka się z pewnymi problemami z danymi. I tak, musiał skonstruować wektor π
e
za
pomoc
ą regresji dla π
t
na opó
źnionych danych i dokonaniu prognozy na jeden okres w przód. Dane do każdej z
regresji [na ka
żdy kolejny okres] były aktualizowane ‘na bieżąco’ dzięki czemu model charakteryzuje się wysokim
dopasowaniem oraz przechodzi testy diagnostyczne na 5% poziomie istotno
ści. Jedynie test na resztach prognozy
jest spe
łniony dopiero na poziomie istotności 10% [test na biały szum]. Kolejnym problemem było to, iż wiarygodne
dane o N dost
ępne były jedynie dla lat 1961 oraz od 1966 wzwyż. Tak więc, dane dla lat 1960 oraz 1962 – 1965
otrzymano z regresji w oparciu o pewn
ą stałą oraz wielkość emigracji przy wykorzystaniu danych z lat 1966 – 1989.
Regresje te zak
ładają iż masowa emigracja z Grecji w latach 60tych była przyczyną trendu spadkowego N w tej
dekadzie. Dodatkowo autor zauwa
żył pewne zróżnicowanie w kształtowaniu się udziału wydatków rządowych w PKB
po roku 1981, jednak
że szybko odkrył iż wynika to z faktu dojścia socjalistów do władzy w 1981. W wyniku tej
zmiany wspomniana warto
ść wzrósł z 23% [1980 rok] do 43% [1993 rok].
Spójrzmy teraz na modele publikowane wcze
śniej. Pierwszy z nich opiera się na zmodyfikowanym równaniu
Eulera, które pozwala na zachowanie zgodne z „regu
łą kciuka”. Ma ono postać (1)
(
)
t
t
t
t
t
e
Y
a
Y
C
a
a
C
+
−
+
+
=
−
−
1
1
1
1
0
λ
, gdzie oczywi
ście e
t
jest b
łędem losowym i jako instrumentów używa trendu
liniowego i pierwszego opó
źnienia konsumpcji, dochodu do dyspozycji, wydatków rządowych i eksportu. Przejście do
nast
ępnego modelu jest proste, przekształcono model pierwszy pracujący na czystych wartościach na model
pracuj
ący na przyrostach: (2)
t
t
t
t
e
Y
u
b
b
C
+
Δ
+
+
=
Δ
−
λ
1
1
0
ˆ
, gdzie jako
1
ˆ
−
t
u
oznaczono reszty z regresji C
przeprowadzonej na Y
t
i pewnej sta
łej. Krok do następnego modelu jest oczywistym następstwem modelu (2).
Zauwa
żono log-liniowe zachowanie konsumpcji i dochodu, co doprowadziło model do postaci (3)
( )
(
)
( )
t
t
t
t
e
Y
r
C
+
Δ
+
+
+
=
Δ
log
1
log
log
λ
θ
μ
, gdzie
θ to elastyczność substytucji międzyokresowej.
Mimo swojej popularno
ści, przekształcenie log-liniowe równania Eulera nie jest do końca dobrym
przekszta
łceniem. Okazuje się, że ‘niszczy’ ono estymatory uzyskane z nie przekształconych równań. Innymi słowy,
estymatory otrzymane z modeli (1) i (2) nie b
ędą dobrymi estymatorami dla modelu (3).
Model opracowany przez Hatzinikolaou’a opiera si
ę na użyteczności konsumenta zdefiniowaną jako:
(
)
[
]
0
,
/
1
1
1
≠
−
=
−
−
γ
γ
γ
β
α
β
α
t
t
t
G
L
C
u
(gdzie
t
C
1
to konsumpcja konsumenta konsumuj
ącego całość dochodu
bie
żącego [konsument typu ‘life - cycle’]) i stąd też wynika postać wykładnicza konsumpcji
(
)
λ
λ
t
t
t
Y
C
C
−
=
1
1
a nie, jak
w dotychczasowych modelach liniowa
(
)
t
t
t
Y
C
C
λ
λ
+
−
=
1
1
. I tak, posta
ć funkcyjna modelu jest wyrażona przez:
[
]
1
)
1
(
1
1
1
1
1
1
)
/(
)
(
1
1
+
−
−
+
+
−
+
+
=
−
−
−
⎟
⎠
⎞
⎜
⎝
⎛
+
+
t
t
t
t
t
t
t
e
g
l
apc
apc
y
r
γ
β
α
βγ
αγ
λ
λ
δ
, gdzie
C
apc
t
t
t
Y
=
.
Wyniki jakie otrzymano przy estymacji zarówno starych [(1)-(3)] modeli jak i nowego modelu przedstawia
poni
ższa tabela.
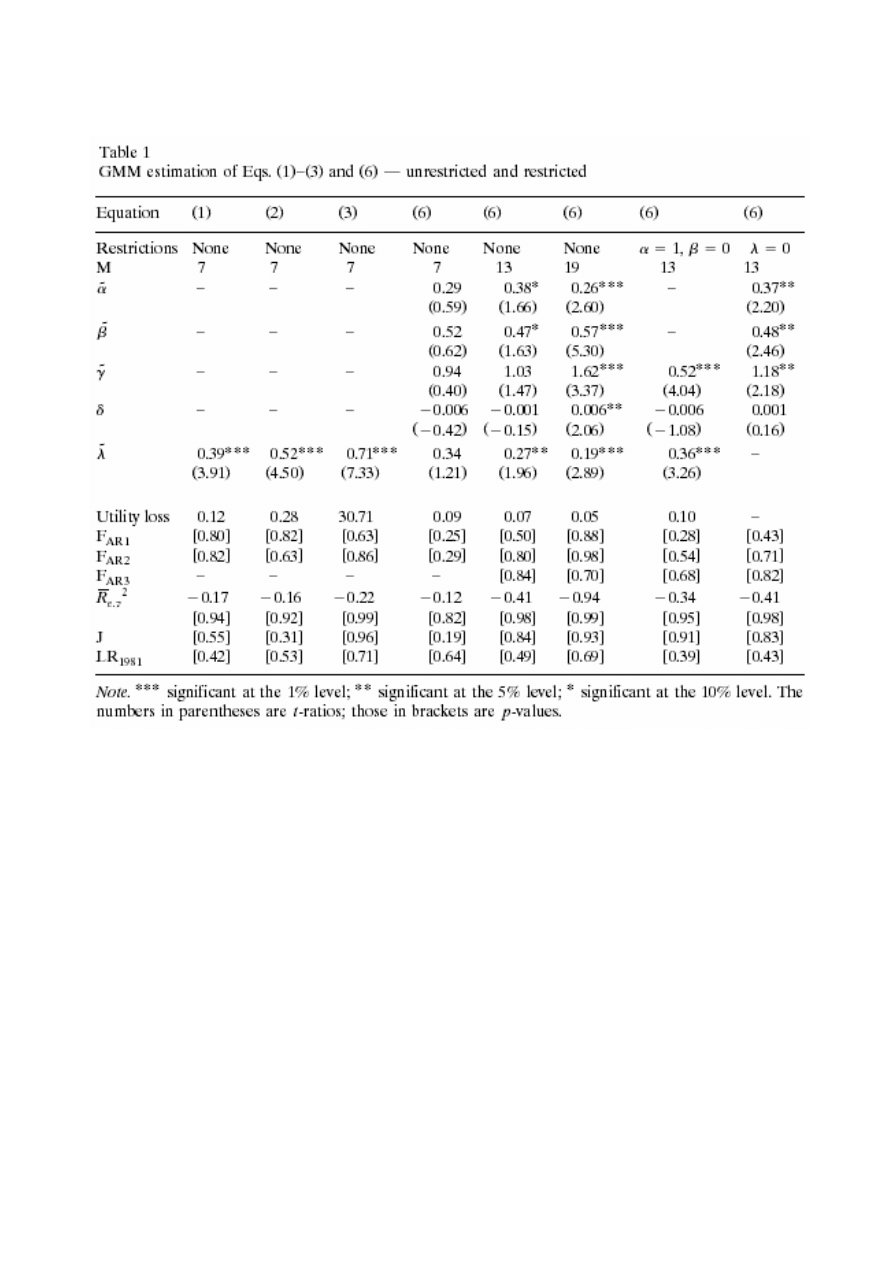
Zanim omówimy wyniki, wpierw kilka uwag. Po pierwsze, ma
ła wielkość próbki utrudnia testowanie założenia
stacjonarno
ści wymaganego przez GMM. Po drugie, zmienne w równaniu (6) nie mają oczywistych trendów,
hipoteza o jednoznaczno
ści rozwiązania może być odrzucona na poziomie istotności 5% dla c, l, g, y, w, r i v, a tylko
na 10 dla apc. I po trzecie, testy parametrów zak
ładają, że wszystkie oszacowania są wylosowane z rozkładu
normalnego.
Wyra
źnie widać, iż wszystkie cztery modele działają dobrze, estymowane parametry leżą w przewidywanym
przedziale, testy diagnostyczne nie wykazuj
ą przeidentyfikowania żadnego z równań. Zauważyć należy, że
estymacje parametrów równania (6), zarówno z restrykcjami jak i bez, wykazuj
ą brak nasycenia, wklęsłość restrykcji
oraz sugeruj
ą, że konsumpcja, czas wolny i wydatki rządowe są komplementarne. Brak narzuconych restrykcji na
równanie (6) dla M=7 powoduje problem identyfikacji i
żadna z estymacji nie jest statystycznie istotna. Podobnie dla
M=13 estymacje
α i β mają istotność zaledwie na poziomie 10%, dopiero dla M=19 poziom istotności wynosi 5%.
Dalej okazuje si
ę, iż nawet jeśli wartości λ są istotne, to dla modelu bez restrykcji należą do przedziału 0,19 do 0,27,
kiedy z równa
ń (1)-(3) wpadają do przedziału 0,39 do 0,71. W równaniu (6) z narzuconą restrykcją λ=0 test
diagnostyczny nie wykazuje przeidentyfikowania, co sugeruje, ze warto
ść λ może być niska. Jednak nie odrzucenie
tego modelu mo
że wskazywać na słabą moc testów, wynika to z małej liczebności próby. Kolejnym wnioskiem, który
si
ę nasuwa jest traktowanie stopy procentowej jako zmiennej w równaniu (1) i (2), co okazuje się mieć mały wpływ
na wyniki estymacji. Wyniki dla równania (6) pokazuj
ą, że zmienne L i G można uznać za istotne. Jednak jeżeli je
usuniemy (przyjmuj
ąc α=1, β=0) nadal przeidentyfikowanie nie będzie wyraźne, ale wartości estymowane λ są
wi
ększe niż w modelach bez restrykcji.