3. Obliczenia hydrologiczne.
Dane:
Powierzchnia zlewni rzeki Iłżanka: A = 133,8 km
2
Średni z wielolecia opad roczny: P = 546,4 mm = 0,5464 m
Konfiguracja terenu: równinna
Podłoże zlewni: średnio przepuszczalne
Szata roślinna w zlewni: silnie rozwinięta
3.1
Obliczenie przepływów charakterystycznych wzorami Iszkowskiego.
3.1.1. Przepływ absolutnie średni dla normalnego roku.
Q
s
= 0,03171 · C
s
· P · A [m
3
· s
-1
]
Q
s
= 0,03171
· 0,25· 0,521·133,8= 0,552 m
3
· s
-1
P
– średni opad roczny [m] P
A
– powierzchnia zlewni [km
2
]
C
s
– współczynnik odpływu zależny od rzeźby terenu zlewni
3.1.2. Przepływ absolutnie najniższy.
Q
0
= 0.2 · · Q
s
[m
3
· s
-1
]
Q
0
= 0,2
· 0,75 · 0,552 = 0,083 m
3
· s
-1
-
Współczynnik zależny od przepuszczalności podłoża i stopnia rozwinięcia roślinności w
zlewni;
= 1,0 ale ze względu na wielkość zlewni zmniejszamy go o 25% i wynosi = 0,75
3.1.3. Przepływ najniższy normalny
Q
1
= 0.4 · · Q
s
[m
3
· s
-1
]
Q
1
= 0,4
· 0,75 · 0,552 = 0,166 m
3
· s
-1
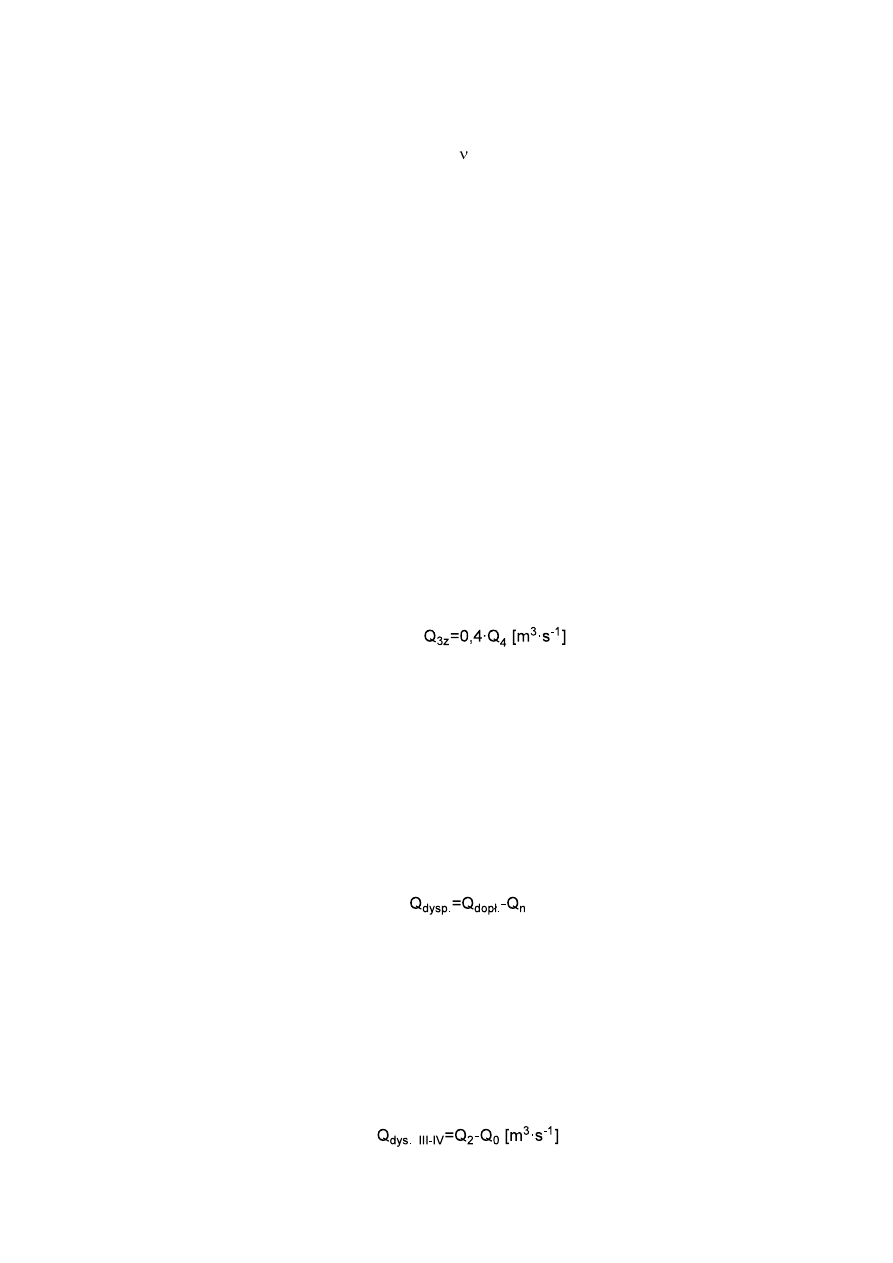
3.1.4. Przepływ średni normalny
Q
2
= 0.7 · · Q
s
[m
3
· s
-1
]
Q
2
= 0,7
· 0,75 · 0,552 = 0,289 m
3
· s
-1
3.1.5. Przepływ najwyższy wielki
Q
4
= C
w
· m · P ∙ A [m
3
· s
-1
]
Q
4
= 0,04
· 7,18· 0,521 ∙ 133,8 = 20,02 m
3
· s
-1
C
w
-
współczynnik zależny od rzeźby terenu i kategorii zlewni, przyjmowany z tabeli 1 i 2
(C
w
- 0,04 dla zlewni kategorii II)
m-
współczynnik zależny od powierzchni i konfiguracji terenu zlewni, przyjmowany
z tabeli 6 (m = 7,09 dla powierzchni zlewni 133,8 km
2
) (Zakaszewski Cz. 1964 Meliora-
cje rolne T. I. str 44-47 tab 6.)
3.1.6.
Przepływ wielki doroczny zimowy (dla terenów nizinnych)
Q
3Z
= 2
0,02 ∙ 0,4 = 8,0 m
3
· s
-1
3.2. Obliczenie przepływów dyspozycyjnych.
Przepływy dyspozycyjne w poszczególnych miesiącach i okresach roku określa się jako róż-
nicę między ilością wody dopływającą (netto) do przekroju-ujęcia i przepływem wody który
musi pozostać w cieku poniżej tego ujęcia (przepływ nienaruszalny).
Q
dysp.
– przepływ dyspozycyjny [m
3
∙s
-1
lub dm
3
∙s
-1
]
Q
dopł.
– ilość wód dopływających do przekroju-ujęcia [m
3
∙s
-1
lub dm
3
∙s
-1
],
Q
n
– przepływ nienaruszalny [m
3
∙s
-1
lub dm
3
∙s
-1
],
3.2.1. Przepływy dyspozycyjne w miesiącu marcu i kwietniu.
3.2.2. Przepływy dyspozycyjne w miesiącach maju i czerwcu
3.2.3. Przepływy dyspozycyjne w miesiącach lipcu i sierpniu
3.2.4. Przepływ dyspozycyjny w pierwszym pokosie (Ip.)
3.2.5. Przepływ dyspozycyjny w drugim pokosie (IIp.)
4.Określenie głębokości i rozstawy rowów odwaniająco – nawadniających.
Założenie: Postuluje się otrzymanie po zmeliorowaniu gleb mineralnych łąk wysoko produk-
cyjnych o
roślinności wartościowej.
Głębokości i rozstawy rowów osuszających na użytkach zielonych ustala się w oparciu o
tabelę 7.
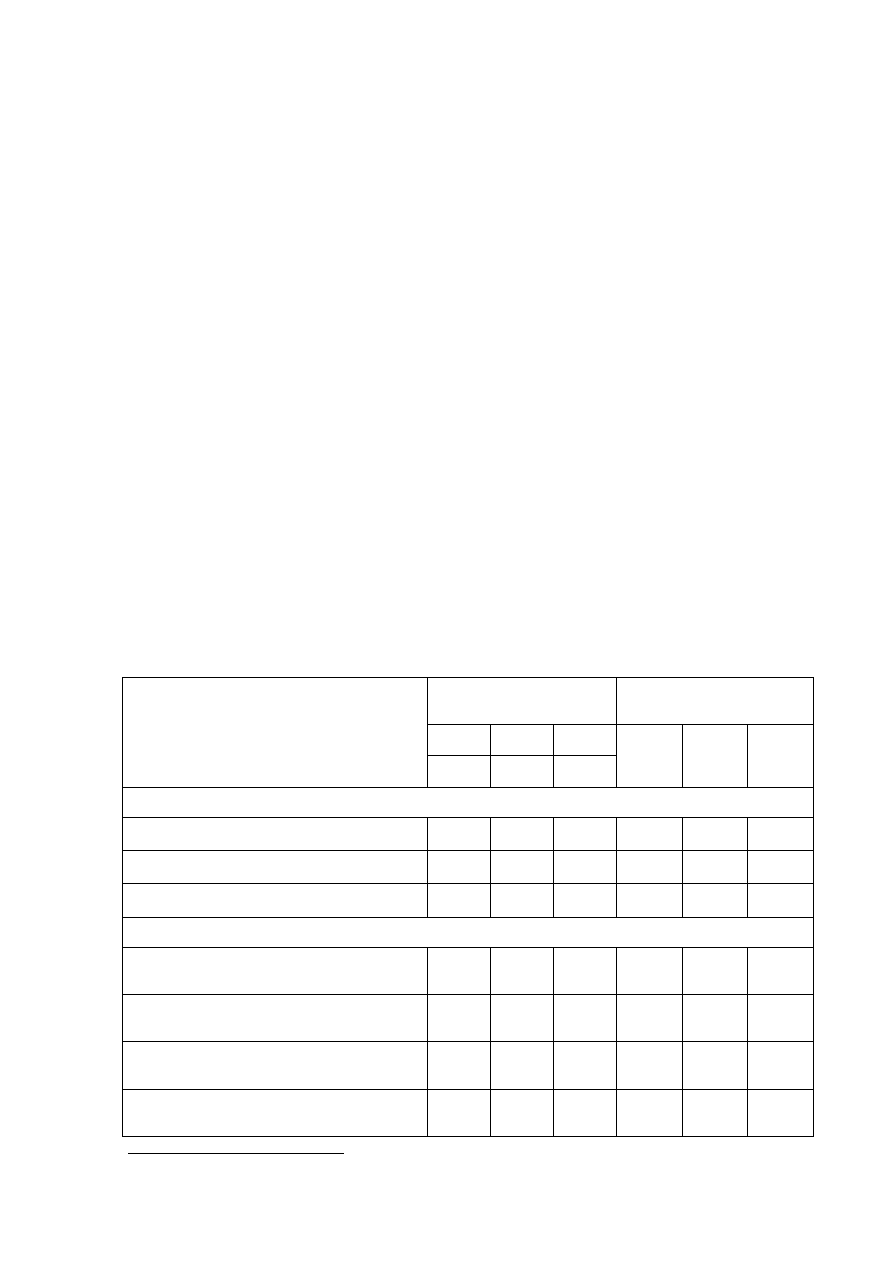
Tabela 7.
Parametry rowów o niezapewnionym nawodnieniu wg Zakaszewskiego
1
Gleba oraz roślinność na łące po jej
zmeliorowaniu
Pożądane obni-
żenie zwiercia-
dła wody grun-
towej [m]
Projektowana głębokość rowów na
glebach
– h
Rozstawa
rowów L
[m]
mineralnych i na
torfach osiadłych
[m]
na torfach nie rozło-
żonych i nie osiadłych
[m]
Łąki na torfach niskich, mało rozłożo-
nych o
roślinności przeważnie kwaśnej
0,25-0,30
-
0,85-1,00
200-300 i
więcej
Łąki o glebie piaszczystej, próchnicz-
nej, lub torfy na piaskach podmokłych,
o roślinności przeważnie słodkiej
0,4
0,60-0,70
-
80-100
Łąki naturalne o roślinności przeważ-
nie słodkiej, na glebie piaszczysto-
gliniastej lub na torfach głębokich
0,40-0,50
0,65-0,75
0,80-0,95
60-80
Łąki o roślinności słodkiej na glebach
zwięzłych i na torfach głębokich w
uprawie
0,50-0,60
0,75-0,90
0,95-1,20
40-60
Dla p
owyższego założenia przyjęto łąki o glebie piaszczystej, próchnicznej lub torfy na
piaskach podmokłych o roślinności przeważnie słodkiej. Dla tej kategorii łąk głębokość wa-
cha się w granicach do 0,60 – do 0,70 m, a rozstawa od 60 do 80 m.
Przy ustalaniu głębokości i rozstawy rowów należy uwzględnić następujące zalecenia:
mniejsze normy głębokości rowów ( dolna granica ) należy stosować dla terenów
o opadach niższych od 500 mm, a większe ( górna granica ) na obszarach niż-
szych od 750 mm,
większe normy rozstawy należy stosować dla obszarów o średniej dobowej tem-
peraturze stycznia wyższej od -2 °C, mniejsze dla obszarów o średniej dobowej
temperaturze stycznia niższej od - 4,5 °C,
dla opadów i temperatur pośrednich głębokości rowów oraz ich rozstawy należy
ustalać przez interpolację, zaokrąglając głębokości do 5 cm, rozstawy zaś do
5 m,
Mając na uwadze powyższe zalecenia i uwzględniając warunki glebowe ( piasek glinia-
sty lekki)
, średnią z wielolecia temperaturę stycznia (-3,0 °C), oraz średnią wielolecia sumę
opadów atmosferycznych (546,4 mm), z interpolacji otrzymano:
głębokość rowów odwaniająco – nawadniających h = 0,658 m – ostatecznie
przyjęto 0,65m,
rozstawę rowów odwaniająco – nawadniających L = 72 m – ostatecznie przyję-
to 70 m
5.
Obliczenie jednorazowej dawki polewowej netto warunkach płytkiego położenia zwierciadła
wody gruntowej.
Na podstawie znajomości profilu glebowego przyjmuje się dla danej rośliny miarodajne
normy osuszenia, a więc: minimalną dopuszczalną, optymalną ( średnią ) i maksymalną do-
puszczalną głębokość zwierciadła wody gruntowej pod powierzchnią terenu. W warunkach
nawadnianego obiektu miarodajne normy osuszenia
– przyjęto z tab. 8 -wynoszą odpowied-
nio:
h
max
=
0,7 m h
min
= 0,50 m
Tabela 8.
Rezerwy użyteczne i wielkości dawek polewowych dla łąk na glebach z bliskim
zaleganiem zwierciadła wody gruntowej
2
Rodzaj i gatunek gleby
Normy osuszenia [m]
Rezerwy lub dawki polewowe
netto [mm]
min
średnia
max
W
1-2
W
2-3
W
1-3
h
1
h
2
h
3
I. Gleby mineralne
a) Lekkie (piasek luźny)
0,35
0,40
0,45
25
25
35
b) Średnie (glina lekka)
0,50
0,55
0,70
20
40
45
c) Ciężkie (mada ciężka)
0,60
0,70
0,90
20
65
70
II. Gleby torfowe
a) Torfy głębokie, słaby stopień zmurszenia,
podsiąk wysoki (>1,0 m)
0,50
0,70
0,90
50
85
100
b) Torfy głębokie, średni stopień zmurszenia,
podsiąk średni (0,7−0,8 m)
0,40
0,55
0,70
60
80
95
c) Torfy głębokie, silny stopień zmurszenia, pod-
siąk mały (poniżej 0,6 m)
0,30
0,45
0,60
50
65
85
d) Torfy płytkie o miąższości 0,6−0,7 m, średnio
zmurszałe na podłożu przepuszczalnym
0,40
0,50
0,60
55
70
80
Dawka polewowa netto uzależniona jest przede wszystkim od właściwości wodnych pro-
filu glebowego i
najczęściej jest obliczana jest w przypadku nawadniania podsiąkowego ze
zmiennym pierzeniem wody jako dawka maksymalna.
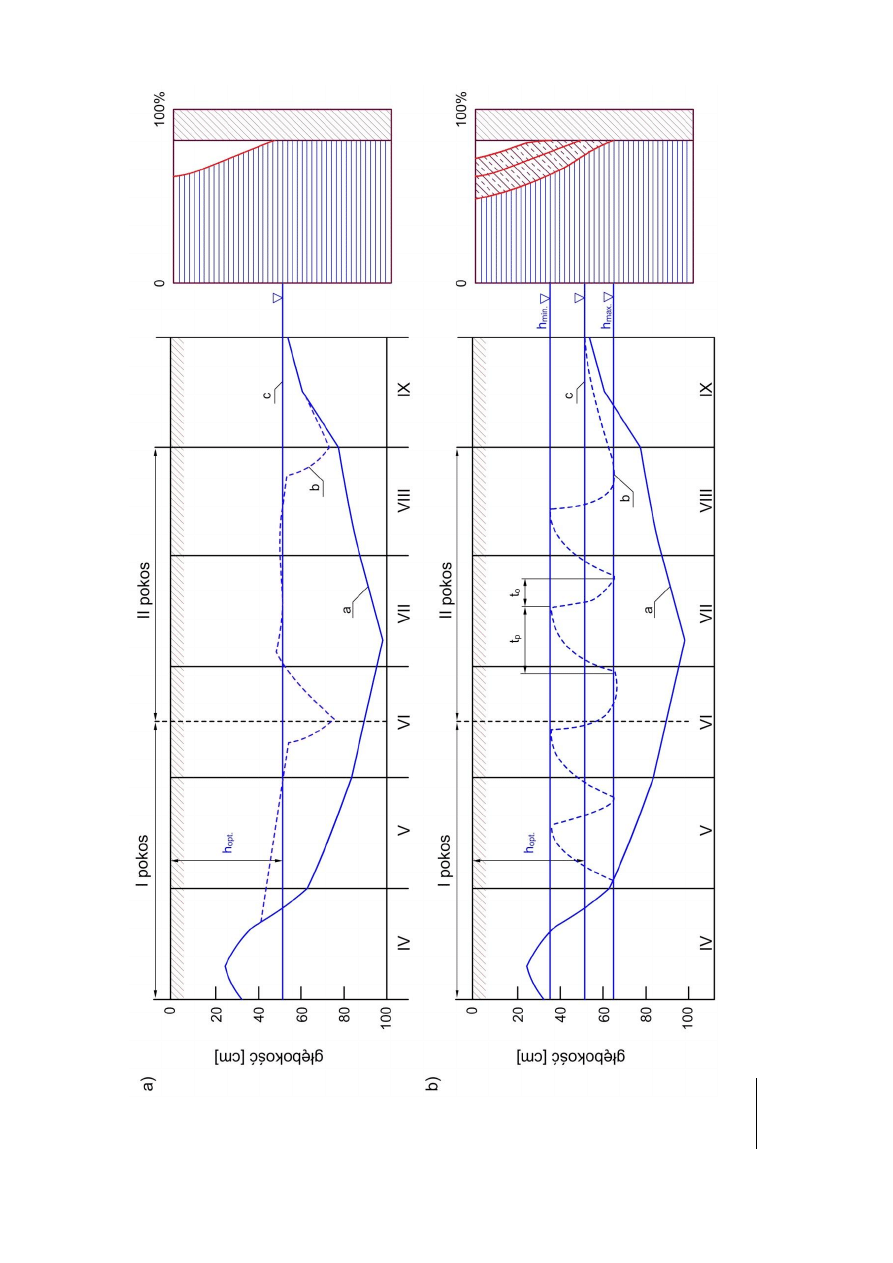
Ryci
n
a
1
.
S
ch
e
m
a
tycz
n
y
p
rze
b
ieg
s
ta
nó
w
g
ru
n
to
wyc
h
i
u
wi
lgo
tn
ie
nia
p
rofilu
g
leb
o
weg
o
w
śr
o
d
ku
łan
u
p
rzy
n
a
w
o
d
n
ie
n
iu
p
o
d
si
ą-
ko
wym
łą
k.
a)
P
od
si
ąk
z
e
stał
ym
p
iętrz
en
iem
,
b)
P
od
si
ąk
z
e
zmi
e
nn
ym
p
iętrz
en
iem
,
a
–
zwi
erc
iad
ło
wo
dy
be
z
na
w
od
n
ień
,
b
–
zw
ierc
iad
ło
w
od
y
w
po
lac
h
na
w
ad
n
ia-
ny
c
h,
c
–
ś
red
n
ie
po
łoż
en
ie
wod
y gru
nto
w
ej
w ok
res
ie
wege
tac
ji, t
p
–
ok
res
p
iętrz
e
ni
a,
t
o
–
ok
res
op
us
z
c
z
an
ia
wo
dy
.
Maksymalną dawkę polewową netto oblicza się z różnicy między polową pojemnością wodną
przy minimalnej normie osuszenia a zapasem wody okresu suszy przy maksymalnej normie
osuszenia oblicza się ze wzoru:
gdzie:
- V
hmax
– objętość rezerw przejściowych przy maksymalnej normie odwodnienia,
- Q
hmin
– ociekalność przy minimalnej normie odwodnienia,
- h
max
– maksymalna norma odwodnienia,
- h
min
– minimalna norma odwodnienia.
Objętość rezerw przejściowych można obliczyć z formuły empirycznej,
natomiast ociekalność ze wzoru:
gdzie:
- a i b
– współczynniki empiryczne zależne od zawartości części spławianych
(< 0,02 mm) w glebie nawadnianego obiektu.
Tabela 9.
Wartość współczynników empirycznych do wzorów na objętość rezerw przejścio-
wych i ociekalność
3
Współczynnik
Zawartość frakcji spławianej (Φ < 0,02 mm) w %
1
5
10
15
20
35
50
60
a
273
128
92
76
66
51
43
40
b
290
168
133
116
105
87
77
73
Przy
zawartości 12 % części spławialnych w glebie nawadnianego obiektu wartości
współczynników a i b ustalono na:
a = 50
b = 86
Q = 50
∙ 0,50
1,73
= 15 mm V = 86
∙ 0,7
1,43
= 51,6 mm
3
Somorowski Cz. 1971. Materiały do ćwiczeń z melioracji rolnych. Cz. II. Stosunki wodne gleb, str. 14,
tab. 1, SGGW Warszawa
d
n
= 51,6 - 15 = 26 mm
d
n
= 36,6 mm
6.Obliczenie po
trzeb wodnych użytków zielonych:
6.1. metodą opadów optymalnych wg Hohendorfa.
ΣP
opt.
– suma opadów optymalnych za rozpatrywany okres
Tabela 10.Optymalne
opady (w mm) dla użytków zielonych w Polsce w okresie wegetacyj-
nym na glebach średnio zwięzłych (wg Hohendorfa)
4
Roślina
X-III
IV
V
VI
VII
VIII
IX
Okres wege-
tacji
Rok
Użytki zielone
200
65
120
115
100
80
70
550
750
Normy opadów optymalnych odczytane z tabeli 10 należy dla gleb lekkich i torfów zwiększyć
o 25%, natomiast dla gleb ciężkich obniżyć o 15%.
6.1.1. dla I pokosu
Wartość poprawiona ( zwiększona o 25 %):
6.1.2. dla II pokosu
Wartość poprawiona ( zwiększona o 25 %):
4
Ostromęcki J. 1973. Podstawy melioracji nawadniających, str. 327, tab. IV.23, PWN
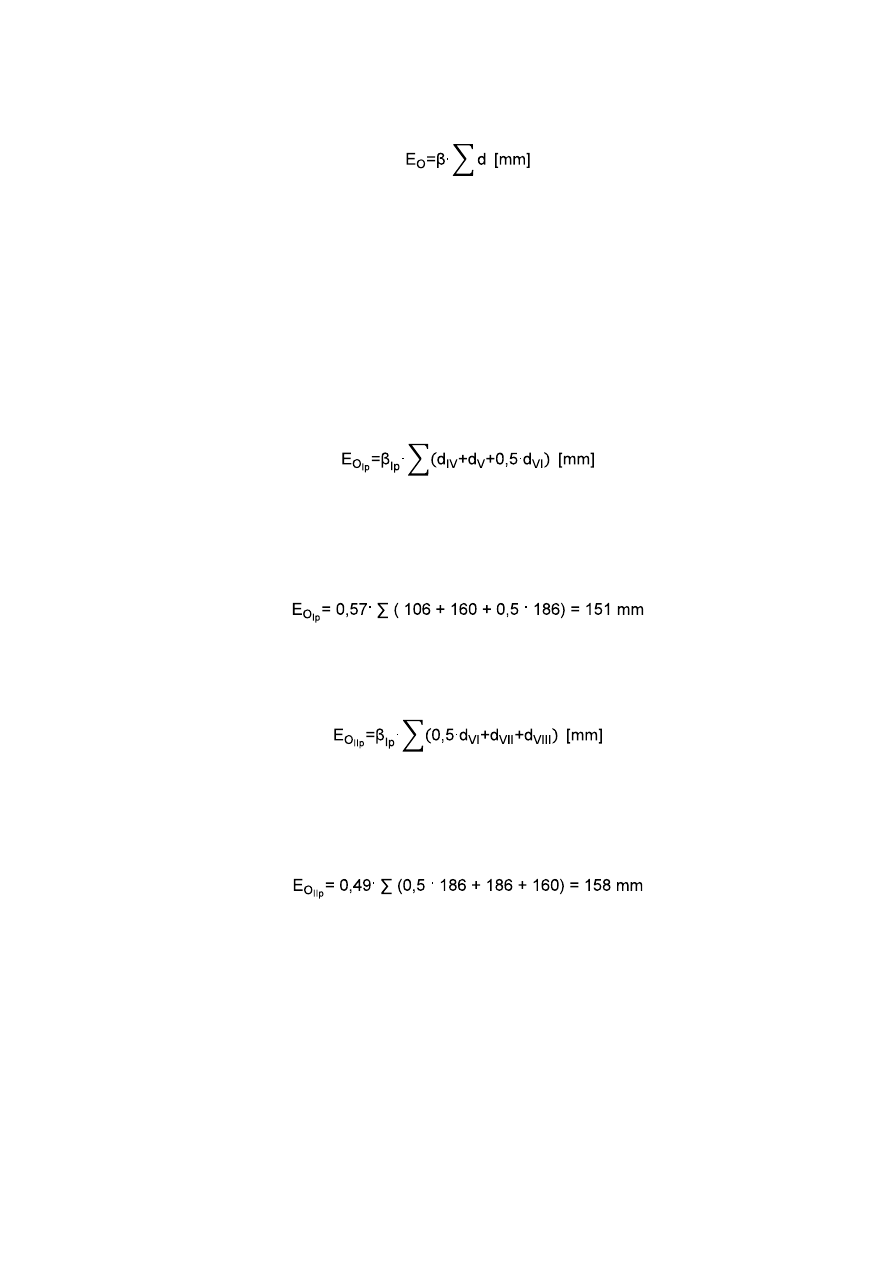
6.2. metodą higrometrycznego współczynnika parowania terenowego wg Ostromęckiego
β – higrometryczny współczynnik parowania [mm∙d
-1
∙hPa
-1
] zależny od rodzaju roślin,
wysokości roślin, wysokości plonu, rodzaju gleby i poziomu zwierciadła wody gruntowej
– wartości β przyjmuje się z tabeli 11
Σd – suma średnich dobowych niedosytów wilgotności powietrza [hPa] za rozpatrywany
okres
6.2.1. dla I pokosu
β
Ip
= 0,57
– przyjęto dla plonu siana 5,0 T∙ha
-1
, zwierciadło wody gruntowej h
opt.
= 1,00 m
i piasku gliniastego lekkiego
6.2.2. dla II pokosu.
β
IIp
= 0,49
– przyjęto dla plonu siana 3,0 T∙ha
-1
, zwierciadło wody gruntowej h
opt.
= 1,00
m i piasku gliniastego lekkiego
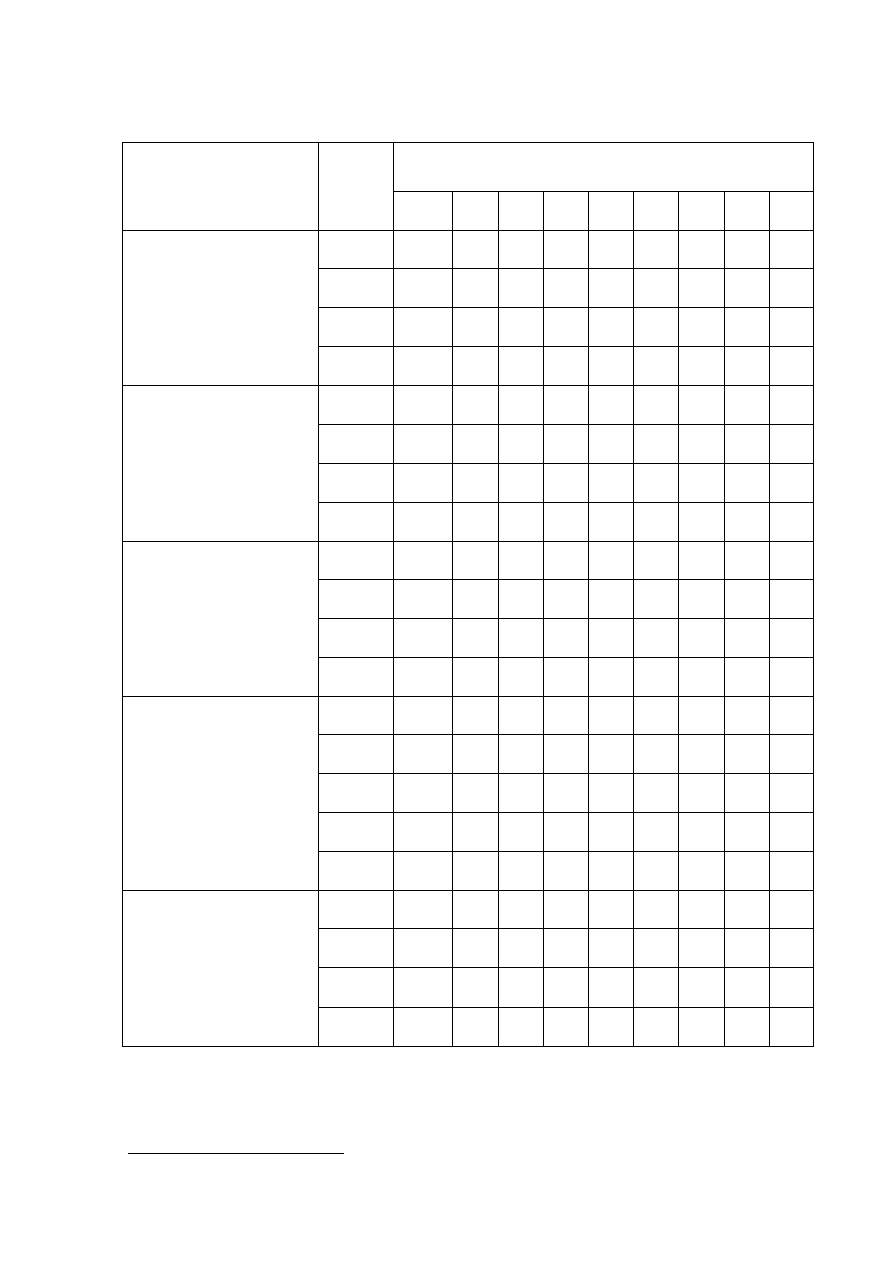
Tabela 11.
Higrometryczne współczynniki parowania (β) w mm na dobę i 1 hPa niedosytu
wilgotności powietrza dla łąk za okres jednego
5
Gleba
Poziom
wody
gruntowej
[cm]
Współczynnik parowania () przy plonie siana w T∙ha
-1
darnina
1
2
3
4
5
6
7
8
Torf niski turzycowo trzcinowy,
średnio rozłożony, o małej
popielności (do 15%) i małej
masie obj. warstwy wierzchniej
(do 200 g
dcm
3
), podsiąkanie
do warstwy wierzchniej inten-
sywne, proces murszenia b.
słaby
25
0,65
0,83
0,91
0,97
1,02
1,06
1,10
1,14
1,17
50
0,53
0,68
0,75
0,80
0,84
0,87
0,91
0,94
0,97
75
0,44
0,57
0,62
0,66
0,69
0,72
0,75
0,77
0,80
100
0,36
0,46
0,51
0,54
0,57
0,59
0,62
0,64
0,66
Torf niski namulony, rozpylo-
ny, popielność ponad 20%,
masa obj. warstwy wierzchniej
200
–400 gdcm
3
, podsiąkanie
słabe, proces murszenia za-
awansowany
25
0,38
0,48
0,54
0,59
0,64
0,68
0,72
0,76
0,79
50
0,32
0,41
0,47
0,51
0,55
0,59
0,62
0,65
0,68
75
0,28
0,36
0,40
0,44
0,47
0,50
0,53
0,56
0,59
100
0,24
0,31
0,35
0,38
0,41
0,43
0,46
0,48
0,50
Torf niski namulony, rozpylo-
ny, popielność ponad 20%,
ciężar obj. warstwy wierzchniej
400
–500 gdcm
3
, podsiąkanie
utrudnione, proces murszenia
bardzo zaawansowany
25
0,33
0,42
0,47
0,51
0,55
0,59
0,63
0,66
0,69
50
0,29
0,37
0,41
0,45
0,49
0,52
0,55
0,58
0,61
75
0,25
0,32
0,36
0,40
0,43
0,46
0,49
0,51
0,53
100
0,22
0,29
0,32
0,35
0,38
0,41
0,43
0,45
0,47
Mada ciężka wiślana, głęboka,
o zawartości 60% części spła-
wialnych
(< 0,01 mm)
25
0,35
0,47
0,53
0,59
0,64
0,69
0,73
0,77
0,81
50
0,33
0,44
0,51
0,56
0,61
0,65
0,69
0,73
0,77
75
0,32
0,42
0,48
0,53
0,58
0,62
0,66
0,70
0,73
100
0,30
0,40
0,46
0,51
0,55
0,59
0,63
0,67
0,70
125
0,29
0,38
0,44
0,48
0,52
0,56
0,60
0,63
0,66
Lekka gleba piaszczysta,
(90 % piasku 0,1 - 1,0 mm),
warstwa próchniczna około 10
-15 cm
25
0,37
0,48
0,55
0,61
0,66
0,71
0,75
0,79
0,83
50
0,31
0,41
0,46
0,51
0,55
0,59
0,63
0,69
0,70
75
0,26
0,34
0,39
0,43
0,47
0,50
0,53
0,56
0,59
100
0,22
0,29
0,33
0,36
0,39
0,42
0,45
0,47
0,49
5
Ostromęcki J. 1973. Podstawy melioracji nawadniających. str. 308–309, tab. IV.11, PWN
6.3. metodą termicznego współczynnika parowania wg Szarowa
α – termiczny współczynnik parowania [mm∙d
-1
∙
o
C
-1
], zależy od rodzaju gleby i jej uwil-
gotnienia oraz wysokości plonu – obliczany ze wzoru = z
z
– stosunek sumy niedosytów wilgotności powietrza do sumy średnich dobowych tem-
peratur powietrza
– wartość przyjmowana z tabeli 12
Σt – suma średnich dobowych temperatur powietrza [°C] za rozpatrywany okres
6.3.1. dla I pokosu
z
Ip
= 0,35 -
przyjęto dla I pokosu i sumy średnich dobowych temperatur powietrza równych
825
o
C
α
Ip
= β
Ip
· z
Ip
= 0,57
· 0,35 = 0,197 mm · 1
o
C
-1
6.3.2. dla II pokosu
z
IIp
= 0,21 -
przyjęto dla II pokosu i sumy średnich dobowych temperatur powietrza równych
1388
o
C
α
IIp
= β
IIp
· z
IIp
= 0,49
· 0,21 = 0,103 mm · 1
o
C
-1
0,103
· 1322 = 136,510 mm
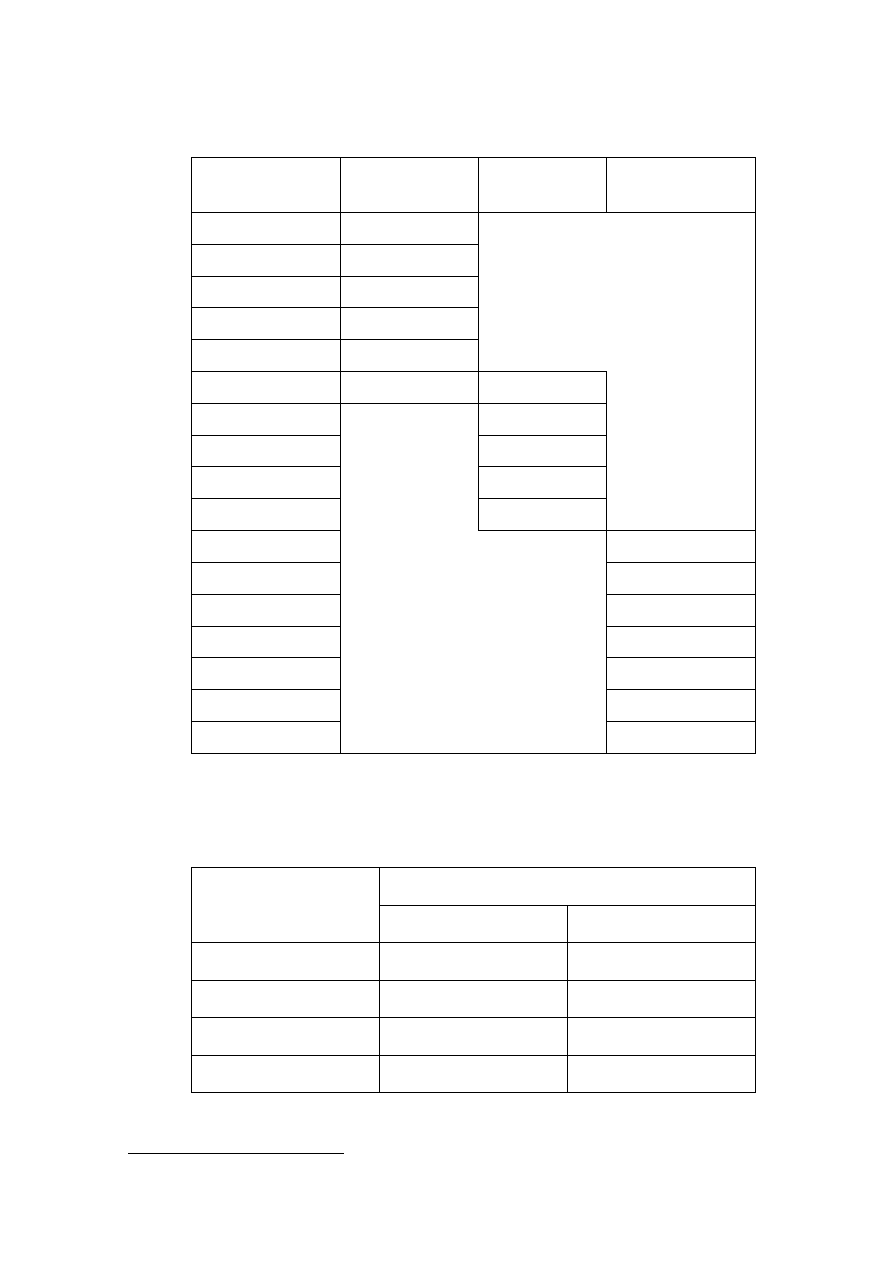
Tabela 12.
Stosunek (z) sum niedosytów wilgotności powietrza i temperatur okresu wegetacji
dla Niżu Polskiego
6
Σ t
0
Pokos I
( IV-VI)
Pokos II
(VII-IX)
Okres wegetacji
(IV-IX)
800
0,34
900
0,37
1000
0,39
1100
0,41
1200
0,43
1300
0,44
0,24
1400
0,29
1500
0,33
1600
0,37
1700
0,40
2200
0,29
2300
0,31
2400
0,33
2500
0,34
2600
0,36
2700
0,37
2800
0,39
6.4. Obli
czenie średnich potrzeb wodnych
Metody Hohendorfa nie uwzględniam do średniej, gdyż znacznie odbiega od pozostałych wyników
Metoda
Potrzeby wodne pokosu
E
Ip
E
IIp
Hohendorfa
243
238
Ostromęckiego
205
228
Szarowa
163
136
Średnia
203
201
6
Ostromęcki J. 1964. Wstęp do melioracji rolnych. Str. 220, tab. 63, PWRiL
7.Obliczenie niedoborów wodnych roślin nawadnianego użytku
7.1. w latach normalnych pod względem opadów
N
n
=E
– P
n
[mm]
E
– średnie potrzeby wodne roślin dla danego pokosu
P
n
– suma opadów dla lat normalnych za rozpatrywany okres
7.1.1. w I pokosie
E
Ip
= 203,6 mm
P
nIp
= P
nIV
+ P
nV
+ 0,5∙ P
nVI
= 33 + 50
+ 0,5 ∙ 62 = 114 mm
N
nIp
= E
Ip
– P
nIp
= 204
– 114 = 90 mm
7.1.2. w II pokosie.
E
IIp
= 200,8 mm
P
nIIp
= 0,5∙P
nVI
+ P
nVII
+ P
nVIII
=0,5∙62 + 92 + 68 = 191 mm
N
nIIp
= E
IIp
– P
nIIp
= 200
– 191 = 9 mm
7.2. w latach średnio-suchych pod względem opadów
N
s
=E
– P
s
[mm]
E
–średnie potrzeby wodne roślin dla danego pokosu [mm]
P
s
– suma opadów dla lat średnio suchych za rozpatrywany okres [mm].
7.2.1. w I pokosie
N
sIp
= E
Ip
– P
sIp
= 203
– 98 = 105 mm
P
sIp
= P
sIV
+ P
sV
+ 0,5∙ P
sVI
=
33 + 44 + 0,5∙43 = 98,5 mm
7.2.2. w II pokosie
N
sIIp
= E
IIp
– P
sIIp
= 201
– 156,5= 44,5 mm
P
sIIp
=0,5∙ P
sVI
+ P
sVII
+ P
sVIII
= 0,5 ∙ 43 + 77 + 58 = 156,5mm
7.3. z określonym prawdopodobieństwem przewyższenia
7.3.1. z 10% prawdopodobieństwem przewyższenia dla lat normalnych
A
10%
– współczynnik regionalny uwzględniający zmienność niedosytów wilgotności powietrza
dla prawdopodobieństwa 10%
B
10%
– współczynnik regionalny uwzględniający zmienność rozkładu opadów dla prawdopo-
dobieństwa 10%
E
O
– potrzeby wodne za rozpatrywany okres wg Ostromęckiego
P
n
– suma opadów atmosferycznych za rozpatrywany okres (opady średnie z wielolecia dla
lat normalnych)
7.3.1.1. w I pokosie.
7.3.1.2.w II pokosie.
7.3.2
. z 10% prawdopodobieństwem przewyższenia dla lat średnio-suchych
A
10%
– współczynnik regionalny uwzględniający zmienność niedosytów wilgotności powietrza
dla prawdopodobieństwa 10%
B
10%
– współczynnik regionalny uwzględniający zmienność rozkładu opadów dla prawdopo-
dobieństwa 10%
E
O
– potrzeby wodne za rozpatrywany okres wg Ostromęckiego
P
n
– suma opadów atmosferycznych za rozpatrywany okres (opady średnie z wielolecia dla
lat
średnio-suchych)
7.3.2.1. w I pokosie.
7.3.2.2.w II pokosie.
7.3.3
. z 25% prawdopodobieństwem przewyższenia dla lat normalnych
A
25%
– współczynnik regionalny uwzględniający zmienność niedosytów wilgotności powietrza
dla
prawdopodobieństwa 25%
B
25%
– współczynnik regionalny uwzględniający zmienność rozkładu opadów dla prawdopo-
dobieństwa 25%
E
O
– potrzeby wodne za rozpatrywany okres wg Ostromęckiego
P
n
– suma opadów atmosferycznych za rozpatrywany okres (opady średnie z wielolecia dla
lat normalnych).
7.3.3.1. w I pokosie.
7.3.3.2. w II pokosie.
7.3.4
. z 25% prawdopodobieństwem przewyższenia dla lat srednio-suchych
A
25%
– współczynnik regionalny uwzględniający zmienność niedosytów wilgotności powietrza
dla prawdopodobieństwa 25%
B
25%
– współczynnik regionalny uwzględniający zmienność rozkładu opadów dla prawdopo-
dobieństwa 25%
E
O
– potrzeby wodne za rozpatrywany okres wg Ostromęckiego
P
n
– suma opadów atmosferycznych za rozpatrywany okres (opady średnie z wielolecia dla
lat normalnych).
7.3.4.1. w I pokosie.
7.3.4.2. w II pokosie.
8.
Obliczenie zapotrzebowania wody do nawodnień zwilżających
8.1
Obliczenie zapotrzebowania wody do nawodnień netto
gdzie:
N
– niedobór wody
ΔR – retencja użyteczna (zapas pozimowy) ≈ dawka polewowa netto (d
n
)
8.1.1. w latach
normalnych pod względem opadów atmosferycznych
8.1.1.1.
w I pokosie
∆R = 36,6 mm
8.1.1.2.
w II pokosie
8.1.2.
w latach średnio-suchych pod względem opadów atmosferycznych
8.1.2.1.
w I pokosie
∆R = 36,6 mm
8.1.2.2.
w II pokosie
8.1.2.3.
z określonym prawdopodobieństwem przewyższenia
8.1.2.3.1.
z 10% prawdopodobieństwem przewyższenia
8.1.2.3.1.1.
w I pokosie
∆R = 36,6 mm
8.1.2.3.1.2.
w II pokosie
8.1.2.3.2.
z 25% prawdopodobieństwem przewyższenia
8.1.2.3.2.1.
w I pokosie
∆R = 36,6 mm
8.1.2.3.2.2.
w II pokosie
8.2.
Obliczenie zapotrzebowania wody do nawodnień brutto
gdzie:
Z
– zapotrzebowanie do nawodnień netto [mm]
η – współczynnik użyteczności
8.2.1.
w latach normalnych pod względem opadów atmosferycznych
8.2.1.1.
w I pokosie
η = 0,5
8.2.1.2.
w II pokosie
η = 0,5
8.2.2.
w latach średnio-suchych pod względem opadów atmosferycznych
8.2.2.1.
w I pokosie
η = 0,5
8.2.2.2.
w II pokosie
η = 0,5
8.2.2.3.
z określonym prawdopodobieństwem przewyższenia
8.2.2.3.1.
z 10% prawdopodobieństwem przewyższenia
8.2.2.3.1.1.
w I pokosie
η = 0,5
8.2.2.3.1.2.
w II pokosie
η = 0,5
8.2.2.3.2.
z 25% prawdopodobieństwem przewyższenia
8.2.2.3.2.1.
w I pokosie
η = 0,5
8.2.2.3.2.2.
w II pokosie
η = 0,5
9.
Obliczenie ilości nawodnień
Przy jednakowej wielości dawek polewowych netto w okresie wegetacyjnym ilość nawodnień
równa się:
gdzie:
Z
– zapotrzebowanie wody do nawodnień zwilżających [mm]
d
n
– jednorazowa dawka polewowa netto [mm]
9.1.
w latach normalnych pod względem opadów atmosferycznych
9.1.1. w I pokosie
d
n
= 26 mm
Należy dostarczyć 2 dawki polewowe netto
9.1.2. w II pokosie
d
n
= 36,6 mm
Należy dostarczyć 1 dawkę polewową netto
9.2.
w latach średnio-suchych pod względem opadów atmosferycznych
9.2.1. w I pokosie
d
n
= 36,6 mm
Należy dostarczyć 2 dawki polewowe netto
9.2.2. w II pokosie
d
n
= 36,6 mm
Należy dostarczyć 2 dawki polewowe netto
9.3.
z określonym prawdopodobieństwem przewyższenia
9.3.1. z 10%
prawdopodobieństwem przewyższenia
9.3.1.1.
w I pokosie
d
n
= 36,6 mm
Należy dostarczyć 4 dawki polekowe netto
9.3.1.2.
w II pokosie
d
n
= 36,6 mm
Należy dostarczyć 5 dawek polewowych netto
9.3.2.
z 25% prawdopodobieństwem przewyższenia
9.3.2.1.
w I pokosie
d
n
= 36,6 mm
Należy dostarczyć 3 dawki polekowe netto
9.3.2.2.
w II pokosie
d
n
= 36,6 mm
Należy dostarczyć 4 dawki polekowe netto
Z przeprowadzonej analizy danych wynika, iż użytki zielone na rozpatrywanym terenie cier-
pią na niedobory wody zarówno w latach normalnych, średnio suchych jak
i
prawdopodobnych pod względem opadów. Zaleca się na analizowanym obszarze przepro-
wadzić nawodnienie użytków zielonych, wybierając optymalny system nawadniający – w tym
przypadku nawodnienie podsiąkowe.
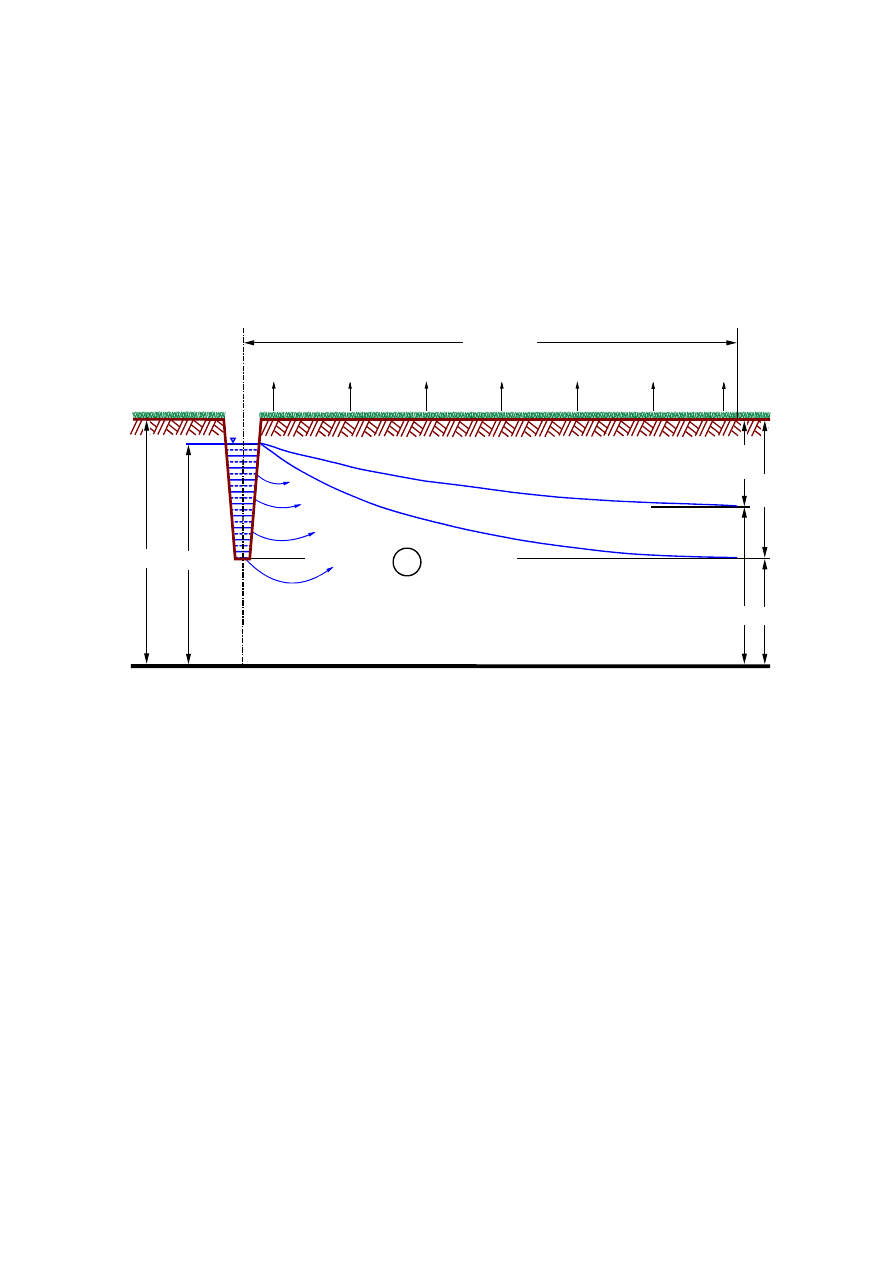
10.
Obliczenie nawodnienia podsiąkowego
Obliczenie nawodnienia podsiąkowego w zasadzie sprowadza się do określenia
czasu trwania poszczególnych faz podsiąku oraz niezbędnych dopływów jednostkowych.
W przypadku realizowania nawodnienia podsiąkowego ze zmiennym piętrzeniem
w
warunkach gleb mineralnych, najczęściej korzysta się ze schematu obliczeniowego Ko-
stiakowa.
Schemat hydrauliczny nawadniania podsiąkowego wg. Kostiakowa
Przyjmowanie powyższego schematu obliczeniowego jest uzależnione od znajomo-
ści współczynnika filtracji oraz głębokości zalegania warstwy nieprzepuszczalnej, będącej
poziomem odniesienia. Jak wykazują doświadczenia praktyczne, dla gleb lekkich
i
średniozwięzłych można przyjmować (przy głębokości rowów do 1,0 m) poziom odniesienia
na głębokości około H = 4 – 5 m. W tym bowiem przypadku warstwy poniżej tego poziomu
uczestniczą w ruchu wody w mniejszym stopniu, a określone czasy podsiąku; przy tym zało-
żeniu, będą tylko nieco dłuższe od faktycznych.
Czas trwania podsiąku oblicza się dla dwóch faz. Fazę pierwszą stanowi czas prze-
siąkania wody do środka łanu. W końcu tej fazy zwierciadło wody gruntowej osiąga w środku
łanu poziom H
0
według krzywej 1. W drugiej fazie odbywa się podnoszenie zwierciadła wody
gruntowej z poziomu H
0
do poziomu H
2
(rycina 4).
l = 0,5L
podłoże nieprzepuszczalne
2
1
H
1
H
2
H
o
k
h
m
in
.
h
m
a
x
.
H
ET
r
10.1.
Obliczenie czasu i niezbędnego dopływu jednostkowego w fazie I
Czas trwania I fazy wynosi:
gdzie:
n
– współczynnik zależny od kształtu krzywej depresji po nawodnieniu jego wartość kształtu-
je się w granicach 0,50-0,66 (do obliczeń przyjęto n = 0,50)
-
wolna porowatość profilu gleby w chwili nawodnienia; wartość równoznaczna z wartością
α
g
i przyjmowana z tabeli 11 (przyjęto σ = 0,31)
k
– współczynnik filtracji w m∙d
-1
, klasy przepuszczalności gleb ( k = 8,5 m ∙ d
-1
)
l
– 0,5 ∙ L [m], gdzie L – rozstawa rowów w m, L = 70 m
H
1
– wartość ustalona ze schematu H
1
= H
– 0,20 [m]; przyjęto H = 5,00 m
H
1
= 5,00
– 0,20 = 4,80 m;
H
0
– wartość ustalona ze schematu H
0
= H
– h
max
[m], h
max
= 0,70 m
H
0
= 5,00
– 0,70
= 4,30 m
Tabela 11. Orientacyjne wartości współczynników α
g
Gatunek gleby
α
g
= σ
Piasek luźny
0,37
Piasek słabo gliniasty
0,31
Glina lekka
0,30
Glina ciężka
0,25
Potrzebny dopływ jednostkowy netto w czasie trwania fazy I wynosi:
Natomiast dopływ jednostkowy brutto w fazie I jest w przybliżeniu równy
gdzie
η – współczynnik wykorzystania wody zależny od systemu nawodnień (dla nawodnienia
podsiąkowego (η = 0,7- 0,8) przyjęto η = 0,7
η = 0,7
10.2.
Obliczenie czasu i niezbędnego dopływu jednostkowego w fazie II
H
2
– wartość ustalona ze schematu H
2
= H
– h
min
e
– parowanie średnie w m∙d
-1
(e = 0,003 -
0,005 m∙d
-1
) (przyjęto e = 0,003 m∙d
-1
)
Q
śr.
– średni dopływ w fazie II [m
3
d
-1
],
Q
1
– dopływ na początku fazy II [m
3
d
-1
],
Q
2
– dopływ na końcu w fazy II w [m
3
d
-1
],
Potrzebny dopływ jednostkowy netto w czasie trwania fazy II wynosi:
dopływ jednostkowy brutto w fazie II jest w przybliżeniu równy:
η = 0,70
10.3.
Obliczenie całkowitego czasu trwania jednego cyklu podsiąku
T
1
= 1,23 dni
T
2
= 1,38 dni
10.4.
Obliczenie całkowitego czasu realizacji jednego nawodnienia
T = 2,61 dni
10.4. Obliczenie powierzchni możliwej do nawodnienia wodą dyspozycyjną.
10.4.1. w pierwszym pokosie
Q
dysp. Ip.
= 247
l ∙ s
-1
10.4.2. w drugim pokosie
Q
dysp. IIp.
= 124
l ∙ s
-1
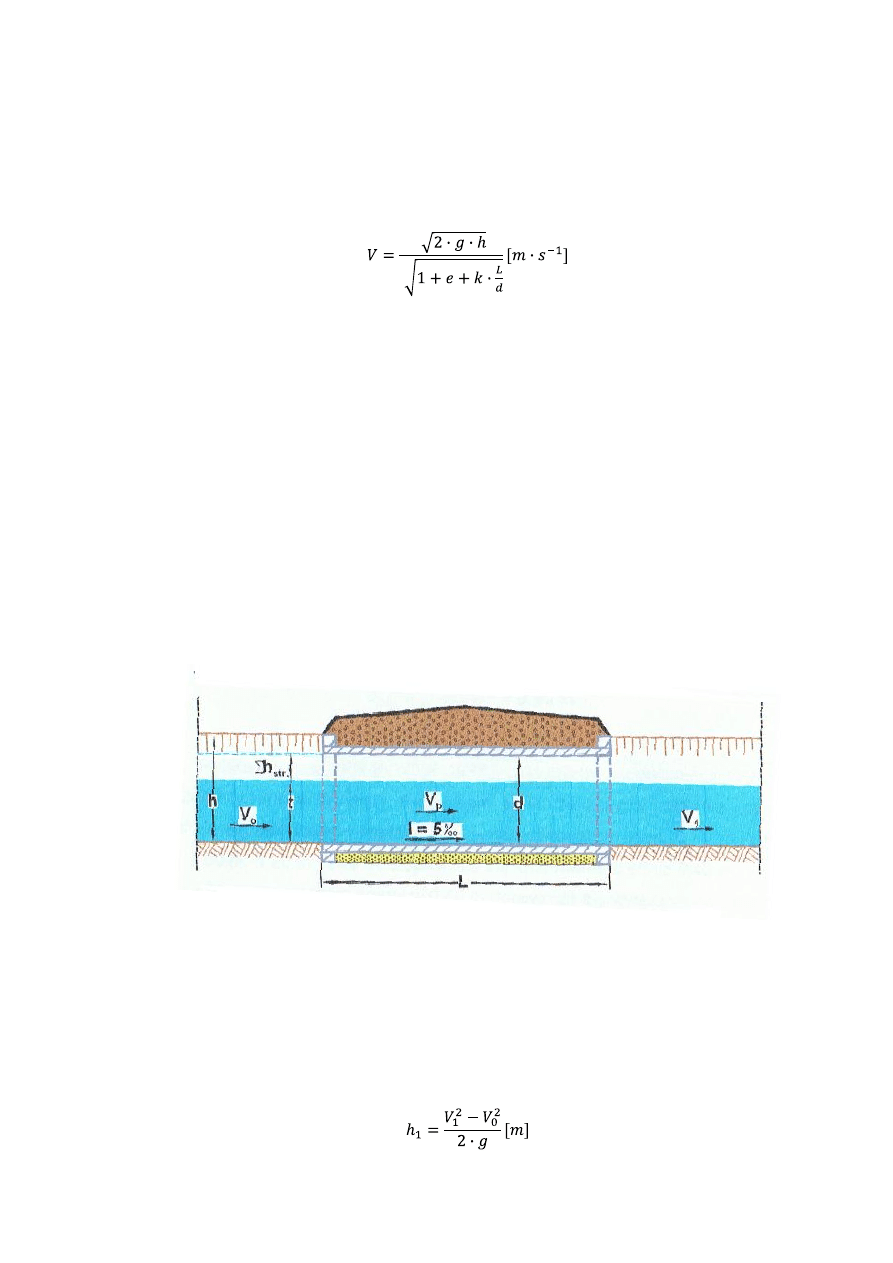
11.
Obliczenia hydrauliczne budowli wodno melioracyjnych
11.1.
Obliczenie światła przepustu wałowego
Krótkie przepusty rurowe prowadzące wodę całym przekrojem, a nawet powodujące pewne
popiętrzenie wody powyżej przepustu, można obliczyć ze wzoru Weissbacha:
gdzie:
h
– różnica poziomów wody powyżej i poniżej przepustu [m]
L
– długość przepustu [m]
d
– średnica rurociągu [m]
e
– współczynnik dławienia przy wlocie, dla przepustów e = 0,5
k
– współczynnik tarcia, zależny od materiału z którego wykonano rurociąg – dla betonu,
żelbetonu, rur żeliwnych i spawanych k = 0,02
g
– przyspieszenie ziemski g =9,81 m
.
s
-2
Ryc. Hydrauliczny schemat obliczeniowy przepustu drogowego
Różnica poziomów wody powyżej i poniżej budowli (h), a więc straty spadu hydraulicznego w
przepuście, powstają wskutek:
zmiany prędkości wody dopływającej (V
0
) i odpływającej (V
1
):
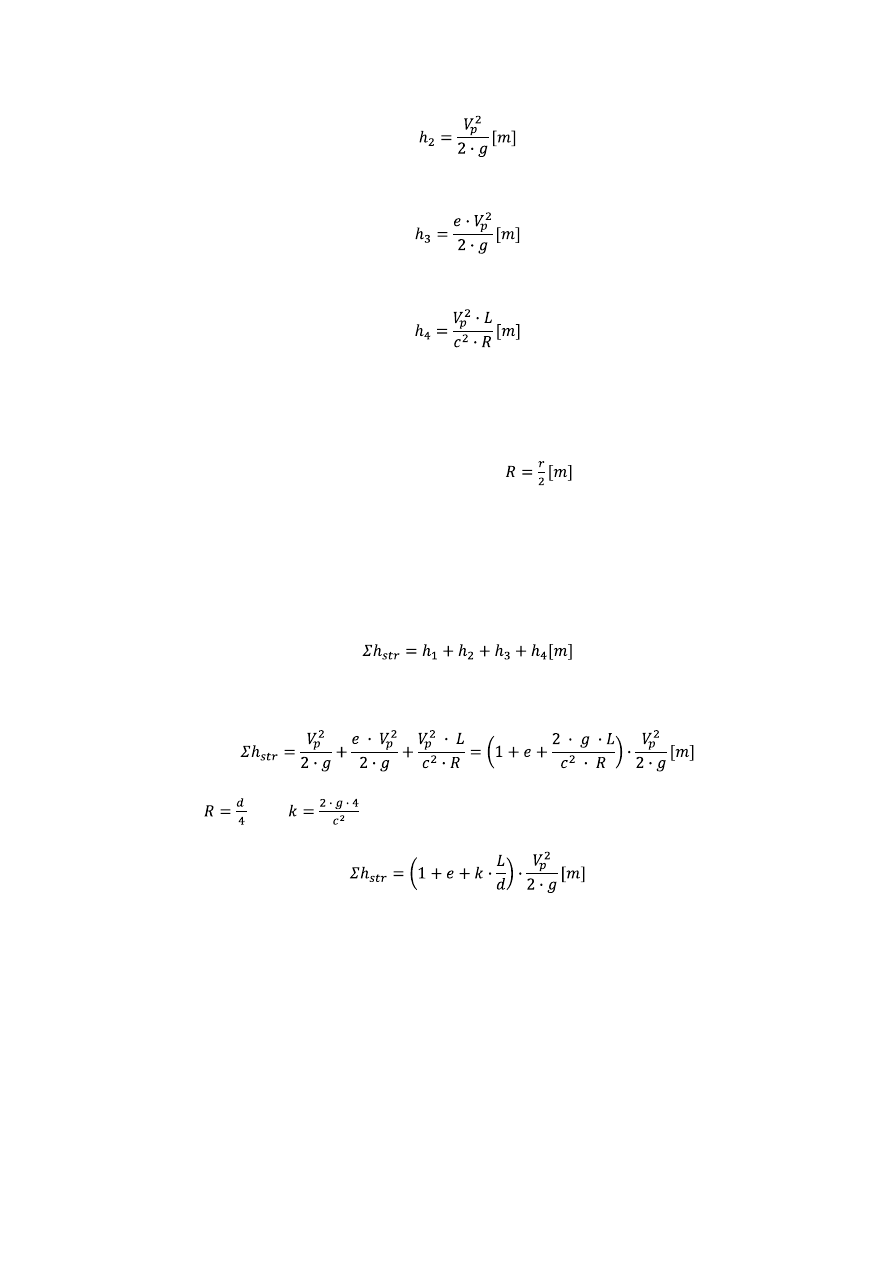
wzrostu prędkości wody w rurociągu (V
p
):
strat na wlocie:
oporów tarcia w rurociągu:
gdzie:
V
p
– prędkość wody w przepuście [m
.
s
-1
]
R
– promień hydrauliczny – dla przekroju kołowego
c
– współczynnik prędkości obliczony ze wzoru Kuttera lub Bazina
Sumaryczne straty w przepuście wynoszą:
ze względów praktycznych pomijane są straty h
1
, a więc:
Ponieważ
oraz
w efekcie formuła przyjmuje postać:
11.1.1.
Obliczanie Światła przepustu drogowego
Aby określić średnicę przepustu drogowego na rowie doprowadzającym wodę do nawodnień,
w pierwszej kolejności należy ustalić przepływ miarodajny (Q
m
) oblicza się go, jako iloczyn
niezbędnego dopływu jednostkowego brutto q
Ibr.
[
l ∙ s
-1
∙ ha
-1
] i powierzerzchnię obiektu
nadadnianego A
n
[ha]
Q
m
= q
Ibr.
∙ A
n
[m
3
∙ s
-1
]
Powierzchnię obiektu nawadnianego ustala się z iloczynu sumarycznej długości rowów
odwadniająco nawadniających (L
CR
) i ich rozstawy (L)
A
n
= L
CR
∙ L [ha]
L
CR
= 4865 m
L = 70
A
n
= 4865 ∙ 70 = 340550 m
2
= 34,05 ha
dysponując wszystkimi danymi można obliczyć przepływ miarodajny
q
Ibr.
= 7,61
l ∙ s
-1
∙ ha
-1
A
n
= 34,05 ha
Q
m
= q
Ibr.
∙ A
n
[m
3
∙ s
-1
]
Q
m
= 7,61
∙ 34,05 = 259,1 l ∙ s
-1
= 0,26 m
3
∙ s
-1
Założenia do światła przepustu:
średnica przepustu nie może być mniejsza niż szerokość dna rowu
b
d
możliwe jest pewne popiętrzenie wody w rowie powyżej przepustu
Dane:
g = 9,81 m
.
s
-2
Q
m
= 0,26 m
3 .
s
-1
L = 8 m
– długość przepustu
V
dop
= 1,50 m
.
s
-1
– dopuszczalna prędkość wody w przepuście
Polska norma (PN-B-
12096:1997. Urządzenia wodno melioracyjne. Przepusty rurowe. Wy-
miary. Polski
Komitet Normalizacyjny.) zawiera zapis: „ustala się następujące średnice prze-
pustu jednootworowego: 0,60m; 0,80m; 1,00m; 1,20m; 1,40m.” Dopuszcza się stosowanie
średnic 0,40 m; 1,25m i 1,50m. Stosowanie średnicy 0,40m dopuszcza się wyłącznie na ro-
wach okre
sowo prowadzących wodę, przy długościach przepustu do 6,0m w przypadku ko-
nieczności zastosowania przepustu dwuotworowego należy stosować średnicę przewodów
rurowych 0,80m in1,00m.
Zgodnie z wytycznymi PN-B-
12096:1997 i mając na uwadze założenie, iż średnica przepustu
nie może być mniejsza od szerokości dna rowu (b = 0,50 m) przyjęto d
kat.
=0,60 m, a więc:
d
kat.
= 0,60 m > d
obl.
= 0,46 m
Następnie oblicza się powierzchnię przekroju przyjętej rury katalogowej:
W dalszej kolejności określa się prędkości rzeczywistą w rurociągu:
11.1.2.
Obliczanie strat wywołanych przepustem
Sprawdzenie warunku czy przyjęta średnica katalogowa jest odpowiednia:
gdzie:
t
– napełnienie rowu wodą przed przepustem [m]; Napełnienie t =0,50 m,
h
– głębokość rowu [m]; h = 0,65
0,50 + 0,08 = 0,58 < 0,65 m -
warunek spełniony
Na podstawie obliczeń hydraulicznych przyjęto przepust jednootworowy o średnicy
Ø 0,60 m
11.2.
Obliczenie światła zastawki
Założenia :
Dopuszcza się nieznaczne piętrzenie nie przekraczające h
s
= 10 cm w momencie gdy
woda powy
żej zastawki zaczyna wylewać się na brzegi i omijać zastawkę, spływa
poniżej niej z powrotem o koryta .
Światło zastawki nie może być mniejsze niż szerokość dna rowu.
Dane :
Obliczenia wykonane dla zastawki: Z - 5
głębokość strugi: h = 0,85 m
spadek
dna: I = 1,98 ‰
przekrój trapezowy koryta: b = 0,5 m
nachylenie skarp; przyjęto dla gleb średniozwięzłych 1: n = 1: 1,5
współczynnik szorstkości dla koryta ziemnego zadarnionego źle utrzymanego do wzoru
Ganguilleta
– Kutnera: n
s
=0,03
współczynniki dławienia bocznego zależne od szerokości otworu
1
=
2
= 0,73 przyjęty z
tabeli 13
Tabela 13 Wartości współczynnika μ w zależności od światła otworu
Szerokość otworu [m]
μ
1
0,73
2
0,74
3
0,75
4
0,76
5
0,76
6
0,77
7
0,78
8
0,78
9
0,79
10
0,80
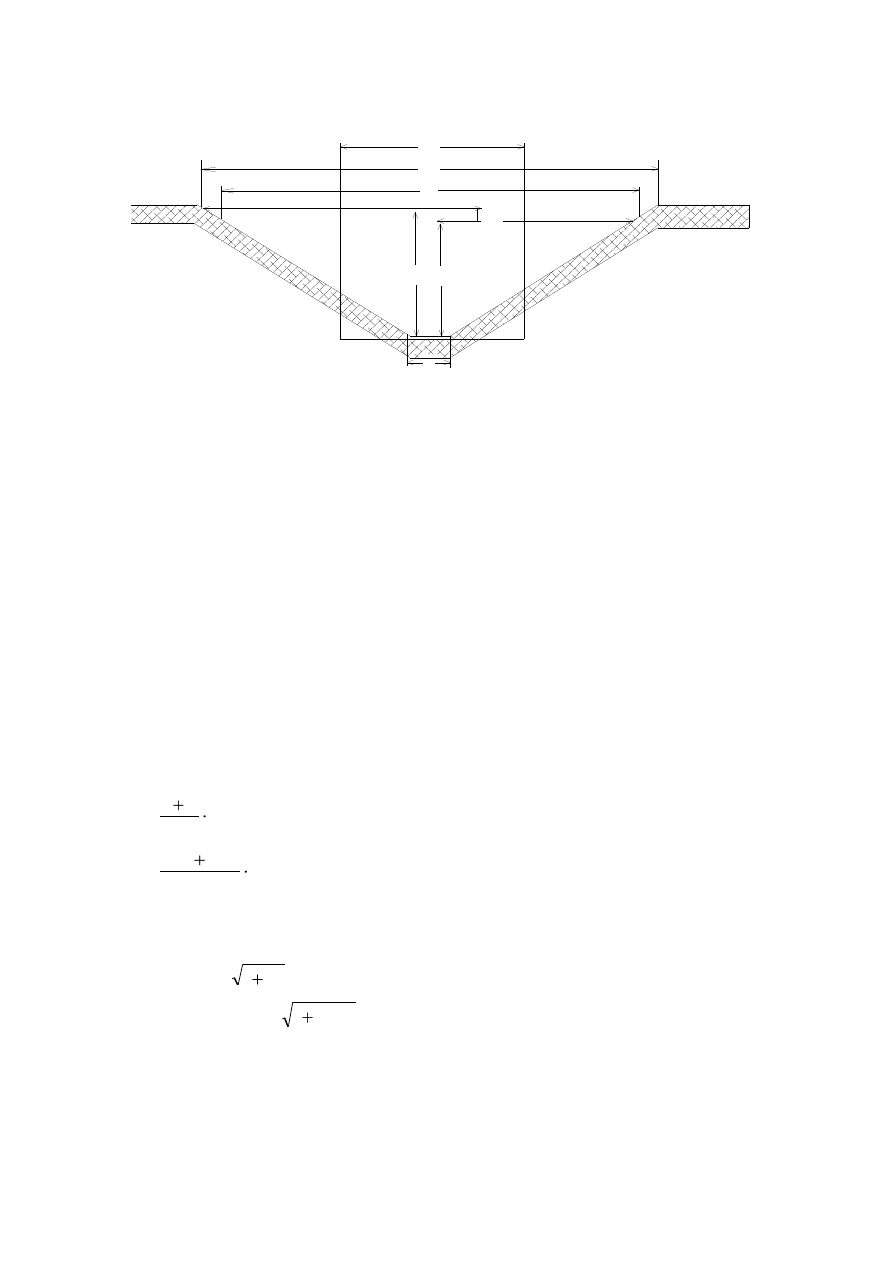
b
h t
h
s
b
z
B
0
B
1:1
,5
Ryc. Hydrauliczny schemat obliczeniowy zastawki
11.2.1.
Obliczenia parametrów hydraulicznych poniżej zastawki:
1. głębokość strugi wody:
t = h
– h
s
[ m ]
t = 0,90
– 0,10 = 0,80 m
2. górna szerokość koryta:
B = b + 2 ∙ n ∙ t [ m ]
B = 0,50 + 2 ∙ 1,50 ∙ 0,80 = 2,75 m
3. użyteczna powierzchnia przekroju koryta:
F =
t
2
B
b
[ m
2
]
F =
80
,
0
2
75
,
2
50
,
0
= 1,30 m
2
4. obwód zwilżony:
O = b + 2 ∙ t ∙
2
n
1
[ m ]
O = 0,50
+ 2 ∙ 0,80 ∙
2
1,50
1
= 3,20 m
5. promień hydrauliczny:
R =
O
F
[ m ]
R =
20
,
3
30
,
1
= 0,41 m
6. współczynnik prędkości wg Ganguilleta – Kuttera:
c =
R
n
I
I
n
s
s
)
00155
,
0
23
(
1
00155
,
0
1
23
[-]
c =
41
,
0
03
,
0
)
00198
,
0
00155
,
0
23
(
1
00198
,
0
00155
,
0
03
,
0
1
23
= 26,96
7. prędkość wody w strudze:
V = c ∙
I
R
[ m ∙ s
-1
]
V = 26,96 ∙
00198
,
0
41
,
0
= 0,77 m ∙ s
-1
8. ilość przepływającej wody:
Q = F ∙ V [ m
3
∙ s
-1
]
Q = 1,30 ∙ 0,77 = 1,00 m
3
∙ s
-1
11.2.2.
Obliczenia parametrów hydraulicznych powyżej zastawki
Prędkość wody dopływającej do zastawki V
o
jest nieco mniejsza od prędkości wody odpływa-
jącej V, gdyż za sprawą popiętrzenia wody przez zastawkę h
s
większy jest przekrój dopływa-
jącej strugi.
1. górna szerokość koryta:
B
o
= b + 2 ∙ n ∙ h [ m ]
B
o
= 0,50 +2 ∙ 1,50 ∙ 0,90 = 3,20 m
2. użyteczna powierzchnia przekroju koryta:
F
o
=
h
B
b
o
2
[ m
2
]
F
o
=
90
,
0
2
20
,
3
50
,
0
= 1,67 m
2
3. prędkość wody:
V
o
=
o
F
Q
[ m ∙ s
-1
]
V
o
=
67
,
1
00
,
1
= 0,60 m ∙ s
-1
11.2.3.
Obliczenia światła zastawki
Q =
5
,
0
5
,
0
5
,
0
k)
(h
g
2
b
t
μ
]
k
k)
[(h
g
2
b
μ
3
2
s
z
2
s
z
1
[m
3
∙ s
-1
]
k =
g
2
V
2
0
k =
81
,
9
2
60
,
0
2
= 0,031
przekształcając powyższy wzór szerokość światła zastawki wyniesie:
5
,
0
5
,
1
5
,
1
k)
(h
g
2
t
μ
]
k
k)
[(h
g
2
μ
3
2
Q
b
s
2
s
1
z
[m]
5
,
0
5
,
1
5
,
1
0,031)
(0,10
9,81
2
0,80
0,75
]
0,031
0,031)
[(0,10
9,81
2
0,73
3
2
1,00
b
z
b
z
= 0,98 m
Polska norma (PN-B-
12092:1997. Urządzenia wodno melioracyjne. Zastawki. Wymiary. Pol-
ski Komitet Normalizacyjny.) zawiera zapis: „ustala się następujące wymiary światła zasta-
wek: 0,60m; 0,80m; 1,00m; 1,25m; 1,50m.”
W oparciu o wytyczne zawarte w PN-B-
12092:1997 i w efekcie obliczeń hydraulicznych przy-
jęto światło zastawki b
z
= 1,00 m
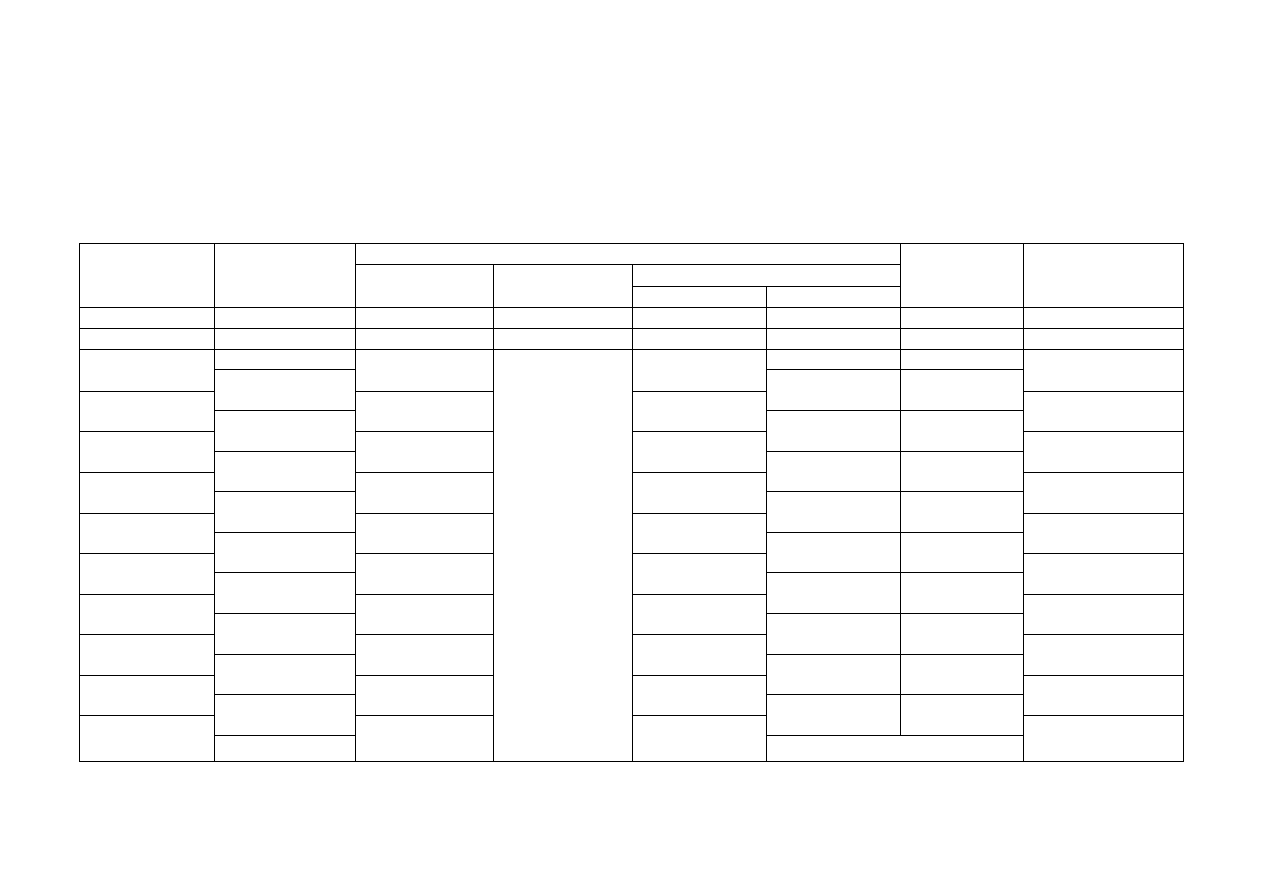
12.
Zestawienie objętości robót ziemnych
12.1.
Kubatura robót ziemnych rowu doprowadzająco - odprowadzającego
Stacja
hektometr
Odległości
Przekrój projektowany
Objętość
Objętość
sumaryczna
głębokość
parametry rowu
powierzchnia
na stacji
średnia
-
m
m
-
m
2
m
2
m
3
m
3
1
2
3
4
5
6
7
8
0 + 00
0,85
S
zerokość
dn
a
b
=
0,
5
m
N
ach
yl
en
ie skar
p
1:n
=
1:1,
50
1,51
0
72
1,56
112,32
0 + 72
0,88
1,60
112,32
140
1,71
239,40
2 + 12
0,95
1,82
351,72
262
1,66
434,92
4 + 74
0,85
1,51
786,64
71
1,66
117,86
5 + 45
0,95
1,82
904,50
121
1,81
219,01
6 + 66
0,94
1,80
1123,51
132
1,81
238,92
7 + 98
0,90
1,82
1362,43
141
1,66
234,06
9 + 39
0,85
1,51
1596,49
62
1,51
93,62
10 + 01
0,85
1,51
1690,11
54
1,51
81,54
11 + 54
0,85
1,51
1771,65
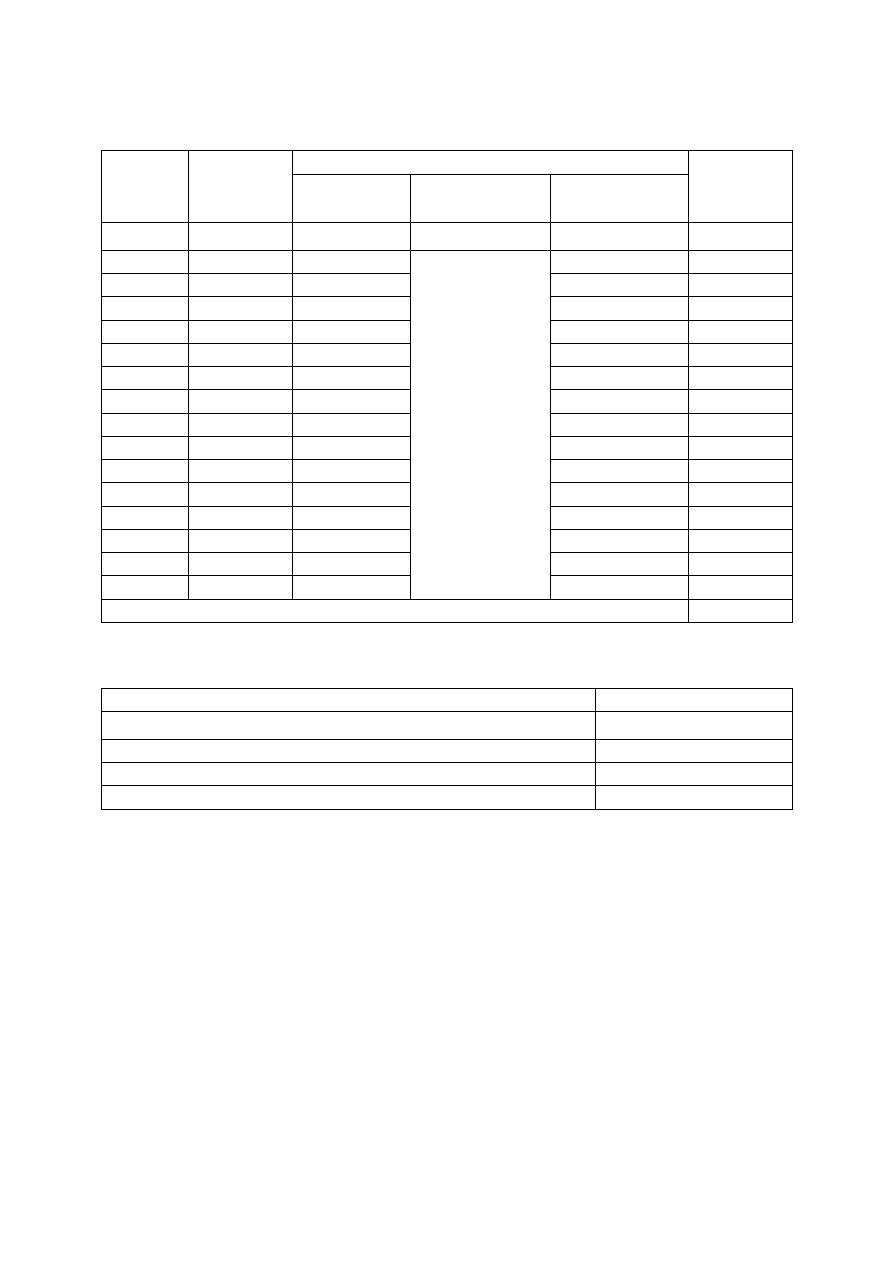
12.2.
Kubatura wykopu rowów odwadniająco - nawadniających
Nr rowu
Długość
rowu
Przekrój projektowany
Objętość
średnia
głębokość
parametry rowu
średnia
powierzchnia
-
m
m
-
m
2
m
3
A1
286
0,65
S
zerokość
dn
a
b
=
0,
5
m
N
ach
yl
en
ie skar
p
1:n
=
1:1,
50
0,96
274,56
A2
568
0,65
0,96
545,28
A3
556
0,65
0,96
533,76
A4
460
0,65
0,96
441,60
A5
456
0,65
0,96
437,76
A6
404
0,65
0,96
387,84
A7
332
0,65
0,96
318,72
A8
270
0,65
0,96
259,20
A9
253
0,65
0,96
242,88
A10
204
0,65
0,96
195,84
A11
146
0,65
0,96
140,16
A12
133
0,65
0,96
127,68
B1
494
0,65
0,96
474,24
B2
333
0,65
0,96
319,68
B3
256
0,65
0,96
245,76
Suma :
4944,96
12.3.
Łączna kubatura robót ziemnych
Rodzaj rowu
Objętość wykopu
-
m
3
Rów odprowadzająco - doprowadzający DA - RA
1771,69
Rowy nawadniająco - odwadniające
4944,96
Suma:
6716,65