Przewodnictwo ciał stałych.

Wyznaczenie zależności rezystancji przewodnika

metalicznego i półprzewodnika od temperatury.

Ćw.10

Cel ćwiczenia

Celem ćwiczenia jest:

a) Zbadanie

zależności rezystancji przewodnika metalowego i półprzewodnika (termistora) od temperatury.

b) Wyznaczenie temperaturowych współczynników zmiany rezystancji dla rezystora metalicznego i dla

półprzewodnika.

c) Obliczenie

szerokości przerwy energetycznej ∆E pomiędzy pasmem przewodzenia i pasmem walencyjnym

dla półprzewodnika, z którego wykonany jest badany termistor.

Zakres obowiązującego materiału teoretycznego

Model pasmowy ciała stałego. Przewodnictwo elektryczne przewodników metalicznych i półprzewodników.

Półprzewodniki samoistne i domieszkowane. Zależność rezystywności (przewodnictwa) przewodników

metalicznych i półprzewodników od temperatury.

Metale

Ogrzanie próbki przewodnika powoduje zmianę jej rezystancji. Na gruncie mechaniki kwantowej wykazano, że

przewodność metali jest dla niezbyt niskich temperatur odwrotnie proporcjonalna do temperatury T w skali

bezwzględnej:

1

T

~

−

σ

(1)

T>>Θ

D

gdzie Θ

D

jest tzw. temperaturą Debye'a. Zależność ta w sposób zadawalający zgadza się z

doświadczeniem. Jeśli zamiast przewodności wprowadzić rezystywność

ρ

, związek (1) uzyska postać:

1

−

σ

=

T

~

ρ

(2)

Jakościowo tłumaczy się zwiększenie rezystywności metali przy podwyższeniu temperatury przez wzrost

rozproszenia cieplnego elektronów na sieci metalicznej.

Dla przewodnika o określonych wymiarach rezystancja jest proporcjonalna do temperatury:

(

)

(

)

o

o

273

t

1

A

273

t

273

A

AT

R

+

=

+

=

=

(3)

gdzie A oznacza stałą, a t jest temperaturą w skali Celsjusza.

Rezystancję w temperaturze 0

o

C oznacza się zwykle przez R

o

. Z równania (3) wynika dla t=0

o

C:

A

273

R

o

o

=

(4)

Wobec tego (3) można zapisać w postaci:

(

)

at

1

R

R

o

+

=

(5)

gdzie a=1/273

o

=0,00366 stop

-1

nazwany jest temperaturowym współczynnikiem zmiany rezystancji.

Z pośród metali platyna ma własności najbliższe przewidywanym przez równanie (5). Równanie to ma

jednak charakter przybliżony, bardziej zgodna z doświadczeniem jest zależność:

1

(

)

...

bt

at

1

R

R

2

o

+

+

+

=

(6)

b jest przy tym często ujemne, przede wszystkim w przypadku stopów. Wówczas pochodna:

(

)

...

bt

2

a

R

dt

dR

o

+

+

=

(7)

osiąga zero dla pewnej temperatury t = t

m

; rezystancja jest wówczas maksymalna i zmienia się nieznacznie z

temperaturą. Wartość t

m

bliską temperaturze pokojowej posiadają niektóre stopy, odznaczające się w związku z

tym stabilnością rezystywności. Należą do nich m.in. manganian, konstantan, nowokonstantan i izabelin.

Półprzewodniki

Własności półprzewodników są bardzo czułe na zmiany temperatury, ponieważ liczba elektronów w paśmie

przewodzenia wzrasta szybko przy ogrzewaniu. Jeśli różnica energii pomiędzy pasmem przewodzenia i

pasmem walencyjnym jest ∆E, to prawdopodobieństwo P tego, że w ciągu jednostki czasu energia równa

szerokości przerwy energetycznej stanie się dostępna dla któregoś z elektronów w paśmie walencyjnym, jest

proporcjonalna do czynnika

(

kT

2

E

∆

−

)

exp

, gdzie k oznacza stałą Boltzmana natomiast T - temperaturę

bezwzględną:

(

)

kT

2

E

exp

~

P

∆

−

(8)

Energia dostarczana z zewnątrz przy ogrzewaniu może zostać zużyta na przeniesienie elektronu z pasma

walencyjnego do pasma przewodzenia. Wynika stad, że liczba elektronów w paśmie przewodzenia, a wiec i

przewodność jest proporcjonalna do czynnika wykładniczego:

(

)

kT

2

E

exp

~

∆

−

σ

(9)

(dokładniej

(

)

kT

2

E

exp

T

~

2

3

∆

−

σ

jednak ze względu na decydujący wpływ czynnika wykładniczego

wyrażenie (9) jest dobrym przybliżeniem).

Szybka zmiana przewodności półprzewodnika przy zmianie temperatury została wykorzystana w urządzeniach

nazwanych termistorami, odznaczających się dużym, najczęściej ujemnym temperaturowym współczynnikiem

zmiany rezystancji. W niezbyt dużym zakresie temperatur przewodność termistora opisuje zależność typu (9),

czyli rezystancję termistora można zapisać w postaci:

( )

T

a

exp

R

R

0

T

T

=

(10)

gdzie

k

2

E

a

∆

=

(11)

Podobne zależności są spełnione dla elementów półprzewodnikowych, w których przeważa przewodność

samoistna - termistor należy do takich elementów. W diodach i tranzystorach decydującą rolę odgrywa

przewodność domieszkowana.

Zastosowanie

Temperaturową zmianę rezystywności przewodników metalicznych wykorzystano przy budowie termometrów

oporowych (dokładność pomiaru rzędu 10

-3 o

C). Do konstrukcji termometrów oporowych używa się najczęściej

platyny, niklu i miedzi, rzadziej żelaza. Z kolei stopy o malej wartości temperaturowego współczynnika

2

rezystywności służą do wytwarzania stabilnych rezystorów. Termistory znalazły zastosowanie jako

ograniczniki prądu w chwili włączania urządzeń elektronicznych, jako kompensatory zmian temperaturowych

parametrów innych elementów półprzewodnikowych, a także w pomiarach temperatury, mocy, przepływu

gazu, poziomu cieczy oraz jako detektory promieniowania wysokiej częstości. Dzięki wysokiej czułości

temperaturowej (rzędu 2×10

-2

1/

o

C) przy użyciu termistorów można rejestrować zmiany temperatury rzędu

10

-6

o

C Typowe dopuszczalne temperatury pracy nie przekraczają zwykle 300

o

C istnieją jednak termistory

pracujące przy dwukrotnie wyższych temperaturach.

Metoda pomiaru

Celem doświadczenia jest wyznaczenie zależności rezystancji od temperatury dla czystego metalu, i materiału

półprzewodnikowego (termistora). Zgodnie z równaniem (5) w pierwszym przypadku oczekujemy zależności

liniowej. Dla termistora, jak to wynika z równania (10), spełniony jest związek:

(

)

( )

T

a

exp

R

kT

2

E

exp

R

R

0

T

0

T

T

=

∆

=

(12)

po zlogarytmowaniu:

T

a

R

ln

R

ln

0

T

T

+

=

(13)

W układzie współrzędnych ln(R)=f(1/T) wykresem zależności (13) jest linia prosta o nachyleniu

k

2

E

a

∆

=

(14)

Doświadczalne wyznaczenie a pozwala określić szerokość przerwy energetycznej ∆E:

ka

2

E

=

∆

(15)

Tradycyjnie stosowaną jednostką jest tutaj elektronowolt (eV).

Część doświadczalna

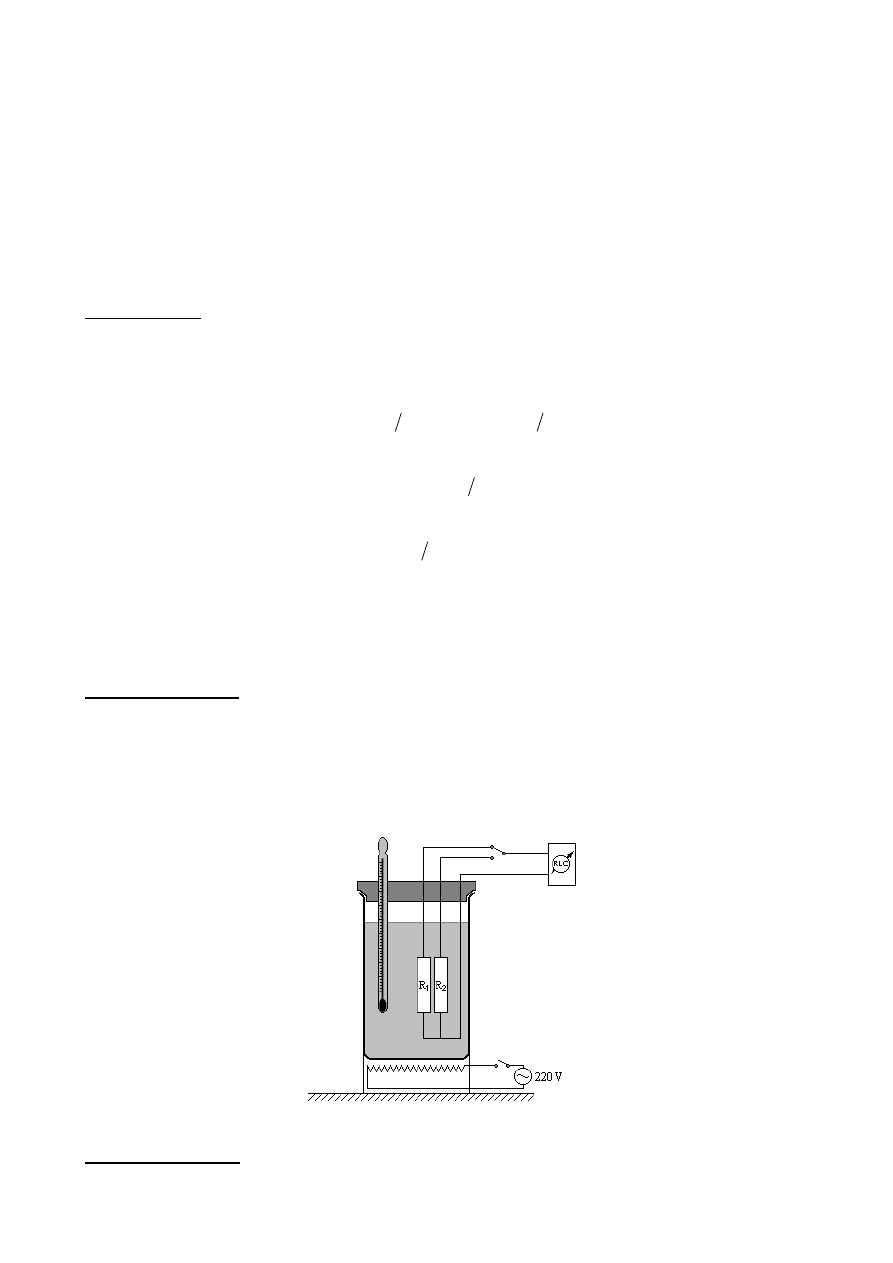
Zestaw przyrządów do wyznaczania temperaturowej zależności rezystancji przedstawia rys.1. Zestaw

pomiarowy składa się z naczynia metalowego napełnionego olejem silikonowym i podgrzewanego prądem

elektrycznym. Badane rezystory znajdują się w kąpieli olejowej. Pomiar rezystancji dla określonej temperatury

wykonujemy miernikiem elektrycznym RLC na zakresie rezystancji.

Rys.1

Wykonanie pomiarów

3

1. Włączyć przełącznikiem odpowiedni rezystor i wykonać pomiary oporu dla opornika metalicznego i

termistora zanurzonego w kąpieli olejowej dla temperatury pokojowej.

2. Włączyć prąd podgrzewający naczynie z kąpielą olejową, w której zanurzone są badane rezystory.

3. Przy

osiągnięciu temperatury ok. 105

o

C wyłączyć ogrzewanie. Po wyłączeniu prądu, temperatura kąpieli

olejowej wzrastać będzie jeszcze do ok. 110-115

o

C, a następnie zacznie opadać.

4. W czasie stygnięcia kąpieli poczynając od ok. 110

o

C wykonać pomiary rezystancji rezystora metalowego i

termistora w odstępach ok. 5-7

o

C. Aby przyśpieszyć obniżanie się temperatury w zakresie niższych

temperatur (poniżej ok. 80

o

C) należy włączyć przepływ wody w wężownicy (Wykonuj pod nadzorem

prowadzącego pracownię !!!) i mieszać olej za pomocą mieszadła (po skończeniu pomiarów zakręcić

zawór wody !).

5. Wyniki pomiarów zapisać w tabeli:

Tabela 1

lp. t

[

o

C] T

[K] R [Ω] R

T

[Ω]

1.

2.

3.

.

.

.

n.

Opracowanie wyników

1. W przypadku czystego metalu wyniki opracować metodą najmniejszych kwadratów (instrukcja nr 17).

Wyniki obliczeń zestawić w tabeli wg. przykładu ze str.21 instrukcji nr 17, przyjmując X = t (

o

C) i Y = R (Ω).

Sporządzić na papierze milimetrowym wykres otrzymanej zależności Y = aX+b i nanieść również punkty

doświadczalne dla metalu. Korzystając z obliczeń metodą najmniejszych kwadratów wyliczyć wartość R

o

odpowiadająca temperaturze t = 0

o

C, oraz wyznaczyć temperaturowy współczynnik rezystywności

(współczynnik a ze wzoru nr 5.) materiału, z którego jest wykonany rezystor metaliczny. Obliczyć

odchylenie standardowe współczynników regresji (instrukcja 17), oraz podać oszacowanie granic

wyników dla R

o

i a.

2. Dla

termistora

obliczyć wartości 1/T (T - temperatura w stopniach Kelvina) i odpowiadające im wartości

ln(R

T

). Wyniki zapisać w tabeli 2. Korzystając z metody najmniejszych kwadratów sporządzić wykres

ln(R

T

)=f(1/T) odzwierciedlający równanie (13).

Tabela 2

lp. T

[K]

R

T

[Ω]

x =1/T [1/K]

y=ln(R

T

) x

2

[1/K

2

] y

2

xy [1/K]

1.

2.

3.

.

.

4

5

.

n.

3. Mając obliczony (metodą najmniejszych kwadratów) współczynnik prostej opisanej równaniem (13) –

y = Ax + B, gdzie x = 1/T, y = ln(R

T

), A = a, B = ln(R

To

)

obliczyć szerokość przerwy energetycznej ∆E

zgodnie z równaniem (15) pomiędzy pasmem przewodnictwa a pasmem walencyjnym (przyjmując

k = 1,38 ×10

-23

J/K = 8,62 ×10

-5

eV K

-1

). Obliczyć odchylenie standardowe współczynników regresji i podąć

oszacowanie granic wyniku pomiaru szerokości przerwy energetycznej ∆E.

Wyniki obliczeń i wnioski

Na osobnej stronie podać wyniki obliczeń rezystancji R

To

oraz współczynnika rezystywności dla metalu wraz z

obliczonymi błędami. Podać obliczoną wartość szerokości przerwy energetycznej pomiędzy pasmem

przewodnictwa a pasmem walencyjnym dla termistora wraz z obliczonym błędem. Napisać wnioski. Poprzez

porównanie z wartościami teoretycznymi przerw energetycznych określić materiał z jakiego wykonano

półprzewodnik.