CHARAKTERYSTYKI CZ

Ę

STOTLIWO

Ś

CIOWE PODSTAWOWYCH

CZŁONÓW LINIOWYCH UKŁADÓW AUTOMATYKI

Do podstawowych form opisu dynamiki elementów automatyki (oprócz równa

ń

ró

żniczkowych) zaliczamy transmitancję operatorową K(s) oraz transmitancję widmową

K(j

ω). Związek pomiędzy tymi transmitancjami wyraża się wzorem:

)

(

0

0

)

(

)

(

)

(

)

(

)

(

)

(

)

(

ω

φ

ω

ω

ω

ω

ω

ω

ω

j

n

i

i

i

m

l

l

l

j

s

e

j

K

j

a

j

b

j

U

j

Y

s

K

j

K

=

=

=

=

∑

∑

=

=

>

−

(1)

Twierdzenie o przechodzeniu sygnału sinusoidalnego przez układ liniowy.

Je

ż

eli na wej

ś

cie układu liniowego podamy sygnał sinusoidalny (u(t)=Asin

w

t), to na wyj

ś

ciu,

w stanie ustalonym (przy zało

ż

eniu

ż

e składowa swobodna y

s

równa si

ę

zero), otrzymamy

tak

ż

e sygnał sinusoidalny o amplitudzie

)

( ω

j

K

A

B

=

i przesuni

ę

ciu fazowym

f

.

Transmitancj

ę

widmow

ą

mo

ż

na przedstawi

ć

tak

ż

e w postaci:

)}

(

Im{

)}

(

Re{

)

(

ω

ω

ω

j

K

j

j

K

j

K

+

=

,

(2)

gdzie: K j

(

)

ω

– moduł transmitancji widmowej (stosunek amplitud sygnału wyj

ś

ciowego do

sygnału wej

ś

ciowego),

Re{K(j

w

)} – cz

ęść

rzeczywista K(j

w

),

Im{K(j

w

)} – cz

ęść

urojona K(j

w

),

ϕ

(

ω

) =

)}

(

Re{

)}

(

Im{

ctg

ω

ω

j

K

j

K

ar

– argument transmitancji widmowej (przesuni

ę

cie

fazowe pomi

ę

dzy sygnałem wyj

ś

ciowym i wej

ś

ciowym).

Zale

ż

no

ść

transmitancji widmowej

φ

ω

ω

j

e

j

K

j

K

)

(

)

(

=

od cz

ę

stotliwo

ś

ci przedstawia si

ę

na

płaszczy

ź

nie Gaussa i nazywa si

ę

charakterystyk

ą

amplitudowo-fazow

ą

.

Charakterystyki amplitudowe i fazowe przedstawia si

ę

cz

ę

sto jako charakterystyki

logarytmiczne Bodego (w logarytmicznej skali cz

ę

stotliwo

ś

ci):

)

(

log

20

)

(

10

ω

ω

j

K

M

=

[dB]

(3)

φ ω

ω

( )

arg[ (

)]

=

K j

.

Zaleta

tego

sposobu

przedstawiania

charakterystyk

cz

ę

stotliwo

ś

ciowych

wynika

z wła

ś

ciwo

ś

ci funkcji logarytmicznej:

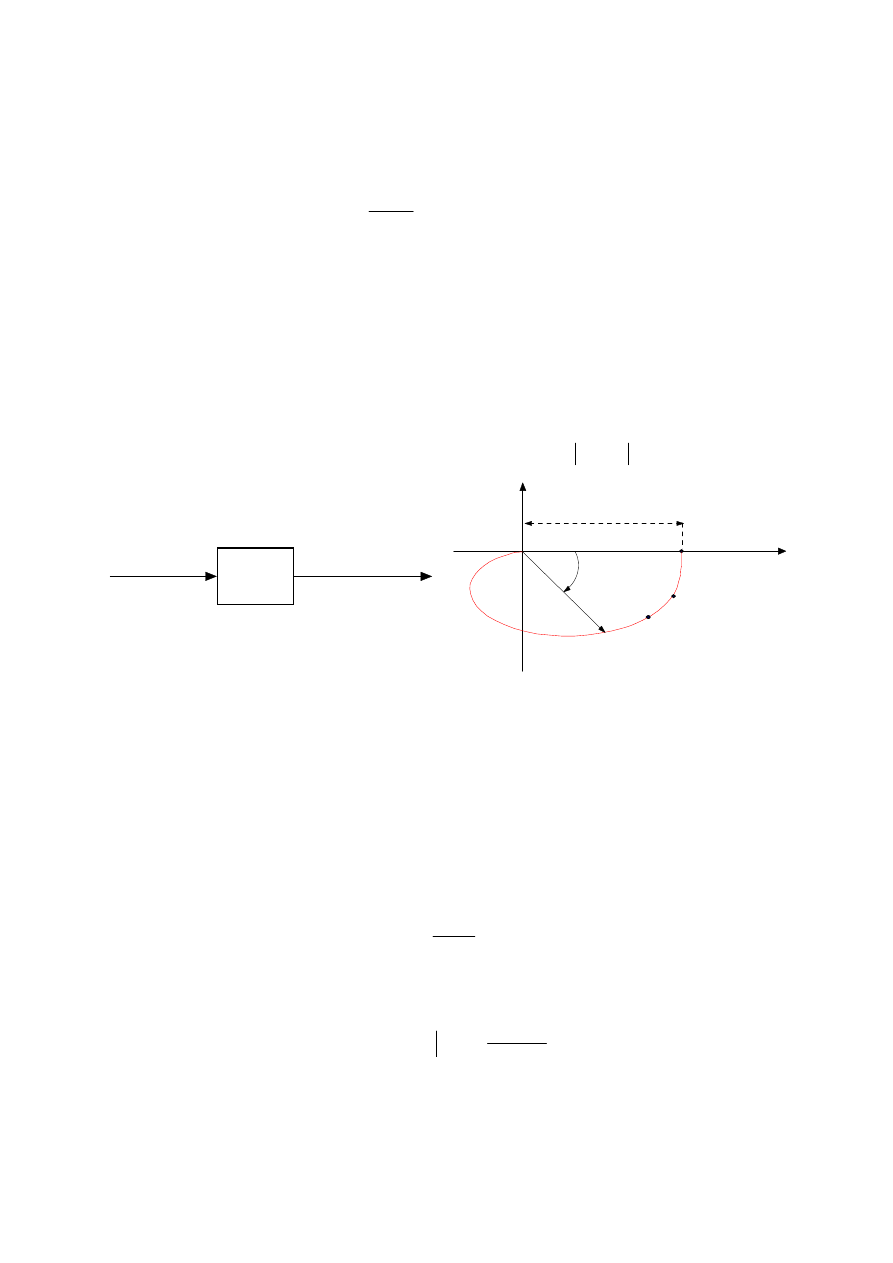
- w skali logarytmicznej zmiana o 10

c

(c –liczba całkowita) jest proporcjonalna do c,

-

logarytm iloczynu jest równy sumie logarytmów, a logarytm ilorazu ró

ż

nicy logarytmów:

3

2

1

3

2

1

log

log

log

log

K

K

K

K

K

K

−

+

=

.

(4)

Pozwala to przedstawi

ć

charakterystyki (modułu i fazy) zło

ż

onego układu automatyki za

pomoc

ą

sumy charakterystyk członów podstawowych.

Eksperymentalne zdejmowanie charakterystyk amplitudowo-fazowych.

W celu okre

ś

lenia charakterystyki amplitudowo-fazowej zmieniamy cz

ę

stotliwo

ść

sygnału

sinusoidalnego wej

ś

ciowego

w

1

,

w

2

w

3

... i okre

ś

lamy parametry

)

( ω

j

K

oraz

)

(

ω

ϕ

.

K(j

ω)

x(t)=Xsin

ωt

y(t)=X

K(jω) sin(ωt+ϕ)

Im {K(j

ω)}

Re {K(j

ω)}

k

ω=0

ω=∝

ω

1

ω

2

-

ϕ(ω)

K(jω)

ω

Rys. 1. Eksperymentalne okre

ślanie charakterystyki częstotliwościowej

W wprowadzeniu do

ć

wiczenia zostan

ą

omówione charakterystyki cz

ę

stotliwo

ś

ciowe

wybranych podstawowych członów automatyki.

I. Człon inercyjny I-rz

ędu

Transmitancja operatorowa opisana jest wzorem:

K(s) =

1

+

Ts

k

(I.1)

Transmitancja widmowa członu inercyjnego pierwszego rz

ę

du:

1

)

(

)

(

+

=

=

=

T

j

k

s

K

j

K

j

s

ω

ω

ω

(I.2)

Przedstawiona w postaci modułu i fazy:

T

ar

j

j

e

T

k

e

j

K

j

K

ω

ω

ϕ

ω

ω

ω

ctg

2

)

(

1

)

(

)

(

)

(

−

+

=

=

.

(I.3)

Wykres charakterystyki amplitudowo-fazowej członu inercyjnego pierwszego rz

ę

du

przedstawiono na rys. I.1.

Im {K(j

ω)}

Re {K(j

ω)}

k

ω=0

ω=∝

-j



k
2

ω= 

1

T



k

2

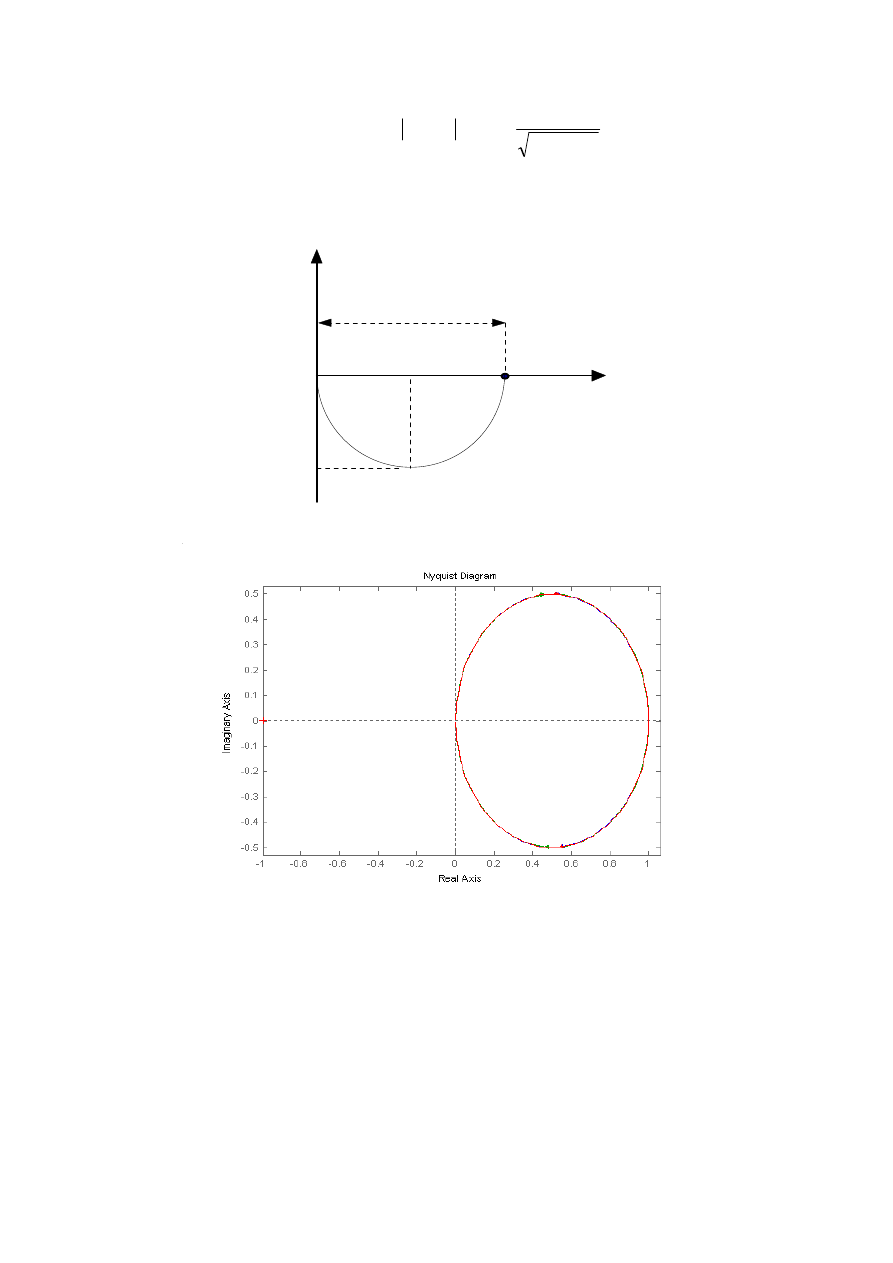
Rys. I.1. Charakterystyka amplitudowo-fazowa członu inercyjnego pierwszego rz

ędu

Rys. I.2. Charakterystyki Nyquista członu inercyjnego pierwszego rz

ędu

Na rys. I.2 przedstawiono charakterystyki Nyquista układu inercyjnego I-rz

ę

du dla trzech

ró

ż

nych stałych czasowych: T1=0,1; T2=1; T3=5. Jak mo

ż

na zauwa

ż

y

ć

z wykresów krzywe

te pokrywaj

ą

si

ę

(przy tym samym wzmocnieniu k=1). Oczywi

ś

cie punkt 0,5 –j0,5 na

wykresach uzyskuje si

ę

dla ró

ż

nych pulsacji

ω

(odpowiednio: 10, 1 i 0,5). Dlatego dogodniej

jest korzysta

ć

z charakterystyk Bode.

Logarytmiczna charakterystyka amplitudowa ma posta

ć

:

1

)

(

log

20

log

20

)

(

2

+

−

=

ω

ω

T

k

M

,

(I.4)

a charakterystyka fazowa:

)

ctg(

)

(

T

ar

ω

ω

−

=

Φ

.

(I.5)

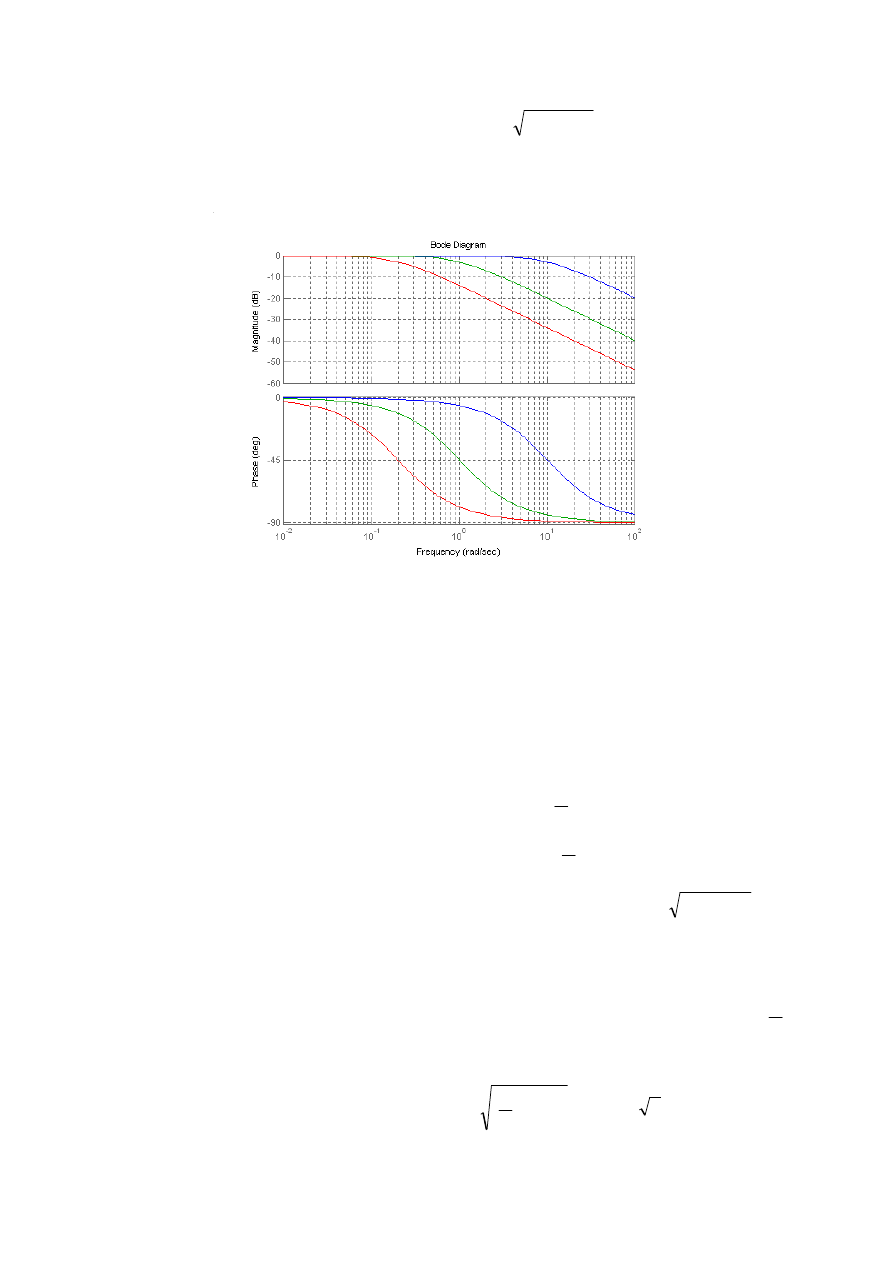
Rys. I.3. Logarytmiczne charakterystyki amplitudy i fazy członu inercyjnego pierwszego rz

ędu

Na wykresie I.3 przedstawiono logarytmiczne charakterystyki amplitudy i fazy, wyznaczone

dla: k=1, oraz T1=0,1; T2=1; T3=5. .

Wykres M(

w

) mo

ż

na przedstawi

ć

w postaci przybli

ż

onej, zast

ę

puj

ą

c krzyw

ą

(I.4) za pomoc

ą

wyra

ż

enia (I.6):













>

−

<

=

,

1

log

20

log

20

1

log

20

)

(

T

dla

T

k

T

dla

k

M

ω

ω

ω

ω

(I.6)

bowiem

dla

małych

cz

ęstotliwości (wT<<1) wyrażenie

0

1

)

(

log

20

2

=

+

T

ω

.

Charakterystyka (I.6) nosi

nazw

ę logarytmicznej asymptotycznej charakterystyki

amplitudowej i składa si

ę z dwóch odcinków prostych. W tym przypadku największa różnica

pomi

ędzy charakterystyką logarytmiczną, a jej przybliżeniem występuje dla pulsacji

T

1

=

ω

i wynosi:

dB

T

T

k

k

3

2

log

20

)

1

)

1

(

log

20

log

20

(

log

20

2

=

=

+

−

−

.

(I.7)

II. Człon oscylacyjny

Transmitancja operatorowa przedstawia si

ę

nast

ę

puj

ą

co:

2

2

2

2

)

(

n

n

n

s

s

k

s

K

ω

ξω

ω

+

+

=

.

(II.1)

Transmitancja widmowa członu oscylacyjnego:

ω

ξω

ω

ω

ω

ω

n

n

n

j

k

j

K

2

)

(

2

2

2

+

−

=

.

(II.2)

Przedstawiona w postaci modułu i fazy:

)

2

(

2

2

2

2

2

2

2

)

2

(

)

(

)

(

ω

ω

ω

ξω

ω

ξω

ω

ω

ω

ω

−

−

+

−

=

n

n

arctg

j

n

n

n

e

k

j

K

.

(II.3)

Logarytmiczna charakterystyka amplitudy członu oscylacyjnego jest równa:

2

2

2

2

2

)

2

(

)

(

log

20

)

log(

20

log

20

(

log

20

)

(

ω

ξω

ω

ω

ω

ω

ω

n

n

n

k

j

K

M

+

−

−

+

=

=

.

(II.4)

Logarytmiczna charakterystyka fazy:

2

2

2

)

(

ω

ω

ξωω

ω

−

−

=

Φ

n

n

arctg

.

(II.5)

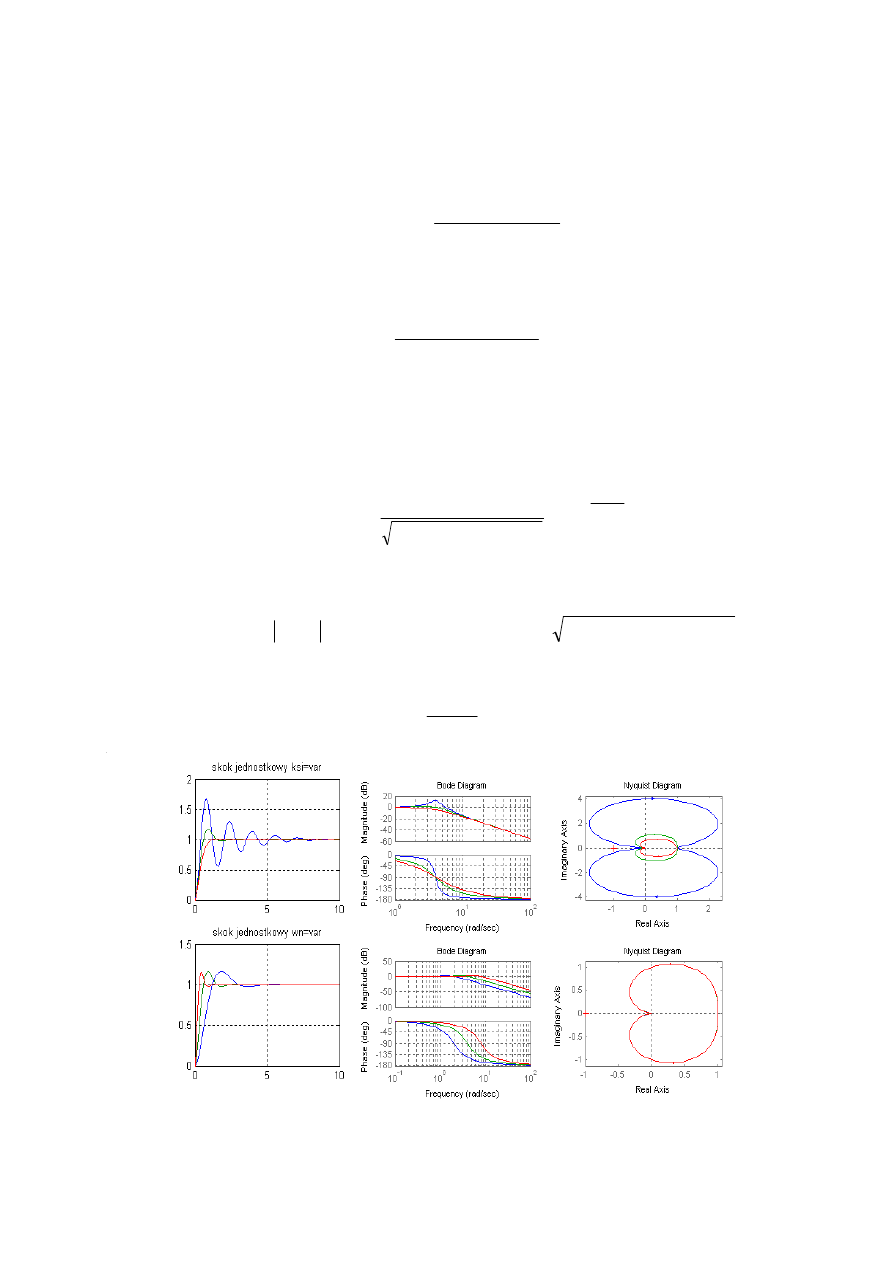
Rys. II.1. Charakterystyki amplitudowo-fazowe członu oscylacyjnego (Bode i Nyquista)

Na rys. II.1 przedstawiono charakterystyki wyznaczone dla: k=1, oraz

-

x

1=0,125;

x

2=0,5;

x

3=0,85 przy

w

n

=4

-

w

n1

=2,

w

n2

=4;

w

n3

=8 przy

x

=0,5.

Na podstawie analizy wzoru II.2 mo

ż

na okre

ś

li

ć

warunki potrzebne do wyznaczenia

parametrów

w

n

i

x

. Parametr

w

n

wyznaczamy z warunku arg{K(j

w

a

)=-

2

π

. Wtedy

w

n

=

w

a

.

Natomiast parametr

x

wyznaczamy dla warunku arg{K(j

w

b

)=-

4

π

. Wtedy

b

n

b

n

ω

ω

ω

ω

ξ

2

2

2

−

=

.

III. Człon ró

żniczkujący rzeczywisty

Transmitancja operatorowa rzeczywistego członu ró

ż

niczkuj

ą

cego:

1

)

(

+

=

Ts

ks

s

K

.

(III.1)

Transmitancja widmowa rzeczywistego członu ró

ż

niczkuj

ą

cego:

)

2

ctg

(

2

1

)

(

)

(

π

ω

ω

ω

ω

−

−

+

=

T

ar

j

e

T

k

j

K

.

(III.2)

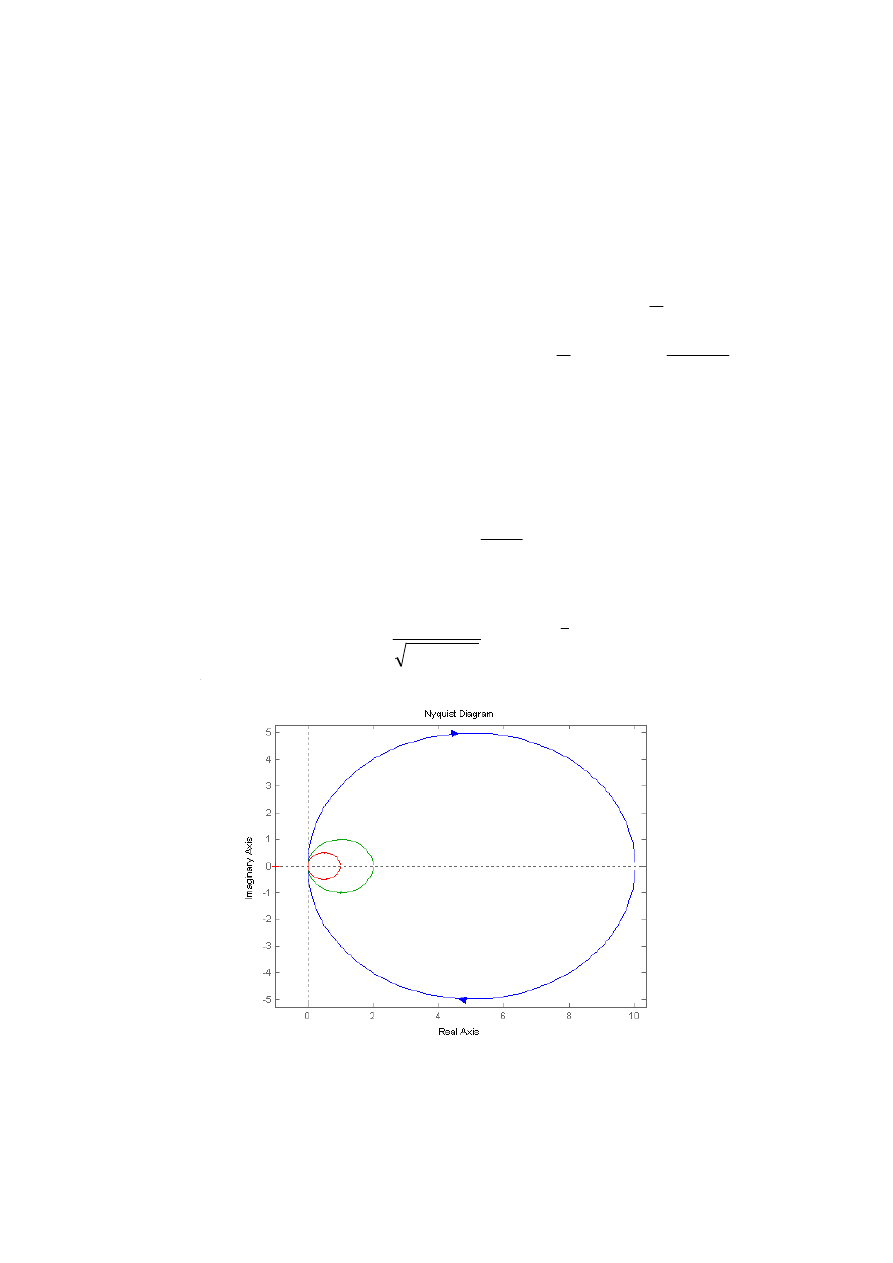
Rys. III.1. Charakterystyka amplitudowo-fazowa rzeczywistego członu ró

żniczkującego

Na rys. III.1 przedstawiono charakterystyki amplitudowo-fazowe członu ró

ż

niczkuj

ą

cego dla

trzech ró

ż

nych stałych czasowych: T1=0,1; T2=0,5; T3=1.

Logarytmiczna charakterystyka amplitudy rzeczywistego członu ró

ż

niczkuj

ą

cego jest równa:

1

)

(

log

20

log

20

log

20

(

log

20

)

(

2

+

−

+

=

=

ω

ω

ω

ω

T

k

j

K

M

.

(III.3)

Logarytmiczna charakterystyka fazy:

ω

π

ω

T

ar ctg

2

)

(

−

=

Φ

.

(III.4)

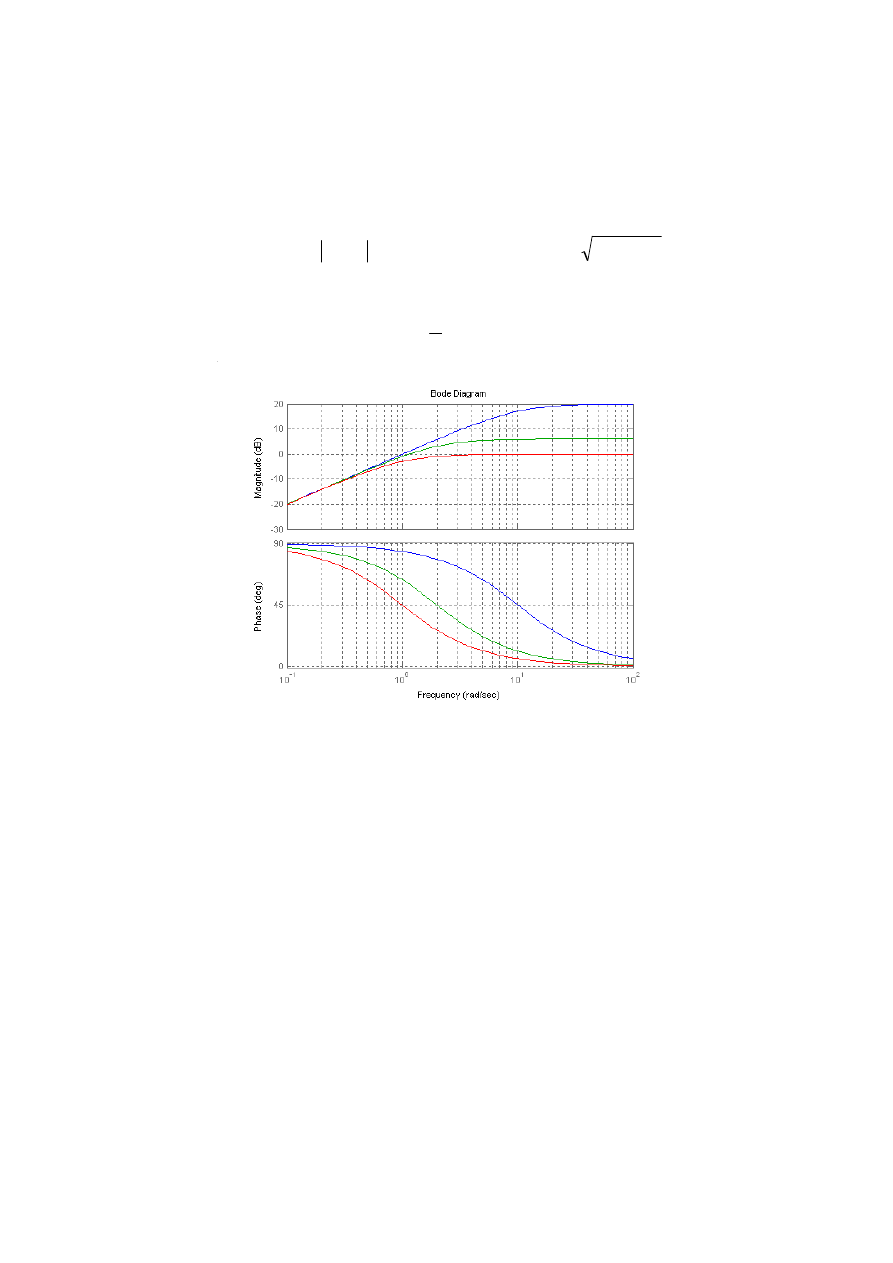
Rys. III.2. Charakterystyki logarytmiczne rzeczywistego członu ró

żniczkującego

Charakterystyki logarytmiczne amplitudy i fazy, wyznaczone dla: T1=0,1; T2=0,5; T3=1

przedstawiono na rys. III.2.