Dynamika Budowli

– laboratorium

Ćwiczenie 4

Magdalena Rucka

Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów

1

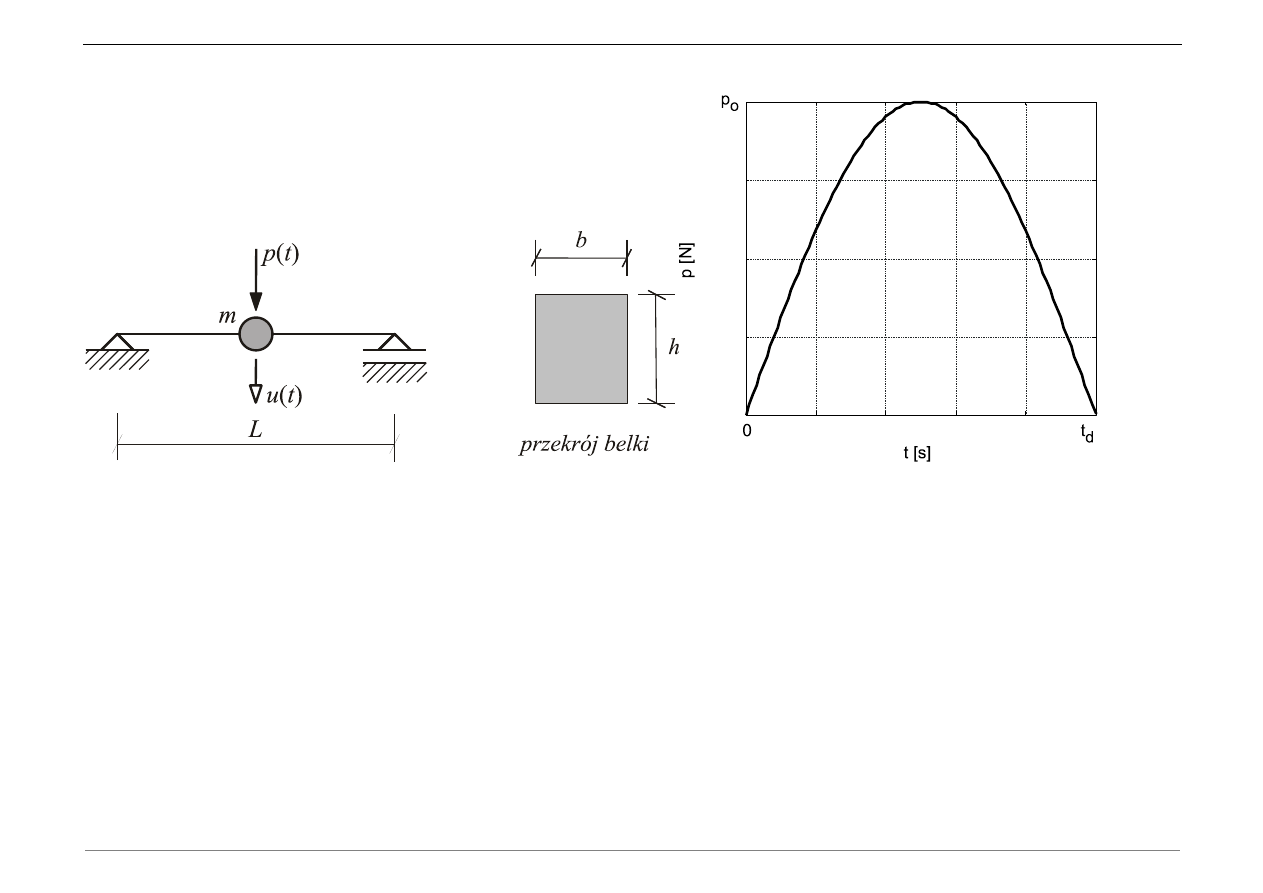
A. Obliczyć przemieszczenie u(t), prędkość v(t) i przyspieszenie a(t) układu o jednym
stopniu swobody obciążonego siłą p(t). Do całkowania równania ruchu w środowisku
MATLAB zastosować metodę różnic centralnych (funkcja mrc). Obliczyć krytyczny krok
całkowania. Dobrać krok całkowania.
Dane: E,



L, b, h,



, u

0

, v

0,

p

o,

t

d

Dynamika Budowli

– laboratorium

Ćwiczenie 4

Magdalena Rucka

Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów

2

Rozwiązanie:
a) Otworzyć nowy plik m-file, zadeklarować wszystkie dane materiałowe i geometryczne.

b=10/100;

% szerokosc [m]

h=20/100;

% wysokosc [m]

L=5;

% dlugosc [m]

E=200e+9;

% modul sprezystosci [Pa]

ro=7850;

% gestosc [kg/m3]

u0= 0 ;

% przemieszczenie poczatkowe [m]

v0= 0;

% predkosc poczatkowa [m/s]

ksi=0.03;

% liczba tłumienia

td=0.01

% czas trwania impulsu [s]

po=2000;

% amplituda impulsu [N]

b) Obliczyć moment bezwładności przekroju

x

I .

c) Obliczyć sztywność k układu wymodelowanego za pomocą jednego stopnia swobody.

d) Obliczyć masę m poprzez skupienie masy z ½ długości belki.

e) Obliczyć częstość kołową drgań własnych

n

k

m





.

f) Obliczyć tłumienie

kr

c

c





,

2

kr

n

c

m





.

Dynamika Budowli

– laboratorium

Ćwiczenie 4

Magdalena Rucka

Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów

3

g) Dobrać krok całkowania dt z warunku stabilności metody różnic centralnych

2

kr

n

dt

dt







.

dt_mrc=2/(wn)

Dla powyższych danych

dt_mrc = 0.0175

. Przyjęto krok czasowy jako:

dt=0.001

h) Utworzyć wektor czasu

t=[0:dt:tk]
Czas końcowy tk dobrać tak, by zaobserwować przejście układu do spoczynku
(ewentualnie skorygować go po przeprowadzeniu pierwszej próby całkowania).
Aby określić długość wektora czasu t użyć funkcji length
nt = length(t)

i) Utworzyć wektor obciążenia p(t) na podstawie zadanego wykresu. Uwaga: wektor

obciążenia musi mieć taką samą długość jak wektor czasu.

j) Wykonać numeryczne całkowanie równania ruchu.
Do całkowania w programie MATLAB zastosować funkcję mrc. Funkcja mrc wykonuje
całkowanie równania ruchu metodą różnic centralnych. W wyniku całkowania otrzymuje
się wektor przemieszczenia, prędkości i przyspieszenia.
Uwaga: funkcję mrc ściągnąć na dysk i umieścić w katalogu bieżącym. W niniejszym
przykładzie liczba stopni swobody wynosi n = 1.

Dynamika Budowli

– laboratorium

Ćwiczenie 4

Magdalena Rucka

Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów

4

[u,v,a]=mrc(m,c,k,p,t,u0,v0);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% funkcja calkowania rownan ruchu metoda roznic centralnych
% [u,v,a]=mrc(M,C,K,P,t,u0,v0)
%---------------------------------------------------------

% WEJSCIE:

% M - macierz mas (n x n)

% C - macierz tlumienia (n x n)

% K - macierz sztywnosci (n x n)

% P - wektor obciazen zewnetrznych (n x nt)

% t - wektor czasu (1 x nt)

% u0 - wektor przemieszczen poczatkowych (1 x n)

% v0 - wektor predkosci poczatkowych (1 x n)

%----------------------------------------------------------

% WYJSCIE:

% u - wektor przemieszczen (n x nt)

% v - wektor predkosci (n x nt)

% a - wektor przyspieszen (n x nt)

%----------------------------------------------------------

Dynamika Budowli

– laboratorium

Ćwiczenie 4

Magdalena Rucka

Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów

5

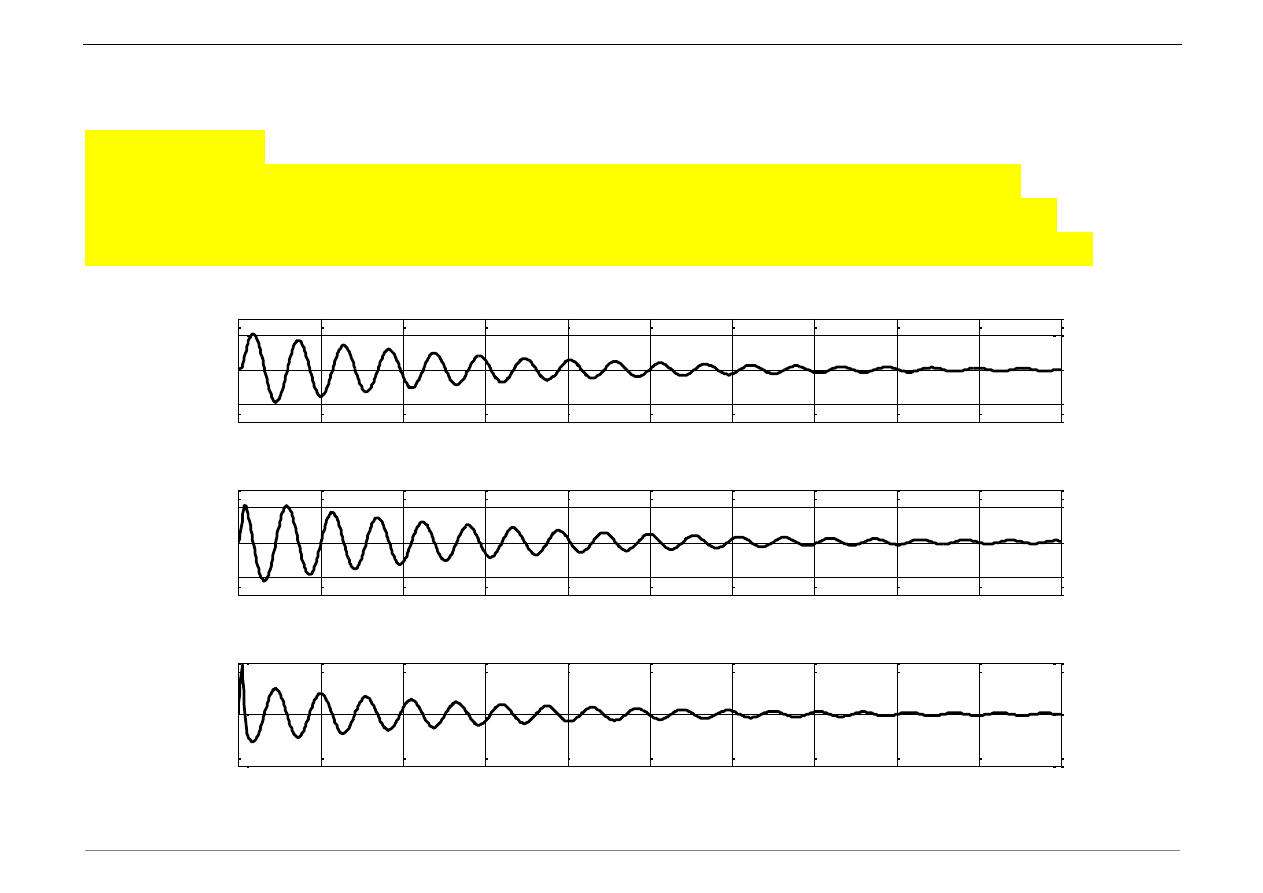
k) Wykreślić przebieg przemieszczenia, prędkości i przyspieszenia w czasie, opisać osie

wykresów

figure(1);
subplot(311); plot(t,u); xlabel(

't'

);ylabel(

'u [m]'

)

subplot(312); plot(t,v); xlabel(

't'

);ylabel(

'v [m/s]'

)

subplot(313); plot(t,a); xlabel(

't'

);ylabel(

'a [m/s^2]'

)

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-2

0

2

x 10

-4

t [s]

u

[

m

]

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-0.02

0

0.02

t

v

[

m

/s

]

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-5

0

5

t [s]

a

[

m

/s

2

]

Dynamika Budowli

– laboratorium

Ćwiczenie 4

Magdalena Rucka

Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów

6

B. Obliczyć przemieszczenie u(t) stosując przybliżone rozwiązanie dla „impulsu
krótkiego”.
Rozwiązanie:

a) Obliczyć wartość impulsu:

J=0.5*td*po;

b) Sprawdzić, czy impuls spełnia warunek krótkiego impulsu

/

0.5

d

n

t

T



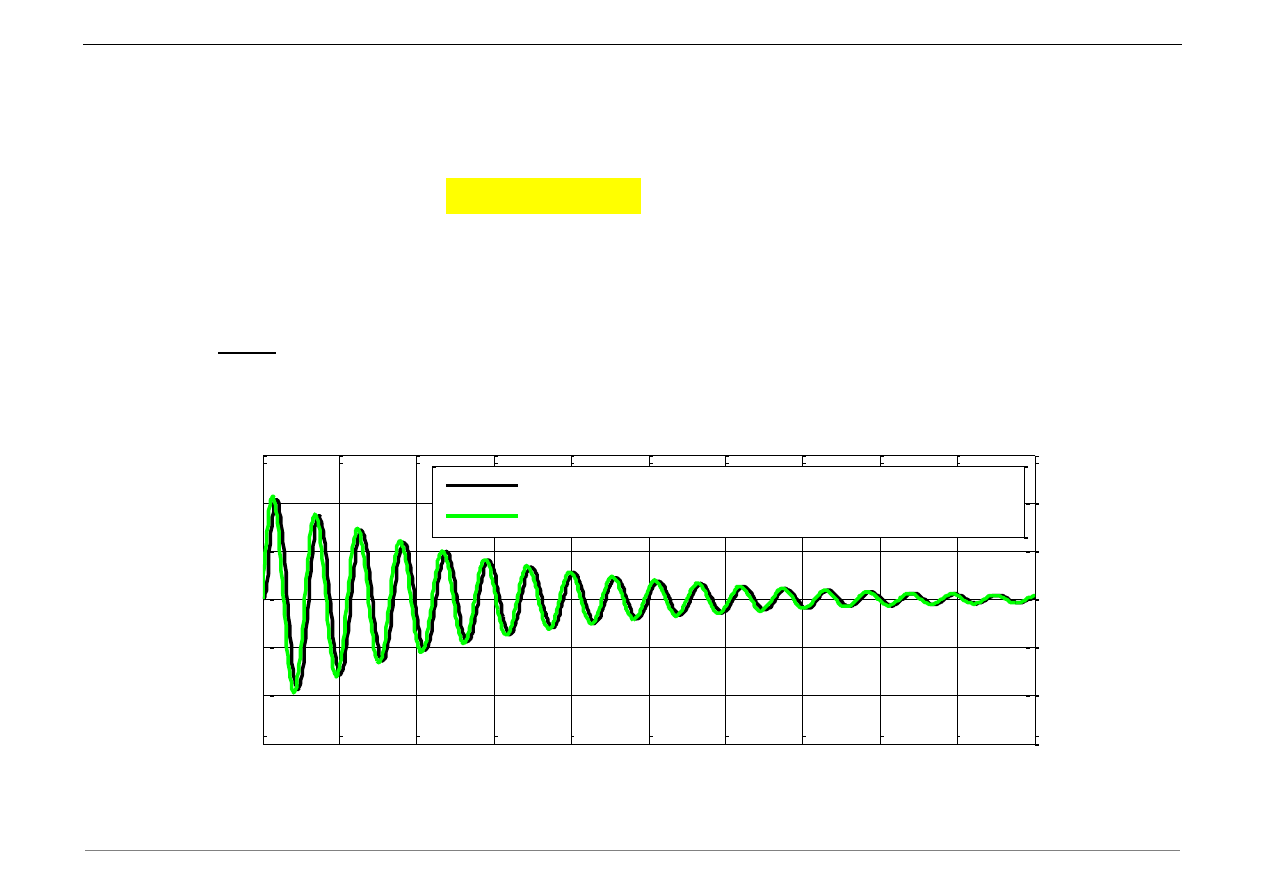
c) Obliczyć przemieszczenie układu

1

( )

sin(

)

n

t

d

d

u t

J

t e

m











0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-2

-1

0

1

2

x 10

-4

t [s]

u

[

m

]

metoda różnic centralnych
rozwiązanie przybliżone dla impulsu "krótkiego"

Dynamika Budowli

– laboratorium

Ćwiczenie 4

Magdalena Rucka

Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów

7

Zadanie do samodzielnego rozwiązania:

Wykonać obliczenia dla różnych wartości t

d

:

t

d

= 0.001 s; t

d

= 0.01 s; t

d

= 0.05 s; t

d

= 0.1 s.

Porównać wyniki u(t) dla różnych szerokości impulsu.

Porównać wyniki u(t) dla rozwiązania metodą różnic centralnych oraz przybliżonego
rozwiązania dla „impulsu krótkiego”.