Politechnika Krakowska im. Tadeusza Kościuszki Katedra Automatyki
i Technik Informacyjnych (E-3)
Automatyka
Laboratorium
– Badanie stabilności liniowego układu 3 rzędu z opóźnieniem. Wpływ
opóźnienia na stabilność – symulacja komputerowa –
1. Cel ćwiczenia
Celem ćwiczenia jest sprawdzenie czy zdefiniowany przez prowadzącego liniowy układ
dynamiczny jest stabilny, stosując kryterium Hurvitza oraz zamodelowanie wyżej wymienionego
układu w środowisku ‘Simulink’. Przy pomocy programu, lub obliczeń należy sprawdzić wpływ
parametrów układu na stabilność.
2. Opis teoretyczny zagadnienia stabilności liniowych układów
2.1. Stabilność układu automatycznej regulacji
Stabilność układu automatycznej regulacji jest to właściwość układu polegająca na powrocie
do stanu równowagi po ustaniu wymuszenia, które wytrąciło układ z tego stanu, lub osiągnięciu
nowego stanu równowagi, jeśli wymuszenie pozostało na stałym poziomie. Jest to jedno
z najważniejszych zagadnień w automatyce, ma też fundamentalne znaczenie w teorii sterowania.
Stabilność jest zatem podstawową własnością jaką powinien spełniać każdy system
automatycznej regulacji. Intuicyjnie pojęcie stabilności mówi, że gdy podamy na wejście systemu
dowolny sygnał ograniczony, wówczas na jego wyjściu y(t) otrzymamy również sygnał ograniczony
(definicja według Laplace’a).
Układ zamknięty liniowy i stacjonarny opisany równaniem (1) jest stabilny, jeżeli dla skończonej
wartości zakłócenia przy dowolnych wartościach początkowych jego odpowiedź ustalona przyjmuje
skończone wartości.
𝑎
𝑛
𝑑
𝑛
𝑥(𝑡)
𝑑𝑡
𝑛
+ 𝑎
𝑛−1
𝑑
𝑛−1
𝑥(𝑡)
𝑑𝑡
𝑛−1
+ ⋯ + 𝑎
0
𝑥(𝑡) = 𝑏
𝑚
𝑑
𝑚
𝑢(𝑡)
𝑑𝑡
𝑚
+ 𝑏
𝑚−1
𝑑
𝑚−1
𝑢(𝑡)
𝑑𝑡
𝑚−1
+ ⋯ + 𝑏
0
𝑢(𝑡)
(1)
Transmitancja operatorowa tego układu ma postać:
𝐺(𝑠) =
𝑏
𝑚
𝑠
𝑚
+ 𝑏
𝑚−1
𝑠
𝑚−1
+ ⋯ + 𝑏
1
𝑠 + 𝑏
0
𝑎
𝑛
𝑠
𝑛
+ 𝑎
𝑛−1
𝑠
𝑛−1
+ ⋯ + 𝑎
1
𝑠 + 𝑎
0
=
𝐿(𝑠)
𝑀(𝑠)
(2)
Stąd jego równanie charakterystyczne:
Automatyka
mgr inż. P. Pytlik, KAiTI (E-3)
2
𝑀(𝑠) = 𝑎
𝑛
𝑠
𝑛
+ 𝑎
𝑛−1
𝑠
𝑛−1
+ ⋯ + 𝑎
1
𝑠 + 𝑎
0
= 0
(3)
Gdzie: a
i
– rzeczywiste współczynniki równania charakterystycznego
W ujęciu matematycznym warunkiem koniecznym i dostatecznym na to, ażeby układ
zamknięty był stabilny jest, aby wszystkie pierwiastki równania charakterystycznego układu
zamkniętego miały ujemne części rzeczywiste, czyli powinny znajdować się w lewej półpłaszczyźnie
płaszczyzny zmiennej zespolonej s. Rozwiązanie tego równania wystarczy, więc dla stwierdzenia czy
dany układ liniowy jest stabilny. Jednak w praktyce ta metoda nie zawsze jest dogodna i wystarczająca.
Z tego względu zostały opracowane metody pozwalające na badanie stabilności bez rozwiązywania
równania charakterystycznego są to tzw. kryteria stabilności. Kryteria te dzielą się na: algebraiczne do,
których należą kryteria Routha i Hurwitza oraz częstotliwościowe Michajłowa i Nyquista.
Pierwiastki równania charakterystycznego mogą być wyrażone jako
𝑠
𝑖
= 𝜎
𝑖
± 𝑗𝜔
𝑖
, 𝑖 = 1,2, … , 𝑛
(4)
Gdzie: 𝜎
𝑖
= 𝑅𝑒(𝑠
𝑖
)
Warunki stabilności:
Re(s
i
)<0 dla i=1,2,3,4... – układ stabilny asymptotycznie
Re(s
i
)=0 dla dowolnego (jednego) i , pozostałe Re(si)<0 – układ na granicy stabilności
Re(s
i
)>0 dla dowolnego (dwóch lub więcej) i – układ niestabilny
Powyższa metoda nazywana jest często „Metodą biegunów”. Wymaga obliczenia pierwiastków
równania charakterystycznego , stąd pojawiły się jej odpowiedniki (wymagające mniej obliczeń
arytmetycznych).
2.2. Transmitancja zastępcza układu regulacji
Rzeczywiste systemy często składają się z mniejszych, połączonych i przez to współzależnych,
prostych obiektów. Dlatego istotna jest ich reprezentacja za pomocą modeli odzwierciedlających
rzeczywiste struktury połączeń. Pojedyncze układy dynamiczne mogą tworzyć struktury o różnym
stopniu złożoności. Najbardziej powszechne są połączenia szeregowe, równoległe, szeregowo-
równoległe i ze sprzężeniem zwrotnym, mające podstawowe znaczenie przy tworzeniu bardziej
złożonych struktur systemów. Stąd wywodzi się, fundamentalny w automatyce, złożony system
dynamiczny zwany Układem Automatycznej Regulacji (UAR). Jest on złożona struktura szeregowa
(najczęściej składająca się z dwóch pojedynczych układów), zawierająca dodatkowo pętlę ujemnego
sprzężenia zwrotnego.
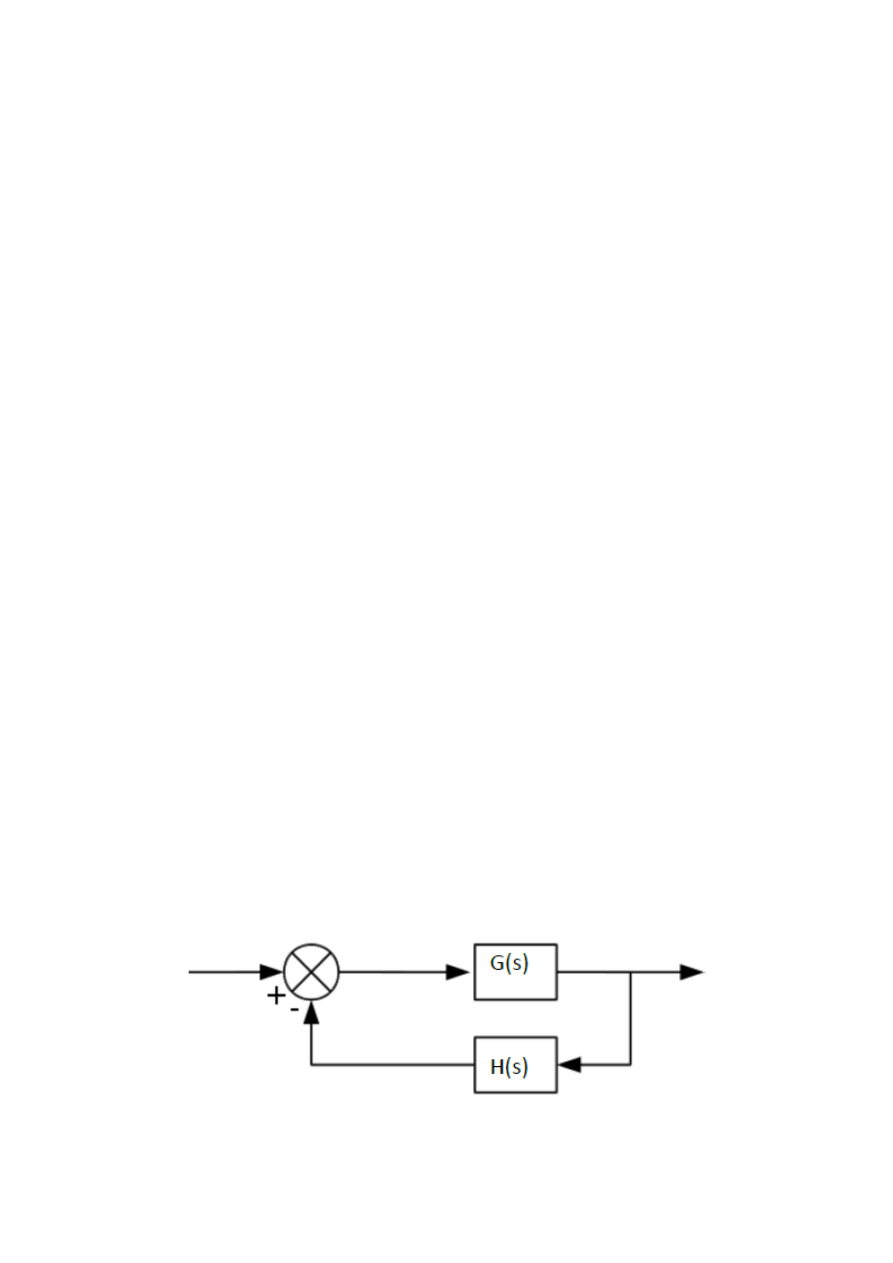
Wyznaczanie transmitancji zastępczej G
z
zamkniętego układu regulacji
Rysunek 1 Schemat blokowy zamkniętego układu regulacji (ze sprzężeniem zwrotnym)
Automatyka
mgr inż. P. Pytlik, KAiTI (E-3)
3
𝐺
𝑧
(𝑠) =
𝐺(𝑠)
1 + 𝐻(𝑠)𝐺(𝑠)
(5)
Gdzie: G(s) – transmitancja toru głównego, H(s) – transmitancja toru sprzężenia zwrotnego
Wyznaczanie transmitancji zastępczej połączenia szeregowego i równoległego
transmitancji.
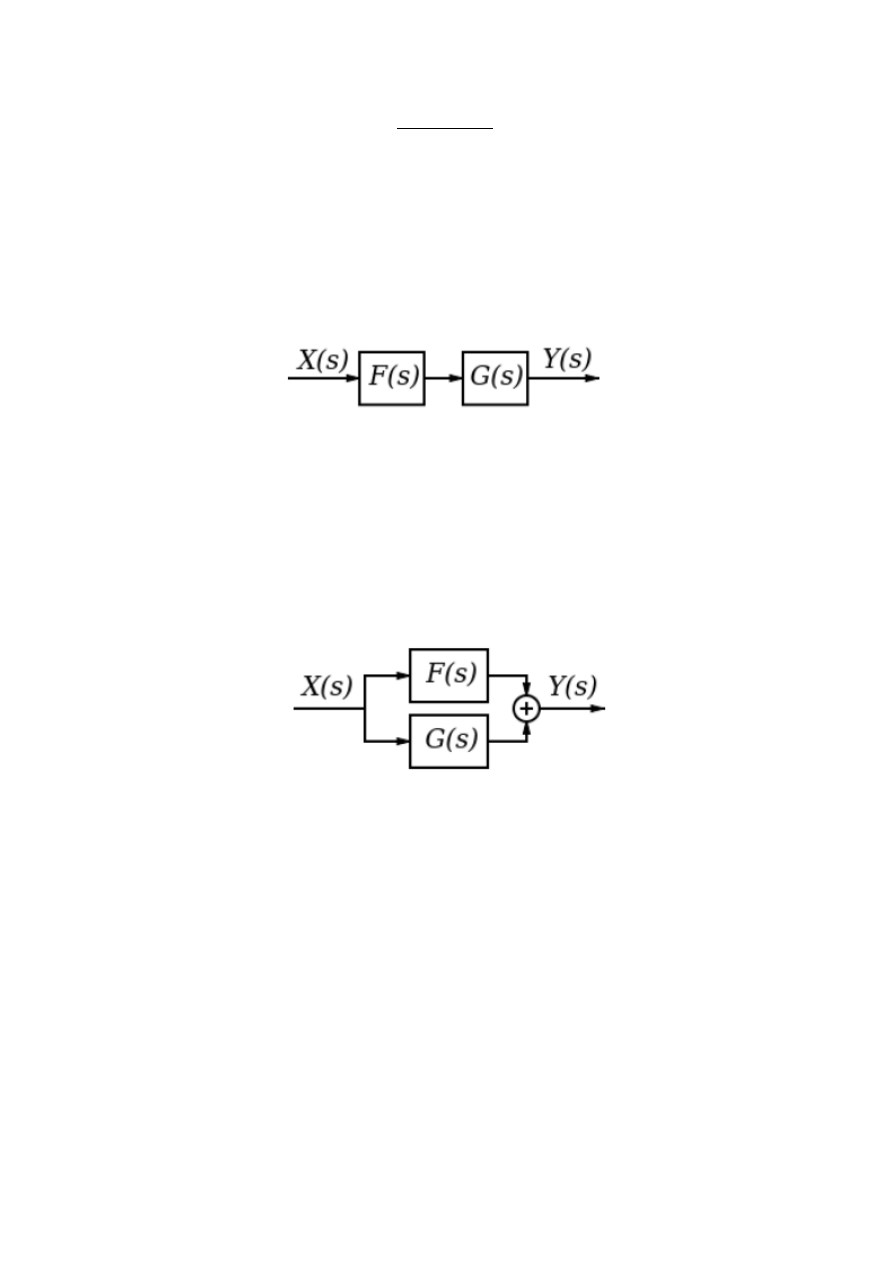
Gdy dwa lub więcej członów zostanie połączone szeregowo, mogą one być wówczas zastąpione
jednym, reprezentującym je członem (układem), którego transmitancją zastępczą będzie iloczyn
transmitancji poszczególnych członów składowych.
Rysunek 2 Szeregowe połączenie transmitancji
𝐺
𝑧
(𝑠) = 𝐹(𝑠)𝐺(𝑠)
(6)
Członów (określonych przez bloki) nie można zestawić równolegle bez użycia sumatora. Człony
połączone sumatorem pokazane powyżej mają całkowitą transmitancję zastępczą będącą sumą
transmitancji poszczególnych członów składowych.
Rysunek 3 Równoległe połączenie transmitancji
𝐺
𝑧
(𝑠) = 𝐹(𝑠) + 𝐺(𝑠)
(7)
2.3. Kryterium stabilności Hutvitza
Kryterium stabilności Hurwitza jest metodą pozwalającą określić stabilność zamkniętego układu
regulacji na podstawie równania charakterystycznego (3) układu.
Z punktu widzenia algebry kryterium Hurwitza pozwala sprawdzić, czy wszystkie pierwiastki równania
charakterystycznego leżą w lewej półpłaszczyźnie zmiennej zespolonej , co pociąga za sobą stabilność
układu. Na potrzeby kryterium wykorzystujemy ciąg wyznaczników, utworzonych ze współczynników
równania charakterystycznego:
Automatyka
mgr inż. P. Pytlik, KAiTI (E-3)
4
Aby układ regulacji był asymptotycznie stabilny muszą zostać spełnione następujące warunki:
1. Wszystkie współczynniki wielomianu charakterystycznego a
i
dla i=0,1,2,…n istnieją i są tego
samego znaku.
2. Wszystkie wyznaczniki Δ
1
, Δ
2
, … , Δ
𝑛
są dodatnie
W przeciwnym razie układ jest niestabilny. Jeśli jednak któryś z podwyznaczników jest równy zeru,
a pozostałe warunki są spełnione, to oznacza, że równanie charakterystyczne układu ma między innymi
pierwiastki urojone i wtedy układ znajduje się na granicy stabilności.
Przykład
Za pomocą kryterium Hurwitza zbadać stabilność układu zamkniętego, którego równanie
charakterystyczne ma postać:
𝑀(𝑠) = 𝑠
5
+ 6𝑠
4
+ 4𝑠
3
+ 7𝑠
2
+ 11𝑠 + 2 = 0
Zauważmy, że spełniony jest warunek konieczny stabilności, ponieważ wszystkie współczynniki
równania charakterystycznego są dodatnie.
Wyznacznik Hurwitza utworzony ze współczynników wielomianu tego równania ma postać:
Obliczamy wartość wyznacznika za pomocą polecenia det(macierz), które wprowadzamy w oknie
poleceń MATLAB-a według poniższej składni. Argumentem polecenia det zapisanym w nawiasach
okrągłych jest macierz współczynników wyznacznika Hurwitza, która z kolei zapisana jest w nawiasach
Automatyka
mgr inż. P. Pytlik, KAiTI (E-3)
5
kwadratowych. Poszczególne elementy wierszy tej macierzy oddzielone są odstępami, natomiast
wiersze – oddzielone są średnikami.
» delta_5=det([6 7 2 0 0;1 4 11 0 0;0 6 7 2 0;0 1 4 11 0;0 0 6 7 2]),
delta_5 = -5846
Wniosek:
Ujemna wartość wyznacznika Hurwitza wskazuje na to, że badany układ jest niestabilny.
3. Instrukcja wykonania ćwiczenia
Dany jest układ dynamiczny zamknięty.
a) Za pomocą kryterium Hurwitza należy zbadać stabilność układu przedstawionego na zajęciach.
Proponowanym sposobem, jest wykonanie obliczeń w programie Matlab, lub ręcznie. Należy
wykreślić na płaszczyźnie zmiennej zespolonej wszystkie bieguny układu zamkniętego. Oprócz
tego należy pokazać jego zachowanie i zapas bezpieczeństwa przy zmianie parametrów układu.
Które parametry mają krytyczny wpływ na stabilność układu, a które znikomy?
Parametry układu należy dobrać samodzielnie tak, aby uzyskać układ stabilny/na granicy
stabilności, niestabilny.
b) W środowisku Simulink należy zbudować model układu dynamicznego przedstawionego przez
prowadzącego ćwiczenie. Rezultatem tej części ćwiczenia powinny być przebiegi wielkości
wyjściowej układu y(t) w dziedzinie czasu. Należy wykreślić odpowiedź stabilnego/na granicy
stabilności i niestabilnego.
4. Sprawozdanie
Forma sprawozdania oraz aspekty, które powinny zostać w nim wymienione, obliczone i opisane
przedstawione zostały poniżej.
1. Wstęp
Czym jest stabilność układów dynamicznych, podział kryteriów badania stabilności, jak
określić stabilność, itp.
2. Przebieg ćwiczenia
Jaki był przebieg ćwiczenia (własnymi słowami)
Co należało wyznaczyć i w jaki sposób
Schemat układu podany przez prowadzącego ćwiczenie
3. Opracowanie ćwiczenia
Schemat symulacyjny z programu Simulink
Kod źródłowy (m-plik)
Dobranie parametrów układu tak, aby uzyskać:
o Układ stabilny.
o Układ niestabilny.
o Układ na granicy stabilności.
Do każdego przypadku wymienionego powyżej należy zamieścić:
o Wartości parametrów dla jakich uzyskano pożądany stan.
Automatyka
mgr inż. P. Pytlik, KAiTI (E-3)
6
o Wykres biegunów transmitancji.
o Odpowiedź układu z ‘Simulink’a’.
o Uzasadnienie dlaczego układ dla tych parametrów uważany jest za stabilny.
4. Wnioski
Ogólne wnioski i obserwacje z wykonanego ćwiczenia
Które parametry układu mają największy wpływ na stabilność, a które znikomy.