
Egzamin dla Aktuariuszy z 15 grudnia 2008 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
(
)
[
]
[
]
=
=
+
+
+
+
=
=
+
+
+
9
2
9
3
2
1
2
4
4
3
2
3
3
2
1
2
4
3
X
X
X
X
X
X
X
E
X
X
X
X
X
E
(
)
(
)
( )
2
4
3
2
1
3
4
3
2
1
2
3
9
2
9
X
E
X
X
X
X
E
EX
X
X
X
X
E
+
=
+
+
+
=
+
+
=
(
) (
)
4
3
2
1
3
3
2
1
4
3
9
9
EX
X
X
X
X
E
X
X
X
X
X
E
+
=
+
+
=
=
+
+
+
dla
)
9
,...,
0
(
∈
i
(
)
(
)
(
)
≅
=
+
+
−
=
+
=
=
=
+
+
=
3
1
;
9
9
9
,
9
3
2
1
2
1
3
3
2
1
3
Bernoulli
X
X
X
P
i
X
X
i
X
P
X
X
X
i
X
P
czyli:
(
)
[
]
181
10
10
3
1
9
10
2
3
1
9
3
2
3
1
9
9
2
2
3
2
1
2
4
3
=
+
+
⋅
⋅
⋅
+
⋅
+
⋅
⋅
=
=
+
+
+
X
X
X
X
X
E
(
)
13
10
3
9
3
2
1
4
3
=
+
=
=
+
+
+
X
X
X
X
X
E
12
)
13
(
181
2
=
−
=
ODP
Zadanie 2
0<X+Y<2
X-Y<0
Sprawdzamy (B)
[
]
(
)
∫ ∫
∫
∫
=
−
=
−
=
=
−
−
−
−
−
−
1
0 0
1
0
1
0
5
,
0
5
,
0
0
5
,
0
5
,
0
5
,
0
5
,
0
2
2
25
,
0
2
25
,
0
25
,
0
x
x
x
x
y
x
x
y
e
e
e
e
dydx
e
e
P
[
]
(
)
1
1
1
0
5
,
0
5
,
0
5
,
0
2
2
5
,
0
5
,
0
2
5
,
0
−
−
−
−
=
−
−
=
−
−
=
e
e
e
x
czyli odpowiedź (B) jest prawidłowa
Zadanie 3
(
)
(
)
1
,
1
1
,
1
,
1
3
2
3
2
1
≠
≠
≠
≠
=
=
X
X
P
X
X
X
P
P
(
)
(
)
=
=
=
≠
≠
=
1
1
1
,
1
1
1
3
2
X
P
X
X
X
P
LICZ
(
)
(
)
[
]
12
1
9
2
8
3
9
1
9
1
8
3
9
4
4
1
9
2
2
1
8
3
....
1
1
1
4
3
2
1
0
0
1
=
⋅
=
+
=
⋅
+
⋅
=
+
=
=
=
⋅
=
X
P
X
X
P
(
)
(
)
(
)
(
)
(
)
∑
=
=
=
+
=
+
=
⋅
=
=
=
≠
≠
=
3
1
1
1
1
1
1
3
2
3
4
3
2
4
3
1
4
3
2
1
1
,
1
i
X
P
X
P
X
P
i
X
P
i
X
X
X
P
MIAN
3
2
12
8
12
3
4
1
4
1
3
1
12
1
3
1
4
3
9
4
4
3
9
2
8
3
9
4
4
3
4
3
3
1
9
2
2
1
4
3
9
4
4
1
9
2
2
1
8
3
=
=
+
+
=
+
+
=
+
+
=
⋅
⋅
+
+
⋅
+
⋅
+
⋅
=
8
1
2
3
12
1
=
⋅
=
ODP
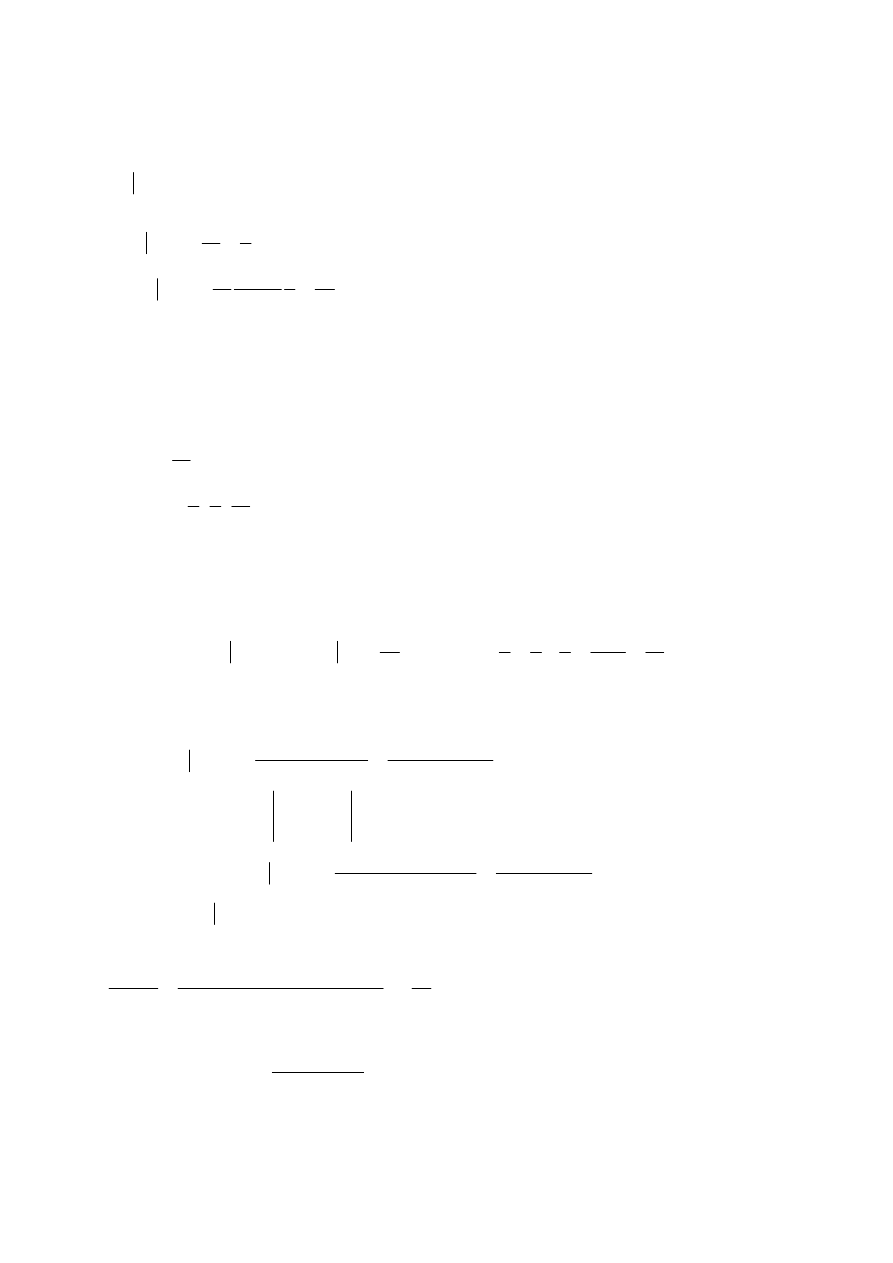
Zadanie 4
B – liczba białych pozostałych po I losowaniu
( )
≅
B
S
2
ma rozkład hipergeometryczny
N=10, M=B, n=5
( )
B
B
B
S
E
2
1
10
5
2
=
⋅
=
( )
(
)
B
B
B
B
B
S
−
=
−
⋅
=
10
36
1
9
5
10
10
10
5
var
2
rozkład B:
X - liczba wylosowanych białych
X=8-B
B=8-X
N=16, n=6, M=8
3
16
8
6
=
⋅
=
EX
1
15
10
2
1
2
1
6
var
=
⋅
⋅
⋅
=
X
10
9
1
2
=
+
=
EX
5
3
8
)
8
(
=
−
=
−
=
X
E
EB
(
)
26
10
3
16
64
16
64
)
8
(
2
2
2
=
+
⋅
−
=
+
−
=
−
=
X
X
E
X
E
EB
1
5
26
var
2
=
−
=
B
( )
(
)
( )
(
)
(
)
12
11
12
3
8
4
1
3
2
4
1
26
5
10
36
1
var
var
2
2
=
+
=
+
=
+
−
⋅
=
+
=
B
S
E
B
S
E
ODP
Zadanie 5
(
)
(
)
)
1
(
1
)
1
(
)
1
(
)
1
(
1
1
1
1
F
F
t
F
X
P
t
X
P
X
t
X
P
−
−
+
=
>
+
<
<
=
>
<
−
∫
∫
−
−
−
−
=
=
=
=
=
=
t
t
t
w
x
X
e
dw
e
dw
xdx
w
x
dx
xe
t
F
0
0
2
2
2
2
1
2
2
)
(
θ
θ
θ
θ
θ
(
)
(
)
t
t
t
t
e
e
e
e
e
e
e
X
t
X
P
t
Y
P
2
)
1
(
)
1
(
2
2
2
1
1
1
1
1
1
1
)
(
+
−
−
+
−
−
−
−
+
−
−
=
−
=
+
−
+
−
−
=
>
<
−
=
<
θ
θ
θ
θ
θ
θ
θ
(
)
(
)
[
]
(
)
t
t
t
t
e
t
t
e
x
x
f
y
f
2
2
2
2
)
1
(
2
2
2
1
1
)
(
+
−
+
−
+
=
−
−
−
=
>
−
=
θ
θ
θ
θ
θ
(
)
(
)
(
)
(
)
(
)
(
)
∑
=
∑
+
∑
+
=
=
=
=
+
−
−
=
+
−
=
+
−
∏
∏
10
1
2
1
2
10
1
2
1
10
1
2
2
1
2
2
10
1
2
10
1
2
10
1
10
10
1
2
10
2
10
1
2
1
2
)
(
)
(
i
i
i
i
i
i
i
i
i
y
y
i
y
y
i
i
y
y
i
e
e
y
e
y
x
p
x
p
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
dla
(
)
(
)
)
(
2
1
)
(
dla
i
10
1
2
1
2
x
T
L
y
y
x
T
i
i
i
∑
=
+
=
>
θ
θ
jest funkcją niemalejącą
czyli
(
)
05
,
0
)
(
3
=
>
=
c
x
T
P
θ
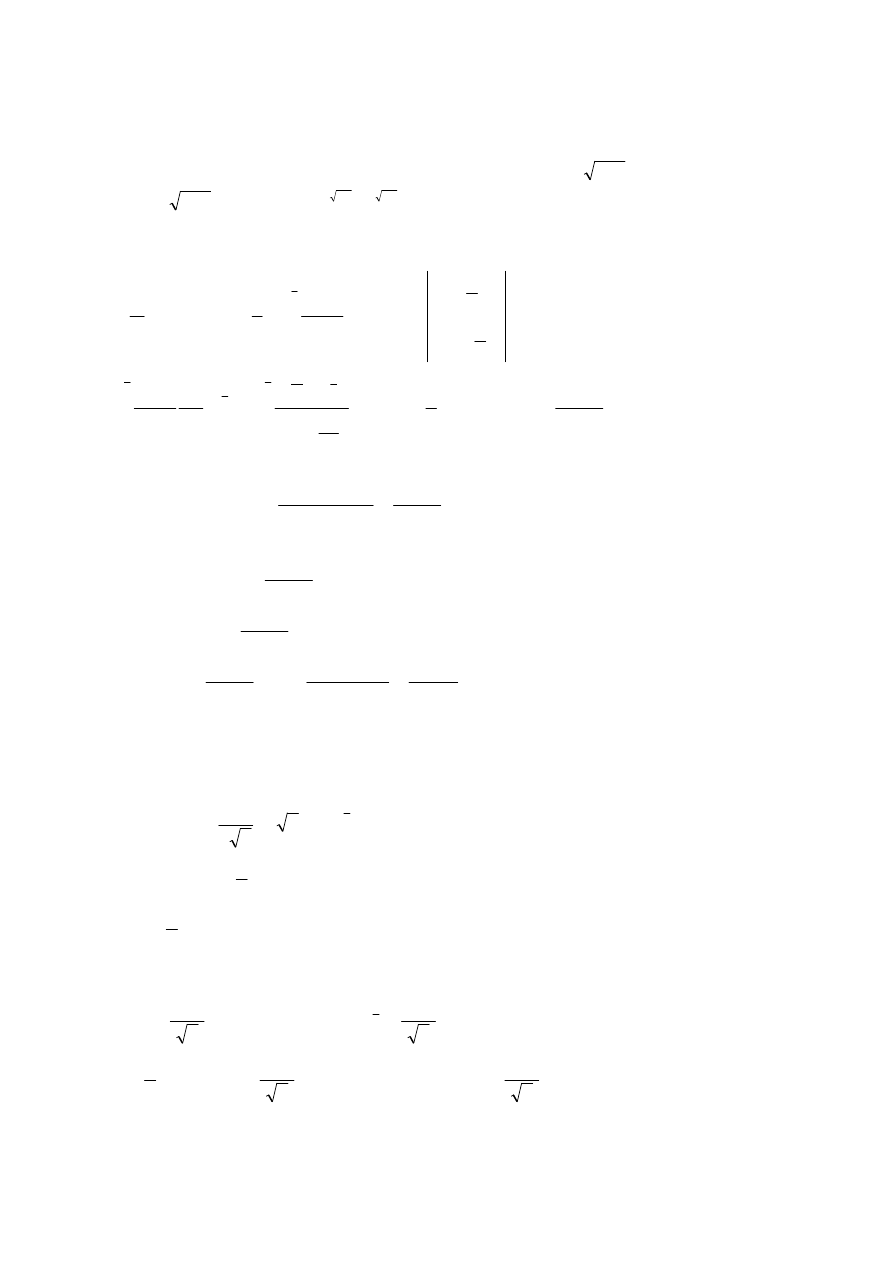
przy
:
3
=
θ
(
)
y
y
e
y
y
f
2
3
2
)
1
(
6
)
(
+
−
+
=
(
) (
) (
)
(
)
=
+
<
+
=
+
<
+
=
<
−
+
=
<
+
1
1
1
)
1
(
1
)
1
(
2
2
2
2
t
y
P
t
y
P
t
y
P
t
y
y
P
(
)
(
)
)
3
(
1
1
1
1
3
2
1
2
1
1
2
1
3
wykl
e
e
t
y
P
t
t
t
t
≅
−
=
−
=
−
+
<
=
−
−
+
+
+
+
−
+
−
(
)
∑
=
≅
Γ
≅
+
10
1
2
)
3
,
10
(
2
i
i
i
Z
y
y
∫
=
=
=
=
Γ
=
<
=
>
−
c
x
dt
dx
t
x
dx
e
x
c
Z
P
c
Z
P
1
0
3
9
10
2
1
3
2
3
)
10
(
3
1
1
∫
∫
=
→
=
→
=
Γ
=
Γ
=
≅
−
−
−
c
c
t
t
c
c
e
t
dt
e
t
6
0
6
0
)
20
(
10
2
1
2
20
2
10
9
10
851
,
10
6
851
,
10
6
05
,
0
2
20
2
6
)
10
(
3
2
43
42
1
χ
czyli odrzucamy, gdy:
(
)
851
,
10
6
2
1
10
1
2
>
+
∑
=
i
i
i
y
y
czyli:
(
)
∑
=
<
+
10
1
2
6
851
,
10
2
i
i
i
y
y
(
)
∑
=
<
−
+
10
1
2
6
851
,
10
10
1
i
i
y
(
)
∑
=
=
=
+
=
+
<
+
10
1
2
8085
,
11
6
851
,
70
6
60
851
,
10
10
6
851
,
10
1
i
i
Y
Zadanie 6
(
)
0
;
∞
−
∈
t
(
)
[ ]
∫
=
=
=
<
t
t
e
t
e
e
x
x
t
X
P
0
2
1
0
2
1
ln
Y
n
X
i
≅
Γ
≅
−
∑
2
1
;
ln
∑
=
i
n
X
n
U
ln
1
ln
sprawdzamy (B)
(
)
=
+
≤
⋅⋅
⋅
=
+
≤
−
−
−
−
2
2
1
1
2
2
4
4
e
n
e
X
X
P
e
n
e
U
P
n
n
n
=
+
>
=
+
>
=
∑
∑
−
−
−
−
2
2
2
2
4
ln
ln
4
ln
ln
1
e
n
e
n
X
P
e
n
e
X
n
P
i
i
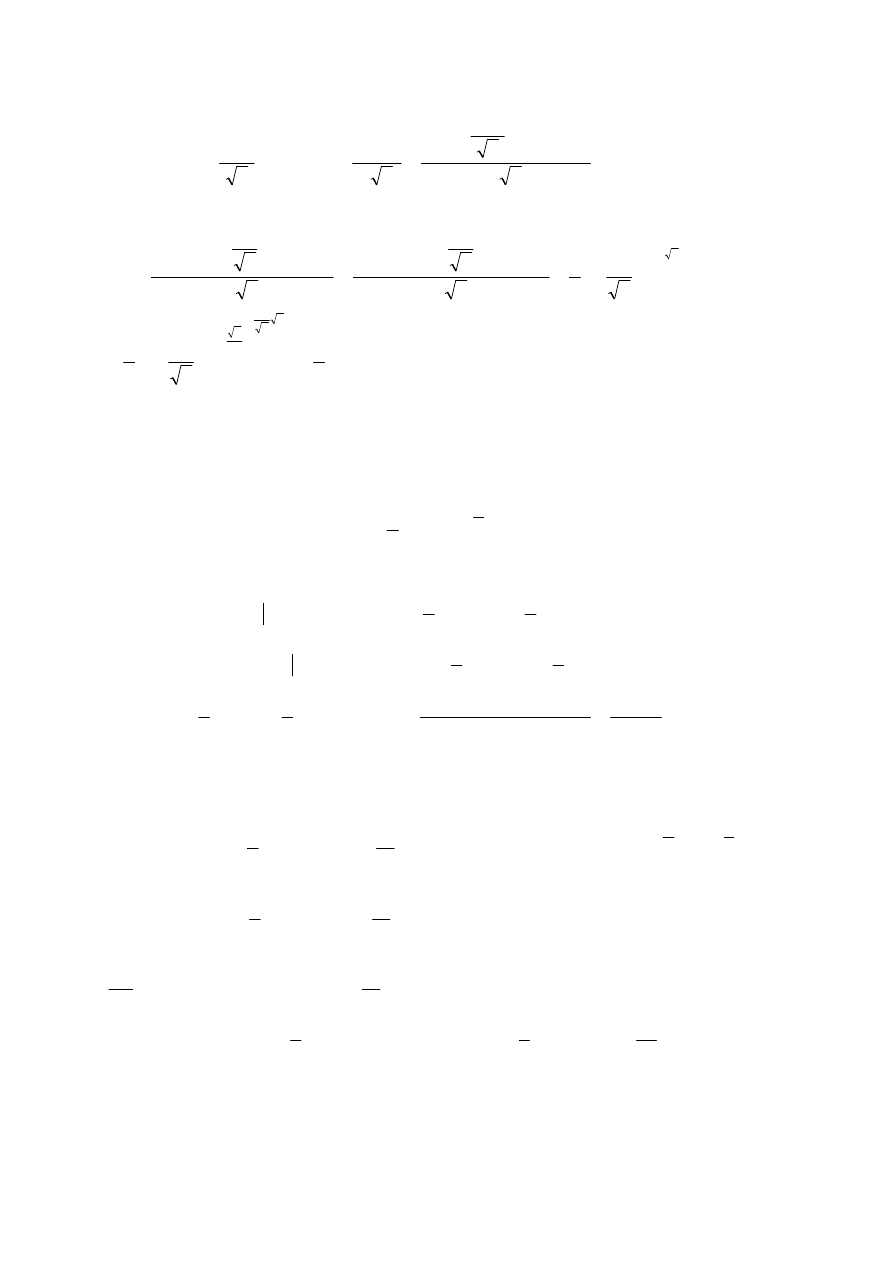
(
)
n
X
X
N
P
n
n
e
n
e
n
n
n
Y
P
e
n
e
n
Y
P
n
lim
2
2
4
ln
2
2
4
ln
2
2
2
2
<
→
−
+
−
<
−
=
+
−
<
=
−
−
−
−
4
4
4
4
3
4
4
4
4
2
1
=
+
=
−
+
+
−
−
=
−
+
−
=
−
n
n
n
n
n
n
n
n
n
n
e
n
X
1
4
ln
2
1
2
2
1
4
ln
2
2
2
1
4
ln
2
2
4
2
1
1
4
ln
2
1
4
4
=
⋅
→
+
=
→
n
n
e
n
n
43
42
1
977
,
0
)
2
(
≈
<
N
P
czyli odpowiedź (B) jest prawidłowa
Zadanie 7
(
)
(
)
t
k
k
t
k
e
e
k
t
P
t
X
X
k
P
2
2
1
1
1
min
1
,...,
min
−
−
−
=
−
=
>
−
=
<
)
2
(
2
)
(
2
min
wykl
e
t
f
t
k
≅
=
−
⋅
(
)
(
)
(
)
∑
∑
∞
=
∞
=
−
=
=
=
=
=
=
1
1
1
2
1
)
(
2
1
)
(
k
r
k
N
N
p
k
N
P
k
N
P
k
N
NZ
E
NZ
E
(
)
(
)
(
)
(
)
∑
∑
∞
=
∞
=
−
=
=
=
=
=
=
1
1
2
2
1
2
1
)
(
2
1
)
(
k
k
r
N
N
p
k
N
P
k
N
P
k
N
NZ
E
NZ
E
(
)
(
) (
)
4
1
4
2
1
2
2
2
1
4
1
1
2
1
var
2
2
2
r
r
r
r
r
r
r
N
p
p
p
p
p
p
p
NZ
−
=
−
+
−
−
=
+
−
−
−
=
Zadanie 8
STAŁE NIEISTOTNE:
(
)
(
)
Y
m
X
m
to
m
Y
m
X
LICZ
i
i
m
m
=
=
→
−
−
−
−
=
∑
∑
2
1
2
2
2
1
,
,
dla
wiemy
18
1
2
1
exp
sup
2
1
(
)
(
)
−
−
−
−
=
∑
∑
4
4
4
4
4
4
3
4
4
4
4
4
4
2
1
)
(
2
2
18
1
2
1
exp
sup
m
f
i
i
m
m
Y
m
X
MIAN
(
)
(
)
=
−
⋅
+
−
⋅
=
∂
∂
∑
∑
m
Y
m
X
m
f
m
i
i
2
18
1
exp(...)
)
(
(
)
∑
∑
∑
∑
+
=
+
→
=
−
+
−
=
m
m
Y
X
m
Y
m
X
i
i
i
i
9
20
20
9
1
0
20
9
1
20
exp(...)
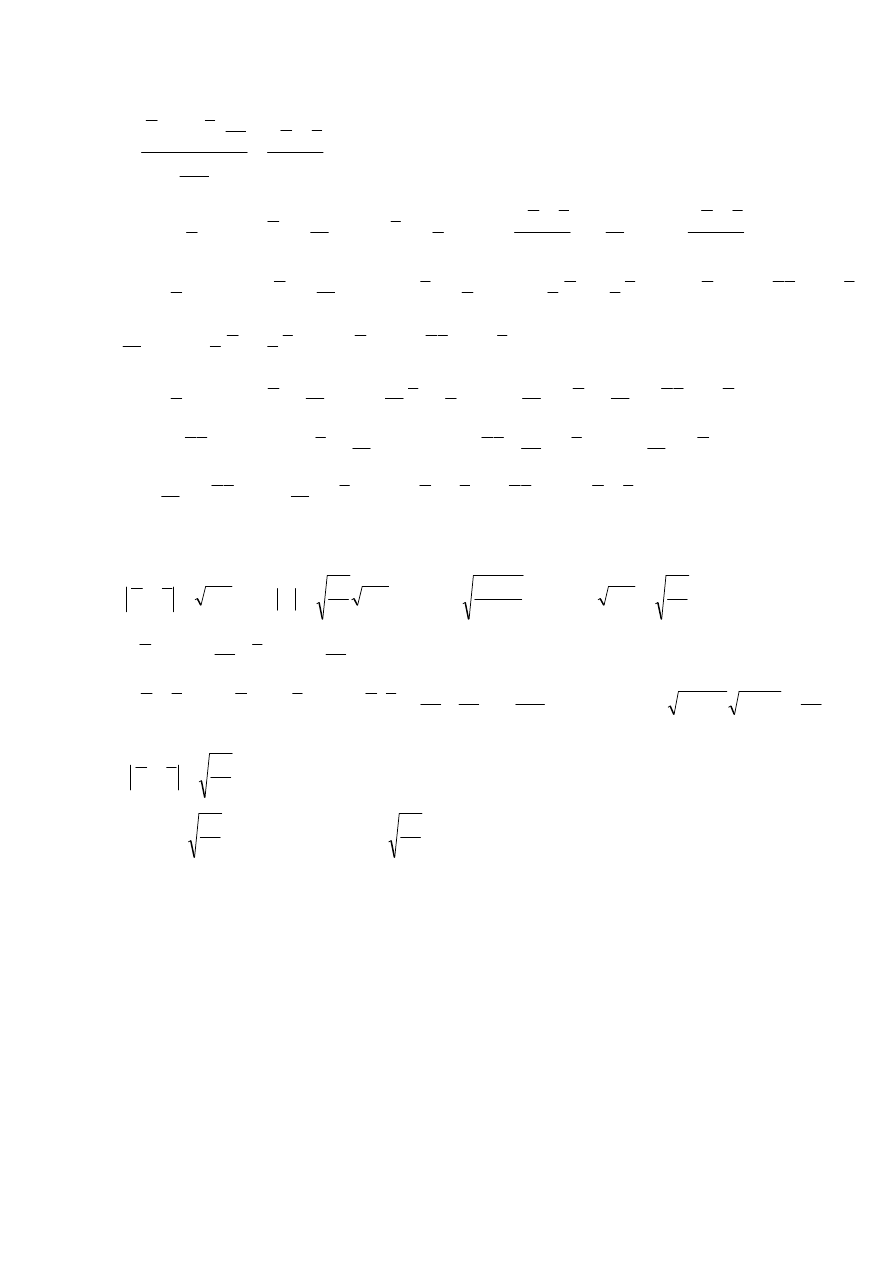
10
9
9
200
9
20
20
Y
X
Y
X
m
+
=
⋅
+
⋅
=
(
)
(
)
=
+
−
+
+
−
+
−
−
−
−
=
∑
∑
∑
∑
2
2
2
2
10
9
18
1
10
9
2
1
18
1
2
1
exp
Y
X
Y
Y
X
X
Y
Y
X
X
i
i
i
i
λ
(
) (
)
+
+
+
−
−
+
−
−
−
−
=
∑
∑
∑
2
2
2
2
2
2
2
01
,
0
18
,
0
81
,
0
5
1
5
9
2
1
20
18
1
20
2
1
exp
Y
Y
X
X
X
Y
X
X
X
Y
y
X
X
i
i
i
i
i
=
+
+
+
−
−
+
∑
2
2
2
01
,
0
18
,
0
81
,
0
5
1
5
9
18
1
Y
Y
X
X
y
Y
y
X
y
i
i
i
+
⋅
−
⋅
−
+
+
−
+
−
=
∑
∑
∑
2
2
2
2
2
2
2
1
,
8
20
10
1
20
10
9
2
1
9
10
18
1
10
2
1
exp
X
Y
X
X
X
Y
y
X
X
i
i
i
∑
⋅
⋅
+
⋅
−
⋅
−
+
⋅
⋅
+
⋅
+
2
2
2
2
20
18
1
81
,
0
20
90
1
20
1
,
0
18
1
20
5
,
0
01
,
0
20
09
,
0
X
Y
Y
X
y
Y
Y
X
i
[
]
(
)
[
]
2
2
2
2
exp
2
exp
20
18
1
01
,
0
20
18
1
18
,
0
Y
X
Y
X
Y
X
Y
Y
X
−
=
−
+
=
⋅
⋅
+
⋅
⋅
+
dla
:
0
H
(
)
64
,
1
20
7
ln
64
,
1
7
ln
20
1
,
0
ln
7
20
ln
=
→
=
→
=
>
=
>
−
c
c
c
N
P
c
Y
X
P
bo:
≅
≅
20
9
;
,
20
1
;
m
N
Y
m
N
X
(
)
( )
(
)
20
7
var
var
,
20
400
1
2
20
9
20
1
,
cov
2
var
var
var
=
⋅
⋅
⋅
−
+
=
−
+
=
−
i
i
i
i
Y
X
Y
X
corr
Y
X
Y
X
Y
X
CHCEMY
1
,
0
64
,
1
20
7
<
<
−
Y
X
P
(
)
(
)
1
,
0
7
20
64
,
1
7
20
64
,
1
2
1
2
1
<
−
−
<
<
−
−
−
m
m
N
m
m
P
sprawdzamy i wychodzi 1,66 (najbliżej)
Zadanie 9
(
)
min
ˆ
2
→
−
m
m
E
(
) ( )
( )
2
2
2
2
ˆ
2
ˆ
ˆ
2
ˆ
m
m
mE
m
E
m
m
m
m
E
+
−
=
+
−
∑
∑
=
=
=
⋅
=
n
i
n
i
i
i
a
m
m
a
m
E
1
1
ˆ
(
)(
)
[
]
=
+
+
+
+
+
+
=
n
n
n
n
X
a
X
a
X
a
X
a
X
a
X
a
E
m
E
...
...
ˆ
2
2
1
1
2
2
1
1
2
(
)
∑
∑
=
≠
=
+
=
n
i
j
i
j
i
j
i
i
i
X
X
E
a
a
EX
a
1
2
2
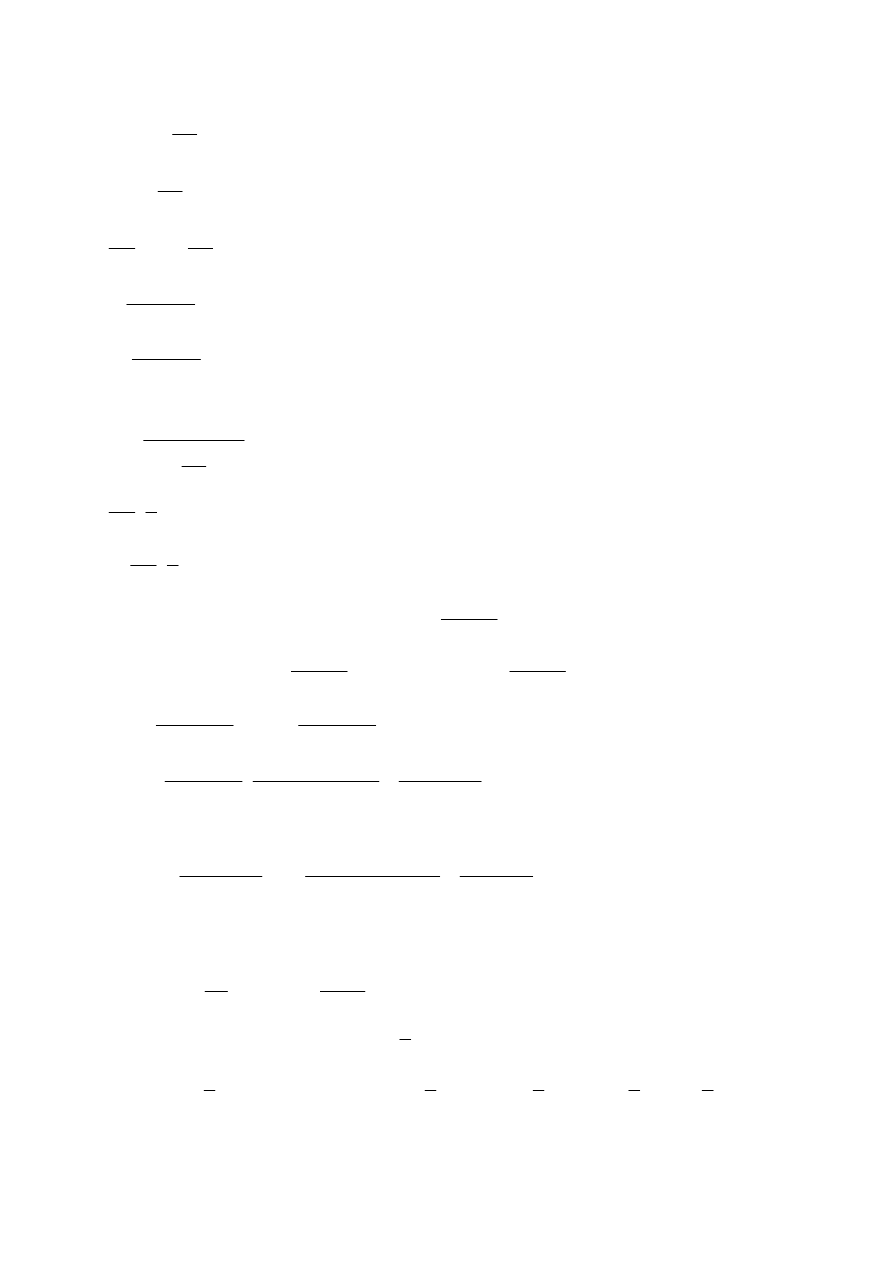
∑
∑
=
≠
+
+
=
n
i
j
i
j
i
i
m
a
a
m
i
m
a
1
2
2
2
2
∑
∑
∑
=
≠
=
→
+
−
+
+
n
i
j
i
n
i
i
j
i
i
m
a
m
m
a
a
m
i
m
a
1
1
2
2
2
2
2
2
min
2
∑
≠
=
−
+
+
=
∂
∂
i
j
j
i
i
m
m
a
m
i
m
a
a
0
2
2
2
2
2
2
2
0
2
1
2
2
2
=
−
−
+
+
∑
=
m
a
a
m
i
im
m
a
n
i
i
i
i
∑
=
−
=
−
+
n
i
i
i
a
m
m
m
i
im
m
a
1
2
2
2
2
2
−
=
−
=
∑
∑
=
=
n
i
i
n
i
i
i
a
i
i
m
a
m
a
1
2
1
2
1
1
(
)
∑
≠
=
−
+
+
=
⋅
∂
∂
i
j
j
i
i
im
m
a
i
im
m
a
i
a
0
2
2
2
2
2
(
)
∑
∑
∑ ∑
∑
=
=
=
≠
=
=
−
+
+
=
⋅
∂
∂
n
i
n
i
n
i
i
j
n
i
j
i
i
im
m
a
i
im
m
a
i
a
1
1
1
1
2
2
2
2
0
2
∑
∑
∑
∑
=
=
=
=
=
+
−
−
+
+
n
i
n
i
n
i
n
i
i
i
i
i
n
n
m
a
a
im
ia
m
a
m
1
1
1
2
1
2
2
2
0
2
)
1
(
∑
∑
∑
∑
=
=
=
=
=
+
−
−
+
+
+
n
i
n
i
n
i
n
i
i
i
i
i
n
n
m
ia
m
a
n
n
m
ia
m
a
m
1
1
1
1
2
2
2
2
2
0
2
)
1
(
2
)
1
(
∑
=
+
=
+
+
n
i
i
n
n
m
a
n
n
m
m
1
2
2
2
2
)
1
(
2
)
1
(
∑
=
+
+
+
=
+
+
⋅
+
=
n
i
i
n
n
n
n
n
n
m
m
n
n
m
a
1
2
2
2
)
1
(
2
)
1
(
)
1
(
2
2
2
)
1
(
Z tego:
n
n
i
n
n
n
n
n
n
i
n
n
n
n
i
a
i
+
+
=
+
+
−
−
+
+
⋅
=
+
+
+
−
=
2
2
2
2
2
)
1
(
2
2
)
1
(
2
)
1
(
1
Zadanie 10
)
(
i
)
1
,
0
(
),
;
0
(
i
U
STAT
J
X
J
X
i
i
≅
≅
≅
θ
θ
θ
[
]
(
)
=
<
>
=
∈
−
−
)
,
2
(
)
,
3
(
:
2
:
3
2
1
i
5
,
0
2
,
2
n
n
n
n
n
n
U
U
P
X
X
P
θ
4
4
4
3
4
4
4
2
1
0
2
3
2
3
2
3
2
1
i
2
1
2
1
2
1
1
5
,
0
lub
2
1
1
=
−
−
−
<
>
+
<
−
>
−
=
≤
≥
−
=
n
n
n
J
J
P
J
P
J
P
J
J
P
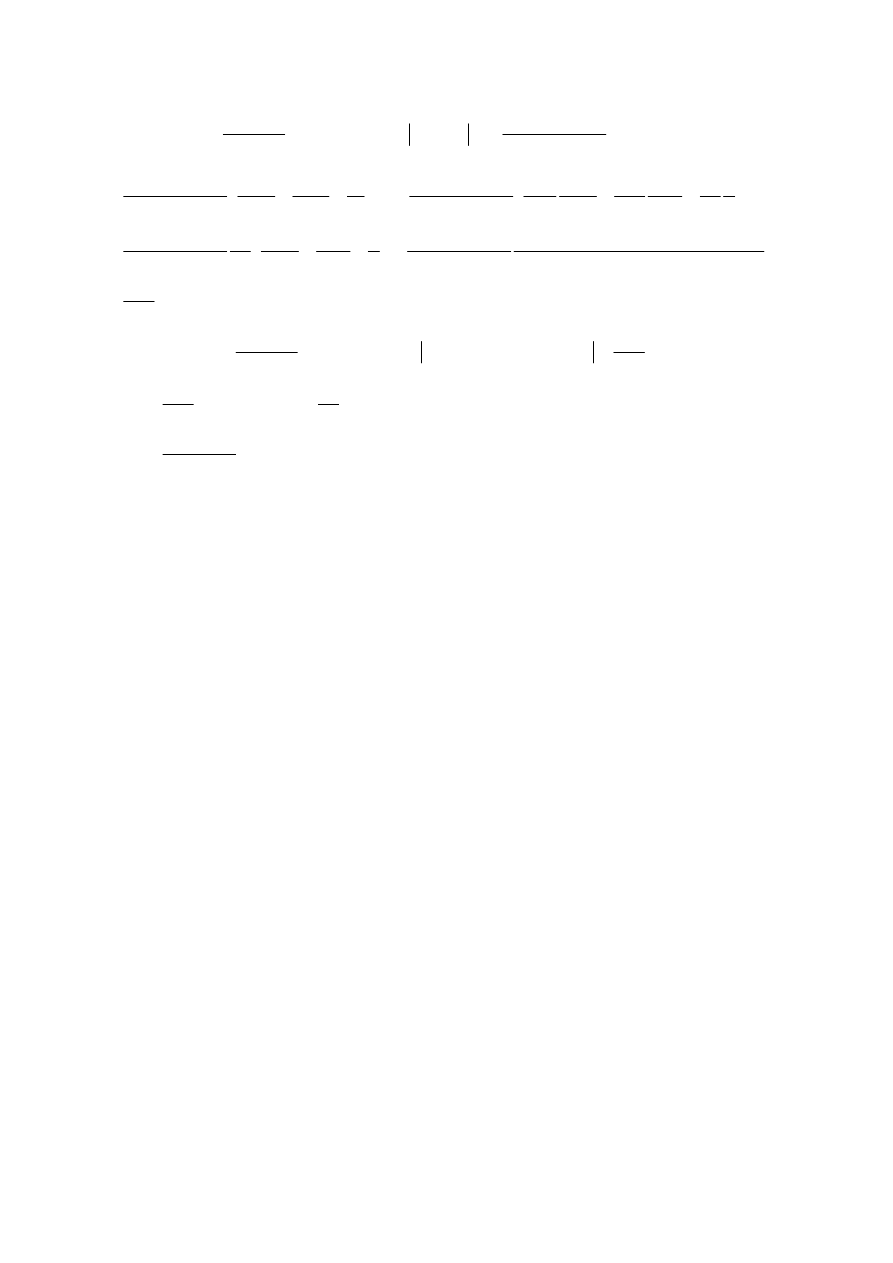
(
)
(
)
∫
∫
=
+
−
−
−
=
=
−
=
−
−
=
>
−
−
1
5
,
0
5
,
0
0
3
2
3
2
3
2
1
2
)
1
)(
2
(
1
)
1
(
)!
3
(
2
!
5
,
0
n
n
t
t
t
n
n
n
t
x
dx
x
x
n
n
J
P
=
+
−
−
−
−
−
=
+
−
−
−
−
−
=
−
−
−
−
n
n
n
n
n
n
n
t
n
t
n
t
n
n
n
n
n
n
n
n
n
1
2
1
1
1
2
2
2
1
2
1
2
)
2
)(
1
(
1
2
2
2
)
2
)(
1
(
1
2
5
,
0
0
1
2
(
) (
)
=
−
−
+
−
+
−
−
−
−
−
=
+
−
−
−
−
−
=
+
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
)
1
)(
2
(
2
3
2
4
4
2
)
2
)(
1
(
1
1
4
2
4
2
1
2
)
2
)(
1
(
2
2
2
1
(
)
2
2
1
2
1
+
+
=
+
n
n
n
(
)
(
)
∫
+
+
=
=
−
−
=
<
+
−
−
5
,
0
0
2
1
2
3
2
2
2
1
SAMO
TO
ZE
WIDAC
)
1
(
2
)!
3
(
!
5
,
0
n
n
dx
x
x
n
n
J
P
n
n
n
(
)
(
)
9
,
0
2
2
1
1
2
2
2
1
2
2
1
≥
+
+
−
=
+
+
−
=
+
n
n
n
n
P
n
n
1
,
0
2
2
)
(
2
≤
+
+
=
n
n
n
n
f
f(n) jest malejąca więc sprawdzamy i wychodzi n=11
Wyszukiwarka
Podobne podstrony:
2008.12.15 prawdopodobie stwo i statystyka
2002 06 15 prawdopodobie stwo i statystykaid 21643
2000 12 09 prawdopodobie stwo i statystykaid 21582
2010 12 13 prawdopodobie stwo i statystykaid 27016
2007 12 03 prawdopodobie stwo i statystykaid 25662
2008.06.02 prawdopodobie stwo i statystyka
2003.12.06 prawdopodobie stwo i statystyka
2005.12.05 prawdopodobie stwo i statystyka
2003 12 06 prawdopodobie stwo i statystykaid 21710
2008 03 17 prawdopodobie stwo i statystykaid 26449
2008 06 02 prawdopodobie stwo i statystykaid 26454
2008.10.06 prawdopodobie stwo i statystyka
1998.12.05 prawdopodobie stwo i statystyka
2007.12.03 prawdopodobie stwo i statystyka
1996.12.07 prawdopodobie stwo i statystyka
1998 12 05 prawdopodobie stwo i statystykaid 18587
2002.06.15 prawdopodobie stwo i statystyka
2000.01.15 prawdopodobie stwo i statystyka
więcej podobnych podstron