Politechnika Świętokrzyska
Wydział Mechatroniki i Budowy Maszyn
Centrum Laserowych Technologii Metali PŚk i PAN
Zakład Informatyki i Robotyki
Przedmiot: Podstawy Automatyzacji – laboratorium, rok III, sem. II

Ćwiczenie nr 3

Badanie stabilności układów automatyki – symulacja komputerowa

1. Stabilność - wprowadzenie

Jedną z podstawowych własności jaką muszą wykazywać układy automatyki to

stabilność. Układ regulacji uważa się za stabilny, gdy wielkość wyjściowa, jako odpowiedz na

dowolne ograniczone wymuszenie, będzie ograniczona. Sytuacja taka będzie miała miejsce,

gdy w układzie będzie tłumiony stan nieustalony.

Wyróżniamy następujące układy pod względem stabilności:

1.

Stabilny asymptotycznie – wszystkie rzeczywiste pierwiastki równania

charakterystycznego lub wszystkie części rzeczywiste pierwiastków zespolonych

muszą być ujemne. W interpretacji graficznej oznacza to, że wszystkie te bieguny

lub wartości własne macierzy stanu, leżą w lewej półpłaszczyźnie zmiennej

zespolonej.

2.

Stabilny nieasymptotycznie (na granicy stabilności) – układ, którego pierwiastki

leżą w lewej półpłaszczyźnie, oraz występują:

•

jeden pierwiastek rzeczywisty równy zero,

•

pojedyncze pary pierwiastków urojonych,

•

jeden pierwiastek rzeczywisty równy zero i pojedyncze pary pierwiastków

urojonych (leżą na osi urojonej).

3.

Układ niestabilny – występuje co najmniej jeden pierwiastek w prawej

półpłaszczyźnie zmiennej zespolonej.

Poprzez rozwiązanie równania charakterystycznego określa się stabilność układu.

Rozwiązanie to pozwala na określenie położenia pierwiastków, a więc dzięki temu można

zbadać odległość od granicy stabilności, którą jest oś urojona zmiennej zespolonej.

2. Algebraiczne kryterium stabilności (kryterium Hurwitza)

Rozwiązywanie równania charakterystycznego często jest kłopotliwe, dlatego

wprowadza się metody oszacowywania stabilności układu.

Warunkiem koniecznym i dostatecznym stabilności układu liniowego i stacjonarnego

(1) jest, ażeby wszystkie współczynniki wielomianu charakterystycznego transmitancji tego

układu istniały i były dodatnie, a ponadto wyznacznik

n

∆

(3),

)

(

)

(

)

(

)

(

)

(

)

(

1

1

1

1

1

1

t

u

b

dt

t

u

d

b

dt

t

u

d

b

t

x

a

dt

t

x

d

a

dt

t

x

d

a

o

m

m

m

m

m

m

o

n

n

n

n

n

n

+

+

+

=

+

+

+

−

−

−

−

−

−

L

L

(1)

zwany wyznacznikiem Hurwitza oraz jego podwyznaczniki

1

3

2

,

,

,

−

∆

∆

∆

n

L

były dodatnie.

Po pewnych przekształceniach otrzymujemy formułę równania charakterystycznego, z

którego tworzymy wyznacznik i podwyznaczniki:

0

...

0

1

1

1

=

+

+

+

+

−

−

a

s

a

s

a

s

a

n

n

n

n

.

(2)

0

2

4

1

3

0

2

3

1

4

2

5

3

1

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

n

n

n

n

n

n

n

n

n

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

−

−

−

−

−

−

−

=

∆

(3)

1

1

−

=

∆

n

a

2

3

1

2

−

−

−

=

∆

n

n

n

n

a

a

a

a

3

1

4

2

5

3

1

3

0

−

−

−

−

−

−

−

=

∆

n

n

n

n

n

n

n

n

a

a

a

a

a

a

a

a

M

1

3

5

0

2

4

1

3

3

1

4

2

5

3

1

1

0

0

0

0

0

0

0

0

0

0

0

0

0

0

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

n

n

n

n

n

n

n

n

n

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

−

−

−

−

−

−

−

−

=

∆

Przykład 1

Zbadać, czy wielomian

4

3

5

2

2

3

4

+

+

+

+

s

s

s

s

(4)

spełnia założenia kryterium Stabilności Hurwitza.

Wszystkie współczynniki wielomianu charakterystycznego są dodatnie, co spełnia

pierwszy warunek kryterium. Wielomian (4) jest czwartego stopnia, wiec należy sprawdzić

wszystkie wyznaczniki kończąc na 3 stopniu, co daje:

0

7

5

3

1

2

2

>

=

=

∆

,

0

5

3

4

0

2

5

3

0

1

2

3

>

=

=

∆

.

Możemy wywnioskować, że wielomian (4) nie posiada pierwiastków o dodatniej

części rzeczywistej.

3. Częstotliwościowe kryterium stabilności

Kryterium częstotliwościowe zwane kryterium Nyquista pozwala badać stabilność

układu zamkniętego na podstawie przebiegu charakterystyki częstotliwościowej układu

otwartego.

1.

Jeżeli układ otwarty jest stabiny asymptotycznie, to układ zamkniety jest

stabilny asymptotycznie wtedy i tylko wtedy, gdy wykres charakterystyki

amplitudowo-fazowej G

0

(jω) układu otwartego przy zmianie pulsacji ω od 0 do

+∞ nie obejmuje punktu (-1, j0).

2.

Jeżeli układ otwarty jest niestabilny i jego transmitancja ma m biegunów

w prawej półpłaszczyźnie zmiennej zespolonej, to układ zamknięty jest stabilny

wtedy i tylko wtedy, gdy wykres charakterystyki amplitudowo-fazowej G

0

(jω)

układu otwartego przy zmianie pulsacji ω od 0 do +∞ obejmuje w kierunku

dodatnim punktu (-1, j0) m/2.

Prz ykł ad 2

Dany jest obiekt o transmitancji

1

2

2

)

(

2

3

+

+

+

=

s

s

s

k

s

G

p

o

(5)

za pomocą polecenia nyquist

z pakietu MatLab-a, wykonamy wykresy charakterystyk

amplitudowo-fazowych układu otwartego G

0

(jω) dla trzech wartości wzmocnienia k

p

=2, 3

i 4.

-3

-2

-1

0

1

2

3

4

-4

-3.5

-3

-2.5

-2

-1.5

-1

-0.5

0

0.5

1

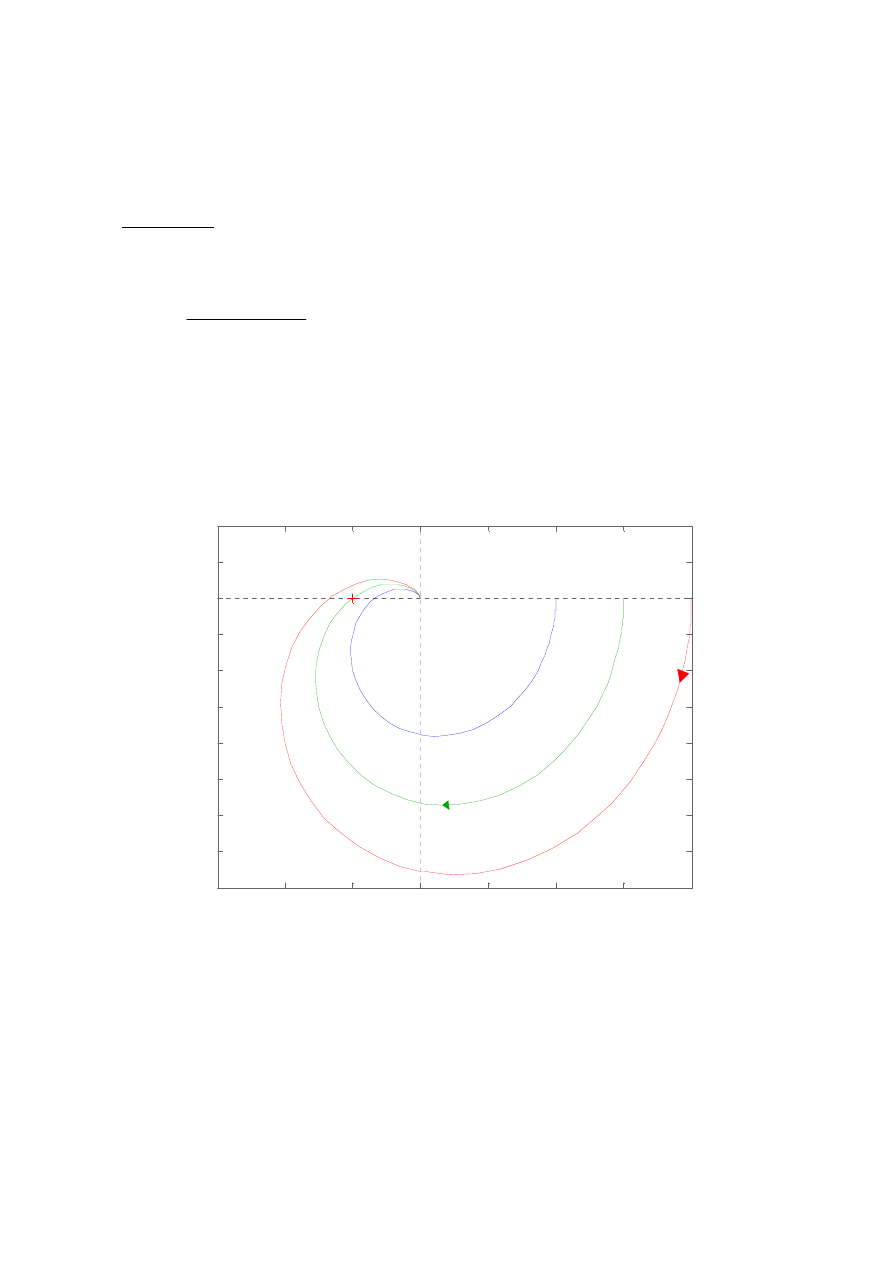
W ykres Nyquista Go(jw)

P (w)

Q

(w

)

k p= 2

k p= 3

kp= 4

w

Rys. 1. Charakterystyki amplitudowo-fazowe układu otwartego G

0

(jω) dla k

p

= 2, 3, 4

Na wykresie charakterystyki Nyquista układu otwartego G

0

(jω) (rys. 2) możemy

zaobserwować trzy charakterystyczne przypadki regulacji. Pierwszy z nich przedstawia

sytuację, gdzie charakterystyka G

0

(jω) wykreślona dla wszystkich wartości częstotliwości ω

nie obejmuje punktu (-1,j0). Powiemy, że układ zamknięty dla k

p

jest stabilny. W drugim

przypadku dla k

p

= 3 charakterystyka G

0

(jω) przechodzi przez punkt (-1,j0), układ ten jest na

granicy stabilności. Dla k

p

= 4 charakterystyka G

0

(jω) przy wzroście ω od 0 do ∞ obejmuje

punkt (-1,j0), w tej sytuacji układ po zamknięciu sprzężenia zwrotnego będzie niestabilny.

Potwierdzenie wcześniejszego wywodu znajdziemy przez sprawdzenie położenia biegunów

transmitancji równania charakterystycznego układu zamkniętego na płaszczyźnie zmiennej

zespolonej.

Wyznaczamy transmitancję układu zamkniętego

,

(6)

oraz jego równanie charakterystyczne

. (7)

Za pomocą komendy roots programu MatLab zbadano pierwiastki (bieguny) równania

(7) dla:

•

k

p

= 2

s

1

= -1.8105

s

2

= -0.0947 + 1.2837j

s

3

= -0.0947 - 1.2837j

Wszystkie pierwiastki mają części rzeczywiste dodatnie, co dowodzi stabilności

układu zamkniętego.

•

k

p

= 3

s

1

= - 2.0000

s

2

= 0.0000 + 1.4142j

s

3

= 0.0000 - 1.4142j

W tym przypadku występują pierwiastki urojone sprzężone posiadające części

rzeczywiste równe 0 (bieguny s

2

i s

3

znajdują się na osi urojonej), zatem układ

zamknięty jest na granicy stabilności.

•

k

p

= 4

s

1

= -2.1509

s

2

= 0.0755 + 1.5228j

0

1

2

2

)

(

2

3

=

+

+

+

+

=

p

z

k

s

s

s

s

M

1

2

2

)

(

1

)

(

)

(

2

3

+

+

+

+

=

+

=

p

p

o

o

z

k

s

s

s

k

s

G

s

G

s

G

s

3

= 0.0755 - 1.5228j

Tym razem występują pierwiastki zespolone sprzężone, których części rzeczywiste są

dodatnie, wobec tego układ zamknięty jest dla tego przypadku niestabilny.

3. Przebieg ćwiczenia

a)

Zbadaj stabilność układów postępując zgodnie z przykładami 1 i 2. Wykreśl

charakterystyki:

•

czasowe (na jednym wykresie) dla przykładu 2,

•

rozmieszczenie biegunów i zer transmitancji na płaszczyźnie zmiennej zespolonej

posługując się poleceniem (pzmap)

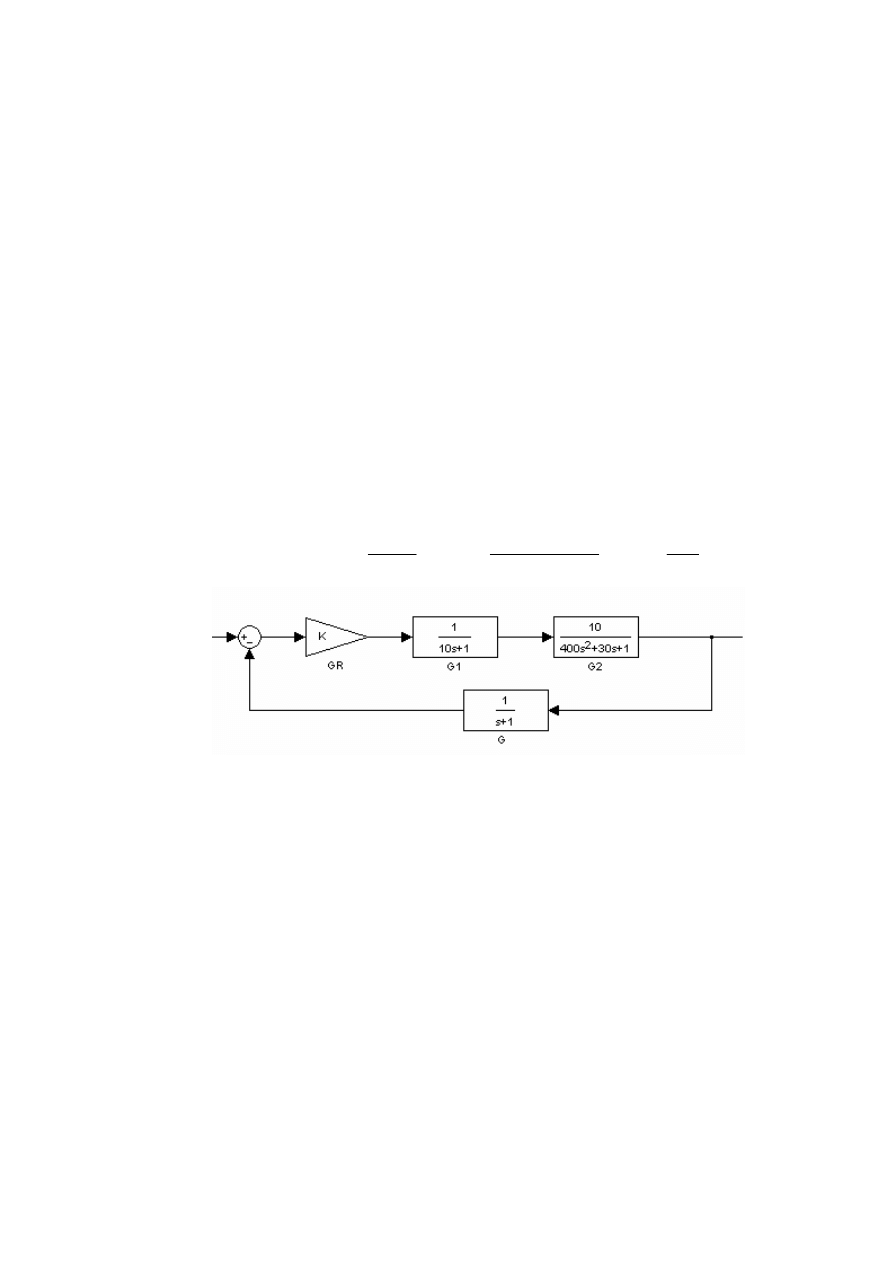
b)

Dla jakiego przedziału wartości parametru K układ jest stabilny. Transmitancje

elementów układu wynoszą:

K

s

G

r

=

)

(

,

1

10

1

)

(

1

+

=

s

s

G

,

1

30

400

10

)

(

2

2

+

+

=

s

s

s

G

,

1

1

)

(

+

=

s

s

G

.

c)

Proszę o wybranie 2 transmitancji (jedna układ stabilny, druga układ niestabilny)

i przedstawienie wyliczeń analitycznych i graficznych. Dla układu stabilnego proszę

o zaznaczenie zapasu stabilność zarówno dla charakterystyki Nyquista jak i Bodego.