28 października 2009
Gracja Bednarz
Kierunek: Ogrodnictwo
Nr grupy: 1
Nr zespołu: 8
Ćwiczenie 19
Wyznaczanie ciepła właściwego ciał stałych
.
1. Tabele
Tabela pomiarów i wyników:
J/K
kg
kg
K
V
K
V
K
J/kg•K
J/kg•K
120
254,910 341,6 ∙ 10 369,4
0,51 ∙ 10
288
0,76 ∙ 10 295
4186
326,9
Tabela cechowania termopary:
ΔT[K]
23
28
33
38
43
48
53
58
U [V]
0,56 ∙ 10 0,75 ∙ 10 0,88 ∙ 10 1,04 ∙ 10 1,22 ∙ 10 1,46 ∙ 10
1,62 ∙ 10
1,65 ∙ 10
a [V/K]
0,034 ∙ 10
2. Znaczenie symboli
– pojemność cieplna kalorymetru
- masa wody w kalorymetrze
– masa ciała (metalu)
– temperatura podgrzanego metalu
- napięcie odpowiadające temperaturze
– temperatura początkowa wody w kalorymetrze
- napięcie odpowiadające temperaturze
– temperatura końcowa mieszaniny w kalorymetrze
- ciepło właściwe wody
- ciepło właściwe metalu użytego do ćwiczenia
- różnica temperatury podgrzewanej wody
- napięcie kontaktowe (energia wewnętrzna układu)
- stała termopary (współczynnik nachylenia krzywej cechowania)
3. Wzory robocze
=
+ 273
=
+ 273
=
( +
∙
) ∙ (
−
)
∙ (
−
)
=
∆
∆
4. Obliczenia
Dla wykresu przecinającego punkty:
(
, ∆ )
(
, ∆ )
gdzie:
= 1,41 ∙ 10
= 0,9 ∙ 10
= 306
= 321
wyliczamy współczynnik nachylenia krzywej cechowania ze wzoru:
=
(
−
)
(
−
)
=
(1,41 ∙ 10
− 0,9 ∙ 10 )
(321 − 306)
=
0,51 ∙ 10
15
= 0,000034
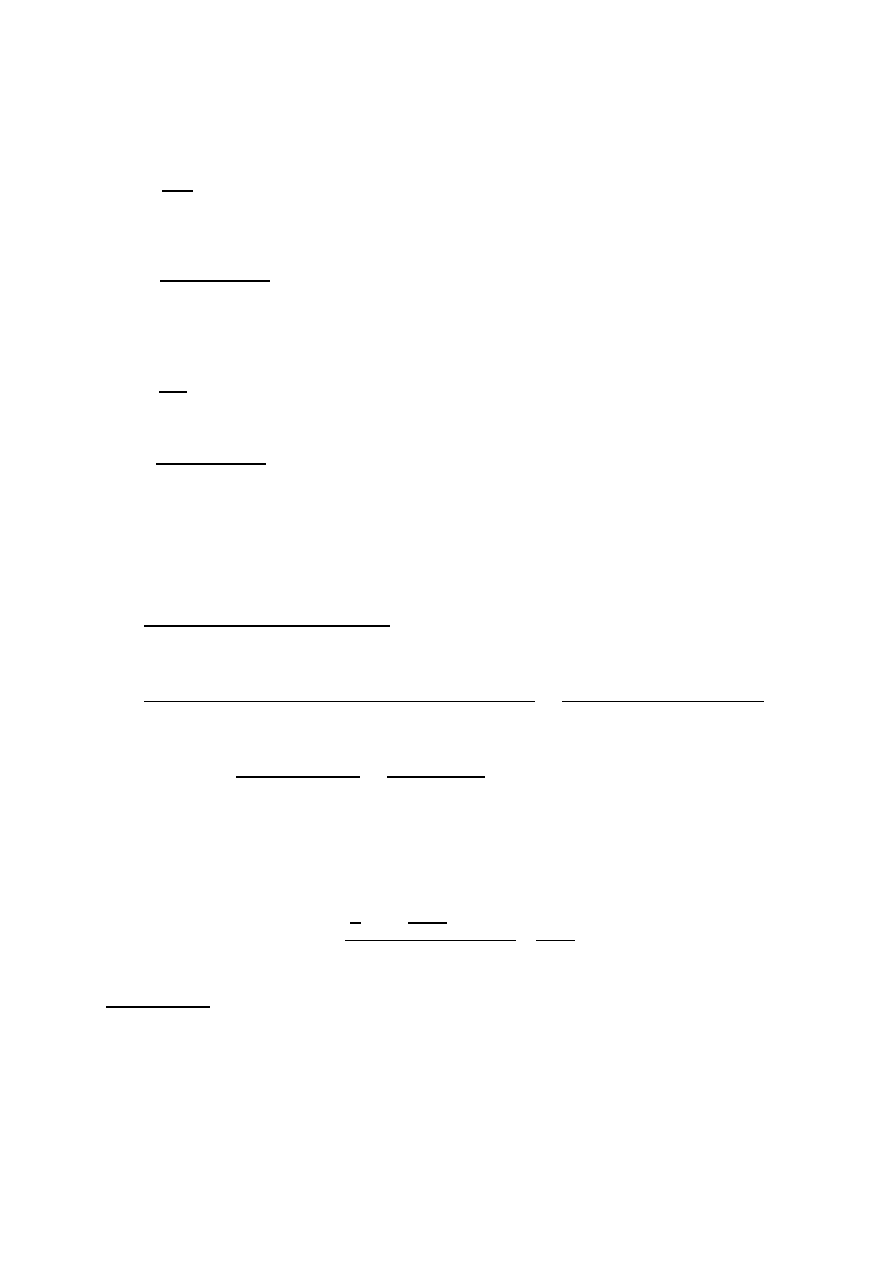
Uzyskany wynik podstawiamy kolejno do wzorów:
=
+
=
0,51 ∙ 10
0,034 ∙ 10
+ 273 = 288 [ ]
oraz
=
+
=
0,76 ∙ 10
0,034 ∙ 10
+ 273 = 295,35294 ≈ 295 [ ]
W celu obliczenia ciepła właściwego podgrzewanego metalu, uzyskane wyniki
podstawiamy do wzoru:
=
( +
∙
) ∙ (
−
)
∙ (
−
)
=
[120 + (254,9 ∙ 10 ) ∙ 4186] ∙ (295 − 288)
(341,6 ∙ 10 ) ∙ (369,4 − 295)
=
(120 + 1067,0114) ∙ 7
(341,6 ∙ 10 ) ∙ 74,4
=
=
1187,0114 ∙ 7
25,41504
=
8309,0798
25,41504
= 326,9355389564 ≈
≈ 326,9
∙
=
+
∙
∙
∙ ( − )
∙ ( − )
=
∙
5. Wniosek
Po porównaniu uzyskanego wyniku ciepła właściwego dla użytego
w ćwiczeniu metalu
( = 326,9 ⁄
∙ ) do tabeli z wartościami ciepła właściwego
dla poszczególnych materiałów stwierdzam, że metalem jaki został użyty do
ćwiczenia jest miedź.