Biotechnologia, 3 rok, 6 semestr 

Instrukcja do laboratorium nr 3 z 

Modelowania Biosystemów 

Modele stochastyczne 

 

Prowadz cy: mgr in . Krzysztof Psiuk-Maksymowicz (p.629) 

krzysztof.psiuk-maksymowicz@polsl.pl 

 

 

 

1.  Zakres materiału laboratorium 

 

Przygotowanie  do  zaj   obejmuje  znajomo   modeli  kompartmentalnych  oraz  podstaw  rachunku 

operatorowego wykorzystuj cego transformat  Laplace’a. 

 

2.  Wprowadzenie 

 

Rachunek operatorowy jest jednym z narz dzi matematycznych słu cych do rozwi zywania liniowych 

równa   ró niczkowych  zwyczajnych.  W  porównaniu  z  metod   klasyczn ,  metoda  transformaty 

operatorowej przekształca równanie ró niczkowe zwyczajne w równanie algebraiczne.  
W  rachunku  operatorowym  najcz ciej  stosowanym  operatorem  jest  liniowy  operator 

,  który 

definiuje tzw. jednostronn  transformat  Laplace’a.  

Jednostronna transformata Laplace’a zdefiniowana jest jako funkcja  

 

Gdzie  zmienna  s  jest  zmienn   zespolon ,  natomiast  argument  t  funkcji  f(t)  jest  zmienn   rzeczywist  

nieujemn . Warto ci funkcji f(t) dla t<0 przyjmowane s  jako 0. Transformata Laplace'a jest zdefiniowana 

dla  przedziału czasu od t = 0

−

 do + . Symbol t = 0

−

 oznacza,  e granica dla czasu t 0 brana jest z lewej 

strony  t  =  0.  Takie  ograniczenie  brane  jest  pod  uwag   w  tych  przypadkach,  gdy  funkcja  f(t)  ma  posta  

funkcji skokowej lub impulsowej, w których to funkcjach zmiana nast puje w chwili t = 0. 

 

Przykład 1 zastosowania transformaty Laplace’a. 

 

Funkcja wykładnicza zdefiniowana jest nast puj co 

 

gdzie A i   s  stałymi. Transformata powy szej funkcji wyznaczana jest nast puj co 

. 

 

Przykład 2 zastosowania transformaty Laplace’a.  

 

Funkcja skokowa zdefiniowana jest nast puj co 

 

gdzie A jest stał . Transformata powy szej funkcji wyznaczana jest nast puj co 

. 

 

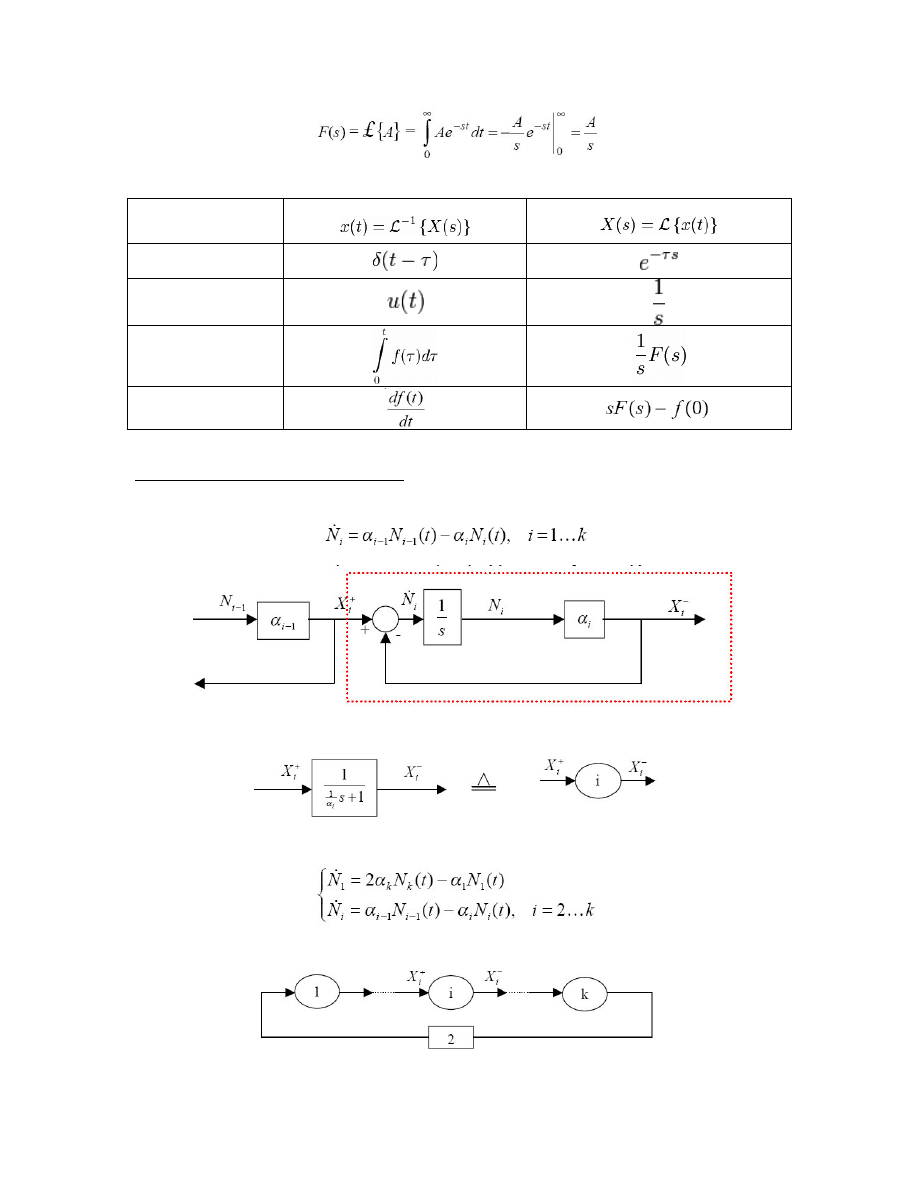
Poni sza tabela przedstawia transformaty najcz ciej wykorzystywanych funkcji b d  operatorów. 

Funkcja/operator 

Domena czasu t 

 

Domena transformaty s 

 

Opó nienie 

 

 

Skok jednostkowy 

 

 

Całkowanie 

 

 

Ró niczkowanie 

 

 

 

 

Modele kompartmentalne – stochastyczne 

 

Maj c układ k równa  ró niczkowych zapisanych w postaci: 

 

ka de i-te równanie mo emy zamodelowa  wykorzystuj c rachunek operatorowy jako: 

 

po  przekształceniu  (cz ci  schematu  zaznaczon   czerwon   lini   punktow )  mo emy  upro ci   do  bloku 

postaci (inercja I rz du, o stałej czasowej 

i

=1/

i

) 

 

Układ  równa   ró niczkowych  wraz  z  równaniem  granicznym  wi

cym  populacje  mo na  zapisa  

nast puj co jako: 

 

co  mo na  zapisa   za  pomoc   schematu,  którego  analizowanie  opiera  si   na  obserwacji  przepływów  

i stanów kompartmentów: 

 

Przykład tworzenia modelu wykładniczego w Simulinku 

 

Model wykładniczy w dziedzinie czasu ma posta  dN(t)/dt = aN(t), natomiast w dziedzinie operatorowej 

(po dokonaniu transformacji Laplace’a) ma posta  sN(s) = aN(s) + N(0). St d N(s) = N(0) / (s-a), sk d po 

zastosowaniu odwrotnej transformaty Laplace’a mo na otrzyma  wzór na rozwi zanie modelu w czasie. 

W  Simulinku  za  całkowanie  odpowiedzialny  jest  bloczek 

,  natomiast  za 

wzmacnianie  sygnału  bloczek 

.  Wszelkiego  rodzaju  bloczki  mo na  znale   w  Simulink 

Library Browser, bloczek Integrator’a w znajduje si  w zbiorze Simulink->Continuous, natomiast bloczek 

Gain  w  zbiorze  Simulink->Math  Operations.  Budowanie  modelu  polega  na  ł czeniu  ze  sob  

poszczególnych bloczków, dodatkowo specyfikuj c odpowiednie parametry poszczególnych bloczków tak 

aby  doprowadzi   do  zbilansowania  sygnałów  wg  równania  modelu.  Dla  bloczka  Integratora  nale y 

zdefiniowa   dodatkowo  warunek  pocz tkowy  całkowania,  natomiast  dla  bloczka  gain  okre li   warto  

wzmocnienia. Parametry bloczków mog  by  definiowane jako konkretne warto ci b d  wektory warto ci 

lub  te   jako  zmienne  zdefiniowane  w  Matlabie.  Wszystkie  zmienne  Matlaba  s   widoczne  z  poziomu 

modelu  Simulinka,  mo liwe  jest  równie   uruchomienie  modelu  Simulinka  z  poziomu  Matlaba  poprzez 

wpisanie nazwy pliku, w którym model został wcze niej zapisany. 

 

Gotowy model ma posta : 

  

 

W  powy szym  modelu  zastosowano  dodatkowo  bloczek  Scope  (Simulink->Sinks),  który  umo liwia 

obserwacj   konkretnych  zmiennych.  W  powy szym  modelu  u yto  warto ci  pocz tkowej  N

0

=100  i 

parametru a=0.2. 

 

 

Statistics toolbox 

 

Matlab posiada szereg toolbox’ów zawieraj cych predefiniowane funkcje. Toolbox Statistics zawiera wiele 

u ytecznych funkcji maj cych zastosowanie w statystyce. Chc c uzyska  informacj  na temat dost pnych 

funkcji  toolboxa  Statictics  nale y  w  linii  komend  Matlaba  wpisa   help  stats.  W  rozwi zaniu  zada  
laboratoryjnych przydatne b d  m.in. funcja generacji histogramów hist, funkcje generatorów losowych 
xxxrnd

, funkcje g sto ci prawdopodobie stw xxxpdf, dystrybuanty xxxcdf, gdzie xxx oznacza skrót 

od danego rozkładu, np. exp, norm, etc.  

 

 

3.  Program zaj  laboratoryjnych 

 

Zadania laboratoryjne wykonywan  s  w  rodowisku Matlab z wykorzystaniem toolbox’ów Simulink oraz 

Statistics. 

 

Zad 1.

  Zbudowa   model  wzrostu  populacji  komórkowej  o  dwóch  kompartmentach 

okre laj cych fazy cyklu komórowego. Zało y ,  e w chwili pocz tkowej w pierwszym 

kompartmencie znajduje si  N

G1S

(0) komórek oraz w drugim N

G2M

(0) komórek. Zało y , 

e komórki przebywaj  w poszczególnych kompartmentach ze  rednimi czasami 

G1S

  i 

G2M

. Wykre li  przebiegi czasowe dla obu kompartmentów. 

 

Zad 2.

  W  oparciu  o  model  z  poprzedniego  zadania  zbada   wpływ  działania  leku 

cytotoksycznego na populacj  komórek wiedz ,  e zabija on p% komórek b d cych w 

fazie  syntezy.  Wiadomo,  e  komórki  przebywaj   w  poszczególnych  kompartmentach  z 

czasami  okre lonymi  rozkładami:  jednorodnym  i  wykładniczym.  Wykre li   przebiegi 

czasowe  dla  obu  kompartmentów.  Za  pomoc   metody  „prób  i  bł dów”  znale   takie  p 

(0<p<100), dla którego populacja osiaga stan ustalony. 

 

Zad 3.

  Zbudowa   model  wzrostu  populacji  komórkowej  o  kompartmentach  okre laj cych 

wszystkie  fazy  cyklu  komórowego.  Zało y ,  e  w  chwili  pocz tkowej  populacja  jest 

zsynchronizowana i znajduje si  wył cznie w fazie G

1

 i osi ga wielko  N

G1

(0). Komórki 

przebywaj   w  poszczególnych  kompartmentach  z  czasami  okre lonymi  rozkładami:  

1  -  gamma,  2  -  jednorodnym,  3  -  zło eniem  dwóch  rozkładów  normalnych  

i 4 - zło eniem rozkładów wykładniczego i normalnego. Wygenerowa  po 1000 realizacji 

zmiennych  losowych  wg  poszczególnych  rozkładów,  wyliczy   redni   warto  

przebywania w ka dym z kompartmentów, któr  nast pnie nale y zastosowa  w modelu. 

Wykre li   przebiegi  czasowe  dla  wszystkich  kompartmentów  oraz  histogramy  dla 

wylosowanych zmiennych.