1

Wprowadzenie do Teorii Algorytmów

(Introduction to Algorithms Theory)

Prof. Dr hab. Alexander Prokopenya

Szkoła Główna Gospodarstwa Wiejskiego w Warszawie

Katedra Zastosowań Informatyki

Wykład 6-7.

Algorytmy grafowe

Grafy są powszechnie stosowane w informatyce, a algorytmy grafowe zaliczają się do podsta-
wowych w tej dziedzienie. Istenieją setki interesujących problemów obliczeniowych, które wy-
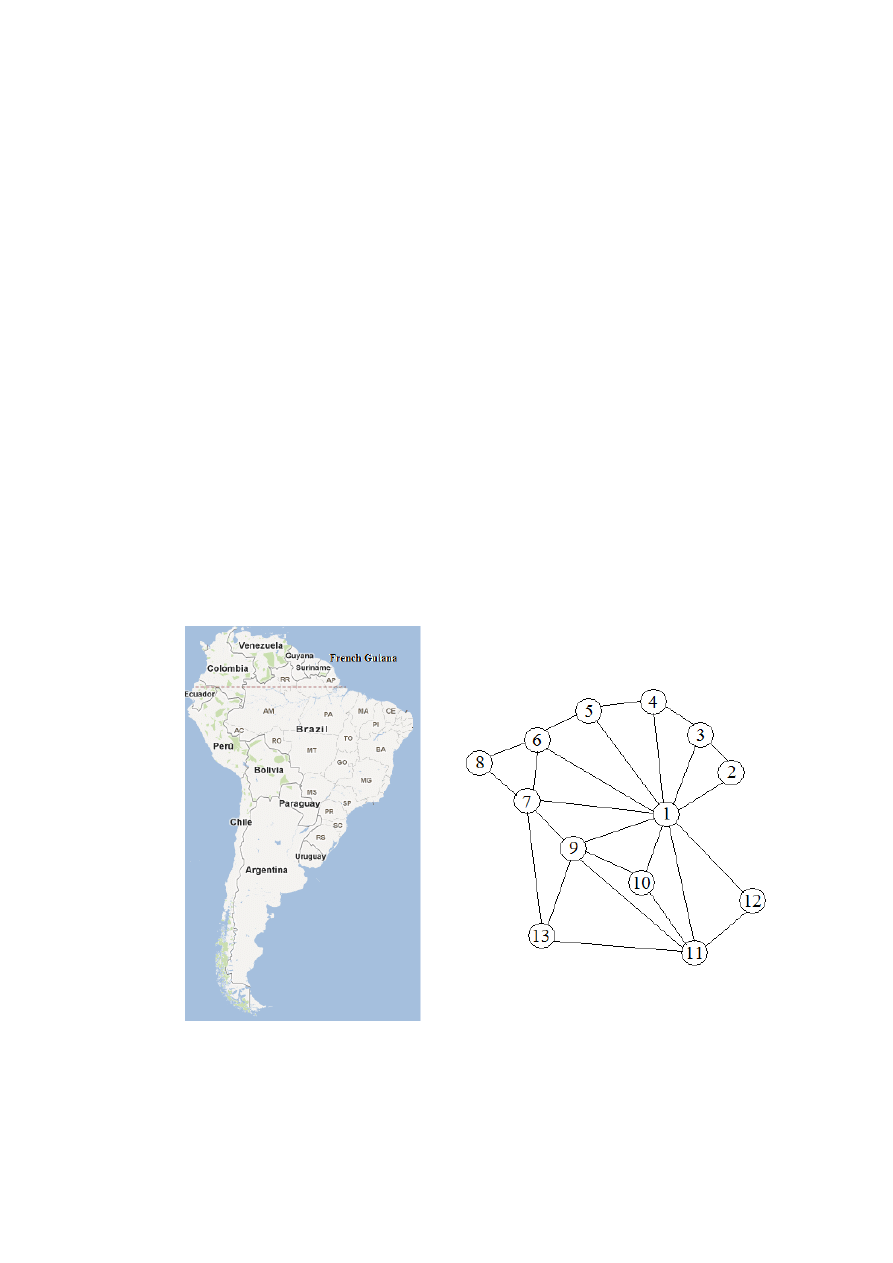
raża się w „języku” grafów. Rozważmy dla przykładu zadanie pokolorowania mapy politycznej.
Jaka jest minimalna liczba kolorów potrzebna do pokolorowania mapy z oczywistym warun-
kiem, że kraje sąsiadujące mają różne kolory? Jedna z trudności, która pojawia się przy próbie
rozwiązania problemu, jest związana z tym, że nawet zredukowana wersja mapy, taka jak na ry-
sunku 1, jest zwykle zaśmiecona nieistotnymi informacjami, jak na przykład: skomplikowane
granice, punkty graniczne, w których zbiega się trzy lub więcej krajów, otwarte morza, wijące
sie rzeki. Tych „zakłóceń” nie ma w matematycznym modelu z rysunku 1, jakim jest graf z jed-
nym wierzchułkiem dla każdego kraju (1 to Brazylia, 11 to Argentyna) oraz krawędziami mię-
dzy sąsiadami. Zawiera on jedynie informacje potrzebne przy kolorowaniu i nic więcej. Precy-
zyjnym celem jest teraz przypisanie wierzchołkom grafu kolorów tak, aby żadna krawędź nie
miała końców w tym samym kolorze.

Rys. 1. Mapa oraz jej graf

Kolorawanie grafu nie jest wyłącznie zadaniem projektantów map. Przypuśćmy, że uni-

wersytet potrzebuje zaplanować egzaminy dla wszystkich grup i chce przeprowadzić je w moż-
liwe najkrótszym czasie. Jedynym ograniczeniem jest, że jeśli jakiś student będzie podchodził do
dwóch egzaminów, to nie mogą one odbywać się w tym samym czasie. Aby wyrazić powyższy
problem za pomocą grafu, przypiszemy jednemu wierzchółkowi jeden egzamin oraz wstawimy

2

krawędź między dwa wirzchółki, dla których ma miejsce konflikt, tzn. gdy istnieje osoba zdająca
egzaminy odpowiadające obu końcom krawiędzi. Przypuśćmy, że każdy przedział czasu, w któ-
rym odbywa się jakiś egzamin, ma przypicany unikatowy kolor. Wtedy przypisanie przedziałów
czasu egzaminom to dokładnie pokolorowanie grafu.

Pewne podstawowe operacje na grafach pojawiają się tak często i w tak przeróżnych kon-

tekstach, że wiele wysiłków włożono w znalezenie dla nich efektywnych procedur. W niniej-
szym wykładzie zajmiemy sie najbardziej podstawowymi algorytmami ukazującymi podstawo-
wą, spójną strukturę grafu.

Formalnie graf jest zdefiniowany jako zbiór wierzchołków (czasem nazywanych także

węzłami) V oraz zbiór krawędzi E między wybranymi parami wierzchołków. Na przykładzie z
mapa

}

13

...,

,

2

,

1

{



V

, a zbiór E zawiera między innymi

}

2

,

1

{

,

}

11

,

9

{

oraz

}

13

,

7

{

. Krawiędź

między wierzchołkami x oraz y oznacza, że „x ma granicę z y”. Jest to relacja symetryczna – im-
plikuje, że także y ma granicę z x – oznaczamy ją, używając notacji dla zbiorów, tzn.

}

,

{

y

x

c



.

Takie krawiędzie są nieskierowane i są częścią grafu nieskierowanego.

Czasami graf opisuje relację, która nie ma wzajemności, w takim przypadku koniecznie

jest użycie krawędzi z oznaczeniem kierunku. Wówczas graf może zawierać skierowaną kra-
wędź c z x do y (co zapisujemy

)

,

(

y

x

c



) albo z y do x (co zapisujemy

)

,

(

x

y

), albo obie.

Szczególnym przypadkiem olbrzymiego grafu skierowanego jest graf zależności w sieci World
Wide Web. Ma on wierzchołek dla każdej strony w Internecie oraz skierowaną krawędź

)

,

(

v

u

,

kiedy ze strony u istnieje połączenie za stroną v; łącznie miliardy wierzchołków i krawędzi! Zro-
zumienie najbardziej podstawowych, spójnych własności sieci WWW jest wielkim ekonomicz-
nym i spółecznym wyzwaniem. Chociaż rozmiar problemu jest zniechęcający, zobaczymy nie-
długo, że wiele wartościowych informacji o strukturze grafu, na szczęście, można określić w
czasie liniowym.

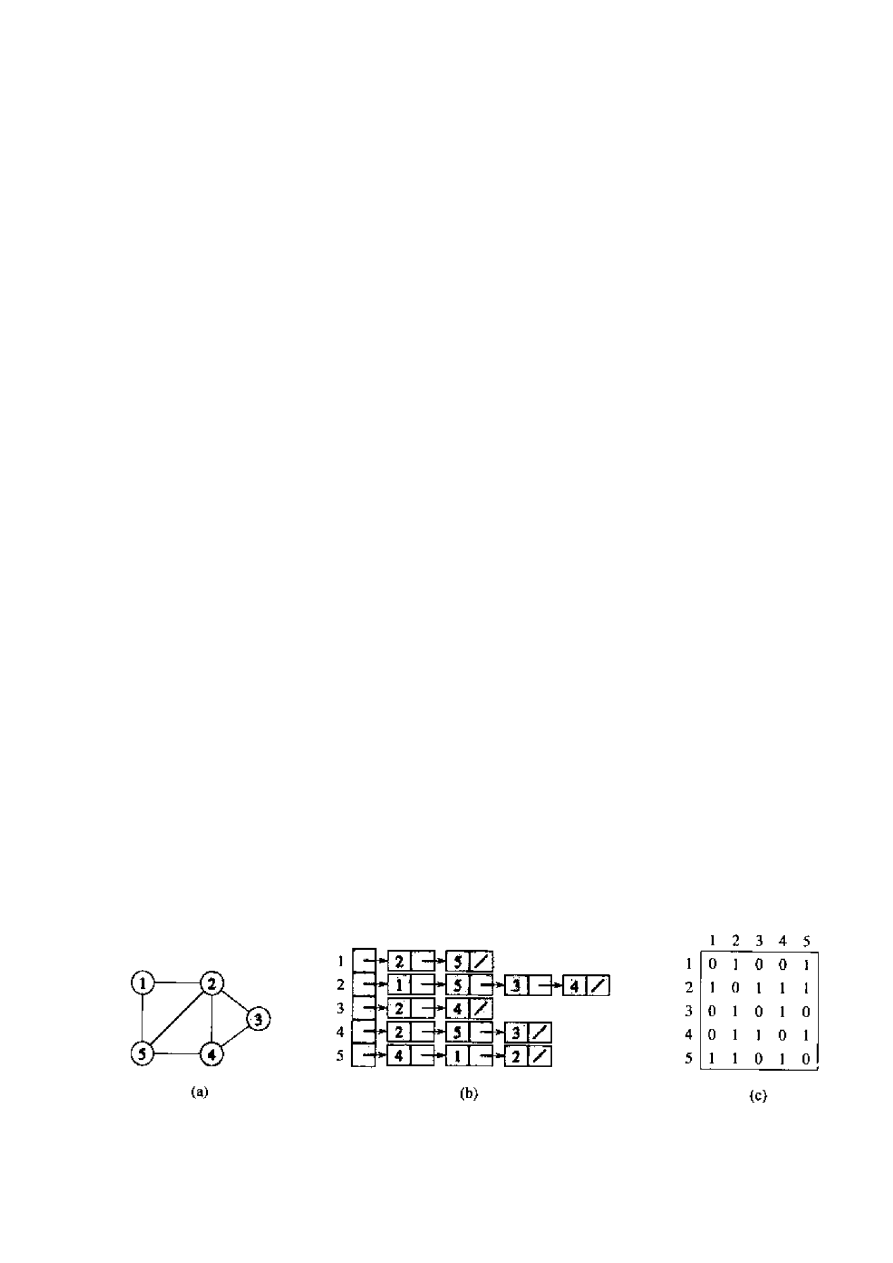
1. Reprezentacje grafów

Istnieją dwa standartowe sposoby reprezentowania grafu

)

,

(

E

V

G



: za pomocą list sąsiedztwa

(ang. adjacency list) lub macierzy sąsiedztwa (ang. adjacency matrix). Jeśli mamy

|

| V

n



wierzchołków

1

v ,

2

v , ...,

n

v , to macierz sąsiedztwa grafu jest tablicą

n

n



, której element

)

,

(

j

i

jest równy









razie

przeciwnym

w

v

do

v

z

krawiedz

istnieje

jesli

a

j

i

ij

,

0

,

1

Dla grafów nieskierowanych macierz ta jest symetryczna, ponieważ krawiędź

}

,

{ v

u

można po-

traktować jako krawiędź w obu kierunkach.

Największą zaletą tej reprezentacji jest to, że istnienie krawiędzi może być sprawdzone w

czasie stałym, z jednym dostępem do pamięci. Jednakż macierz zajmuje

)

(

2

n

O

miejsca, co jest

marnotrawstwem pamięci, gdy graf nie ma zbyt dużo krawiędzi.

Alternatywną reprezentacjaą grafu, której rozmiar jest proporcjonalny do liczby krawię-

dzi, są listy sąsiedztwa. Zawierają one

|

| V list z dowiązaniami, jedną dla każdego wierzchołka.

Na liście sąsiedztwa wierzchołka u są przechowywane nazwy wierzchołków, do których z u jest

3

wychodząca krawiędź – tzn. wierzchołki v, dla których

E

v

u



)

,

(

. Każda krawiędź pojawia się

na dokładnie jednej liście z dowiązaniami, gdy graf jest skierowany, a na dwóch listach, gdy graf
jest nieskierowany. W obu przypadkach całkowity rozmiar struktury wynosi

|)

(| E

O

. Wyszuki-

wanie konkretnej krawiędzi nie zajmuje już czasu stałego, gdyż wymaga przefiltrowania listy
sąsiedztwa dotyczącej wierzchołka u. Jednakże łatwe jest powtórzenie obliczeń dla wszystkich
sąsiadów danego wierzchołka (przez przeglądanie odpowiednej listy), co jak zobaczymy póżniej,
jest bardzo użyteczną operacją w algorytmach grafowych. Dla grafów nieskierowanych repre-
zentacja jest symetryczna: v jest na liście sąsiedztwa u wtedy i tylko wtedy, gdy u jest na liście
sąsiedztwa v.

Która z dwu opisanych reprezentacji jest lepsza: macierz sąsiedztwa czy listy sąsiedztwa?

Zależy to od relacji między liczbą wierzchołków grafu

|

| V

oraz liczbą krawiędzi

|

| E

. Zazwy-

czaj preferuje się reprezentację listową, ponieważ umożliwia ona przedstawienie w zwarty spo-
sób grafów rzadkich (ang. sparse) – to jest takich, dla których

|

| E

jest dużo mniejsze od

2

|

| V

.

Kiedy graf jest gęsty (ang. dense) –

|

| E

jest blizkie

2

|

| V

– lub gdy istnieje potrzeba szybkiego

stwierdzania, czy istnieje krawiędź łącząca dwa dane wierzchołki, wtedy może być korzystniej-
sza reprezentacja macierzowa.

2. Przeszukiwanie grafu nieskierowanego

2.1. Przeszukiwanie wszerz

Przeszukiwanie wszerz jest jednym z najprostszych algorytmów przeszukiwania grafu i pierwo-
wzorem wielu innych algorytmów grafowych. Dane są graf

)

,

(

E

V

G



i wyróżniony wierzcho-

łek początkowy s (nazywany dalej źródlem). W przeszukiwaniu grafu wszerz są systematycznie
badane krawiędzie G w celu odwiedzania każdego wierzchołka, który jest osiągalny z s. Jedno-
cześnie są obliczne odleglości (najmniejsza liczba krawiędzi) od źródła s do wszystkich osiągal-
nych wierzchołków. Wynikiem działania algorytmu jest też dzewo przeszukiwania wszerz o ko-
rzeniu w s, które zawiera wszystkie osiągalne wierzchołki. Dla każdego wierzchołka v osiągal-
nego z s ścieżka w drzewie przeszukiwania wszerz od s do v odpowiada najkrótszej ścieżkie od s
do v w G, tzn. ścieżce zawieralącej najmniejszą możliwą liczbę krawiędzi. Algorytm przeszuki-
wania wszerz działa zarówno dla grafów skierowanych, jak i nieskierowanych.

Nazwa przeszukiwanie wszerz bierze się stąd, że w tym algorytmie granica między

wierzchołkami odwiedzonymi i nie odwiedzonymi jest przekraczana jednocześnie na calej jej
szerokości. To znaczy, wierzchołki w odległości k od źródla są odwiedzane przed wierzchołkami
w odległości

1



k

.

Podczas przeszukiwania wszerz każdy wierzchołek jest kolorowany na biało, szaro lub

czarno. Początkowo wszystkie wierzchołki są białe i mogą potem zmienić kolor na szary lub
czarny. Podczas przeszukiwania każdy nowo napotkany wierzchołek staje się odwiedzony, a je-
go kolor zmienia się na inny niż biały. Zatem wierzchołki szare i czarne są już odwiedzone, ale
rozróżnia się je w celu zapewnienia poprawności wykonywania przeszukiwania. Jeśli

E

v

u



)

,

(

i wierzchołek u jest czarny, to wierzchołek v jest albo szary albo czarny; tzn. wszystkie wierz-
chołki sąsiadujące z u są już odwiedzone. Wierzchołki szare mogą mieć białych sąsiadów; two-
rzą one granicę między odwiedzonymi i nie odwiedzonymi wierzchołkami.

Algorytm przeszukiwania wszerz buduje drzewo przeszukiwania wszerz, początkowo

zawierające tylko korzeń, który jest wierzchołkiem źródłowym s. Gdy podczas przeglądania listy
sąsiedztwa odwiedzonego wierzchołka u napotkany jest nie odwiedzony wierzchołek v, krawiędź

)

,

( v

u

i wierzchołek v są dodawane do drzewa. Mówimy, że u jest poprzednikiem lub ojcem v

w drzewie przeszukiwania wszerz. Ponieważ wierzchołek jest odwiedzany co najmniej raz, ma
zatem co najwyżej jednego ojca. Relacje przodek-potomek w drzewie przeszukiwania wszerz są
definiowane względem korzenia s jak zazwyczaj: jeśli u znajduje się na ścieżce prowadzącej od
s do wierzchołka v, to u jest przodkiem v i v jest potomkiem u.

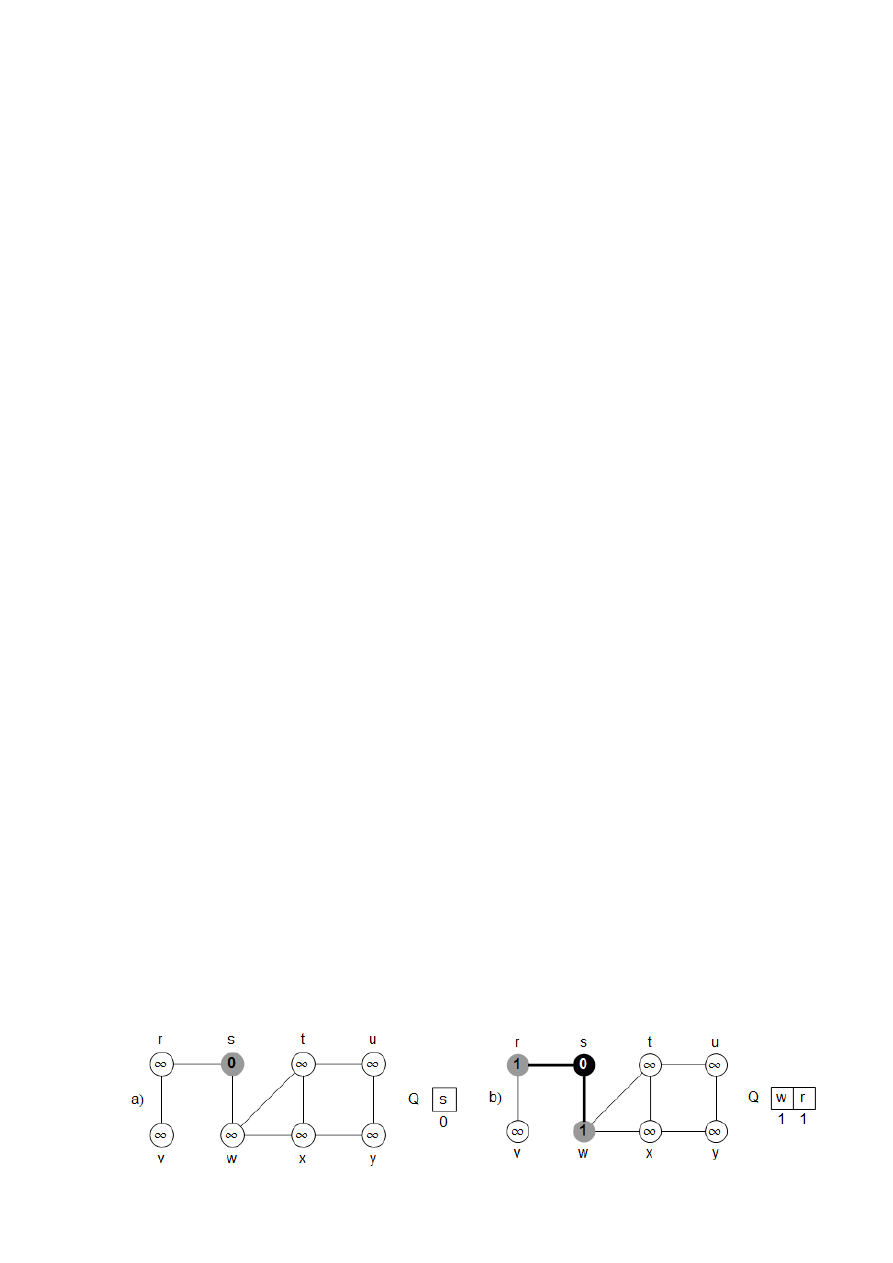
4

W algorytmie przeszukiwania wszerz BFS (ang. breadth-first search) zakłada się, że wej-

ściowy graf

)

,

(

E

V

G



jest reprezentowany przez listy sąsiedztwa. Z każdym wierzchołkiem w

grafie wiążemy kilka dodatkowych zmiennych. Kolor każdego wierzchołka

V

u



jest pamięta-

ny w zmiennej

]

[u

color

, a poprzednik u jest pamiętany w zmiennej

]

[u



. Jeśli u nie ma po-

przednika (np. jeśli

s

u



lub u nie zastał odwiedzony), to

NIL

u



]

[



. Odleglość od źródła s do

wierzchołka u jest obliczana w zmiennej

]

[u

d

. W algorytmie jest używana też kolejka Q typu

FIFO, w której pamięta się szare wierzchołki.
Implementacja kolejki w tablicy

]

..

1

[ n

Q

: Atrybut

]

[Q

head

takiej kolejki wskazuje na jej głowę,

tj. początek, natomiast atrybut

]

[Q

tail

wyznacza następną wolną pozycję, na którą można wsta-

wić do kolejki nowy element. Elementy kolejki znajdują się na pozycjach

]

[Q

head

,

1

]

[



Q

head

, ...,

1

]

[



Q

tail

; umawiamy się tutaj, że tablica Q jest „cykliczna”, tzn. pozycja o

numerze 1 jest bezpośrednim następnikem pozycji o numerze n. Jeśli

]

[

]

[

Q

tail

Q

head



, to ko-

lejka jest pusta. Początkowo

1

]

[

]

[





Q

tail

Q

head

. Jeżeli kolejka jest pusta, to próba usunięcia

elementu z kolejki za pomocą operacji Dequeue (element może zostać usunięty z kolejki tylko
wtedy, gdy znajduje się na jej początku) jest sygnalizowana jako błąd niedomiaru. Jeśli

1

]

[

]

[





Q

tail

Q

head

, to kolejka jest pełna. Próba wstawienia nowego elementu do kolejki za

pomocą operacji Enqueue (zostaje on umieszczony na końcu kolejki) jest w takiej sytuacji sy-
gnalizowana jako błąd przepełnienia.

BFS(G, s)

1

for każdy wierzchołek

}

{

]

[

s

G

V

u





2

do

]

[u

color

:= Biały

3





:

]

[u

d

4

NIL

u



]

[



od

5

]

[s

color

:= Szary

6

0

:

]

[



s

d

7

NIL

s



:

]

[



8

Q := {s}

9

while



Q



10

do

]

[

:

Q

head

u



11

for każdy

]

[u

Adj

v



12

do if

]

[v

color

= Biały

13

then

]

[v

color

:= Szary

14

1

]

[

:

]

[





u

d

v

d

15

u

v



:

]

[



16

Enqueue(Q, v) fi od

17

Dequeue(Q)

18

]

[u

color

:= Czarny od

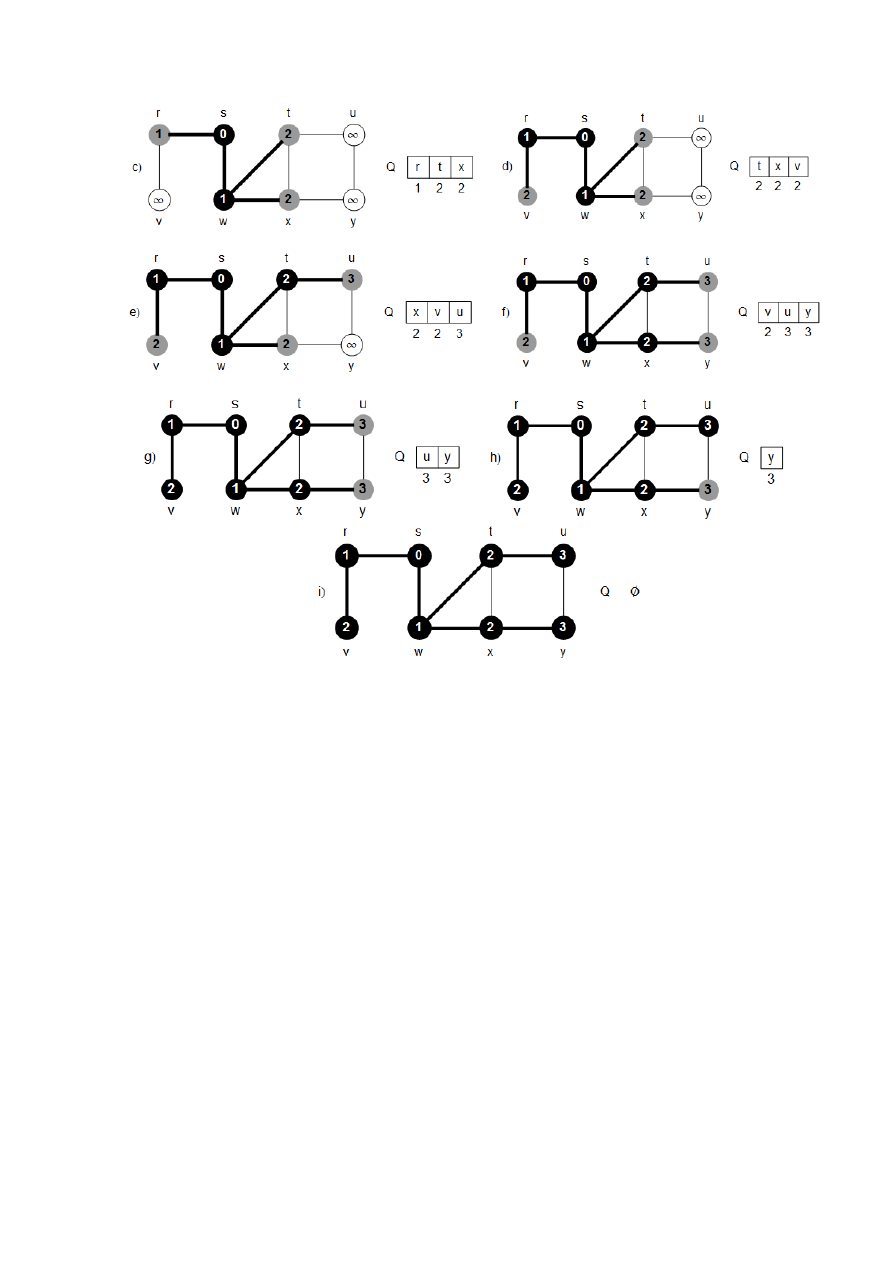
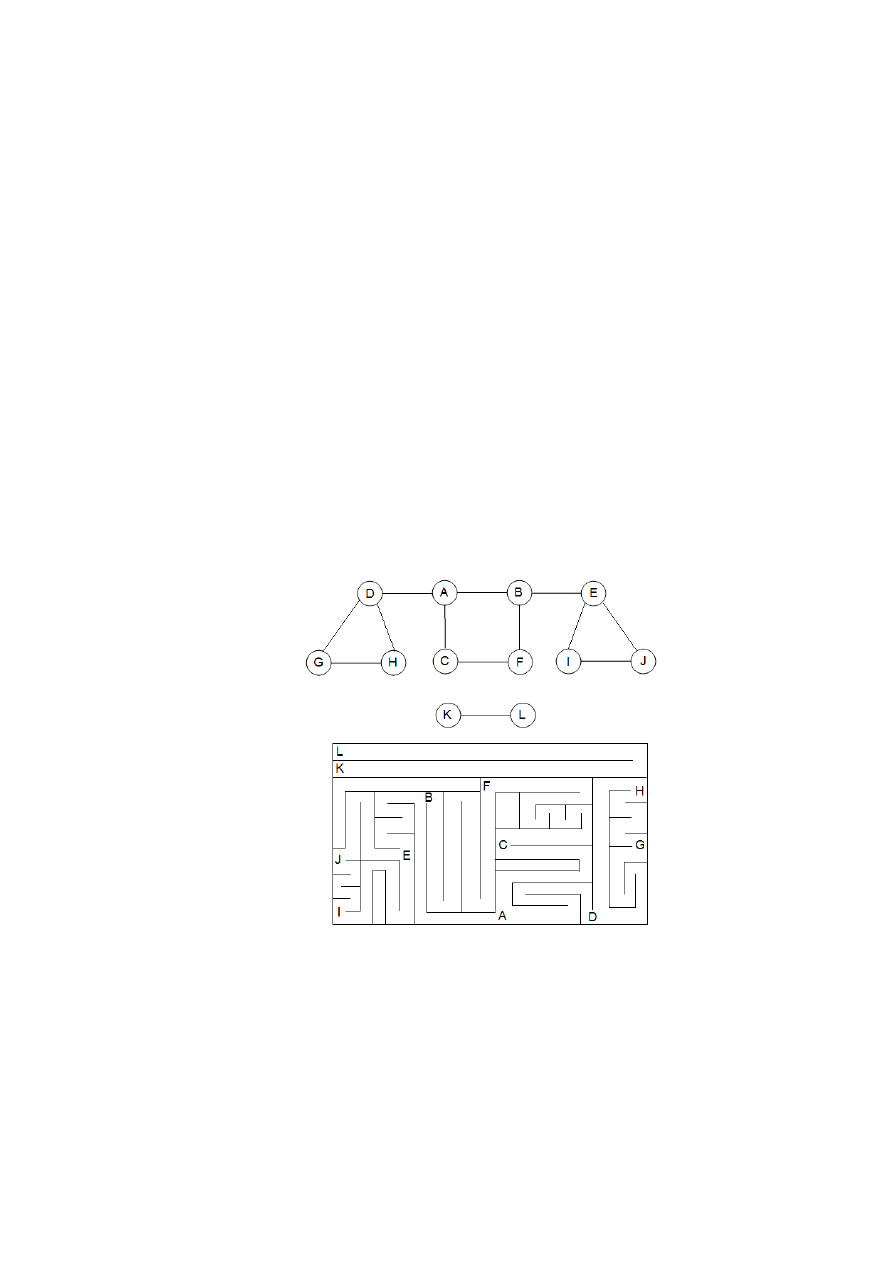
Rysunek 2 ilustruje działanie procedury BFS na przykładowym grafie.

5

Rys. 2. Działanie procedury BFS na grafie nieskierowanym. Krawiędzie drzewowe tworzone

przez BFS są zacieniowane. W każdym wierzchołku u jest podana wartość

]

[u

d

. Stan kolejki Q

przedstawiony na początku każdej iteracji instrukcji while (wiersze 9-18). Poniżej wierzchołków

w kolejce znajdują się ich odległości od źródła.

Procedura BFS działa w następujący sposób. W wierszach 1-4 każdy wierzchołek u różny

od korzenia jest kolorowany na biało, zmienna

]

[u

d

jest inicjowana na nieskończoność, a

wskaźnik

]

[u



do ojca u przyjmuje wartość NIL. W wierszu 5 źródło s jest kolorowane na sza-

ro, ponieważ przyjmuje się, że s zostaje odwiedzony na początku działania procedury. W wier-
szu 6 odległość

]

[s

d

jest inicjowana na 0, a w wierszu 7 wskaźnik do ojca s przyjmuje wartość

NIL. W wierszu 8 jest inicjowana kolejka Q. Początkowo Q zawiera tylko wierzchołek s, później
Q zawiera zawsze szare wierzchołki.

Główna pętla programu jest zapisana w wierszach 9-18. Pętla jest wykonywana tak dłu-

go, jak długo istnieją szare wierzchołki. Szare wierzchołki są wierzchołkami odwiedzonymi, któ-
rych listy sąsiedztwa nie zostały jeszcze w całości przejrzane. W wierszu 10 jest pobierany szary
wierzchołek u z początku kolejki Q. Każdy wierzchołek v na liście sąsiedztwa u jest rozważany
w pętli for w wierszach 11-16. Jeśli v jest biały, to nie był dotychczas odwiedzony. Wierzchołek
v jest kolorowany na szaro, a

]

[v

d

przyjmuje wartość

1

]

[



u

d

. Następnie wierzchołek u jest za-

pamiętywany jako ojciec wierzchołka v. Na koniec v jest umieszczany jako ostatni element w
kolejce Q. Kiedy wszystkie wierzchołki z listy sąsiedztwa u są już zbadane, jest usuwany z Q i
kolorowany na czarno (wiersze 17-18).

Operacje wstawiania do kolejki i usuwania z kolejki zajmują czas

)

1

(

O

. Stąd lączny czas

wykonywania operacji na kolejce wynosi

)

(V

O

. Ponieważ lista sąsiedztwa każdego wierzchołka

6

jest przeglądana tylko wtedy, gdy wierzchołek zostanie usunięty z kolejki, lista sąsiedztwa każ-
dego wierzchołka jest przeglądana co najwyżej raz. Ponieważ suma długości wszystkich list są-
siedztwa wynosi

)

(E



, łączny czas spędzany na przeglądaniu list sąsiedztwa wynosi

)

(E

O

. Ini-

cjowanie zabiera czas

)

(V

O

i dlatego łączny czas dzialania procedury BFS wynosi

)

(

E

V

O



.

Tak więc przeszukiwanie wszerz jest wykonywane w czasie liniowo zależnym od rozmiaru re-
prezentacji liniowej grafu

)

,

(

E

V

G

.

2.2. Przeszukiwanie w głąb

Przeszukiwanie w głąb (ang. depth-first search) jest zaskakująco wszechstronną procedurą dzia-
łająca w czasie liniowym, która polega na sięganiu „głębiej” w graf, jeżeli jest to tylko możliwe.
Najbardziej podstawowe pytanie, na które znajduje odpowiedź, brzmi następująco:

Jaka część grafu jest osiągalna z danego wierzchołka?

Aby zrozumieć, na czym polega to zadanie, spróbujmy postawić się na miejscu kompute-

ra, któremu właśnie dano nowy graf, powiedzmy w postaci list sąsiedztwa. Wykorzystując tę
reprezentację, można wykonać tylko jedną podstawową operację: wyszukiwanie sąsiadów
wierzchołka. Z tym podstawowym narzędziem problem osiągalności da się porównać do cho-
dzenia po labiryncie (Rys. 3). Rozpoczynamy w ustalonym miejscu, a po dotarciu do skrzyżo-
wania (wierzchołka), dostrzegamy dużą liczbę korytarzy (krawędzi), którymi możemy iść dalej.
Nieostrożny wybór korytarza może prowadzić do chodzenia w kółko lub spowodować przega-
pienie pewnej osiągalnej części labiryntu. Jasne jest zatem, że podczas przeglądania musimy za-
pisywać pewne informacje.

Rys. 3. Badanie grafu przypomina nawigacjcę w labiryncie

Każdy wie, że wszystko, czego potrzebujemy do przejścia labiryntu, to kłębek sznurka i

kawałek kredy. Zaznaczając kredą skrzyżowania, które już odwiedziliśmy, chronimy się przed
zapętleniem. Używając sznurka, możemy zawsze wrócić do punktu wyjścia oraz do korytarzu,
które ostatnio widzieliśmy, a które nie zostały jeszcze zbadane.

W jaki sposób możemy symulować za pomocą komputera te prymitywne narzędzia, ja-

kimi są kreda i sznurek? Ślady kredą łatwo jest zrealizować: dla każdego wierzchołka przecho-
wujemy zmienną boolowską wskazującą, czy dany wierzchołek był już przeglądany. Odpowied-
nią informatyczną analogią do kłębka sznurka jest stos. Za pomocą sznurka mamy realizować
dwie podstawowe operacji – rozwijanie, aby dotrzeć do kolejnego skrzyżowania (odpowiedni-

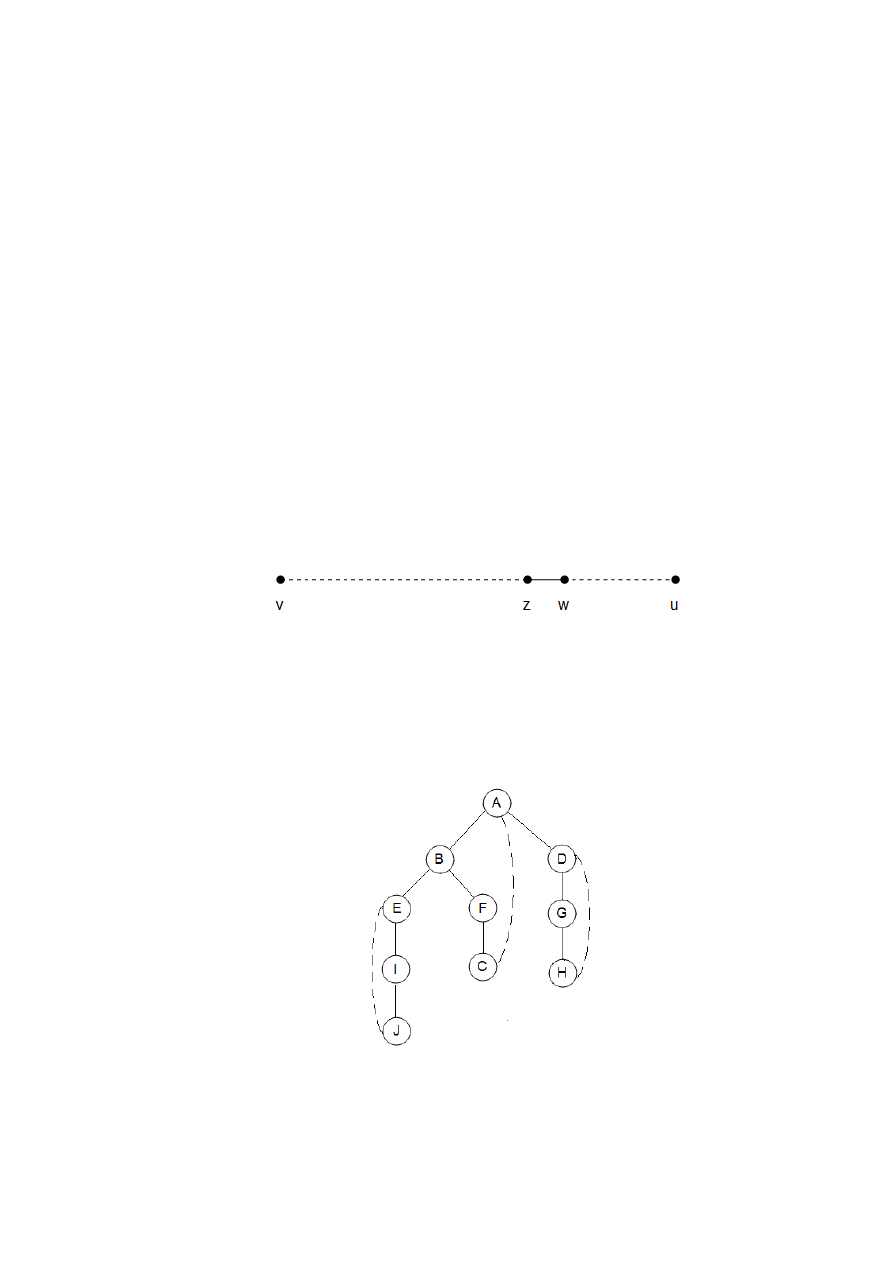
7

kiem dla stosu jest operacja push – wstaw nowy wierzchołek), i zawijanie, by wrocić do ostat-
niego skrzyżowania (operacja pop – zdejmij ze stosu).

W procedurze użyjemy stosu w sposób pośredni – poprzez rekursję (która jest implemen-

towana z użyciem stosu aktywnych rekordów). Uzyskany algorytm jest przedstawiony na rysun-
ku 4. Procedury previsit oraz postvisit są opcjonalne, służą one do oznaczenia operacji wykony-
wanych na wierzchołku, kiedy jest on odkryty po raz pierwszy i kiedy wychodzimy z nego po
raz ostatni. Zobaczymy wkrótce ciekawe ich zastosowania.

procedura explore (v)
Wejście:

)

,

(

E

V

G



jest grafem;

V

v



Wyjście: visited(u) ma wartość true dla wszystkich wierzchołków u osiągalnych z v

visited(v) := true
previsit(v)
for każda krawędź

E

u

v



)

,

(

do if not visited(u) then explore(u) fi od
postvisit(v)

Najpierw należy potwierdzić, że operacja explore zawsze działa poprawnie. Z pewnością

nie jest to zbyt trudne, gdyż poruszamy się jedynie z wierzchołków do ich sąsiadów oraz nigdy
nie wskoczymy do obszaru nieosiągalnego z v. Ale czy znajdziemy wszystkie wierzchołki osią-
galne z v? Załóżmy, że jest pewien u, który został pominięty, wybierzmy ścieżkę z v do u,
spójrzmy na ostatni wierzchołek na tej ścieżce, który był przeglądany, i oznaczmy go przez z.
Niech w będzie wierzchołkiem następnym po z na tej samej ścieżce.

Wiemy, że z był przeglądany, natomiast w nie był. Mamy sprzeczność. Kiedy operacja explore
była w wierzchołku z, zauważyłaby w oraz poszła go odwiedzić.

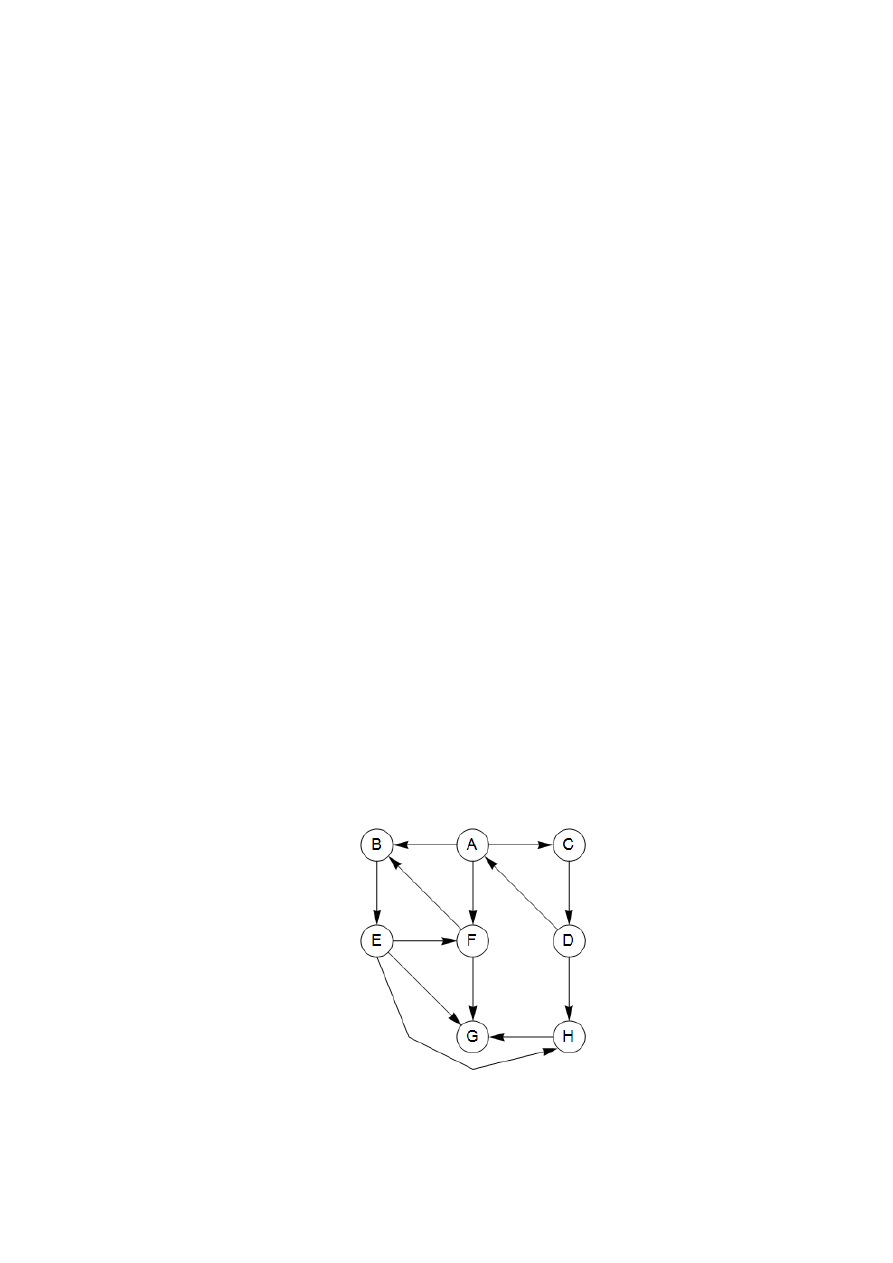
Na rys. 4 przedstawiony jest wynik działania procedury explore na naszym przykłado-

wym grafie, stratującej w węźle A i przeglądającej wierzchołki w porządku alfabetycznym, kiedy
jest możliwość wybory kolejnego wierzchołka. Krawiędzie proste to te, przez które algorytm
wędrował, każda z nich była związana z wywołaniem operacji explore i prowadziła do odwie-
dzenia nowego wierzchołka.

Rys. 4. Wynik działania procedury explore(A) na grafie z rys. 3

Na przykład, podczas przeglądania B została zauważona krawiędź B-E, a ponieważ E nie

był jeszcze przeglądany, algorytm przeszedł ją przez wywołanie explore(E). Krawędzie zazna-
czone na rysunku linią ciągła tworzą drzewo (spójny graf bez cykli) i dlatego są nazywane kra-

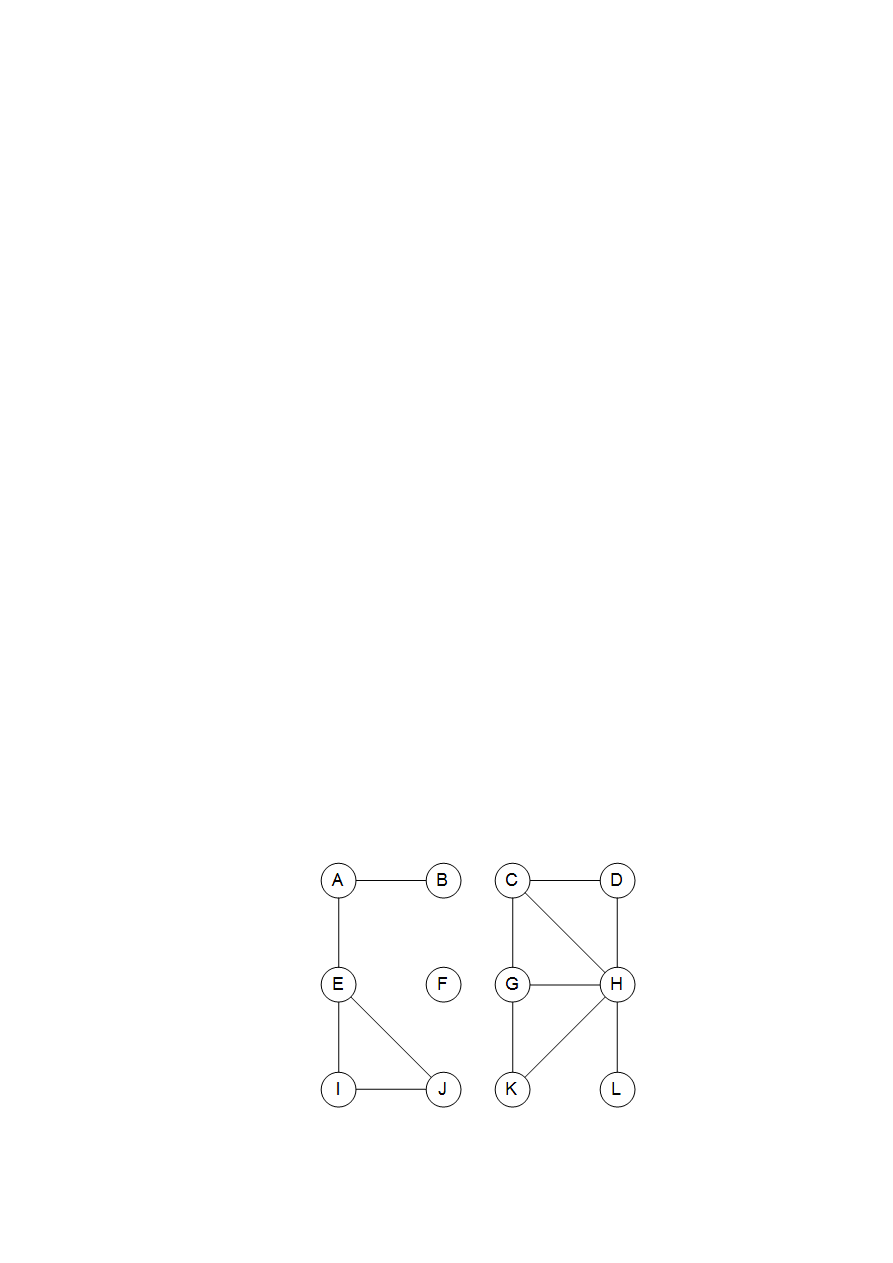
8

wędziami drzewowymi. Krawędzie zaznaczone linią przerywaną były pomijane, ponieważ pro-
wadziły z powrotem do znajomego terenu, do wierzchołków wcześniej odwiedzonych. Są one
nazywane krawędziami powrotnymi.

Procedura explore odwiedza tylko ta część grafu, która jest osiągalna z punktu startowe-

go. Aby przebadać pozostałą część grafu, należy uruchomić procedurę kolejny raz w innym
miejscu, na jeszcze nieprzeglądanym wierzchołku. Algorytm, zwany przeszukiwaniem w gląb
(ang. depth-first search, DFS), wykonuje procedurę explore wielokrotnie, dopóki cały graf nie
zostanie przemierzony.

procedura dfs (G)
for każdy wierzchołek

V

v



do visited(v) := false od

for każdy wierzchołek

V

v



do if not visited(v) then explore(v) fi od

Analizując czas działania algorytmu DFS, możemy zauważyć, że dzięki użuciu tablicy

visited (kredowym znakom) każdy wierzchołek jest odwiedzany tylko raz. Podczas przeglądania
wierzchołka wykonywane są:

1. Zaznaczenie wierzchołka, że jest już odwiedzony, oraz operacje pre/postvisit, co po-

chłania pewną stałą ilość pracy.

2. Pętla, w której przeglądane są sąsiadujące krawędzie, w celu znalezenia nieodwie-

dzonych wierzchołków.

Dla każdego wierzchołka pętla ta zajmuje różną ilość czasu, rozważmy zatem wszystkie

wierzchołki razem. Łączna praca wykonana w kroku 1 to

|)

(| V

O

. W kroku 2, podczas przebie-

gu całego algorytmu DFS, każda krawiędź

E

y

x



}

,

{

jest rozważana dokładnie dwa razy, raz

podczas explore(x), drugi raz podczas explore(y). Łączny czas kroku 2 jest więc równy

|)

(| E

O

,

czyli czas działania przeszukiwania w głąb wynosi

|)

|

|

(|

E

V

O



– jest liniowy względem roz-

miaru wejścia. Czas działania algorytmu jest możliwe najlepszy, jest to tylko czas potrzebny do
przeczytania list sąsiedztwa.

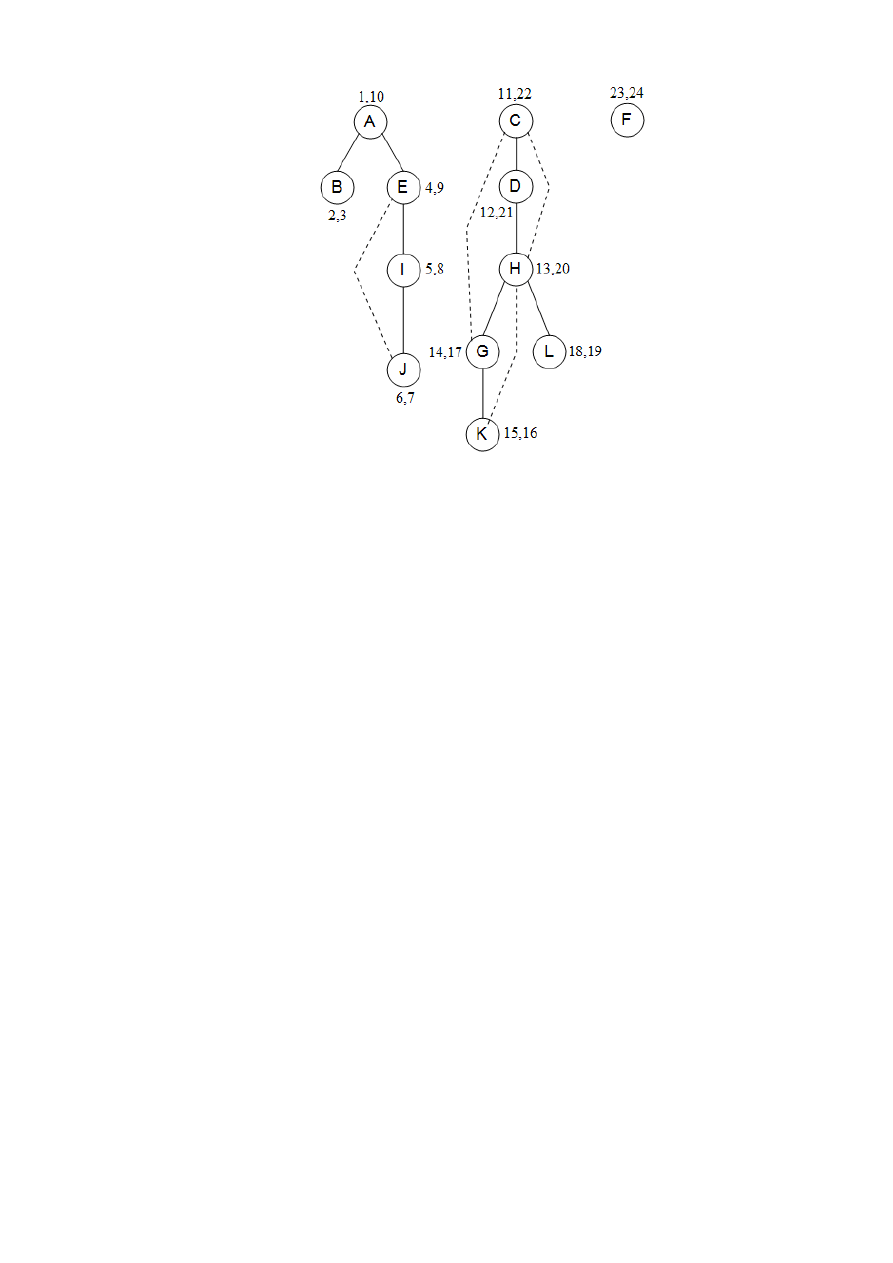
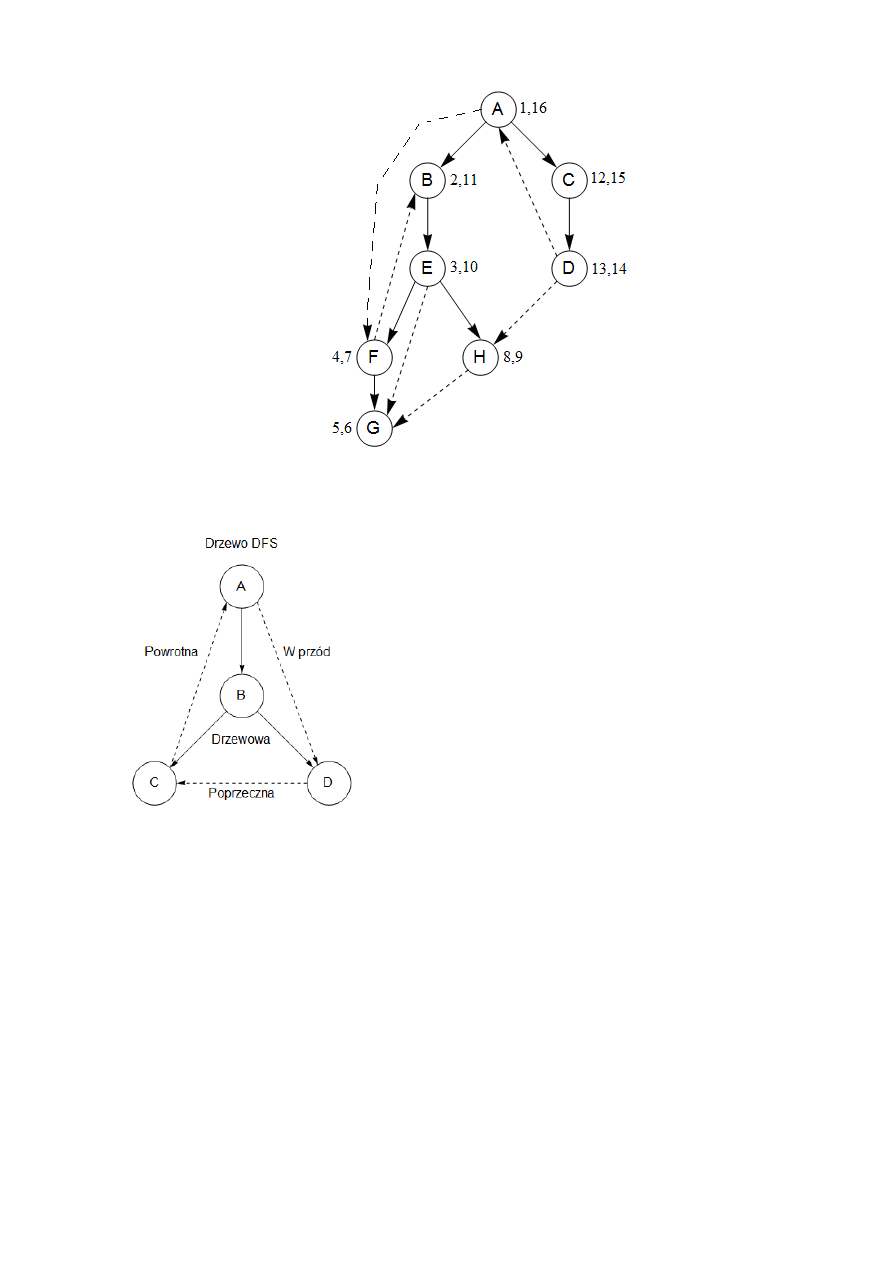
Na rys. 5 przedstawiony jest wynik przeszukiwania w głąb na grafie 12-

wierzchołkowym, w którym wierzchołki były przeglądane w kolejności alfabetycznej (ignoru-
jemy na razie pary numerów oznaczające czasy bycia w wierzchołku). Zewnętrzna pętla algo-
rytmu DFS wywołuje operację explore trzy razy, na A, C i w końcu na F. Jako wynik uzyskuje-
my trzy drzewa, każde z korzeniem w wierzchołku startowym. Tworzą one razem las.

9

Rys. 5. Graf 12-wierzchołkowy oraz las przeglądania DFS

2.3. Spójność w grafie nieskierowanym

Nieskierowany graf jest spójny (ang. connected), jeśli między każdą parą jego wierzchołków ist-
nieje ścieżka. Graf z rysunku 5 nie jest spójny, ponieważ nie ma na przykład ścieżki od A do K.
Ma on jednak trzy rozłączne spójne obszary odpowiadające zbiorom wierzchołków:

}

,

,

,

,

{

J

I

E

B

A

,

}

,

,

,

,

,

{

L

K

H

G

D

C

,

}

{F

.

Obszary te są nazywane spójnymi składowymi; każdy z nich jest podgrafem, który jest

spójny i nie ma krawędzi do pozostalych wierzchołków. Kiedy dla konkretnego wierzchołka
wywołana jest operacja explore, wyznacza ona precyzyjne spójną składową zawierającą ten
wierzchołek. Za każdym razem, kiedy zewnętrzna pętla algorytmu DFS wywołuje explore, wy-
znaczona jest nowa spójna skaładowa.

Przeszukiwanie w głąb można w trywialny sposób wykorzystać do sprawdzenia, czy graf

jest spójny, i bardziej ogólnie do przypisania każdemu wierzchołkowi v numeru ccnum[v], który
oznacza spójną skaładową, do której on należy. Wszystko, co wystarczy zrobić, to

procedura previsit (v)
ccnum[v] := cc

gdzie początkowa wartość cc jest równa zeru i jest incrementowana za każdym razem, kiedy
procedura DFS wywołuje explore.

2.4. Porządki previsit i postvisit

Zobaczyliśmy, w jaki sposób przeszukiwanie w głąb – kilka skromnych wierszy kodu – jest w
stanie odkrywać spójną strukturę grafu nieskierowanego w liniowym czasie. Opisane wyszuki-
wanie jest jednak daleko bardziej wszechstronne. Aby rozwinąć tę myśl, podczas procesu prze-
glądania zbierzemy trochę więcej informacji o grafie: dla każdego wierzchołka zapiszemy czasy
dwóch ważnych wydarzeń, moment pierwszego odwiedzenia wierzchołka (odpowiadający ope-
racji previsit) oraz moment opuszczenia wierzchołka (postvisit). Na rysunku 5 pokazane są
omawiane czasy dla wcześniejszego przykładu, w którym są 24 wydarzenia. Piąte wydarzenie to
odwiedzenie I. Wydarzenie 21 to opuszczenie na dobre wierzchołka D.

10

Jedną z metod wyznaczenia tablic pre oraz post z numerami w porządku previsit oraz

postvisit jest zdefiniowanie zwykłego licznika clock, ustawionego początkowo na 1, który jest
modyfikowany w następujący sposób.

procedura previsit (v)
pre[v] := clock
clock := clock + 1

procedura postvisit (v)
post[v] := clock
clock := clock + 1

Okaże się wkrótce, że odmierzenie czasu będzie miało duże znaczenie. Tymczasem, ko-

rzystając z rysunky 4, zauważmy, że:
Własność. Dla każdych dwóch wierzchołków u oraz v dwa przedziały [pre(u), post(u)] oraz
[pre(v), post(v)] są albo rozłączne, albo jeden zawiera się w drugim.

Dlaczego? Ponieważ [pre(u), post(u)] jest w istocie przedziałem czasu, w którym wierz-

chołek u jest na stosie. Zasada działania stosu: ostatni wchodzi, pierwszy wychodzi, wyjaśnia
resztę.

3. Przeszukiwanie w głąb grafu skierowanego

3.1. Rodzaje krawędzi

Nasze przesukiwanie grafu w głąb możemy zastosować bez żadnych zmian dla grafu skierowa-
nego, uważając jedunie, aby przechodzić krawędzie tylko w zalecanym kierunku. Na rysunku 6
przedstawiony jest przykład grafu i jego drzewo przeszukiwań, które uzyskamy, kiedy rozważ-
my wierzchołki w porządku leksykograficznym. Podczas analizy grafów skierowanych pomocna
będzie terminologia dla ważnych relacji między węzlami drzewa. Wierzchołek A jest korzeniem
drzewa (ang. root), wszystkie pozostałe wierzchołki są jego potomkami (ang. descendant). Po-
dobnie, wierzchołek E ma potomków F, G oraz H i odwrotnie – jest przodkiem (ang. ancestor)
tych trzech wierzchołków. Analogia rodziny jest przenoszona dalej: C jest ojcem D (ang. pa-
rent), które z kolei jest jego dzieckiem (ang. child).

Dla grafów nieskierowanych wyróżnialiśmy krawiędzie drzewowe oraz niedzewowe. W

przypadku grafu skierowanego taksonomia jest nieco bardziej złożona:

11

Rys. 6. Algorytm DFS na grafie skierowanym

Krawędzie drzewowe śa częścią lasu DFS.
Krawędzie w przód prowadzą od węzła do jego potomka w
dzewie DFS, który nie jest jego dzieckiem.
Krawędzie powrotne prowadzą do przodka w drzewie DFS.
Krawędzie poprzeczne nie prowadzą ani do przodka, ani do
potomka; prowadzą do węzła, który już był przeanalizowany
dokładnie (tzn. była dla niego wywołana procedura postvisit).

Graf na rysunku 6 ma dwie krawędzie w przód, dwie

powrotne i dwie poprzeczne.

Relacje bycia potomkiem i przodkiem, jak i typu kra-

wędzi wynikają wprost z numerów porządków pre i post.
Zgodnie ze strategią przesukiwania w głąb wierzchołek u jest
przodkiem wierzchołka v wtedy, gdy u jest odwiedzany jako
pierwszy oraz v jest przeglądane wewnątrz operacji explore(u).

Inaczej mówiąc

)

(

)

(

)

(

)

(

u

post

v

post

v

pre

u

pre







, co możemy przedstawić jako dwa za-

gnieżdżone przedziały:

u

v

v

u

]

]

[

[

Przypadek bycia potomkiem jest symetryczny, ponieważ u jest potomkiem v wtedy i tyl-

ko wtedy, gdy v jest przodkiem u. Ponieważ kategorie krawędzi są w zupełności oparte na relacji
bycia przodkiem i potomkiem, także mogą być zapisane za pomocą numerów porządków pre i
post. Poniżej znajduje się podsumowanie różnych możliwości dla krawędzi

)

,

( v

u

:

Porządek pre/post dla

)

,

( v

u

:

u

v

v

u

]

]

[

[

– krawiędź drzewowa / w przód;

v

u

u

v

]

]

[

[

– powrotna;

u

u

v

v

]

[

]

[

– poprzeczna.

Każdy z powyższych porządków pre/post można uzasadnić, patrząc na diagram typów krawędzi.

12

3.2. Skierowany graf acykliczny

Cykl (ang. cycle) w grafie skierowanym to ścieżka rozpoczynająca się i kończąca się w tym sa-
mym wierzchołku

0

2

1

0

...

v

v

v

v









. Graf z rysunku 6 ma ich wiele, na przykład,

B

F

E

B







. Graf bez cykli jest nazywany acyklicznym (ang. acyclic). Okazuje się, że

możemy sprawdzić, czy graf jest acykliczny w czasie liniowym za pomocą zwykłego przeszuki-
wania w głąb.

Własność. Graf skierowany ma cykl wtedy i tylko wtedy, gdy przeszukiwanie w głąb wy-

krywa krawędź powrotną.

Dowód. W jedną stronę jest w miarę łatwy: jeśli

)

,

( v

u

jest krawędzią powrotna, to istnie-

je cykl składający się z tej krawędzi oraz ze ścieżki z v do u w drzewie przeszukiwań.

W drugą stronę, jeśli graf ma cykl

0

2

1

0

...

v

v

v

v

v

k











, to wybierzmy pierwszy

odwiedzony wierzchołek na tym cyklu (wierzchołek z najmniejszym numerem pre). Przypuść-
my, że jest to wierzchołek

i

v . Wszystkie pozostałe wierzchołki na cyklu są z niego osiągalne,

zatem są jego potomkami w drzewie. W szczególności krawędź

i

i

v

v





1

(lub

0

v

v

k



, jeśli

0



i

) prowadzi od wierzchołka do jego poprzednuka i z definicji jest to krawędź powrotna.

Skierowany graf acykliczny (ang. directed acyclic graph), czyli w skrócie dag, pojawia

się często. Jest on wygodny do modelowania różnych związków takich jak przyczynowość, hie-
rarchia, zależności czasowe. Przypuśćmy na przykład, że musimy wykonać wiele zadań, a nie-
które z nich nie mogą się rozpocząć, zanim pewne inne nie zostaną zakończone (musisz się obu-
dzić, zanim będziesz mógł wstać z łóżka, musisz wstać z łóżka, ale jeszcze nie być ubranym, by
wziąć prysznic itd.). Pytamy zatem, jaka jest właściwa kolejność wykonawania zadań?

Takie związki przyczynowe wygodnie jest reprezentować za pomocą skierowanego gra-

fu, w którym każde zadanie jest wierzchołkiem i w którym występuje krawędź z u do v, jeśli u
jest warunkiem dla v. Innymi słowy, zanim wykonamy określone zadanie, wszystkie inne zada-
nia, które na niego wskazują, muszą być już wykonane. Jeśli taki graf ma cykl, to nie ma żadnej
możliwości wykonania wszystkich zadań – grafu nie da się uporządkować. Jednakże jeśli graf
jest dagiem, to chcielibyśmy, o ile to możliwe, uporządkować go liniowo (posortować topolo-
gicznie), ustawiając wierzchołki jeden za drugim w taki sposób, aby każda krawędź prowadziła
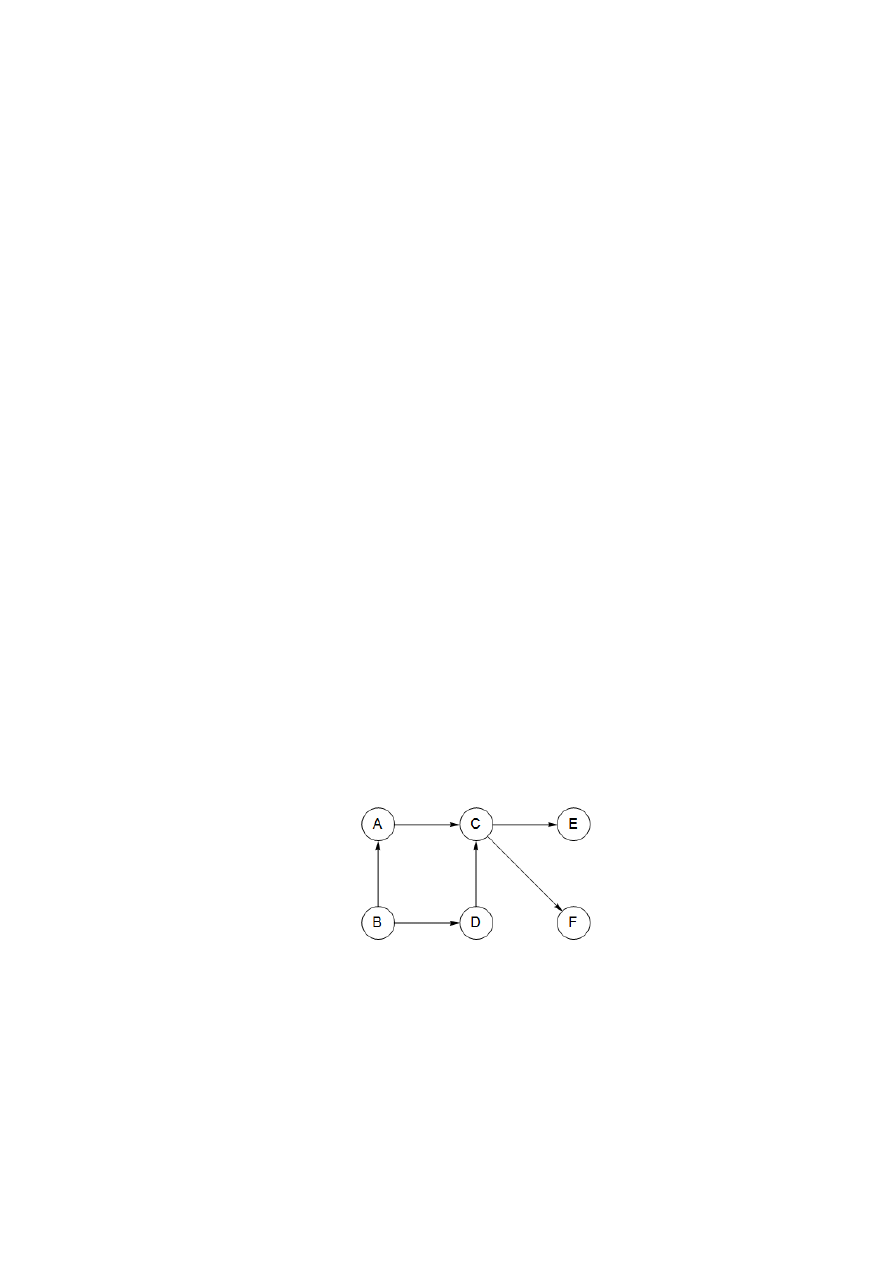
od wierzchołka wcześniejszego do póżniejszego, czyli aby wszystkie warunki były spełnione. Na
przykład, na rys. 7 jednym z odpowiednich uporządkowań jest B, A, D, C, E, F. (Jakie są inne
trzy?)

Rys. 7. Skierowany graf acykliczny z jednym żródłem, dwoma ujściami i czterema

możliwymi uporządkowaniami liniowymi

Jakie acykliczne grafy skierowane możemy uporządkować liniowo? Wszystkie. I znów

przeszukiwanie w głąb wskazuje metodę, jak to zrobić: należy po prostu wykonać zadania w po-
rządku malejących numerów porządków post. Jedyne krawędzie

)

,

( v

u

w grafie, dla których

)

(

)

(

v

post

u

post



(patrz opis typów krawędzi powyżej) to krawędzi powrotne – a jak wiemy, w

dagu takich krawędzi nie ma. Otrzymujemy zatem:

Własność. W skierowanym grafie acyklicznym każda krawędź prowadzi do wierzchołka z

mniejszym numerem porządków post.

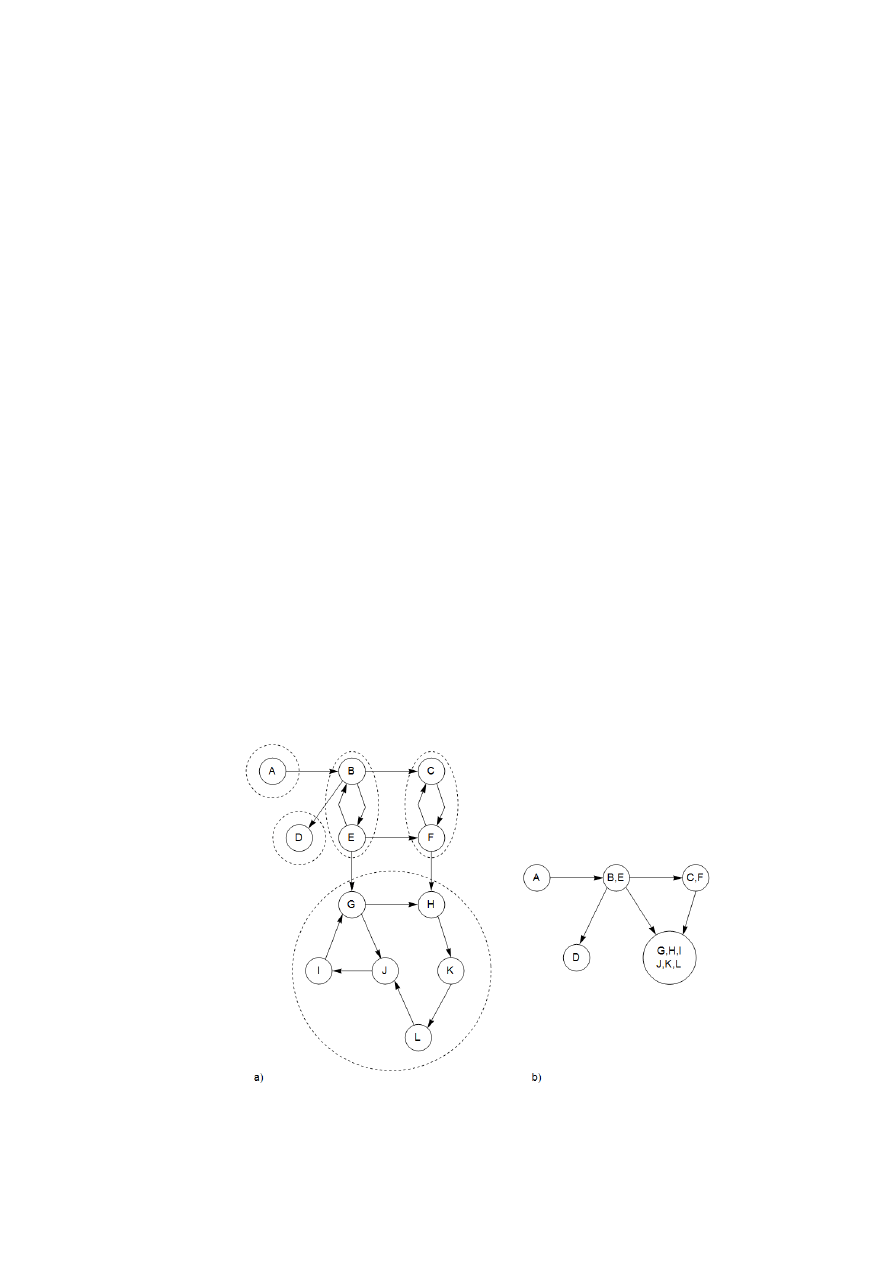
13

W ten sposób uzyskaliśmy algorytm liniowy wyznaczania porządku wierzchołków w da-

gu. Stąd oraz z naszych wcześniejszych obserwacji wynika, że trzy różnie nazwane własności –
acykliczność, możliwość liniowego uporządkowania oraz brak krawędzi powrotnych w drzewie
przeszukiwania w głąb – są w istocie tymi samymi rzeczami. Ponieważ dag możemy uporząd-
kować loniowo za pomocą malejących numerów post, wierzchołek o najmniejszym numerze
post pojawia się jako ostatni w porządku i jest ujściem – wierzchołkiem bez wychodzących kra-
wędzi. I na odwrót, ten z największą wartością post jest źródłem, wierzchołkiem bez wchodzą-
cych krawędzi.

Własność. Każdy skierowany graf acykliczny ma co najmniej jedno źródło i co najmniej

jedno ujście.

Z tego, że zagwarantowane jest istnienie źródła w dagu, wynika alternatywny sposób wy-

znaczania porządku liniowego:

Znajdź źródło, wypisz je i usuń z grafu.

Powtarzaj dopoki graf jest niepusty.

Czy umiesz pokazać, dlaczego wyznacza to właściwy liniowy porządek każdego skierowanego
grafu acyklicznego?

4. Składowe silnie spójne

4.1. Definicja spójności dla grafów skierowanych

Spójność grafu nieskierowanego jest pojęciem naturalnym: graf, który jest niespójny, można ła-
two rozłożyć na kilka składowych spójnych (trafnym przykładem jest graf z rys. 5). Jak widzieli-
śmy w punkcie 2.3, operacja explore robi to zręcznie, przy każdym wywołaniu zaznaczając no-
wą spójną składową.

W grafach skierowanych spójność jest bardziej wyrafinowana. W najprostszym sensie

graf skierowany z rys. 8 jest „spójny”, bo nie można go „rozdzielić” – nieformalnie mówiąc –
bez przecinania krawędzi. Taka definicja jest jednak mało interesująca i pouczająca. Nie może-
my uważać grafu z rys. 8 za spójny, ponieważ nie ma on ścieżki na przykład z G do B oraz z F
do A. Precyzyjne spójność dla grafów skierowanych definiuje się następująco:

Dwa wierzchołki u oraz v w grafie skierowanym są połączone, jeśli istnieje ścieżka z u do

v oraz ścieżka z v do u.

Rysunek 8. Graf skierowany i jego silnie spójne składowe a) oraz metagraf b)

Powyższa relacja dzieli V na rozłączne zbiory, które nazywamy składowymi silnie spój-

nymi (ang. strongly connected components). Graf z rys. 8 ma ich pięć.

14

Zastąpimy teraz każdą składową jednym metawierzchołkiem. Między jednym meta-

wierzchołkiem a drugim narysujemy krawiędź, jeśli instnieje krawiędź (w tą samą stronę) mię-
dzy odpowiadającymi im składowymi (rys. 8). Wynikowy metagraf musi być skierowanym gra-
fem acyklicznym. Powód jest prosty: cykl zawierający kilka silnie spójnych składowych łączyłby
je w jedną, silnie spójną składową. Stwierdzamy, że:
Własność. Każdy graf skierowany jest skierowanym grafem acyklicznym swoich silnie spójnych
składowych.

Własność ta mówi coś ważnego: spójna struktura grafu skierowanego jest dwuwarstwo-

wa. W wyższej warstwie mamy skierowany graf acykliczny, który ma raczej prostą strukturę – w
szczególności, może być liniowo uporządkowany. Jeśli interesują nas szczególy, to możemy zaj-
rzeć wewnątrz jednego z jego wierzchołków i zbadać istniejącą w nim właściwą silnie spójną
składową.

4.2. Efektywny algorytm

Rozkład grafu skierowanego na silnie spójne składowe jest barszo pouczający i użyteczny. Oka-
zuje się, że może on być wykonany w czasie loniowym znów przy użyciu przeszukiwania w
głąb. Algorytm bazuje się na pewnych własnościach, które już poznaliśmy, a które teraz przea-
nalizujemy dokładniej.

Własność 1. Jeśli podprogram explore startuje w wierzchołku u, to zatrzyma się on dokladnie
wtedy, kiedy wszystkie wierzchołki osiągalne z u zostaną odwiedzone.

Jeśli wywołujemy explore na wierzchołku, który leży gdzieś w ujściowej silnie spójnej

składowej (silnie spójnej składowej, która jest ujściem w metagrafie), to uzyskamy dokładnie
całą tą składową. Graf z rys. 8 ma dwie ujściowe silnie spójne składowe. Na przykład, wywołu-
jąc explore na węźle K, przewędrujemy w całości największą składową i się zatrzymamy.

Z powyższego rozumowania wynika sposób znalezienia jednej silnie spójnej składowej,

ale wciąż pozostają otwarte dwa główne problemy: (A) w jaki sposób wyznaczyć wierzchołek, o
którym wiemy z pewnością, że leży w ujściowej silnie spójnej składowej i (B) jak kontynuować,
kiedy już wyznaczymy pierwszą składową?

Zacznijmy od problemu (A). Nie ma łatwiej, bezpośredniej metody wyznaczenia wierz-

chołka, który z pewnością leży w ujściowej silnie spójnej składowej. Znamy jednak sposób uzy-
skania wierzchołka ze źródłowej silnie spójnej składowej.
Własność 2. Wierzchołek, który otrzymuje największy numer post w porządku postvisit w prze-
szukiwaniu s głąb, musi leżeć w źródłowej silnie spójnej składowej.

Wynika to z następującej, bardziej ogólnej własności.

Własność 3. Jeśli C oraz C’ są silnie spójnymi składowymi oraz jeśli istnieje krawiędź z wierz-
chołka w C do wierzchołka w C’, to największy numer post w porządku postvisit w C jest większy
niż największy numer post w porządku postvisit w C’.
Dowód. Podczas dowodzenia własności 3 rozważmy dwa przypadki. Jeśli przy przeszukiwaniu
w głąb składowa C jest przeglądana przed składowa C’, to oczywiste jest, że wszystko z C oraz z
C’ będzie odwiedzone, zanim procedura się zatrzyma (patrz własność 1). Czyli pierwszy wierz-
chołek odwiedzony w C będzie miał większy numer post od każdego wierzchołka w C’. Jednak-
że jeśli C’ jest przeglądane wcześniej, to przeszukiwanie w głąb zatrzyma się po odwiedzeniu
wszystkich wierzchołków z C’, a przed odwiedzeniem czegokolwiek z C. Również w tym przy-
padku dowodzona własność jest zachowana.

Z własności 3 możemy wywnioskować, że silnie spójne składowe mogą być uporządko-

wane liniowo przez ustawienie ich w kolejności malejących ich największych numerów post.
Jest to uogólnienie naszego wcześniejszego algorytmu sortującego dag; w dagu każdy wierzcho-
łek jest jednoelementową silnie spójną składową.

Własność 2 pomaga nam znaleźć wierzchołek w źródłowej silnie spójnej składowej G.

To, czego potrzebyjemy, to wierzchołek w ujściowej składowej. To, co many, jest przeciwień-

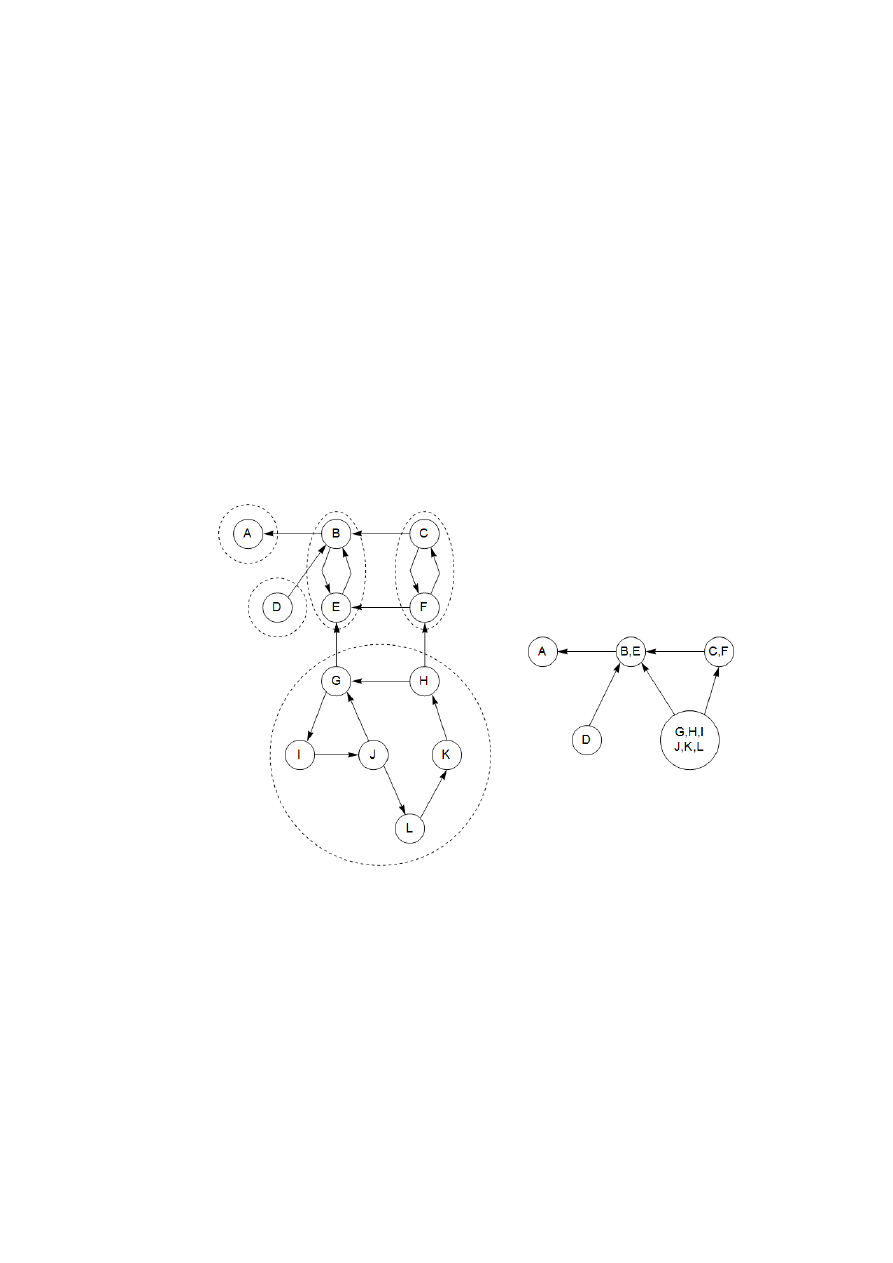
15

stwem tego, czego potrzebujemy. Rozważmy teraz graf odwrócony G

R

, taki sam jak G, tylko z

odwróconymi krawędziami (rys. 9). G

R

ma dokładnie takie same silnie spójne składowe jak G.

Jeśli zatem wykonamy przeszukiwanie w głąb na G

R

, wierzchołek z największym numerem post

jest w źródłowej silnie spójnej składowej G

R

, czyli w ujściowej silnie spójnej składowej grafu G.

Tym samym rozwiązaliśmy problem (A).

Przechodzimy do problemu (B). W jaki sposób kontynuować algorytm po zidentyfiko-

waniu pierwszej ujściowej składowej? Rozwiązanie dostarcza nam własność 3. Najpierw znajdu-
jemy pierwszą silnie spójną składową i usuwamy ją z grafu, wierzchołek z największym nume-
rem post spośród pozostałych wierzchołków będzie należał do ujściowej silnie spójnej tego, co
pozostało w G. Możemy więc użyć kolejności numerów post z początkowego przeszukiwania w
głąb G

R

do sukcesywnego wyznaczania drugiej silnie spójnej składowej, trzeciej silnie spójnej

składowej itd. Uzyskujemy następujący algorytm:

1. Wykonaj przeszukiwanie w głąb na grafie G

R

.

2. Wykonaj algorytm znajdowania nieskierowanych spójnych składowych na grafie G, a

podczas wyszukiwania w głąb przeglądaj wierzchołki w kolejności malejących nume-
rów post z kroku 1.

Algorytm ten działa w czasie liniowym, jedyna stała w liniowym wyrażeniu jest związa-

na z dwukrotnym wywołaniem zwykłego przeszykiwania w głąb.

Rysunek 9. Odwrócenie grafu z rys. 8

Wykonajmy teraz ten algorytm na grafie z rys. 9. Jeśli w kroku 1 rozważane są wierz-

chołki w kolejności leksykograficznej, wówczas porządek wyznaczony dla kroku 2 (tzn. maleją-
ca kolejność numerów zdarzeń post wyznaczonych przez przeszukiwanie w głąb grafu G

R

) jest

następujący: G, I, J, L, K, H, D, C, F, B, E, A. Następnie w kroku 2 zostaną wyznaczone skła-
dowe w następującej kolejności: {G, H, I, J, K, L}, {D}, {C, F},{B, E},{A}.