Analityka Medyczna zaliczenie wykładów z Biofizyki. Wersja A
Łącznie 33 pkt.
3 styczeń 2012 r.
1. (1 pkt) Wyjaśnij pojęcie: czułość narzędzia pomiarowego.
Czułość c informuje o ile zmieni się wskazanie narzędzia pomiarowego Δy, na skutek jednostkowej zmiany
wartości wielkości mierzonej Δx, czyli
Δ
Δ
y
c
x
(1 pkt)
2. (2 pkt.) Co oznacza następujący zapis wyniku pomiaru długości odcinka a: a = (11 ± 1) mm (1 pkt)? Ob-
licz procentowy błąd względny tego pomiar. Pamiętaj o zasadach zaokrąglania błędów (1 pkt).
Oznacza to, że rzeczywista wartość długości odcinka należy do przedziału obustronnie zamkniętego od 10
do 12 mm (1 pkt).
Δ
1 mm
. . .
100%
100%
9,09%
9,1%
11 mm
a
b w p
a
(1 pkt).
3. (5 pkt.) W czasie t = (115 7) s organizm zużył V = (8,5 0,5) cm
3
tlenu. Oblicz wielkość szybkości P
przemiany materii
V
P
w
t
tego organizmu, jeśli kaloryczność tlenu w = (20 2)10
3
J/O
2
(1 pkt).
Zwróć uwagę na jednostki. Wymień metody szacowania błędu wielkości złożonej (1 pkt). Jedną z nich,
krok po kroku (nazwa metody, odpowiedni wzór/wzory lub bez wzoru, rachunki (2 pkt.), końcowy za-
pis błędu i wyniku (1 pkt)) oszacuj błąd pomiaru szybkości przemiany materii w rozpatrywanym przy-
padku.
3
3
J
8,5 cm
20
1,453 W
cm
115 s
V
P
w
t
(1 pkt)
Metody: (a) liczba cyfr znaczących, (b) najmniej korzystnego przypadku i (c) metoda logarytmiczna (1 pkt)
Metoda logarytmiczna:
Δ
Δ
Δ
Δ
1,45 0,100
0,0609
0,0588
1,45 0,220
0,319.
w
t
V
P
P
w
t
V
Ostatecznie
Δ
0,32 W
P
(za wzór i obliczeni a 2 pkt.)
Końcowy zapis:
1,45 0,32 W
P
(1 pkt).
4. (3 pkt.) Jakich trzeba użyć podstawień, aby zlinearyzować następująca zależność:
5 log( ) 10,
y
x
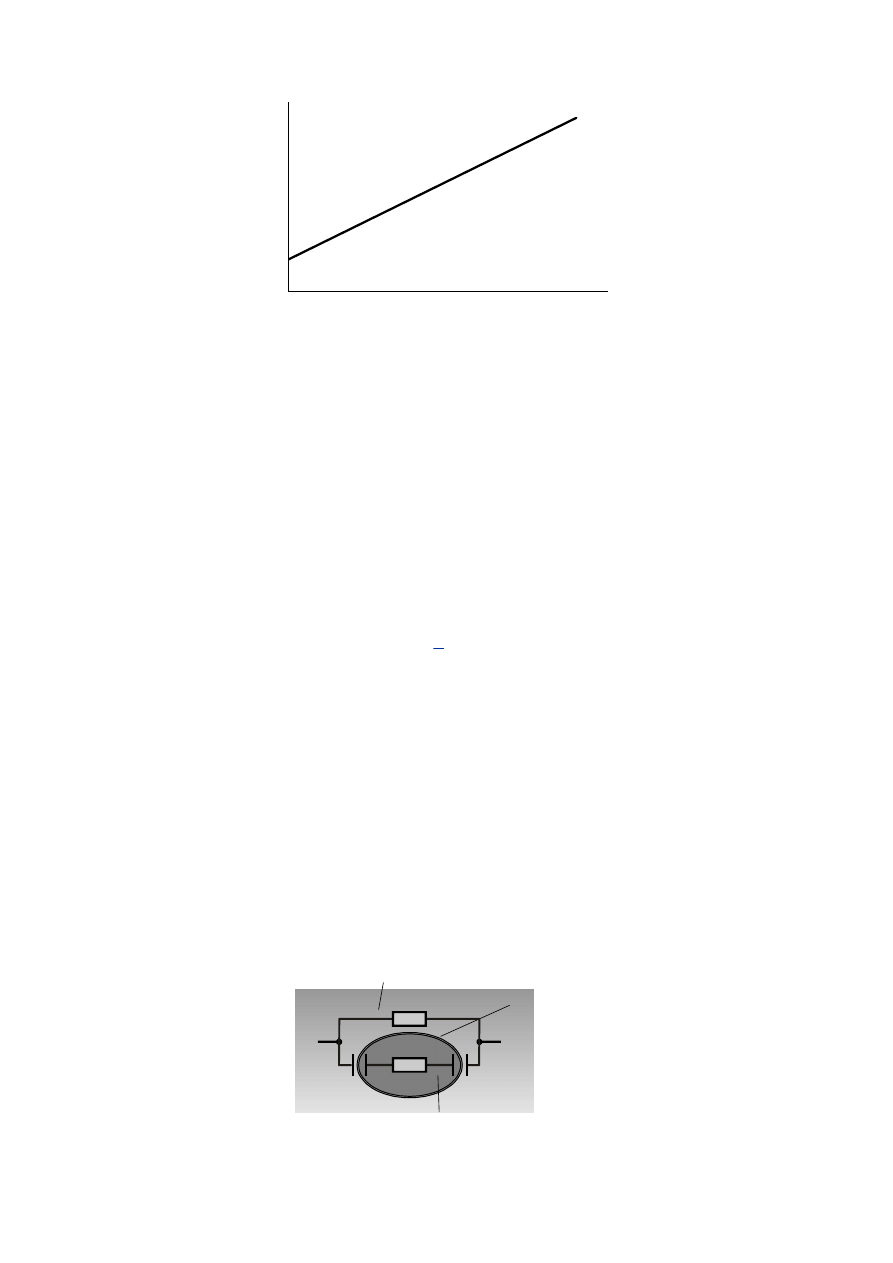
gdzie zmienną niezależną jest x, a zmienną zależną y (1 pkt.). Narysuj wykres ilustrujący tę zależność
w nowym układzie współrzędnych (1 pkt.). Jaką wartość ma współczynnik kierunkowy linii uzyskanej w
tym nowym układzie współrzędnych (1 pkt).
Właściwe podstawienie, to
Y
y oraz log( )
X
x (1 pkt).
2
Zadanie 4. (1 pkt za poprawny rysunek opis osi i początek wykresu).
Współczynnik kierunkowy jest równy 5
k
(1 pkt).
5. (3 pkt.) Jakie substancje (nie chodzi o nazwy poszczególnych substancji, ale o ich budowę i nazwę całej
ich klasy) tworzą warstwy monomolekularne na powierzchni wody (1 pkt)? Co to jest ciśnienie po-
wierzchniowe (1 pkt)? Jaki jest związek pomiędzy napięciem powierzchniowym i ciśnieniem po-
wierzchniowym (1 pkt)?
Surfaktanty, substancje powierzchniowo czynne; są amfifilowe (mają jedną końcówkę hydrofobową i drugą
hydrofilową) (1 pkt.).
Ciśnienie powierzchniowe σ
p
jest równe sile F, jaką molekuły surfaktantu działają na jednostkę długości, li-
nii oddzielającej powierzchnię pokrytą surfaktantami i tę, która nie jest pokryta:
p
F
σ
(1 pkt)
Istnieje formalny związek pomiędzy ciśnieniem powierzchniowym σ
p
i napięciem powierzchniowym wody
i wody pokrytej surfaktantem:
,
p
wody
wody
surfaktatnty
σ
σ
σ
gdzie σ
wody
i σ
wody+surfaktanty
oznaczają odpowiednio napięcie powierzchniowe wody i wody pokrytej surfaktan-
tami (1 pkt).
6. (2 pkt.) Narysuj i opisz elektryczny model zastępczy komórki (1 pkt). Wyjaśnij dlaczego właśnie takich
elementów użyto w tym modelu (1 pkt).
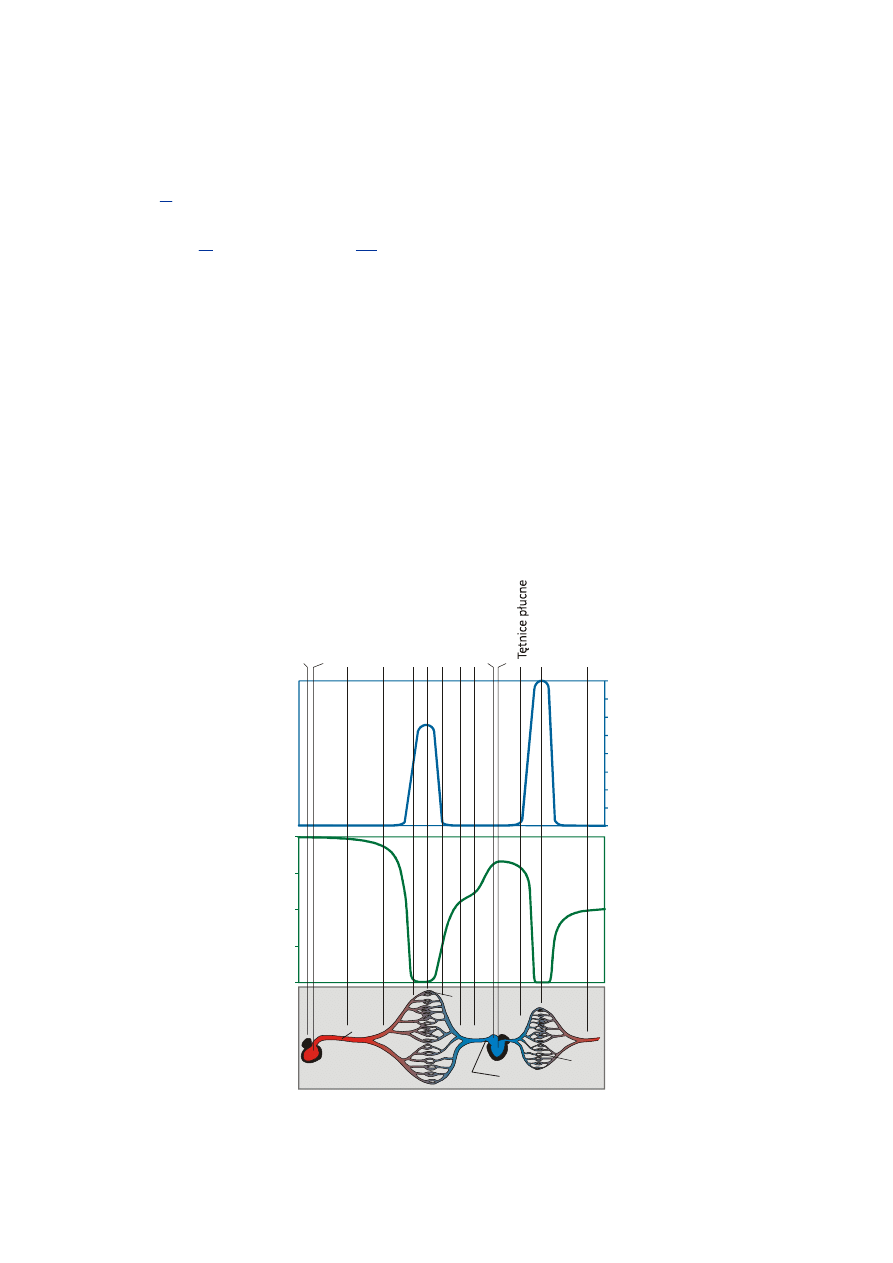
Poniższy rysunek przedstawia elektryczny model zastępczy komórki i wyjaśnia dlaczego użyto właśnie takich
elementów. Właściwości elektryczne komórki dobrze opisują dwa wielkości fizyczne zastępczy opór elek-
tryczny R
Śr
i R
C
i zastępcza pojemność elektryczna błony C
B
.
Rysunek do zadania 6.
y
log(x)
0
dobrze przewodząca cytoplazma
błona komórkowa
o właściwościach
izolatora
dobrze przewodzący płyn śródkomórkowy
C
B
C
B
R
Śr
R
C
3
7. (2 pkt.) Przepuszczalność błony o grubości 9 nm dla jonów sodowych wynosi 10
−14
m/s. Oblicz współ-
czynnik dyfuzji przez tę błonę. Wzór 1 pkt, obliczenia i wynik 1 pkt.
Wzór
D
P
D
P x
x
(1 pkt),
2
14
9
23
m
m
10
9 10 m
9 10
s
s
D
P x
(1 pkt).
8. (4 pkt.) Prawo ciągłości strumienia (kiedy jest spełnione, treść prawa 2 pkt.). Wyjaśnij przy jego pomo-
cy, jak zmienia się prędkość przepływu krwi w różnych częściach układu krążenia (2 pkt.). Dobrze spo-
rządzony odpowiedni wykres jest punktowany dodatkowo.
Ciecz powinna być nieściśliwa, płynąć laminarnie w sztywnym naczyniu (1 pkt).
Prawo to mówi, że suma strumieni objętości cieczy wpływających do węzła jest równa strumieni wypływają-
cych z węzła (1 pkt).
Jego konsekwencją jest następujące równanie:
,
S v
const co oznacza, że iloczyn łącznego pola przekroju
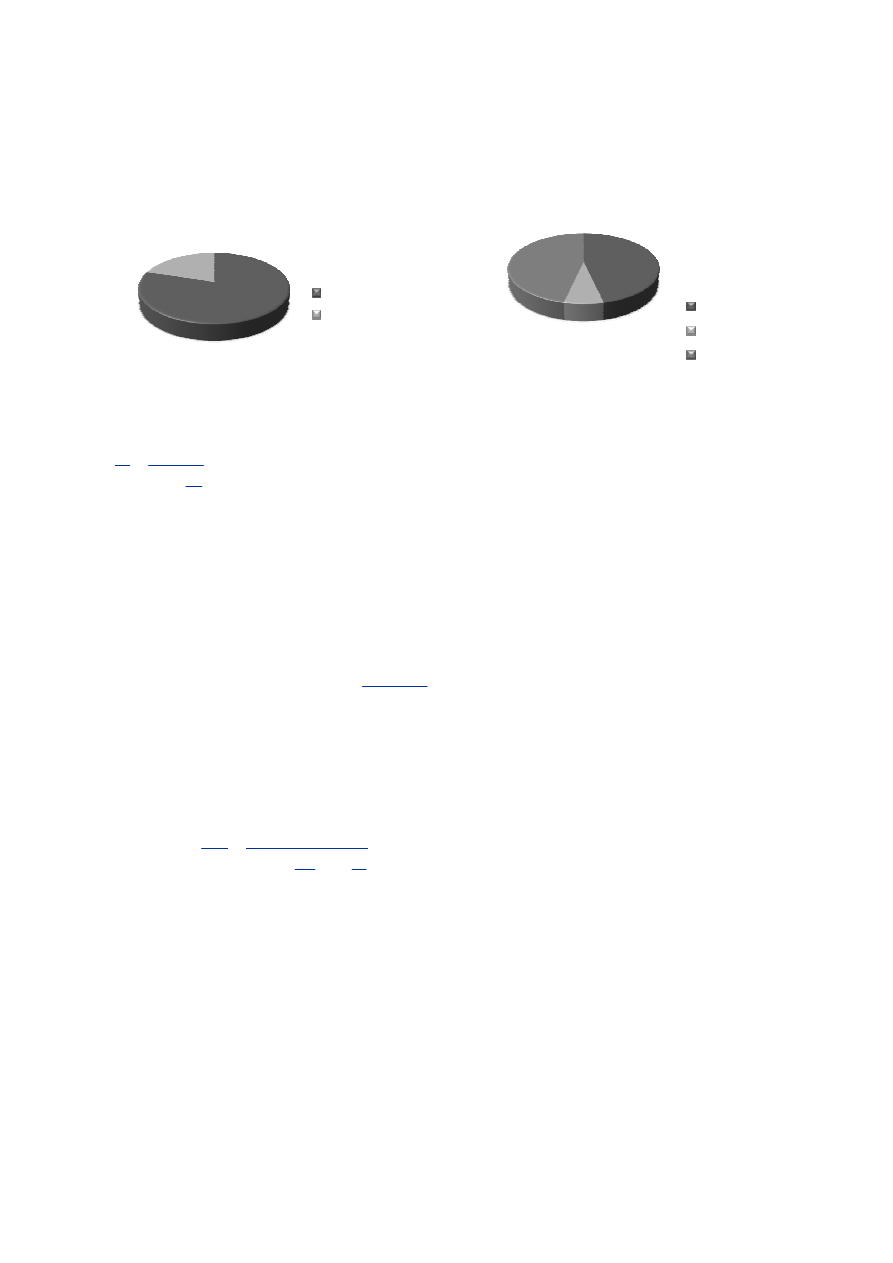
naczyń i średniej prędkości przepływu cieczy jest stały. Wynika stąd, że krew płynie z duża prędkością przez
te obszary układy krążenia, które mają małe łączne pole przekroju poprzecznego (np. aorta) i wolno, tam,
gdzie pole przekroju jest duże (np. kapilary) (2 pkt). Można dołączyć rysunek:
Rysunek do zadania 8
.
4000
P
o
w
ie
rz
ch
n
ia
p
rz
ek
ro
ju
p
o
p
rz
e
cz
n
e
go
, c
m
2
3000
1000
2000
0
S
a
= 4 cm
2
P
rę
d
ko
ść
li
n
io
w
a
cm/s
5
10
15
20
0
v = 0,03 cm/s
S
ż
= 6 cm
2
Le
w
y
p
rz
ed
si
o
n
e
k
P
ra
w
y
p
rz
e
d
si
o
n
ek
Le
w
a
ko
m
o
ra
P
ra
w
a
ko
m
o
ra
A
o
rt
a
Tę
tn
ic
e
K
ap
ila
ry
Tę
tn
ic
zk
i
W
ło
śn
ic
zk
i
Ży
łk
i
Ży
ły
Ży
ła
g
ło
w
n
a
Ży
ły
p
łu
cn
e
v = 0,02 cm/s
4
9. (4 pkt.) Oblicz objętość krwi zgromadzonej w tętnicach małego krążenia u człowieka o masie 80 kg. Za-
łóż, że 7% masy człowieka stanowi masa krwi, a jej gęstość ma wartość 1080 kg/m
3
. Wykorzystaj dane
z poniższego diagramu.
Rozkład krwi w krążeniu.
Rozkład krwi w krążeniu płucnym
Masa krwi ma wartość:
80 kg 0,07
5,6 kg
m
(1 pkt), jej objętość obliczymy ze wzoru:
5,6 kg
5,19
kg
1,08
m
V
d
(1 pkt).
Z diagramów wynika, ze w małym krążeniu jest 20% krwi z czego w jego tętnicach (100 – 47 – 7 = 46) 46%,
zatem w tętnicach małego krążenia objętość krwi wynosi:
5,19 0,2 0,46
0,477
tmk
V
(2 pkt.).
10. (2 pkt.) Oblicz liczbę skurczy serca w czasie 2 minut, gdy objętość minutowa serca wynosi 5,9 , a jego
objętość wyrzutowa ma wartość 85 cm
3
.
Liczba skurczy w czasie 1 minuty wynosi:
3
3
5900 cm
69
85 cm
(1 pkt). Zatem w czasie 2 minut ma wartość 138 (1
pkt).
11. (2 pkt.) Przelicz ciśnienie 15 kPa na mmHg (gęstość rtęci wynosi 13600 kg/m
3
, a przyspieszenie ziem-
skie przyjmij jako równe 9,8 m/s
2
).
3
2
15000 Pa
0,112 m
kg
m
13600
9,8
m
s
p
p
d g h
h
d g
Zatem ciśnienie to wynosi 112 mmHg (2 pkt.).
12. (3 pkt.) Co to jest potencjał spoczynkowy komórki (np. nerwowej) (1 pkt). Rozkład jonów K
+
wewnątrz
i na zewnątrz neuronu (0,5 pkt.); Określ kierunki transportu dyfuzyjnego (wywołanego różnicą stężeń),
elektrycznego (wywołanego różnicą potencjałów elektrycznych) i transportu aktywnego jonów pota-
sowych w stanie spoczynku przez błonę komórki (1,5 pkt.).
Potencjał spoczynkowy to różnica potencjałów pomiędzy wnętrzem komórki i jej zewnętrzem, gdy komórka
jest niepobudzona (1 pkt).
W tabeli zebrano wartości stężeń wybranych jonów wewnątrz, c
W
i na zewnątrz, c
Z
komórek mięśniowych
zwierząt stałocieplnych.
80%
Obwodowe
Płucne
7%
47%
Układ tętniczy
Kapilary
Układ żylny
5
Rodzaj jonów
c
W
mmol/
c
Z
mmol/
c
Z
/c
W
Na
+
12
145
12:1
K
+
155
4
1:39
Inne kationy
0
5
Cl
−
4
120
32:1
B
−
155
−
Inne aniony
8
34
1:4
Zmierzony potencjał spoczynkowy: −90 mV
Wystarczyło jednak podać, że potasu jest dużo w cytoplazmie, a mało w płynie śródkomórkowym (0,5 pkt.).
Transport dyfuzyjny odkomórkowy (0,5 pkt.).
Transport elektryczny dokomórkowy (0,5 pkt.).
Transport aktywny dokomórkowy (0,5 pkt.).