
1
Magnetyzm cz.I
Oddziaływanie magnetyczne
Siła Lorentza
Prawo Biote’a Savart’a
Prawo Ampera
2
Magnesy
Zjawiska magnetyczne (naturalne magnesy) były obserwowane i
badane już w starożytnej Grecji 2500 lat temu.
Własności „magnesów”:
mogą wywierać siłę na inne magnesy,
mogą „magnetyzować” przez dotyk kawałki żelaza
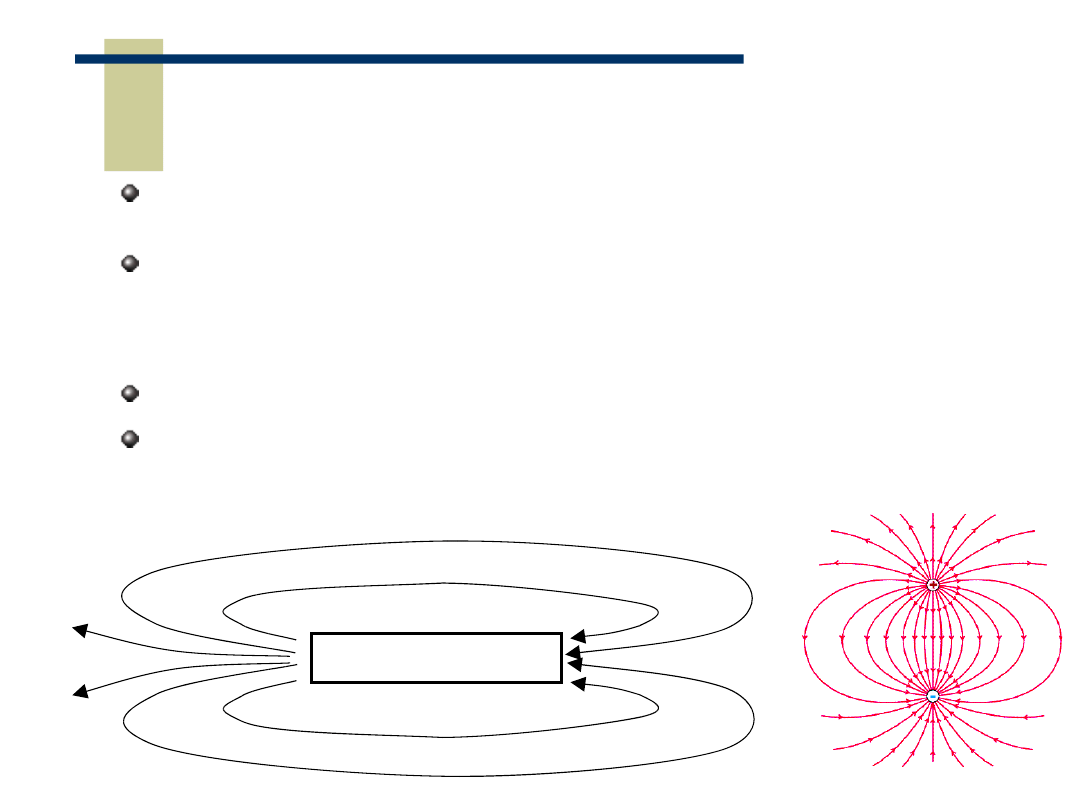
Magnes trwały
... dwa bieguny : N i
S
Pole magnetyczne, linie pola magnetycznego
są zamknięte.
N
S
Analogia do pola
elektrycznego dipoli
3
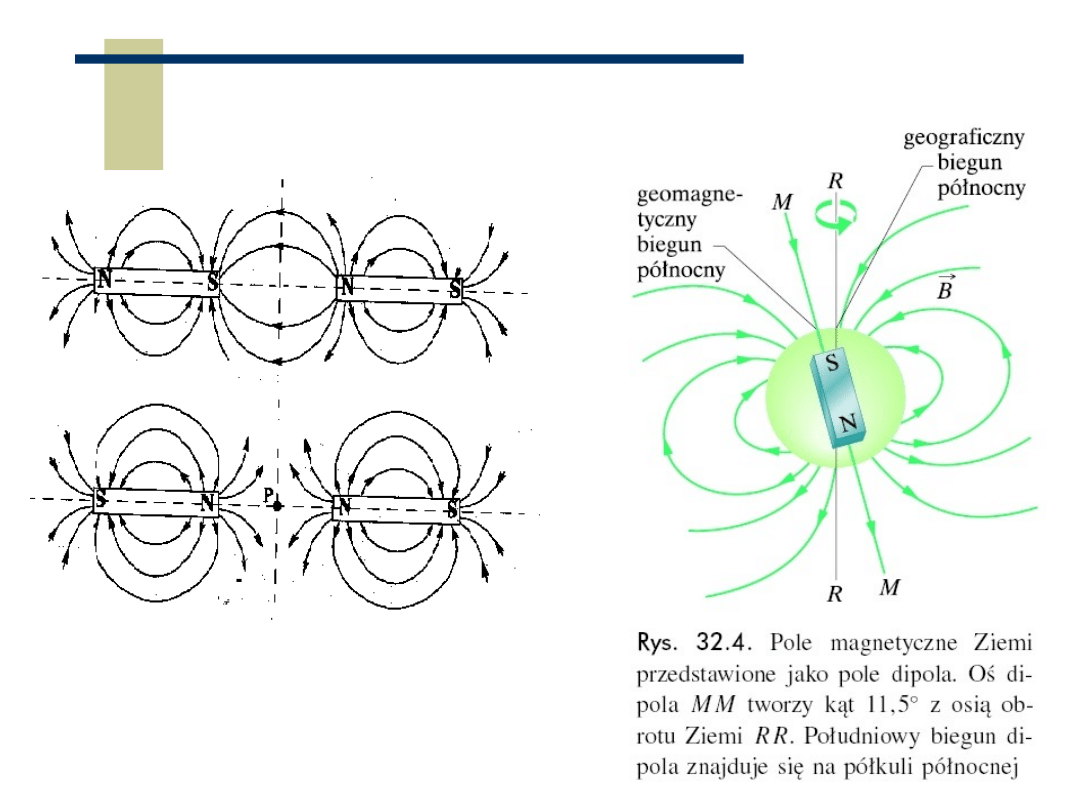
Oddziaływanie magnesów,
pole magnetyczne Ziemi
Bieguny jednoimienne
odpychają się
Bieguny różnoimienne
przyciągają się
4
Dipole magnetyczne, źródło pola magnetycznego
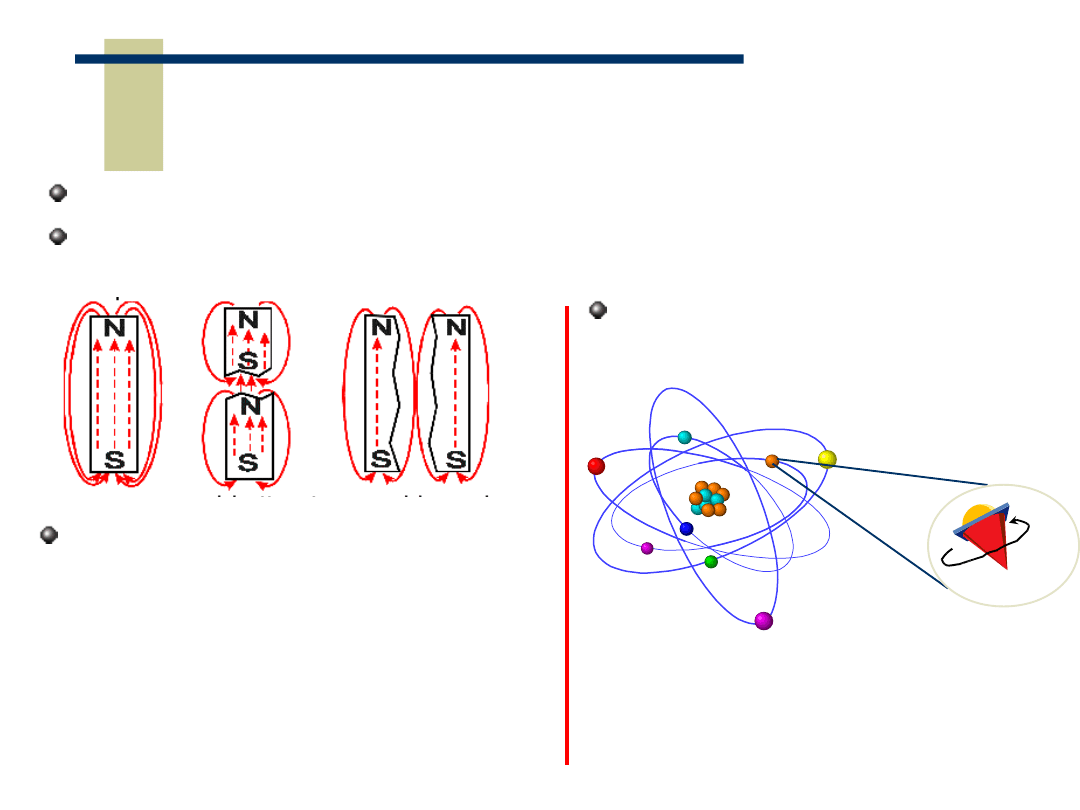
magnesy trwałe mają zawsze dwa bieguny – są „dipolami magnetycznymi”
nie znaleziono dotychczas magnetycznego „mono-pola” czyli pojedynczego
„ładunku magnetycznego”
co jest zatem źródłem pola
magnetycznego jeśli nie znamy „ładunku
magnetycznego”?
ładunek elektryczny w ruchu!
pole magnetyczne wytwarzane
jest przez wszelkiego rodzaju
prądy elektryczne!
źródłem pola magnetycznego w
magnesach trwałych jest też ruch
ładunków elektrycznych w atomach
• elektrony krążą po orbitach wokół jądra
• nawet sam elektron ma własny “dipol
magnetyczny” związany z jego spinem
• wektorowa suma tych “dipoli” stanowi o
całkowitym momencie magnetycznym atomu

5
Porównanie: pole elektryczne i magnetyczne
Pole elektryczne
Pole elektryczne
rozkład ładunków wytwarza pole elektryczne
E(r)
wokół otaczającej
przestrzeni
pole elektryczne oddziałuje siłą
F=q E(r)
ona ładunek
q
w punkcie
r
Pole magnetyczne
Pole magnetyczne
poruszający się ładunek wytwarza pole magnetyczne
B(r)
wokół
otaczającej przestrzeni
pole magnetyczne oddziałuje siłą
F
na poruszający się ładunek
q
w
punkcie
r
jaka to siła
F
?
co to jest B(r) ?
wektor natężenia pola
wektor indukcji pola
magnetycznego
6
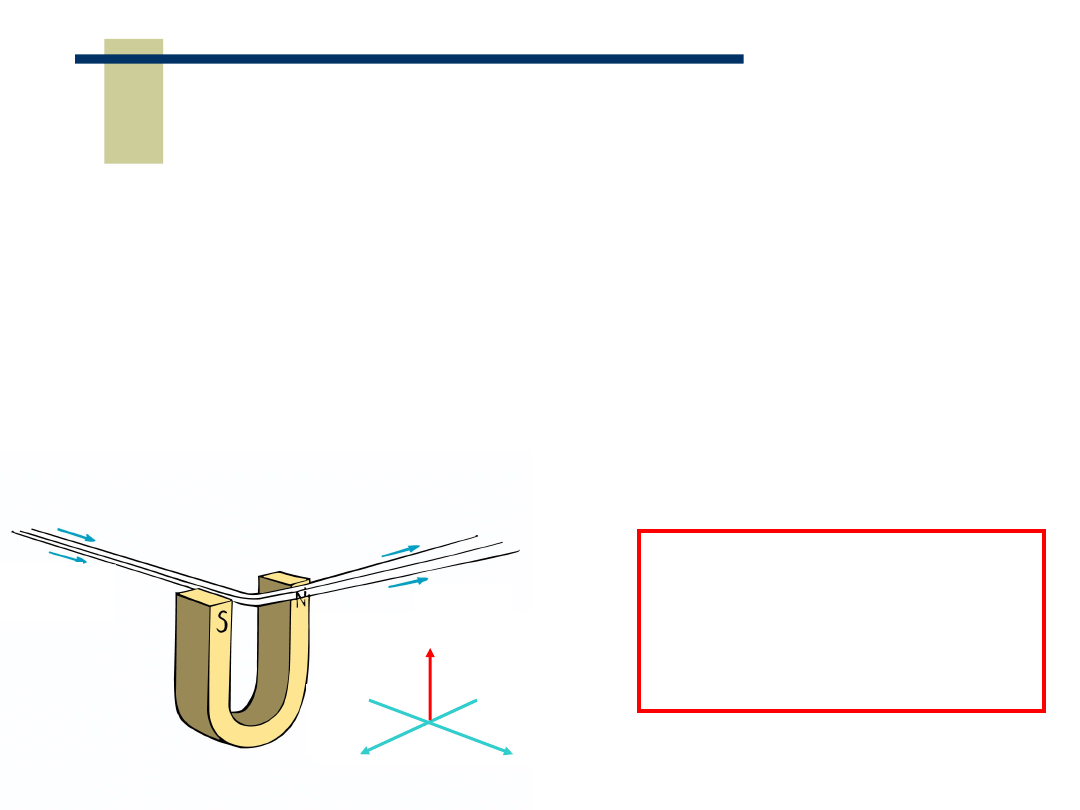
Siła Lorentz'a
siła
pole
magnetyczne
wiązka
wiązka
elektronów
Fakty doświadczalne dotyczące oddziaływania pola indukcji
magnetycznej na poruszające się elektrony:
• poruszające się elektrony są odchylane ,
• działająca na ładunki siła F jest
⊥
do kierunku wskazywanego przez
igłę magnetyczną, czyli do kierunku wektora B,
• siła F
⊥
do prędkości ładunku v,
• siła F
∝
| v |,
• wartość siły F
∝
q.
)
(
→
→
→
×
=
B
v
q
F
Wszystkie te wyniki doświadczalne
zebrał Hendrik Lorentz(1853-1928)
definiując siłę nazwaną obecnie
siłą
Lorentza
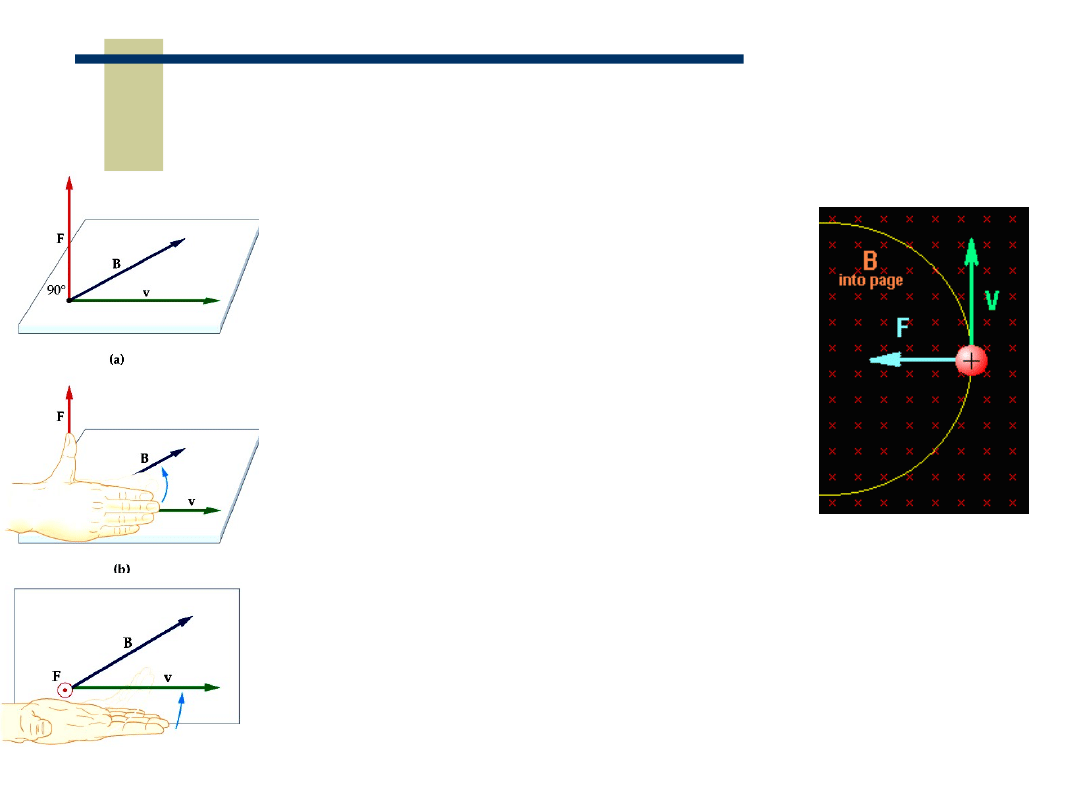
7
Kierunek siły Lorentza
)
(
→
→
→
×
=
B
v
q
F
Jednostki:
[F] = N
[v] = m/s
[q] = C
[B] = T (tesla).
.
1 T = 1 Wb/m
2
.
1 T = 1 N s m
-1
C
-1
.
1 T = 1 N A
-1
m
-1
.
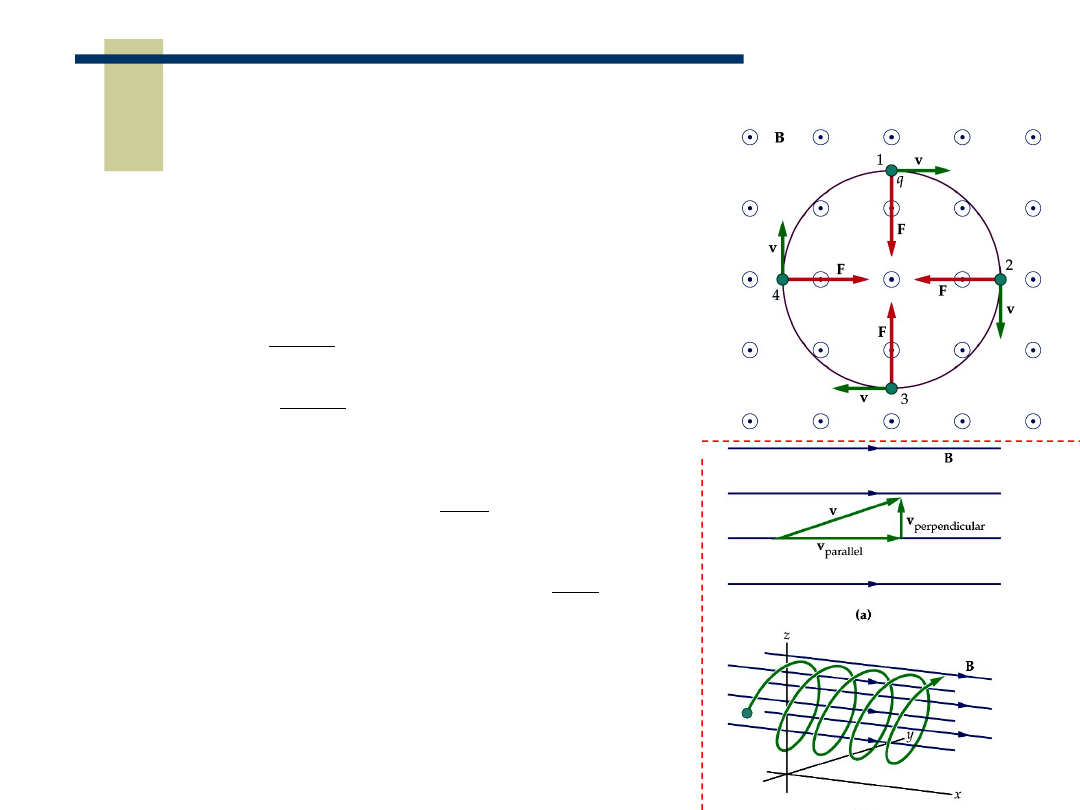
8
Ruch ładunku w polu magnetycznym
Jeśli ładunek q porusza się w kierunku prostopadłym do
pola magnetycznego wówczas jego trajektoria będzie
okręgiem ponieważ siła F = q v B jest zawsze
prostopadła do ruchu ładunku (dośrodkowa
)
r
mv
ma
F
2
=
=
F
qvB
mv
r
=
=
2
r
mv
qB
=
Promień okręgu po
którym porusza się
ładunek q
m
qB
f
=
=
π
ω
2
Częstość obrotów
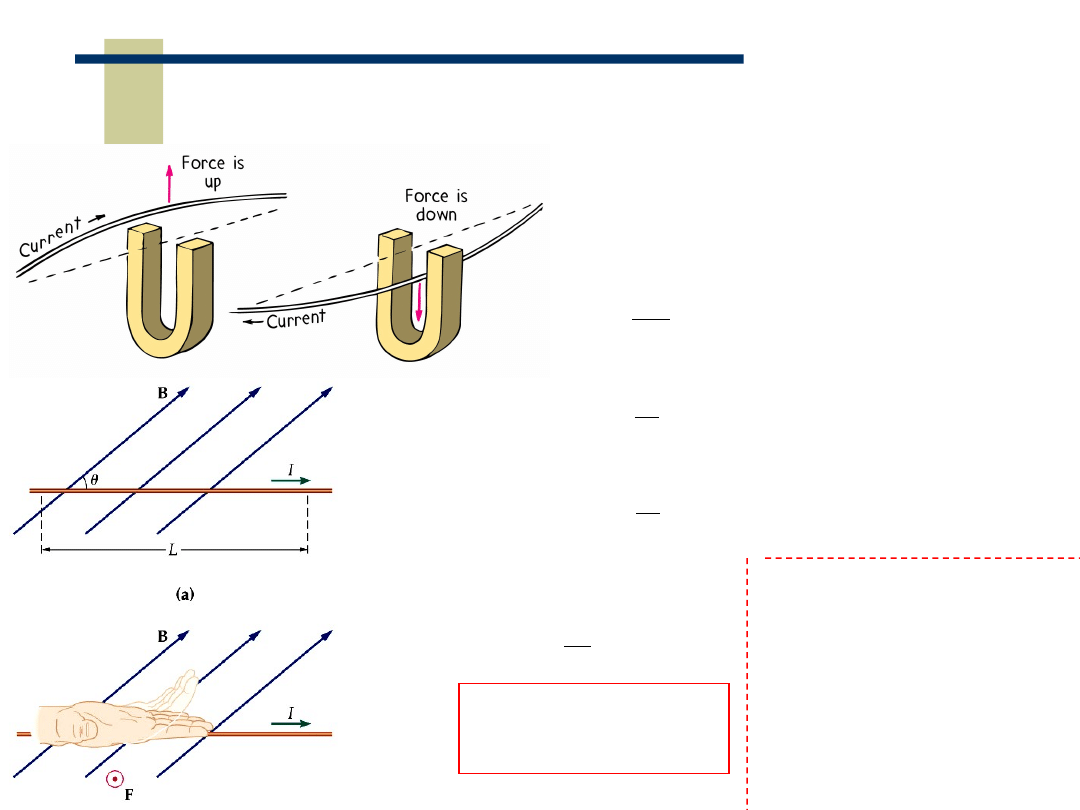
9
Oddziaływanie pola magnetycznego na
przewodnik z prądem
)
(
→
→
→
×
=
B
v
q
F
t
L
v
=
prędkość ład. q
dt
dq
i
=
prąd jako ładunek, który
przepłynął w czasie
czas w jakim ład. q przebył
drogę L
v
L
t
=
)
(
→
→
→
×
=
B
v
v
L
i
F
)
(
→
→
→
×
=
B
L
i
F
zatem
)
(
→
→
→
×
=
B
dl
i
dF
Jeśli linia nie jest prosta
wówczas musimy podzielić
ją na małe dl i sumować
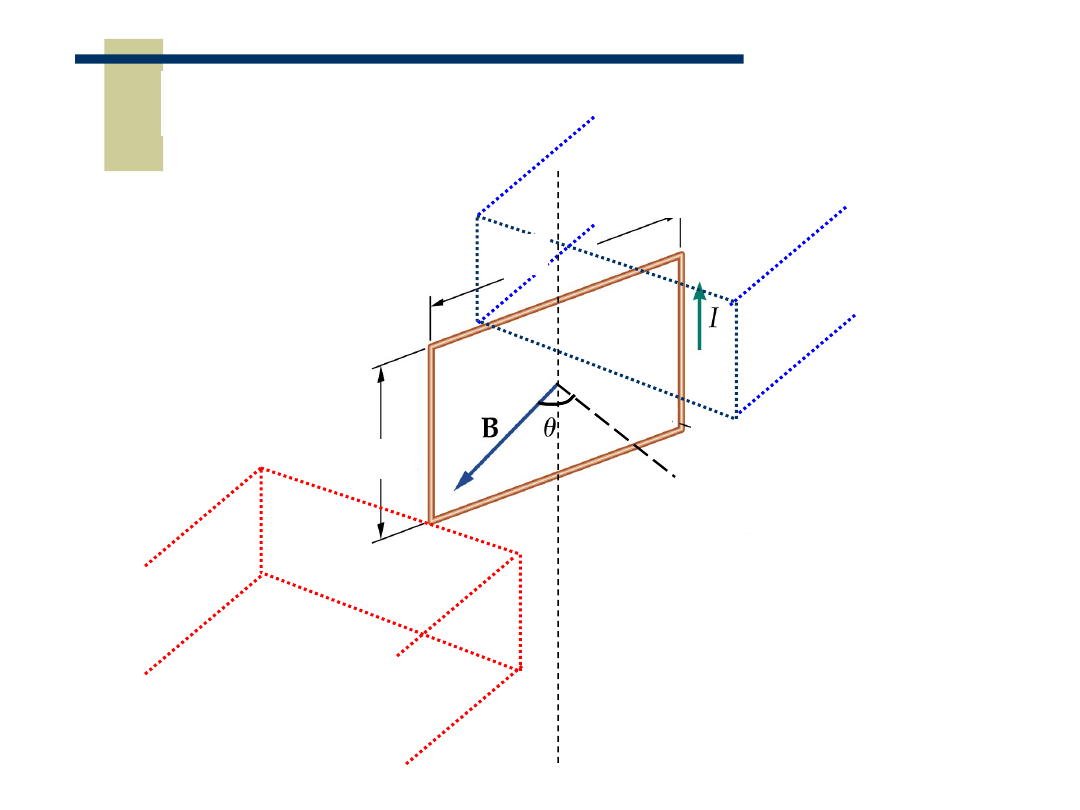
10
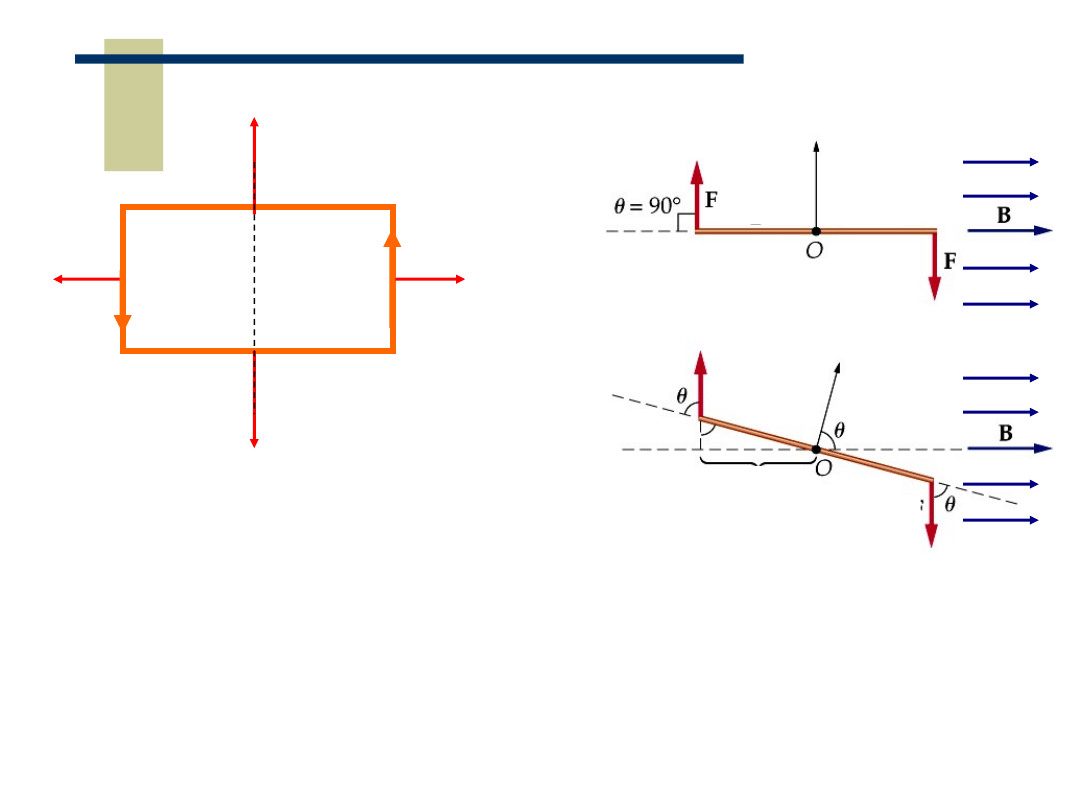
Ramka z prądem w polu magnetycznym
S
N
a
b
oś
obrotu
normalna do
powierzchni
11
Ramka z prądem w polu magnetycznym
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
F
2
F
4
F
3
F
1
a
b
b/2
b/2
b/2 sin
θ
F
1
F
3
F
1
F
3
i
θ = 0°
Siły F
2
i F
4
równoważą się niezależnie od
orientacji ramki
→
→
→
→
−
=
×
=
4
2
)
(
F
B
b
i
F
Siły F
1
i F
3
obracają ramkę
)
(
1
→
→
→
×
=
B
a
i
F
3
1
)
90
(
)
(
F
sin
B
a
i
F
=
°
=
→
n
→
n
12
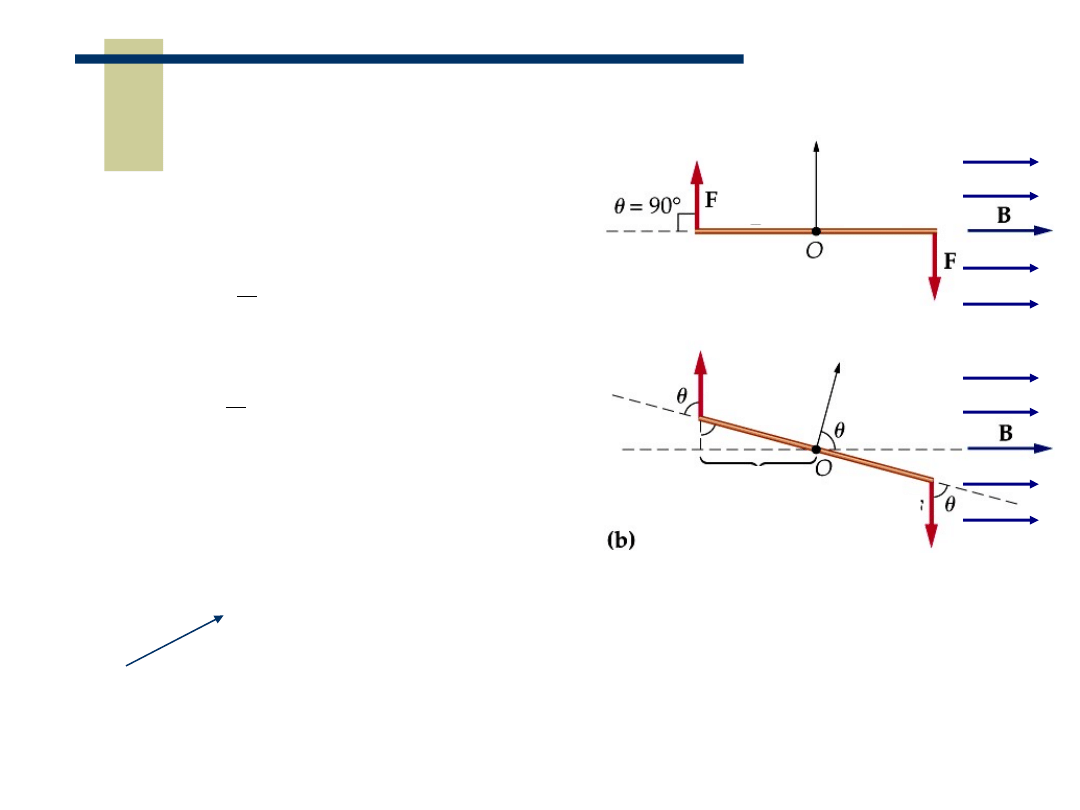
Ramka z prądem w polu magnetycznym
b/2
b/2
b/2 sin
θ
F
1
F
3
F
1
F
3
Moment sił które obracają ramkę
)
2
(
2
1
→
→
→
×
=
F
b
M
)
(
2
2
1
θ
sin
F
b
M
=
→
n
→
n
Def. magnetycznego mementu
dipolowego
→
→
→
=
=
n
S
i
n
ab
i
µ
powierzchnia ramki S
→
→
→
×
=
=
B
M
sin
B
ab
i
M
µ
θ
)
(
Moment sił które obracają ramkę
13
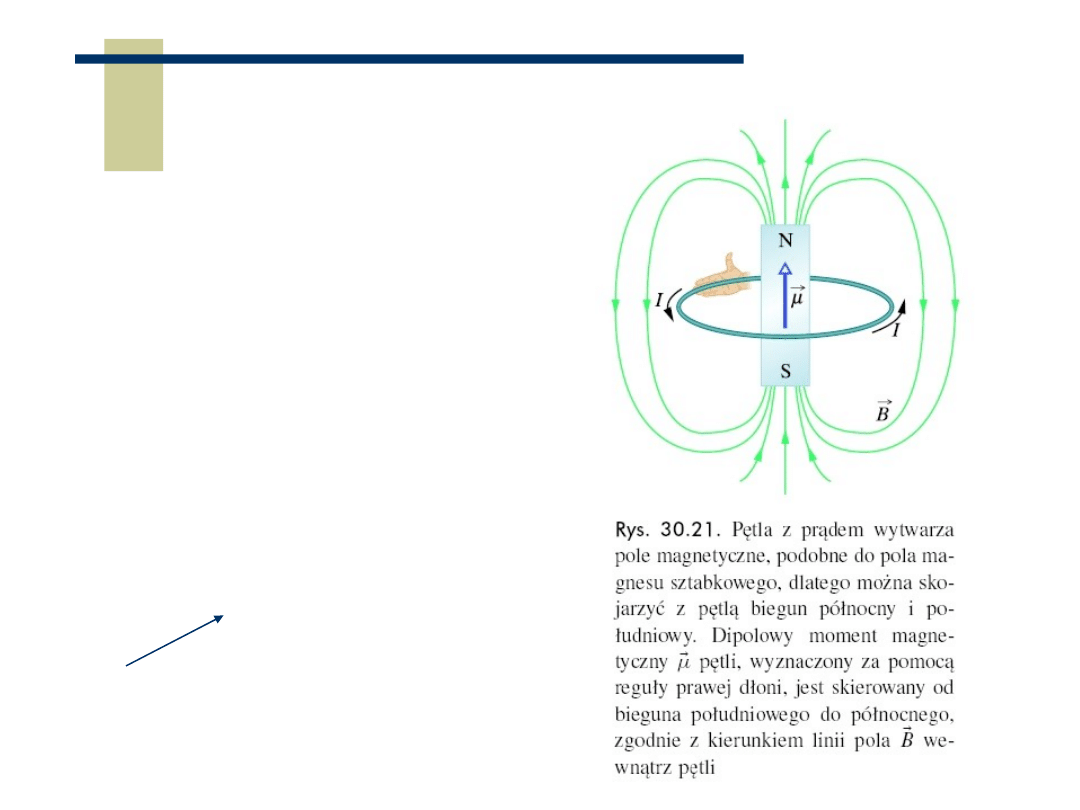
Ramka z prądem w polu magnetycznym
Def. magnetycznego mementu
dipolowego
→
→
→
=
=
n
S
i
n
ab
i
µ
powierzchnia ramki S
14
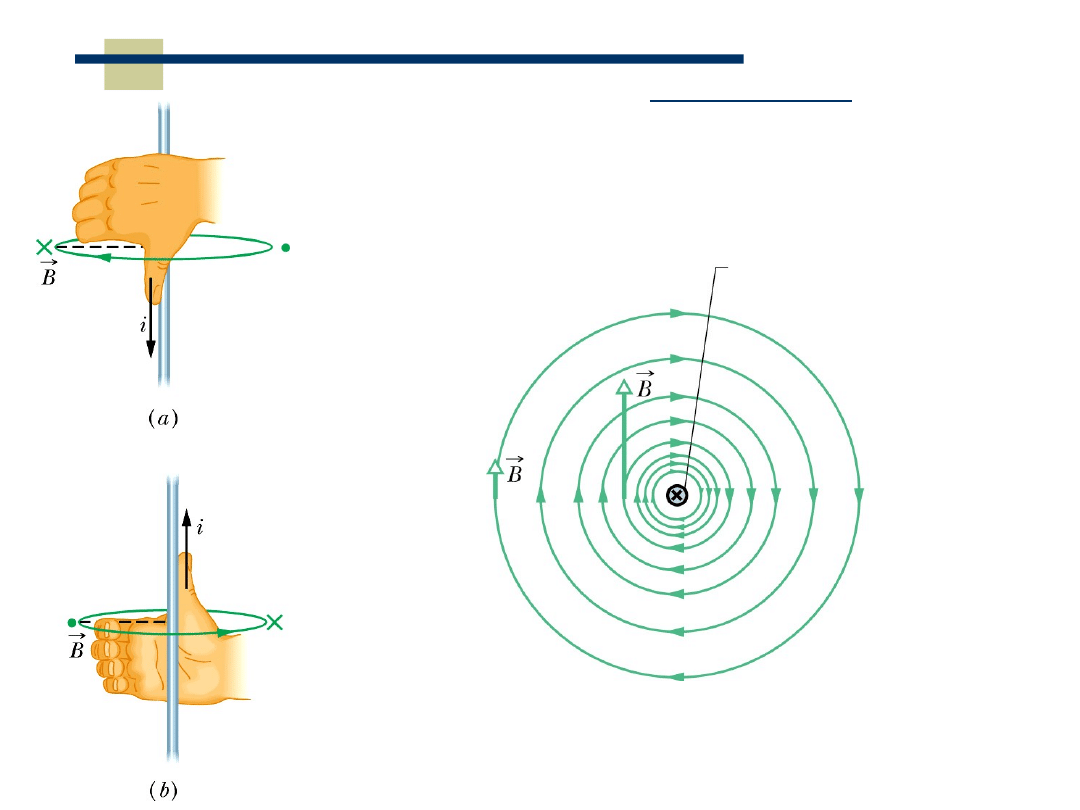
Pola magnetyczne wytwarzane
przez przewodnik z prądem
Przewodnik z prądem i
skierowanym do płaszczyzny
15
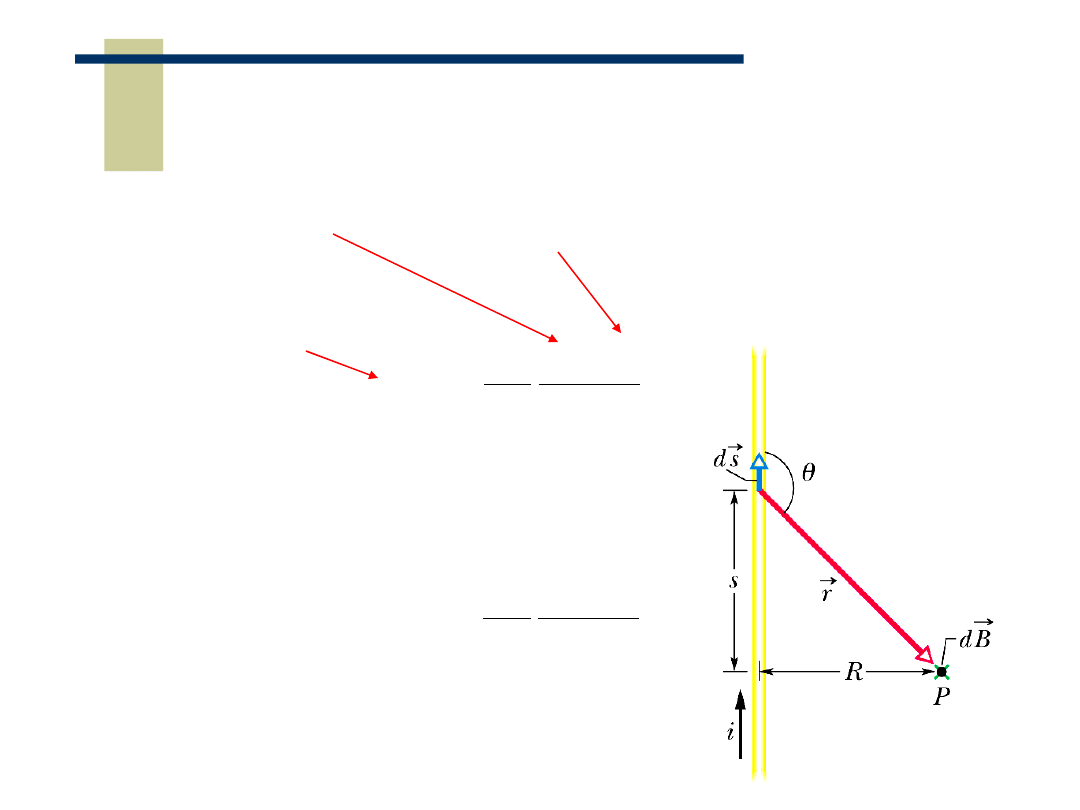
Prawo Biot’a-Savart’a- pole magnetyczne wytwarzane
przez dowolny przewodnik z prądem
3
0
4
r
r
s
id
B
d
×
=
π
µ
Pole mag. pochodzące od
odcinka przewodnika ds
µ
0
przenikalność magnetyczna
próżni = 4π x 10
-7
= 1.26 x 10
-6
Tm/A
wektor styczny do przewodnika
skierowany zgodnie z
kierunkiem prądu i
wektor łączący punkt P z
elementem ds
Aby policzyć pole w punkcie P
trzeba sumować (całkować)
odpowiednie dB po całej
długości przewodnika
∫
×
=
3
0
4
r
r
s
id
B
π
µ
16
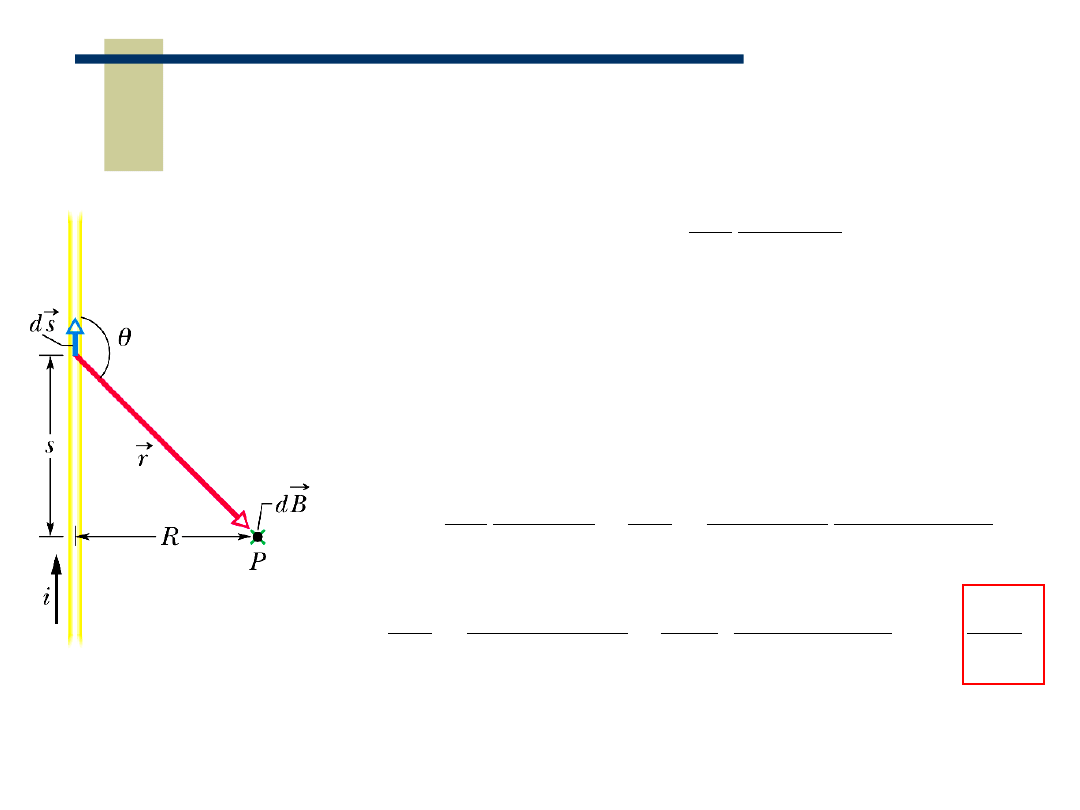
Prawo Biot’a-Savart’a- pole magnetyczne wytwarzane
przez prostoliniowy przewodnik z prądem
dB
=
µ
0
4
π
idssin
θ
r
2
W punkcie P:
Zauważ, że kierunek dla wszystkich małych dB
jest do płaszczyzny kartki, obojętnie czy ds jest
powyżej czy poniżej punktu P
Używając zależności r
2
= (s
2
+ R
2
) i sin
θ
= R/r
B
=
µ
0
4
π
ids sin
θ
r
2
− ∞
+ ∞
∫
=
µ
0
i
4
π
ds
(s
2
+
R
2
)
− ∞
+ ∞
∫
R
(s
2
+
R
2
)
1/ 2
=
µ
0
i
4
π
Rds
(s
2
+
R
2
)
3/ 2
− ∞
+ ∞
∫
=
µ
0
i
4
π
R
s
(s
2
+
R
2
)
1/ 2
− ∞
+ ∞
=
µ
0
i
2
π
R
17
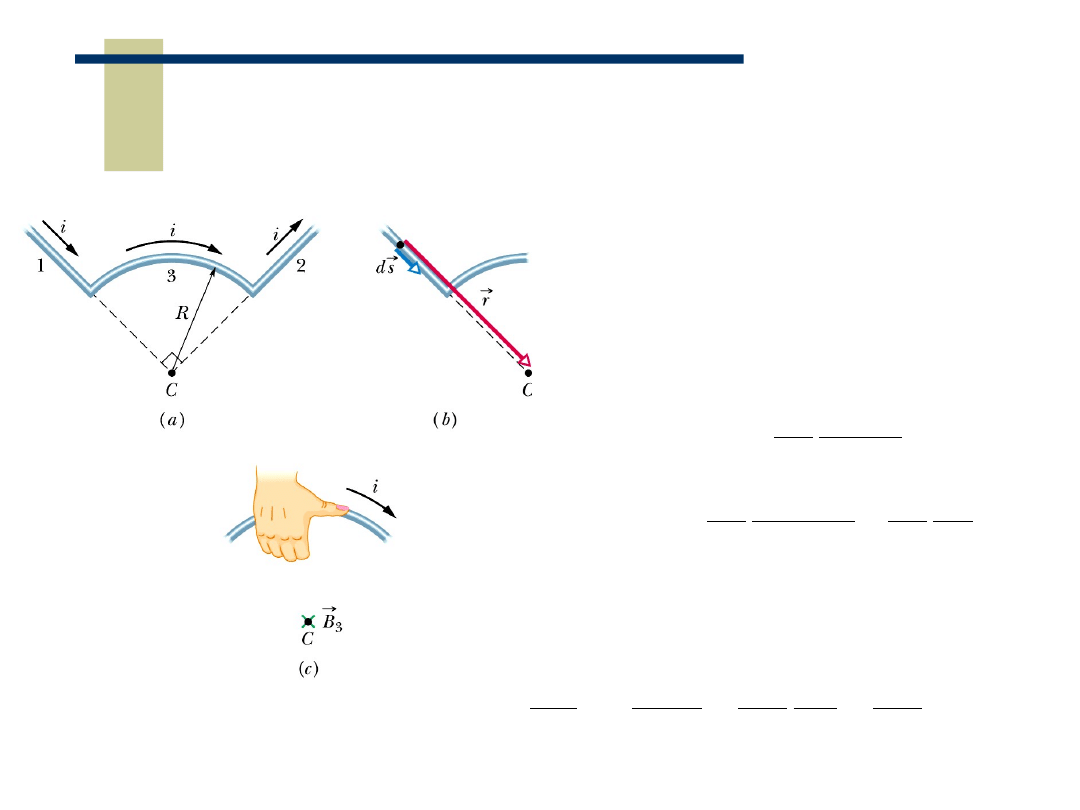
Prawo Biot’a-Savart’a- pole magnetyczne wytwarzane
przez przewodnik z prądem o przykładowym kształcie :
Dla odcinków 1 i 2 :
)
sin(0
sinθ
r
s
d
°
=
=
×
0
2
0
2
0
3
0
4
sin
4
4
R
ids
R
ids
r
r
s
id
B
d
π
µ
θ
π
µ
π
µ
=
=
×
=
Dla odcinka 3 :
B
=
µ
0
4
π
iRd
θ
R
2
0
π
/ 2
∫
=
µ
0
i
4
π
π
2R
=
µ
0
i
8R
Sumowanie (całkowanie) odbywa się po ds, które
można wyrazić ds = R d
θ
:
18
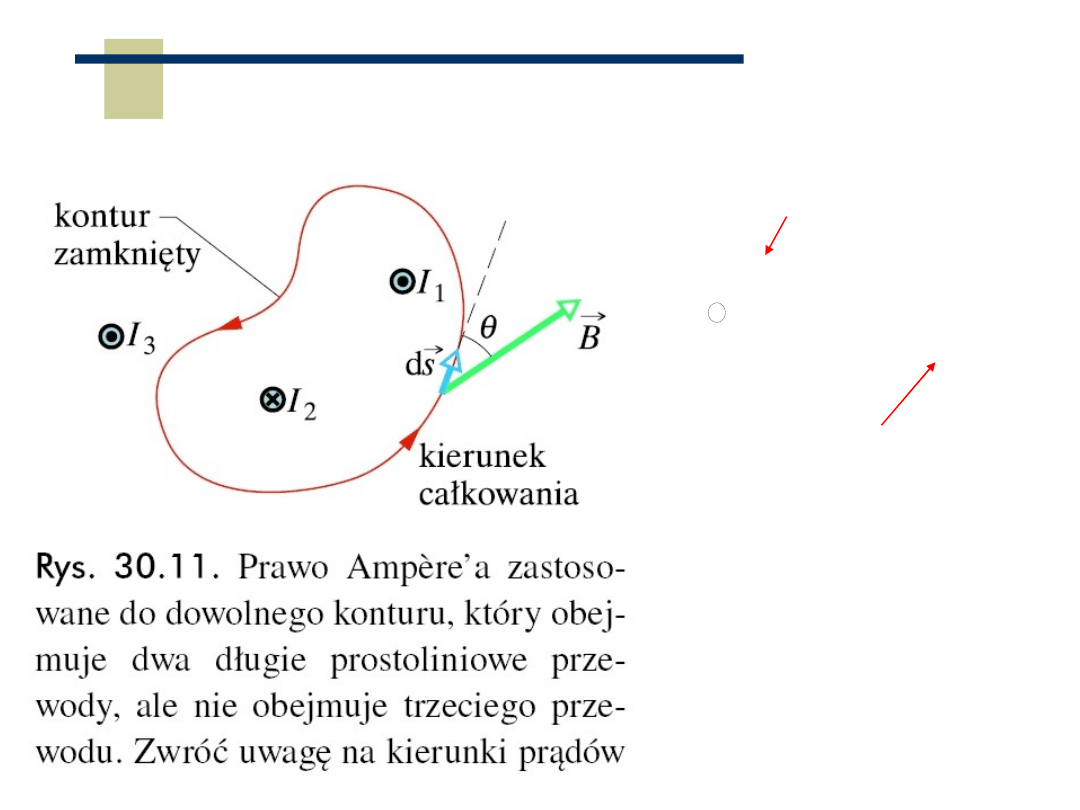
Prawo Ampera
∑
∫
=
⋅
→
→
k
k
I
ds
B
0
µ
„krążenie” wektora B po
zamkniętej krzywej
suma prądów
przecinających
powierzchnię rozpiętą
na zamkniętej krzywej
pole magnetyczne
wytwarzane przez
prądy
19
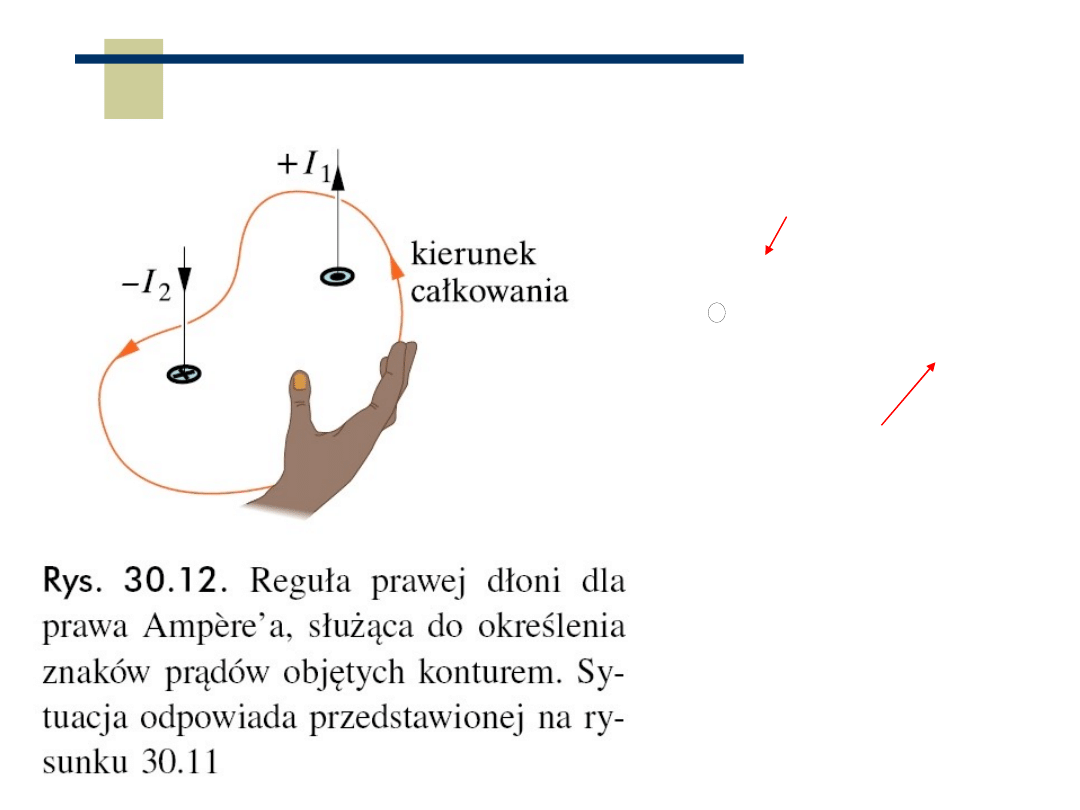
Prawo Ampera
∑
∫
=
⋅
→
→
k
k
I
ds
B
0
µ
„krążenie” wektora B po
zamkniętej krzywej
suma prądów
przecinających
powierzchnię rozpiętą
na zamkniętej krzywej
20
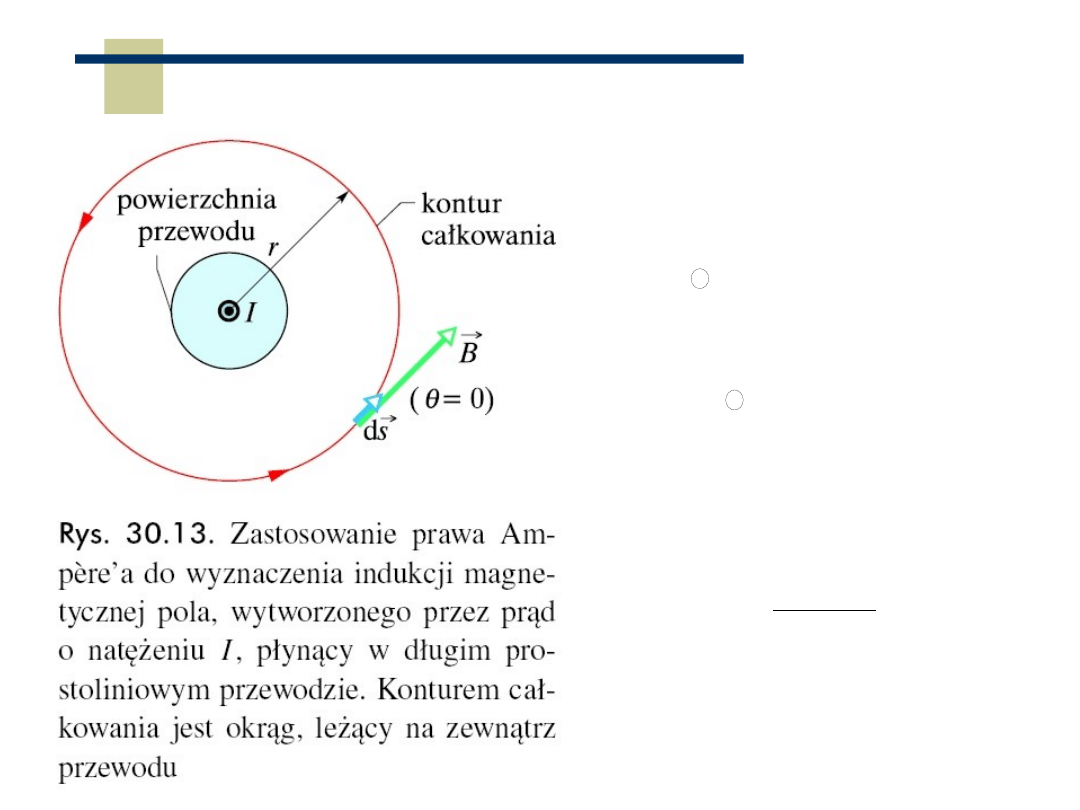
Prawo Ampera
R
I
B
I
R
B
I
ds
B
I
ds
B
π
µ
µ
π
µ
µ
2
)
2
(
0
0
0
0
=
=
=
=
⋅
∫
∫
→
→
21
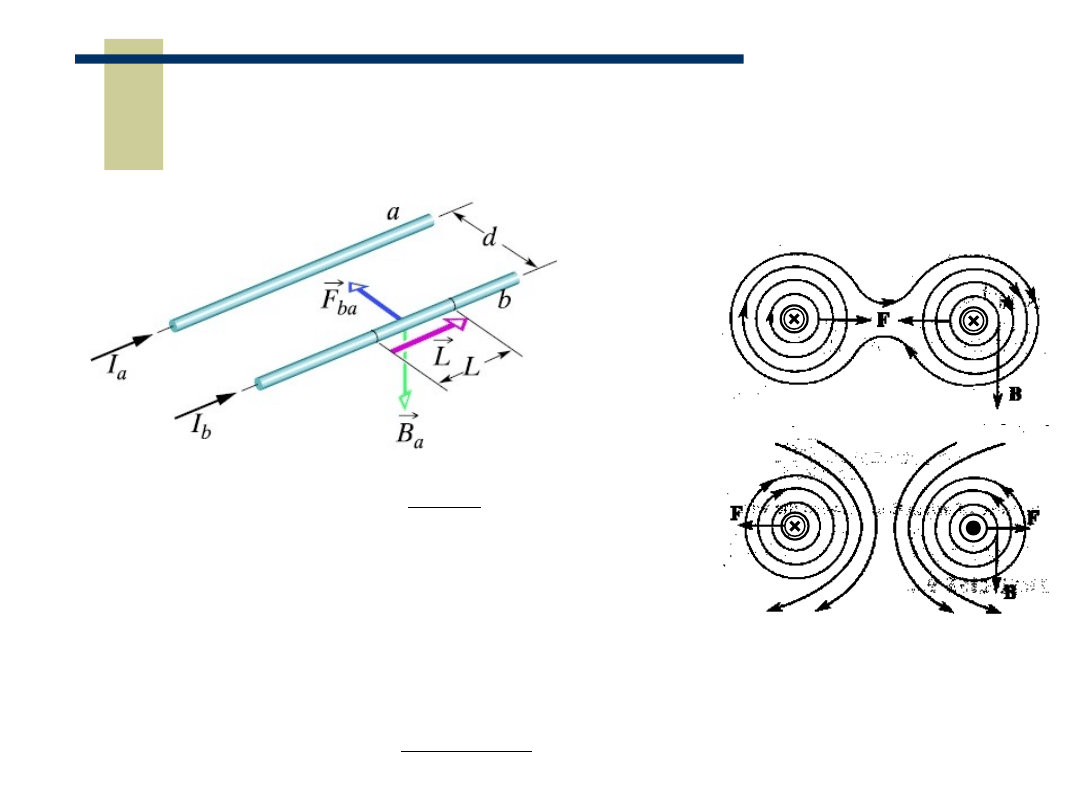
Oddziaływanie magnetyczne dwóch równoległych
przewodników z prądem
prądy skierowane do tablicy
prądy przeciwnie skierowane
d
I
LI
LB
I
F
B
L
I
F
b
a
b
ba
b
ba
π
µ
2
0
=
=
×
=
→
→
→
Siła działająca na przewodnik b w polu
B
a
, działająca na odcinek L
d
I
B
a
a
π
µ
2
0
=
→
22
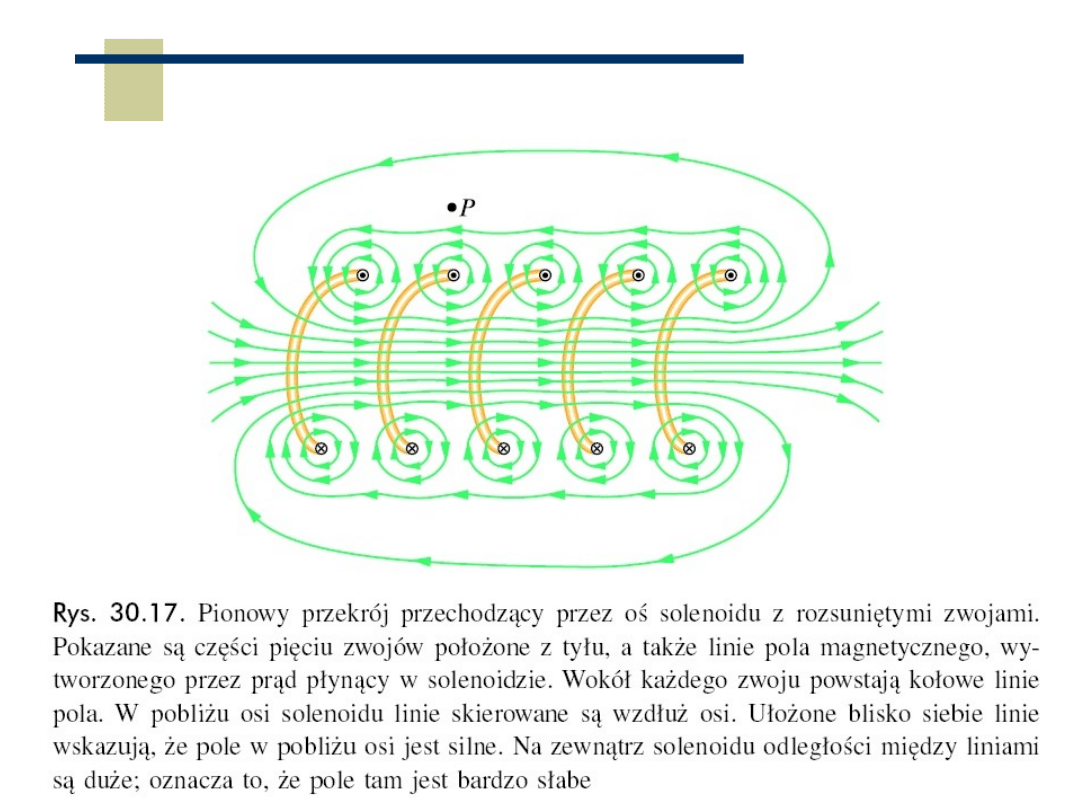
Pole magnetyczne solenoidu (elektromagnes)
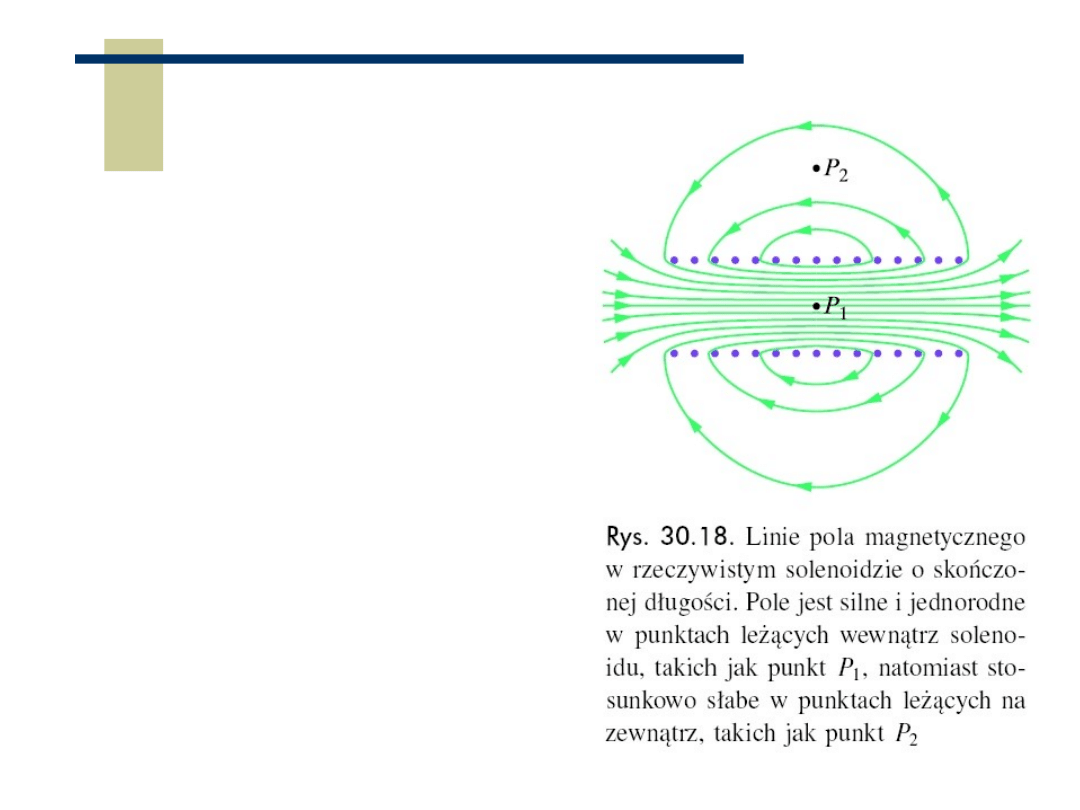
23
Pole magnetyczne
solenoidu
(elektromagnes)
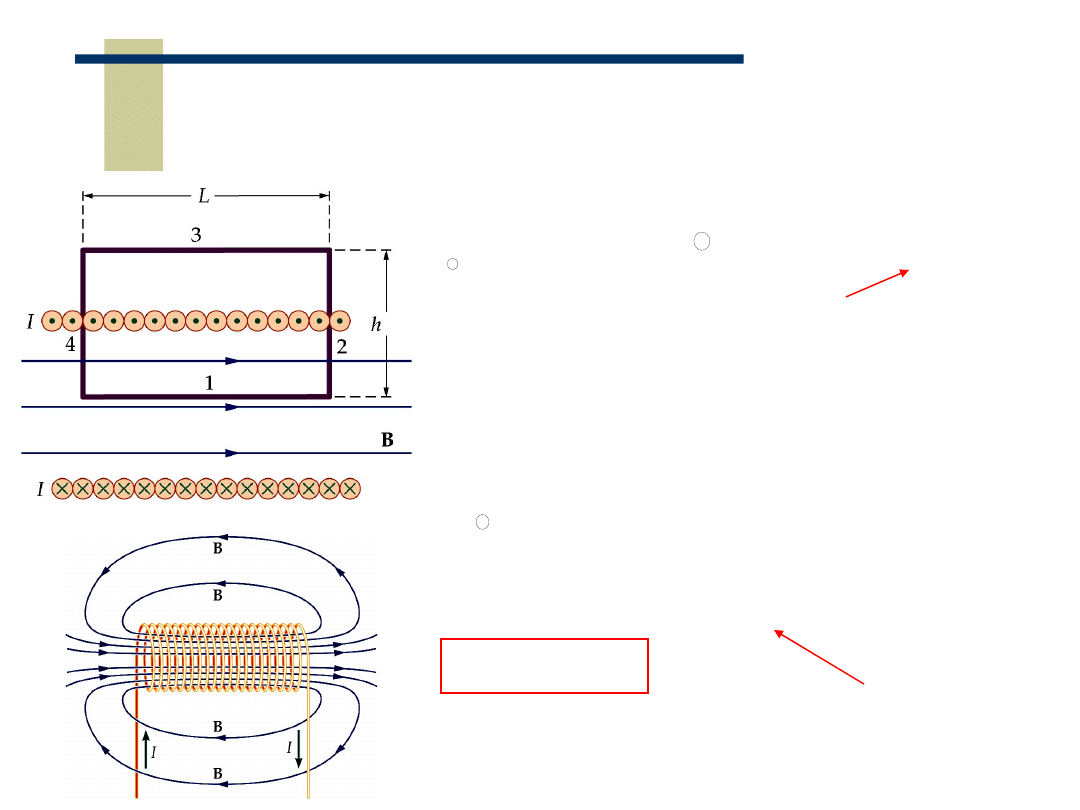
24
Pole magnetyczne solenoidu (elektromagnes)
a
b
c
d
i
0
n
i
B
nL
i
BL
dl
B
dl
B
dl
B
dl
B
dl
B
a
d
d
c
c
b
b
a
0
0
0
0
0
0
0
µ
µ
=
=
+
+
+
⋅
+
⋅
+
⋅
+
⋅
=
⋅
→
→
→
→
→
→
→
→
→
→
∫
∫
∫
∫
∫
Na odcinku cd wektor B = 0
Na odcinku bd, da wektor B
⊥
(prostopadły do) dl
Liczba zwojów na jednostkę
długości solenoidu
Wartość wektora indukcji p.mag. jest
proporcjonalna do prądu płynącego w
elektromagnesie
N
i
dl
B
0
0
µ
=
⋅
→
→
∫
Z prawa Ampera
Liczba zwojów przecinających
powierzchnię rozpiętą na
konturze abcd
∑
∫
=
⋅
→
→
k
k
i
dl
B
0
µ
N
S
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
- Slajd 16
- Slajd 17
- Slajd 18
- Slajd 19
- Slajd 20
- Slajd 21
- Slajd 22
- Slajd 23
- Slajd 24
Wyszukiwarka
Podobne podstrony:
2010 w16B Magnetyzm materii
2010 czerwiec klucz cz I
Sp asp proc kom cz VII 2010
Kom multimed cz I 2010
odp cz II(5)2010
cywil ogolna 1 wyklad do wywalenie 2 wyklad od str 5, prawo cywilne - cz੠ogˇlna (5) - 18.12.2010
2010 SP Kat prawo cywilne cz III
Wyznaczanie ładunku właściwego, Wyznaczanie ładunku właściwego e do m metodą magnetronową 12, 1.1. C
cywil ogolna 1 wyklad do wywalenie 2 wyklad od str 5, prawo cywilne - cz੠ogˇlna (3) - 6.11.2010
cywil ogolna 1 wyklad do wywalenie 2 wyklad od str 5, prawo cywilne - cz੠ogˇlna (2) - 16.10.2010
Kult uwar kom cz VIII 2010
Kom multimed cz II 2010
Kom multimed cz VII 2010
Sp asp cz V 2010 Kom Sp 24 01 10
MAGNETOTERAPIA I MAGNETOSTYMULACJA 2010
więcej podobnych podstron