AKADEMIA GÓRNICZO

– HUTNICZA

KATEDRA METROLOGII I ELEKTRONIKI

TEORIA I PRZETWARZANIE SYGNAŁÓW

Zadanie projektowe pt.:

FILTRACJA ADAPTACYJNA

– IDENTYFIKACJA OBIEKTÓW

Wykonał:

RADZIK

Jarosław

Jarosław RADZIK

AKADEMIA GÓRNICZO-HUTNICZA W KRAKOWIE , KATEDRA METROLOGII I
ELEKTRONIKI

rok akademicki 2014/2015

Filtracja adaptacyjna

– identyfikacja obiektów

 

)

(

1

)

(

n

dx

n

xx

o

p

R

w





STRESZCZENIE

Celem projektu jest demonstracja zasad i efektów

działania filtrów adaptacyjnych. Spo ród różnych

zastosowań filtrów adaptacyjnych, dla celów tej
prezentacji wybrano system identyfikacji.

W czę ci

teoretycznej

zostały

zaprezentowane

ogólne

wiadomo ci odno nie filtracji adaptacyjnej oraz

konkretne jej metody oraz rodzaje filtrów. Czę ć
praktyczna przedstawia wyniki symulacji dwóch
typów identyfikacji parametrycznej opartej na
przetworzonych

splotowo sygnałów pomiarowych

oraz bezpo rednio aproksymowanych funkcjami

sklejanymi sygnały pomiarowe. Dodatkowo zostanie
przeprowadzona identyfikacja odpowiedzi impulsowej

układu LTI za pomocą filtru RLS.

Słowa kluczowe: filtracja adaptacyjna, filtr RLS,

sklejanie sygnałów.

1. WSTĘP

Filtracja

adaptacyjna

jest

szeroko

wykorzystywana w przypadkach, gdy parametry

systemu (procesu) są zmienne w czasie, a statystyczne

cechy sygnałów nie są znane. Algorytmy filtracji,

przeprowadzające proces optymalizacji, wspomagają
wówczas zadanie identyfikacji takiego systemu.

Wydajno ć algorytmów okre lana jest przez

liczbę czynników takich jakŚ

— dokładno ć otrzymanego rozwiązania,

— prędko ć zbieżno ci,

— zdolno ć ledzenia dla procesów

zmiennoczasowych,

— złożono ć obliczeniowa,

— odporno ć na błędy zaokrągleń,

— równoległe operacje dla platform

wieloprocesorowych.

W pracy przedstawione zostają podstawowe i

szeroko wykorzystywane algorytmy gradientowe

(rozdziały 3, 4).

2. FILTR WIENERA

Model

systemu

opisany

jest

równaniem

różnicowymŚ

(2.1)

gdzie: x(n)

-

sygnał wej ciowy,

d(n)

-

sygnał wyj ciowy,

w

i

o

-

współczynniki filtru.

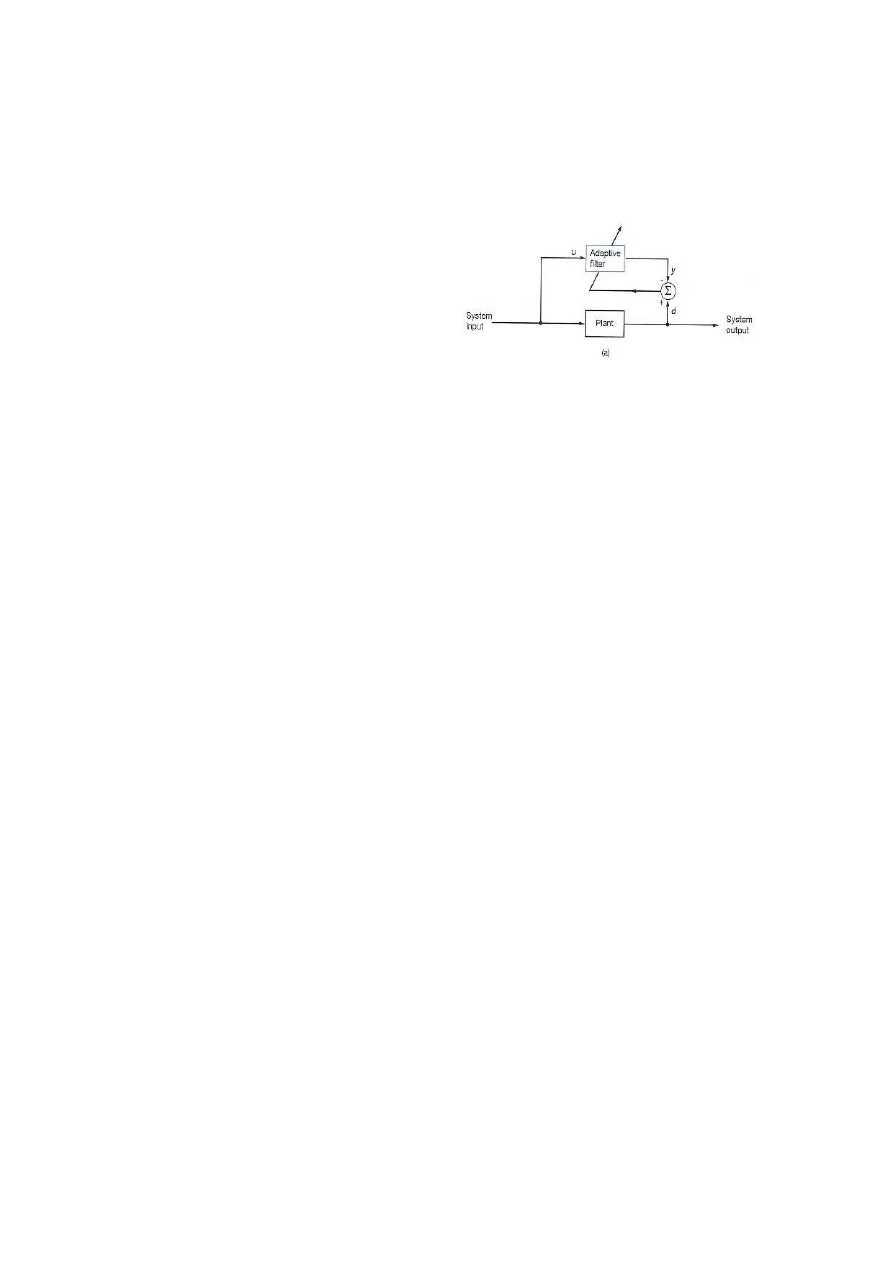
Rys.1

. Filtr adaptacyjny w konfiguracji identyfikacji

obiektu

[źródło: Internet]

Powyższy wzór można zapisać w formie

� =

�

� ∙

(2.2)

� = [ � , … , � − � + ]

�

(2.3)

�

= [

�

, … ,

−

�

]

�

(2.4)

Estymatorem FIR powyższego systemu jestŚ

� =

�

� ∙

(2.5)

gdzie w=[w

0

, …, w

M-1

] są estymatami parametrów

rzeczywistego systemu. Celem jest takie wyznaczenie
w

M

aby błąd

redniokwadratowy pomiędzy

zmierzonym sygnałem d(n) (sygnałem odniesienia) a

sygnałem wyj ciowym modelu y(n) był minimalny.

Kryterium błędu wygląda następującoŚ

� = � ∙ [

� ] = � ∙ [( � − � ) ] (2.6)

gdzie E

[.] oznacza warto ć oczekiwaną. Podstawienie

(2.5) do (2.6) daje w rezultacie:

�

= � ∙ [

� −

�

�

] (2.7)

Proste przekształcenia i obliczenie pochodnej

względem w oraz przyrównanie jej do zera prowadzi

do wyrażenia na optymalne warto ci wag w filtra,

który nosi nazwę filtru WieneraŚ

(2.8)

gdzie: R

xx

(n)

- estymata

macierzy

autokorelacji

sygnału x(n) w n-tej chwili czasowej,
p

dx

(n)

- estymata wektora korelacji wzajemnej

sygnału wej ciowego i odniesienia,











1

0

)

(

)

(

M

i

o

i

i

n

x

w

n

d

))

(

(

)

(

2

1

)

(

)

1

(

n

J

n

n

n

w

w

w















1

2

))

(

(

)

(







n

J

n

w

W

(n)

n

n

v

w

w









)

(

)

1

(

))

(

(

)

(

)

(

2

1

)

(

)

1

(

n

J

n

n

n

n

w

W

w

w











3. METODY GRADIENTOWE

Praktyczne wykorzystanie równania (2.8) dla

każdej chwili czasu n pociąga za sobą kłopot z

poprawną

estymacją

warto ci

oczekiwanych,

co

jest

typowym

problemem

stochastycznej

optymalizacji. Wynika to z faktu, że w większo ci

przypadków

funkcje

rozkładu

gęsto ci

prawdopodobieństwa obserwowanych zmiennych

losowych nie są znane lub też zmienne te są

niestacjonarne. Aby przezwyciężyć ten problem

adoptuje się zazwyczaj znane iteracyjne metody

optymalizacji okre lone dla deterministycznych
funkcji kosztu.

Najczę ciej

stosowanymi

algorytmami

optymalizującymi deterministyczną funkcję kosztu

(celu) są adaptacyjne algorytmy gradientowe.

Rekursywny estymator ma postaćŚ

(3.1)

gdzie: w(n+1)

– wektor współczynników filtru w

chwili n+1,
w(n)

– wektor współczynników filtru w chwili n,

μ(n) – współczynnik skalujący (w ogólno ci zmienny
w czasie),
v(n)

– kierunek modyfikacji.

Wzór (3.1) pokazuje uaktualnianie parametrów

filtru w kierunku v(n

). Najczęstszym wyborem v(n)

jest kierunek przeciwny do okre lonego przez gradient
z funkcji celu J(.).

3.1. Algorytmy najszybszego spadku

Mają one postaćŚ

(3.2)

gdzie:



J

(w(n))

–

wektor gradientu funkcji

kosztu,

μ(n) – współczynnik skalujący.

3.2. Algorytmy Newtona-Raphsona

Przyjmują postaćŚ

(3.3)

gdzie W(n

) jest macierzą wagową, poprawiającą

zbieżno ć (szybko ć adaptacji). W algorytmach
Newtona-Raphsona za macierz W(n

) przyjmuje się

odwrotno ć hesjanu funkcji celu J(w(n)) w n-tej
chwili czasowej:

(3.4)

3.3. Algorytmy Quasi-Newtona

W przypadkach gdy wyznaczenie warto ci

hesjanu jest trudne, wykorzystywana jest jego
aproksymata A(n):

� +

=

� −

� [� � ]

−

��

� (3.5)

4. ADAPTACYJNE ALGORYTMY GRADIENTU

STOCHASTYCZNEGO (LMS)

Niech minimalizowana funkcja kosztu wynosi:

� =

�

(4.1)

Filtr adaptacyjny ma zatem za zadanie mi

nimalizować

chwilową a nie oczekiwaną warto ć błędu. Równanie

(3.3) przyjmuje postać (4.2) charakteryzującą szeroką

grupę filtrówŚ

� +

=

� + � � �

�

� (4.2)

� = � − � = � −

�

�

� (4.3)

gdzie: W(n)

– macierz wagowa o wymiarach MxM,

e

(n)

– sygnał błędu w chwili n.

4.1. Filtr LMS

Otrzymywany

jest

po

uniezależnieniu

współczynnika skalującego od czasu (μ(n) = μ) oraz

po wprowadzeniu identyczno ciowej macierzy
wagowej W(n) = I.

� +

=

� +

�

�

(4.4)

Zalety:

— prosta implementacja,

— mała złożono ć obliczeniowa.

Wady:

— czuło ć na rozrzut warto ci własnych macierzy

autokorelacji R,

— wolna zbieżno ć algorytmu zależna od stosunku

λ

min

/ λ

max

czyli minimalnej do

maksymalnej warto ci

własnej macierzy R.

W rezultacie warto ć parametru skalującego μ

dobierana jest w następujący sposób, zapewniający

dążenie do zera błędu dopasowania wag filtra do

warto ci optymalnych dla n→∞:

< <

�

��

(4.5)

4.2. Filtr NLMS

Unormowany filtr LMS (NLMS) otrzymywany

jest po następującym uzależnieniu w równaniu (4.4)
parametru

μ od czasu:

(4.6)

gdzie niewielki parametr γ zapobiega zerowaniu się

mianownika. Zaletą unormowanego algorytmu LMS

jest poprawienie zbieżno ci w stosunku do
podstawowego algorytmu LMS.

Niestety złożono ć

obliczeniowa jest większa, co skutkuje wydłużeniem
czasu potrzebnego do przeprowadzenia filtracji .

5. Blokowe filtry adaptacyjne

Je li w dziedzinie czasu użyty zostanie algorytm

LMS wymagający dużej ilo ci pamięci, można

zaobserwować

znaczący

wzrost

złożono ci

obliczeniowej. Problem ten może być rozwiązany na
dwa sposoby:
1.

Wybór algorytmu o nieskończonej odpowiedzi

impulsowej. Rozwiązanie takie niesie za sobą

kolejny problem związany z niestabilno cią
algorytmu.

2. Filtracja adaptacy

jna w dziedzinie częstotliwo ci,

łącząca dwie uzupełniające się metody stosowane

w cyfrowym przetwarzaniu sygnałówŚ
a)

blokowa implementacja filtru o skończonej

odpowiedzi impulsowej, pozwalająca na

skuteczne

wykorzystanie

równoległego

przetwarzania, skutk

ującego przyspieszeniem

działania algorytmu,

b) algorytmy szybkiej transformaty Fouriera

(FFT)

do

wykonywania

splotów,

umożliwiające w efektywny sposób adaptować

parametry filtru w dziedzinie częstotliwo ci.

Powyższe podej cie nazywane jest często

blokowym algorytmem LMS (BLMS). Jak wskazuje
nazwa rodziny filtrów, adaptacja przeprowadzana jest

na zasadzie „blok po bloku” zamiast „próbka po

próbce” (LMS, NLMS). Umożliwia to wykorzystanie

wspomnianej wyżej szybkiej transformaty Fouriera,
co prowadzi do oszcz

ędno ci obliczeniowych.

Zastosowanie blokowej struktury wiąże się

jednak z dodatkowym opóźnieniem w cieżce sygnału,

które wynika z konieczno ci zebrania całego bloku
danych przed jego dalszym przetwarzaniem. Im

większy blok tym opóźnienie jest większe.

6.

Porównanie

dwóch

typów

identyfikacji

W rozdziale tym zaprezentowane zostaną

wyniki

porównania

2

typów

identyfikacji

parametrycznej:

- w oparciu

o przetworzone splotowo sygnały

pomiarowe

-

w oparciu o bezpo rednio aproksymowane

funkcjami sklejanymi sy

gnały pomiarowe

Parametry obiektu identyfikowanego w testach będą
stałe lub będą zmieniały się skokowo.

Dla celów identyfikacji splotowej znajdują
zastosowanie

metody

filtracji

nieadaptacyjnej.

Symulacje przeprowadzono dla czasu T=30 i czasie
dyskretyzacji dt=0.01, zarejestrowano M=3000 próbek
pomiarowych

dla

sygnału

wej ciowego

i

wyj ciowego. Jako sygnał wymuszający u(t) przyjęto
przebieg prostokątny z okresem T

U

=10 i amplitudą

±0.5.

Następnie w t=15 nastąpiła skokowa zmiana

parametru transmitancji co spo

wodowało zmianę

wszystkich

współczynników

transmitancji

unormowanej. Szum pomiarowy nie został dodany do
sygnału wej ciowego u i na wyj ciu y, dzięki czemu
metoda identyfikacji wprowadza mniejsze błędy na
estymowane parametry i łatwiejsza jest analiza
otrzymanych wyników.

Dla pierwszego typu identyfikacji długo ć

okna filtru h=3, czas dyskretyzacji ∆t=0.01, funkcja
modulująca ᶲ(t)=t

2

(h-t)

5

(gdzie: h=3). Dokonano

operacji spalania sygnałów pomiarowych z kolejnymi
pochodnymi funkcji modulującej. W chwili t=3
równej h możliwe jest wyliczenie pierwszego splotu.
Sploty sygnałów wej ciowych i wyj ciowych
przedstawione są na rys. 2

Dla drugiego t

ypu identyfikacji rząd funkcji

modulującej k=4, ilo ć węzłów N=50. Na rys. 2
wykre lono

wyniki

aproksymacji

sygnałów

pomiarowych wej ciowego u i wyj ciowego y
funkcjami sklejanymi. Dodatkowo przedstawiono
przebiegi kolejnych pochodnych aproksymaty dla
zare

jestrowanych

sygnałów

pomiarowych.

Założono

odpowiednio

równe

identyfikowanej transmitancji rzędy licznika m=1 i
mianownika n=2. Na rys.3 przedstawiono przebieg
identyfikowanych parametrów metodą dokładną
poprzez rozwiązanie pełnego zagadnienia własnego
dla symulowanego obiektu. Długo ć przesuwanego
okna została przyjęta jako dwukrotnie większa od
długo ci funkcji modulującej h i wynosi T=6. Dla t=5
sploty już nie są na tyle długie by warto ci własne
macierzy Grama zaczęły się stabilizować.

















1

0

2

)

(

)

(

)

(

)

(

M

k

T

k

n

x

n

n

n











x

x

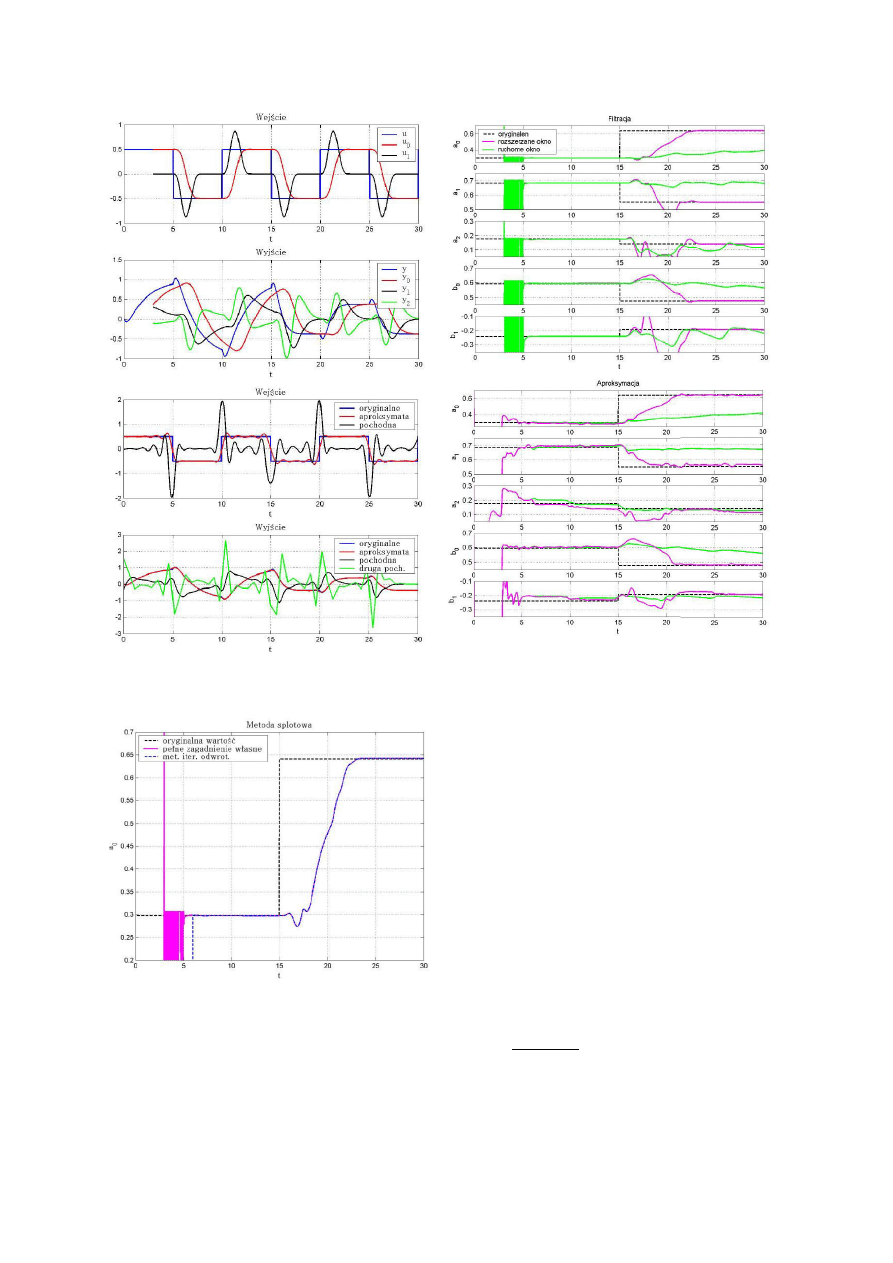
Rys.2 Wynik

i filtracji i aproksymacji z sygnałami

pomiarowymi wej cia i wyj cia.

Rys.3

Porównanie wyników rozwiązania pełnego i

przybliżonego zagadnienia własnego

Rys. 4 Przebieg identyfikacji parametrów w

rozszerzanym i ruchomym oknie

7. Filtry adaptacyjne RLS

Implementacja algorytmu RLS wymaga znajomo ci

warto ci początkowej macierzy odwrotnej P,

przyjmuje się, że jest nią macierz diagonalna z
warto ciami δ

-1

na przekątnej, gdzie δ jest małą

warto cią dodatnią.

Podsumowując, algorytm RLS jest następującyŚ
I. Inicjalizacja

1. Wybór długo ci filtra M,

2. Początkowe współczynniki filtra można ustawić na
zero h

0

=0,

Początkowa macierz odwrotna P

0

=

δ

-1

I, gdzie

δ jest

małą warto cią dodatnią.

IIa. Obliczenia dla N=1,2,3,...

. � =

�

�−1 �

+

�

�

�

−1 �

(7.1)

.

=

�

ℎ

−

(7.2)

. ℎ = ℎ

−

+ �

(7.3)

. � = �

−

− �

�

�

−

(7.4)

W przypadku, kiedy filtr RLS wykorzystywany jest do

ledzenia parametrów zmiennych w czasie, stosuje się

wykładnicze zapominanie najstarszych pomiarów i

obliczenia przebiegają następującoŚ
IIb. Obliczenia dla N=1,2,3,...

. � =

�

−1

�

�−1 �

+�

−1

�

�

�

−1 �

(7.5)

.

=

�

ℎ

−

(7.6)

. ℎ = ℎ

−

+ �

(7.7)

. � =

−

�

−

−

−

�

�

�

−

(7.8)

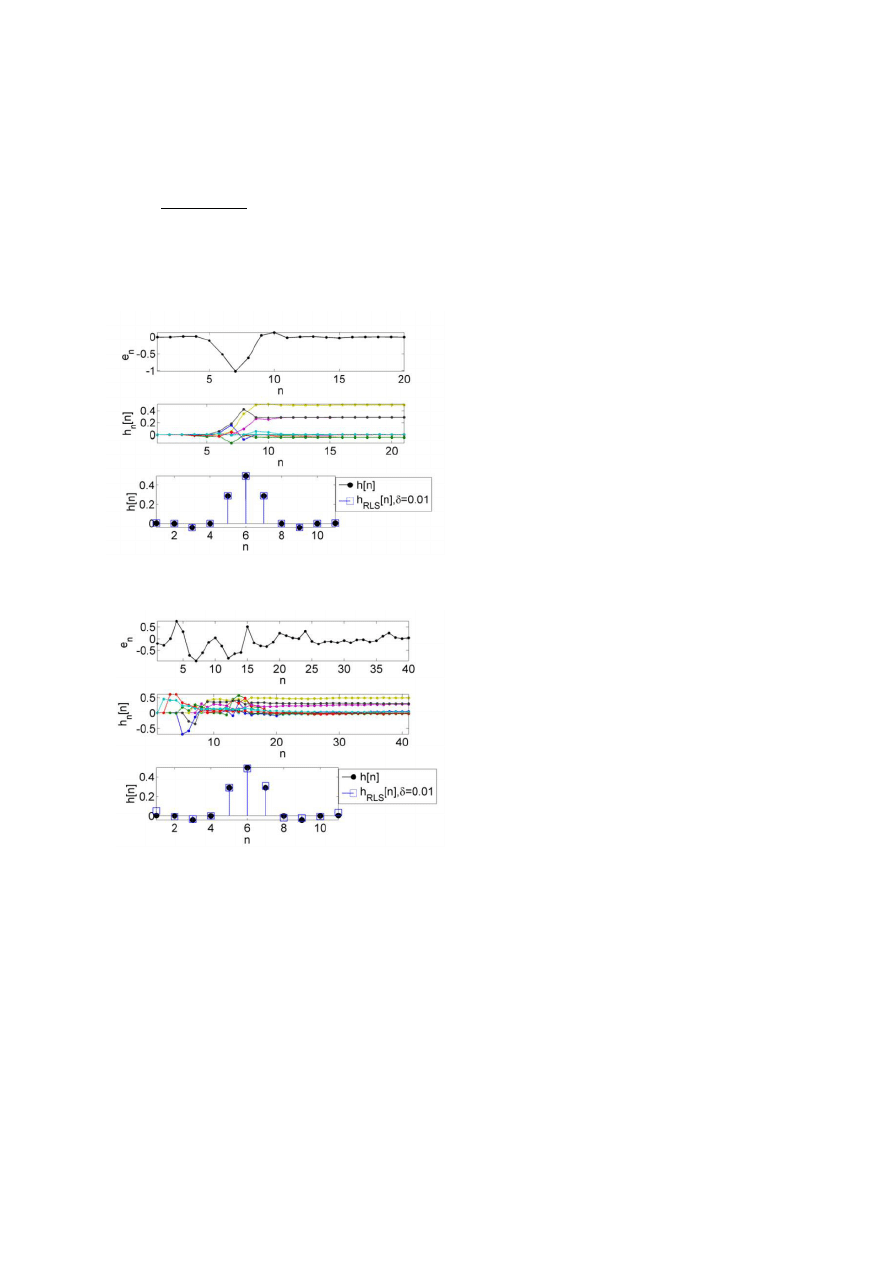
Rys.5 Identyfikacja odpowiedzi impulsowej filtrem

RLS -

pomiar bez zakłóceń.

Rys. 6 Identyfikacja odpowiedzi impulsowej filtrem

RLS -

pomiar zakłócony szumem addytywnym.

Pierwszy przebieg w rys.5 przedstawia

wyniki identyfikacji odpowiedzi impulsowej układu

LTI za pomocą filtra RLS. Wej ciowym sygnałem
testowym x[n

] był szum o rozkładzie normalnym, a

sygnałem odniesienia d[n] odpowiedź układu
identyfikowanego na to wymuszenie zarejestrowana

bez zakłóceń. rodkowy wykres rys.6 przedstawia

błąd dopasowania w kolejnych chwilach czasu. Błąd

ten szybko maleje, co oznacza, że sygnały x[n] i d[n]

zostały dopasowane. Dolny przebieg rys. 6

przedstawia współczynniki filtra w kolejnych

chwilach czasu. Algorytm został uruchomiony z

początkowymi współczynnikami filtra równymi zeroś

w kolejnych iteracjach współczynniki filtra szybko

osiągają warto ci zadane. Dolny przebieg rys.5

przedstawia

odpowiedź

impulsową

układu

identyfikowanego h[n

] i współczynniki odpowiedzi

impulsowej wyznaczone filtrem RLS w N=21 iteracji.
Rys.6 przedstawia wykresy analogiczne do rys.5 dla

przypadku, kiedy sygnał odniesienia d[n] został

zarejestrowany z zakłóceniem w postaci szumu
addytywnego. Rys.6 (

dolna czę ć) przedstawia

odpowiedź impulsową układu identyfikowanego h[n] i

współczynniki odpowiedzi impulsowej wyznaczone
filtrem RLS w N=41 iteracji.

8. Podsumowanie

Zaobserwowano podobne wyniki dla metody

identyfikacji z użyciem aproksymacji funkcjami
sklejanymi.

Przykładowo dla parametru a

0

i b

0

metoda

daje nam lepsze wyniki niż metoda identyfikacji w
oparciu o filtracje. W metodzie aproksymacyjnej
otrzymano

poprawne

identyfikowane

parametry

wcze niej o długo ć okna h metody splotowej.

Natomiast dla pozostałych parametrów można

zauważyć gorsze wyniki.

Problem filtracji optymalnej w sensie

najmniejszych kwadratów sprowadza się do
odwrócenia macierzy R=A

H

A

. Rozwiązanie jest

uzyskiwane dla całego wektora dostępnych danych,

tzn. blokowo. Innym sposobem uzyskania rozwiązania
jest adaptacyjny algorytm rekurencyjny RLS, który

wyznacza współczynniki filtra h[n] w miarę jak

napływają kolejne próbki sygnału.

9. Literatura

[1] K.

DudaŚ Analiza sygnałów biomedycznych,

Kraków 2010, str. 145-161

[2]

T. P. ZielińskiŚ Cyfrowe przetwarzanie sygnałów

– od teorii do zastosowania, wydanie1, Warszawa
2005, str. 247-286

[3]

M. Pionke, Ł. TuzŚ Projekt „Zastosowania

procesorów sygnałowych”. Demonstracja filtracji

adaptacyjnej, Gdańsk 2008

[4]

M. W. NowakŚ Metody identyfikacji układów

ciągłych z wykorzystaniem funkcji modulujących
i sklejanych i ich zastosowanie w regulatorze
adaptacyjnym, Kraków 2007

[5] D.

Rzepka,

P.

Otfinowski:

Identyfikacja

systemów

nieliniowych

przy

pomocy

kernelowego algorytmu LMS z ograniczeniem
zasobów