1
BUDOWA I PROMIENIOWANIE
ATOMÓW
1
BUDOWA I PROMIENIOWANIE
ATOMÓW
2
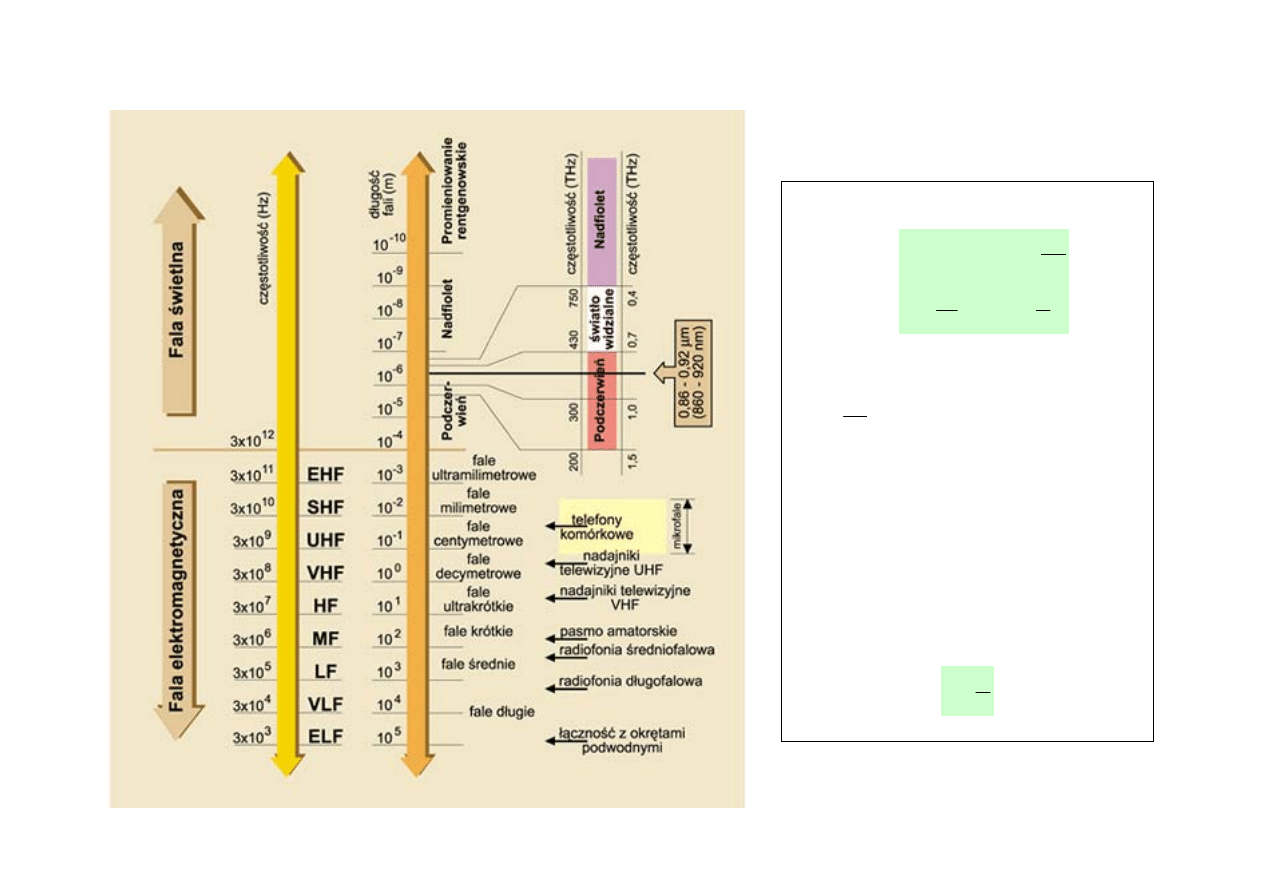
FALE ELEKTROMAGNEYCZNE – WIDMO FAL ELEKTROMAGNETYCZNYCH
Teoria korpuskularna
foton
λ
λ
ν
ν
1
~
,
,
E
hc
E
c
h
p
h
E
=
=
=
stała Plancka h = 6,6·10
-34
J·s
1J =
eV
19
10
6
,
1
1 ⋅
Prędkość fal świetlnych w próżni
c = 3·10
8
m/s.
Związek między częstotliwością
i długością fali elektromagnetycznej
λ
ν
c
=
3
Zakres długości fali
Nazwa
Energia
0,38 < λ < 0,77 µm (1 µm = 10
-6
m)
światło widzialne (fale świetlne)
3800 Å
< λ <
7700 Å
(1 Å = 10
-10
m)
od
fioletu
do
czerwieni
λ > (7700 Å) 770 nm
podczerwień
λ < 380 nm (1 nm = 10
-9
m)
nadfiolet (ultrafiolet)
λ < 380 nm
130 < λ < 380 nm
nadfiolet bliższy
~ eV
10 < λ <130 nm
nadfiolet dalszy
~ eV
0,01 < λ < 10 nm
fale rentgenowskie
~ 10
3
eV (keV)
10
-4
< λ < 0,01 nm
promienie γ
~ MeV
λ< 10
-4
nm
składowa γ promieniowania kosmicznego
> MeV
λ > 770 nm
770 < λ < 3000 nm
podczerwień bliższa
< eV
3 < λ < 100 µm
podczerwień dalsza
< eV
10
-3
< λ < 1 m
mikrofale(~cm), radarowe
λ > 10
-2
m
fale radiowe i telewizyjne
może być λ ~ 10
3
km (ν ~ 10
2
Hz)
4
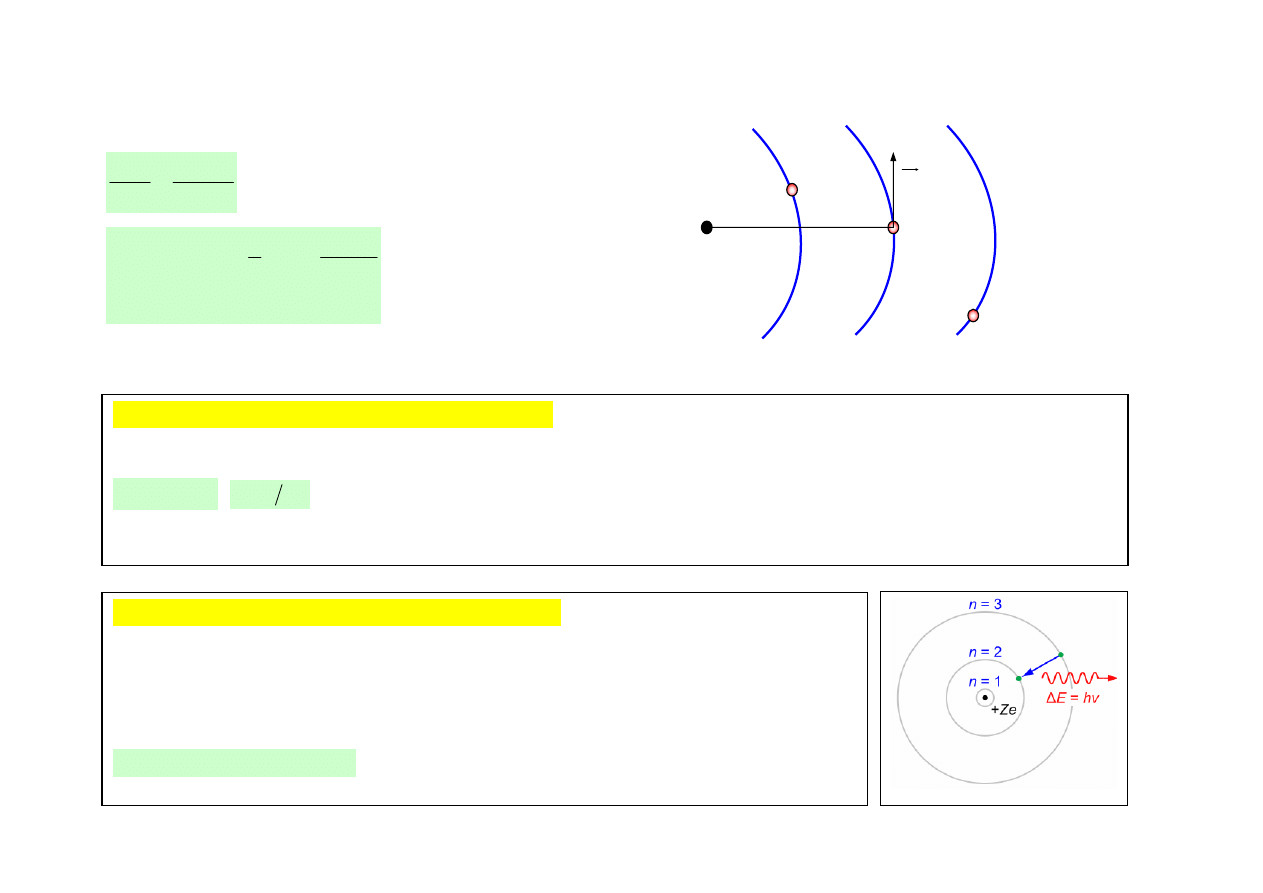
ŹRÓDŁO FAL ŚWIETLNYCH – WZBUDZONE ATOMY - ŹRÓDŁO PROMIENIOWANIA ŚWIETLNEGO
Promieniowanie atomów według modelu Bohra
2
0
2
2
2
4
n
n
n
r
Ze
r
m
πε
υ
=
k
c
k
pot
n
n
pot
k
n
E
E
E
E
r
Ze
m
E
E
E
−
=
−
=
−
=
+
=
,
2
4
2
1
0
2
2
πε
υ
n = 1, 2, 3, ... główna liczba kwantowa
+Ze
e
e
e
r
n
n
υ
I postulat kwantowy (stan stacjonarny atomu)
W atomie istnieją takie orbity, po których poruszające się elektrony nie promieniują energii.
h
n
r
m
n
n
=
υ
,
π
2
h
=
h
n = 1, 2, 3, ... główna liczba kwantowa
II postulat kwantowy (stan stacjonarny atomu)
Każda emisja lub też absorpcja energii promieniowania odpowiada przejściu elektronu
pomiędzy dwoma orbitami stacjonarnymi. Promieniowanie emitowane w czasie takiego
przejścia jest określone wzorem:
nm
nm
m
n
nm
h
E
E
E
ω
ν
h
=
=
−
=
5
Atomy wodoropodobne (1 elektron w atomie)
Rozmiar atomu wodoru w stanie podstawowym:
m
r
Z
n
r
r
n
10
1
1
10
53
,
0
,
−
⋅
=
=
Prędkość:
c
c
n
Z
c
n
Z
n
⋅
=
⋅
=
⋅
=
⋅
⋅
=
137
1
,
1
1
α
υ
υ
α
υ
, c – prędkość światła w próżni
Stała struktury subtelnej:
137
1
=
α
Skwantowane stany energii atomu:
(
)
2
1
2
2
2
0
2
2
1
1
2
1
n
E
Z
n
c
m
Z
E
n
=
−
=
α
Energia stanu podstawowego atomu wodoru:
(
)
eV
c
m
E
6
,
13
2
1
2
0
2
1
−
=
−
=
α
(
)
wodoru
atom
Z
n
1
,
1
=
=
Energia spoczynkowa elektronu swobodnego:
MeV
c
m
511
,
0
2
0
=
Widmo wodoru
−
=
=
2
2
1
2
1
1
1
m
n
hc
E
Z
hc
h
λ
λ
ν
takie „długości fal” promieniują atomy
Stała Rydberga:
1
1
807
,
109736
−
∞
=
=
cm
R
hc
E
M
stała Rydberga dla skończonej masy jądra:
1
580
,
109677
1
−
∞
=
+
=
cm
m
m
R
R
p
e
M
M
=
1836
1
p
e
m
m
6
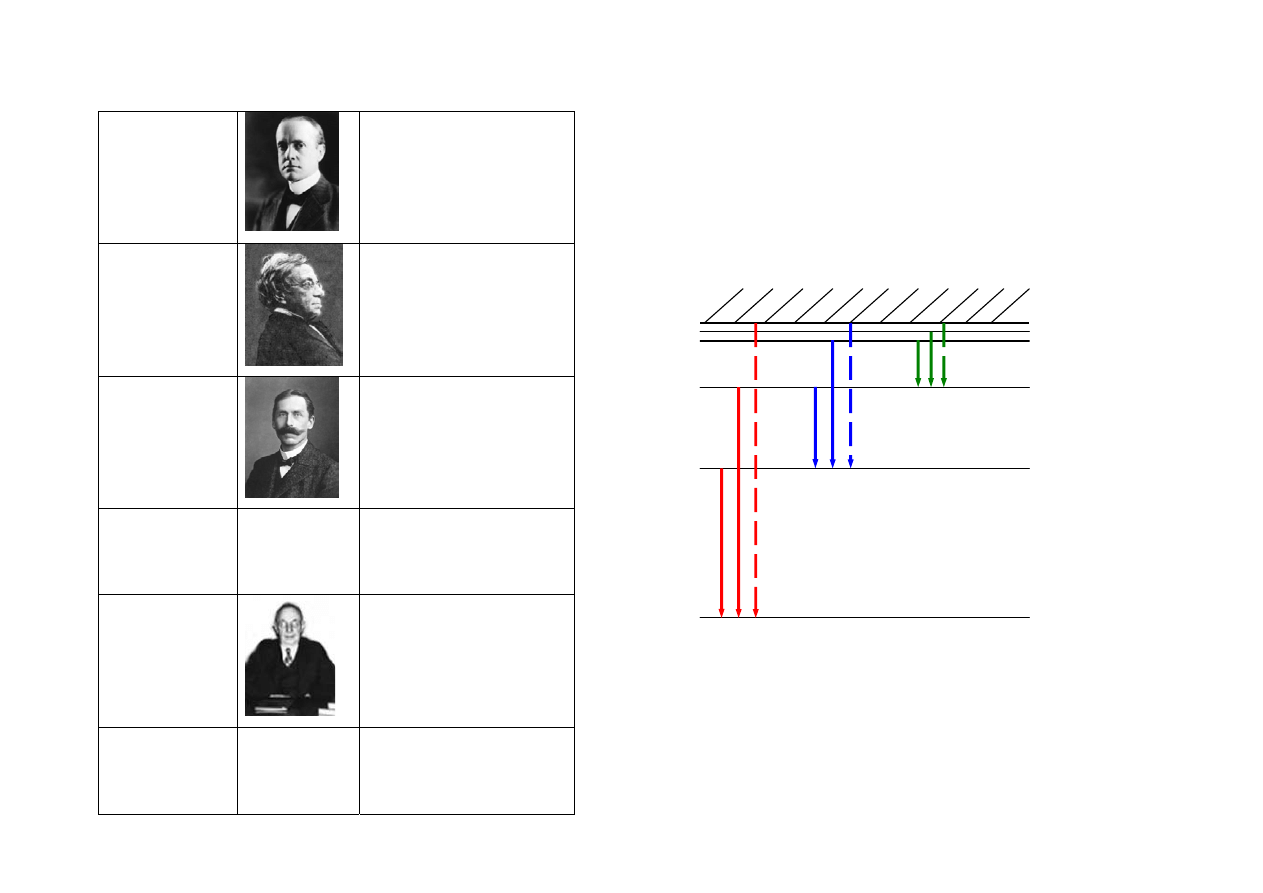
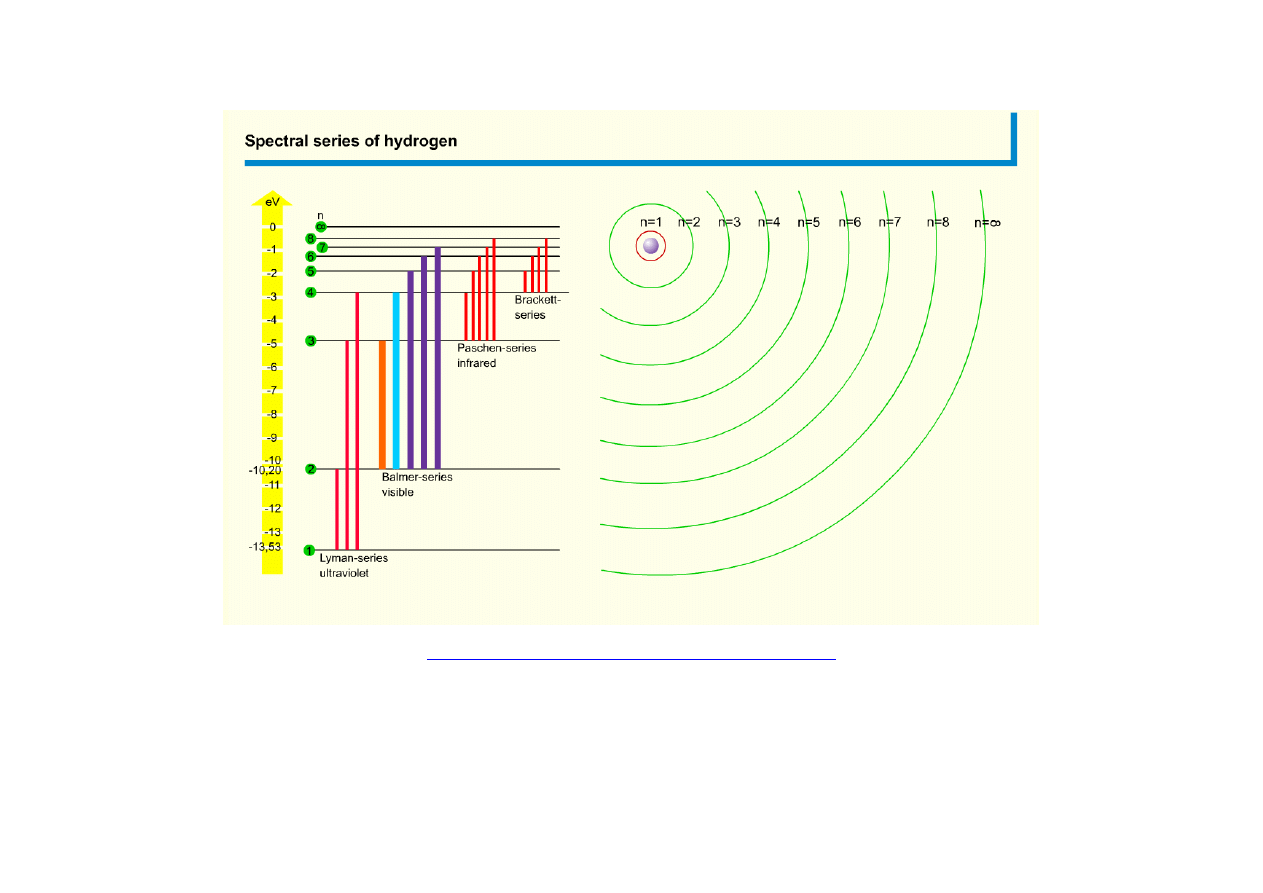
Serie widmowe
Lymanna
n=1
Theodore Lyman
(1874 - 1954)
Balmera
n=2
Johann J. Balmer
(1825 –1898)
Rok odkrycia: 1885
Paschena
n=3
Louis K.H.F. Paschen
(1865 -1947)
Rok odkrycia: 1908
Bracketta
n=4
Frederick S. Brackett
(1896 – 1988)
Rok odkrycia: 1922
Pfunda
n=5
August H. Pfund
(1879–1949)
Rok odkrycia: 1924
Humphreysa
n=6
Curtis J. Humphreys
(1898- 1986)
Rok odkrycia: 1953
Elektron swobodny
E > 0
n
∞
3
2
1
E
0
s. Paschena
s. Balmera
(widzialne linie serii)
s. Lymanna
-13,6 eV
Dozwolone przejścia elektronu
7
Animacja serii widmowych w atomie wodoru
http://www.bigs.de/en/shop/anim/termsch01.swf
8
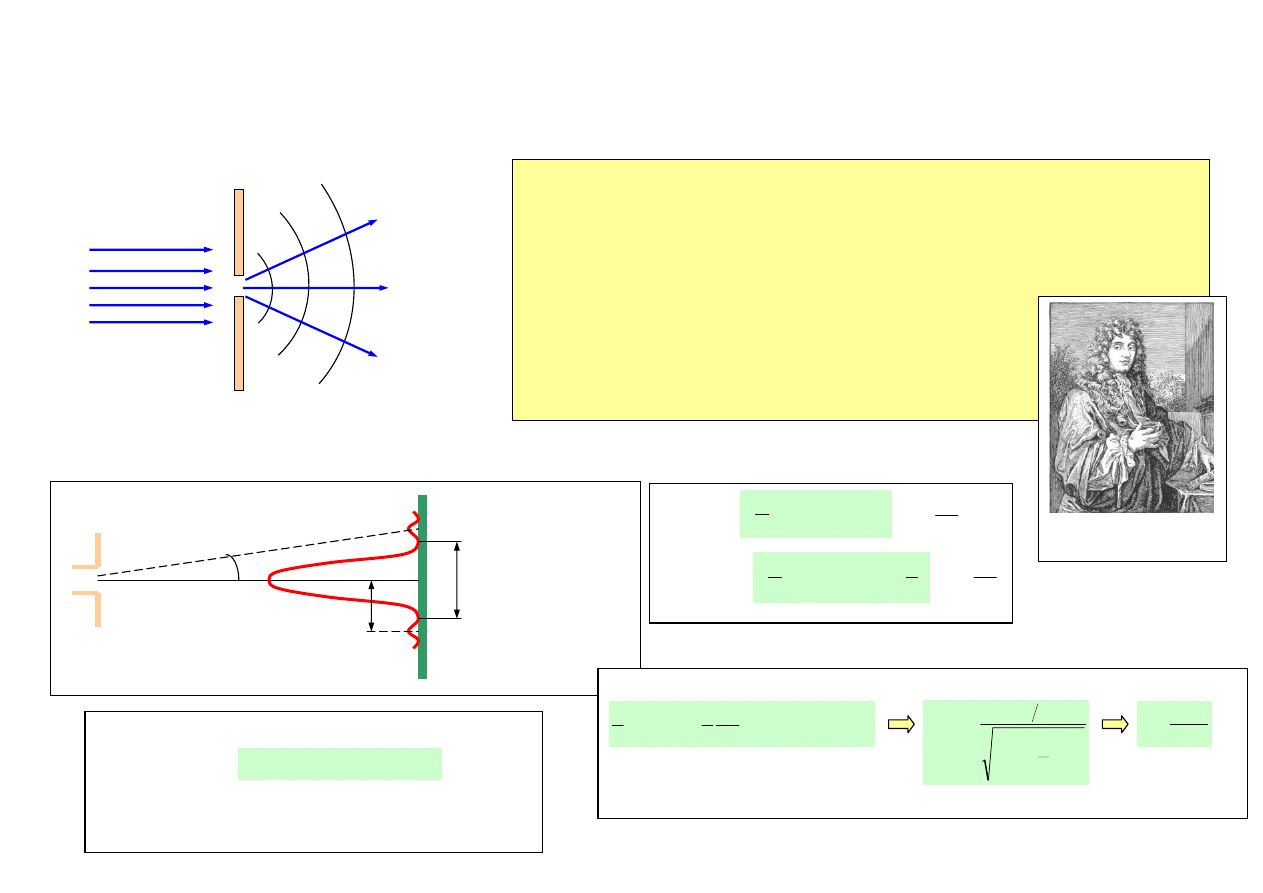
ISTOTA DYFRAKCJI (UGIĘCIA)
Dyfrakcja – zespół zjawisk, które występują, gdy fale rozchodzą się w obecności przeszkód.
Dyfrakcja na pojedynczej szczelinie
Obraz ugiętego światła = obraz po przejściu światła przez siatkę dyfrakcyjną
L
Zasada Huygensa
każdy punkt ośrodka, do którego dotarło czoło fali w chwili
wcześniejszej, jest źródłem wtórnej fali kulistej o tej samej częstości,
co fala(padająca) pierwotna.
λ – długość fali padającej, L – rozmiar otworu
Gdy λ ≈ L, na otworze występuje dyfrakcja.
Christiaan Huygens
(1629-1695)
minima
n
L
k
mw
⋅
±
=
π
α
sin
2
,
λ
π
2
≡
k
maksima
+
±
=
2
1
sin
2
n
L
k
n
π
α
,
λ
π
2
≡
k
L
x >> L
α
α
α
k=1
k=1
α
ekran
Prążek centralny
0
D
Wyznaczenie szerokości szczeliny z obserwacji obrazu ugiętego
1
,
sin
2
2
1
sin
2
1
=
=
=
n
L
kL
π
α
λ
π
α
2
2
2
1
2
sin
+
=
D
x
D
α
α
λ
sin
=
L
(np. L ~ mikronów można wyznaczyć)
- Dyfrakcja elektronów (fali de Broglie’a elektronów)
rozmiar atomu:
(
)
m
eV
E
e
10
3
10
10
~
−
≈
λ
obserwacja struktur krystalicznych
- Dyfrakcja promieni X (E~keV)
9
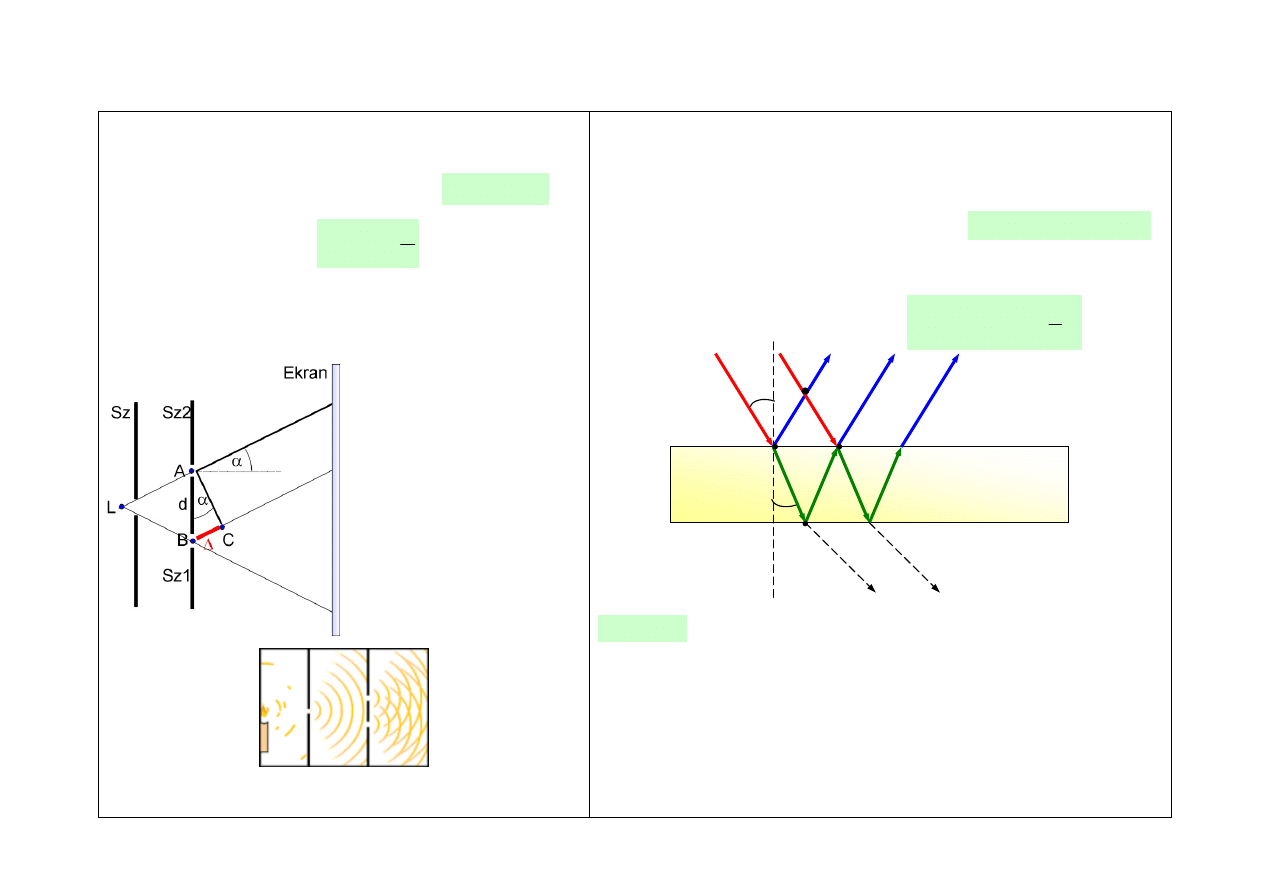
INTERFERENCJA FAL ŚWIETLNYCH
Doświadczenie Younga
różnica dróg optycznych promieni
k
d
α
sin
=
∆
położenie maksimów
d
k
k
λ
α
=
sin
d – odległość szczelin
k – rząd prążka interferencyjnego
Ilustracja doświadczenia Younga
Odbicie światła od cienkich płytek
(prążki jednakowej grubości)
różnica dróg interferujących promieni
(
)
LM
n
CD
LC
−
+
=
∆
n – współczynnik załamania
różnica dróg promieni odbitych
λ
β
2
1
cos
2
+
=
∆
hn
( )
λ
,
n
∆
=
∆
- obraz barwny, gdy mamy źródło światła
białego (kolorowe smugi na powierzchni, np. plama
oliwy)
może wystąpić interferencja promieni przechodzących
L – źródło światła
S
Z
– szczeliny
(siatka interferencyjna
– zasada działania)
h
α
β
C
L
D
M
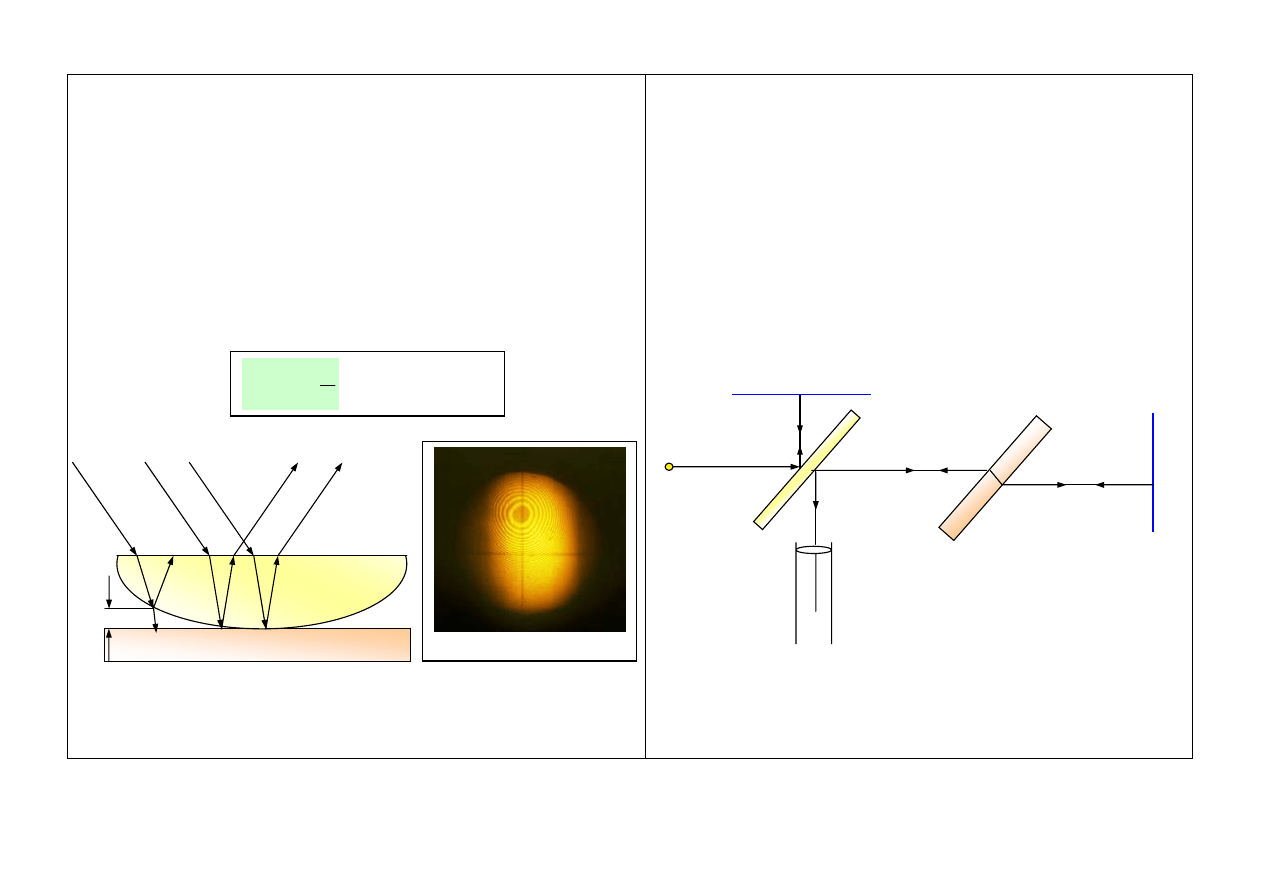
10
Pierścienie Newtona
Prążki są wynikiem interferencji promieni odbitych od
tylnej powierzchni soczewki z odbitych od przedniej
powierzchni płytki płasko – równoległej.
Dla światła
białego powstają wielobarwne prążki dla
monochromatycznego jasne i ciemne prążki.
Interferometr Michelsona
D
1
, D
2
– płytki płasko – równoległe
Z
1
, Z
2
– zwierciadła
L – źródło światła
Pierwszy bardzo dokładny
pomiar prędkości światła (c = const)
h
Układ do obserwacji
Z
1
D
D
L
Z
2
Luneta
Pierścienie Newtona
2
2
λ
+
=
∆
h
h – zmienne
11
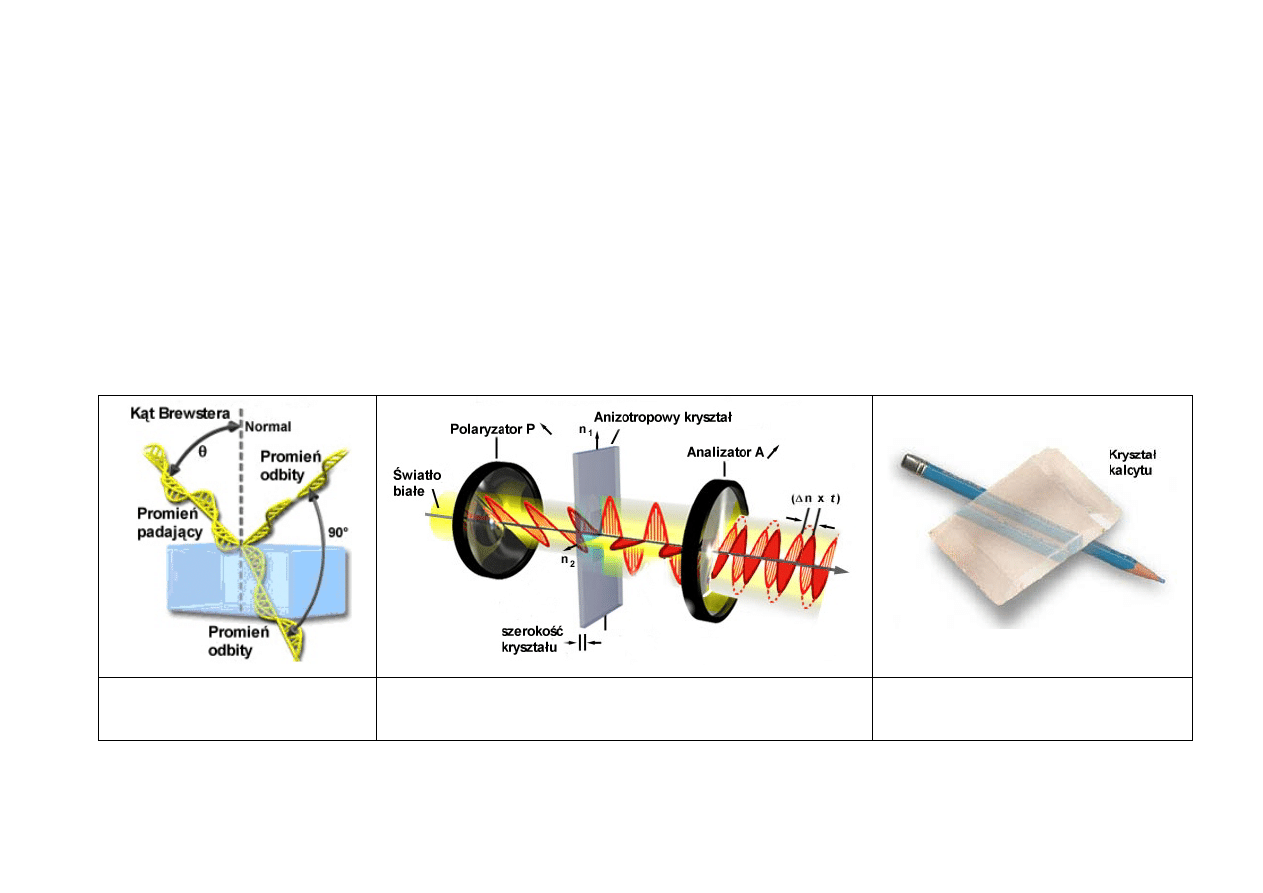
POLARYZACJA ŚWIATŁA
• podwójne załamanie światła w kryształach i polaryzacja światła przy podwójnym załamaniu
• zasada działania Nikola; polaryzatory i analizatory
• prawo Malusa
• polaryzacja przez odbicie, kąt Brewstera
• polaryzacja przez załamanie
Polaryzacja przez odbicie,
kąt Brewstera
Zasada działania Nikola;
polaryzatory i analizatory
Dwójłomność kryształów