L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe - przykłady
208
Inżynieria systemów dynamicznych
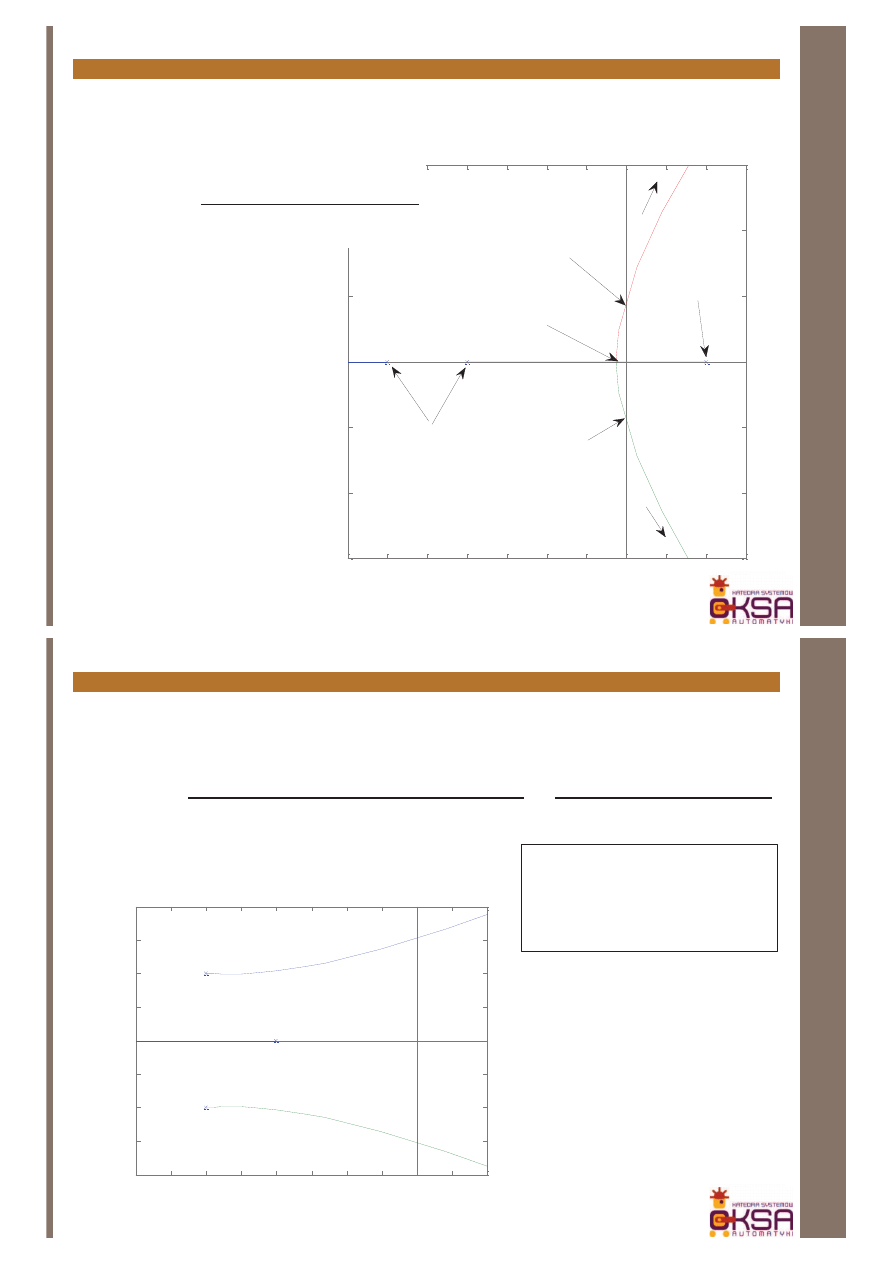
Przykład:
Wykreślić linie pierwiastkowe dla układu objętego sprzężeniem zwrotnym
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
-3
-2
-1
0
1
2
3
Root Locus
Real Axis
Im
a
g
in
a
ry
A
x
is
k=6,06
s
12
=-0,13
k=10
s=j
k=10
s=-j
k=0
k=0
k =
¥
k =
¥
)
3
)(
2
)(
1
(
)
(
+
+
-
=
s
s
s
k
s
kG
P
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – przykłady
209
Inżynieria systemów dynamicznych
Przykład:
Korzystając z Matlaba wykreślić linie pierwiastkowe dla układu
50
37
8
)
2
)(
3
4
)(
3
4
(
)
(
2
3
+
+
+
=
+
+
+
+
-
=
s
s
s
k
s
j
s
j
s
k
s
kG
P
clear
all
; close
all
; clc;
s= tf('s');
Gp=1/((s-j*4+3)*(s+j*4+3)*(s+2))
rlocus(Gp);
axis([-4,1,-8,8]);
-4
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
-8
-6
-4
-2
0
2
4
6
8
Root Locus
Real Axis
Im
a
g
in
a
ry
A
x
is
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – przykłady
210
Inżynieria systemów dynamicznych
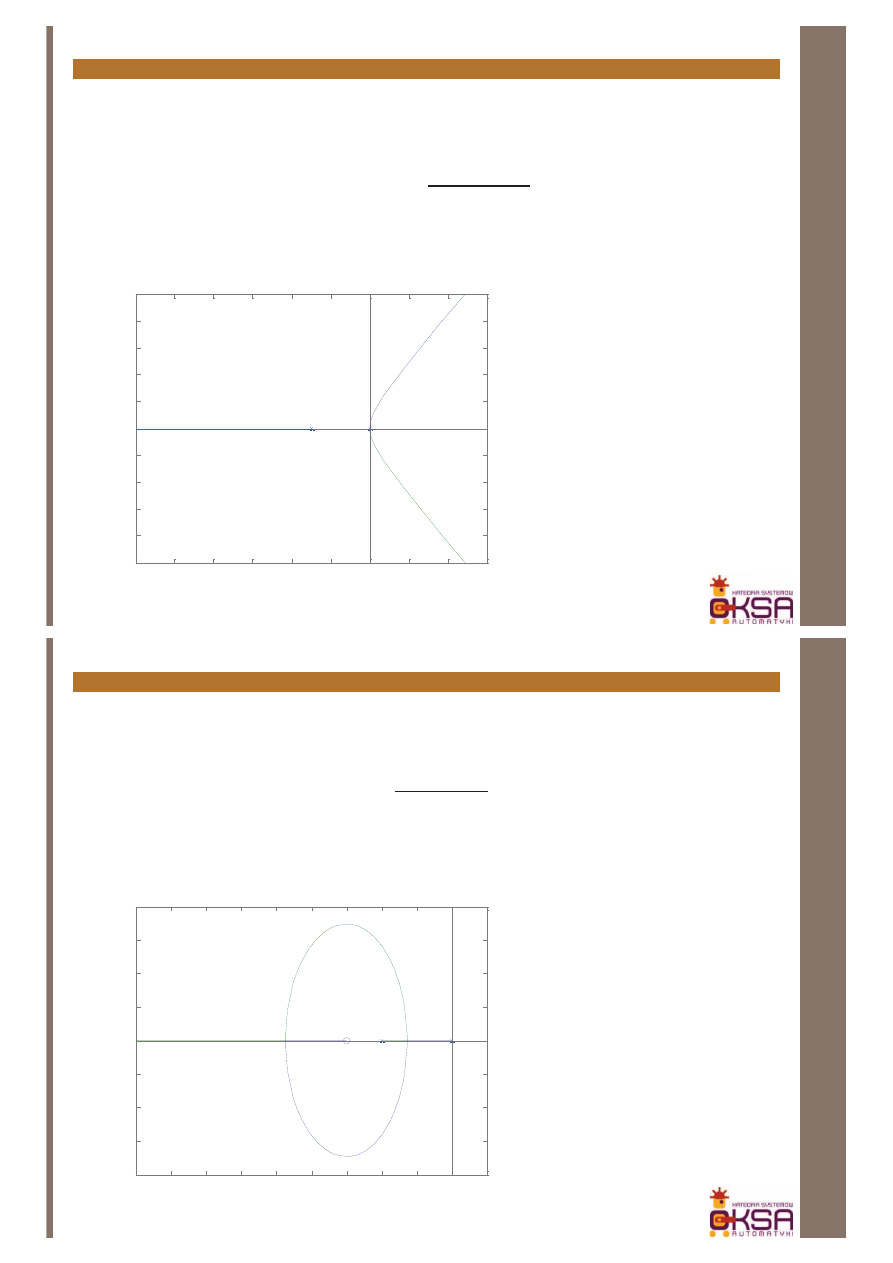
Przykład:
Wykreślić linie pierwiastkowe dla układu
)
3
(
)
(
2
+
=
s
s
k
s
kG
P
-12
-10
-8
-6
-4
-2
0
2
4
6
-10
-8
-6
-4
-2
0
2
4
6
8
10
Root Locus
Real Axis
Im
a
g
in
a
ry
A
x
is
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – przykłady
211
Inżynieria systemów dynamicznych
Przykład:
Wykreślić linie pierwiastkowe dla układu
)
4
(
)
6
(
)
(
+
+
=
s
s
s
k
s
kG
P
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
2
-4
-3
-2
-1
0
1
2
3
4
Root Locus
Real Axis
Im
a
g
in
a
ry
A
x
is
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – dodatkowy biegun
212
Inżynieria systemów dynamicznych
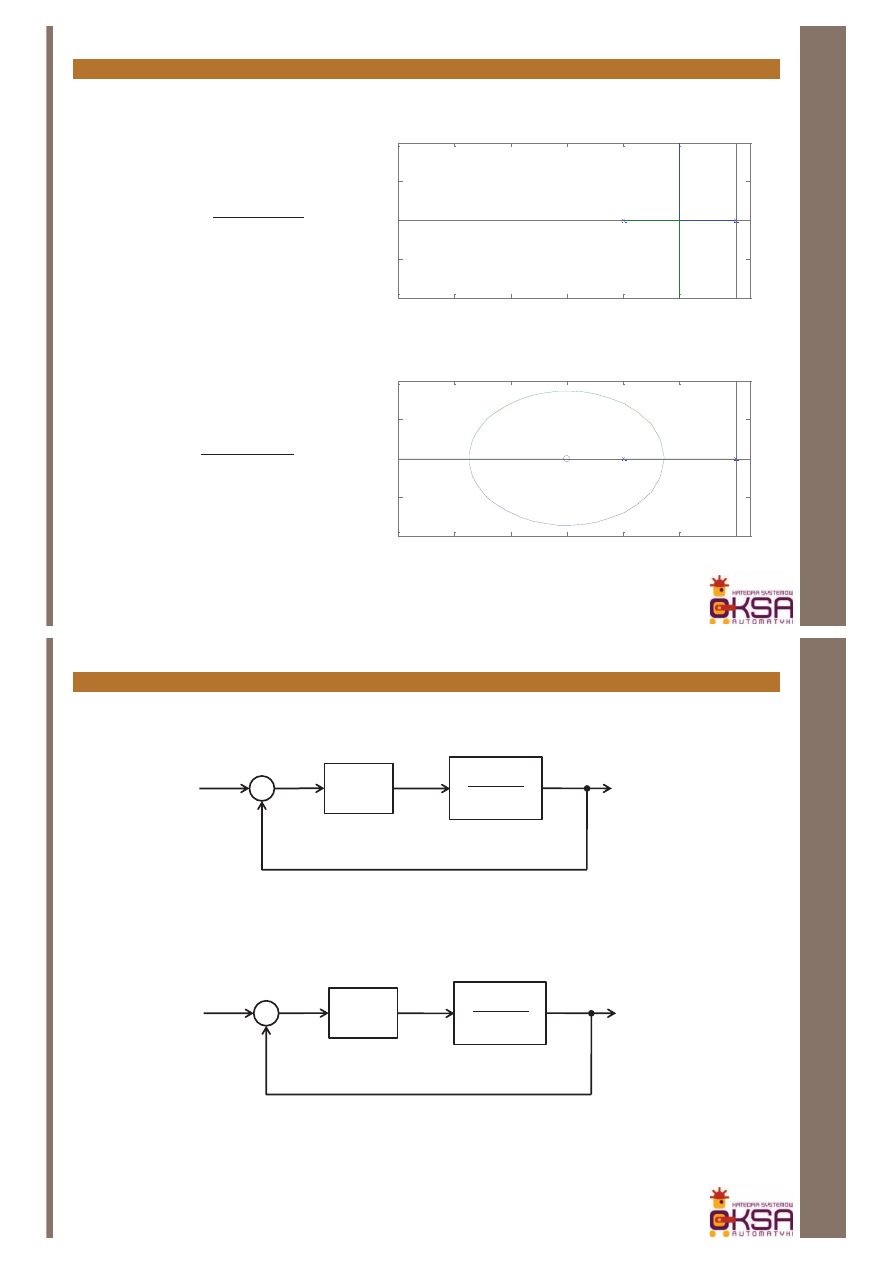
Porównajmy wyniki
)
4
(
)
6
(
)
(
+
+
=
s
s
s
k
s
kG
P
)
4
(
)
(
+
=
s
s
k
s
kG
P
-12
-10
-8
-6
-4
-2
0
-4
-2
0
2
4
Root Locus
Real Axis
Im
a
g
in
a
ry
A
x
is
-12
-10
-8
-6
-4
-2
0
-4
-2
0
2
4
Root Locus
Real Axis
Im
a
g
in
a
ry
A
x
is
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – regulator PD
213
Inżynieria systemów dynamicznych
Jeśli dodatkowe zero wprowadziliśmy celowo, to uzyskany regulator
nosi nazwę regulatora proporcjonalno-różniczkującego
R(s)
Y(s)
_
k
)
4
(
1
+
s
s
R(s)
Y(s)
_
)
6
( +
s
k
)
4
(
1
+
s
s
regulator P
regulator PD
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – regulator PD
214
Inżynieria systemów dynamicznych
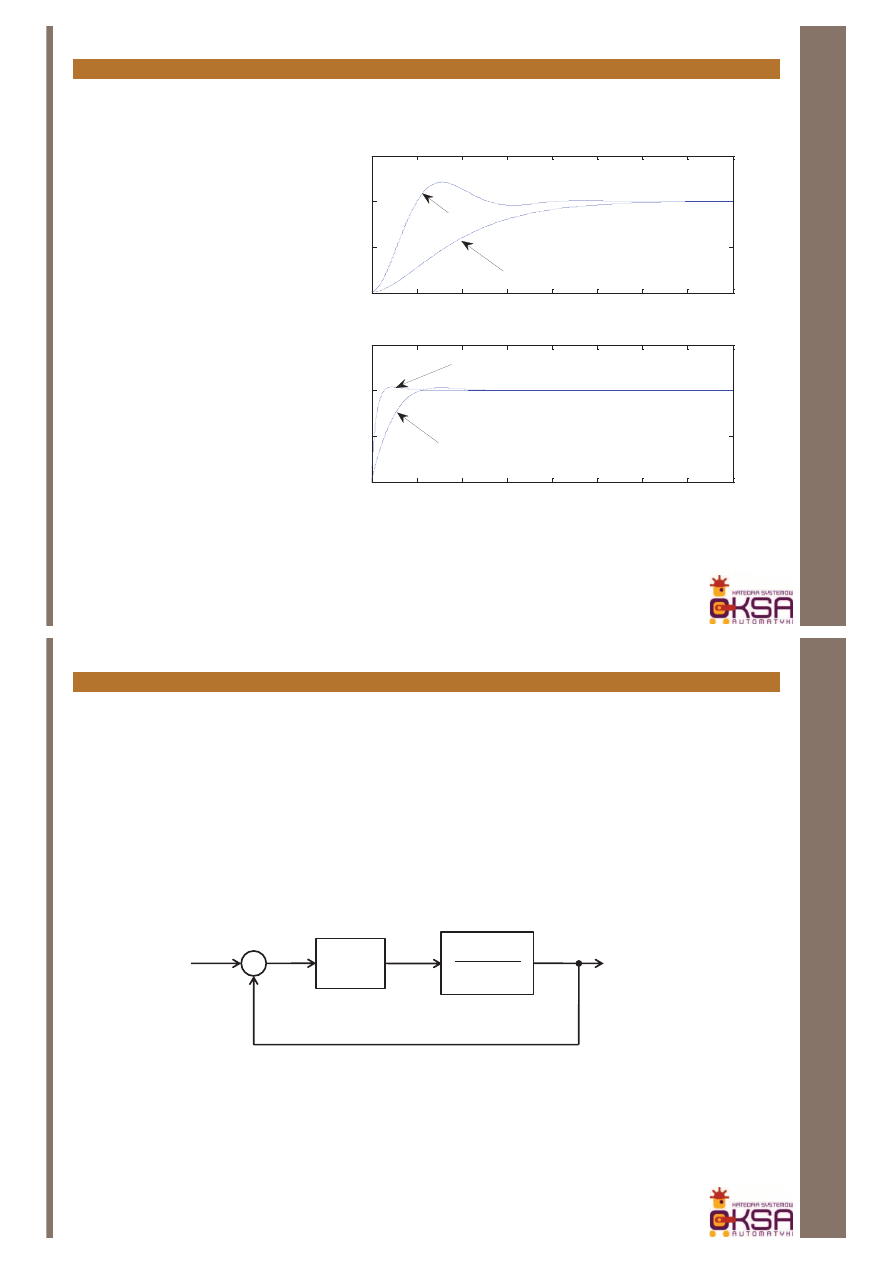
Porównanie odpowiedzi
skokowych układów z
regulatorem proporcjonalnym i
proporcjonalno-różniczkującym
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.5
1
1.5
t
y
(t
)
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.5
1
1.5
y
(t
)
t
k=4
k=20
k=4
k=20
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – zależność od parametru innego niż wzmocnienie
215
Inżynieria systemów dynamicznych
Czasami interesuje nas wpływ na bieguny innego niż wzmocnienie parametru
układu (np. stałej czasowej, współczynnika tłumienia). W takim przypadku należy
sprowadzić równanie charakterystyczne układu do postaci (a-zmienny parametr):
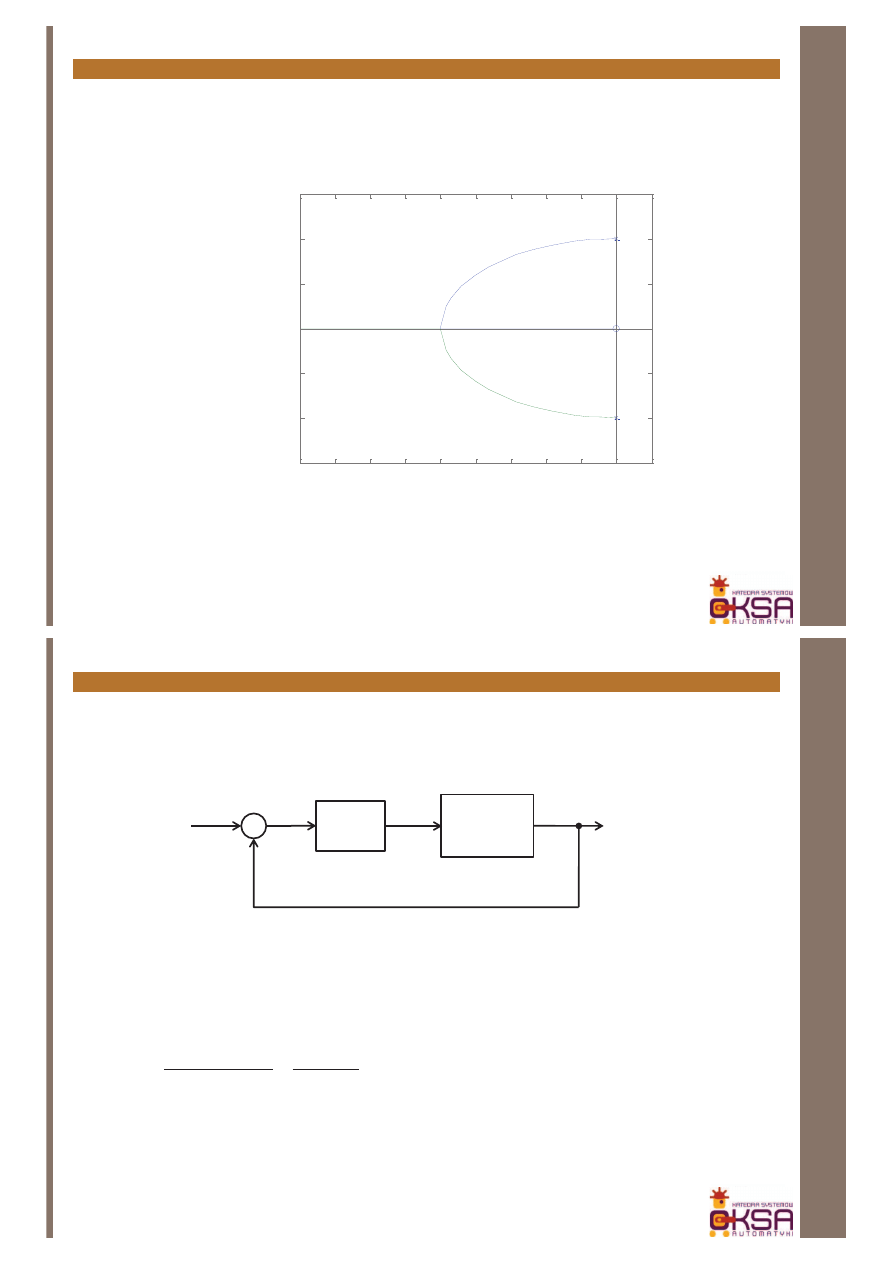
Przykład: określić, jak zmieni się położenie biegunów układu w zależności od
współczynnika ζ układu pokazanego na schemacie
0
)
(
)
(
=
+
×
s
M
s
L
a
a
a
R(s)
Y(s)
_
1
)
2
(
1
x
+
s
s
regulator P
L
IN
IE
P
IE
RW
IA
S
T
K
O
W
E
Linie pierwiastkowe – zależność od parametru innego niż wzmocnienie
216
Inżynieria systemów dynamicznych
równanie charakterystyczne
0
1
2
2
=
+
+
s
s
x
s
L
2
=
x
1
2
+
= s
M
x
-1.8
-1.6
-1.4
-1.2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
-1.5
-1
-0.5
0
0.5
1
1.5
Root Locus
Real Axis
Im
a
g
in
a
ry
A
x
is
C
Z
Ę
S
T
O
T
LI
W
O
Ś
C
IO
W
E
K
RY
T
E
RI
A
S
T
A
B
IL
N
O
Ś
C
I
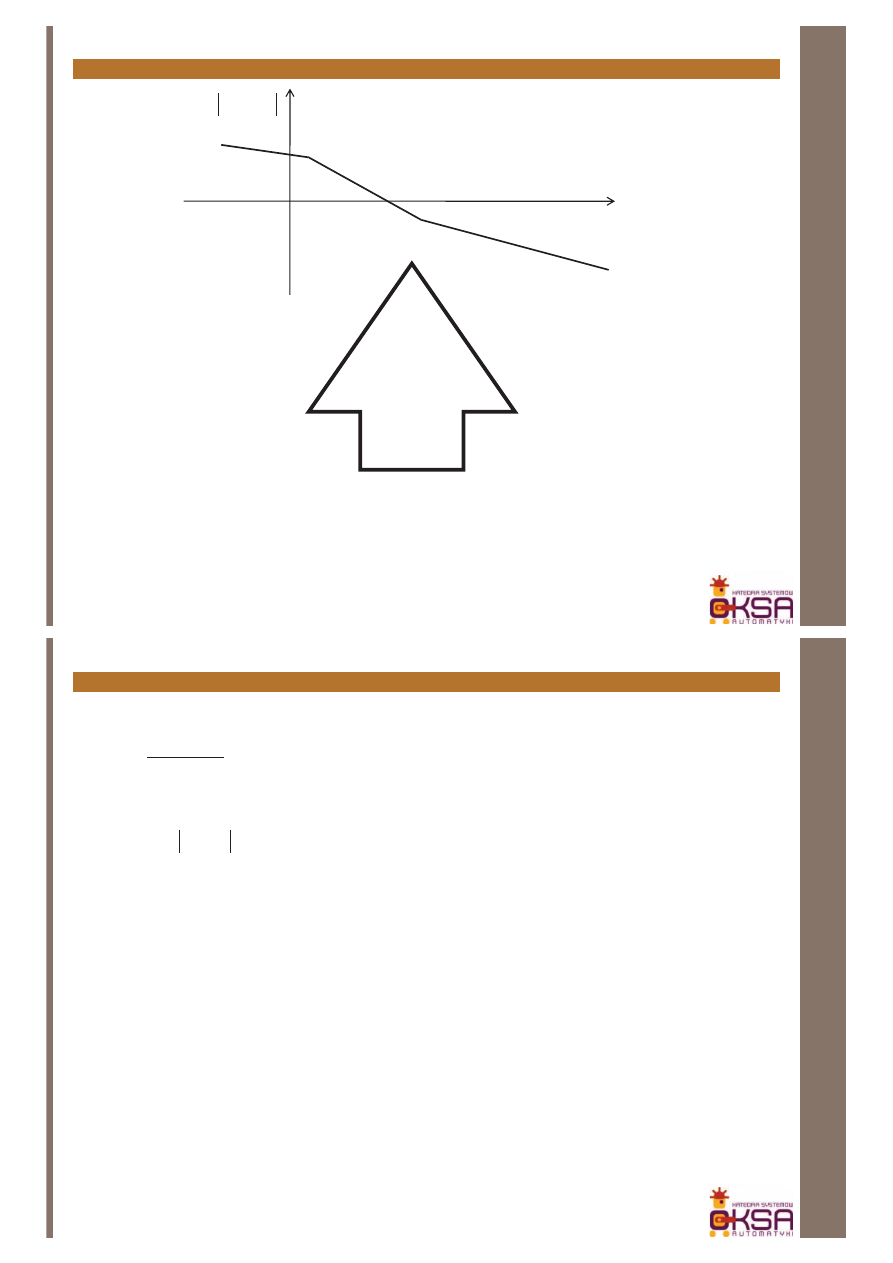
Wprowadzenie
217
Inżynieria systemów dynamicznych
R(s)
Y(s)
_
)
(s
G
C
)
(s
G
P
regulator
obiekt
Transmitancja układu otwartego:
)
(
)
(
)
(
s
G
s
G
s
G
P
C
o
=
Transmitancja układu zamkniętego:
)
(
1
)
(
)
(
1
)
(
)
(
)
(
s
G
G
s
G
s
G
s
G
s
G
s
G
O
O
P
C
P
C
+
=
+
=
C
Z
Ę
S
T
O
T
LI
W
O
Ś
C
IO
W
E
K
RY
T
E
RI
A
S
T
A
B
IL
N
O
Ś
C
I
Wprowadzenie – charakterystyka amplitudowa układu otwartego
218
Inżynieria systemów dynamicznych
)
(
log
20
w
j
G
o
małe częstotliwości:
decydują o stanie ustalonym
w
(skala log)
duże częstotliwości:
decydują o tłumieniu zakłóceń
ty
po
wa
ch
arak
te
ry
sty
ka
C
Z
Ę
S
T
O
T
LI
W
O
Ś
C
IO
W
E
K
RY
T
E
RI
A
S
T
A
B
IL
N
O
Ś
C
I
Wprowadzenie – charakterystyka amplitudowa
219
Inżynieria systemów dynamicznych
Wykreśl asymptotyczne charakterystyki amplitudowo-fazowe Bodego dla układu o transmitancji:
2
)
1
10
(
100
)
(
+
=
s
s
s
G
P
)
1
10
log(
40
)
log(
20
40
)
1
10
log(
40
)
log(
20
)
100
log(
20
)
(
log
20
)
(
+
-
-
=
+
-
-
=
=
w
w
w
w
w
w
j
G
L
uwaga: amplituda w dB, pulsacja w skali logarytmicznej
rozpatrzmy drugi składnik:
)
log(
20
w
-
załóżmy, że pulsacja wzrosła 10 razy:
)
log(
20
20
)
log(
20
)
10
log(
20
)
10
log(
20
w
w
w
-
-
=
-
-
=
-
w takim przypadku wzmocnienie tego składnika spadło o 20dB
rozpatrzmy trzeci składnik:
)
1
10
log(
40
+
-
w
Dla pulsacji mniejszych od 1/10 wartość tego składnika jest stała i jest bliska zero. Dla pulsacji
dużo większych od 1/10 wzmocnienie tego składnika spada z szybkością 40dB na każdą
dekadę. Maksymalny błąd jaki popełniamy wyniesie 6dB i wystąpi dla pulsacji 1/10.

C
Z
Ę
S
T
O
T
LI
W
O
Ś
C
IO
W
E
K
RY
T
E
RI
A
S
T
A
B
IL
N
O
Ś
C
I
Wprowadzenie – charakterystyka amplitudowa
220
Inżynieria systemów dynamicznych
Na podstawie naszego rozumowania, możemy wyciągnąć wnioski:
1.
człon (Tjω+1) dla pulsacji ω<<1/T wnosi wzmocnienie 0dB
2.
wzmocnienie członu (Tjω+1) dla pulsacji ω>>1/T wnosi wzmocnienie 0dB wprowadza
wzmocnienie narastające z szybkością 20dB/dek (gdy człon znajduje się w liczniku) lub
zmniejszające się z szybkością 20dB/dek (gdy człon znajduje się w mianowniku) . Jeśli
wykreślimy asymptotyczną charakterystykę amplitudową członu, to największy błąd popełnimy
dla pulsacji 1/T. Wyniesie on 3dB
Podobne wnioski możemy wysnuć dla członów wyższych rzędów:
1.
człon (Tjω+1)
n
dla pulsacji ω<<1/T wnosi wzmocnienie 0dB
2.
wzmocnienie członu (Tjω+1)
n
dla pulsacji ω>>1/T wnosi wzmocnienie 0dB wprowadza
wzmocnienie narastające z szybkością n*20dB/dek (gdy człon znajduje się w liczniku) lub
zmniejszające się z szybkością n*20dB/dek (gdy człon znajduje się w mianowniku) . Jeśli
wykreślimy asymptotyczną charakterystykę amplitudową członu, to największy błąd popełnimy
dla pulsacji 1/T. Wyniesie on n*3dB
Składnik jω powoduje wzrost wzmocnienia z szybkością 20dB/dek (gdy znajduje się w liczniku
transmitancji) lub spadek z szybkością 20dB/dek (gdy znajduje się w mianowniku transmitancji)
C
Z
Ę
S
T
O
T
LI
W
O
Ś
C
IO
W
E
K
RY
T
E
RI
A
S
T
A
B
IL
N
O
Ś
C
I
Wprowadzenie – charakterystyka fazowa
221
Inżynieria systemów dynamicznych
{
}
{ }
{
}
1
10
arg
2
arg
)
(
arg
+
-
-
=
w
w
w
j
j
j
G
P
pierwszy składnik wprowadza przesunięcie fazowe -90°
drugi składnik wprowadza przesunięcie 0° dla ω <<1/10, -90° dla ω ==1/10 oraz -180° dla ω >>1/10
Na podstawie naszego rozumowania, możemy wyciągnąć wnioski:
1.
człon (Tjω+1) dla pulsacji ω<<1/T wnosi przesunięcie fazowe 0°
2.
przesunięcie fazowe wnoszone przez człon(Tjω+1) dla pulsacji ω>>1/T wynosi 90°(gdy człon
znajduje się w liczniku) lub -90°(gdy człon znajduje się w mianowniku) .
Podobne wnioski możemy wysnuć dla członów wyższych rzędów:
1.
człon (Tjω+1)
n
dla pulsacji ω<<1/T wnosi przesunięcie fazowe 0°
2.
przesunięcie fazowe wnoszone przez człon(Tjω+1)
n
dla pulsacji ω>>1/T wynosi n*90°(gdy
człon znajduje się w liczniku) lub -n*90°(gdy człon znajduje się w mianowniku) .
Składnik jω wnosi przesunięcie fazowe +90° gdy znajduje się w liczniku i -90° gdy znajduje się w
mianowniku
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron