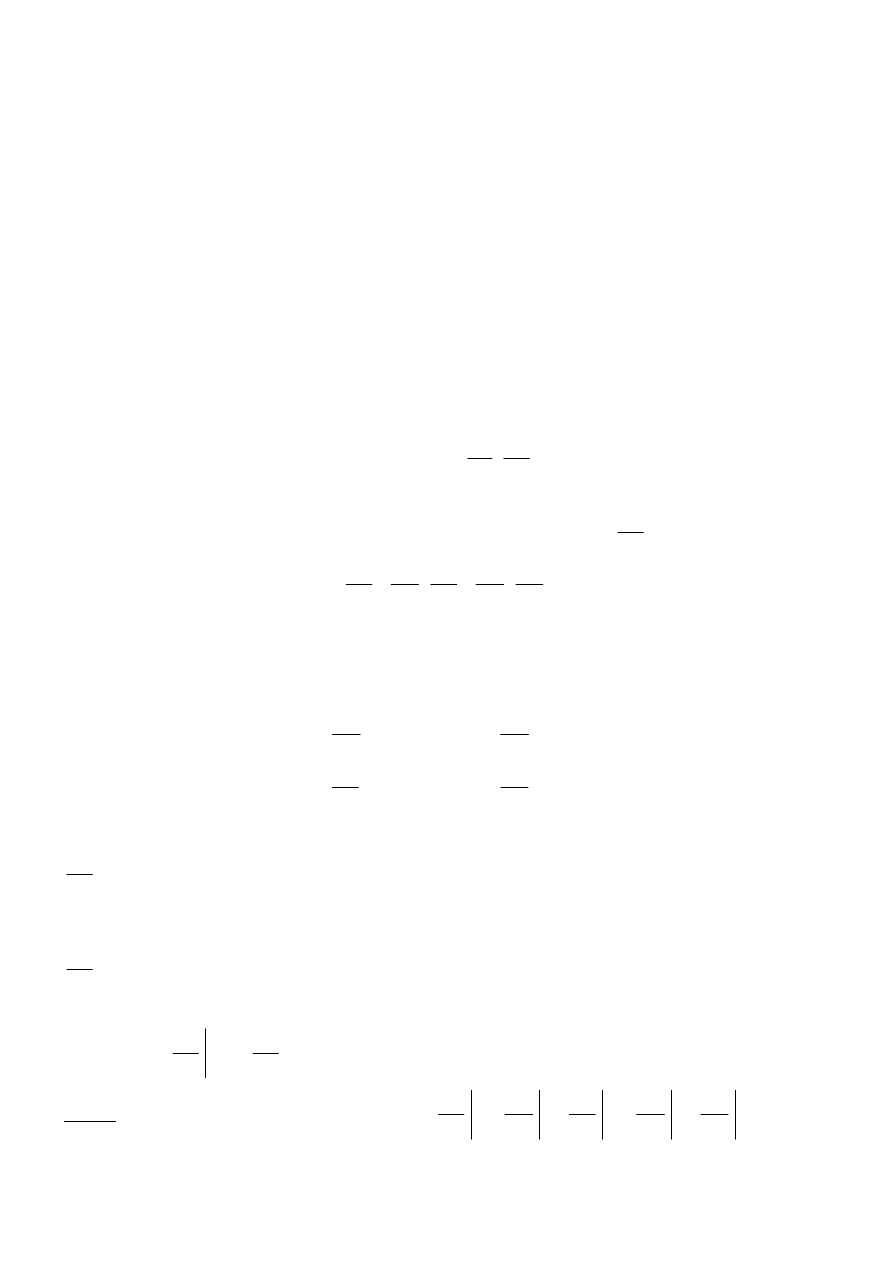
207
WYKŁAD Nr 16
FUNKCJE DWÓCH ZMIENNYCH – c. d.
6. POCHODNA FUNKCJI ZŁOŻONEJ
POCHODNA FUNKCJI ZŁOŻONEJ JEDNEJ ZMIENNEJ NIEZALEŻNEJ
A) Pochodna funkcji
(
)
)
(
),
(
t
y
t
x
f
z
=
Tw.6.1. (o pochodnej funkcji
(
)
)
(
),
(
t
y
t
x
f
z
=
)
Jeżeli:
-
funkcja
)
,
( y
x
f
jest określona w obszarze D,
-
funkcje
)
(
),
(
t
y
t
x
określone w przedziale
(
)
β
α,
, takie że para
(
)
D
y
x
∈
,
odwzorowuje
przedział
(
)
β
α,
w obszar D,
-
funkcje
)
(
),
(
t
y
t
x
są różniczkowalne dla
(
)
β
α
∈
,
t
,
-
funkcja
(
)
)
(
),
(
t
y
t
x
f
z
=
ma pochodne
y
f
x
f
∂
∂
∂
∂
,
dla każdej pary
(
)
D
y
x
∈
,
oraz są one
ciągłe
to wówczas funkcja złożona
(
)
)
(
),
(
t
y
t
x
f
z
=
ma dla argumentu t pochodną
t
d
z
d
określoną następująco
(1)
t
d
y
d
y
f
t
d
x
d
x
f
t
d
z
d
⋅
∂
∂
+
⋅
∂
∂
=
Przykład: Niech będzie dana funkcja
x
y
x
y
x
f
z
sin
)
,
(
2
+
=
=
mająca ciągłe pochodne w całej
przestrzeni
2
R oraz niech
R
∈
−
=
=
t
t
e
y
t
x
t
,
,
2
2
2
. Obliczyć pochodną funkcji
(
)
)
(
),
(
t
y
t
x
f
z
=
dla
0
0
=
t
.
Rozwiązanie:
Ponieważ
x
y
f
x
y
x
x
f
sin
,
cos
2
=
∂
∂
+
=
∂
∂
t
e
t
d
y
d
t
t
d
x
d
t
2
,
4
−
=
=
oraz spełnione są założenia tw.6.1, więc wstawiając powyższe pochodne cząstkowe do wzoru (1) mamy:
(
)
(
)
t
e
x
t
x
y
x
t
d
z
d
t
2
sin
4
cos
2
−
⋅
+
⋅
+
=
Stąd podstawiając za
2
2
,
2
t
e
y
t
x
t
−
=
=
otrzymujemy
(
) ( )
[
]
( ) (
)
=
−
⋅
+
⋅
−
+
⋅
=
t
e
t
t
t
t
e
t
t
d
z
d
t
t
2
2
sin
4
2
cos
2
2
2
2
2
2
(
) ( )
[
]
( ) (
)
t
e
t
t
t
t
e
t
t
t
2
2
sin
4
2
cos
4
2
2
2
2
−
⋅
+
⋅
−
+
=
Zatem
( ) (
)
0
1
0
0
1
1
0
0
0
0
=
⋅
+
⋅
⋅
+
=
=
=
t
d
z
d
t
d
z
d
t
Uwaga
: Można również zastosować wzór
0
0
0
0
0
t
P
t
P
t
t
d
y
d
y
f
t
d
x
d
x
f
t
d
z
d
⋅
∂
∂
+
⋅
∂
∂
=
,
gdzie
( ) ( )
(
)
0
0
0
, t
y
t
x
P
208
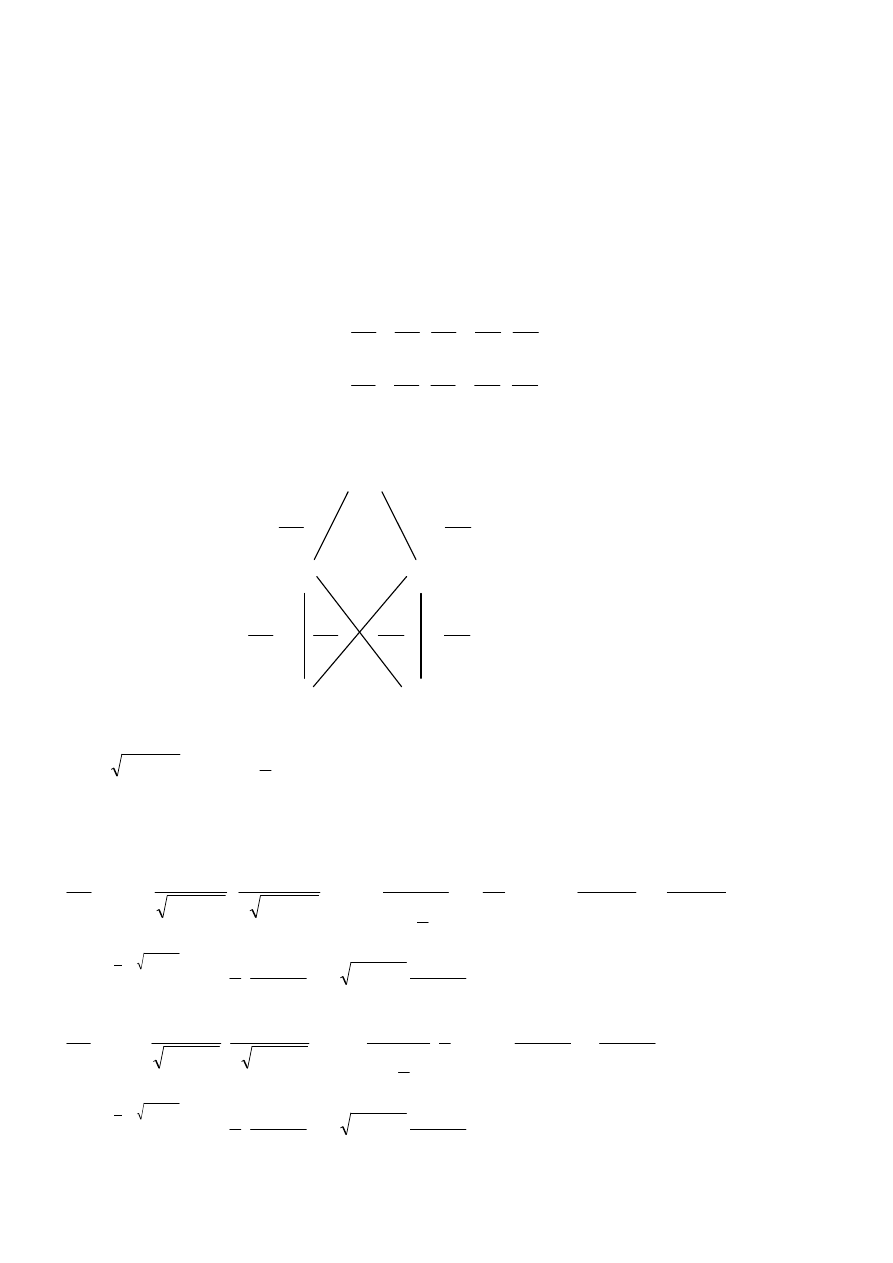
SCHEMAT OBLICZANIA POCHODNEJ
t
d
z
d
)
,
( y
x
f
z
=
y
f
x
f
∂
∂
∂
∂
y
x
t
d
y
d
t
d
x
d
t
t
d
y
d
y
f
t
d
x
d
x
f
t
d
z
d
⋅
∂
∂
+
⋅
∂
∂
=
Druga pochodna funkcji
(
)
)
(
),
(
t
y
t
x
f
z
=
Zachowując założenia z tw.6.1. zakładamy dodatkowo, że występujące tam funkcje mają ciągłe pochodne
do rzędu drugiego włącznie (tzn. są klasy
2
C
).
SCHEMAT OBLICZANIA POCHODNEJ
2
2
t
d
z
d
=
=
t
d
z
d
t
d
d
t
d
z
d
2
2
{wstawiamy wzór (1)}
=
⋅
∂
∂
+
⋅
∂
∂
=
⋅
∂
∂
+
⋅
∂
∂
=
t
d
y
d
y
f
t
d
d
t
d
x
d
x
f
t
d
d
t
d
y
d
y
f
t
d
x
d
x
f
t
d
d
{pochodne iloczynu}
=
⋅
∂
∂
+
⋅
∂
∂
+
⋅
∂
∂
+
⋅
∂
∂
=
2
2
2
2
t
d
y
d
y
f
t
d
y
d
y
f
t
d
d
t
d
x
d
x
f
t
d
x
d
x
f
t
d
d
{należy zróżniczkować względem
zmiennej t człony
y
f
x
f
∂
∂
∂
∂
,
patrz poniższe schematy, a następnie wstawić otrzymane wyrażenia} (*)
x
f
∂
∂
y
f
∂
∂
x
y
f
x
f
∂
∂
∂
∂
∂
2
2
2
2
2
2
y
f
y
x
f
∂
∂
∂
∂
∂
y
x
y
x
t
d
y
d
t
d
x
d
t
d
y
d
t
d
x
d
t
t
czyli wracając do (*):
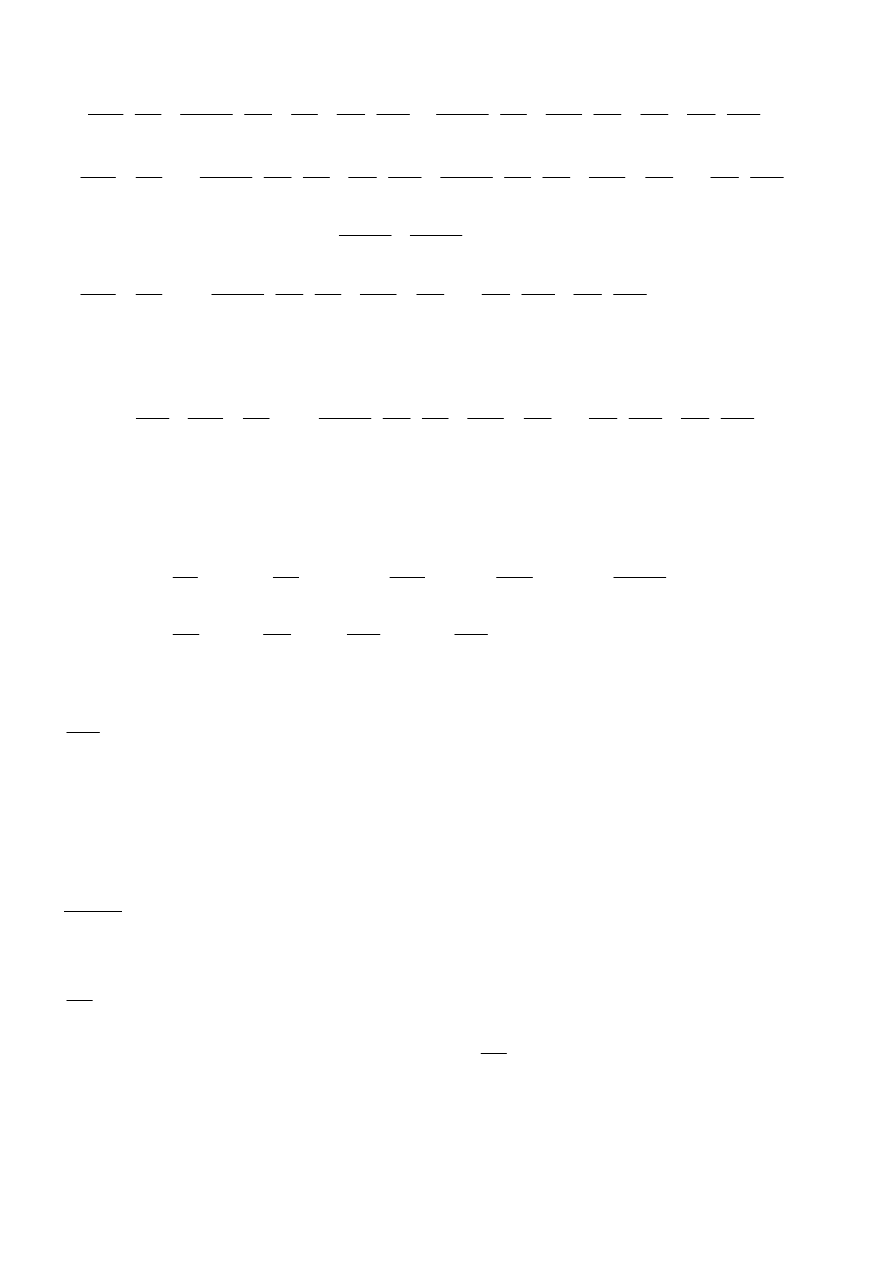
209
=
⋅
∂
∂
+
⋅
⋅
∂
∂
+
⋅
∂
∂
∂
+
⋅
∂
∂
+
⋅
⋅
∂
∂
∂
+
⋅
∂
∂
=
2
2
2
2
2
2
2
2
2
2
t
d
y
d
y
f
t
d
y
d
t
d
y
d
y
f
t
d
x
d
y
x
f
t
d
x
d
x
f
t
d
x
d
t
d
y
d
x
y
f
t
d
x
d
x
f
=
⋅
∂
∂
+
⋅
∂
∂
+
⋅
⋅
∂
∂
∂
+
⋅
∂
∂
+
⋅
⋅
∂
∂
∂
+
⋅
∂
∂
=
2
2
2
2
2
2
2
2
2
2
2
2
t
d
y
d
y
f
t
d
y
d
y
f
t
d
y
d
t
d
x
d
y
x
f
t
d
x
d
x
f
t
d
x
d
t
d
y
d
x
y
f
t
d
x
d
x
f
{korzystamy z twierdzenia Schwarza
x
y
f
y
x
f
∂
∂
∂
=
∂
∂
∂
2
2
}
2
2
2
2
2
2
2
2
2
2
2
2
t
d
y
d
y
f
t
d
x
d
x
f
t
d
y
d
y
f
t
d
x
d
t
d
y
d
x
y
f
t
d
x
d
x
f
⋅
∂
∂
+
⋅
∂
∂
+
⋅
∂
∂
+
⋅
⋅
∂
∂
∂
+
⋅
∂
∂
=
Ostatecznie
(2)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
t
d
y
d
y
f
t
d
x
d
x
f
t
d
y
d
y
f
t
d
x
d
t
d
y
d
x
y
f
t
d
x
d
x
f
t
d
z
d
⋅
∂
∂
+
⋅
∂
∂
+
⋅
∂
∂
+
⋅
⋅
∂
∂
∂
+
⋅
∂
∂
=
Przykład: Obliczyć drugą pochodną funkcji
y
x
e
z
2
−
=
, gdzie
3
,
sin
t
y
t
x
=
=
Rozwiązanie: Podana funkcja spełnia założenia w
2
R .
Ponieważ
y
x
y
x
y
x
y
x
y
x
e
y
x
z
e
y
z
e
x
z
e
y
z
e
x
z
2
2
2
2
2
2
2
2
2
2
2
,
4
,
,
2
,
−
−
−
−
−
−
=
∂
∂
∂
=
∂
∂
=
∂
∂
−
=
∂
∂
=
∂
∂
t
t
d
x
d
t
t
d
x
d
t
t
d
y
d
t
t
d
x
d
6
,
sin
,
3
,
cos
2
2
2
2
2
=
−
=
=
=
Zatem
(
)
(
)
=
⋅
−
−
⋅
+
⋅
+
⋅
⋅
−
⋅
+
⋅
=
−
−
−
−
−
t
e
t
e
t
e
t
t
e
t
e
t
d
z
d
y
x
y
x
y
x
y
x
y
x
6
2
sin
9
4
3
cos
2
2
cos
2
2
4
2
2
2
2
2
2
2
{wstawiamy
3
,
sin
t
y
t
x
=
=
}
=
−
⋅
−
+
⋅
−
+
⋅
=
−
−
−
−
−
3
3
3
3
3
2
sin
2
sin
2
sin
4
2
sin
2
2
2
sin
12
sin
36
cos
12
cos
t
t
t
t
t
t
t
t
t
t
te
e
t
e
t
t
e
t
t
e
(
)
t
t
t
t
t
t
e
t
t
12
sin
36
cos
12
cos
4
2
2
2
sin
3
−
−
+
−
=
−
Uwaga:
Przykład ten możemy rozwiązać również innym sposobem.
W tym celu obliczamy:
=
⋅
−
⋅
=
−
−
2
2
2
3
2
cos
t
e
t
e
t
d
z
d
y
x
y
x
{wstawiamy
3
,
sin
t
y
t
x
=
=
} =
=
(
)
2
2
sin
2
sin
2
2
sin
6
cos
6
cos
3
3
3
t
t
e
e
t
t
e
t
t
t
t
t
t
−
=
−
−
−
−
, czyli
(
)
2
2
sin
6
cos
3
t
t
e
t
d
z
d
t
t
−
=
−
Wówczas obliczając drugą pochodną traktujemy ją jako pochodną z pierwszej pochodnej funkcji jednej
zmiennej t.
210
B) Pochodna funkcji
(
)
)
(
,
x
y
x
z
z
=
Jeżeli przyjmiemy
t
x
= to otrzymamy funkcję złożoną, której pochodną obliczamy korzystając ze
schematu:
(
)
)
(
,
x
y
x
z
z
=
y
z
x
z
∂
∂
∂
∂
y
x
x
d
y
d
x
Zatem
(3)
x
d
y
d
y
z
x
z
x
d
z
d
⋅
∂
∂
+
∂
∂
=
W przypadku drugiej pochodnej mamy:
=
⋅
∂
∂
+
⋅
∂
∂
+
∂
∂
=
⋅
∂
∂
+
∂
∂
=
=
2
2
2
2
x
d
y
d
y
z
x
d
y
d
y
z
x
d
d
x
z
x
d
d
x
d
y
d
y
z
x
z
x
d
d
x
d
z
d
x
d
d
x
d
z
d
+
⋅
∂
∂
∂
+
∂
∂
=
⋅
∂
∂
+
⋅
⋅
∂
∂
+
∂
∂
∂
+
⋅
∂
∂
∂
+
∂
∂
=
x
d
y
d
x
y
z
x
z
x
d
y
d
y
z
x
d
y
d
x
d
y
d
y
z
y
x
z
x
d
y
d
x
y
z
x
z
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
x
d
y
d
y
z
x
d
y
d
y
z
⋅
∂
∂
+
∂
∂
+
Ostatecznie
(4)
2
2
2
2
2
2
2
2
2
2
2
x
d
y
d
y
z
x
d
y
d
y
z
x
d
y
d
x
y
z
x
z
x
d
z
d
⋅
∂
∂
+
∂
∂
+
⋅
∂
∂
∂
+
∂
∂
=
Przykład: Obliczyć pierwszą i drugą pochodną funkcji
(
)
3
,
ln
x
y
e
e
z
y
x
=
+
=
Rozwiązanie:
Ponieważ
(
)
2
2
2
,
,
y
x
y
x
y
x
y
y
x
x
e
e
e
x
z
e
e
e
y
z
e
e
e
x
z
+
=
∂
∂
+
=
∂
∂
+
=
∂
∂
+
(
)
2
2
2
,
y
x
y
x
e
e
e
y
z
+
=
∂
∂
+
,
(
)
x
x
d
y
d
x
x
d
y
d
e
e
e
x
y
z
y
x
y
x
6
,
3
,
2
2
2
2
2
=
=
+
−
=
∂
∂
∂
+
Zatem
3
3
3
3
3
3
2
2
3
3
3
x
x
x
x
x
x
x
x
x
x
y
x
y
y
x
x
e
e
e
x
e
x
e
e
e
e
e
e
x
e
e
e
e
e
e
x
d
z
d
+
+
=
⋅
+
+
+
=
⋅
+
+
+
=
(
)
(
)
(
)
=
⋅
+
+
⋅
+
+
⋅
+
−
+
+
=
+
+
+
x
e
e
e
x
e
e
e
x
e
e
e
e
e
e
x
d
z
d
y
x
x
y
x
y
x
y
x
y
x
y
x
y
x
6
9
3
2
4
2
2
2
2
2
2
x
e
e
e
x
e
e
e
x
e
e
e
e
e
e
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
6
9
3
2
3
3
3
3
3
3
3
4
2
2
2
2
⋅
+
+
⋅
+
+
⋅
+
−
+
+
=
+
+
+
211
POCHODNA FUNKCJI ZŁOŻONEJ DWÓCH ZMIENNYCH NIEZALEŻNYCH
Tw.6.2. (o pochodnej funkcji
(
)
)
,
(
),
,
(
v
u
y
v
u
x
f
z
=
)
Jeżeli:
-
funkcja
(
)
)
,
(
),
,
(
v
u
y
v
u
x
f
z
=
klasy
1
C
jest określona w obszarze
2
R
⊂
D
,
-
funkcje
)
,
(
),
,
(
v
u
y
v
u
x
mają ciągłe pochodne I –go rzędu w obszarze D,
-
(
)
D
v
u
y
v
u
x
∈
)
,
(
),
,
(
gdy
(
)
1
,
D
v
u
∈
to wówczas funkcja złożona dwóch zmiennych
(
)
)
,
(
),
,
(
v
u
y
v
u
x
f
z
=
ma pochodne cząstkowe I go rzędu
określone następująco:
(5)
u
y
y
z
u
x
x
z
u
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
(6)
v
y
y
z
v
x
x
z
v
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
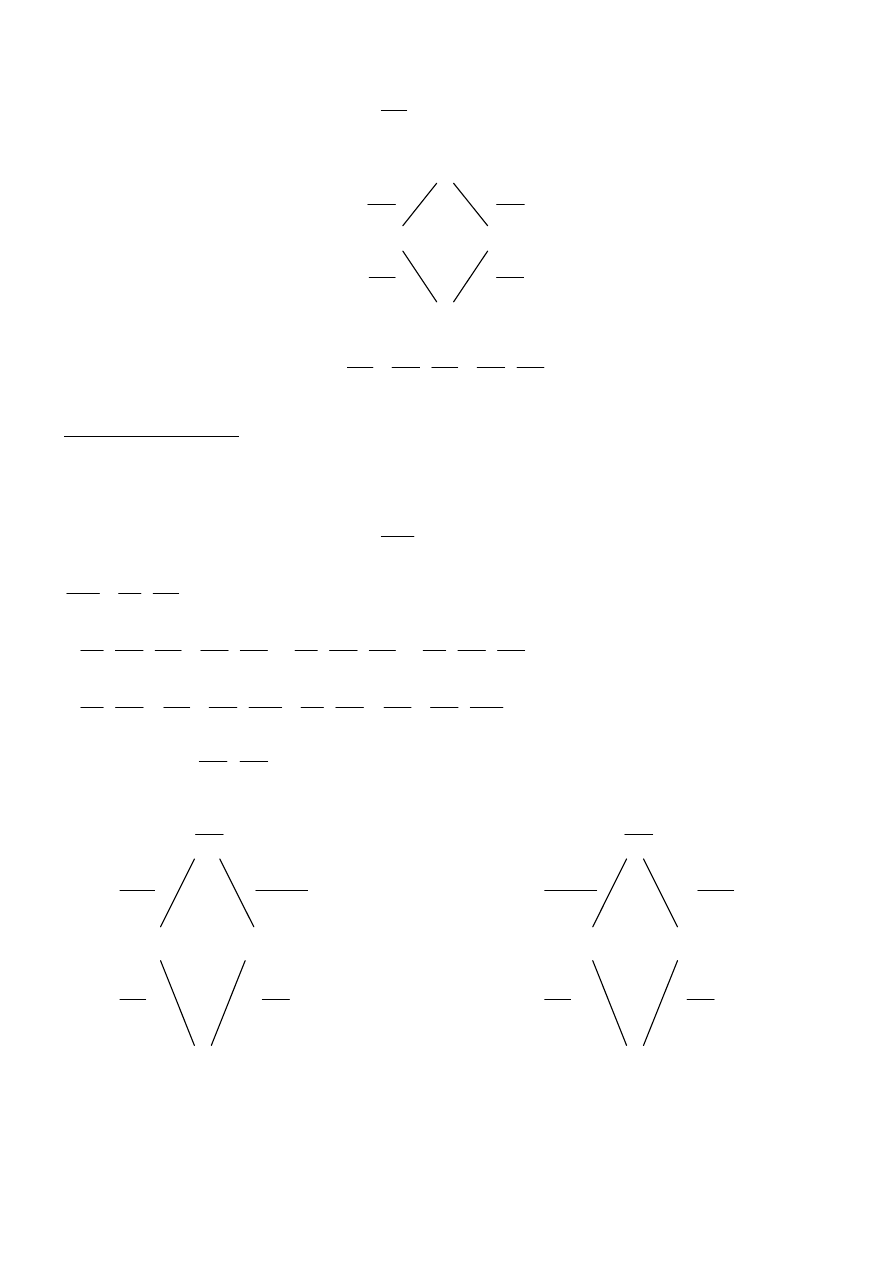
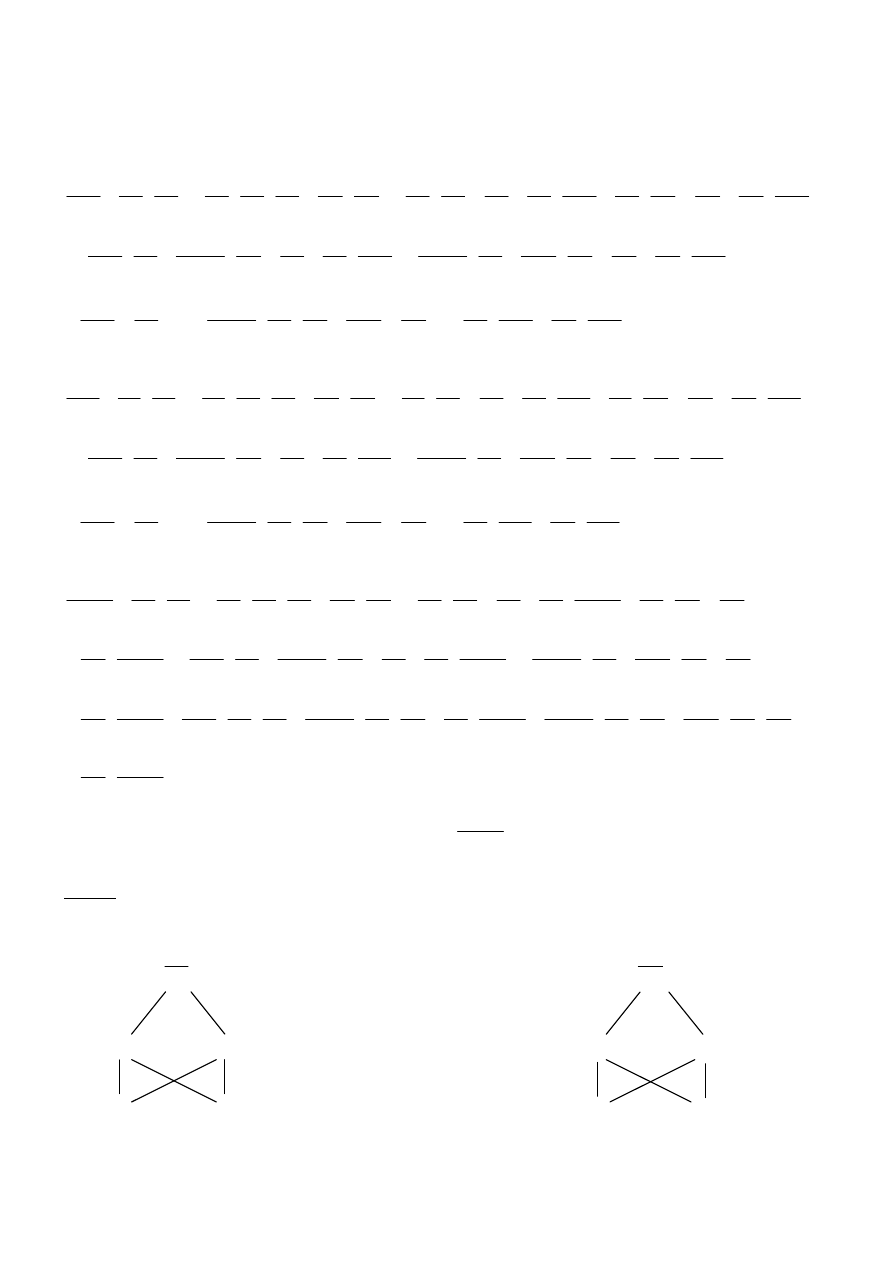
SCHEMAT OBLICZANIA POCHODNYCH CZĄSTKOWYCH I – GO RZĘDU
)
,
( y
x
f
z
=
y
z
x
z
∂
∂
∂
∂
y
x
v
y
u
y
v
x
u
x
∂
∂
∂
∂
∂
∂
∂
∂
v
u
Przykład: Obliczyć pochodne cząstkowe I – go rzędu względem u i v funkcji
xy
e
z
=
, gdzie
u
v
y
v
u
x
arctg
,
ln
2
2
=
+
=
.
Rozwiązanie:
Korzystając ze wzorów (5) i (6) dla
(
) ( )
0
,
0
,
≠
v
u
i
0
≠
u
mamy:
=
+
−
+
+
=
−
⋅
+
⋅
+
+
⋅
+
⋅
=
∂
∂
2
2
2
2
2
2
2
2
2
2
1
1
2
2
1
v
u
v
x
v
u
u
y
e
u
v
u
v
xe
v
u
u
v
u
ye
u
z
xy
xy
xy
+
−
+
+
+
⋅
=
+
⋅
2
2
2
2
2
2
ln
arctg
ln
arctg
2
2
v
u
v
v
u
v
u
u
u
v
e
v
u
u
v
=
+
+
+
=
⋅
+
⋅
+
+
⋅
+
⋅
=
∂
∂
2
2
2
2
2
2
2
2
2
1
1
1
2
2
1
v
u
u
x
v
u
v
y
e
u
u
v
xe
v
u
v
v
u
ye
v
z
xy
xy
xy
+
+
+
+
⋅
=
+
⋅
2
2
2
2
2
2
ln
arctg
ln
arctg
2
2
v
u
u
v
u
v
u
v
u
v
e
v
u
u
v
212
POCHODNE CZĄSTKOWE RZĘDU II – GO FUNKCJI ZŁOŻONEJ DWÓCH ZMIENNYCH
NIEZALEŻNYCH
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
u
y
y
z
u
x
x
z
u
y
y
z
u
y
u
x
y
x
z
u
x
x
z
u
y
y
z
u
y
u
y
y
z
u
x
y
x
z
u
x
x
z
u
x
u
y
x
y
z
u
x
x
z
u
y
y
z
u
y
y
z
u
u
x
x
z
u
x
x
z
u
u
y
y
z
u
x
x
z
u
u
z
u
u
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
v
y
y
z
v
x
x
z
v
y
y
z
v
y
v
x
y
x
z
v
x
x
z
v
y
y
z
v
y
v
y
y
z
v
x
y
x
z
v
x
x
z
v
x
v
y
x
y
z
v
x
x
z
v
y
y
z
v
y
y
z
v
v
x
x
z
v
x
x
z
v
v
y
y
z
v
x
x
z
v
v
z
v
v
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
v
u
y
y
z
v
y
u
y
y
z
v
y
u
x
y
x
z
v
u
x
x
z
u
y
v
x
x
y
z
v
x
u
x
x
z
v
u
y
y
z
v
y
u
y
y
z
u
x
y
x
z
v
u
x
x
z
v
x
u
y
x
y
z
u
x
x
z
v
u
y
y
z
v
y
y
z
u
v
u
x
x
z
v
x
x
z
u
v
y
y
z
v
x
x
z
u
v
z
u
v
u
z
∂
∂
∂
⋅
∂
∂
+
+
∂
∂
⋅
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
∂
+
∂
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
=
∂
∂
∂
⋅
∂
∂
+
+
∂
∂
⋅
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
+
∂
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
∂
⋅
∂
∂
+
+
∂
∂
⋅
∂
∂
∂
∂
+
∂
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Analogicznie można wyprowadzić wzór na pochodną
u
v
z
∂
∂
∂
2
.
Uwaga
: Przy wyprowadzaniu powyższych wzorów korzystaliśmy ze wzorów (5), (6), reguł
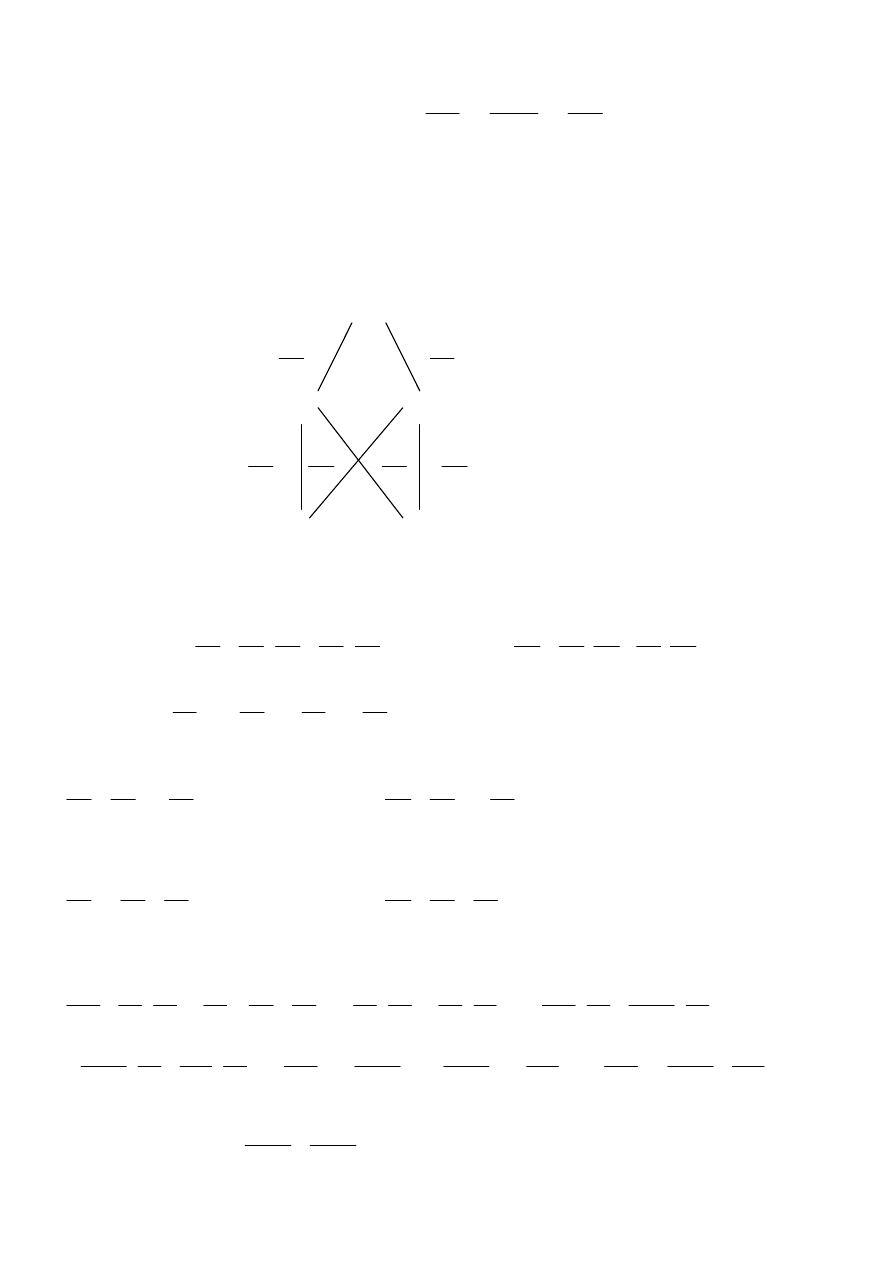
różniczkowania sumy i iloczynu oraz następujących schematów:
x
z
∂
∂
y
z
∂
∂
x
y
x
y
u
v
u
v
213
Przykład: Przekształcić wyrażenie różniczkowe
2
2
2
2
2
3
4
y
z
y
x
z
x
z
∂
∂
+
∂
∂
∂
−
∂
∂
wprowadzając zmienne u i v
określone następująco:
y
x
v
y
x
u
+
=
+
=
,
3
.
Rozwiązanie:
W zadaniu mamy do czynienia z pewną funkcją z dwóch zmiennych u i v, z których każda jest funkcją
dwóch zmiennych niezależnych x i y. Zatem
(
)
)
,
(
,
)
,
(
y
x
v
y
x
u
f
z
=
.
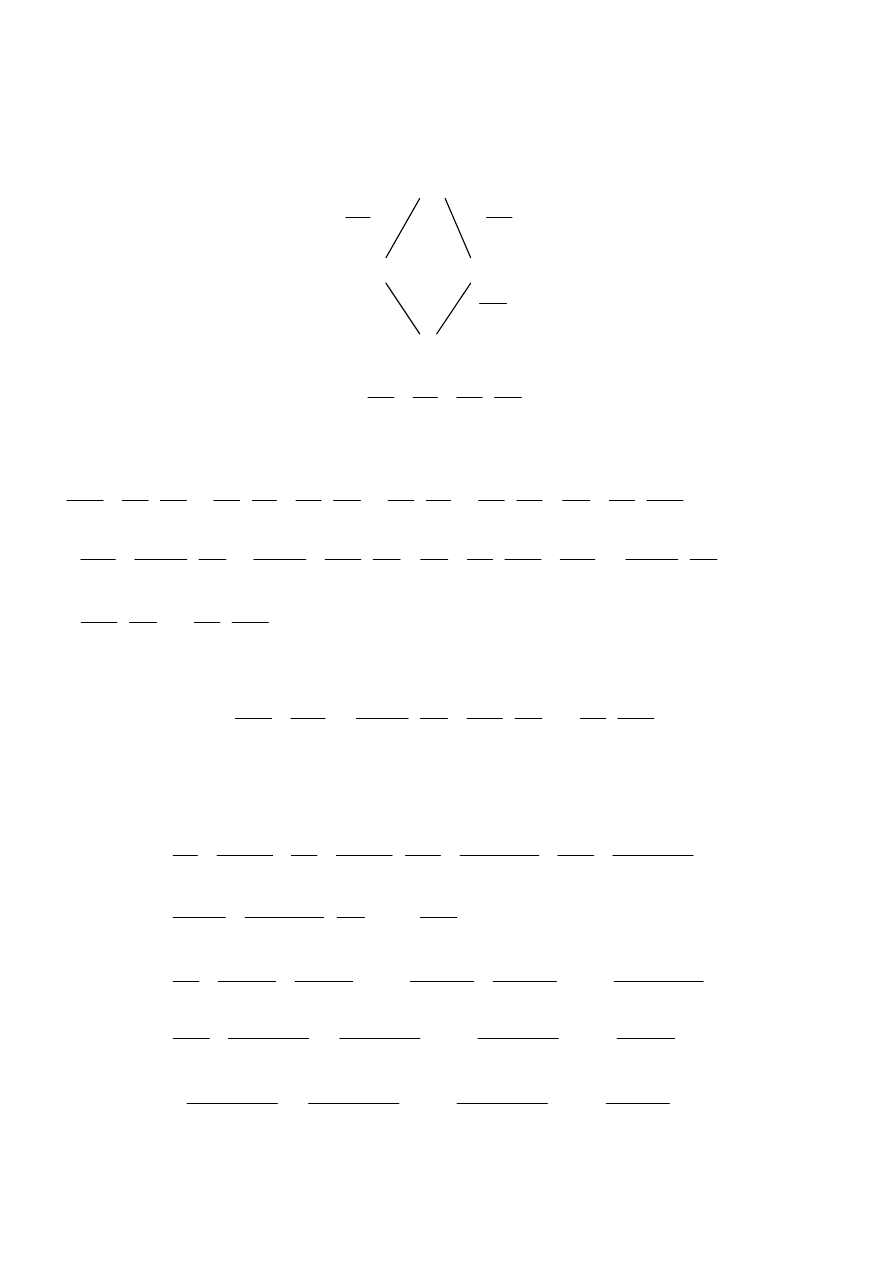
Schemat obliczania pochodnych cząstkowych I – go rzędu tej funkcji przedstawia się następująco:
)
,
( v
u
f
z
=
v
z
u
z
∂
∂
∂
∂
v
u
y
v
x
v
y
u
x
u
∂
∂
∂
∂
∂
∂
∂
∂
y
x
Korzystając z powyższego schematu otrzymujemy następujące wzory na pochodne cząstkowe I – go
rzędu:
x
v
v
z
x
u
u
z
x
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
,
y
v
v
z
y
u
u
z
y
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
Ponieważ
1
,
1
,
1
,
3
=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
y
v
x
v
y
u
x
u
Zatem
1
3
⋅
∂
∂
+
⋅
∂
∂
=
∂
∂
v
z
u
z
x
z
,
1
1
⋅
∂
∂
+
⋅
∂
∂
=
∂
∂
v
z
u
z
y
z
czyli
v
z
u
z
x
z
∂
∂
+
∂
∂
=
∂
∂
3
v
z
u
z
y
z
∂
∂
+
∂
∂
=
∂
∂
Obliczamy pochodne cząstkowe rzędu II – go występujące w naszym wyrażeniu różniczkowym:
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
6
9
1
3
1
3
3
3
3
3
v
z
v
u
z
u
z
v
z
v
u
z
u
v
z
u
z
x
v
v
z
x
u
v
u
z
x
v
u
v
z
x
u
u
z
v
z
x
u
z
x
v
z
u
z
x
x
z
x
x
z
∂
∂
+
∂
∂
∂
+
∂
∂
=
⋅
∂
∂
+
⋅
∂
∂
∂
+
⋅
∂
∂
∂
+
⋅
∂
∂
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
+
+
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
+
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
Z twierdzenie Schwarza
u
v
z
v
u
z
∂
∂
∂
=
∂
∂
∂
2
2
, co zostało powyżej wykorzystane w końcowych obliczeniach.

214
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
v
z
v
u
z
u
z
v
z
v
u
z
u
v
z
u
z
y
v
v
z
y
u
v
u
z
y
v
u
v
z
y
u
u
z
v
z
y
u
z
y
v
z
u
z
y
y
z
y
y
z
∂
∂
+
∂
∂
∂
+
∂
∂
=
⋅
∂
∂
+
⋅
∂
∂
∂
+
⋅
∂
∂
∂
+
⋅
∂
∂
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
+
+
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
+
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
3
1
3
1
3
v
z
v
u
z
u
z
v
z
v
u
z
u
v
z
u
z
x
v
v
z
x
u
v
u
z
x
v
u
v
z
x
u
u
z
v
z
x
u
z
x
v
z
u
z
x
y
z
x
y
x
z
∂
∂
+
∂
∂
∂
+
∂
∂
=
⋅
∂
∂
+
⋅
∂
∂
∂
+
⋅
∂
∂
∂
+
⋅
∂
∂
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
∂
+
+
∂
∂
⋅
∂
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
+
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
Ostatecznie otrzymaliśmy następujące pochodne cząstkowe II – go rzędu wyrażone za pomocą
zmiennych u i v.
2
2
2
2
2
2
2
6
9
v
z
v
u
z
u
z
x
z
∂
∂
+
∂
∂
∂
+
∂
∂
=
∂
∂
,
2
2
2
2
2
2
2
2
v
z
v
u
z
u
z
y
z
∂
∂
+
∂
∂
∂
+
∂
∂
=
∂
∂
,
2
2
2
2
2
2
4
3
v
z
v
u
z
u
z
y
x
z
∂
∂
+
∂
∂
∂
+
∂
∂
=
∂
∂
∂
Wstawiając powyższe zależności do podanego wyrażenia różniczkowego otrzymujemy:
v
u
z
v
z
v
u
z
u
z
v
z
v
u
z
u
z
v
z
v
u
z
u
z
v
z
v
u
z
u
z
v
z
v
u
z
u
z
v
z
v
u
z
u
z
y
z
y
x
z
x
z
∂
∂
∂
−
=
∂
∂
+
∂
∂
∂
+
∂
∂
+
+
∂
∂
−
∂
∂
∂
−
∂
∂
−
∂
∂
+
∂
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
∂
−
∂
∂
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
3
6
3
4
16
12
6
9
2
3
4
3
4
6
9
3
4
Ostatecznie wyrażenie różniczkowe
2
2
2
2
2
3
4
y
z
y
x
z
x
z
∂
∂
+
∂
∂
∂
−
∂
∂
po wprowadzeniu zmiennych
y
x
u
+
= 3
,
y
x
v
+
=
przedstawia się następująco:
v
u
z
y
z
y
x
z
x
z
∂
∂
∂
−
=
∂
∂
+
∂
∂
∂
−
∂
∂
2
2
2
2
2
2
4
3
4
.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron